在螺旋桨飞机的气动布局设计和性能分析中,存在着滑流和全机的气动干扰,预测螺旋桨滑流对飞机气动特性的影响一直是螺旋桨飞机设计中亟待解决又难度很大的问题[1]。由于螺旋桨的滑流是一种非管道控制的流动,不仅轴向速度较远方的来流速度大,而且还有一定的回转运动,流线呈螺旋状[2],因此流动特性非常复杂。国内外学者长期以来不断尝试着用各种理论和方法来研究螺旋桨滑流的机理,目前螺旋桨气动特性计算的方法主要有:动量理论、叶素理论、涡流理论、升力线理论、升力面理论以及各种CFD方法[3]。20世纪70年代以来,Strash[4]等将动量理论与叶素理论结合构造了等效盘模型用于螺旋桨/短仓/机翼组合部件的数值模拟;Sullivan[5]和陈泽民、潘杰元[6]提出了改进的升力线方法,并在此基础上发展了螺旋桨的升力面方法;西工大的左岁寒等[7]采用基于动量理论的等效盘模型与CFD相结合的方法对螺旋桨/机翼的三维流场进行了求解;南航的李博等[8]发展了考虑螺旋桨滑流旋转速度的等效盘模型,并与CFD相结合对某四发涡桨飞机的气动性能进行了计算。以上的这些方法基于不同理论,对真实螺旋桨三维流场都有一定程度的简化。随着数值方法和计算机技术的发展,使得对螺旋桨三维流场直接进行Euler/N-S方程求解变得可能。近年来,国内许和勇[9]、杨小川[10]等用非定常Euler方程数值模拟了螺旋桨飞机的滑流影响并进行了分析。由于RANS方程考虑了气体的黏性,可以更加深入地研究螺旋桨大侧流、桨叶失速、滑流扫过机身部件的干扰等复杂流动现象的流场细节,采用URANS方程对单个螺旋桨的气动特性开展数值模拟研究已有不少成果[11-12],但对螺旋桨/全机的URANS方程数值模拟及验证的工作还很少。
本文为了研究螺旋桨滑流对某涡桨飞机气动特性的影响,运用自主开发的大型三维可压缩RANS方程解算器——PMBNS3D软件,采用动态重叠网格技术实现桨叶的相对运动,计算采用双时间步方法,SA一方程湍流模型和k-ω SST两方程湍流模型,在内循环迭代当中,通过隐式求解、多重网格方法以及结合并行化算法加速收敛过程。通过以上方法对某螺旋桨飞机起飞构型下的低速特性流动进行了研究,并与试验结果进行了对比,在确保计算结果总体可信的基础上总结了螺旋桨滑流动对飞机全机及部件气动特性和操控性能的影响规律,然后通过对螺旋桨滑流影响边界区域定义及分析,对滑流干扰现象以及背后的物理流动机理进行了研究和探索。通过这些工作的开展,表明本文所发展的螺旋桨/机身流场的URANS方程数值方法可以为我国涡桨飞机操纵性及稳定性设计及分析提供技术支撑。
1 数值方法 1.1 控制方程在惯性坐标下,针对任意运动控制体的的可压缩N-S方程的积分形式为:
| $ \frac{\text{d}}{\text{d}t}\iiint\limits_\mathit{\Omega }{\mathit{\boldsymbol{Q}}}\text{d}\mathit{\Omega }+\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S \left( {{H}^{I}}-\mathit{\boldsymbol{Q}}{{\mathit{\boldsymbol{V}}}_\mathit{\Omega }} \right) \cdot \mathit{\boldsymbol{n}}\text{d}\mathit{\boldsymbol{S}}=\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S {{\mathit{\boldsymbol{H}}}^{V}}\cdot \mathit{\boldsymbol{n}} \text{d}\mathit{\boldsymbol{S}} $ | (1) |
其中,Ω表示控制体的体积;S表示控制体边界面的面积;VΩ为边界面上的网格运动速度;Q为状态变量:Q={ρ, ρu, ρv, ρw, e}T,这里ρ、u、v、w、e分别表示流体的密度、速度矢量在三个坐标方向(x、y、z)上的分量和单位体积的总能量。压力p和内能ε以及和总能e之间满足如下状态方程:
| $ p=\rho RT=\rho (\gamma -1)\varepsilon $ | (2) |
| $ p=(\gamma -1)\left[ e-\frac{1}{2}\rho \left( {{u}^{2}}+{{v}^{2}}+{{w}^{2}} \right) \right] $ | (3) |
无黏项的空间离散采用Roe平均迎风通量差分分裂格式,黏性项采用中心差分格式离散,计算分别采用了SA一方程湍流模型和k-ω SST二方程湍流模型[13-14]。非定常计算采用双时间步方法[15],除了真实时间t之外,引入伪时间τ,好处是使原来只适用于定常计算的隐式时间迭代、局部时间步长、多重网格等方法都可以运用到非定常计算的伪时间迭代当中[16-17]。
1.2 多重网格方法限制URANS方程应用的一个重要因素是对计算资源的要求过高。对双时间步方法来说,提高子迭代过程的收敛速率是衡量方法的一个重要指标,而在加速方法中多重网格法被证明是最有效的手段之一[18-19]。多重网格方法的原理就是利用高频误差比低频误差更容易被迭代格式消除的特点,通过引入系列逐步粗化网格的办法,将低频误差转化为高频误差,消除各种误差分量,再用套迭代技术将粗网格上的解返回到各级细网格上。多重网格法从理论上被证明至少对于线性椭圆型问题是一种最优化的数值方法,其计算工作量仅仅与网格节点数的一次方成正比,并且收敛速度与网格的尺度大小无关,从而特别适合于应用在超大型工程数值计算问题中。本文采用了多重网格法中非线性方程的全近似格式(FAS),套迭代技术为W循环。
1.3 动态重叠网格技术在采用时间精确的数值方法求解中,网格运动是一个比较棘手的问题,较为成熟的方法是结构网格框架下的动态重叠网格方法。重叠网格[20-21]对相对运动的部件生成不同的网格,分别随各自部件运动,相互之间构成动态的重叠关系。由于部件运动的关系,有必要在网格生成上对运动路径上的网格进行互相适应,照顾好这个区域的网格密度以及均匀程度,以满足重叠插值的要求;同时要求不同部件的网格在接合区域相互匹配,对它们之间流场的光滑过渡也是十分必要的[22-23]。
1.4 并行化计算并行计算采用基于消息传递(MPI)的并行化算法,用区域分割方法将计算域映射到多个CPU上分别进行计算[24-25]。由于计算网格采用多块结构网格方法,在网格块数小于节点数或者现有网格分块不足以使负载平衡的情况下,对最大块进行剖分,剖分需要满足两个条件,一是沿最大维数方向进行剖分,这样保证信息交换量最少;第二要求剖分后网格满足多重网格计算条件。如果最大维数方向满足不了该条件的话就沿次大维数方向进行剖分,依次进行。按这种方法划分的网格可以在各计算节点上进行多重网格计算,提高整体计算效率[26]。
在发展了动态重叠网格的快速自动查询方法基础之上,实现了重叠网格挖洞、插值关系建立的完全并行化。其中找插值关系的具体过程可以描述如下:对任意插值点而言,首先在本节点查找贡献单元,在没有找到的情况下将该插值点信息发送到其余各个节点上,由这些节点同时查找该插值点的贡献单元,如果找到,将该贡献单元信息返回,并且建立两个节点之间的消息传递关系。这种做法的最大好处就是去掉了所谓的根节点,即任何节点的重叠网格计算不须收集网格全局信息,降低了单节点的内存要求,同时避免了单个节点计算重叠插值关系,其余节点等待的局面,提高了计算效率。
2 螺旋桨单桨计算验证研究模型为单独涡桨发动机吊舱带六片桨叶模型,见图 1。螺旋桨直径4 m,桨叶角为36°,转速为7550 r/min,来流风速25 m/s,迎角为0°,模型缩比为1:12。

|
图 1 带六片桨叶的涡桨发动机外形 Fig.1 The propeller engine with six blades |
计算网格采用重叠网格方法。分别对运动部件(桨叶及轮毂)和静止部件(发动机吊舱)生成各自的网格。图 2中给出了桨叶网格和发动机吊舱背景网格的重叠关系,桨叶网格随桨叶一起作刚体运动,动态地与发动机吊舱背景网格构成重叠关系。桨叶网格的拓扑结构为O型。为了模拟黏性附面层的需要,第一层网格距离物面的距离约为1×10-5m,网格单元总数约330万。
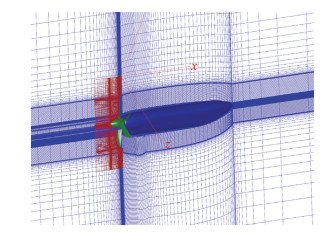
|
图 2 桨叶网格和发动机吊舱背景网格的重叠关系 Fig.2 Overlap relationship between blades grids and engine background grids |
流场计算从初场开始进行非定常计算,计算采用在惯性坐标系下求解URANS方程方法,在时间上计算采用双时间步方法,每个真实时间步桨叶在周向运动3°,即每个旋转周期包含真实时间步数为120步,每个真实时间步内的子迭代步数为50步,采用隐式LU-SGS方法进行迭代,空间格式采用Roe通量差分分裂方法,湍流模型分别采用了SA一方程湍流模型和k-ω SST二方程湍流模型。
并行计算在工作站集群上完成,计算结点为12核至强芯片(Intel(R) Xeon(R) CPU X5670,主频2.93 GHz,内存48 GB),该单桨计算验证采用了8核的并行计算,加速比为7,并行效率约为87%。
图 3给出了总的拉力系数CT和功率系数CP的收敛历程,横坐标表示桨叶周向角的变化,从图中看到,拉力系数在桨叶运动1.5周以后基本达到收敛状态。由于螺旋桨包含6片桨叶,每片桨叶的运动规律相同,所以流场变化的周期实际上是1/6周。
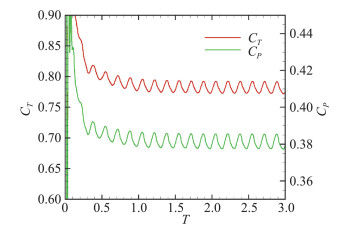
|
图 3 总的拉力系数和功率系数的收敛历程 Fig.3 Convergence course of propeller thrust coefficient and power coefficient |
图 4给出的是螺旋桨效率计算结果与试验结果的比较,可以看出采用SST湍流模型的计算结果与试验值吻合的很好,误差最大不超过2%,因此在以后的计算中均采用了SST湍流模型。涡桨发动机吊舱带六片桨叶模型的计算结果证实了动态重叠网格及非定常方法解算器的可靠性,可用于螺旋桨飞机的初步气动特性计算分析。
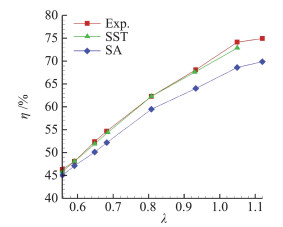
|
图 4 螺旋桨效率计算结果与试验结果的比较 Fig.4 Comparison of propeller efficiency between calculation and experimental data |
某涡桨飞机起飞构型无动力及带动力外形如图 5所示,模型基本参数如下:
模型缩比:1:12
机翼面积:0.4626 m2
机翼平均气动弦长:0.20125 m
试验风速:30 m/s
螺旋桨转速:4977 r/min(拉力TC=0.15)
襟翼偏度:35°
螺旋桨旋转方向为双发同向顺时针旋转(飞行员视角),对该起飞构型下的低速特性流动进行了计算分析。
3.1 计算结果的可靠性验证计算网格分为无动力全机和带动力全机两套网格,见图 5,无动力全机网格采用对接网格方法,网格单元总数约为2200万,无动力全机单个定常计算状态采用8核并行计算,迭代计算1万步取收敛结果,耗时约为24 h。带动力全机计算网格采用重叠网格方法,分别对运动部件(桨叶及轮毂)和静止部件(全机其它部分)生成各自的网格,桨叶网格随桨叶一起运动,动态地与全机背景网格构成重叠关系,为了模拟黏性附面层的需要,第一层网格距离物面的距离约为3×10-5m,y+=O(1),湍流模型采用了k-ω SST二方程湍流模型。全机网格规模约3050万,带动力全机单个非定常计算状态采用64核并行计算,加速比为49,并行效率约为75%,迭代计算2520个真实时间步数(螺旋桨旋转21转)取流场变化的周期值,耗时约135个小时。
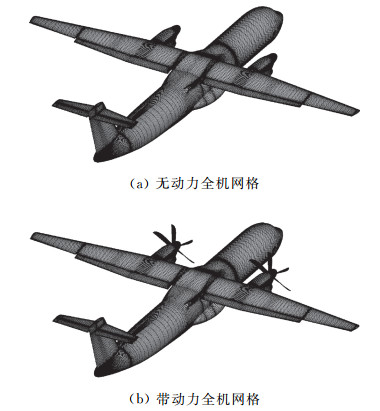
|
图 5 全机无动力及带动力起飞构型物面网格 Fig.5 Grid of takeoff airplane surface without and with propellers |
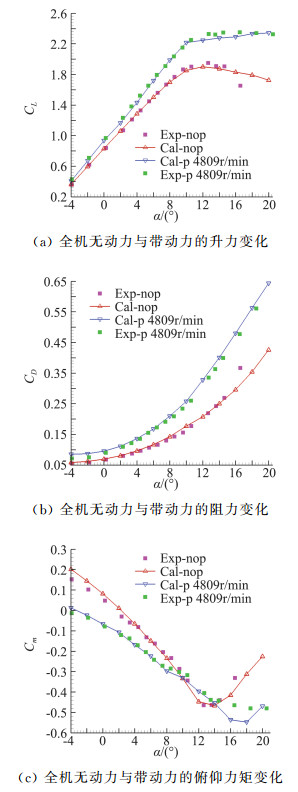
图 6给出了无动力及带动力不同情况下气动特性随迎角变化的计算值与试验值的比较。需要特别说明的是为了和试验结果对比,图中的升力和阻力特性曲线乃是扣除了桨叶的直接拉力,而带动力的俯仰力矩曲线则是考虑了桨叶的俯仰力矩。从试验结果和计算结果的对比情况来看,升力系数在线性段几乎重合,计算结果与试验值在线性段的总体误差不超过2%,在失速点附近因为机翼上出现的分离区导致数值模拟的难度较大,造成了计算与实验的一些偏差;阻力系数计算结果相对试验值整体偏大,但误差基本控制在8%以内,偏大原因应该来自于数值计算解的耗散行为以及采用全湍流模型带来的摩阻的增加;俯仰力矩曲线在线性段带动力情况的计算值与试验值吻合较好,而在勺型区域计算值与试验值差别较大,只有带动力情况的计算值与试验值出现拐点的迎角一致;在滑流影响作用下,全机升力、阻力系数有明显提升,且随着迎角的变大,升阻系数的增量值也开始放大,而俯仰力矩系数斜率的绝对值减小,说明带螺旋桨动力的全机俯仰安定性对比无动力有所降低。
|
图 6 全机无动力与带动力的气动特性变化 Fig.6 Change of takeoff airplane's aerodynamics characteristics(without and with propellers) |
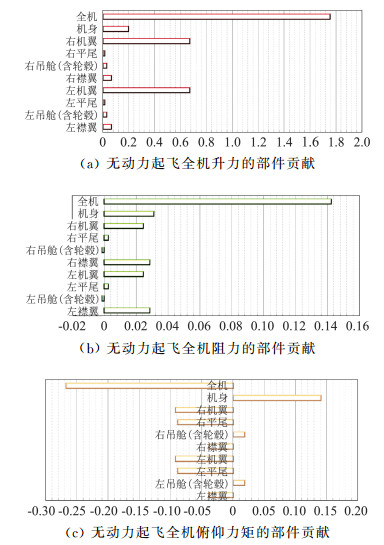
与巡航状态不同的是,即使在小迎角状态下,滑流对起飞状态飞机的升力及阻力亦有明显的放大作用,可见襟翼的打开导致流场阻塞效应进一步增大,这个阻塞作用通过压力场施加给螺旋桨一个反作用力,从而使螺旋桨拉力及滑流效应进一步增强。由于低速起飞时迎角8°为典型飞行状态,下面对该状态进行细节上的分析,图 7是无动力巡航的全机各部件对气动力特性的贡献图,图 8给出了带动力巡航的全机各部件对气动力特性的贡献图。在升力的贡献图对比中可以看到,有无动力全机的升力都主要来自于机翼的贡献,它占到总升力的70%左右,其次机身贡献占总升力的11%左右,另外襟翼贡献能占到总升力的9%左右;受滑流影响,带动力影响的机翼升力比无动力偏大了约10%,机身升力比无动力偏大了约19%,襟翼升力比无动力偏大约60%;由于螺旋桨同向旋转的原因,左侧(即关键发动机侧)的机翼升力比右侧机翼大2%;在滑流影响下左右平尾的升力发生明显不对称变化,值得注意的是机身和立尾受到的是右向侧力,其中立尾的右向侧力非常明显,而左机翼和右机翼受到的侧力值亦不小,但它们各自反向而近似抵消;俯仰力矩的贡献图中可以发现,机翼、襟翼、平尾和桨叶的低头力矩有利于纵向的静稳定性,特别是右平尾的低头力矩相比无动力时明显减弱,而此时机身有很大的抬头力矩,轮毂也有一定的抬头力矩,它们对全机的纵向安定性带来了不利的影响。
|
图 7 无动力起飞的全机各部件的气动力特性(α=8°) Fig.7 Parts contribution in takeoff airplane's aerodynamics characteristics(without propellers, α=8°) |

|
图 8 带动力起飞的全机各部件的气动力特性(α=8°) Fig.8 Parts contribution in takeoff airplane's aerodynamics characteristics(with propellers, α=8°) |
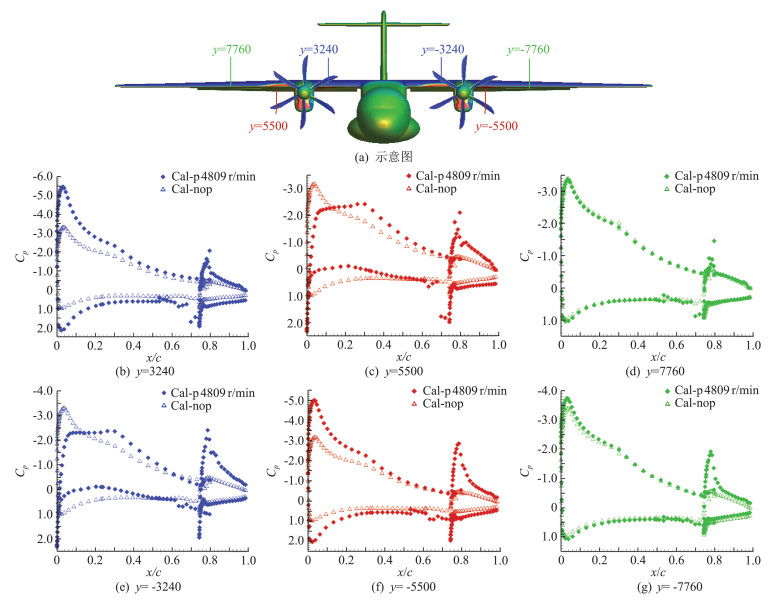
图 9给出了低速起飞迎角8°时无动力及带动力机翼的弦向截面站位压力系数对比图,可以看到经过机翼的导流作用后,滑流对襟翼的洗流不像机翼那么明显,但由于滑流区襟翼上的动压还是得到明显增加,同时高速滑流也起到一个吹除在大偏度襟翼上堆积的附面层作用,延迟了襟翼上气流的分离,这两个因素明显提高了襟翼效率。另外左侧(即关键发动机侧)的襟翼升力比右侧偏大一些,这是因为左侧襟翼的当地来流迎角比右侧的略大一点。
|
图 9 有动力及无动力机翼弦向站位的压力系数比(Ma=0.088, α=8°, TC=0.15) Fig.9 Cp distributions for different stations located on wing chordwise (without and with propellers, Ma=0.088, α=8°, TC=0.15) |
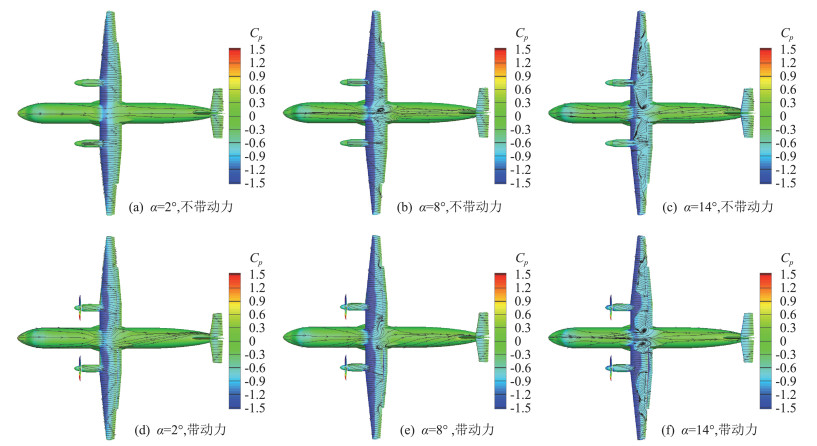
图 10(a~c)给出了无动力起飞外形随迎角变化的物面极限流线图。图中显示在小迎角2°条件下起飞状态的机翼没有分离;迎角到8°时靠近襟翼外侧的机翼上表面出现了小范围的展向分离流动,它是由襟翼的翼尖涡诱导而引起的;迎角增大到14°后,机翼上表面的出现了大范围的分离,靠近襟翼外侧的机翼展向分离已经接近到了吊舱的外侧机翼位置,而吊舱内侧的机翼翼根大面积分离是由吊舱的干扰诱发的,机翼明显产生了失速现象。图 10(d~f)是带动力起飞外形不同迎角的物面极限流线图,与无动力外形相比,迎角14°时,左机翼上靠近襟翼外侧的机翼展向分离面积扩大,这是由于滑流旋转与机翼翼尖涡方向同一侧而更容易诱发展向分离,左边发动机内侧的机翼翼根分离被抑制是受到滑流对左机翼当地迎角的上洗影响,同理右机翼上靠近襟翼外侧的机翼展向分离被抑制是由于滑流旋转与右机翼翼尖涡方向反向,关键发动机内侧的机翼翼根分离被扩大是因为滑流对右机翼当地迎的下洗影响。
|
图 10 无动力和带动力全机物面极限流线随迎角变化情况(Ma=0.088) Fig.10 Comparison of the pressure coefficients and streamlines on airplane's surface(without and with propellers, Ma=0.088) |
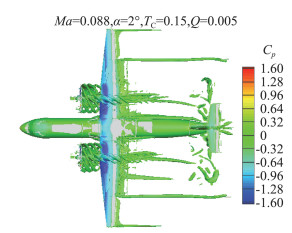
图 11给出的是带动力在低速起飞状态下的空间涡量等值面图。这时可以看到螺旋桨后拖出的涡量, 经过机翼及襟翼进一步被切割打散后拖出的尾涡圈数明显减少,相互融合成带状分布, 并在向下游发展的过程中逐渐淡化变得不再明显。
|
图 11 带动力起飞状态空间涡量等值面图 Fig.11 Iso-surfaces of the Q-criterion colored by Cp |
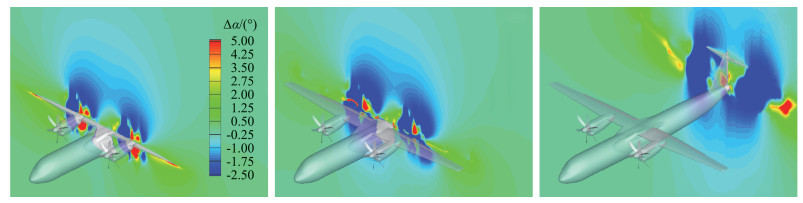
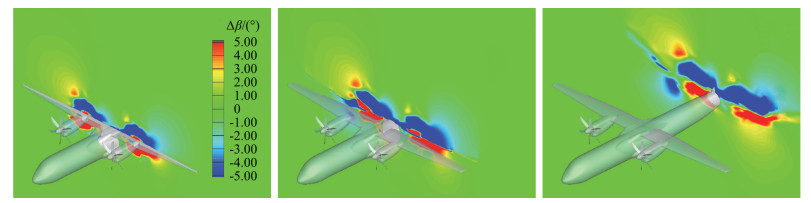
为了研究滑流的周期时均影响效果,这里采用有无滑流不同情况下对比当地动压增量来定义滑流的加速效应边界,对比当地气流角增量来定义滑流的洗流效应边界,期望通过对滑流起主要影响作用的参数分解来判定滑流的影响区域。为了达到以上目的,需要将螺旋桨停止旋转时定常状态的流场和螺旋桨正常旋转的非定常滑流的周期时均流场进行对比,得到两者间的加速作用和洗流的增量变化。图 12~图 14分别给出了在滑流影响作用下,低速起飞状态空间流场不同截面的动压增量Δq、当地迎角增量Δα和当地侧滑角增量Δβ的变化情况。可以发现空间中除桨叶卷出的滑流流管以外的地方动压增量Δq近似为0,流管中机翼上下翼面附近处的动压增量能达到0.006左右,相比流场远处来流的动压q增加了近1.5倍以上(远方来流的动压q等于0.00387),相比巡航状态,起飞状态下滑流流管的范围经过襟翼后变得更大, 且动压增量Δq的值更高,说明起飞状态下襟翼打开后相比巡航状态对滑流的阻塞效应进一步增强,会增大螺旋桨拉力,使滑流的加速效应和洗流效应更明显。图 13中能明确看到在襟翼打开后空间中下洗范围比巡航状态扩大且被进一步增强,右侧平尾的前方有约-3°左右的下洗增量,左侧平尾的前方却有约1°左右的上洗增量,左右不对称效应被放大, 导致飞机更低的纵向静安定度。图 14中给出了有无滑流情况下当地气流侧滑角增量Δβ的空间剖面图,能够看到滑流对空间流场侧洗的影响,在立尾翼根的前缘处来流相比巡航状态有更明显的右偏斜,而机身后段右侧的来流相比巡航状态不再存在明显的右偏斜,这样使得机身受到的侧力相比巡航状态发生了方向性的变化。

|
图 12 带动力起飞状态动压增量变化的空间剖面图(α=8°) Fig.12 Incremental of dynamic pressure for different sections in flow field(with propellers, α=8°) |
|
图 13 带动力起飞状态当地迎角增量变化的空间剖面图(α=8°) Fig.13 Incremental of local angle of attack for different sections in flow field(with propellers, α=8°) |
|
图 14 带动力起飞状态当地侧滑角增量变化的空间剖面图(α=8°) Fig.14 Incremental of local angle of sideslip for different sections in flow field(with propellers, α=8°) |
本章对有无滑流影响作用的某双发同向旋转涡桨飞机分别进行了巡航和起飞状态的数值模拟,与试验结果进行了对比并对滑流的影响作用开展了详细的分析,得到了以下一些结论:
(1) 螺旋桨后拖出的螺旋状滑流改变了机翼的流态,其影响大致可以分为两个方面:首先螺旋桨的转动给气流注入了能量,使得滑流区域机翼、襟翼上的动压和静压都明显增加,产生了一个升力增量和诱导阻力增量;其次改变了机翼上的局部迎角,使滑流区内螺旋桨上行桨叶侧上洗增强,增加了局部有效迎角,从而在机翼上诱导出一个正升力增量,同理,滑流区内螺旋桨下行桨叶侧下洗增强,减小了局部有效迎角,在机翼上诱导出一个负升力增量。
(2) 当飞机襟翼打开后,滑流区内襟翼上的动压得到明显增强,同时高速滑流也起到一个吹除在大偏度襟翼上堆积的附面层作用,延迟了襟翼上气流的分离,这两个因素明显提高了襟翼效率。
(3) 采用有无滑流不同情况下对比当地动压增量和当地气流角增量来定义滑流的加速效应和洗流效应边界,采用该方法能较好地捕捉和解释由于滑流对飞机尾翼干扰而使得飞机方向安定性呈现的很大非线性现象,增进了滑流对扫过飞机部件的气动干扰作用机理的认识。
| [1] |
鄂秦, 杨国伟, 李凤蔚, 等. 螺旋桨滑流对飞机气动特性影响的数值分析[J]. 西北工业大学学报, 1997, 15(4): 511-516. E Q, YANG G W, LI F W, et al. On coupling effect of two vortex systems of Chinese aircraft with turbo-propellers[J]. Journal of Northwestern Polytechnical University, 1997, 15(4): 511-516. (in Chinese) |
| [2] |
《航空工业科技词典》编辑委员会. 航空工业科技词典[M]. 北京: 国防工业出版社, 1982: 1-83. Editorial Committee of Aviation Industry Science & Technology Dic-tionary. Aviation industry science & technology dictionary[M]. Beijing: National Defence Industry Press, 1982: 1-83. (in Chinese) |
| [3] |
刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006.
|
| [4] |
STRASH D J, LEDNICER D A, ROUBIN T D. Analysis of propeller induced aerodynamic effects[R]. AIAA-98-2414, 1998.
|
| [5] |
SULLIVAN J P. The effect of blade sweep on propeller perfromance[R]. AIAA-77-716, 1977.
|
| [6] |
陈泽民, 潘杰元. 一种计算螺旋桨性能的高效升力线方法[J]. 航空动力学报, 1991, 6(4): 295-299. CHEN Z M, PAN J Y. Efficient lifting line method for computing performance of propeller[J]. Journal of Aerospace Power, 1991, 6(4): 295-299. (in Chinese) |
| [7] |
左岁寒, 杨永. 螺旋桨滑流对带后缘襟翼机翼气动特性影响的数值分析[J]. 航空计算技术, 2007, 37(1): 54-57. ZUO S H, YANG Y. Numerical simulation of propeller/high-lift system interaction[J]. Aeronautical Computing Technique, 2007, 37(1): 54-57. DOI:10.3969/j.issn.1671-654X.2007.01.016 (in Chinese) |
| [8] |
李博, 梁德旺, 黄国平. 基于等效盘模型的滑流对涡桨飞机气动性能的影响[J]. 航空学报, 2008, 29(4): 845-852. LI B, LIANG D W, HUANG G P. Propeller slipstream effects on aerodynamic performance of turbo-prop airplane based on equivalent actuator disk model[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 845-852. DOI:10.3321/j.issn:1000-6893.2008.04.013 (in Chinese) |
| [9] |
许和勇, 叶正寅. 螺旋桨非定常滑流数值模拟[J]. 航空动力学报, 2011, 26(1): 148-153. XU H Y, YE Z Y. Numerical simulation of unsteady propeller slipstream[J]. Journal of Aerospace Power, 2011, 26(1): 148-153. (in Chinese) |
| [10] |
杨小川, 王运涛, 王光学, 等. 螺旋桨非定常滑流的高效数值模拟研究[J]. 空气动力学学报, 2014, 32(3): 289-294. YANG X C, WANG Y T, WANG G X, et al. Numerical simulation of unsteady propeller slipstream[J]. Acta Aerodynamica Sinica, 2014, 32(3): 289-294. (in Chinese) |
| [11] |
ERICW M ROOSENBOOM, ARNE STURMER. Advanced experimental and numerical validation and analysis of propeller slipstream flows[J]. Journal of Aircraft, 2010, 47(1): 284-291. DOI:10.2514/1.45961 |
| [12] |
许建华, 宋文萍, 韩忠华, 等. 基于CFD技术的螺旋桨气动特性研究[J]. 航空动力学报, 2010, 47(5): 1103-1109. XU J H, SONG W P, HAN Z H, et al. Aerodynamic performance research of propellers based on CFD technology[J]. Journal of Aerospace Power, 2010, 47(1): 284-291. (in Chinese) |
| [13] |
MENTER F. Zonal two equation turbulence models for aerodynamic flows[R]. AIAA-93-2906, 1993.
|
| [14] |
HELLSTEN A. Some improvements in menter's k-ω SST turbulence model[R]. AIAA-98-2554, 1998.
|
| [15] |
GAITONDE A L. A dual-time method for the solution of the unsteady euler equation[J]. Aeronautical Journal, 1994. |
| [16] |
牟斌.流动控制数值模拟研究[D].绵阳: 中国空气动力研究与发展中心, 2006, 3. MOU B. Numerical simulation and investigation of flow control[D]. Mianyang: China Aerodynamics Research and Development Center, 2006, 3. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1015891 |
| [17] |
肖中云.旋翼流场数值模拟方法研究[D].绵阳: 中国空气动力研究与发展中心, 2007. XIAO Z Y. Investigation of computational modeling techniques for rotor flowfields[D]. Mianyang: China Aerodynamics Research and Development Center, 2007. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-90113-2007189440.htm |
| [18] |
陈作斌, 周铸, 牟斌.多重网格技术研究及其应用[C]//第四届海峡两岸航空航天学术研讨会论文集, 2004. CHEN Z B, ZHOU Z, MOU B. The research and application of multigrid techniques[C]//Fourth Symposium on Cross-Strait Aerospace, 2004. (in Chinese) |
| [19] |
LYLE D DAILEY, RICHARD H PLETCHER. Evaluation of multigrid acceleration for preconditioned time-accurate Navier-Stokes algorithms[R]. AIAA-95-1668, 1995.
|
| [20] |
STEGER J L, DOUGHERTY F C. Chimera grid scheme, american society of mechanical engineers[J]. Fluids Engineering Division, 1983, 5: 59-69. |
| [21] |
HARIHARAN N, SANKAR L N. Unsteady overset simulation of rotor-airframe interaction[J]. Journal of Aircraft, 2003, 40(4). |
| [22] |
周铸, 江雄.多块重叠网格技术研究及其应用[C]//十二届全国计算流体力学会议论文集, 陕西西安, 2004. ZHOU Z, JIANG X. Overlapping multi-block grid technology research and application[C]//Twelfth Session of the National CFD Conference Proceedings. Xi'an, 2004(in Chinese) |
| [23] |
MEAKIN R L. Object X-rays for cutting holes in composite overset structured grid[R]. AIAA 2001-2537, 2001.
|
| [24] |
LANTERI S. Parallel solutions of compressible flow using overlapping and non-overlapping mesh partitioning strategies[J]. Parallel Computing, 1996(22): 943-968. |
| [25] |
朱国林, 徐庆新. 计算流体力学并行计算技术研究综述[J]. 空气动力学学报, 2002(S1): 1-6. ZHU G L, XU Q X. Review on parallel computation technique on computational fluid dynamics in CAI[J]. Acta Aerodynamica Sinica, 2002(S1): 1-6. (in Chinese) |
| [26] |
肖中云, 江雄, 牟斌, 等. 并行环境下外挂物动态分离过程的数值模拟[J]. 航空学报, 2010, 31(8): 1509-1516. XIAO Z Y, JIANG X, MOU B, et al. Numerical simulation of dynamic process of store separation in parallel environment[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(8): 1509-1516. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


