2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
近年来,国际火星探测迎来了新的高潮。由于进入火星大气时减速的需要,火星探测器为球冠倒锥构型的钝体飞行器[1-3]。对于此类飞行器,其后体流动较为复杂,存在大范围的分离与再附、激波/旋涡干扰等,相应地,其动态特性也较为复杂,是设计关键问题之一。对于再入地球大气的球冠倒锥钝体飞船返回舱,其动态特性问题已有较多研究。但由于火星大气与地球大气差异较大,平均大气密度约为地球的1.6%,表面大气压力仅为700 Pa,相当于地球30~40 km高度时大气压力[4-5]。这么稀薄的大气环境下,火星探测器进入火星大气环境的动态特性问题,已成为火星探测项目发展面临的挑战之一。
国内外火星环境的动态特性研究方法与地球环境的动态特性研究方法类似,主要有半经验理论方法、数值模拟方法和火星风洞实验方法。
由于探测器在火星环境中的流场十分复杂,理论分析方法往往难以奏效。目前对返回舱的动稳定性研究主要依靠地面模拟试验,包括强迫振荡法、自由振动法、自由翻滚法和模型自由飞试验法等[6-7]。然而,由于地面风洞设备试验气体以模拟空气为主,主要针对地球环境的返回舱动稳定性问题。目前关于火星环境探测器动态特性预测的公开数据相对匮乏,其中,又以弹道靶中进行的模型自由飞试验数据为主。如美国空军ARF在常温、常压的空气环境下进行了MER火星探测器模型的弹道靶试验[8]。试验表明,在迎角较小的状态下,这种短钝头体外形是不稳定的,并且随着速度的降低,稳定性进一步减弱;随着质心的前移,模型稳定性增加。然而,常规空气介质风洞所得的数据需要进行地火相关性修正,才能模拟火星大气相关气动问题。美国阿姆斯研究中心的HFFAF (The Hypervelocity Free Flight Aerodynamics Facility)弹道靶中,进行了二氧化碳环境下MSL (The Mars Smart Lander)探测器模型自由飞试验[9],获得了静、动导数等动态数据,但公开的试验数据很少。
火星探测的飞行数据稀缺,地面试验难度大,工程计算方法进展缓慢,目前,数值模拟可作为火星探测气动问题研究的重要工具。其中,近似比热比数值模拟方法很大程度地简化了计算模型[10-11],但国内外在近似比热比的取值上有所不同,且研究尚显不足。
因此,着眼于我国火星探测项目需求、亟需解决探测器进入火星大气环境中所遇到的气动问题,开展火星探测器气动稳定性的研究。本文采用近似比热比数值模拟方法,基于软件in-house programm FLY3D-Mars,针对火星探测器弹道靶自由飞试验外形,进行了火星大气模拟环境下俯仰气动特性的数值模拟研究。
1 数值模拟方法 1.1 控制方程直角坐标系中,不计体积力和外加热量的无量纲化、守恒形式Navier-Stokes方程组为:
| $ \frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial y}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial z}} = \frac{1}{{\mathit{Re}}}\left( {\frac{{\partial {\mathit{\boldsymbol{E}}_v}}}{{\partial x}} + \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial y}} + \frac{{\partial {\mathit{\boldsymbol{G}}_v}}}{{\partial z}}} \right) $ | (1) |
其中,Q为守恒变量,E、F和G为对流项、无黏通矢量,Ev、Fv和Gv为黏性通矢量,具体形式分别为:
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {\rho u}\\ {\rho {u^2} + p}\\ {\rho uv}\\ {\rho \tau v}\\ {(E + p)u} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{E}}_v} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{xx}}}\\ {{\tau _{xy}}}\\ {{\tau _{xz}}}\\ {v{\tau _{xx}} + u{\tau _{xy}} + w{\tau _{xz}} + {q_x}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\rho v}\\ {\rho uv}\\ {\rho {v^2} + p}\\ {\rho wv}\\ {(E + p)v} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{F}}_v} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{yx}}}\\ {{\tau _{yy}}}\\ {{\tau _{yz}}}\\ {v{\tau _{yx}} + v{\tau _{yy}} + w{\tau _{yz}} + {q_y}} \end{array}} \right] $ |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {\rho w}\\ {\rho uw}\\ {\rho vw}\\ {\rho {w^2} + p}\\ {(E + p)w} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{G}}_v} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\tau _{zx}}}\\ {{\tau _{zy}}}\\ {{\tau _{zz}}}\\ {v{\tau _{zx}} + v{\tau _{zy}} + w{\tau _{zz}} + {q_z}} \end{array}} \right] $ |
通过坐标变换,可将方程组(1)转化为一般曲线坐标系中的形式:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{J^{ - 1}}\mathit{\boldsymbol{Q}}} \right)}}{{\partial \tau }} + \frac{{\partial \bar E}}{{\partial \xi }} + \frac{{\partial \bar F}}{{\partial \eta }} + \frac{{\partial \bar G}}{{\partial \zeta }} = }\\ {\frac{1}{{Re}}\left( {\frac{{\partial {{\bar E}_v}}}{{\partial \xi }} + \frac{{\partial {{\bar F}_v}}}{{\partial \eta }} + \frac{{\partial {{\bar G}_v}}}{{\partial \zeta }}} \right)} \end{array} $ | (2) |
将一般曲线坐标系中的Navier-Stokes方程组(2)写作:
| $ {J^{ - 1}}\frac{{\partial \mathit{\boldsymbol{Q}}}}{{\partial \tau }} = - R\left( \mathit{\boldsymbol{Q}} \right) - \mathit{\boldsymbol{Q}}\frac{{\partial {J^{ - 1}}}}{{\partial \tau }} $ | (3) |
其中:
| $ \begin{array}{l} R\left( \mathit{\boldsymbol{Q}} \right) = \left[ {\frac{{\partial \bar E}}{{\partial \xi }} + \frac{{\partial \bar F}}{{\partial \eta }} + \frac{{\partial \bar G}}{{\partial \xi }} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\frac{1}{{Re}}\left( {\frac{{\partial {{\bar E}_v}}}{{\partial \xi }} + \frac{{\partial {{\bar F}_v}}}{{\partial \eta }} + \frac{{\partial {{\bar G}_v}}}{{\partial \zeta }}} \right)} \right] \end{array} $ | (4) |
动态非定常数值模拟与定态数值模拟的区别之一是需要建立相对于地面系的动坐标系,以描述飞行器的姿态和运动。本文使用的地面系与飞行力学习惯建立的地面系之间的差别在于:y轴方向不变,x、z轴方向相反。同样,本文使用的体轴系的差别在于:yb轴方向不变,xb、zb轴方向相反。
一般俯仰运动计算时,可使用半流场网格;偏航、滚转运动计算,使用全流场网格。对于网格运动要求满足几何守恒律,即:
| $ {H_{{\rm{GCL}}}} = \frac{{\partial {J^{ - 1}}}}{{\partial t}} + {\left( {\frac{{{\xi _t}}}{J}} \right)_\xi } + {\left( {\frac{{{\eta _t}}}{J}} \right)_\eta } + {\left( {\frac{{{\zeta _t}}}{J}} \right)_\zeta } = 0 $ | (5) |
由于计算非定常动态流场需要每一时间步都更新网格,因此动网格生成技术的计算量小就显得尤为重要。目前,刚性运动网格生成和超限插值生成动网格是两种常用的方法。刚性运动网格生成技术就是计算网格随物体一起作刚体运动,其计算量小,并可保持初始网格的品质,但不适于生成较复杂的网格,也使运动开边界的处理不易。超限插值生成动网格方法就是外边界保持静止,物面边界由物体运动规律或运动方程得到,内场网格由超限插值的方法代数生成,其计算量也较小,能够生成复杂网格,但不易保证网格品质,尤其是不能保证物面网格的正交性。可用加权技术来综合这两种方法的优点[3]。
首先,由初始网格Xn生成刚性运动网格Xref 1, 再由n时刻的开边界和n+1时刻的物面边界代数插值得到n+1时刻的网格Xref 2,最后由两者加权得到新时刻的动网格:
| $ \begin{array}{l} {X^{n + 1}} = (1 - \omega ){X^{{\rm{ref}}1}} + \omega {X^{{\rm{ref}}2}},\quad 0 \le \omega \le 1\\ X = {(x,y,z)^{\rm{T}}} \end{array} $ | (6) |
只要适当选择加权因子ω,就既可保证物面附近网格质量,又可使外边界保持静止而易于处理。可构造如下加权因子,计算表明效果较好,令j为法向网格指标,则有:
| $ \begin{array}{l} \chi = {\left( {\frac{{j - 1}}{{{j_{\max }} - 1}}} \right)^{\bar \gamma }},\\ \omega = \omega (j) = 3{\chi ^2} - 2{\chi ^3} \end{array} $ | (7) |
式中,γ为一个控制加权因子的经验常数,本文一般取γ=2。
1.3 静、动态气动稳定性参数计算辨识方法在预测静、动态气动稳定性参数方面,数值计算明显优于地面模拟试验方法:数值计算费用低,可提供较长的非定常动态气动力周期,振心位置可与实际重心位置一致[6]。静、动导数参数辨识的思路在火星环境中仍然适用,主要是将动态气动力进行Taylor级数展开,保留线性部分,以俯仰运动为例,对于单自由度俯仰运动,根据Etkin经典动态气动力模型,有
| $ {C_m}\left( t \right) = {C_m}\left[ {\alpha \left( t \right),\dot \alpha \left( t \right),\ddot \alpha \left( t \right), \cdots ,q\left( t \right),\dot q\left( t \right), \cdots } \right] $ | (8) |
将其在迎角α0处进行Taylor展开,可得:
| $ {C_m} = {\left( {{C_m}} \right)_0} + {\left( {\frac{{\partial {C_m}}}{{\partial \alpha }}} \right)_0} \cdot \theta + \left[ {{{\left( {\frac{{\partial {C_m}}}{{\partial \dot \alpha }}} \right)}_0} + {{\left( {\frac{{\partial {C_m}}}{{\partial q}}} \right)}_0}} \right] \cdot \dot \theta + \cdots $ | (9) |
其中,θ=α-α0,
本文采用强迫振动法求取动导数。以单自由度俯仰强迫振动为例,给定简谐振荡(无量纲化)形式如下:
| $ \begin{array}{l} \alpha (t) = {A_0} + {A_m}\sin \left( {\omega {t^*}} \right)\\ \;\;\;\;\;\;\; = {A_0} + {A_m}\sin (2kt) = {\alpha _0} + \theta \end{array} $ | (10) |
其中,α0为振荡的中心迎角,Am为振荡的幅值,ω为振荡的圆频率,k=ωLref/2V∞为减缩频率(无量纲量),θ为俯仰振荡角。对动态俯仰力矩系数在振荡中心迎角处展开如下:
| $ {C_m} = {\left( {{C_m}} \right)_0} + {\left( {\frac{{\partial {C_m}}}{{\partial \theta }}} \right)_0} \cdot \theta + {\left( {\frac{{\partial {C_m}}}{{\partial \dot \theta }}} \right)_0} \cdot \dot \theta + {\left( {\frac{{\partial {C_m}}}{{\partial \ddot \theta }}} \right)_0} \cdot \ddot \theta + \cdots $ | (11) |
| $ \begin{array}{l} {\left( {\frac{{\partial {C_m}}}{{\partial \theta }}} \right)_0} = \frac{{2k}}{{{A_m}{\rm{ \mathsf{ π} }}}}\int_t^{t + T} {\left( {{C_m} - {C_{m0}}} \right)} \sin 2kt{\rm{d}}t\\ {\left( {\frac{{\partial {C_m}}}{{\partial \dot \theta }}} \right)_0} = \frac{1}{{{A_m}{\rm{ \mathsf{ π} }}}}\int_t^{t + T} {\left( {{C_m} - {C_{m0}}} \right)} \cos 2kt{\rm{d}}t \end{array} $ | (12) |
其中,T=π/k为强迫振荡的周期。强迫振荡的振幅对辨识结果的影响不大,一般取为1°。由于飞行器在空中的真实频率并不知道,需要考察多个频率对动稳定性方面的影响,才能得到有效结果。单自由度强迫偏航/滚转及其静、动导数的辨识类似。
2 算例验证第2节针对非轴对称M3外形,开展俯仰强迫振动数值模拟,通过将数值模拟结果与弹道靶试验结果对比,考核in-house programm FLY3D-MARS软件在火星环境动态计算中的适用性。
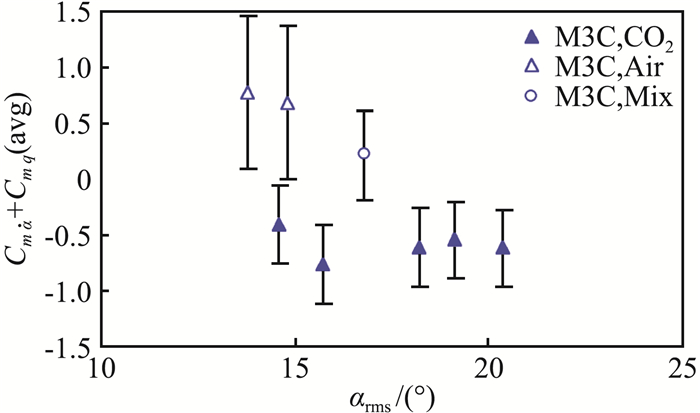
2.1 MSL弹道靶试验动态结果在美国NASA阿姆斯研究中心,针对MSL弹道靶模型进行的弹道靶模型自由飞试验中,采用44.5 mm口径的喷气枪[9],在纯CO2、CO2混合少量空气以及空气介质中进行对比试验,得到了探测器M3模型的动态数据。弹道靶试验动态结果并未全部公开,并且缺乏动态试验中的减缩频率等条件,相关动态结果十分匮乏,文献仅仅给出了M3外形在不同介质中的少量动导数结果,如图 1所示,图中为弹道靶试验中,三种不同的气体介质试验中,M3模型动导数结果。由图可知,在考察的弹道靶试验状态中,空气介质以及空气与CO2混合介质中进行试验,所得动导数为正,M3模型不稳定;在CO2介质中进行试验,动导数为负,模型稳定。三种介质中,CO2分子质量最大,空气介质分子质量最小。分析认为,随着分子质量的增大,气体的可压缩性增强,通过试验得到的动导数越小,动稳定性越强。
2.2 M3模型计算条件及网格数值计算模拟弹道靶试验中的马赫数与雷诺数,表 1给出了M3模型的弹道靶试验状态,采用三种不同的气体介质,分别为纯CO2、CO2混合少量空气以及空气介质,研究试验气体成分对气动特性特别是俯仰振荡的影响。表中,带*号的为空气介质,其余状态的试验气体介质采用纯CO2。
| 表 1 M3模型弹道靶试验状态 Table 1 Test condition of ballistic range of M3 model |
|
|
根据质心位置的不同,将弹道靶试验分为M3A、M3B、M3C、M3Ax以及M3A(high-M)五类状态,其中,前四类状态的质心位置有所不同,M3Ax状态中,质心在M3A的基础上再偏离10%,质心的具体位置如表 2所示。M3A(high-M)与M3A状态中质心位置相同,马赫数存在一定的差异,high-M状态中马赫数高于M3A状态中马赫数。
| 表 2 弹道靶模型的惯性特征 Table 2 Inertia characteristics of ballistic range model |
|
|
由于动态试验条件的缺失,本文根据弹道靶试验状态,考察了多种减缩频率以及时间步长对动态结果的影响。具体计算条件见表 3。
| 表 3 M3模型动态数值计算条件 Table 3 Dynamic numerical conditions of M3 model |
|
|
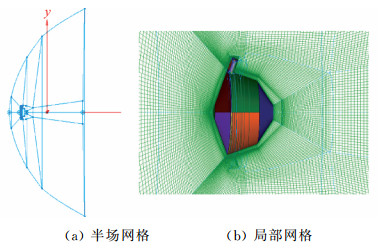
M3外形采用含奇性轴的网格进行数值计算,M3网格如图 2所示,半场网格规模为90万,壁面最小网格间距0.03 mm,网格雷诺数范围为4~10。
|
图 2 计算网格 Fig.2 Computing mesh |
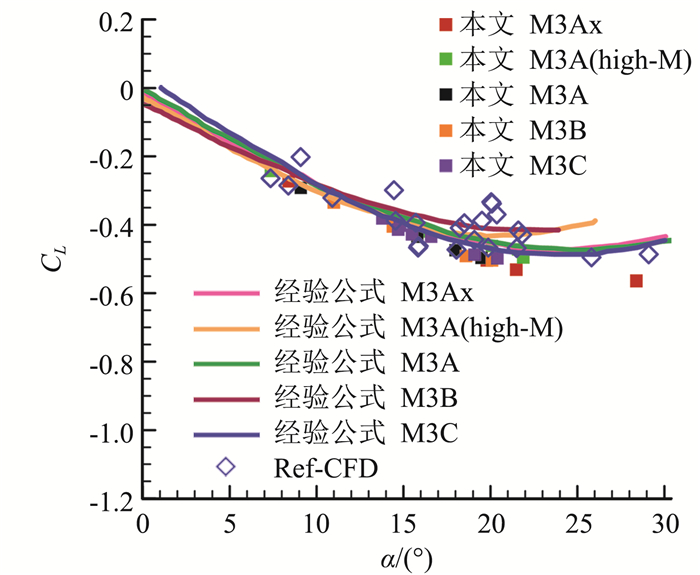
图 3展示了本文数值模拟结果与国外数值模拟结果以及经验公式所得升力系数的对比验证,结果吻合。
|
图 3 升力系数对比图 Fig.3 Comparison of lift coefficients |
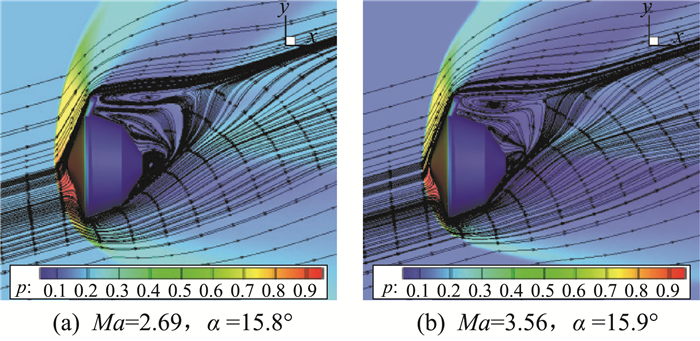
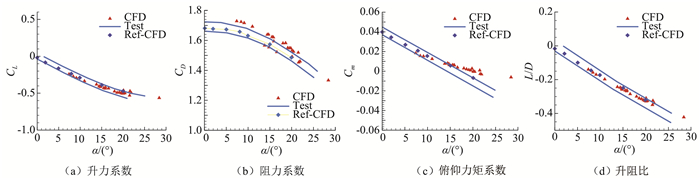
图 4为不同马赫数状态下的流场云图,其中图 4(a)为M3A类对应的一个计算状态,马赫数为2.69,迎角为15.8°,图 4(b)为M3A(high-M)类对应的一个计算状态,马赫数为3.56,迎角为15.9°。由图可知,流线穿过脱体激波,壁面极限流线由驻点向四周散开,前体上半部流线绕过肩部耳片部件,出现内折角,产生膨胀波,向后流动加速,与绕过底部的尾流汇合,形成与来流方向平行的二次压缩波,耳片后侧形成大范围回流区。马赫数对M3模型的脱体激波位置存在影响,马赫数越大,脱体激波越靠近物面,尾部回流区域变窄。图 5展示了本文数值模拟结果与弹道靶试验结果以及文献数值模拟结果进行对比,其中,test为不确定度为3倍标准差的弹道靶试验结果,ref-CFD为文献中采用GASP程序进行静态数值预测的结果。结果表明,本文的数值结果与弹道靶试验结果基本吻合。
|
图 4 不同马赫数下的流场云图 Fig.4 Flow field contour under different Mach number |
|
图 5 气动力系数与弹道靶试验结果以及文献数值模拟结果对比图 Fig.5 Comparison of ballistic range test results and dynamic force coefficient |
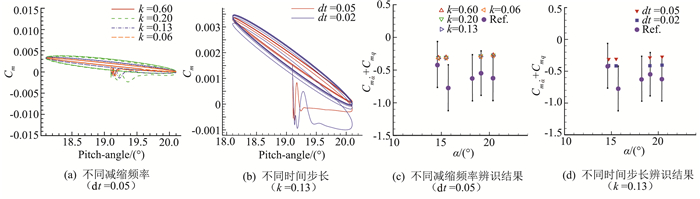
针对表 3中的计算状态,开展M3模型俯仰强迫振动数值模拟计算,获得了俯仰角-俯仰力矩迟滞曲线,如图 6(a,b)所示。
|
图 6 M3模型俯仰强迫振动数值模拟计算结果 Fig.6 Numerical simulation results of M3 model forced pitching motion |
根据迟滞曲线,通过参数计算辨识方法获得了俯仰动导数结果,将结果与弹道靶试验结果进行对比,试验不确定度为3倍标准差(3σ),结果如图 6(c,d)所示。结果表明,在所考察的弹道靶试验状态下,M3模型的动导数均小于0,飞行稳定;减缩频率对参数辨识的结果影响较小,时间步长对动导数计算辨识结果存在一定的影响,时间步长取无量纲时间0.02时,动导数的结果更接近试验值。数值结果与弹道靶试验的结果基本吻合,本文发展的FLY3D-MARS软件适用于火星大气环境的动态数值模拟计算。
3 模型俯仰强迫振荡及动态流场分析本节通过数值模拟M1模型在火星环境中的俯仰强迫振荡,研究探测器前、后体以及压缩性效应等在俯仰动态稳定性中所起的作用和流动机理。为了保证时间精度,采用双时间步隐式方法求解非定常绕流问题。振荡幅值为1°,减缩频率为0.13。远场采用适用于动态边界的无反射边界条件,壁面无滑移边界,物面温度采用等温壁假设,Twall=1500 K。
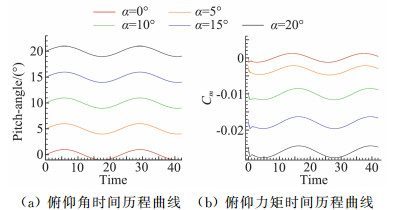
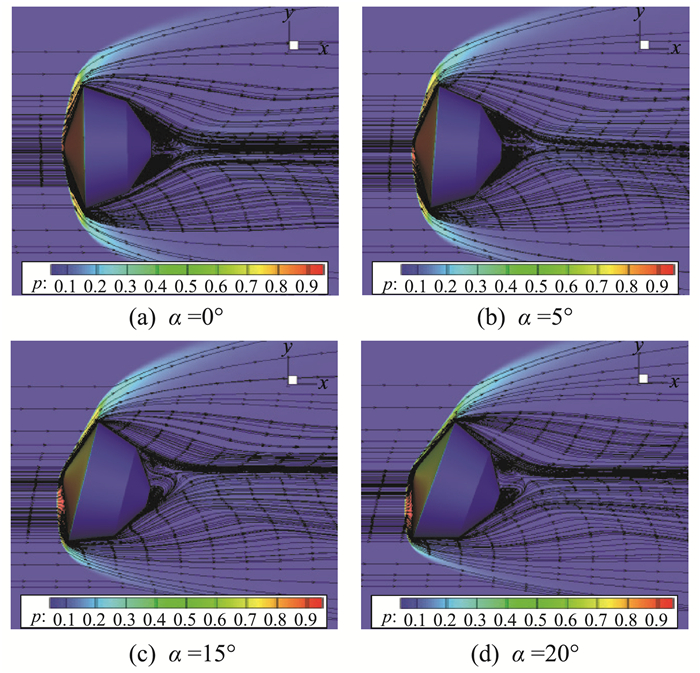
3.1 压缩性效应对高超阶段静、动导数影响规律图 7为火星环境中,不同初始迎角下的俯仰角和俯仰力矩时间历程曲线,图 8为马赫数17.59,近似比热比取值1.15时,不同迎角下动态流场分布。
|
图 7 俯仰角、俯仰力矩时间历程曲线(Ma=17.59) Fig.7 Time history of pitching angle and moment(Ma=17.59) |
|
图 8 动态流场分布(Ma=17.59) Fig.8 Dynamic flow field contour(Ma=17.59) |
上述结果表明,俯仰力矩曲线出现相位滞后。探测器在振荡过程中,每一次位置的调整都是对周围流场的一种扰动,流场达到稳定需要一定的延迟时间。前体大部分为超声速或高超声速流动,所需的调整时间很短;后体流场中,颈部点附近的流场受到剪切层、二次压缩波、回流区内流场以及尾流流场之间的相互作用,流场十分复杂,受到扰动后,需要一定的调整时间,所以后体流场存在较大的滞后。随着迎角的增加,滞后相位越大。
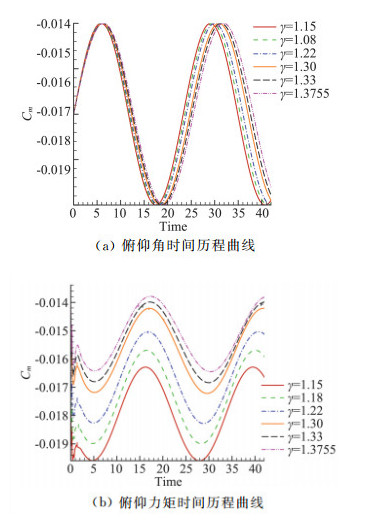
图 9为初始迎角为15°时,不同比热比条件下俯仰角和俯仰力矩的时间历程曲线。相同迎角下,随着比热比的增加,俯仰角和俯仰力矩系数的滞后相位越大。
|
图 9 俯仰角、俯仰力矩时间历程曲线(Ma=17.59,α=15°) Fig.9 Time history of pitching angle and moment (Ma=17.59, α=15°) |
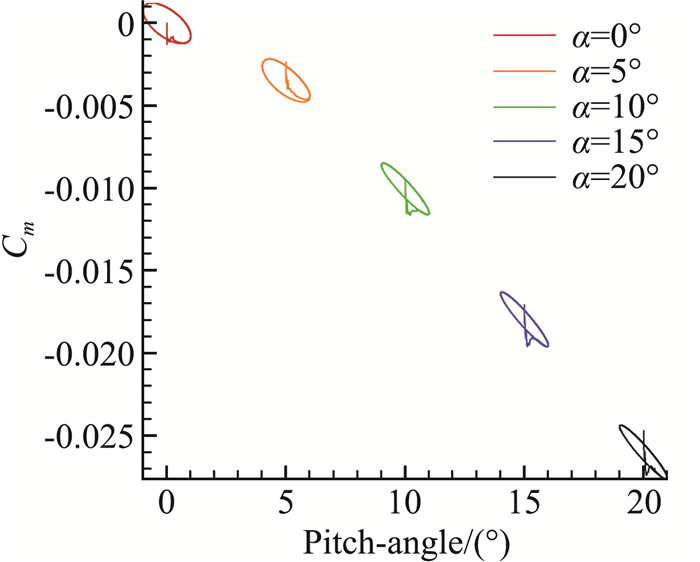
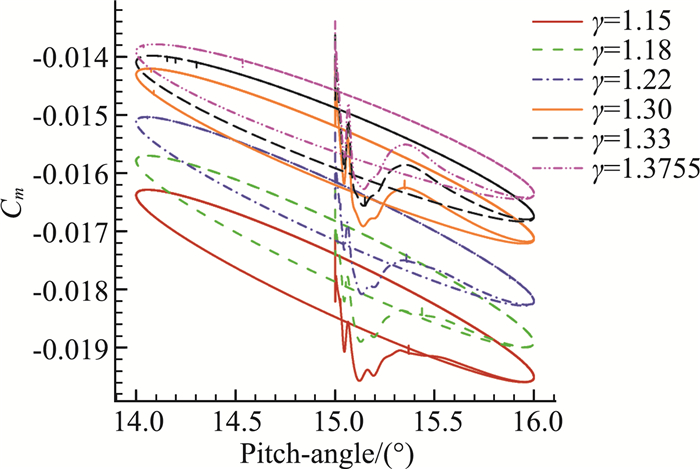
图 10是在火星环境中,不同初始迎角下的迎角-俯仰力矩迟滞曲线,迟滞曲线的形状存在明显的差异。迟滞曲线的面积和旋转方向决定了动导数的数值和符号,进而影响动导数的结果。图 11为初始迎角为15°时,不同比热比条件下迎角-俯仰力矩迟滞曲线,结果表明,相同计算状态下,不同的比热比条件的迟滞圈的面积不同,静、动导数存在差异。
|
图 10 火星环境不同初始迎角下的迟滞圈(Ma=17.59,γ=1.15) Fig.10 Hysteresis loops of different initial angles under Mars environment (Ma=17.59, γ=1.15) |
|
图 11 不同比热比条件的迟滞圈(Ma=17.59,α=15°) Fig.11 Hysteresis loops of different specific heat ratio (Ma=17.59, α=15°) |
根据迟滞曲线,通过参数计算辨识方法获得了俯仰静、动导数。图 12为相同比热比条件下,静、动导数随迎角的变化曲线。结果表明:随着迎角、比热比等变化,静、动导数只存在数值大小上的改变,符号并未发生变化;在所考察的范围内,探测器均为静稳定、动稳定状态。
|
图 12 俯仰静、动导数随迎角的变化曲线(Ma=17.59) Fig.12 Changing curves of pitching static /dynamic derivative according to attack angle (Ma=17.59) |
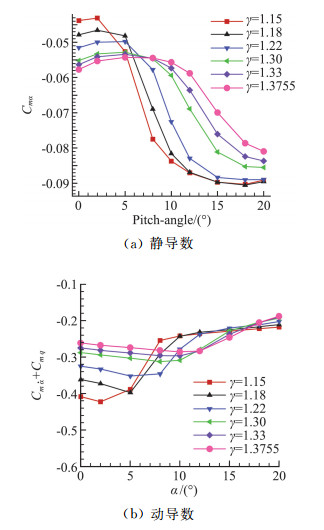
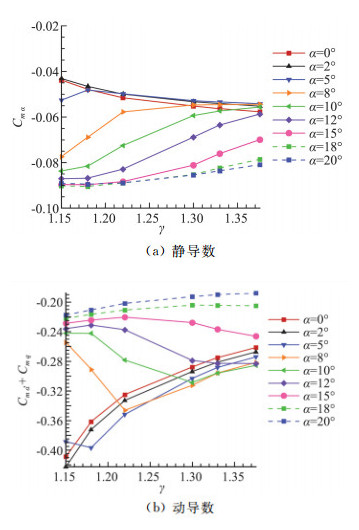
图 13为相同迎角条件下,静、动导数随比热比的变化曲线。由静导数结果(图 13a)可知,比热比对静导数结果存在影响,0°、2°迎角下,静导数随比热比的增加而减小,静稳定性增强;5°迎角下,静导数随比热比先增大后减小,静稳定性先减弱后增强;8°~ 20°迎角下,静导数随比热比的增加而增加,静稳定性减弱。由动导数随比热比变化曲线(图 13b)可知,5°~15°迎角除外,其余状态相同的计算条件下,动导数随着比热比的增加,呈单调递增变化,比热比影响着动导数的结果;随着比热比的增加,动导数增加,动稳定性减弱。分析认为,5°~15°迎角时,由于不同比热比状态下的参考时间不一致,导致动导数的单调性不明显。
|
图 13 俯仰静、动导数随比热比的变化曲线(Ma=17.59) Fig.13 Changing curves of pitching static /dynamic derivative according to attack angle (Ma=17.59) |
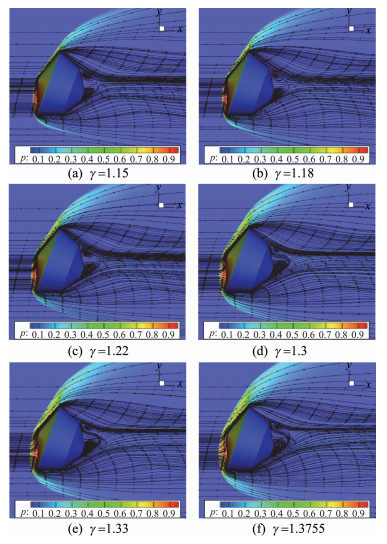
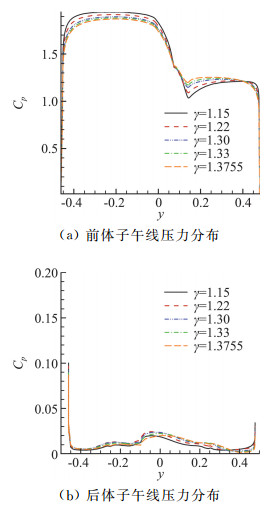
图 14为马赫数17.59、迎角20°、不同比热比条件下的动态流场结果,图中显示,不同比热比条件下脱体激波位置、通过激波后的压强存在差异:比热比越小,脱体激波越靠近物面,波后压强越大。图 15为不同比热比条件下,前、后体子午线动态压力分布曲线,结果表明,前体壁面驻点以下部分,比热比越小,压力越大,体现了压缩性效应的影响。
|
图 14 不同比热比流场结果(Ma=17.59,α=20°) Fig.14 Flow field contour under different specific heat ratio (Ma=17.59, α=20°) |
|
图 15 不同比热比条件下的动态压力分布(Ma=17.59,α=20°) Fig.15 Pressure distribution under different specific heat ratio (Ma=17.59, α=20°) |
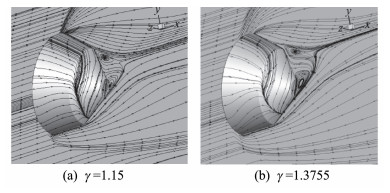
图 16为马赫数17.59、迎角20°,两种不同比热比条件下的俯仰强迫振荡瞬态壁面极限流线分布。由图中可知,迎风面流线穿过脱体激波后改变流动方向,绕过物面向四周发散,流经物面的流线在第二段倒锥尾段物面汇合,后体下部形成半结点。
|
图 16 动态流线分布(Ma=17.59,α=20°) Fig.16 Dynamic streamline distribution (Ma=17.59, α=20°) |
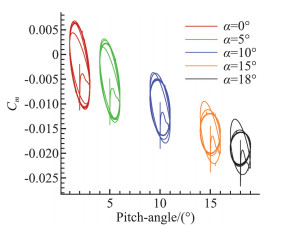
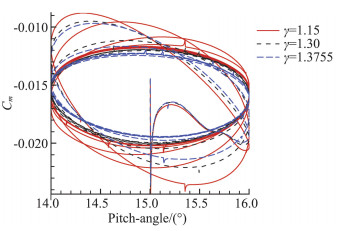
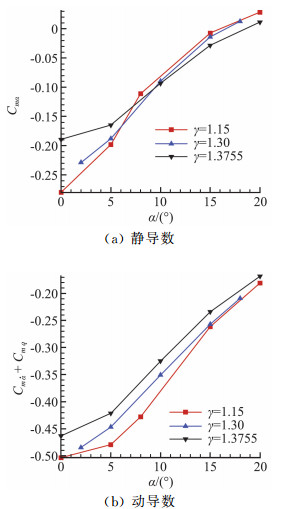
由于超声速环境下的近似比热比取值与高超声速环境中有所不同,本节针对超声速计算状态(马赫数2.5),根据不同迎角下的比热比(1.15、1.3、1.3755)状态展开了数值模拟,得到了俯仰角-俯仰力矩迟滞曲线随迎角、比热比的变化,如图 17和18所示。通过参数计算辨识方法所得的俯仰静、动导数结果如图 19所示,结果表明,超声速状态,相同比热比条件下,随着迎角的增加,静导数增大,静稳定性减弱。在所考察的几种计算状态下,动导数的符号均为负,弹道靶模型为动稳定状态。火星环境中的近似比热比取值1.3,与此同时,γ取1.3755最接近于地球大气比热比1.4,两种比热比条件下,通过参数计算辨识方法所得结果最接近,由此可知,相同迎角下,地球环境所得动导数的数值小于火星环境中动导数的数值,即,在超声速阶段相同计算状态下,火星环境中探测器具有较强的动稳定性。由此可以得出结论:在所考察范围内,随着比热比的减小,流体压缩性增强,动稳定性增强,与弹道靶试验所得结论一致(图 1)。
|
图 17 火星环境不同初始迎角下的迟滞圈(Ma=2.5,γ=1.3) Fig.17 Hysteresis loops of different initial angles under Mars environment (Ma=2.5, γ=1.3) |
|
图 18 不同比热比条件的迟滞圈(Ma=2.5,α=15°) Fig.18 Hysteresis loops of different specific heat ratio (Ma=2.5, α=15°) |
|
图 19 俯仰静、动导数随迎角的变化曲线(Ma=2.5) Fig.19 Changing curves of pitching static/dynamic derivative according to attack angle (Ma=2.5) |
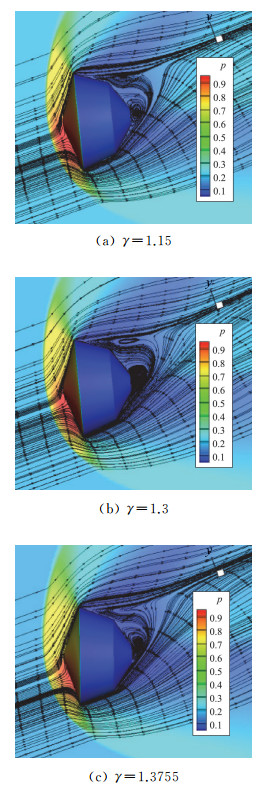
图 20为不同比热比条件的动态流场分布,结果表明,超声速状态中,比热比越小,脱体激波越靠近物面,波后压强越大,与高超声速状态下所得结论一致。
|
图 20 不同比热比的动态流场分布(Ma=2.5,α=15°) Fig.20 Dynamic flow field distribution under different specific heat ratio (Ma=2.5, α=15°) |
本文考核了FLY3D-MARS软件在火星环境动态特性计算中的适用性,进一步确保流动模型的准确性;通过开展M1模型俯仰强迫振荡数值模拟,系统分析压缩性效应对动态特性的影响规律,结果表明,在所考察范围内,比热比越小,压缩性增强,动导数减小,动稳定性增强。导致动稳定性随γ变化的原因是不同γ流场压缩性不同,与弹道靶试验结论一致。
| [1] |
WAY D W, POWELL R W, CHEN A, et al. Mars science laboratory: entry, descent, and landing system performance[C]//IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 2007. 03. 3-10, IEEE: 1-19. https://ieeexplore.ieee.org/document/4526283/
|
| [2] |
EDQUIST K T, HOLLIS B R, DYAKONOV A A, et al. Mars science laboratory entry capsule aerothermodynamics and thermal protection system[C]//IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 2007, 03, 3-10, IEEE: 1-13. http://www.mendeley.com/research/mars-science-laboratory-entry-capsule-aerothermodynamics-thermal-protection-system/
|
| [3] |
ALKANDRY H, BOYD I D, REED E M, et al. Numerical study of hypersonic wind tunnel experiments for mars entry aeroshells: AIAA 2009-3918[R]. Reston: AIAA, 2009.
|
| [4] |
STELTZNER A, KIPP D, CHEN A, et al. Mars science laboratory entry, descent, and landing system[C]//Aerospace Conference, 2006 IEEE. http://adsabs.harvard.edu/abs/2014JSpRo..51..993.%201
|
| [5] |
贾贺, 荣伟. 火星探测器减速着陆技术分析[J]. 航天返回与遥感, 2010, 31(3): 6-14. DOI:10.3969/j.issn.1009-8518.2010.03.002 |
| [6] |
袁先旭.非定常流动数值模拟及飞行器动态特性分析研究[D].绵阳: 中国空气动力研究与发展中心, 2002.
|
| [7] |
赵海洋.返回舱动态稳定性物理机理分析及被动/主动控制方法研究[D].长沙: 国防科学技术大学, 2007. http://cdmd.cnki.com.cn/article/cdmd-90002-2008098773.htm
|
| [8] |
SCHOENENBERGER M, HATHAWAY W, YATES L, et al. Ballistic range testing of the mars exploration rover entry capsule[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, 2005. https://www.mendeley.com/catalogue/ballistic-range-testing-mars-exploration-rover-entry-capsule/
|
| [9] |
BROWN J, YATES L, BOGDANOFF D, et al. Free-flight testing in support of the mars science laboratory aerodynamics database[J]. Journal of Spacecraft and Rockets, 2006, 43(2): 293-302. DOI:10.2514/1.19221 |
| [10] |
LIEVER P, HABCHI S, BURNELL S, et al. CFD prediction of the Beagle 2 aerodynamic database[C]//40th AIAA Aerospace Sciences Meeting & Exhibit. 2002. https://arc.aiaa.org/doi/abs/10.2514/6.2002-683
|
| [11] |
VIVIANI A, PEZZELLA G. Aerodynamic analysis of a capsule vehicle for a manned exploration mission to mars[C]//AIAA/dlr/dglr International Space Planes & Hypersonic Systems & Technologies Conference, 2011. https://arc.aiaa.org/doi/abs/10.2514/6.2009-7386
|
 2019, Vol. 37
2019, Vol. 37