2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
飞机结冰是典型的动态冻结过程,在宏观上表现为冰层的不断累积。在这一过程中,由于伴随液滴撞击和破碎现象,结冰内部会夹杂一定量的空气,从而在微观上形成类似多孔材料的孔隙结构。受结冰条件的共同影响,结冰微观结构呈现出较大的差异,同时直接决定包括密度、黏附力、导热系数等在内的结冰物理特性。
在多种结冰条件中,温度被认为是影响结冰类型的主要因子。在冰点以下时,温度越高,结冰越趋于明冰,反之趋于霜冰[1]。温度还被认为是影响结冰形核、即冻结速度的主要内在动力[2-4],温度越低,基底(包含超疏水材料)表面延缓结冰的性能减弱,甚至会出现瞬间接触结冰[5-6]。相应地,由于温度越高,水滴冻结速度越慢,相互间融合的时间就较长,结冰微观结构中夹杂的空气就越少[7-8]。因此,温度越低,结冰的密度、应力、致密度等越小。
现阶段关于温度对飞机结冰影响的定性讨论取得了较大成果,但随着研究的深入,需要更精细化和定量化的结果,使得多种物理量间的关系或者现象背后的规律以数学形式表示,并方便应用于其他相关方向的研究。然而,在定量方面,尤其是微观的定量方面缺少必要的成果。针对温度对飞机结冰微观结构特性定量研究不足这一关键和难点问题,本文研究结冰二维显微图像结构信息的提取方法,以及结冰三维微观结构数学模型的建立方法,并基于此,研究结冰内部孔隙分布特性的定量表征方法。在试验部分,对所提方法的适用性与合理性进行验证,并开展了温度对微观结构特性的定量影响研究。通过研究,以期为结冰物理现象及物理特性的深入认识提供定量依据。
1 结冰微观信息定量提取方法结冰微观信息的提取是孔隙特性分析的前提,是关乎后期结果正确与否的关键,是本文的基础与难点问题。
1.1 结冰显微图像的获取结冰风洞试验相较于真实飞行试验或者数值仿真具有安全、经济、准确等特点,是研究飞机结冰的重要手段之一。本文的结冰均取自结冰风洞试验中,所使用的喷雾用水经过有效过滤,含有杂质较少,不会对显微结果造成影响。试验所用结冰模型为超临界翼型剖面的缩比模型。
结冰显微图像由电子显微镜连接电脑采集得到,结冰图片为低温切割得到,表面处理光滑平整。显微试验所用结冰选自结冰稳定生长段,如图 1中红线框所示,这一阶段的结冰微观特征不受试验件物面的性质影响,生长速度近似于线性。

|
图 1 结冰稳定生长段 Fig.1 Steady growing part of ice |
图像分割是图像信息提取及定量分析的有力工具,已在结冰研究中得到广泛应用[9-11]。然而目前大多采用的是传统的阈值分割方法,这种方法简单地以某一灰度值作为区分背景和目标的阈值,未考虑目标的完整性及噪声影响,容易产生分割误差。本文采用基于变分思想的图像分割方法,它能较好融入人类的分割思想,包括考虑目标的拓扑特点,或者加入抑制因噪声产生多余曲线的数学项。相比于传统方法,它具有较高的精度。具体地,本文采用前期所提出的变分模型[12],以其作为微观信息提取工具。它的主要做法是给定初始水平集函数,其0-水平集表示演化曲线,并提出关于水平集函数的能量泛函,进而应用最优化算法求解,最优解对应的0-水平集便是最终的分割结果。
定义u0: Ω→R为灰度图像,其中Ω是矩形区域,表示的是图像定义域。文献[12]提出的最小化问题为:
| $ \begin{array}{*{20}{l}} {{\rm{min}}\{ - {\rm{ }}\int {\left[ {1 - H\left( \phi \right)} \right]{\rm{d}}x + } }\\ {\mu \int {{{\left( {{u_0} - c} \right)}^2}\left[ {1 - H\left( \phi \right)} \right]{\rm{d}}x} + \upsilon {\rm{ }}\int {\left| {\nabla H\left( \phi \right)} \right|{\rm{d}}x} \} } \end{array} $ | (1) |
其中:x为图像像素点坐标,也可视为(x, y); ϕ(x)是水平集函数; H(·)是一维Heaviside函数; c=
关于ϕ对式(1)进行求导,可以得到其对应的Euler-Lagrange方程,再应用最速下降法,便可得到对应的水平集演化方程:
| $ \frac{{\partial \phi }}{{\partial t}} =\delta \left( \phi \right)\left[ { - 1 + \mu {{\left( {{u_0} - c} \right)}^2} + \upsilon \cdot \nabla \left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right)} \right] $ | (2) |
其中δ(ϕ)是Dirac函数,仅在ϕ=0处有取值。这样离演化曲线远的区域,ϕ值更新较慢,影响曲线收敛至目标区域边界的速度。为了克服δ(ϕ)对求解速度带来的不利影响,对其做近似处理,令δ(ϕ)≈1,得到最终的求解方程:
| $ \frac{{\partial \phi }}{{\partial t}} = - 1 + \mu {\left( {{u_0} - c} \right)^2} + \upsilon \cdot \nabla \left( {\frac{{\nabla \phi }}{{\left| {\nabla \phi } \right|}}} \right) $ | (3) |
式(3)的离散求解主要采用差分方法。这样求解所得的最优解ϕ*的0-水平集就代表最终的分割曲线,区域{x|ϕ*(x)>0}是目标,在本文中对应着结冰显微图像中的孔隙部分。
2 结冰微观结构特性定量表征结冰中含有一定量的孔隙,其形态、半径、分布较为不统一,但是存在一定的规律性。鉴于此,本节对结冰微观结构提出合理假设,建立结冰微观结构的三维数学模型,并提出表征微观结构特征的量化指标——计算密度。
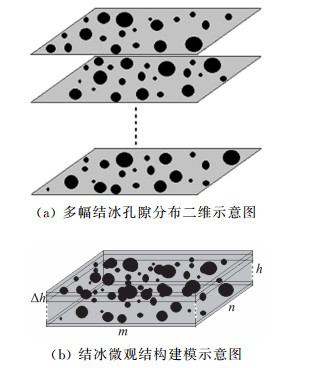
2.1 结冰微观结构三维数学建模飞机结冰属于典型的动态生长过程,常伴随着过冷水的溢流现象。在这一过程中,过冷水不断冻结,部分空气来不及逃逸,在冰层中形成不同大小的孔隙,如图 2(a)所示。借助显微成像系统,可以清晰地得到孔隙的分布图像。
|
图 2 结冰微观结构数学建模 Fig.2 Mathematical modeling of ice micro-structure |
为了合理构造结冰的微观结构,基于已有文献结果和结冰图像特点,进行如下假设:
① 孔隙呈球形。在文献[7, 13, 14]中均有结冰气泡孔隙呈球形的假设或结论;
② 结冰微观结构模型由多个冰层叠加而成。试验或者理论中,都将动态结冰的形成视为不断冻结累积的过程;
③ 结冰微观结构每个截面含有相近甚至相同的孔隙分布。
基于以上假设,在构造结冰微观结构时,多个冰层(图 2(a))相互叠加,孔隙交错分布,就可以建立其数学模型,如图 2(b)所示。其中m和n分别表示显微图像的长和宽,单位均为像素点; Δh为冰层厚度,其值由假设②得到。假设生成的结冰由k个冰层组成,则结冰厚度为h=k·Δh。
2.2 结冰计算密度提出给定大小为m×n×h的结冰,其三维微观结构由2.1节建模方法得到。假设该结冰每个截面具有相同的孔隙分布特性,定义结冰计算密度为:
| $ \begin{array}{l} \rho = 900\frac{{mnh - Sh}}{{mnh}}\\ \;\; = 900\frac{{mn - S}}{{mn}} \end{array} $ | (4) |
其中S是高度方向截面的孔隙面积。
求解计算密度ρ的主要难点在于S,由于同一结冰条件下结冰孔隙分布服从一定的分布[7],且每个观察面内的孔隙孔径不尽相同,因此以各孔径面积和作为S的值时,容易使计算失去一般性,这里采用带有“平均”意义的求解方式。
主要做法是将孔隙按半径大小分成若干组,分别计算每组的平均半径,并以此作为每组孔隙的半径,进而计算出面积S。假设显微镜观察到某一层含有n个孔隙,面积从大到小依次为{si|i=1, 2, …, n},视其为圆后计算的半径对应为{ri|i=1, 2, …, n}。以步长为Δr,将其分为q组,每组包含nj(j=1, 2, …, q)个数,则
| $ \overline {{r_j}} = \frac{{{r_{{a_j} + 1}} + \ldots + {r_{{a_j} + {n_j}}}}}{{{n_j}}} $ | (5) |
其中
那么,可以得到S的表达式如下:
| $ S = \sum\limits_{j = 1}^q {{n_j} \cdot {\rm{ \mathsf{ π} }} {{\overline {{r_j}^2} }}} $ | (6) |
将式(6)代入式(4),得到最终的计算密度表达式为:
| $ \rho = 900\frac{{mm - \sum\limits_{j = 1}^q {{n_j} \cdot {\rm{ \mathsf{ π} }}{{\overline {{r_j}^2} }}} }}{{mn}} $ | (7) |
前面部分给定了结冰微观结构三维建模方法以及代表微观特征的定量指标,本节针对结冰试验采集的显微图像,对不同温度下的结冰微观结构特征进行定量分析。结冰试验条件为v=25 m/s,MVD=38 μm,LWC=0.75 g/m2,温度条件在文中具体给出。所有微观图像均为40倍放大倍率下采集得到。
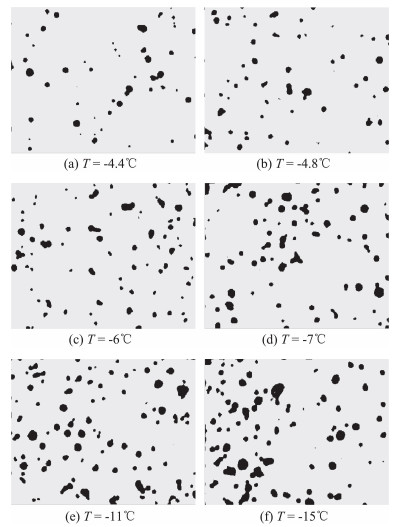
3.1 结冰孔隙提取结果应用1.2节方法对不同温度下的显微图像进行分割处理,并对分割得到的背景区域和目标区域进行二值化处理,结果展示于图 3中。由于光线折射原因,孔隙中心会有不同于周围的亮点,传统方法是不能很好处理的。但是从图中可以看出本文的方法很好保持了孔隙的完整性。另外,图中给出了不同温度的孔隙分割结果,显然孔隙在尺寸、分布等方面存在不同,直观体现在温度越高,孔隙越稀疏。这与结冰宏观特性是高度相关的,即温度越高,孔隙较少,密度越大,反之则相反。
|
图 3 不同温度的微观图像分割结果 Fig.3 Segmentation results for microscopic images of ice at different temperatures |
微观结构建模过程中假设每层观察得到的孔隙数量和半径分布是一致的,为了验证假设的合理性,本小节进行分析讨论。
定义数量分布函数为:
| $ N\left( r \right) = nP\{ X \le r\} $ |
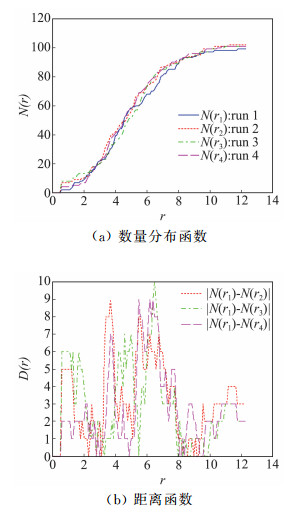
其中: n为图像内孔隙总数,P为概率运算,N(r)表示的是半径小于r的气泡数量。本文选用T=-11 ℃的状态进行验证,试验图像取自四组不同位置的结冰。它们的数量分布函数依次记为N(ri)(i=1, …, 4),分别展示于图 4(a)中,可以看出它们的趋势比较相近,即每个半径的孔隙数量几乎相等,这就说明同一状态不同位置的孔隙分布具有较高的相似性,建模中的假设较为合理。
|
图 4 同一结冰状态不同位置孔隙分布情况 Fig.4 Pores distribution of ice in different locations |
另外,以其中的第一组微观图像的数量分布函数为基准,定量给出了其它三组数据与它的距离(|N(r1)-N(ri),i=2, 3, 4),结果展示于图 4(b)中。从图中可以看出最大距离约为10,约为总数的10%,即对于任意的半径rε,同一结冰状态下,不同显微图像的分割结果中,半径小于rε的孔隙个数之差始终不大于10,这就量化说明了同一状态不同位置孔隙分布具有较高的相似性。
3.3 温度对孔隙分布的影响3.1节中得到了不同温度下的孔隙信息,可以看出它们的分布存在着不同程度的差异,本节中对其进行定量分析,主要包括不同温度下的孔隙数量和半径分布情况。表 1中给出了不同温度下孔隙数量的统计信息,从结果可以看出随着温度降低,孔隙数量增加,并且孔隙所占的空间也增加,这是由于温度越低时,水滴撞击基底表面发生冻结的速度越快,结冰表面存在溢流现象的可能性就越小,从而结冰中夹杂气泡孔隙的概率就越大。
| 表 1 不同温度下孔隙数量 Table 1 Number of porous at different temperatures |
|
|
为了解不同状态下孔隙半径的分布特点,根据模型假设,使用如下的概率密度函数f(ri):
| $f\left( {{r_i}} \right) = \frac{{{n_i}}}{n} \times 100\% $ |
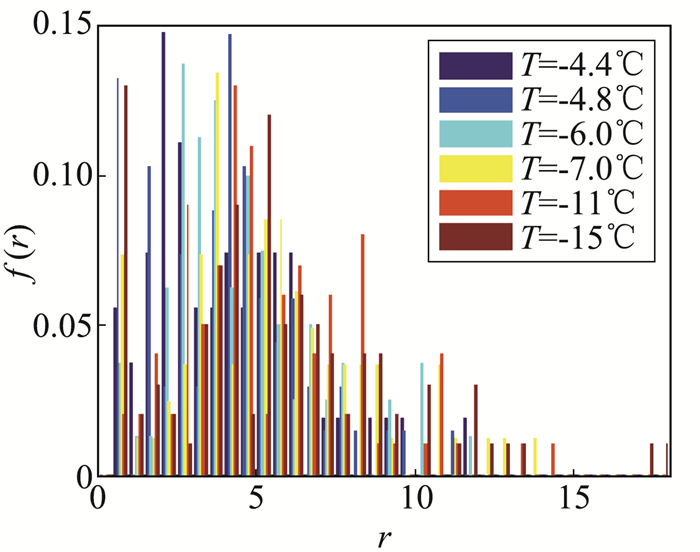
其中:ri=0.25+(i-1)Δr, (i=1, 2, …, q),ni是半径属于((i-1)Δr, iΔr]区间的孔隙个数,图 5中分别给出了与图 3对应的孔隙分布密度函数,其中半径步长取为Δr=0.5。从图中可以看出,孔隙的尺寸较为不均匀,主要集中分布于中小尺寸,其中大尺寸气泡最少,小尺寸气泡较多,这是因为气泡在冻结过程中受到挤压,容易破碎变为小气泡。另外,当温度较低时,由于冻结速度较快,空气来不及逃逸或者分裂,会形成较大的孔隙,这点从图 3中也可以得到印证。
|
图 5 气泡半径概率密度函数 Fig.5 Distribution density function of porous radius |
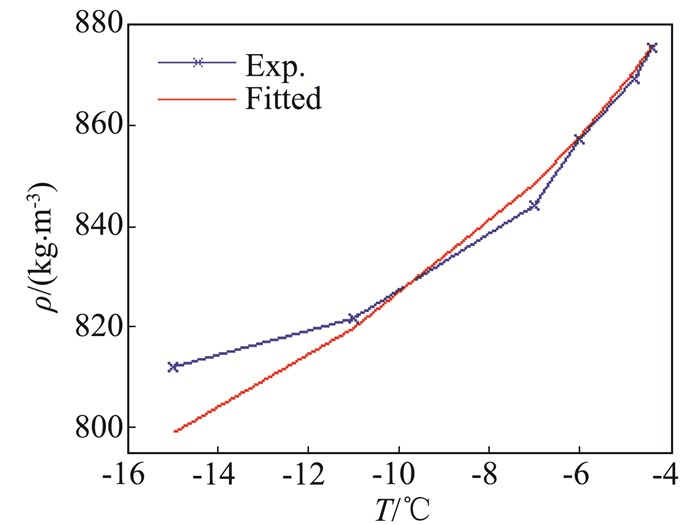
结合式(7),计算不同温度下的计算密度,并对其进行定量分析。不同温度下的计算密度绘制于图 6的蓝色线条中,从曲线的走势可以看出,其与真实密度随温度的变化较为相似,即随着温度减小,结冰密度减小,结冰更趋于霜冰。另外,应用Jones的结冰密度经验公式[15]的形式对试验数据进行了拟合,拟合曲线如图 6中的红色曲线所示,其表达式为:
| $ \begin{array}{*{20}{c}} {f\left( T \right) = 1000{{\rm{e}}^{0.15[1 - 1.34{{\left( { - T} \right)}^{0.23}}]}}, }\\ {T \in [ - 3, - 40]} \end{array} $ |
|
图 6 温度-计算密度及其拟合曲线图 Fig.6 Curve and fitted curve of computational density at different temperatures |
从图中可以看出,拟合结果吻合度较高,可以用该表达式预测任意温度下的计算密度,进而分析不同温度下的结冰特性。
4 结论采用变分图像分割的方法对结冰图像进行孔隙提取,并基于此建立了结冰微观结构的数学模型,提出了表征微观特征的定量指标——计算密度。在试验部分对所提模型和定量指标进行了分析讨论,得到如下结论:
(1) 提出了表征结冰微观结构的三维数学模型和定量指标。文中建立了结冰微观结构三维模型,试验中验证了模型的合理性;在所建立数学模型的基础上,提出了计算密度的概念,并给出了不同温度下计算密度及其拟合曲线,它与真实密度随温度的变化较为相似,即取值随着温度减小而减小,因此计算密度可以作为微观结构的定量指标。
(2) 温度是影响孔隙分布的重要因素。随着温度降低,孔隙数量增加,并且孔隙所占的空间也增加;孔径分布不均匀,主要集中于中小尺寸,其中大尺寸气泡较少,小尺寸气泡较多。另外,温度越低,结冰中所有孔隙的半径最大值越大。
(3) 文中方法具有较大的应用空间。结冰微观三维模型和计算密度是结冰微观的定量反映,更是宏观形貌的另一种体现,具有定量差异的特点,这种方法同样适用于速度、MVD等对结冰微观结构的影响研究。另外,在本文基础上,也可开展温度、速度、MVD等多因素对结冰微观结构的耦合影响定量研究。
| [1] |
HANSMAN R J, KIRBY M S. Comparison of wet and dry growth in artificial and flight icing conditions[J]. Journal of Thermophysics and Heat Transfer, 1987, 1(3): 215-221. DOI:10.2514/3.30 |
| [2] |
ZHOU W W, LIU Y, HU H, et al. Utilization of thermal effect induced by plasma generation for aircraft icing mitigation[J]. AIAA Journal, 2018, 56(3): 1097-1104. DOI:10.2514/1.J056358 |
| [3] |
杜雁霞, 李明, 桂业伟, 等. 飞机结冰热力学行为研究综述[J]. 航空学报, 2017, 38(2): 25-36. DU Y X, LI M, GUI Y W, et al. Review of thermodynamic behaviors in aircraft icing process[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 25-36. (in Chinese) |
| [4] |
LEI G L, DONG W, ZHENG M, et al. Numerical investigation on heat transfer and melting process of ice with different porosities[J]. International Journal of Heat and Mass Transfer, 2017, 107: 934-944. DOI:10.1016/j.ijheatmasstransfer.2016.11.004 |
| [5] |
武卫东, 王菲菲, 申瑞, 等. 不同基底温度下铝基超疏水表面的抗结冰性能实验[J]. 制冷学报, 2017, 38(3): 82-88. WU W D, WANG F F, SHEN R, et al. Experimental study on anti-icing performance of aluminium-based super-hydrophobic surface under different substrate temperatures[J]. Journal of Refrigeration, 2017, 38(3): 82-88. DOI:10.3969/j.issn.0253-4339.2017.03.082 (in Chinese) |
| [6] |
JIN Z Y, WANG Z N, SUI D Y, et al. The impact and freezing processes of a water droplet on different inclined cold surfaces[J]. International Journal of Heat and Mass Transfer, 2016, 97: 211-223. DOI:10.1016/j.ijheatmasstransfer.2016.02.024 |
| [7] |
李伟斌, 魏东, 杜雁霞, 等. 动态结冰微观孔隙结构定量分析[J]. 航空学报, 2018, 39(2): 107-114. LI W B, WEI D, DU Y X, et al. Quantitative analysis of micro porous structure of dynamic icing[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(2): 107-114. (in Chinese) |
| [8] |
雷桂林, 郑梅, 董威, 等. 积冰密度对机翼除冰过程影响的数值研究[J]. 空气动力学学报, 2018, 36(06): 958-965. LEI G L, ZHENG M, DONG W, et al. Numerical investigation of ice density effects on airfoil de-icing process[J]. Acta Aerodynamica Sinica, 2018, 36(06): 958-965. DOI:10.7638/kqdlxxb-2016.0144 (in Chinese) |
| [9] |
WANG X P, HU J L, WU B, et al. Study on edge extraction methods for image-based icing on-line monitoring on overhead transmission lines[J]. High Voltage Engineering, 2008, 34(12): 2687-2693. |
| [10] |
WANG X P, HU J L, SUN C, et al. On-line monitoring of icing-thickness on transmission line with image edge detecting method[J]. High Voltage Apparatus, 2009, 6: 019. |
| [11] |
ZHANG K, WEI T, HU H. An experimental investigation on the surface water transport process over an airfoil by using a digital image projection technique[J]. Experiments in Fluids, 2015, 56(9): 173. DOI:10.1007/s00348-015-2046-z |
| [12] |
LI W B, YI X, SONG S H. Convex background removed model for image segmentation using the split Bregman method[J]. Journal of Information and Computational Science, 2015, 12(17): 6641-6652. |
| [13] |
KINTEA D M, ROISMAN I V, TROPEA C. Transport processes in a wet granular ice layer:Model for ice accretion and shedding[J]. International Journal of Heat and Mass Transfer, 2016, 97: 461-472. DOI:10.1016/j.ijheatmasstransfer.2016.01.076 |
| [14] |
KRZYSZTOF S, EDWARD P. Three-dimensional modelling of ice accretion density[J]. Quarterly Journal of the Royal Meteorological Society, 2000, 126(568): 2395-2404. DOI:10.1002/qj.49712656803 |
| [15] |
JONES K F. The density of natural ice accretions related to nondimensional icing parameters[J]. Quarterly Journal of the Royal Meteorological Society, 2010, 116(492): 477-496. |
 2019, Vol. 37
2019, Vol. 37


