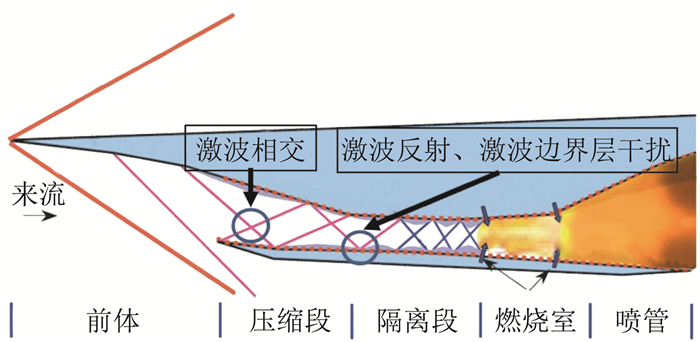
由于超声速飞行的速度特点(Ma>5,例如X-43,Ma=9.8)以及其高度特点(H>30000 m),在飞行器表面会形成厚边界层,另外由于飞行器的几何外形特点,在超声速气流中会产生一系列的激波,激波打在飞行器物面上会发生激波反射,遭遇物面的边界层会形成激波/边界层干扰现象。在高超声速飞行器流场的多个部位存在着形式多样的激波/边界层干扰现象。如在进气道内流场中,存在着复杂的激波反射、激波相交以及激波/边界层干扰现象,如图 1所示,可能造成结构破坏和快速疲劳,气动弹性以及热防护困难,进气气流畸变,甚至不启动等等,对发动机性能及稳定性等有着重要的影响,在设计中需要充分考虑。
1939年,Ferri[2]首次在试验中观察到机翼后缘附近的激波/边界层干扰现象。随后,Fage和Sargent[3]、Barry等[4]、Liepmann等[5]以及Johannesen[6]等均在试验中观察到了不同类型的激波/边界层干扰现象。典型的二维激波边界层干扰有入射斜激波反射、压缩拐角、正激波、压力突增以及迎风台阶[7]。Green[8]基于大量试验数据认为压缩拐角干扰与入射激波边界层干扰流场具有相似性,并指出当拐角为入射激波对应的气流偏转角两倍时,两者的干扰近似一致。
随着计算技术的发展,1971年MacCormack[9]首次开展了激波与层流边界层干扰的数值模拟工作。Beam等[10]研究了复杂几何条件的激波与层流边界层干扰问题,采用有限差分法求解可压缩的N-S方程。Bodonyi等[11]数值模拟跨声速流的入射激波层流边界层干扰,发现分离区和再附区的大小随激波强度增加变化较大。Mailison[12]利用试验方法研究压缩拐角流动,分析表面压力与热流密度的分布规律以及确定初始分离出现的条件。结果表明分离流动的出现及分离区的大小与压缩角的大小相关。Price等[13]研究了高超声速湍流压缩拐角激波边界层干扰,随着压缩角的增加,压力和热流迅速上升,但压力分布在压缩面上缓慢地趋于平缓,而热流在达到峰值后迅速下降。龚安龙等数值仿真双锥分离流动,认为分离流动特性及流场物理参数对计算网格比较敏感,过稀的网格将导致分离区减小,压力和热流峰值增大[14]。赵云飞采用WCNS格式数值分析非定常激波/边界层干扰对于边界层转捩的影响[15]。童福林等采用DNS数值模拟压缩拐角激波/转捩边界层干扰,研究转捩过程对干扰区内分离泡结构的影响[16]。董祥瑞等采用DES方法对激波边界层干扰诱导的分离流动进行数值模拟,并采用单、双微楔对齐进行控制,获得其最佳安装位置[17]。宋友富等发展可压缩湍流模型CKDO,其对壁面压力和摩擦阻力系数的捕捉能力优于其他模型[18]。陈宣亮等采用分离涡模拟方法,对X-37B机翼副翼偏转拐角的激波边界层干扰做非定常数值分析,捕捉该类干扰下的脉动压力[19]。王娇等探索Bump进气道中鼓包诱导的锥形激波和机身湍流边界层干扰问题,同样采用数值仿真,认为鼓包最适合作为超声速进气道前缘压缩面[20]。2016年,Kotov等考虑通过亚格子模型以及数字模拟两方面的改进来实现湍流流动激波附近的精度提高[21]。
1958年,Chapman等[22]基于大量的试验数据,发现分离流动的一些特点并不依赖于引起分离的形式。把这种不受下游几何形状影响也不受引起分离的形式的影响的干扰叫做“自由干扰”。并针对自由干扰给出简单的理论分析——自由干扰理论(FIT)。
在分离区长度方面,Burggraf[23]基于Neiland[24]以及Stewartson和Williams[25]提出的渐进理论,针对激波层流边界层干扰产生较强分离时的分离区长度给出数学模型。同时,对于上游影响长度,即无黏激波入射点至干扰起始点的长度,Miller等[26]以及Ramesh等[27]学者也给出了工程拟合公式。
2011年,Babinsky和Harvey基于前人的试验结果描绘入射激波层干扰分离流场的流动图画和壁面压力分布规律。典型流动结构包括分离泡、入射激波、膨胀波以及反射激波,压增主要分为分离阶段以及再附阶段两个部分[7]。
前人基于大量的试验以及数值手段,已经给出了分离流动的基本流动结构以及典型流动参数的分布规律。但是尚没有完整的理论求解模型,干扰的关键点位置不能明确,对于波系结构的定量描述也少有研究。工程实际中,迫切地需要快速获得流动图画,定位波系位置,明确流动参数具体分布,捕获高压高热流区,为整体流场分析提供帮助。
本文基于对入射激波致边界层分离流场的分析建立完整的理论求解模型,该模型可以根据来流条件(来流马赫数、入射激波强度以及边界层参数)给出局部干扰流场结构以及流动参数分布。
1 干扰流场本文用ρ、p、V、a、Ma、γ分别表征密度、压力、速度、声速、马赫数以及比热比,考虑的流体为量热完全气体。另外,激波角(亦即激波与上游流体的夹角)用β表示,气流穿越激波或膨胀波的偏转角用θ表示。
1.1 流场结构入射激波与平板边界层发生干扰,当入射激波足够强时,引起边界层分离,产生分离泡,如图 2所示。

|
图 2 入射激波致边界层分离流场结构 Fig.2 Sketch of the flow induced by an incident shock wave boundary layer interaction with separation |
分离泡起点S上游流体发生偏转,产生压缩波系,压缩波系合并为分离激波。入射激波与分离激波发生正规相交,产生透射激波。透射激波穿越自由剪切层并反射为膨胀波,使得自由剪切层向壁面偏转,到达再附点R,R下游流体转为与壁面平行,产生压缩波系,压缩波系合并为再附激波[7]。因此,已知的主要结构包括入射激波、边界层、分离激波、干扰点膨胀波、分离泡以及再附激波。工程实际中已知的参数通常包括来流马赫数、干扰点雷诺数以及入射激波强度。由此需要获得各区流动参数、各干扰波的方向和强度以及压力沿壁面分布等。
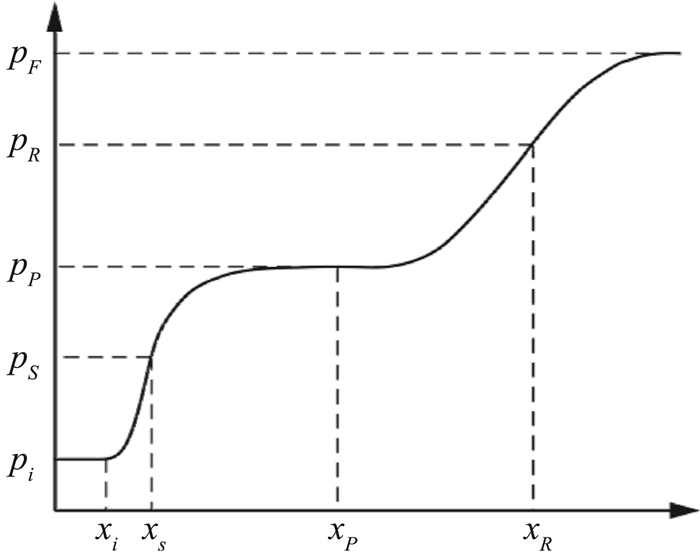
1.2 壁面压力入射激波致边界层分离流场的壁面压力分布如图 3所示,分离点S上游的i点(干扰起始点)压力即开始增加,对应干扰起始点压力pi,通常近似认为pi等于来流压力。伴随分离阶段,压力历经第一个突增,分离阶段下游接着为分离流动的典型压力平台段。激波穿越边界层内的外部区域,但是内部亚声速流不能承受较大的压力梯度,因而局部形成一个近似等压边界。下游伴随再附阶段,压力经历第二次增加,达到最终压力峰值pF。相比分离阶段压增,再附阶段压增比较平缓[7]。
|
图 3 入射激波致边界层分离流场壁面压力 Fig.3 Wall pressure distribution induced by an incident shock wave boundary layer interaction with separation |
Chapmen等[21]基于大量的试验数据,发现分离流动的一些特点并不依赖于引起分离的形式。并把这种不受下游几何形状影响也不受引起分离的形式的影响的干扰叫做“自由干扰”,同时对于这种干扰给出简单的理论分析,即自由干扰理论(FIT),得出平台压力pP:
| $ \frac{{p - {p_0}}}{{{q_0}}} = F\left( {\bar x} \right)\sqrt {\frac{{2{C_{{f_i}}}}}{{{{\left( {Ma_0^2 - 1} \right)}^{0.5}}}}} $ | (1) |
式中:q0为来流动压,Cfi为壁面摩擦力系数,无量纲函数F被认为是普适函数,和马赫数以及雷诺数无关,由试验确定, 见表 1。
| 表 1 特定点处的F值 Table 1 Values of F at special points |
|
|
Katzer[28]针对入射激波层流边界层干扰,进行绝热壁面情况下的数值模拟,其模拟工况范围为1.4≤ Ma∞≤3.4, 1×105≤ ReL≤ 6×105,1.2≤pF/p∞≤3.4。基于这些数值数据,给出了入射激波层流边界层干扰的分离区长度工程拟合公式:
| $ \frac{{{l_{{\rm{sep }}}}}}{{\delta _L^*}}\frac{{Ma_\infty ^3}}{{{{\left( {\frac{{R{e_L}}}{C}} \right)}^{0.5}}}} = 4.4P $ | (2) |
式中:P=(pF-pinc)/p∞,δL*为未受干扰时的平板无黏激波入射点xL处边界层位移厚度:
| $ \delta _L^* = \frac{{{x_L}}}{{{{\left( {\frac{{R{e_L}}}{C}} \right)}^{0.5}}}}\left( {1.72 + 2.22\frac{{\gamma - 1}}{2}Ma_\infty ^2} \right) $ | (3) |
pinc为引起初始分离的激波强度,通过自由干扰理论给出:
| $ \frac{{{p_{{\rm{inc}}}} - {p_i}}}{{{p_i}}} = \frac{1}{2}\gamma Ma_i^2{P_{{\rm{inc}}}}{\left[ {\frac{{{C_{{f_L}}}}}{{{{\left( {Ma_i^2 - 1} \right)}^{0.5}}}}} \right]^{0.5}} $ | (4) |
CfL为未受干扰时平板边界层xL处的壁面摩擦系数:
| $ {C_{{f_L}}} = \frac{{0.664}}{{{{\left( {\frac{{R{e_L}}}{C}} \right)}^{0.5}}}} $ | (5) |
常数Pinc = 1.85
Krishnan等[29]将Katzer公式的范围拓展到Ma∞≤6.85和pF/p∞≤5.89:
| $ \frac{{{l_{{\rm{sep }}}}}}{{\delta _L^*}}\frac{{Ma_\infty ^3}}{{{{\left( {\frac{{R{e_L}}}{C}} \right)}^{0.5}}}} = \frac{{4.4P}}{{1 + 0.1P}} $ | (6) |
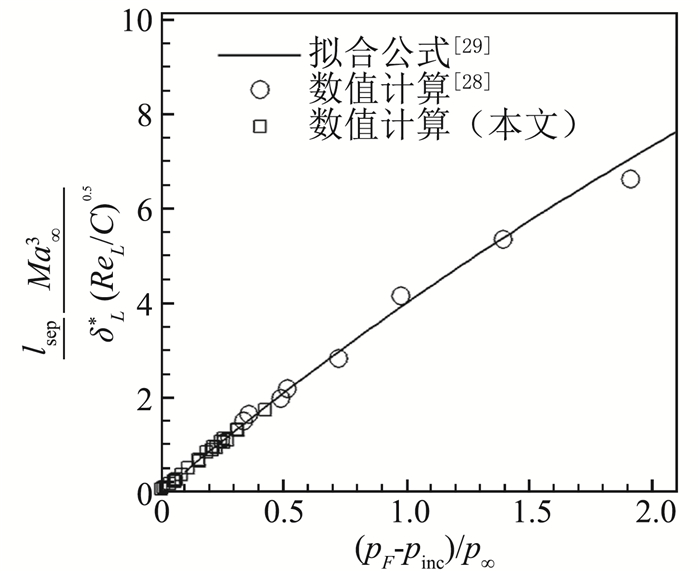
本文运用数值方法并结合文献数据进行验证,如图 4所示。
数值计算数据基本与拟合公式吻合。由于拟合公式适用范围所限,若马赫数较大,其误差将超出工程允许的范围。
2 理论模型 2.1 模型简介基于第1节对激波致边界层分离流场的分析,将局部流场结构进行简化,建立理论模型,如图 5所示。

|
图 5 入射激波致边界层分离流场理论模型 Fig.5 Analytical model of the flow induced by an incident shock wave boundary layer interaction with separation |
首先将分离泡假定为一个三角形。壁面压力分布大致分为如下几个阶段:干扰上游与无干扰平板边界层分布基本一致,分离阶段经历第一个压增,随后为压力平台,再附阶段经历第二个压增,到达压力峰值。由此假设第一个压增完全由分离激波(C2)引起,分离角θS为引起分离激波(C2)的气流偏转角,波后(2)区压力为平台压力。第二个压增完全由再附激波(C6)引起,再附角θR为引起再附激波(C6)的气流偏转角,波前(6)区压力亦为平台压力。入射激波(C1)与分离激波(C2)发生正规相交,产生透射激波(C3)与(C4)以及滑移线(Σ),(R4)反射为膨胀波,(6)区气流转平产生再附激波(C6)。该模型忽略分离激波和再附激波根部的压缩波系以及各激波在穿越边界层时的弯曲,将分离激波及再附激波简化为直接从壁面引出的两道平直斜激波。
以来流(0)区气流状态作为参考,运用极曲线理论描述流场结构,如图 6所示。p0/p0=1, θ0=0°, 因此(0)区状态点位于原点。所有由(0)区穿越斜激波可能达到的状态由极曲线Γ0表征。(0)区气流穿越入射激波(C1)到达(1)区,因此根据区(1)相对于(0)区的压力比以及气流偏转角(此处即为楔角θw,由于气流向下偏转,为负值)可以确定其在极曲线Γ0上的位置。所有由(1)区穿越斜激波可能达到的状态由极曲线Γ1表征。同时,(0)区气流穿越分离激波(C2)到达(2)区,由于假设(2)区压力等于平台压力(即p2=pP),并且(2)区气流必定向上偏转,由此可以确定其在极曲线Γ0上的位置,同时给出分离角θS的大小。所有由(2)区穿越斜激波可能到达的状态由极曲线Γ2表征。入射激波(C1)与分离激波(C2)在H点发生正规相交,产生透射激波(C3),波后(3)区;以及透射激波(C4),波后(4)区。(3)区与(4)区压力相等且气流平行,因此两者状态点位于极曲线Γ1和Γ2的交点上。紧接着,(4)区气流穿越膨胀波到达(6)区,由于假设(6)区压力与(2)区一样,同为平台压力(即p6=pP),因此(6)区状态点位于经过(2)区的等压线(图 6中点划线)与经过(4)区的等熵膨胀极曲线Γ4的(图 6中虚线)的交点处。所有由(6)区穿越斜激波可能达到的状态由极曲线Γ6表征。(6)区气流穿越再附激波(C6)到达(8)区,此时气流转为与壁面平行(即与来流一致,θS=0)。因此(8)区状态点位于极曲线Γ6与竖轴的交点处。

|
图 6 入射激波致边界层分离极曲线示意图 Fig.6 Polar of the flow induced by an incident shock wave boundary layer interaction with separation |
首先,分离激波波后为平台压力,可由自由干扰理论获得。分离角θS和分离激波(C2)波后参数可由激波关系式获得。
| $ \left\{ {\begin{array}{*{20}{l}} {Ma_2^2 = f\left( {M{a_0},{\beta _2}} \right)}\\ {{p_2}/{p_0} = g\left( {M{a_0},{\beta _2}} \right)}\\ {S\left( {M{a_0},{\beta _2},{\theta _s}} \right) = 0} \end{array}} \right. $ | (7) |
式中:
| $ \begin{array}{l} f(Ma,\beta ) \equiv \\ \frac{{M{a^2} + \frac{2}{{\gamma - 1}}}}{{\frac{{2\gamma }}{{\gamma - 1}}M{a^2}{{\sin }^2}\beta - 1}}{\rm{ + }}\frac{{M{a^2}{\rm{co}}{{\rm{s}}^{\rm{2}}}\beta }}{{\frac{{\gamma - 1}}{2}M{a^2}{{\sin }^2}\beta + 1}} \end{array} $ | (8) |
| $ \left\{ {\begin{array}{*{20}{l}} {g\left( {Ma,\beta } \right) \equiv \frac{{2\gamma }}{{\gamma + 1}}M{a^2}{{\sin }^2}\beta - \frac{{\gamma - 1}}{{\gamma + 1}}}\\ {S\left( {Ma,\beta ,\theta } \right) \equiv 2\cot \beta \frac{{M{a^2}{{\sin }^2}\beta - 1}}{{M{a^2}(\gamma + \cos 2\beta ) + 2}} - \tan \theta } \end{array}} \right. $ | (9) |
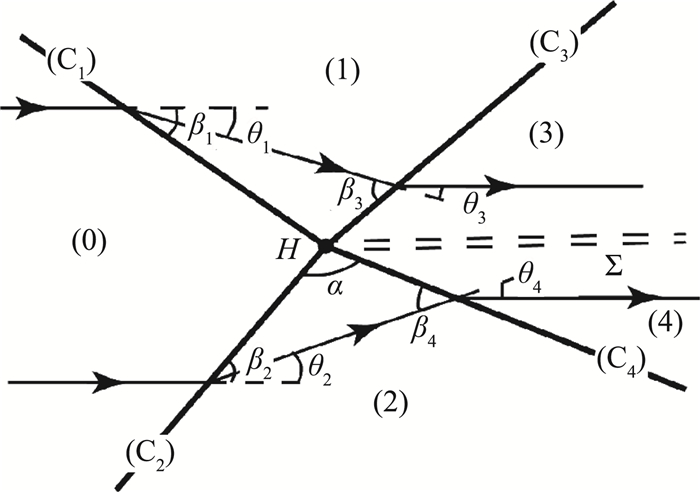
入射激波(C1)与分离激波(C2)发生异侧正规相交,产生透射激波以及滑移线,如图 7所示。
|
图 7 入射激波与分离激波异侧相交 Fig.7 Regular intersection of incident shock and separation shock |
已知(0)区参数以及入射激波(C1),波后参数可由斜激波关系式获得:
| $ \left\{ {\begin{array}{*{20}{l}} {Ma_1^2 = f\left( {M{a_0},{\beta _1}} \right)}\\ {{p_1}/{p_0} = g\left( {M{a_0},{\beta _1}} \right)}\\ {S\left( {M{a_0},{\beta _1},{\theta _1}} \right) = 0} \end{array}} \right. $ | (10) |
(1) 区气流穿越透射激波(C3):
| $ \left\{ {\begin{array}{*{20}{l}} {Ma_1^2 = f\left( {M{a_0},{\beta _1}} \right)}\\ {{p_1}/{p_0} = g\left( {M{a_0},{\beta _1}} \right)}\\ {S\left( {M{a_0},{\beta _1},{\theta _1}} \right) = 0} \end{array}} \right. $ | (11) |
(2) 区气流穿越透射激波(C4):
| $ \left\{ {\begin{array}{*{20}{l}} {Ma_4^2 = f\left( {M{a_2},{\beta _4}} \right)}\\ {{p_4}/{p_2} = g\left( {M{a_2},{\beta _4}} \right)}\\ {S\left( {M{a_2},{\beta _4},{\theta _4}} \right) = 0} \end{array}} \right. $ | (12) |
滑移线两侧气流参数满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _1} - {\theta _3} = - {\theta _2} + {\theta _4}}\\ {{p_3} = {p_4}} \end{array}} \right. $ | (13) |
如图 8所示,(4)区气流穿越分离泡顶点A处的膨胀波(RA)到达(6)区,运用膨胀波关系式:

|
图 8 再附阶段示意图 Fig.8 Schematic of reattachment |
| $ \left\{ {\begin{array}{*{20}{l}} {\nu \left( {M{a_4}} \right) - \nu \left( {M{a_4}} \right) = {\theta _6}}\\ {{p_6}/{p_4} = \chi \left( {M{a_4},M{a_6}} \right)} \end{array}} \right. $ | (14) |
式中:
| $ \begin{array}{l} \nu \left( {Ma} \right) = \sqrt {\frac{{\gamma + 1}}{{\gamma - 1}}} \arctan \sqrt {\frac{{\gamma - 1}}{{\gamma + 1}}\left( {M{a^2} - 1} \right)} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\arctan \sqrt {M{a^2} - 1} \end{array} $ | (15) |
| $ \chi \left( {M{a_0}M{a_1}} \right) = {\left[ {\frac{{2 + (\gamma - 1)Ma_0^2}}{{2 + (\gamma - 1)Ma_1^2}}} \right]^{\frac{\gamma }{{\gamma - 1}}}} $ | (16) |
(6) 区气流穿越再附激波(C6)到达(8)区,运用斜激波关系式:
| $ \left\{ {\begin{array}{*{20}{l}} {Ma_8^2 = f\left( {M{a_6},{\beta _6}} \right)}\\ {{p_8}/{p_6} = g\left( {M{a_6},{\beta _6}} \right)}\\ {S\left( {M{a_6},{\beta _6},{\theta _8}} \right) = 0} \end{array}} \right. $ | (17) |
简化模型假设膨胀波波后(6)区的压力与(2)区一样,等于平台压力,即:
| $ {p_6} = {p_P} $ | (18) |
联立式(7~18)就可以完整求解整个干扰流场波系结构、各区流动参数以及各干扰点位置。
最后求解分离区长度以及几何关系可以进一步确定分离泡个关键点的位置坐标。
如图 9所示,在ΔASR中:

|
图 9 局部结构关键点示意图 Fig.9 Schematic of key points in local flow filed |
| $ {h_{{\rm{sep}}}} = \frac{{{l_{{\rm{sep}}}}}}{{\cot {\theta _S} + \cot {\theta _R}}} $ | (19) |
在ΔSHA中:
| $ \overline {SH} = \overline {SA} \frac{{\sin \left[ {{\rm{ \mathsf{ π} }} - \alpha - \left( {{\beta _2} - {\theta _S}} \right)} \right]}}{{\sin \alpha }} $ | (20) |
式(20)中,SA=hsep/sinθS,在ΔSBH中:
| $ \left\{ {\begin{array}{*{20}{l}} {\overline {HB} = \overline {SH} \sin {\beta _2}}\\ {\overline {SB} = \overline {SH} \cos {\beta _2}} \end{array}} \right. $ | (21) |
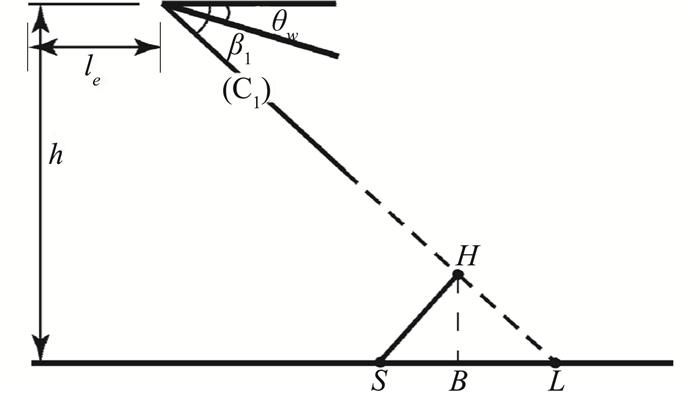
从总体结构来看,如图 10所示,干扰点H的坐标为:
|
图 10 整体结构关键点示意 Fig.10 Schematic of key points in whole flow filed |
| $ \left\{ {\begin{array}{*{20}{l}} {{x_H} = {l_e} + \left( {h - \overline {HB} } \right)\cot {\beta _1}}\\ {{y_H} = \overline {HB} } \end{array}} \right. $ | (22) |
分离点S的坐标:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_S} = {x_H} - \overline {SB} }\\ {{y_S} = 0} \end{array}} \right. $ | (23) |
在ΔASR中,SD= hsep·cotθS,因此分离泡顶点A的坐标:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_A} = {x_S} + \overline {SD} }\\ {{y_A} = {h_{{\rm{sep}}}}} \end{array}} \right. $ | (24) |
再附点R的坐标:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_R} = {x_S} + {l_{{\rm{sep}}}}}\\ {{y_R} = 0} \end{array}} \right. $ | (25) |
由式(19~25)可确定各干扰点的具体位置。
3 结果与分析 3.1 流场结构根据第2节建立的理论模型可以预测入射激波致边界层分离流场,此处用数值计算结果进行验证。
考虑工况Ma∞=2.15、θw=3.75°、ReL=9.91×104, 对比数值计算与理论结果的局部流场结构,如图 11所示。入射激波(C1)、(C1)与分离激波(C2)干扰后的透射激波(C4)以及反射膨胀波(R)等波系位置与形状均与数值计算结果吻合较好,同时分隔流线也与数值结果基本重合。理论预测的分离点位置ST=0.0633525 m,与数值计算结果的分离点位置SC=0.0610716 m相差3.7%;理论预测再附点位置RT=0.0964525 m,与数值计算结果的再附点位置RC=0.097169 m相差仅0.74%。由于理论模型里忽略了边界层的逐渐变形过程,而是将分离点S以及再附点R的气流偏转作为突变处理,因此由分离点S以及再附点R处分别直接引出分离激波(C2)以及再附激波(C6),与数值计算结果中两处形成压缩波系进而合并为激波不同。各区流动参数的预测也相当准确,如表 2所示。

|
图 11 理论预测与数值计算局部流场结构对比 Fig.11 Comparison of wave structure between theoretical prediction and numerical result |
| 表 2 理论预测与数值计算结果各区流场参数对比 Table 2 Comparison of flow parameters |
|
|
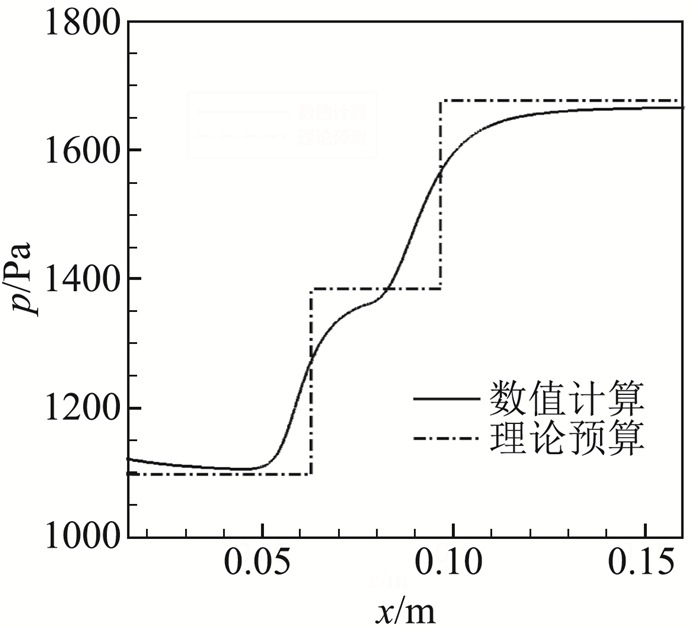
壁面压力分布对比如图 12所示。由于理论模型忽略了激波根部的压缩波系,因此壁面压力分布呈台阶状,不似实际情况的平滑过渡,但是关键位置如干扰起始点、压力平台以及压力峰值均吻合较好,因此整体分布趋势一致。
|
图 12 理论预测与数值计算壁面压力分布对比 Fig.12 Comparison of wall pressure distribution between theoretical prediction and numerical result |
运用该理论模型可进行参数化分析,例如分离泡高度。
考虑工况Ma∞=2.15, θw=3.75°和ReL=9.91×104,根据式(3)可知无干扰情况下入射点xL处的边界层位移厚度为9.1873×10-4m。而理论模型预测的分离泡的高度为1.0524×10-3m,相比没有考虑干扰情况增厚的14.5%。此处考虑来流马赫数、飞行高度以及气流偏转角对分离泡高度的影响,工况列于表 3。分离泡高度与分离角及分离区长度直接相关,分离角越大或者分离区长度越长则分离泡高度越大。而分离角与分离区长度主要由来流参数(包括来流马赫数与压力或者飞行高度)和压缩角确定。
| 表 3 分离角参数化分析的工况 Table 3 Condition for parametric analysis |
|
|
对于表 3中的工况1,在相同的外压缩角以及飞行高度下,来流马赫数的影响如图 13所示。随着马赫数(2≤Ma∞≤6)的增大,分离泡的高度先略微降低随后增大。这是由于随着马赫数的增大,平台压力缓慢减小(接近正比于Ma-1/2),分离角也随之缓慢减小;而总压增随着马赫数的增大迅速增大,导致分离区长迅速增长。两者相互制约,小Ma时,分离区长度变化较小,分离角的变化起主导因素,因此分离区高度有轻微的降低;大Ma时,分离区长度变化剧烈,起主导因素,因此分离区高度随马赫数的增大逐渐增大。

|
图 13 分离泡高度随来流马赫数的变化 Fig.13 Influence of incoming Mach number |
对于表 3中的工况2,在2°~15°范围内,在相同的来流马赫数以及飞行高度下,分离泡高度是入射激波气流偏转角的增函数,如图 14所示。根据自由干扰理论,平台压力基本不随外压缩角变化,因而分离角也基本不变。而总压增随着外压缩角的增大而增大,因此分离泡高度也随之单调增大。

|
图 14 分离泡高度随外压缩角的变化 Fig.14 Influence of flow deflection for incident shock |
对于表 3中的工况3,保持来流马赫数以及外压缩角不变,在20 km到50 km范围内,分离泡高度随飞行高度的升高而增大,在30 km高度时略有减小,如图 15所示。由自由干扰理论结合激波关系式可知,来流压力的降低并不会改变分离角的大小,但引起初始分离的pinc随之显著降低,造成分离区长度增大,因而分离泡高度增大。30 km高度处压力并未平缓降低,而是出现小的增加,因此分离区高度也略有减小。

|
图 15 分离泡高度随飞行高度的变化 Fig.15 Influence of flight altitude |
本文针对激波致边界层分离流场建立了理论预测模型。将分离泡简化为三角形,总压增分为分离阶段以及再附阶段两部分。假设分离阶段的压增完全由分离激波完成,分离角为引起分离激波的气流偏转角;再附阶段的压增完全由再附激波完成,再附角为引起再附激波的气流偏转角。分离激波与再附激波之间的壁面压力一直为平台压力,并运用极曲线方法描述了该局部流场波系结构。该模型可以给出包括分离激波、反射膨胀波以及再附激波等波系结构的位置和形状以及各区流动参数,并得到了很好的CFD验证。运用该理论模型,发现分离泡高度随来流马赫数的增大先略有减小再增大,同时是外压缩角以及飞行高度的增函数。该模型忽略分离激波和再附激波根部的压缩波系以及各激波在穿越边界层时的弯曲,将分离激波及再附激波简化为直接从壁面引出的两道平直斜激波。
本文所建立的理论模型是对真实流动结构进行了一定简化,后续还有以下工作可考虑开展:
(1) 本文模型忽略了分离激波和再附激波根部的压缩波系以及各激波在穿越边界层时发生的弯曲。可以将Henderson[30]的方法添加到模型中,将边界层分层,建立更为详细的理论模型。
(2) 本文采用的是理想气体模型,对于高超声速流动,伴随高温真实气体效应,可以采用考虑复杂化学反应的气体模型,其对波系结构以及流动参数均会产生影响。
| [1] |
Stanford Flow Physics and Computational Engineering. FPCE research[EB/OL].[2006-02-09]. http://www.stanford.edu/group/fpc/cgi-bin/fpcwiki/Main/Research/
|
| [2] |
FERRI A. Experimental results with airfoils tested in the high-speed tunnel at guidonia[R]. National Advisory Commitee for Aeronautics, 1940. https://digital.library.unt.edu/ark: /67531/metadc63187/
|
| [3] |
FAGE A, SARGENTR F. Shock wave and boundary layer phenomena near a flat surface[C]//Proceedings of the Royal Society of London, Series A: Mathematical and Physical Sciences, 1947, 190(1020): 1-20. https://royalsocietypublishing.org/doi/abs/10.1098/rspa.1947.0058
|
| [4] |
BARRY F W, SHAPIRO A H, NEUMANN E P. The interaction of shock waves with boundary layers on a flat surface[J]. Journal of Aerospace Sciences, 1951, 18(4): 229-238. |
| [5] |
LIEPMANN H W, ROSHKO A, DHAWANS. On reflection of shock waves from boundary layers[R]. NACA Rept. 1100, 1952. https://authors.library.caltech.edu/431/
|
| [6] |
JOHANNESEN N H. Experiments on two-dimensional supersonic flow in corners and over concave surfaces[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1952, 43(340): 568-580. DOI:10.1080/14786440508520212 |
| [7] |
BABINSKY H, HARVEY J K. Shock wave boundary layer interactions[M]. Cambridge University Press, 2011.
|
| [8] |
GREEN J E. Interactions between shock waves and turbulent boundary layers[J]. Progress in Aerospace Sciences, 1970, 11: 235-340. DOI:10.1016/0376-0421(70)90018-7 |
| [9] |
MACCOMACK R W. Numerical solution of the interaction of a shock wave with a laminar boundary layer[J]. Lecture Notes in Physis, 1971, 151-163. |
| [10] |
BEAM R M, WARMING R F. An implicit factored scheme for the compressible Navier-Stokes equation[J]. AIAA J, 1978, 16(4): 393-402. DOI:10.2514/3.60901 |
| [11] |
BODONYI R J, SMITHF T. Shock wave laminar boundary layer interaction in supercritical transonic flow[J]. Computers & Fluids, 1986(2): 92-108. |
| [12] |
MALLINSON S G, GAI S L, MUDFORD N R. The interaction of a shock wave with a laminar boundary layer at a compressing corner in high-enthalpy flows including real gas effects[J]. Journal of Fluid Mechanics, 1997, 342: 1-35. DOI:10.1017/S0022112097005673 |
| [13] |
PRINCE S A, Vannahme M, Stollery J L. Experiments on the hypersonic turbulent shock-wave/boundary-layer interaction and the effects of surface roughness[J]. The Aeronautical Journal, 2005, 109(1094): 177-184. DOI:10.1017/S0001924000000683 |
| [14] |
龚安龙, 刘周, 杨云军, 等. 高超声速激波/边界层干扰流动数值模拟研究[J]. 空气动力学学报, 2014, 32(32): 767-771. GONG A L, LIU Z, YANG Y J, et al. Numerical study on hypersonic double cone separated flow[J]. Acta Aerodynamica Sinica, 2014, 32(06): 767-771. DOI:10.7638/kqdlxxb-2014.0083 (in Chinese) |
| [15] |
赵云飞.高精度方法在激波边界层干扰及转捩问题中的应用研究[D].长沙: 国防科技大学, 2015. ZHAO Y F. Study of shock wave/boundary layer interaction and boundary layer transition using high-order numerical scheme[D]. Changsha: National University of Defense Technology, 2015. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-90002-1017834438.htm |
| [16] |
童福林, 李新亮, 唐志共, 等. 转捩对压缩拐角激波-边界层干扰分离泡的影响[J]. 航空学报, 2016, 37(10): 2909-2921. TONG F L, LI X L, TANG Z G, et al. Transition effect on separation bubble of shock wave/boundary layer interactions in a compression ramp[J]. Acta Aeronautica et AstronauticaSinica, 2016, 37(10): 2909-2921. (in Chinese) |
| [17] |
董祥瑞, 陈耀慧, 董刚, 等. 基于DES方法的高超声速激波-边界层干扰的双微楔控制数值研究[J]. 航空学报, 2016, 37(6): 1771-1780. DONG X R, CHEN Y H, DONG G, et al. DES numerical study of shock wave/boundary layer interactions in hypersonic flows controlled by double micro-ramps[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1771-1780. (in Chinese) |
| [18] |
宋友富, 徐晶磊, 张扬, 等. 压缩拐角激波-边界层干扰的可压缩湍流模型研究[J]. 推进技术, 2017, 38(2): 281-288. SONG Y F, XU J L, ZHANG Y, et al. Research of compressible turbulence model in shock wave/boundary-layer interaction flow at a compression corner[J]. Journal of Propulsion Technology, 2017, 38(2): 281-288. (in Chinese) |
| [19] |
陈宣亮, 郭文, 覃湘桂, 等.高超声速激波边界层干扰脉动压力分析[C]//2017年(第三届)中国航空科学技术大会论文集(上册): 141-146. CHEN X L, GUO W, QIN X G, et al. Hypersonic shock wave boundary layer interaction and fluctuation pressure research[C]//The 3rd China aeronautical science and technology conference proceedings (part one): 141-146. (in Chinese) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGHU201709001027.htm |
| [20] |
王娇, 谭慧俊, 黄河峡. Bump进气道中鼓包诱导的激波-边界层干扰特性[J]. 航空动力学报, 2018, 31(1): 91-107. WANG J, TAN H J, HUANG H X. Shock wave/boundary layer interactions induced by bump in the Bump inlet[J]. Journal of Aerospace Power, 2018, 31(1): 91-107. (in Chinese) |
| [21] |
KOTOV D V, YEE H C, WRAY A, 等. 含激波的湍流流动高精度大涡数值模拟方法(英文)[J]. 空气动力学学报, 2016, 34(2): 190-203. KOTOV D V, YEE H C, WRAY A, et al. High order numerical methods for LES of turbulent flows with shocks[J]. Acta Aerodynamica Sinica, 2016, 34(2): 190-203. DOI:10.7638/kqdlxxb-2016.0009 (in Chinese) |
| [22] |
CHAPMAN D R, KUEHN D K, LARSON H K. Investigation of separated flows in supersonic and subsonic with emphasis on the effect of transition[R]. NACA Report, 1958. https://digital.library.unt.edu/ark: /67531/metadc60772/
|
| [23] |
BURGGRAFO R. Asymptotic theory of separation and reattachment of a laminar boundary layer on a compression ramp[R]. NASA STI/Recon Technical Report N, 1975, 76: 10435. http://adsabs.harvard.edu/abs/1975STIN...7610435B
|
| [24] |
NEILAND V. Flow behind the boundary layer separation point in supersonic stream[J]. Fluid Dynamics, 1971, 6(3): 378-384. |
| [25] |
STEWARTSON K, WILLIAMS P. On self-induced separation Ⅱ[J]. Mathematika, 1973, 20(1): 98-108. DOI:10.1112/S0025579300003673 |
| [26] |
MILLER J H, TANNEHILLJ C, LAWRENCE S L. PNS algorithm for solving supersonic flows with upstream influences[J]. AIAA Journal, 1998, 38: 1837-1845. |
| [27] |
RAMESH M D, TANNEHILL J C. Correlations to predict the streamwise influence regions in supersonic turbulent flows[J]. Journal of Aircraft, 2004, 41(2): 274-283. DOI:10.2514/1.9322 |
| [28] |
KATZER E. On the lengthscales of laminar shock boundary layer interaction[J]. Journal of Fluid Mechanics, 1989, 206: 477-496. DOI:10.1017/S0022112089002375 |
| [29] |
KRISHNAN L, YAO Y, SANDHAM N D, et al. On the response of shock-induced separation bubble to small amplitude disturbances[J]. Modern Physics Letters B, 2005, 19(28n29): 1495-1498. DOI:10.1142/S0217984905009742 |
| [30] |
HENDERSON L F. The reflection of a shock wave at a rigid wall in the presence of a boundary layer[J]. Journal of Fluid Mechanics, 1967, 30(4): 699-722. DOI:10.1017/S0022112067001715 |
 2019, Vol. 37
2019, Vol. 37