2. 北京航空航天大学 航空科学与工程学院, 北京 100191;
3. 华中科技大学 能源与动力工程学院 煤燃烧国家重点实验室, 武汉 430074
2. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, China;
3. State Key Laboratory of Coal Combustion, School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
跨流域流动广泛存在于航空航天工程问题中,如航天器微喷管中的流动[1-2]和航天飞行器的再入过程[3]。流动的跨流域特性可以由克努森数(Kn)表述,其为分子平均自由程和流动特征尺度的比值,因此分子平均自由程和流动特征尺度的变化均会使流动呈现多尺度的特点。前者如,在高空真空环境下,喷管中的流动由连续流过渡到自由分子流;而在海拔100~50 km飞行的再入飞行器,由于钝头体背风面气流急剧膨胀产生低压低密度区,其流动也具有稀薄/连续流共存的跨流域特点。后者如,在临近空间飞行器的前缘、表面微结构以及激波附近[4],特征尺度小于平均自由程,流动在局部是非平衡的,这一多尺度的流动特性显著影响着临近空间飞行器的气动力、热[5-6]。除航空航天工程以外,在微纳尺度的机电器件(MEMS)中,由于微纳器件特征尺度的变化,跨流域流动问题同样广泛存在,如微纳器件壁面附近的流动和催化反应往往也都具有典型的多尺度非平衡流动[7]特点。
当流动的特征尺度相当于气体分子平均自由程量级时,流动处于稀薄流区域,此时分子的间断效应变得显著,Navier-Stokes(N-S)方程的连续性假设失效,因此基于N-S方程的CFD方法无法模拟包含稀薄气体效应的跨流域流动。发展CFD和稀薄气体求解格式的混合方法是一种有效的解决途径[8-10]。但由于两种格式基于不同形式和尺度的控制方程,它们的耦合界面处会遇到数值和物理的困难[11]。其一,是耦合界面位置的选取,物理上要求两种方法的分界面位于近平衡态区域。其二,是微观和宏观计算信息在耦合界面处的传递。特别当稀薄气体求解格式选取随机粒子方法时(如DSMC方法),还需要额外处理粒子方法统计噪声的影响。这些问题在混合算法的发展过程中虽已有改善,但对算法实现仍然提出了较高要求。
如直接从介观统计物理出发,各尺度的气体流动均满足基于气体分子几率密度分布函数的Boltzmann方程。相比于N-S方程,Boltzmann方程对气体流动适用范围更宽泛,从形式上看,其与N-S方程有两点差别:
其一, 该方程不仅描述了流场的时空分布,还包含了气体分子速度在速度空间的分布。因此,对高维速度分布函数(VDF)的求解使动理学方法的计算量远大于传统的CFD格式[12]。具体来说,速度分布函数可以在速度空间中直接离散,通过速度离散坐标点确定性的表示;也可以对速度空间随机采样,通过随机的模拟粒子概率性的表示。前者如离散速度法[13]、Boltzmann方程谱方法[14-15]、离散Galerkin方法[16]、有限差分法[17]等,后者如蒙特卡洛直接模拟方法(DSMC)[18]。相比概率性的随机粒子模拟方法,确定性方法,没有统计涨落,因此对低速的非平衡流动,以及非定常问题具有很好的适用性。但对于高速流动,随着速度相空间增大,确定性方法需要的计算内存急剧增加,需要发展速度空间自适应[19]、无存储[20]、大规模并行计算[21-22]等技术提高计算效率。相反,对概率性的随机粒子方法,随着流动速度增加,统计涨落的影响逐渐减小,计算效率将大大提高。特别的,在包含化学反应、气体离解等复杂物理化学过程的高超声速稀薄气体流动模拟中,以DSMC为代表的随机粒子方法具有显著优势。
其二,Boltzmann方程中除了流动特征尺度外,还包括分子碰撞尺度(如分子平均自由程和平均碰撞时间),气体分子所具有的碰撞松弛演化特性决定了Boltzmann方程碰撞项的刚性较强。因此,对确定性方法,Boltzmann方程显式离散求解的时间步长受到格式稳定性条件的限制,例如对于大尺度非规则尖前缘飞行器绕流,由物形的非规则性网格确定的格式稳定条件时间步长甚至小于气体分子平均碰撞时间[23-24];而对概率性的随机粒子模拟方法,虽然不存在稳定性问题,但由于计算中将分子运动和碰撞解耦求解,当时间步长大于分子平均碰撞时间时,将会引入较大的数值黏性。对Kn数远小于1的连续流动而言,时空步长的限制使直接模拟Boltzmann方程的计算量变得非常巨大。因此,Boltzmann方程计算格式虽然理论上可以模拟多尺度流动,但实际求解跨流域流动时的效率是极低的。
提高Boltzmann方程动理学格式对高超声速复杂飞行器跨流域流动的计算效率有两个主要途径:
一是从碰撞项的物理模型出发,利用Boltzmann模型方程近似处理碰撞项,减小碰撞项的计算量,因为碰撞项是连续流动计算中占比最大的部分。如采用BGK和Fokker-Planck方程:
| $ {S^{({\rm{BGK}})}}(f) = v\left( {{f_e} - f} \right) $ | (1) |
| $ \begin{array}{*{20}{l}} {{S^{{\rm{(Fokker-Planck) }}}}(f) = }\\ {\quad \frac{\partial }{{\partial {c_i}}}\left[ {\zeta \left( {{c_i} - {u_i}} \right)f} \right] + \frac{{{\partial ^2}}}{{\partial {c_i}\partial {c_i}}}\left( {\frac{{\zeta {k_B}T}}{m}f} \right)} \end{array} $ | (2) |
其中:f和fe分别是气体的速度分布函数和平衡态分布,ci和ui分别是气体分子运动速度和宏观流动速度,T为温度,m为分子质量,kB为玻尔兹曼常数,υ和ζ分别是BGK和Fokker-Planck模型的松弛系数。上述两类Boltzmann模型方程利用速度分布函数的碰撞松弛演化特性来近似碰撞过程,对概率性粒子方法,近年来发展了一系列基于Fokker-Planck[25]或者BGK模型[26]的随机粒子方法,并在高速气体流动以及多组分流场的模拟中得到了成功的应用。
二是从碰撞项的求解格式出发,减少Boltzmann方程中碰撞松弛演化特性对数值上时空离散的限制,发展多尺度的动理学方程计算格式[27-28]。如基于随机粒子的多尺度Fokker-Planck[29]、BGK[30]和DSMC[31]方法,和基于离散速度坐标法,对Boltzmann模型方程分别在位置空间、速度空间离散数值求解的GKUA[21-22, 32-33]及利用上述方法离散速度坐标法与BGK型有限体积格式相耦合发展的统一格式UGKS[34-35]、DUGKS[36]等。
本文将从对随机粒子方法模拟得到的气体输运系数离散误差的分析出发,分别介绍基于BGK和Fokker-Planck模型的两类多尺度随机粒子方法。区别于传统的BGK和Fokker-Planck随机粒子方法,多尺度随机粒子方法不仅在分子自由运动主导的稀薄流域,能够模拟分子的间断碰撞效应,反应流动的非平衡现象;在碰撞主导的连续流域,也能够通过在分子运动中耦合连续碰撞作用,反应物理上正确的分布函数演化,满足宏观流体力学方程的输运性质。如Chen等在文献[37]中分析,无论从Kn数还是Ma数的角度,N-S方程主导的黏性流区域在跨流域流动中都是不可忽视的。因此,连续区满足N-S方程的宏观输运性质,可以使气体动理论方法在物理上满足模拟跨流域流动的要求。最后,我们将给出几种随机粒子方法的数值比较分析。
1 随机粒子方法模拟得到的输运系数离散误差 1.1 DSMC方法澳大利亚科学家Bird在20世纪60年代提出的直接模拟Monte Carlo(DSMC)方法是目前解决稀薄气体流动最有力的数值计算工具。DSMC方法采用拉格朗日方法跟踪模拟分子,首先在网格中选取分子碰撞对,其次将分子运动和碰撞解耦处理,其模拟得到的输运系数与网格大小和时间步长有关。利用统计物理的Green-Kubo理论[38],Garcia和Hadjiconstantinou等[39-40]分析了DSMC方法的时空离散误差(Green-Kubo理论将流体的输运系数与平衡态下的时空涨落关联在一起,因此可以分析随机粒子方法模拟得到的气体输运系数的时空离散误差)。以黏性系数为例,当Δ/λ和Δt/τc在1附近,DSMC方法硬球模型的数值黏性与网格大小和时间步长的依赖关系分别为:
| $ \begin{array}{l} {\mu _{{\rm{DSMC}}}} = \frac{5}{{16{\sigma ^2}}}\sqrt {\frac{{m{k_B}T}}{{\rm{ \mathsf{ π} }}}} \left[ {1 + \frac{{32}}{{135{\rm{ \mathsf{ π} }}}}\frac{{{\Delta ^2}}}{{{\lambda ^2}}}} \right]\\ {\mu _{{\rm{DSMC}}}} = \frac{5}{{16{\sigma ^2}}}\sqrt {\frac{{m{k_B}T}}{{\rm{ \mathsf{ π} }}}} \left[ {1 + \frac{{32}}{{150{\rm{ \mathsf{ π} }}}}\frac{{{{\left( {{c_0}\Delta t} \right)}^2}}}{{{\lambda ^2}}}} \right] \end{array} $ | (3) |
其与时间步长和网格大小的平方成正比。式(3)中,σ为碰撞截面,λ和τc分别为平均自由程和平均碰撞时间,Δ和Δt分别为网格大小和时间步长。当DSMC方法的时间步长和网格大小分别和分子平均碰撞时间和平均自由程相当时,数值黏性的相对误差Δμ/μ分别约为5%和10%。因此,为了保证流动物理上的正确性,这就要求DSMC方法的时间步长要比分子平均碰撞时间小,选取碰撞对的距离也要小于分子平均自由程。
1.2 BGK模型随机粒子方法BGK模型的气体输运系数可以根据Chapman-Enskog展开得到[41],同样以黏性系数为例,BGK模型的气体黏性系数为:
| $ {\mu _{{\rm{BGK \;model}}}} = p/v $ | (4) |
其中p为压强。不同于DSMC方法直接求解气体分子的双体碰撞,BGK模型通过分布函数的碰撞松弛演化特性来近似表征Boltzmann方程碰撞项(方程(1)),因此BGK模型方法得到的气体输运系数的空间离散误差小于DSMC方法。但在传统的BGK模型的数值求解中,因BGK模型将其碰撞频率视为常数进行完全积分,假设首先自由对流Δt≫τc的时间,然后以常数碰撞频率松弛至当地平衡态,则BGK模型方法得到的气体黏性正比于时间步长:
| $ {\mu _{{\rm{BGK}}\;{\rm{method}}}} \approx p\Delta t $ | (5) |
Fokker-Planck模型也是采用松弛过程近似Boltzmann方程中的碰撞项。与BGK模型不同的是,Fokker-Planck模型中的松弛过程针对气体分子的速度,而BGK模型针对的是速度分布函数整体。因此物理上,Fokker-Planck方程等价于单个分子运动的Uhlenbeck-Ornstein随机过程[42],分子速度和位移由Langevin方程表征:
| $ \frac{{{\rm{d}}{X_i}}}{{{\rm{d}}t}} = {c_i} $ | (6a) |
| $ \frac{{{\rm{d}}{c_i}}}{{{\rm{d}}t}} = - \zeta \left( {{c_i} - {u_i}} \right) + {\left( {\frac{{2{k_B}\zeta T}}{m}} \right)^{0.5}}\frac{{{\rm{d}}{W_i}(t)}}{{{\rm{d}}t}} $ | (6b) |
其中, ci和Xi分别代表分子速度和位置,Wi(t)代表Wiener过程。Fokker-Planck模型的气体输运系数同样可以根据Chapman-Enskog展开求取[43],如黏性系数为:
| $ {\mu _{{\rm{FP}}\;{\rm{model}}}} = p/\left( {2\zeta } \right) $ | (7) |
Jenny等基于Langevin方程(6)构造了Fokker-Planck模型的积分格式(FPM)[25]。Langevin方程的演化包含了随机粒子当地的宏观平均速度和温度,和其它随机粒子方法一样,FPM方法中假设模拟分子的宏观平均速度和温度为当前时刻值,并显式求解分子运动过程。因此,当Δt>τc时,Fokker-Planck模型积分格式得到的气体黏性将会偏离方程(7)的理论值。通过分析Fokker-Planck方程动量和能量矩方程的积分形式,并利用Green-Kubo理论,可以给出FPM方法得到的气体输运系数与时间离散尺度的解析表达式[29],以黏性为例:
| $ {\mu _{{\rm{FP}}\;{\rm{method}}}} = \frac{p}{\zeta }\left[ {1 - tgh\left( {\frac{{\zeta \Delta t}}{2}} \right)\frac{1}{{\zeta \Delta t}}} \right] $ | (8) |
综上,图 1给出了DSMC、BGK、FPM三种随机粒子方法得到的气体流动数值黏性(Δμ=μBGK/FP method-μ0, μ0为动理学方程的物理黏性)随时间步长变化的曲线。三种方法对应时间步长得到的气体黏性系数分别通过Couette流动计算得到。可以看出,当Δt/τc≫1时,DSMC和BGK方法得到的气体数值黏性与Δt的一次方成正比;在Δt/τc=1附近时,DSMC的结果与Δt的二次方成正比;数值结果与方程(3)和方程(5)的理论预测一致。FPM方法得到的气体数值黏性与时间步长的依赖关系稍复杂,在大时间步长时收敛至2μ0,从图 1可以看出我们给出的解析结果(8)与数值实验相符合。
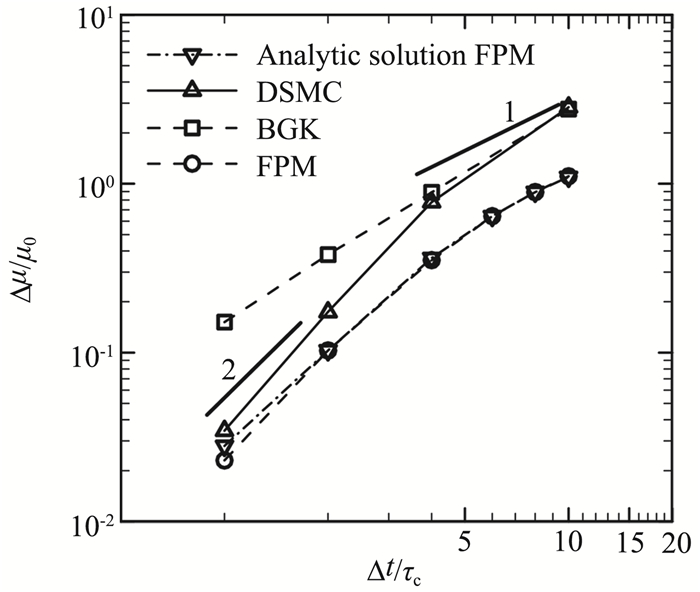
|
图 1 DSMC、BGK、FPM方法黏性系数与时间步长的关系 Fig.1 Relation of the viscosity and time step for the DSMC, BGK and FPM method |
从上节随机粒子方法模拟得到的气体输运系数的时空离散误差的分析可以看出,DSMC、Fokker-Planck或BGK模型随机粒子方法的黏性系数与时间步长相关,对连续流动,随着时间步长的增加这些计算方法并不满足N-S方程的输运性质。造成较大时间离散尺度下数值黏性的主要原因是,这些随机粒子方法求解中将分子运动和碰撞解耦处理。因此,随着时间步长的增加,速度分布函数的演化过程存在显著误差,流场中的动量和能量输运被大大高估了。在小Re数或中等Kn数的区域,跨流域流动中黏性和热传导的作用较为重要,直接采用传统的随机粒子方法显然无法得到与物理流动一致的结果。为了克服随机粒子方法这一困难,我们将分别介绍基于FPM和BGK方法发展的两种适用与跨流域流动计算的多尺度随机粒子方法。
2.1 多尺度Fokker-Planck模型随机粒子方法对连续流,为了构造大时间步长下仍满足N-S方程输运性质的随机粒子方法,需要将分子运动和碰撞过程耦合计算[37]。在Fokker-Planck模型方法中,这一要求可以通过联合求解Langevin方程(6)实现,解析得到Δt时间后分子速度和位移的联合分布函数为:
| $ \begin{array}{l} W\left( {{R_x},{S_x}} \right) = \\ \frac{1}{{2{\rm{ \mathsf{ π} }}{{\left( {FG - {H^2}} \right)}^{0.5}}}}\exp \left[ { - \frac{{R_x^2}}{{2F}} - \frac{{{{\left( {F{S_x} - H{R_x}} \right)}^2}}}{{2F\left( {FG - {H^2}} \right)}}} \right] \end{array} $ | (9) |
其中:
| $ \begin{array}{*{20}{l}} {{R_x} = x - {x_0} - {c_{x0}}\left( {1 - {{\rm{e}}^{ - \xi \Delta t}}} \right)/\zeta }\\ {{S_x} = {c_x} - {c_{x0}}{{\rm{e}}^{ - \zeta \Delta t}}}\\ {F = \frac{{{k_B}T}}{{m{\zeta ^2}}}\left( {4{{\rm{e}}^{ - \zeta \Delta t}} - {{\rm{e}}^{ - 2\zeta \Delta t}} + 2\zeta \Delta t - 3} \right)}\\ {G = \frac{{{k_B}T}}{m}\left( {1 - {{\rm{e}}^{ - 2\zeta \Delta t}}} \right)}\\ {H = \frac{{{k_B}T}}{{m\zeta }}{{\left( {1 - {{\rm{e}}^{ - \zeta \Delta t}}} \right)}^2}} \end{array} $ | (10) |
则Δt时间步长后分子的速度和位移,通过取样联合分布函数(9)得到,这即是FPM积分格式的核心思想。当Δt/τc≫1时,根据方程(9)和式(10),分子的速度分布满足平衡态,而其位移分布满足分子的扩散,满足N-S方程的输运特性。但由方程(8)可知,FPM方法模拟得到的气体输运系数在Δt/τc≪1和Δt/τc≫1两个条件下是不一致的。以黏性系数为例,根据方程(8),两个时间尺度极限下的黏性系数分别为p/(2ζ)和p/ζ。如将Langevin方程(6)中的阻力系数选为恒定值ζ=p/(2μ),正如传统FPM方法的做法,对较大的时间步长是不合适的。因此,多尺度Fokker-Planck模型随机粒子方法(Particle Fokker-Planck Algorithm with Multiscale Temporal Discretization, MTD-FPM)在FPM积分格式基础上,根据其黏性系数与时间步长的表达式(8),选取阻力系数为时间步长的函数ζ(μ, Δt),从而保证对任意的时间步长,随机粒子方法模拟得到的气体输运系数与模型方程的物理值保持一致。类似FPM方法,对等温流动,MTD-FPM方法的主要步骤如下:
(1) 模拟分子速度和位置的初始化;
(2) 根据流场宏观量及式(8),计算阻力系数ζ(μ, Δt);
(3) 根据联合分布函数(9)取样模拟分子Δt时间后分子速度和位移;
(4) 计算补偿压力项对模拟分子速度的贡献,并更新分子速度;
(5) 统计流场宏观量。如未计算结束,从步骤2继续下个时间步循环。
步骤(4)中MTD-FPM方法额外的压力项修正是因为在FPM积分格式中,压力项也是时间步长的函数:
| $ {p_{{\rm{FPM}}}} = \frac{1}{{\Delta t}}\int_{t0}^{{t_0} + \Delta t} {p{\rm{d}}t} = \frac{p}{{\zeta \Delta t}}\left( {1 - {{\rm{e}}^{ - \zeta \Delta t}}} \right) $ | (11) |
当Δt/τc≫1,pFPM→0。假设压力修正项对计算网格内的每个模拟粒子都是相同的,那么,模拟粒子的速度在步骤4后更新为:
| $ {c_{i,n + 1}} = c_i^* - \frac{{\zeta \Delta t + {{\rm{e}}^{ - \zeta \Delta t}} - 1}}{{\zeta \rho }}\frac{{\partial p}}{{\partial {x_i}}} $ | (12) |
其中压力梯度∂p/∂xi由宏观方程差分计算得到。对于非等温流动,MTD-FPM方法的计算步骤也是相似的,具体介绍可以参考文献[29]。
2.2 多尺度BGK模型随机粒子方法和Fokker-Planck模型类似,另一常见的模型方程——BGK模型为:
| $ \frac{{\partial f(c,x,t)}}{{\partial t}} + {c_i}\frac{{\partial f(c,x,t)}}{{\partial {x_i}}} = J(f) $ | (13) |
其中碰撞项J=υ(fe-f)。BGK模型的普朗特数为1,为了得到正确的普朗特数,在计算中一般采用修正后的BGK模型,如Shakhov (SBGK)模型和Ellipsoidal Statistical BGK (ESBGK)模型。ESBGK模型由Holway[44]和Cercignani[45]提出,并满足H定理[46]。本文将重点讨论基于ESBGK模型的多尺度随机粒子方法。
ESBGK模型的碰撞项可写为:
| $ {J_{{\rm{ESBGK}}}} = {v_{{\rm{ES}}}}\left( {{f_G} - f} \right) $ | (14) |
其中υES=Pr·υ,fG为各向异性的Gaussian分布函数:
| $ {f_G} = \rho {\left[ {\frac{1}{{{\rm det}\left( {2{\rm{ \mathsf{ π} }}{\lambda _{ij}}} \right)}}} \right]^{0.5}}\exp \left( { - \frac{1}{2}\lambda _{ij}^{ - 1}{C_i}{C_j}} \right) $ | (15) |
其中, Ci=ci-ui,
| $ {\lambda _{ij}} = RT{\delta _{ij}} + \left( {1 - \frac{1}{{Pr}}} \right)\frac{{{\sigma _{ij}}}}{\rho } $ | (16) |
R=kB/m,σij为剪切应力。ESBGK模型的随机粒子方法(SP-ESBGK)由Gallis、Torczynski[47]发展。SP-ESBGK方法同样将分子对流运动和碰撞解耦处理,由方程(13),SP-ESBGK方法分子对流运动和碰撞松弛步的控制方程可以分别写为,
对流运动:
| $ {\left[ {\frac{{\partial f}}{{\partial t}}} \right]_{{\rm{convection}}}} = - {c_i}\frac{{\partial f}}{{\partial {x_i}}} $ | (17a) |
碰撞松弛:
| $ {\left[ {\frac{{\partial f}}{{\partial t}}} \right]_{{\rm{relaxation}}}} = {v_{{\rm{ES}}}}\left( {{f_G} - f} \right) $ | (17b) |
SP-ESBGK方法的算法实现与DSMC方法类似,唯一区别是碰撞项的处理。根据方程(17b),模拟分子自由运动一个时间步长后,网格中Ns=int{Nc[1-exp(-υESΔt)]}个粒子被随机选中并重新根据Gaussian分布函数(15)取样分子速度;剩余的模拟分子速度保持不变。Nc为网格中的模拟分子个数,“int”为取整操作。因为无需取样双体碰撞,所以对连续流动, SP-ESBGK方法的效率远高于DSMC方法,其主要实现步骤可总结为:
(1) 模拟分子速度和位置的初始化;
(2) 模拟分子位置更新,分子对流,式17(a);
(3) 模拟分子速度更新,分子碰撞,式17(b);
(4) 统计流场宏观量。如未计算结束,从步骤2继续下个时间步循环。
虽然SP-ESBGK方法通过采用近似的碰撞项,提高了对连续流的计算效率,但由于分子运动和碰撞的解耦处理,随着时间步长增加,其时间离散误差将使模拟得到的输运系数远大于物理值(见图 1),因此对黏性和热传导不可忽略的流动区域是不准确的。为了减小时间离散误差,构造满足N-S方程输运性质的ESBGK模型随机粒子方法,我们在原对流运动和碰撞松弛步中分别考虑了它们之间的耦合作用,因此,控制方程(17)需改写为:
| $ {\left[ {\frac{{\partial f}}{{\partial t}}} \right]_{{\rm{convection}}}} = - {c_i}\frac{{\partial f}}{{\partial {x_i}}} + {J_{{\rm{USP - ESBGK}}}} $ | (18a) |
| $ {\left[ {\frac{{\partial f}}{{\partial t}}} \right]_{{\rm{relaxation}}}} = {v_{{\rm{ES}}}}\left( {{f_G} - f} \right) - {J_{{\rm{USP - ESBGK}}}} $ | (18b) |
在多尺度ESBGK随机粒子方法(Unified stochastic particle method with ESBGK model, USP-ESBGK)[30]中我们假设对流步式(18a)的碰撞项为:
| $ {J_{{\rm{USP - ESBGK}}}} = v{P_{ne}}\left( {{f_e} - {f_{\left| {{\rm{Grad}}} \right.}}} \right) $ | (19) |
其中Pne=e-KnGLL, MAX/Knc与当地流动的稀薄程度相关,Knc是Kn数的参考值,KnGLL, MAX是以梯度计算的当地Kn数的最大值[48]。碰撞项(19)中速度分布函数以Grad分布函数近似:
| $ \begin{array}{l} {f_{\left| {{\rm{Grad}}} \right.}} = {f_{\left| {{\rm{13}}} \right.}} = \\ {f_e}\left[ {1 + \frac{{{\sigma _{ik}}}}{{2p}}\frac{{{C_{ < i}}{C_{k > }}}}{\theta } + \frac{2}{5}\frac{{{q_k}}}{{p\theta }}Pr{C_k}\left( {\frac{{{C^2}}}{{2\theta }} - \frac{5}{2}} \right)} \right] \end{array} $ | (20) |
其中θ=kBT/m,qk为热流。
形式上看,方程(18)右端两项将原ESBGK模型的碰撞项分解为两部分,式(18a)的部分表示碰撞项对连续流动的贡献,式(18b)的部分表示剩余对非平衡流动的贡献,而模型方程(18)的多尺度特性可以由Pne表征。当KnGLL, MAX≪1时,将JUSP-ESBGK做Chapman-Enskog展开可以发现其一阶展开部分与连续流下的碰撞项一致:
| $ J_{{\rm{USP}} - {\rm{ESBGK}}}^{(1)} = J_{{\rm{ESBGK}}}^{(1)} $ | (21) |
因此,随机粒子运动过程(18a)中分布函数的演化与BGK方程一致,其输运性质收敛于N-S方程。反之当KnGLL, MAX≫1时,JUSP-ESBGK→0,USP-ESBGK方法的控制方程退化到与传统的SP-ESBGK方法一致,可以准确捕捉小尺度的非平衡流动。
综上,相比于传统的DSMC和SP-ESBGK方法,USP-ESBGK方法是一种适用于对跨流域流动问题的多尺度随机粒子方法。
USP-ESBGK方法与SP-ESBGK方法算法实现的主要区别在对流项式(18a)的求解。数值实现上,USP-ESBGK方法通过引入辅助函数,
| $ \tilde f = f - \frac{{\Delta t}}{2}{J_{{\rm{USP}} - {\rm{ESBGK}}}} $ | (22a) |
和
| $ \hat f = f + \frac{{\Delta t}}{2}{J_{{\rm{USP - ESBGK}}}} $ | (22b) |
并按照梯形公式离散控制方程[36],将对流步式(18a)中对流和碰撞的耦合过程,转化为求解显式的分子对流:
| $ \tilde f\left( {c,{x_{n + 1}},{t_{n + 1}}} \right) = \hat f\left( {c,{x_n},{t_n}} \right) $ | (23) |
因此,类似SP-ESBGK方法,USP-ESBGK方法的主要实现步骤可以概括为:
(1) 模拟分子速度和位置的初始化;
(2) 构造对流项的辅助分布函数,式(23);
(3) 模拟分子位置更新,分子对流,式(24);
(4) 模拟分子速度更新,分子碰撞,式(21b);
(5) 统计流场宏观量。如未计算结束,从步骤2继续下个时间步循环。
步骤(2)中辅助分布函数,可以通过添加满足速度分布Δt/2JUSP-ESBGK的模拟粒子实现。同时,在步骤4的碰撞过程中添加的模拟粒子被平衡态分布吸收,因此在整个模拟过程中,模拟粒子的总数是守恒的。详细的计算过程可参考文献[30]。
2.3 数值算例比较通过两个简单的一维流动,Couette流动和Sod管流,我们将给出DSMC方法与两种多尺度流动随机粒子方法的比较。
2.3.1 Couette流动Couette流动是两个相反运动的平板驱使的定常流动。上、下平板的运动速度分别为正负Uwall=10 m/s,两平板的温度保持Twall=273 K。初始时刻平板间的气体为标准条件(1 atm, 273 K)下的氩气。Couette流动的Kn=λ/H=0.01,H为平板间距。对应不同的时间步长,如表 1,我们分别计算了DSMC、MTD-FPM和USP-ESBGK的剪切应力值,并给出了与时间步长为0.2Δt/τc时DSMC结果的相对误差(见括号)。对较小的时间步长,三种方法给出一致的结果。随着时间步长增加,DSMC的结果逐渐偏离准确值,而MTD-FPM和USP-ESBGK方法的结果并不明显依赖于时间步长选择,对较大的时间步长仍然能够给出正确的剪切应力值。其中MTD-FPM计算结果稍大,这是与其较大的普朗特数有关。对跨流域流动而言,各计算区域的稀薄程度可能相差极大的,相异的Δt/τc使传统随机粒子方法在不同区域具有不一致的输运系数。相反,从算例1可以看出,本文提出的改进的BGK/Fokker-Planck模型随机粒子方法的时间分辨率更高,相比于传统方法具有较小的数值黏性,因此在计算黏性区域不可忽略的多尺度流动时具有显著优势。
| 表 1 Couette流动计算结果比较(单位: N/m2) Table 1 Comparison of Couette flow results (unit: N/m2) |
|
|
最后,我们利用MTD-FPM和USP-ES BGK方法计算典型的一维Sod激波管问题[49]。
选取文献[50]中算例2和算例3,Sod激波管的长度为1 m,左右两端的边界取为开放边界条件。在初始时刻,激波管中间x=0.5 m处有一个密度间断,管中的流体为静止条件。左右两段间断区域的初始温度分别为Tl=Tr=273 K。和文献[51]一致,模拟的时间长度为tfinal =6.8×10-4 s。
其他的计算参数见表 2,其中初始时刻左右两段的密度为ρl和ρr,τc, l为初始时刻激波管左端的平均碰撞时间。两个算例中,Sod管流Kn数分别在0.01 ~0.08和0.001~0.008之间变化,因此其是典型的多尺度流动。
| 表 2 Sod管流动的计算参数 Table 2 Computational parameter for Sod flows |
|
|
图 2和图 3分别给出了算例1和算例2中Sod激波管内tfinal时刻MTD-FPM和USP-ESBGK方法计算的速度、温度和密度分布,其结果与DSMC方法一致[50]。图 4给出了沿管的时间步长与当地平均碰撞时间的比值,可见流场的稀薄程度是沿管长变化的:从左端至右端,流体从连续区域逐渐过渡到稀薄区域。在DSMC方法中,时间步长一般需小于流场中最小的平均碰撞时间,以保证计算得到物理上准确的流场,而MTD-FPM和USP-ESBGK方法中时间步长的选择仅需考虑流动特征时间,并不受分子平均碰撞时间的限制,因此通过选取较大的时间步长,两种多尺度随机粒子方法可以大大提高跨流域流动的计算效率, 例如算例1和算例2中分别选取时间步长为1.5τc, l和4.0τc, l。另外,图 2(b)中,MTD-FPM方法的温度分布与DSMC的结果存在差异,这是因为在Fokker-Planck方程中普朗特数为1.5,不同于DSMC方法中的值,而ESBGK模型具有正确的Pr,因此温度分布同DSMC方法也是一致的。
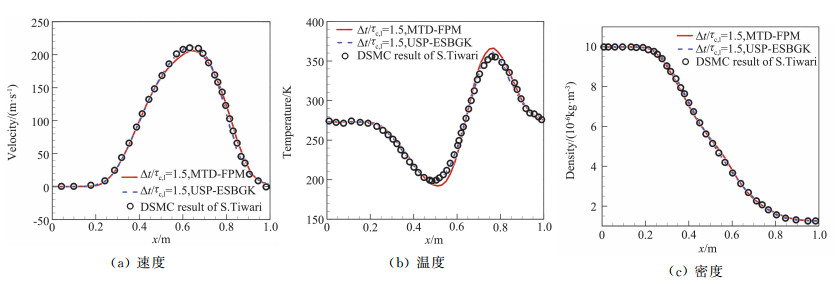
|
图 2 算例1,Sod管流动的速度、温度和密度在tfinal时刻沿管的分布[29-30] Fig.2 Case 1. Velocity, temperature and density at the end time tfinal for Sod flow[29-30] |
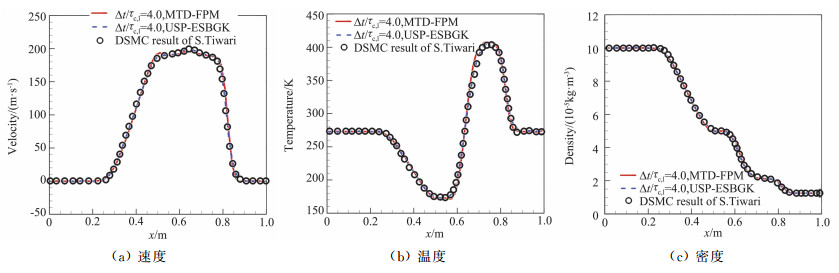
|
图 3 算例2,Sod管流动的速度、温度和密度在tfinal时刻沿管的分布[19-20] Fig.3 Case 2. Velocity, temperature and density at the end time tfinal for Sod flow[19-20] |
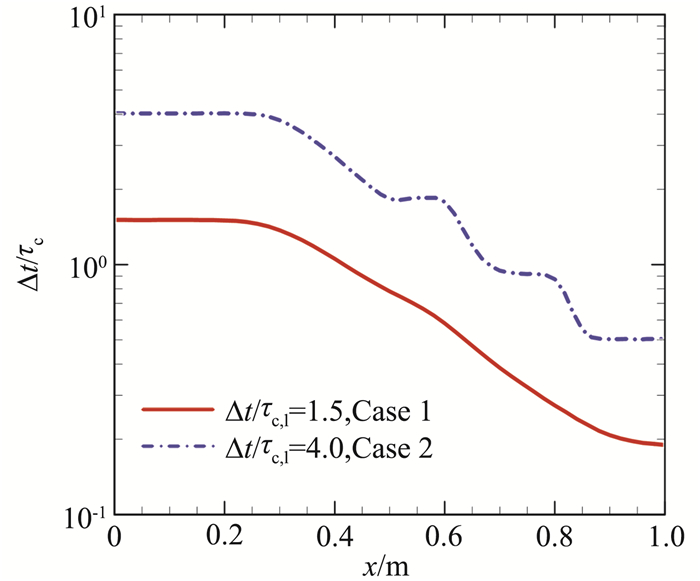
|
图 4 Sod管流动的时间步长与当地分子平均碰撞时间的比值在tfinal时刻沿管的分布[19] Fig.4 The ratio of time step and local mean collision time at the end time tfinal for Sod flows[19] |
本文首先总结了传统随机粒子方法,如DSMC、FPM和BGK等随机粒子方法模拟得到的气体输运系数的时空离散误差。DSMC方法计算得到的输运系数的离散误差与网格大小/分子平均自由程和时间步长/平均碰撞时间的比值相关。而FPM和BGK随机粒子方法由于采用速度分布函数的碰撞松弛演化特性来近似碰撞过程,减小了碰撞项的计算量的同时也降低了对网格的限制,但是因为分子运动和碰撞的解耦求解,它们对时间步长的计算要求依然存在,这影响了传统随机粒子方法模拟跨流域气体流动的计算效率。针对随机粒子方法的这一困难,我们基于Fokker-Planck和BGK模型分别讨论了它们的多尺度算法。该方法的主要思想是在碰撞主导的连续流域,通过在分子自由运动计算中耦合连续碰撞作用,反应物理上正确的分布函数演化过程,从而满足连续流下宏观的输运性质。具体来说,分子运动和碰撞即可以通过模拟分子的运动方程耦合;也可以通过分布函数的动理学方程耦合。前者如Fokker-Planck模型中的Langevin方程,通过积分求解该运动方程,并选取合适的松弛系数,可以构造多尺度时间离散的Fokker-Planck模型方法(MTD-FPM)。后者如BGK模型方程,通过对连续流碰撞项的建模和耦合求解,可以构造多尺度的ESBGK随机粒子方法(USP-ESBGK)。综合看,这两种多尺度粒子方法具有如下优势:
(1) 相较于传统的随机粒子方法,如DSMC方法,它们的网格大小和时间步长无需满足分子碰撞尺度(平均自由程和平均碰撞时间)的限制,并在连续流区域满足宏观流体力学方程的输运性质,具有较小的数值黏性,因此对多尺度流动具有更高的计算效率和分辨率;
(2) 相对于确定性的离散速度坐标方法,它们无需离散巨大的速度空间,概率性的随机粒子模拟方法,更适合跨流域高超声速流动的模拟计算。
(3) 它们在算法实现上与DSMC方法类似,可以同DSMC方法耦合计算,从而方便拓展至包含复杂物理和化学过程的跨流域流动问题。
| [1] |
LA TORRE F, KENJEREŠ S, MOEREL J L, et al. Hybrid simulations of rarefied supersonic gas flows in micro-nozzles[J]. Computers & Fluids, 2011, 49(1): 312-322. |
| [2] |
TITOV E, GALLAGHER-ROGERS A, LEVIN D, et al. Examination of a collision-limiter, DSMC method for predicting micro-propulsion thruster performance[J]. Journal of Propulsion and Power, 2008, 24(2): 311-321. DOI:10.2514/1.28793 |
| [3] |
IVANOV M S, GIMELSHEIN S F. Computational hypersonic rarefied flows[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 469-505. DOI:10.1146/annurev.fluid.30.1.469 |
| [4] |
陈伟芳, 赵文文, 江中正, 等. 稀薄气体动力学矩方法研究综述[J]. 气体物理, 2016, 1(5): 9-24. CHEN W F, ZHAO W W, JIANG Z H, et al. A review of moment equations for rarefied gas dynamics[J]. Physics of Gases, 2016, 1(5): 9-24. (in Chinese) |
| [5] |
罗金玲, 周丹, 康宏琳, 等. 典型气动问题试验方法研究的综述[J]. 空气动力学学报, 2014, 32(5): 600-609. LUO J L, ZHOU D, KANG H G, et al. Summarization of experimental methods associated with typical aerodynamic issues[J]. Acta Aerodynamica Sinica, 2014, 32(5): 600-609. (in Chinese) |
| [6] |
方明, 李志辉, 李中华, 等. 球锥钝头体再入稀薄气体电离过程三维DSMC模拟与验证[J]. 空气动力学学报, 2017, 35(1): 39-45. FANG M, LI Z H, LI Z H, et al. Three dimensional DSMC simulation and validation of rarefied air ionization process for sphere-cone blunt body re-entry[J]. Acta Aerodynamica Sinica, 2017, 35(1): 39-45. DOI:10.7638/kqdlxxb-2015.0086 (in Chinese) |
| [7] |
JU Y, MARUTA K. Microscale combustion:technology development and fundamental research[J]. Progress in Energy and Combustion Science, 2011, 37(6): 669-715. DOI:10.1016/j.pecs.2011.03.001 |
| [8] |
HASHD B, HASSAN H A, Assessment of schemes for coupling Monte Carlo and Navier Stokes solution methods[J]. J Thermophys Heat Transf, 10(1996), 242-249. https://arc.aiaa.org/doi/abs/10.2514/3.781
|
| [9] |
SUN Q, BOYD I D, CANDLER G V. A hybrid continuum/particle approach for modeling rarefied gas flows[J]. J Comput Phys, 194(2004), 256-277. https://www.sciencedirect.com/science/article/pii/S0021999103004698
|
| [10] |
吴俊林, 彭傲平, 李志辉, 等. 分区对接网格在跨流域气体运动论统一算法的应用研究[J]. 空气动力学学报, 2015, 33(5): 624-630. WU J L, PENG A P, LI Z H, et al. Multi-block patched mesh in gas-kinetic unified algorithm[J]. Acta Aerodynamica Sinica, 2015, 33(5): 624-630. (in Chinese) |
| [11] |
WIJESINGHE H S, HADJICONSTANTINOU N G. Discussion of hybrid atomistic-continuum methods for multiscale hydrodynamics[J]. International Journal for Multiscale Computational Engineering, 2004, 2(2): 189-202. DOI:10.1615/IntJMultCompEng.v2.i2.20 |
| [12] |
DIMARCO G, PARESCHI L. Numerical methods for kinetic equations[J]. Acta Numerica, 2014, 23: 369-520. DOI:10.1017/S0962492914000063 |
| [13] |
MIEUSSENS L, Discrete velocity model and implicit scheme for the BGK equation of rarefied gas dynamics[J]. Mathematical Models and Methods in Applied Sciences, 2000, 10(08): 1121-1149. https://www.worldscientific.com/doi/abs/10.1142/S0218202500000562
|
| [14] |
PARESCHI L, PERTHAME B. A spectral method for the homogeneous Boltzmann equation[J]. Transport Theory Statist Phys, 1996, 25: 369-383. DOI:10.1080/00411459608220707 |
| [15] |
WU L, WHITE C, SCANLON T J, et al. Deterministic numerical solutions of the Boltzmann equation using the fast spectral method[J]. Journal of Computational Physics, 2013, 250: 27-52. DOI:10.1016/j.jcp.2013.05.003 |
| [16] |
ALEKSEENKO A, JOSYULA E. Deterministic solution of the spatially homogeneous Boltzmann equation using discontinuous Galerkin discretizations in the velocity space[J]. Journal of Computational Physics, 2014, 272: 170-188. DOI:10.1016/j.jcp.2014.03.031 |
| [17] |
TCHEREMISSINE F G. Solution to the Boltzmann kinetic equation for high-speed flows[J]. Computational Mathematics and Mathematical Physics, 2006, 46(2): 315-329. DOI:10.1134/S0965542506020138 |
| [18] |
BIRD G A. Molecular gas dynamics and direct simulation of gas flows[M]. Oxford: Clarendon Press, 1994.
|
| [19] |
CHEN S, XU K, LEE C, et al. A unified gas kinetic scheme with moving mesh and velocity space adaptation[J]. Journal of Computational Physics, 2012, 231(20): 6643-6664. DOI:10.1016/j.jcp.2012.05.019 |
| [20] |
CHEN S, ZHANG C, ZHU L, et al. A unified implicit scheme for kinetic model equations. Part Ⅰ. Memory reduction technique[J]. Science Bulletin, 2017, 62(2): 119-129. DOI:10.1016/j.scib.2016.12.010 |
| [21] |
LI Z H, PENG A P, ZHANG H X, et al. Rarefied gas flow simulations using high-order gas-kinetic unified algorithms for Boltzmann model equations[J]. Progress in Aerospace Sciences, 2015, 74: 81-113. DOI:10.1016/j.paerosci.2014.12.002 |
| [22] |
李志辉, 吴俊林, 蒋新宇, 等. 跨流域高超声速绕流模型方程并行算法[J]. 航空学报, 2015, 36(1): 201-212. LI Z H, WU J L, JIANG X Y, et al. A massively parallel algorithm for hypersonic covering various flow regimes to solve Boltzmann model equation[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(1): 201-212. (in Chinese) |
| [23] |
LI Z H, FANG M, JIANG X Y, et al. Convergence proof of the DSMC method and the Gas-kinetic Unified Algorithm for the Boltzmann equation[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(2): 404-417. DOI:10.1007/s11433-013-4999-3 |
| [24] |
WU J, LI Z, PENG A, et al. Numerical simulations of unsteady flows from rarefied transition to continuum using gas-kinetic unified algorithm[J]. Advances in Applied Mathematics and Mechanics, 2015, 7(5): 569-596. DOI:10.4208/aamm.2014.m523 |
| [25] |
JENNY P, TORRILHON M, HEINZ S. A solution algorithm for the fluid dynamic equations based on a stochastic model for molecular motion[J]. Journal of Computational Physics, 2010, 229(4): 1077-1098. |
| [26] |
TUMUKLU O, LI Z, LEVIN D A. Particle ellipsoidal statistical Bhatnagar-Gross-Krook approach for simulation of hypersonic shocks[J]. AIAA Journal, 2016. |
| [27] |
FILBET F, JIN S. A class of asymptotic-preserving schemes for kinetic equations and related problems with stiff sources[J]. Journal of Computational Physics, 2010, 229(20): 7625-7648. DOI:10.1016/j.jcp.2010.06.017 |
| [28] |
JIN S, LI Q. A BGK penalization based asymptotic preserving scheme for the multispecies Boltzmann equation[J]. Numerical Methods for Partial Differential Equations, 2013, 29(3): 1056-1080. |
| [29] |
FEI F, LIU Z, ZHANG J, et al. A Particle Fokker-Planck algorithm with multiscale temporal discretization for rarefied and continuum gas flows[J]. Communications in Computational Physics, 2017, 22(2): 338-374. |
| [30] |
FEI F, ZHANG J, LIU Z. A unified stochastic particle Bhatnagar-Gross-Krook method for multiscale gas flows[J]. arXiv: 1808.03801[physics. comp-ph]. 2018. https://www.sciencedirect.com/science/article/pii/S0021999119306771
|
| [31] |
REN W, LIU H, JIN S. An asymptotic-preserving Monte Carlo method for the Boltzmann equation[J]. Journal of Computational Physics, 2014, 276: 380-404. DOI:10.1016/j.jcp.2014.07.029 |
| [32] |
LI Z H, ZHANG H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Journal of Computational Physics, 2004, 193(2): 708-738. DOI:10.1016/j.jcp.2003.08.022 |
| [33] |
李志辉, 张涵信. 稀薄流到连续流的气体运动论统一算法研究[J]. 空气动力学学报, 2003, 21(3): 255-266. LI Z H, ZHANG H X. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum[J]. Acta Aerodynamica Sinica, 2003, 21(3): 255-266. DOI:10.3969/j.issn.0258-1825.2003.03.001 (in Chinese) |
| [34] |
XU K, HUANG J C. A unified gas-kinetic scheme for continuum and rarefied flows[J]. Journal of Computational Physics, 2010, 229(20): 7747-7764. DOI:10.1016/j.jcp.2010.06.032 |
| [35] |
XU K. Direct modeling for computational fluid dynamics: construction and application of unified gas-kinetic schemes[M]. World Scientific, Singapore, 2015.
|
| [36] |
GUO Z, XU K, WANG R. Discrete unified gas kinetic scheme for all Knudsen number flows:low-speed isothermal case[J]. Physical Review E, 2013, 88(3): 033305. DOI:10.1103/PhysRevE.88.033305 |
| [37] |
CHEN S, XU K. A comparative study of an asymptotic preserving scheme and unified gas-kinetic scheme in continuum flow limit[J]. Journal of Computational Physics, 2015, 288: 52-65. DOI:10.1016/j.jcp.2015.02.014 |
| [38] |
ZWANZIG R. Nonequilibrium statistical mechanics[M]. USA: Oxford University Press, 2001.
|
| [39] |
ALEXANDER F J, GARCIA A L, ALDER B J. Cell size dependence of transport coefficients in stochastic particle algorithms[J]. Physics of Fluids, 1998, 10(6): 1540-1542. DOI:10.1063/1.869674 |
| [40] |
HADJICONSTANTINOU N G. Analysis of discretization in the direct simulation Monte Carlo[J]. Physics of Fluids, 2000, 12(10): 2634-2638. DOI:10.1063/1.1289393 |
| [41] |
XU K. A gas-kinetic BGK scheme for the Navier-Stokes equations and its connection with artificial dissipation and Godunov method[J]. Journal of Computational Physics, 2001, 171(1): 289-335. |
| [42] |
CHANDRASEKHAR S. Stochastic problems in physics and astronomy[J]. Reviews of Modern Physics, 1943, 15: 1-89. DOI:10.1103/RevModPhys.15.1 |
| [43] |
MATHIAUD J, MIEUSSENS L. A Fokker-Planck model of the Boltzmann equation with correct Prandtl number[J]. Journal of Statistical Physics, 2016, 162: 397-414. DOI:10.1007/s10955-015-1404-9 |
| [44] |
HOLWAY L. Kinetic theory of shock structure using an ellipsiodal distribution function[C]. Rarefied Gas Dynamics: Proceedings of the 4th International Symposium, Vol. 1, Academic Press, New York, 1965: 193-215. http://adsabs.harvard.edu/abs/1965rgd1.conf..193H
|
| [45] |
CERCIGNANI C. The Boltzmann equation and its applications[M]. Applied Mathematical Sciences, Springer-Verlag, New York, 1988.
|
| [46] |
ANDRIES P, PERTHAME B. The ES-BGK model equation with correct prandtl number[C]//BARTEL T J, GALLIS M A Eds. Proceedings of the 22nd International Symposium on Rarefied Gas Dynamics, Sydney, Australia, vol. 585, AIP Conference Proceedings, Melville, New York (2001), p. 30. http://extras.springer.com/2001/978-0-7354-0025-2/pdfs/585_030.pdf
|
| [47] |
GALLIS M A, TORCZYNSKI J R. The application of the BGK model in particle simulations[C]. 34th AIAA Thermophysics Conference, AIAA 2000-2360, Denver, CO, June 2000. https://digital.library.unt.edu/ark: /67531/metadc716141/m2/1/high_res_d/760783.pdf
|
| [48] |
WANG W L, BOYD I D. Predicting continuum breakdown in hypersonic viscous flows[J]. Physics of Fluids, 2003, 15(1): 91-100. DOI:10.1063/1.1524183 |
| [49] |
SOD G A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J]. Journal of computational physics, 1978, 27(1): 1-31. |
| [50] |
TIWARI S, KLAR A, HARDT S. A particle-particle hybrid method for kinetic and continuum equations[J]. Journal of Computational Physics, 2009, 228(18): 7109-7124. DOI:10.1016/j.jcp.2009.06.019 |
 2019, Vol. 37
2019, Vol. 37

