2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China
自从20世纪中叶计算流体力学(Computational Fluid Dynamics, CFD)诞生以来,随着计算机技术和计算方法的迅速发展,CFD数值模拟技术已经广泛应用于以航空航天为代表的诸多领域,革命性地改变了这些领域内传统的研究和设计方法[1]。但是CFD数值模拟的先天不足在于控制流动的偏微分方程组的可解性以及解的唯一性仍没有得到理论严格证明,因此CFD数值结果的可信度就非常值得关注。
验证与确认(Verification and Validation,V & V)是评价CFD数值模拟结果可信度的重要手段[2]。验证的目的在于验证离散格式、数值方法、程序代码是否正确地离散并求解了控制方程;而确认的意义在于确认所求解的控制方程及边界条件是否真实地反映了实际物理流动问题。
20世纪八九十年代,国外就开始对验证与确认的研究给予高度重视,并逐步开展相关研究工作。1998年,AIAA在总结之前工作的基础上发布了第一部系统阐述CFD验证与确认的指南[3]。而国内在验证与确认研究方面起步较晚,2007年,有学者建议在国内广泛开展验证与确认研究,提升国内CFD应用的可信度[4]。
在CFD数值模拟精度的验证工作中,主要有两种手段:第一种即通过采用精确解方法[5-6]或制造解方法[7-8],结合网格收敛性测试研究微分方程的求解精度及数值精度阶,验证算法或者求解代码的正确性。第二种则是通过Richardson插值法[9-10]结合网格收敛性研究进行复杂问题的CFD数值模拟精度验证。而计算结果的确认,一般采用与高可信度的风洞实验或飞行试验结果进行对比,确认计算模型的合理性和准确性。
网格收敛性研究是CFD数值模拟精度验证必不可少的手段。网格收敛性研究[11]通常是在一系列依次加密的网格上进行数值模拟,并考察计算结果随网格加密的收敛性;严格的网格收敛性研究要求网格自相似加密,即在加密过程中,不改变网格拓扑和网格质量,这样才能保证计算结果仅仅只受网格尺度的影响。但是自相似加密仅仅能够在简单、规则的网格上实现;在一般的网格上,如无黏流模拟中使用的不规则三角形网格,特别是黏性流模拟使用的物面法向存在增长率的各向异性拉伸网格,均难以实现严格的网格自相似加密。这样将导致无法进行严格的网格收敛性测试,如果网格加密不恰当,甚至可能无法得到网格收敛解。
在这样的背景下,Hebert等[12]提出基于网格缩小(Downscaling, DS)的网格收敛性研究方法,并分析了DS方法的优缺点。Diskin等[13]将DS方法应用于一般非结构网格上有限体积离散格式截断误差和离散误差的网格收敛性研究。除此之外,DS方法的应用并不多见。
考虑到黏性流动模拟精度一直是CFD工程应用关注的重点问题之一,以往的研究往往按照一定的规范生成粗中密三套网格,结合Richardson外插法进行网格收敛性研究,这种方法能够在复杂外形上进行网格收敛性研究,但是由于这些网格加密并不自相似,因此并不能对数值算法的精度阶做出严格判断。
本文针对难以实现自相似加密的非结构网格,在典型的各向同性和各向异性拉伸网格上,利用网格缩小精度测试方法分别考察梯度重构精度以及制造解流动模拟精度,验证网格缩小精度测试方法与网格加密精度测试方法及理论分析的一致性。然后将网格缩小精度测试方法应用到各向异性拉伸网格黏性制造解流动精度测试中考察其优势。最后还在各向异性拉伸网格上初步考察了梯度重构方法、网格类型对制造解流动模拟精度的影响。
1 数值精度测试方法离散方法的数值精度由数值误差(Numerical error, N.E.)定量衡量,在不考虑机器舍入误差(Round-off error, R.E.)时,数值误差等于离散误差(Discretization error, D.E.)。
| $ \mathrm{N.E.}=\mathrm{D.E.}+\mathrm{R.E.} \approx \mathrm{D.E.} $ | (1) |
离散误差产生的原因则是由方程的截断误差以及边界条件的离散误差直接导致。通常,对于精度阶达到p阶的离散方法,其离散误差与网格尺度之间存在以下定量关系:
| $ f_{\text {numerical }}=f_{\text {exact }}+O\left(h^{p}\right) $ | (2) |
| $ \mathrm{D.E.}=O\left(h^{p}\right)=f_{\text {numerical }}-f_{\text {exact }} $ | (3) |
式中h为网格全局尺度,可以定义为[14]:
| $ h=\left(\frac{V_{\text {total }}}{n_{\text {dof }}}\right)^{\frac{1}{d}} $ | (4) |
式中:Vtotal为计算域内所有单元的体积之和,ndof为计算域内自由度数。对于格心型格式,ndof为单元数,d为计算域空间维数。
在本文中,不管是考察梯度重构精度还是制造解流动模拟精度,均是考察离散误差随网格尺度的变化情况,考察数值精度阶是否与理论精度阶吻合,以及不同方法离散误差的大小比较。
在两套依次加密的网格上比较离散误差随网格尺度h的变化,由式(2)、式(3)可以得到数值精度阶的计算公式:
| $ p=\frac{\ln \left(\frac{E_{2}}{E_{1}}\right)}{\ln \left(\frac{h_{2}}{h_{1}}\right)} $ | (5) |
式中:E1和E2分别为加密前后计算域内统计意义的数值误差,本文考虑离散误差的L1模,即平均值,h1和h2分别为加密前后计算域内网格尺度。
1.1 网格加密精度测试方法严格的网格收敛性测试不单要求网格全局尺度(式(4))按照一定比例进行缩小,更要求计算域内相应局部网格尺度(如矩形网格的hx和hy)按照统一的比例c进行缩小,以保证每个网格单元在加密的过程中保持其原有的形状,即网格自相似加密,这样才能保证在统计误差计算精度阶(式(5))时,两套网格之间相应网格尺度之比h2/h1=c为常数,而不是随着网格单元变化的值,这样才能得到准确的全局数值精度阶。
对于常规的网格收敛性测试,譬如在二维各向同性矩形网格上常常通过将边界上的节点数加倍来实现网格加密一倍;对于二维各向同性三角形网格,则将每个三角形单元每边的中点连起来,将原三角形单元剖分成4个自相似的三角形单元,此时网格单元数增加到原来的4倍,相应三维情况网格单元数增加到原来的8倍(金字塔单元为10倍)。比如,对于y方向拉伸比(Stretching Ratio, 或增长率)r=1的无拉伸矩形网格,网格数量为10×10,则将网格数量增加为20×20则可以实现网格加密一倍的目的,如图 1所示。

|
图 1 传统网格加密方法示意图 Fig.1 Schematic diagram of traditional mesh refinement |
相反,在遇到各向异性拉伸网格时,由于拉伸比的存在,导致不能简单地通过将节点数加倍来实现网格尺度的统一减小。比如,对于长细比AR=1×102,y方向拉伸比r=1.4,网格数量为20×20的各向异性拉伸网格不能通过将网格数量增加为40×40来实现网格加密一倍、网格尺度减小一倍的目的。在一般的非结构网格上,尤其是在各向异性拉伸网格上,通过传统的自适应方法来加密网格的方法都无法实现严格的网格自相似加密,从而导致测得的数值精度阶不准确。
1.2 网格缩小精度测试方法网格缩小精度测试方法不是通过增加网格点数来减小局部网格尺度,而是直接将原有网格进行缩小。比如,原来在[0, 1]范围内均匀分布10个单元的一维网格,网格尺度为0.1。传统网格加密方法是将网格节点数增加到21,此时单元数增加一倍,网格尺度减小为0.05;而网格缩小方法则是直接将[0, 1]范围的10个单元整体缩小一倍,计算域缩小到[0, 0.5]的范围内,网格单元数不变,网格尺度同样减小为0.05。
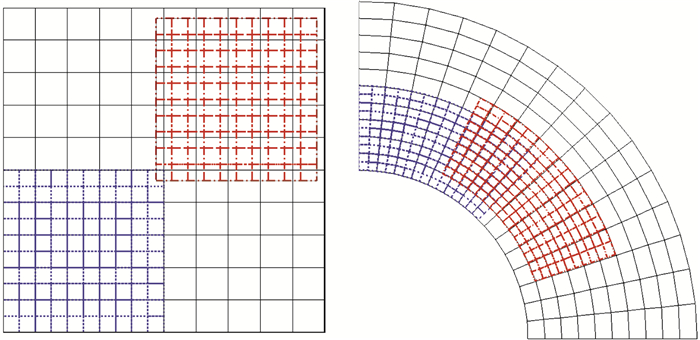
但是,由于网格缩小后,新计算域缩小为原计算域的一部分,因此在统计误差时,如果仅仅统计新计算域上的误差,那么会导致网格缩小前后误差统计区域发生变化,缩小网格上统计得到的误差不完整。因此,考虑将缩小后的网格在初始计算域范围内进行随机平移,取多个在初始计算域内随机平移的网格样本,使样本网格叠加后覆盖的计算域与初始计算域相同,平均统计所有样本网格上的计算误差,得到新网格上的误差。图 2给出了网格缩小精度测试示意图,蓝色虚线网格为缩小一倍的网格,红色点画线网格为随机平移后的一个误差统计样本。
|
图 2 网格缩小精度测试方法示意图 Fig.2 Schematic diagram of mesh downscaling accuracy tests |
由以上的分析可以看到,与传统网格加密方法相比,网格缩小精度测试具有以下优点:(1)适用于难以进行严格自相似加密的一般非结构网格;(2)容易实现并行操作,多个样本可以同时计算;(3)网格量不大,传统加密方法网格量呈4倍(二维)或者8倍(三维)增加,但是DS精度测试方法网格量保持不变;(4)不改变初始网格的拓扑和网格质量。
另一方面,尽管网格缩小精度测试方法在一般的非结构网格上存在一些优势,但是也存在以下一些缺点,比如:(1)重复考虑边界,Dirichlet精确边界条件的施加可能会使流动模拟误差降低;(2) DS方法认为各个网格样本之间的误差是独立的,但实际上,不同样本之间的误差会互相影响;(3)虽然多个样本可以并行操作,但是总计算量较大。
2 DS精度测试方法的验证由上述的分析可知,DS网格样本数量要足够大,以满足“样本网格覆盖的计算域与初始计算域相同”的要求。但是在流动模拟精度测试时,也要注意到,每个样本网格上的数值模拟均采用了精确的Dirichlet边界条件,样本数量过多不仅可能使样本统计的误差低于真实误差,也增加了计算量。通过与传统网格加密方法对比验证,本文所有的DS精度测试均取100个样本。事实上,我们比较过不同样本数的影响,发现样本数大于50后,样本数量对计算结果基本没有影响。由于验证过程比较简单,加之篇幅限制,在此不再赘述。
本节主要考察3种情况:各向同性网格梯度重构精度测试、各向异性拉伸网格梯度重构精度测试、各向同性网格制造解流动精度测试[15],将DS精度测试结果与传统网格加密精度测试结果及附录中的梯度重构模板理论分析结果进行对比,验证网格缩小精度测试方法在各向同性网格、各向异性网格上精度测试结果的准确性。
2.1 各向同性网格梯度重构精度梯度重构采用的测试函数形式为:
| $ \begin{aligned} f(x, y) &=x+y+C_{x} \sin \left(\frac{{\rm{ \mathsf{ π} }} x}{L_{x \text { ret }}}\right)+\\ & C_{y} \sin \left(\frac{{\rm{ \mathsf{ π} }} y}{L_{y \text {ref }}}\right)+C_{x y} \cos \left(\frac{{\rm{ \mathsf{ π} }} x y}{L_{x \text { rel }} L_{y\text {ref }}}\right) \end{aligned} $ | (6) |
该流场函数包含参考尺度Lxref、Lyref,加权系数Cx、Cy、Cxy以及线性项以确保梯度场不存在零点,可以模拟多种光滑的梯度场,可根据不同的测试需求进行选择参考尺度及加权系数。本文取Cx=Cy=Cxy=1.0,Lxref=Lyref=30。
本文重点考察基于格林-高斯(Green-Gauss)公式的梯度重构GG-Cell方法[15-17],该方法面心值采用单元值算术平均求解,在非规则网格上精度会降阶至0阶[17];以及采用基本模板、加权的最小二乘梯度重构方法,记为WLSQ-basic[15-18]。
分别采用传统网格加密方法和网格缩小方法测试GG-Cell梯度重构方法在以下两种网格(图 3)上的精度及精度阶。
|
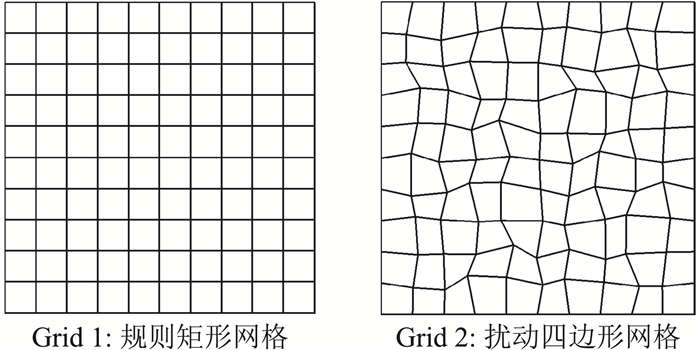
图 3 精度测试各向同性网格 Fig.3 Isotropic grids for accuracy tests |
(1) Grid 1矩形网格:传统网格加密方法采用5套依次加密的矩形网格,网格数量分别为20×20,40×40,80×80,160×160,320×320;DS测试方法的初始网格为20×20。
(2) Grid 2扰动四边形网格:即在矩形网格的基础上,引入网格节点位置的随机扰动,随机扰动量定义为rh/4,其中r是[-1, 1]区间内的随机数,h是局部网格尺度。
传统网格加密方法和DS方法测试得到的x方向梯度离散误差如表 1和表 2所示。
| 表 1 网格加密精度测试与DS精度测试离散误差的比较(Grid 1:规则矩形网格) Table 1 Comparison between mesh refinement tests and DS tests (discretization error of x-direction gradient on Grid 1) |
|
|
| 表 2 网格加密精度测试与DS精度测试离散误差的比较(Grid 2:扰动四边形网格) Table 2 Comparison between mesh refinement tests and DS tests (discretization error of x-direction gradient on Grid 2) |
|
|
结果显示,DS方法的离散误差略小于网格加密方法的误差,这是因为尽管DS方法样本数量较大,但是缩小后的网格样本并不一定能够完全覆盖初始计算域,即DS方法统计误差的区域与网格加密方法统计误差的区域存在一定差异,因此统计到的误差也存在一定的差异。但是这并不影响对精度高低的判断以及数值精度阶的计算,如在矩形网格Grid 1上,如表 1所示,两种方法测得的精度阶(按式(5)计算)均为2阶。而在扰动网格Grid 2上,如表 2所示,两种方法测得的精度阶均为0阶,其主要原因是在扰动网格上面心值插值精度无法达到二阶。文献[17]对GG-Cell方法在扰动网格上精度降阶的原因做了详细解释,在此不再赘述。因此,在各向同性网格梯度重构精度测试中,DS精度测试方法能够得到与传统网格加密方法一致的结果。
2.2 各向异性拉伸网格梯度重构精度正如第1节中所述,对于各向异性的拉伸网格,无法通过加密网格点数来实现严格的网格自相似加密,从而导致无法通过传统的网格加密方法来准确测试各向异性拉伸网格上各种离散格式的精度阶。
在此,为说明传统网格加密方法在各向异性拉伸网格上无法准确测试方法的精度阶,以下给出采用传统网格加密方法测试得到的离散误差和精度阶。传统网格加密方法采用5套依次加密的各向异性拉伸矩形网格,第一层网格长细比AR=1×102,网格数量分别为20×20,40×40,80×80,160×160,320×320,保持计算域大小不变,显然这样在加密的过程中,网格的拉伸比r会发生改变,各套网格的拉伸比分别为:r=1.4,r=1.18,r=1.085,r=1.04,r=1.02,其中第一套20×20的网格如图 4所示。

|
图 4 精度测试的各向异性拉伸矩形网格 Fig.4 Anisotropic stretched quadrilateral grids for accuracy tests |
表 3和表 4分别给出了GG-Cell梯度重构和WLSQ-basic梯度重构方法在各向异性拉伸网格上的离散误差和精度阶,测试方法为网格加密方法。
| 表 3 网格加密精度测试的离散误差与精度阶(GG-Cell) Table 3 Discretization error and accuracy order of mesh refinement tests (GG-Cell) |
|
|
| 表 4 网格加密精度测试的离散误差与精度阶(WLSQ-basic) Table 4 Discretization error and accuracy order of mesh refinement tests (WLSQ-basic) |
|
|
结果显示GG-Cell和WLSQ-basic方法在x、y两个方向均能达到二阶精度,显然,该结果与附录中各向异性梯度重构模板分析的结论不一致,模板分析结果显示GG-Cell方法在x方向可以达到二阶精度,但是在y方向降阶至0阶精度;WLSQ-basic方法在x方向可以达到二阶精度,但是在y方向也只能达到一阶精度。可以看到,传统网格加密方法在各向异性拉伸网格上是不适用的,测得的结果也是错误的。
由于传统方法在各向异性拉伸网格上不适用,因此以下采用20×20、第一层网格长细比AR=102、拉伸比r=1.4的各向异性拉伸矩形网格作为初始网格,对GG-Cell梯度重构方法和WLSQ-basic方法进行DS精度测试。测试函数仍然为光滑非线性函数式(6)。
表 5和表 6分别给出了GG-Cell梯度重构方法和WLSQ-basic梯度重构方法在各向异性拉伸矩形网格上的离散误差和精度阶。结果显示,在x方向,GG-Cell和WLSQ-basic均能达到2阶精度;而在y方向,GG-Cell降阶至0阶精度,而WLSQ-basic仍然保持1阶精度。这与附录中的模板分析结果是完全一致的,因此这体现出DS方法在各向异性拉伸网格计算精度测试与验证上的优势。
| 表 5 DS精度测试的离散误差与精度阶(GG-Cell) Table 5 Discretization error and accuracy order of DS tests (GG-Cell) |
|
|
| 表 6 DS精度测试的离散误差与精度阶(WLSQ-basic) Table 6 Discretization error and accuracy order of DS tests (WLSQ-basic) |
|
|
制造解方法[7-8]是验证的重要手段,与精确解方法需要确定控制方程组的精确解(解析解)不同,制造解方法通过人为设计“制造解”,将制造解代入原始的控制方程得到修正的控制方程,制造解即为修正方程的精确解,数值求解修正控制方程得到数值解,通过比较数值解与制造解的差值即可量化离散误差。文献[15]对制造解方法在代码验证、精度分析、边界条件验证等方面的应用作了详细描述,并实现了分量制造解方法和标量制造解方法。
| $ \begin{aligned} \rho(x, y) &=\rho_{0}+\rho_{x} \sin \left(\frac{\alpha_{\rho x} {\rm{ \mathsf{ π} }} x}{L}\right)+\\ & \rho_{y} \sin \left(\frac{\alpha_{\rho y} {\rm{ \mathsf{ π} }} y}{L}\right)+\rho_{x y} \cos \left(\frac{\alpha_{\rho x y} {\rm{ \mathsf{ π} }} x y}{L^{2}}\right) \\ u(x, y) &=u_{0}+u_{x} \sin \left(\frac{\alpha_{u x} {\rm{ \mathsf{ π} }} x}{L}\right)+ \\ & u_{y} \sin \left(\frac{\alpha_{u y} {\rm{ \mathsf{ π} }} y}{L}\right) +u_{x y} \cos \left(\frac{\alpha_{u x y} {\rm{ \mathsf{ π} }} x y}{L^{2}}\right) \\ v(x, y) &=v_{0}+v_{x} \sin \left(\frac{\alpha_{v x} {\rm{ \mathsf{ π} }} x}{L}\right)+\\ & v_{y} \sin \left(\frac{\alpha_{v y} {\rm{ \mathsf{ π} }} y}{L}\right)+v_{x y} \cos \left(\frac{\alpha_{ {vxy}} {\rm{ \mathsf{ π} }} x y}{L^{2}}\right) \\ P(x, y) &=P_{0}+P_{x} \sin \left(\frac{\alpha_{P x} {\rm{ \mathsf{ π} }} x}{L}\right)+\\ & P_{y} \sin \left(\frac{\alpha_{P y} {\rm{ \mathsf{ π} }} y}{L}\right)+P_{x y} \cos \left(\frac{\alpha_{P x y} {\rm{ \mathsf{ π} }} x y}{L^{2}}\right) \end{aligned} $ | (7) |
本文采用2.1节中图 3所示的矩形网格Grid 1和扰动四边形Grid 2,采用Euler分量制造解进行精度测试,制造解形式为式(7),采用的是“名义”上二阶精度的有限体积格式,即网格交界面上的物理量通过单元中心的物理量平均值线性展开得到。方法具体实现可参考文献[15, 19]。本算例梯度重构方法采用GG-Cell方法,无黏通量格式选择Roe格式。比较传统网格加密方法与DS精度测试得到的密度离散误差和精度阶。
表 7和表 8分别给出了矩形网格(Grid 1)和扰动四边形(Grid 2)上网格加密精度测试及网格缩小精度测试得到的密度离散误差及相应精度阶。结果显示在规则矩形网格上,制造解模拟精度能够达到二阶精度,而在扰动网格上,流动模拟精度降阶至一阶精度,网格加密精度测试与DS精度测试得到完全相同的精度阶;在离散误差的绝对大小上,DS方法与传统网格加密方法也比较接近,这进一步证实了DS方法在流动模拟精度测试上的有效性。扰动网格上流动模拟精度降阶是因为GG-Cell梯度重构在扰动网格上精度下降至0阶,详细分析可参考文献[17]。
| 表 7 网格加密精度测试与DS精度测试的比较(Grid 1) Table 7 Comparison between mesh refinement tests and DS tests (density discretization error of Euler manufactured solution on Grid 1) |
|
|
| 表 8 网格加密精度测试与DS精度测试的比较(Grid 2) Table 8 Comparison between mesh refinement tests and DS tests (density discretization error of Euler manufactured solution on Grid 2) |
|
|
经过第2节中三个算例的验证,证实了DS精度测试方法在各向同性网格和各向异性网格上的可行性和有效性,以下将DS精度测试方法应用于图 4所示的各向异性拉伸矩形网格,对其进行对流扩散方程的标量制造解[15]DS精度测试,采用对流扩散方程是为了考虑扩散项,即黏性项的作用。对流扩散方程形式为式(8),各项系数为a=b=c=1,ν=1×10-4,标量制造解形式为式(9)。
| $ \frac{\partial \phi}{\partial t}+\boldsymbol{A} \cdot \nabla \phi-\nu \nabla^{2} \phi=S $ | (8) |
式中ϕ为任意标量场,A=(a, b, c),A和ν分别为线性对流项和线性扩散项的常系数。
| $ \begin{aligned} \phi(x, y) &=\phi_{0}+\phi_{x} \sin \left(\frac{\alpha_{\phi x} {\rm{ \mathsf{ π} }} x}{L}\right)+\\ & \phi_{y} \sin \left(\frac{\alpha_{\phi y} {\rm{ \mathsf{ π} }} y}{L}\right)+\phi_{x y} \cos \left(\frac{\alpha_{\phi x y} {\rm{ \mathsf{ π} }} x y}{L^{2}}\right) \end{aligned} $ | (9) |
梯度重构方法分别选择GG-Cell和WLSQ-basic,根据2.2节中的梯度重构精度测试结论,在各向异性拉伸网格y方向上,GG-Cell方法精度下降到0阶,而WLSQ-basic方法仍然保持一阶精度,因此可以预测GG-Cell和WLSQ-basic的制造解流动模拟精度分别为一阶和二阶。
表 9给出了两种梯度重构方法在各向异性拉伸矩形网格上的制造解流动数值离散误差及相应的精度阶,DS测试结果与预期完全吻合。对于传统方法无法自相似加密的各向异性拉伸网格,DS精度测试方法显示出其优势。
| 表 9 DS精度测试的离散误差与精度阶(各向异性拉伸矩形网格) Table 9 Discretization error and accuracy order of DS tests (anisotropic stretched quadrilateral grids) |
|
|
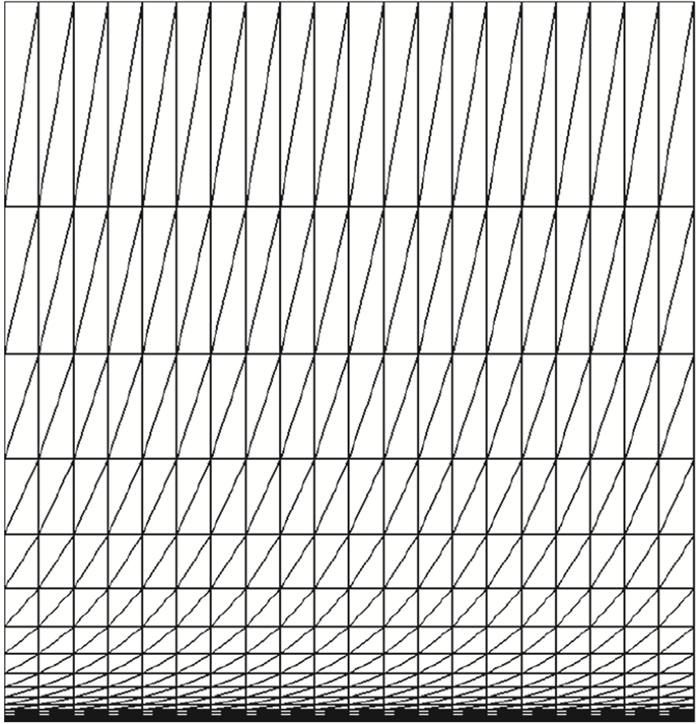
最后,在图 5所示的各向异性拉伸三角形网格上进行与各向异性拉伸矩形网格类似的精度测试。梯度重构方法仍然选择GG-Cell和WLSQ-basic方法。
|
图 5 精度测试各向异性拉伸三角形网格 Fig.5 Anisotropic stretched triangular grids for accuracy tests |
表 10给出了两种梯度重构方法在各向异性拉伸三角形网格上的制造解流动数值离散误差及相应的精度阶。结果显示GG-Cell方法只有一阶精度,已经不满足二阶有限体积离散的精度要求,而WLSQ-basic则仍然保持二阶精度,且离散误差明显比GG-Cell方法离散误差小。
| 表 10 DS精度测试的离散误差与精度阶(各向异性拉伸三角形网格) Table 10 Discretization error and accuracy order of DS tests (anisotropic stretched triangular grids) |
|
|
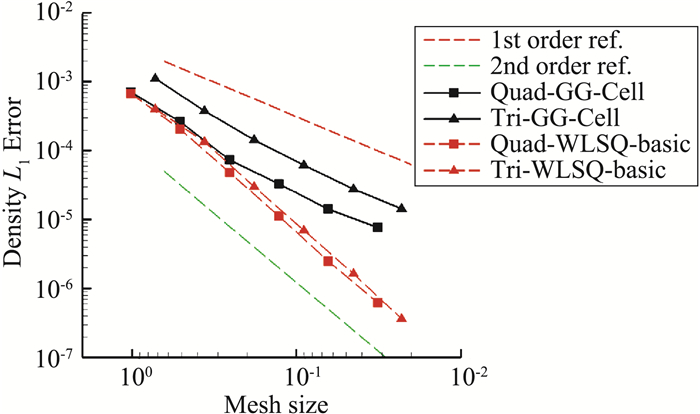
进一步还可比较四边形网格与三角形网格离散误差的大小,比较结果如图 6所示。结果显示,在同等的网格尺度情况下,采用GG-Cell方法时,矩形网格精度更高,而在采用WLSQ-basic方法时,矩形网格和三角形网格精度相差不大。
|
图 6 矩形网格与三角形网格精度的比较 Fig.6 Comparison between quadrilateral grids and triangular grids on solution accuracy |
但是,如果从计算效率的角度来看,一个四边形网格可以剖分为两个三角形,因此整体的网格数量仅为三角形网格的1/2,因此计算效率更高。因此,在实际应用中,结合网格生成的易用性和黏性流动的模拟精度和效率,大多采用混合网格[20]。
4 结论本文实现了基于网格缩小的精度测试方法,在各向同性网格梯度重构精度测试、各向同性网格无黏制造解流动精度测试,及各向异性拉伸网格梯度重构精度测试等三类算例中,将网格缩小测试结果与传统网格加密精度测试结果和理论分析结果进行对比,验证了网格缩小精度测试方法的可行性和有效性。
进一步将网格缩小精度测试应用于传统方法无法处理的各向异性拉伸网格黏性制造解流动精度测试,得到了与预期中完全一致的精度阶结果,证明网格缩小精度测试方法适用于更一般的非结构网格的精度测试。
此外,本文还初步考察了梯度重构方法、网格类型对黏性制造解流动模拟精度的影响。结果显示GG-Cell在各向异性拉伸网格上会导致流动模拟精度降阶,在相同网格尺度下,离散误差显著增大;而WLSQ-basic方法则能够保持流动模拟精度达到二阶。在采用GG-Cell方法时,四边形网格精度更高,而在采用WLSQ-basic方法时,三角形网格能够达到与四边形网格相当的计算精度,但是三角形网格计算效率更低。
需要指出的是,虽然GG-Cell梯度重构方法的精度在各向异性网格上会降至0阶,但是由于空间离散采用了线性重构,因此其计算结果的绝对误差仍较真正的一阶格式(单元内常值分布)小。另一方面,由于梯度重构精度未达到一阶以上精度,因此虽然采用了“名义”上的二阶有限体积离散格式,但是其实际数值精度阶会达不到理想的二阶精度。这正是我们希望避免的。
下一步可以将网格缩小精度测试方法应用于更一般的非结构网格精度测试,同时,也可以作为精度测试工具,详细定量考察不同网格类型、网格质量对数值模拟精度的影响。在此基础上,实际黏性流动模拟精度测试、验证与计算精度的提高也是值得深入研究的方向。
附录A 网格模板梯度重构精度分析模板分析是在特定梯度重构网格模板上,分析在不同梯度重构方法对解析函数的梯度重构精度。本节将基于格心型格式,在典型的各向异性网格模板上分析两种常用梯度重构方法(GG-Cell和WLSQ-basic)的重构精度。具体来说,采用非线性函数f(x, y)=sinx+siny+cos(xy)作为重构测试函数,考察各向异性网格上的梯度重构离散误差(即重构梯度与精确梯度的差值)。
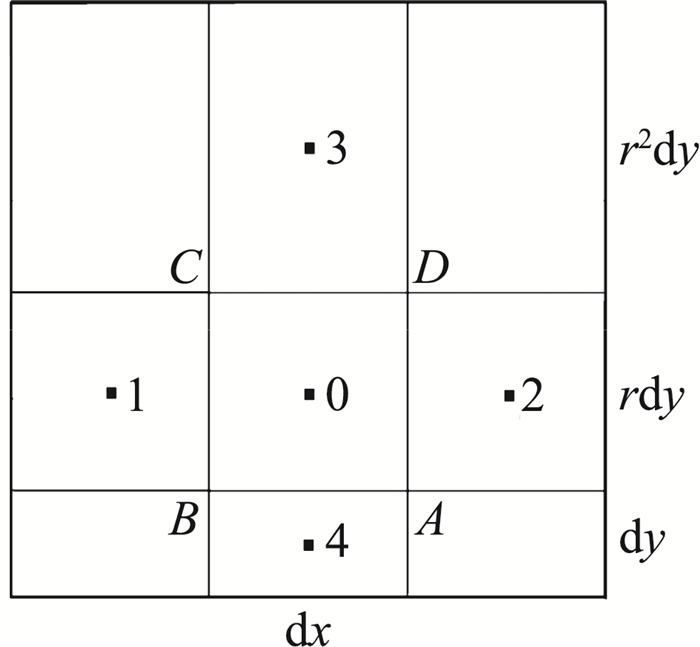
A.1 各向异性四边形网格基于格心型格式,选择如图A.1所示的各向异性四边形网格进行模板梯度重构精度分析,第一层网格长细比(Aspect Ratio)为AR=dy/dx,网格拉伸比(或网格增长率,Stretching Ratio)为r,图A.1中点0为梯度待求点,坐标假设为(x, y),点1~点4均为梯度重构模板点,其坐标容易确定,在此不再列出。
|
图 A.1 梯度重构测试四边形网格模板 Fig.A.1 Quadrilateral grid stencils for reconstruction tests |
表A.1给出了GG-Cell和WLSQ-basic方法的在各向异性四边形网格上的梯度重构误差。格心位置为(x, y)的网格单元,其梯度重构误差是网格长细比AR,拉伸比r及网格尺度dy的函数,对于各向异性网格,AR≫1,r接近1。
| 表 A.1 不同梯度重构方法的离散误差(各向异性四边形网格) Table A.1 Discretization errors of different reconstruction methods (anisotropic quadrilateral grid stencils) |
|
|
当拉伸比r=1,即网格无拉伸时,显然两种梯度重构方法均能达到二阶精度,梯度离散误差的量级为O(dy2),但是值得注意的是网格尺度较大的x方向离散误差的量级为O(AR2dy2)=O(dx2),而y方向的离散误差的量级为O(dy2),并不受AR的影响,当AR≫1时,尽管两个方向上的离散误差均呈现出二阶精度,但是网格尺度较大的x方向绝对误差将会远大于y方向,梯度重构精度呈现出各向异性的特性。
而当拉伸比r≠1时,显然GG-Cell方法在x方向仍然呈现出二阶精度(梯度离散误差的量级为O(AR2dy2)=O(dx2)),这是因为网格在x方向上是均匀的;而在拉伸的y方向,GG-Cell梯度重构精度下降到0阶(梯度离散误差的量级为O(1))。相反,此时WLSQ-basic方法在x方向呈现出二阶精度,y方向则呈现出一阶精度,不会出现精度降阶至0阶的情况。由于梯度重构只跟局部重构模板相关,以上的模板分析结论是严格的,可以为本文2.2节提供参考。
| [1] |
阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562-589. YAN C, YU J, XU J L, et al. On the achievements and prospects for the methods of computational fluid dynamics[J]. Advances in Mechanics, 2011, 41(5): 562-589. (in Chinese) |
| [2] |
OBERKAMPF W L, ROY C J. Verification and validation in scientific computing[M]. Cambridge University Press, 2010.
|
| [3] |
OBERKAMPF W L, SINDIR M N, CONLISK A T. Guide for the verification and validation of computational fluid dynamics simulations[M]. Sponsor American Institute of Aeronautics and Astronautics, 1998.
|
| [4] |
邓小刚, 宗文刚, 张来平, 等. 计算流体力学中的验证与确认[J]. 力学进展, 2007, 37(2): 279-288. DENG X G, ZONG W G, ZHANG L P, et al. Verification and validation in computational fluid dynamics[J]. Advances in Mechanics, 2007, 37(2): 279-288. DOI:10.3321/j.issn:1000-0992.2007.02.011 (in Chinese) |
| [5] |
GHIA U, BAYYUK S, ROY C, et al. The AIAA code verification project-test cases for CFD code verification[R]. AIAA 2010-125, 2010.
|
| [6] |
IANNELLI J. An exact non-linear Navier-Stokes compressible-flow solution for CFD code verification[J]. International Journal for Numerical Methods in Fluids, 2013, 72: 157-176. DOI:10.1002/fld.3731 |
| [7] |
ROACHE P J, STEINBURG S. Symbolic manipulation and computational fluid dynamics[J]. AIAA Journal, 1984, 22(10): 1390-1394. DOI:10.2514/3.8794 |
| [8] |
ROACHE P J. Code verification by method of manufactured solutions[J]. Transactions of ASME, 2002, 124: 4-10. |
| [9] |
陈坚强, 张益荣. 基于Richardson插值法的CFD验证和确认方法的研究[J]. 空气动力学学报, 2012, 30(2): 176-183. CHEN J Q, ZHANG Y R. Verification and validation in CFD based on the Richardson extrapolation method[J]. Acta Aerodynamica Sinica, 2012, 30(2): 176-183. DOI:10.3969/j.issn.0258-1825.2012.02.007 (in Chinese) |
| [10] |
李钊, 陈海昕, 张宇飞. 基于广义Richardson外插方法的阻力预测精度分析[J]. 航空学报, 2015, 36(7): 2105-2114. LI Z, CHEN H X, ZHANG Y F. Accuracy analysis of drag prediction based on generalized Richardson extrapolation[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2105-2114. (in Chinese) |
| [11] |
ROY C J. Review of code and solution verification procedures for computational simulation[J]. Journal of Computational Physics, 2005, 205: 131-156. DOI:10.1016/j.jcp.2004.10.036 |
| [12] |
HEBERT S, LUKE E A. Honey, I shrunk the grids! A new approach to CFD verification studies[R]. AIAA 2005-685, 2005.
|
| [13] |
DISKIN B, THOMAS J L. Accuracy analysis for mixed-element finite volume discretization schemes[R]. National Institute of Aerospace, NIA Report No.2007-08. https://fun3d.larc.nasa.gov/papers/nia_2007_08.pdf
|
| [14] |
KATZ A, SANKARAN V. Mesh quality effects on the accuracy of CFD solutions on unstructured meshes[J]. Journal of Computational Physics, 2011, 230: 7670-7686. DOI:10.1016/j.jcp.2011.06.023 |
| [15] |
王年华, 张来平, 赵钟, 等. 基于制造解的非结构二阶有限体积离散格式的精度测试与验证[J]. 力学学报, 2017, 49(3): 627-637. WANG N H, ZHANG L P, ZHAO Z, et al. Accuracy verification of unstructured second-order finite volume discretization schemes based on the method of manufactured solutions[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 627-637. (in Chinese) |
| [16] |
SOZER E, BREHM C, KIRISC C. Gradient calculation methods on arbitrary polyhedral unstructured meshes for cell-centered CFD solvers[R]. AIAA 2014-1440, 2014. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140011550.pdf
|
| [17] |
王年华, 张来平, 马戎, 等. 非结构网格质量对梯度重构及无黏流动模拟精度的影响[J]. 计算力学学报, 2017, 34(5): 555-563. WANG N H, ZHANG L P, MA R, et al. Mesh quality effects on the accuracy of gradient reconstruction and inviscid flow simulation on isotropic unstructured grids[J]. Chinese Journal of Computational Mechanics, 2017, 34(5): 555-563. (in Chinese) |
| [18] |
MAVRIPLIS D J. Revisiting the least-squares procedure for gradient reconstruction on unstructured meshes[R]. AIAA 2003-3986, 2003. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20040070704.pdf
|
| [19] |
赫新, 赵钟, 马戎, 等. HyperFLOW亚跨声速流动验证(英文)[J]. 空气动力学学报, 2016, 34(2): 267-275. HE X, ZHAO Z, MA R, et al. Validation of HyperFLOW in subsonic and transonic flow[J]. Acta Aerodynamica Sinica, 2016, 34(2): 267-275. DOI:10.7638/kqdlxxb-2016.0002 (in Chinese) |
| [20] |
BAKER T J. Mesh generation:art or science[J]. Progress in Aerospace Science, 2005, 41: 29-63. DOI:10.1016/j.paerosci.2005.02.002 |
 2019, Vol. 37
2019, Vol. 37


