2. 新加坡国立大学 工程学院, 新加坡 117576
2. Faculty of Engineering, National University of Singapore, Singapore 117576, Singapore
具有动态复杂物面边界物体的绕流问题,是非定常流体力学研究的一个重要课题。特别地,在以仿生微型飞行器为代表的低雷诺数大变形柔性结构流固耦合仿真中具有重要的研究价值[1-2]。在流固耦合数值模拟中,非定常边界流场与柔性结构变形需要进行耦合计算,无法事先预测的动态变形物面对所使用的非定常流场求解器的动边界处理能力提出了特殊的要求。基于贴体网格的流场求解器在处理此类问题时需要进行动态网格重构,这往往带来复杂繁琐的计算,一般会增加计算时间并降低求解鲁棒性。而基于非贴体网格的流场求解方法,如基于笛卡尔网格的浸润边界法(Immersed Boundary Method,IBM)有效地规避了网格重构过程。在浸润边界法中,物面与流体物质之间的相互作用被转化为流场方程中的一个体积力项,可对物面两侧区域不加区分地进行流场统一求解。
格子波尔兹曼方法(Lattice Boltzmann Method,LBM)在处理低速不可压流动问题时,相对于直接求解N-S方程,无需处理压力泊松方程和应用交错网格算法,具有相对简便高效的特性。基于相同的非贴体笛卡尔网格框架,可将LBM与浸润边界法相结合,产生了浸润边界-格子波尔兹曼方法(IB-LBM)[3, 5]。为将其应用有限体积框架内以求解更广泛的问题,学术界近年来提出了一种新的求解方案,即格子波尔兹曼通量求解器(Lattice Boltzmann Flux Solver, LBFS)[5-9, 11]。该方法通过在单元界面处的LBM模型计算流场通量值,且由于无需存储密度分布函数节约了内存空间。由于该方法基于有限体积法,故可使用非均匀网格求解,从而摆脱了计算时间步长和单元网格尺寸之间的绑定关系,提高了流场数值计算的灵活性和效率。进一步将LBFS与浸润边界法相结合以处理复杂动态边界流动问题,构建了浸润边界-格子波尔兹曼通量求解器(IB-LBFS)。同时,引入了隐式速度边界修正方程,实现了物面无滑移流场边界条件的精确满足。
在当前IB-LBFS方法的基础上,为了将其应用于真实三维大变形柔性结构的流固耦合数值模拟,还需要进行两方面的工作:首先,需要提升当前IB-LBFS求解器的计算效率,实现可处理大规模网格的并行化计算;同时,需要建立柔性结构动力学求解器,并构建其与IB-LBFS流场求解器之间的流-固交互界面。本文搭建了基于IB-LBFS和绝对节点坐标板壳单元结构力学求解器的流固耦合求解平台,并通过几个典型算例确认了该耦合求解器的有效性。
1 浸润边界-格子波尔兹曼通量求解器 1.1 控制方程宏观流动的Navier-Stokes方程为:
| $ \begin{array}{l} \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{u}}} \right) = 0\\ \frac{{\partial \rho \mathit{\boldsymbol{u}}}}{{\partial t}} + \nabla \cdot \left[ {\rho \mathit{\boldsymbol{uu}} + p\mathit{\boldsymbol{I}} - \mu \left( {\nabla \mathit{\boldsymbol{u}} + {{(\nabla \mathit{\boldsymbol{u}})}^{\rm{T}}}} \right)} \right] = \mathit{\boldsymbol{F}} \end{array} $ | (1) |
在格子波尔兹曼通量计算中,动量通量ρu和黏性-无黏通量Π的表达式为:
| $ \rho \mathit{\boldsymbol{u}} = \sum\limits_{\alpha = 0}^N {{e_\alpha }} f_\alpha ^{{\rm{eq}}} $ | (2) |
| $ \begin{array}{l} {\mathit{\Pi }_{\beta \gamma }} = \rho \mathit{\boldsymbol{uu}} + p\mathit{\boldsymbol{I}} - \mu \left[ {\nabla \mathit{\boldsymbol{u}} + {{\left( {\nabla \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}} \right]\\ \;\;\;\;\;\; = \sum\limits_{\alpha = 0}^N {{{\left( {{\mathit{\boldsymbol{e}}_\alpha }} \right)}_\beta }} {\left( {{\mathit{\boldsymbol{e}}_\alpha }} \right)_\gamma }\left[ {f_\alpha ^{{\rm{eq}}} + \left( {1 - \frac{1}{{2\tau }}} \right)f_\alpha ^{{\rm{neq}}}} \right] \end{array} $ | (3) |
其中:eα为粒子速度,fα为α方向上的密度分布函数,fαeq是相应方向上的平衡状态分布函数,fαneq为非平衡状态分布函数。根据LBGK模型,fαeq的表达式为:
| $ \begin{array}{*{20}{l}} {f_\alpha ^{{\rm{eq}}}\left( {\mathit{\boldsymbol{r}},t} \right) = }\\ {\rho {w_\alpha }\left[ {1 + \frac{{{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{u}}}}{{c_s^2}} + \frac{{{{\left( {{\mathit{\boldsymbol{e}}_\alpha } \cdot \mathit{\boldsymbol{u}}} \right)}^2} - {{\left( {{c_s}\left| \mathit{\boldsymbol{u}} \right|} \right)}^2}}}{{2c_s^4}}} \right]} \end{array} $ | (4) |
eα和系数wα的选择取决于不同的格子速度模型。IB-LBFS的控制方程组为:
| $ \begin{array}{l} \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\sum\limits_{\alpha = 0}^N {{\mathit{\boldsymbol{e}}_\alpha }f_\alpha ^{{\rm{eq}}}} } \right) = 0\\ \frac{{\partial \rho \mathit{\boldsymbol{u}}}}{{\partial t}} + \nabla \cdot \mathit{\Pi } = \mathit{\boldsymbol{F}} \end{array} $ | (5) |
其中F为浸润边界法中物面边界对应的体积力项。
1.2 离散求解将式(5)进行时间离散,将求解过程分裂为一个预测步和一个修正步(分别对应式(6)和式(7)):
| $ \begin{array}{l} \frac{{{\rho ^{n + 1}} - {\rho ^n}}}{{\Delta t}} + \nabla \left( {\sum\limits_{\alpha = 0}^N {{\mathit{\boldsymbol{e}}_\alpha }f_\alpha ^{{\rm{eq}}}} } \right) = 0\\ \frac{{{\rho ^{n + 1}}{\mathit{\boldsymbol{u}}^*} - {\rho ^n}{\mathit{\boldsymbol{u}}^n}}}{{\Delta t}} + \nabla \cdot \mathit{\Pi } = 0 \end{array} $ | (6) |
| $ {\rho ^{n + 1}}\frac{{\delta \mathit{\boldsymbol{u}}}}{{\Delta t}} = \mathit{\boldsymbol{F}} $ | (7) |
分别求解式(6)和式(7),可得到中间速度u*和修正速度δu,二者之和为真实流场速度un+1。
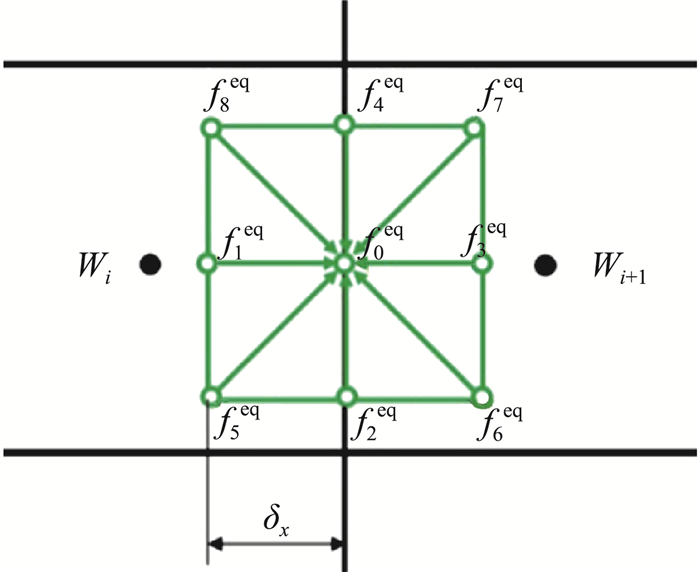
将式(6)离散于有限体积的单元控制体,各个速度方向α上的平衡状态函数fαeq的值由相邻单元的守恒变量在相应位置插值并转换得到。经界面重构(图 1),得到界面上的密度ρ、动量通量ρu、无黏-黏性通量Π,使用单元有限体积控制方程解得流场密度场和中间速度场u*。
|
图 1 相邻单元界面上的LBM重构(D2Q9模型) Fig.1 LBM reconstruction at cell interface (D2Q9 model) |
为了满足无滑移边界条件,引入了隐式边界修正法,即将体积力项F的计算转化为物面边界引起的流场修正速度δu的求解。根据无滑移条件,物面速度矢量Un+1(XBl)的值应与流场在物面相应位置上的流场速度相同,这一关系可由如下的插值关系得到:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}^{n + 1}}\left( {\mathit{\boldsymbol{X}}_B^l} \right) = \sum\limits_j {{\mathit{\boldsymbol{u}}^{n + 1}}\left( {{\mathit{\boldsymbol{r}}_j}} \right)} \cdot D\left( {{\mathit{\boldsymbol{r}}_j} - \mathit{\boldsymbol{X}}_B^l} \right){h^2},}\\ {l = 1, \cdots ,N;\quad j = 1, \cdots ,M} \end{array} $ | (8) |
其中un+1=u*+δu。作为未知数的物面网格速度修正量假定为δuBlΔsl,作从物面拉格朗日网格点至流场欧拉网格点的插值,有:
| $ \begin{array}{*{20}{c}} {\delta \mathit{\boldsymbol{u}}\left( {{r_j}} \right) = \sum\limits_l {\delta \mathit{\boldsymbol{u}}_B^l\Delta s} \cdot D\left( {{\mathit{\boldsymbol{r}}_j} - \mathit{\boldsymbol{X}}_B^l} \right),}\\ {l = 1, \cdots ,N} \end{array} $ | (9) |
将式(9)代入式(8),有:
| $ \begin{array}{l} {\mathit{\boldsymbol{U}}^{n + 1}}\left( {\mathit{\boldsymbol{X}}_B^l} \right) = \sum\limits_i {{\mathit{\boldsymbol{u}}^*}\left( {{\mathit{\boldsymbol{r}}_j}} \right)} \cdot D\left( {{\mathit{\boldsymbol{r}}_j} - \mathit{\boldsymbol{X}}_B^l} \right){h^2} + \\ \;\;\;\sum\limits_j {\sum\limits_k {\delta \mathit{\boldsymbol{u}}_B^k\Delta {s^k}} } \cdot D\left( {{\mathit{\boldsymbol{r}}_j} - \mathit{\boldsymbol{X}}_B^l} \right) \cdot D\left( {{\mathit{\boldsymbol{r}}_j} - \mathit{\boldsymbol{X}}_B^k} \right){h^2} \end{array} $ | (10) |
将δuBkΔsk设为未知向量X,式(10)可整理为线性方程组形式AX=B。其中
| $ \mathit{\boldsymbol{X}} = {\left[ {\delta \mathit{\boldsymbol{u}}_B^1\Delta {s^1},\delta \mathit{\boldsymbol{u}}_B^1\Delta {s^1}, \cdots ,\delta \mathit{\boldsymbol{u}}_B^N\Delta {s^N}} \right]^{\rm{T}}} $ | (11) |
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{D}}_{N \times M}} \cdot \mathit{\boldsymbol{D}}_{M \times N}^{\rm{T}} $ | (12) |
| $ \mathit{\boldsymbol{B}} = {\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_B^1}\\ {\mathit{\boldsymbol{U}}_B^1}\\ \vdots \\ {\mathit{\boldsymbol{U}}_B^1} \end{array}} \right)^{n + 1}} - \left( {\begin{array}{*{20}{c}} {{D_{11}}}&{{D_{12}}}& \cdots &{{D_{1M}}}\\ {{D_{21}}}&{{D_{22}}}& \cdots &{{D_{2M}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{D_{N1}}}&{{D_{N2}}}& \cdots &{{D_{NM}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}_1^*}\\ {\mathit{\boldsymbol{u}}_2^*}\\ \vdots \\ {\mathit{\boldsymbol{u}}_M^*} \end{array}} \right) $ | (13) |
N为构成物面的拉格朗日表面点总数;M为Euler网格点总数;Dij是连续核插值函数,对三维情况有(R为临界半径):
| $ \begin{array}{*{20}{c}} {\delta \left( \mathit{\boldsymbol{r}} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{4}(1 + \cos \left( {{\rm{ \mathsf{ π} }}\left| r \right|/2} \right)),}&{\left| r \right| \le R}\\ {0,}&{\left| r \right| > R} \end{array}} \right.}\\ {D\left( {{\mathit{\boldsymbol{r}}_j} - \mathit{\boldsymbol{X}}_B^l} \right) = \delta \left( {\mathit{\boldsymbol{r}}_j^x - \mathit{\boldsymbol{X}}_B^l} \right)\delta \left( {\mathit{\boldsymbol{r}}_j^y - \mathit{\boldsymbol{X}}_B^l} \right)\delta \left( {\mathit{\boldsymbol{r}}_j^z - \mathit{\boldsymbol{X}}_B^l} \right)} \end{array} $ | (14) |
在非定常动边界流动的IB-LBFS计算中,修正速度方程系数矩阵A的相关计算步骤(矩阵计算、存储、线性方程组求解)占据了相当的计算时间,为了提高运算效率,有对其进行算法优化的必要。进行了以下三处算法优化:
(1) 利用变量物理意义,加速矩阵A生成计算:由于动态边界的存在,每个非定常时间步中,必须重新计算物面边界点和背景点的相关系数Dij,再由式(12)得到Aij。Dij的列向量代表了一个物面拉格朗日节点(j=1, …, N; N为物面点总数)与每个Euler背景网格点(i=1, …, M; M为背景网格点总数)的相关关系。每个物面拉格朗日点对应的背景欧拉网格点数相对于总网格点数极为有限,这意味着D和A为稀疏矩阵,背景欧拉相关点必须在以该物面点为球心的周围半径为R的空间内。因此,在A生成计算中可忽略两个间距大于2R的物面点之间的相关系数计算。通过添加这一筛选条件,可大大减少A矩阵重构的计算时间。
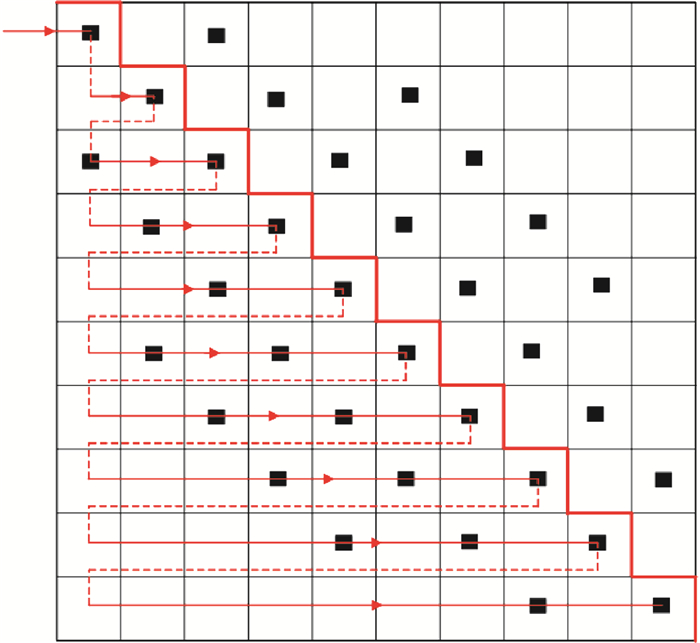
(2) 利用A矩阵的稀疏对称性使用一维存储。由于D为M×N的实系数稀疏矩阵,且A可以写成D·DT的形式,故由矩阵性质可知A亦为正定矩阵。在A生成过程中可扫描其下三角部分,以一维向量形式存储其下三角非零元素的值及位置信息(图 2)。应用一维存储可以极大减小稀疏矩阵的内存占用和相关计算时间。
|
图 2 一维存储:按行搜索稀疏对称矩阵A的下三角部分 Fig.2 One dimensional storage: search the lower triangle part of the coarse matrix A along each row |
(3) 利用矩阵A的对称正定性,使用共轭梯度法对以A为系数矩阵的线性方程组进行迭代求解。对正定对称矩阵,相对于LU分解求逆等直接解法,共轭梯度法作为一种快速迭代法可以极大加速线性方程组AX=B的求解。
由于A矩阵的规模取决于所要计算的物面拉格朗日节点数N,故当物面网格规模越大,所使用的加速效率就相对越高。
对典型的动边界非定常物面绕流问题,在其迭代周期中,单一进程中更为主要的计算时间包括界面单元通量重构计算。该部分的计算量与当前计算进程中处理的背景欧拉网格量成正相关关系。因此,为了实现工程实用的数值模拟能力,有必要将背景流场计算的笛卡尔网格块划分为若干子块进行并行计算。
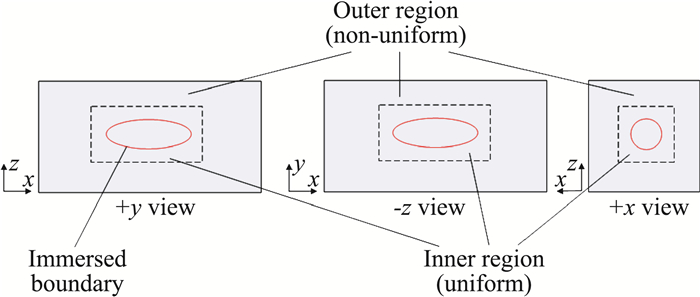
对单进程IB-LBFS程序,其流场Euler笛卡尔网格由1个块(Block)构成,构成物面的Lagrange边界面位于该块的中心部位(图 3)。为了减小物面边界和背景网格的插值搜索计算量,该单一块被分为两个区域:位于物体周围的内部区域和位于远场的外部区域。在内部区域,其Euler网格为均匀网格,在外部区域,Euler网格分布则由于远场条件逐渐变稀疏。
|
图 3 欧拉背景网格块分区:单块单进程 Fig.3 Euler grid domain: single block for serial computation |
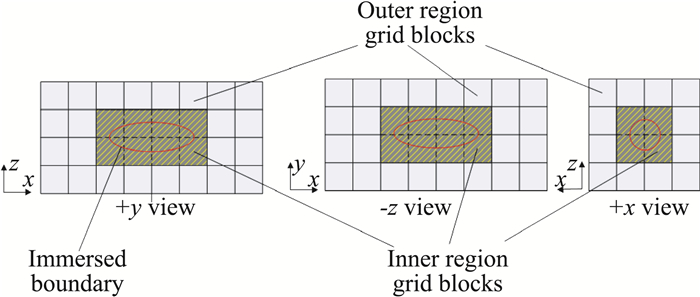
参考单进程情况下的网格块结构特性,在并行计算中,对背景网格进行了如图 4所示的分块处理:原内部均匀区的对应区域被分割为内部子块(Inner region grid blocks),原外部非均匀区域的对应区域被分割为外部子块(Outer region grid blocks)。每个子块对应一个并行进程进行块内部流场方程的求解。在部分内部子块中,需要额外进行浸润边界的搜索插值和物面边界修正速度计算。块与块之间的内部边界需要进行必要的数据传输,邻近外边界的子块的外边界面需要给定相应的边界条件。
|
图 4 欧拉背景网格块分区:多块多进程 Fig.4 Euler grid domain: multi-block for parallel computation |
在进行修正速度方程组求解时,由于矩阵A具有全局性质,故每一个相关内部子块进程中均需求解以该矩阵为系数的线性方程组。在计算AX=B中,A具有全局变量的特性,同时右端项B亦须由各边界插值进程中的值叠加得到(分裂求解方程组,再进行解X的叠加会导致数值误差)。因此,限于修正速度的基本求解算法,并行计算的并行效率由于全局变量和增加的数据交换量会受到一定的影响,为此需要在编程时尽量减少涉及的进程数和数据传递量。
3 绝对节点坐标板单元在传统有限元方法中,对柔性体的描述基于微小变形和转动量作为其广义坐标,这一形式难以描述其刚体运动模态,同时对柔性体大变形则需要大量的计算单元求解。绝对节点坐标法(Absolute Nodal Coordinate Formula,ANCF)则基于非增量的在全局坐标系中描述的广义坐标求解,这一方法可以准确描述柔性体的刚性运动,同时保证了质量阵为常数,可以以较少单元描述柔性体的大变形运动。
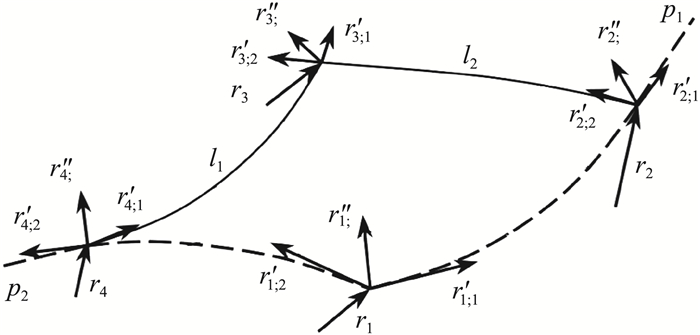
对矩形板结构进行了基于ANCF的4节点48自由度薄板单元建模[12-14](见图 5)。在这一模型中假定该板具有如下性质:
|
图 5 48自由度绝对节点坐标薄板单元 Fig.5 48 degree of freedom ANCF thin plate element |
(1) 板的相对厚度很小,在厚度方向上应力/应变均匀;
(2) 初始形状为矩形。
如图 5所示,该单元节点为4个角点,每个节点包括12个广义坐标自由度。第i个节点的广义坐标向量ei包括节点的绝对位置坐标r、节点在两个物质坐标方向(l1,l2)上的切向梯度∂r/∂p1、∂r/∂p2,以及交叉梯度∂2r/(∂p1∂p2)。
| $ {\mathit{\boldsymbol{e}}_i} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{r}}&{\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial {p_1}}}}&{\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial {p_2}}}}&{\frac{{{\partial ^2}\mathit{\boldsymbol{r}}}}{{\partial {p_1}\partial {p_2}}}} \end{array}} \right] $ | (15) |
板中任一点的坐标由单元插值函数决定:r=S·e,其中S为二维Hermite广义坐标插值函数,由两组一维Hermite插值函数相乘得到。
根据Kirchhoff定律,薄板弹性能可分解为两部分:一部分为薄板中面产生的拉伸应变能和剪切弹性能,另一部分为板的弯度引起的弯曲弹性能和扭转弹性能。薄板单元的弹性能U和单元广义弹性力Qe的表达式为:
| $ U = \frac{1}{2}\iint_S {{\mathit{\boldsymbol{\varepsilon }}^{\text{T}}}{\mathit{\boldsymbol{E}}_\varepsilon }\mathit{\boldsymbol{\varepsilon }}{\text{d}}S} + \frac{1}{2}\iint_S {{\mathit{\boldsymbol{\kappa }}^{\text{T}}}{\mathit{\boldsymbol{E}}_\kappa }\mathit{\boldsymbol{\kappa }}{\text{d}}S} $ | (16) |
| $ {\mathit{\boldsymbol{Q}}_e} = \iint_S {{{\left( {\frac{{\partial \mathit{\boldsymbol{\varepsilon }}}}{{\partial \mathit{\boldsymbol{e}}}}} \right)}^{\text{T}}}{\mathit{\boldsymbol{E}}_\varepsilon }\mathit{\boldsymbol{\varepsilon }}{\text{d}}S} + \iint_S {{{\left( {\frac{{\partial \mathit{\boldsymbol{\kappa }}}}{{\partial \mathit{\boldsymbol{e}}}}} \right)}^{\text{T}}}{\mathit{\boldsymbol{E}}_\kappa }\mathit{\boldsymbol{\kappa }}{\text{d}}S} $ | (17) |
其中拉伸和剪切应变ε和侧向曲率κ的分量表达式为:
| $ \begin{array}{l} {\varepsilon _{ij}} = \frac{1}{2}\left( {{{\mathit{\boldsymbol{r'}}}_i}{{\mathit{\boldsymbol{r'}}}_j} - {\delta _{ij}}} \right) = \frac{1}{2}\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{S}}_{ij}^\varepsilon \mathit{\boldsymbol{e}} - {\delta _{ij}}} \right)\\ {\mathit{\boldsymbol{\kappa }}_{ij}} = {{\mathit{\boldsymbol{r''}}}_{ij}^{\rm T}}\mathit{\boldsymbol{n}} \end{array} $ | (18) |
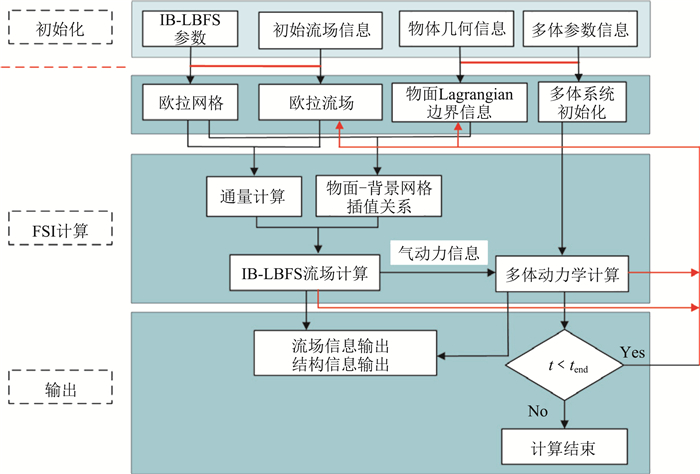
基于绝对节点坐标单元的结构力学求解器合适于与多体动力学求解框架相结合。综合第2节和第3节理论和算法,搭建了基于IB-LBFS流场求解器和绝对节点坐标单元柔性结构动力学的流固耦合数值计算程序,其计算流程图和模块功能图如图 6所示。
|
图 6 流固耦合求解器计算流程图 Fig.6 Flowchart of FSI solver |
旋转球体的绕流问题是一类典型的动边界非定常绕流问题,其流动特性由物体外形和运动的边界条件共同决定。进行横向旋转(旋转角速度与来流方向垂直)的球体绕流作为一个典型问题,可以有效检验IB-LBFS求解器的加速优化方法和并行算法。如图 7所示,本算例采用文献[9]中的参数:来流雷诺数Re=300,无量纲来流速度U∞=0.1(该变量与马赫数的关系有Ma=

|
图 7 绕y轴(垂直来流方向)转动的球体绕流问题 Fig.7 Flow around rotating sphere (ωy in y direction) |
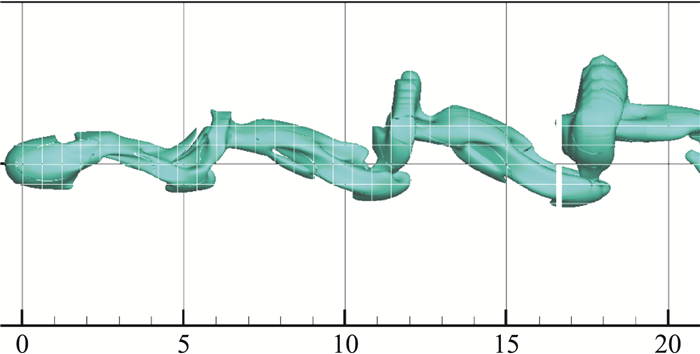
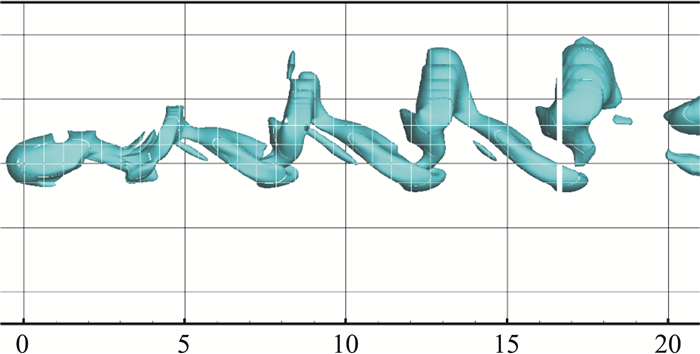
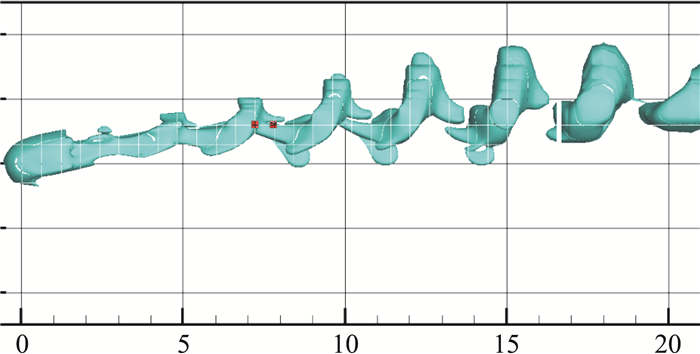
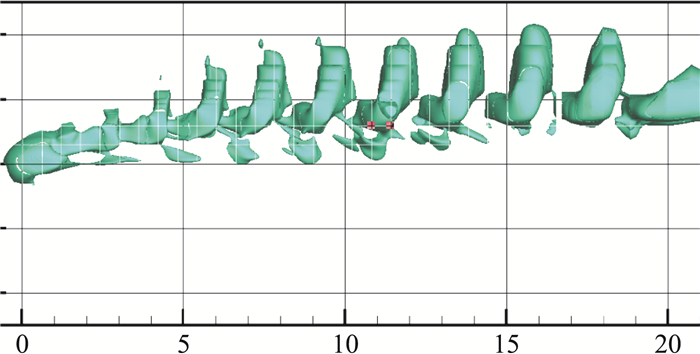
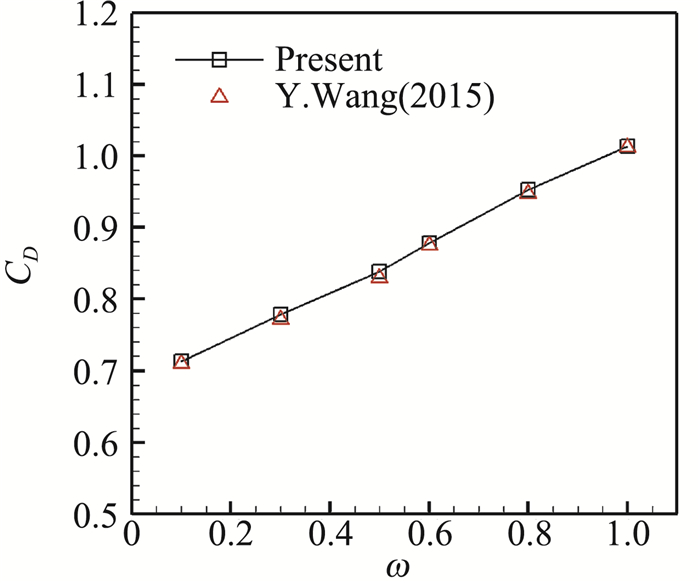
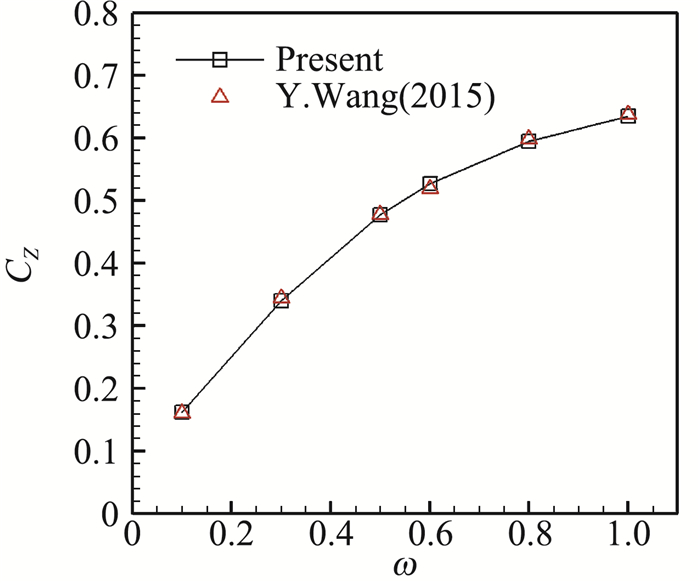
图 8至图 11为ω=0.1、0.3、0.5、1.0四个角速度下的绕流涡量等值面图,显示了相应的脱落涡序列结构。随着球旋转角速度的增加,脱落涡的间隔越小,且其脱落轨迹逐渐沿着球面后部切向旋转速度(+z方向)方向偏移。图 12和图 13分别给出了球体所受的呈周期性振荡的阻力系数CD(+x方向)和侧向力系数Cz(+z)的时均值。计算结果与文献[9]中的值相符,验证了流场计算的准确性。
|
图 8 无量纲角速度ω=0.1:绕流涡结构 Fig.8 Angular velocity ω=0.1: vortex structure |
|
图 9 无量纲角速度ω=0.3:绕流涡结构 Fig.9 Angular velocity ω=0.3: vortex structure |
|
图 10 无量纲角速度ω=0.5:绕流涡结构 Fig.10 Angular velocity ω=0.5: vortex structure |
|
图 11 无量纲角速度ω=1.0:绕流涡结构 Fig.11 Angular velocity ω=1.0: vortex structure |
|
图 12 球体时均阻力系数CD(对比文献[8]) Fig.12 Drag coefficient CD of rotating sphere |
|
图 13 球体时均侧向力系数CZ(对比文献[8]) Fig.13 Lateral force coefficient CZ of rotating sphere |
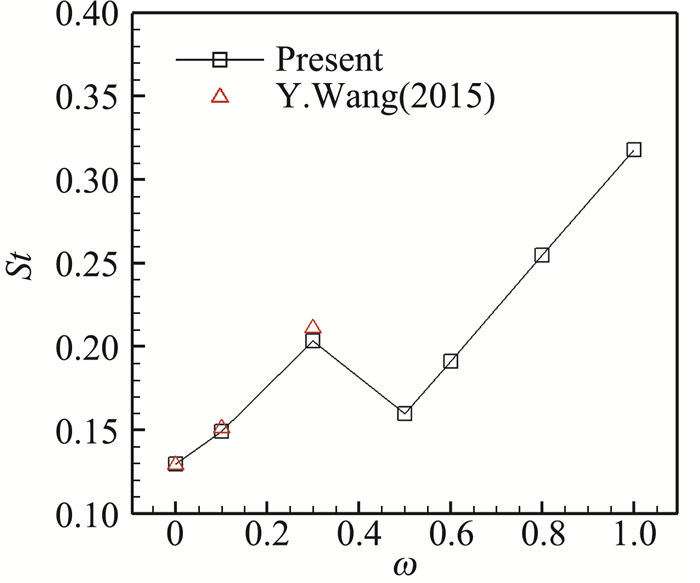
图 14给出了不同角速度下的气动力St数,可视为涡脱落的无量纲频率。当ω≤0.3时,St数与角速度ω成正比;0.3≤ω≤0.5为过渡区间;当ω>0.5后,St数与角速度ω重新具有正比线性关系。
|
图 14 不同旋转角速度下的斯特劳哈尔数St Fig.14 St Number with different rotating velocities |
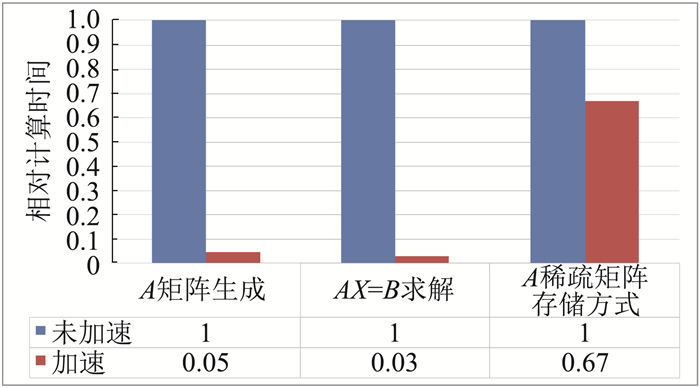
图 15显示了本算例中,应用本文第2节中的各种IB-LBFS加速计算方法在其对应计算步骤中所获得的加速比。其中,使用矩阵生成加速技术可使A矩阵的生成时间减少至直接生成法所需时间的0.05倍;使用共轭梯度法求解线性方程组问题可使计算时间减少为直接解法的0.03倍;在求解方法相同时,应用A矩阵的一维存储替代其全元素二维存储可减少1/3的计算时间。
|
图 15 加速运算方法加速比 Fig.15 Accelerating ratio for the optimization method |
表 1给出了在本算例进行定常初始场计算中,对相同的整体背景欧拉网格,采用不同的并行进程计算得到的单步迭代时间和相对并行效率。进程数从256增长至576时,其并行效率保持不变;并行进程数进一步增加至1152后,迭代时间进一步减小,但由于单核网格量较少(2.7万个),数据交换时间占比增加,其并行效率有一定下降。
| 表 1 定物面计算中不同并行进程数下的并行效率 Table 1 Parallel efficiency for different parallel process number without body surface updating |
|
|
表 2给出了在1152核并行球体旋转计算中,增加了物面边界-背景笛卡尔网格重构计算的非定常迭代步中各部分计算的时间占比。其中物面边界-背景网格重构计算时间在优化后占比仍在60%以上,这说明了本文相关优化算法的必要性。
| 表 2 非定常并行计算中单步迭代各计算步骤所占时间比例 Table 2 Time fraction of computation steps in unsteady surface IB-LBFS parallel computation |
|
|
本节通过研究柔性物面在流场中的变形,考核了基于IB-LBFS和绝对节点坐标法的的流固耦合求解器。矩形柔性旗帜在均匀来流中的摆动运动,是一个典型的三维空间中柔性体的流固耦合问题[15-16]。来流雷诺数为Re=200,在初始时刻旗帜与均匀来流方向存在夹角α=0.1π(图 16),厚度为dh=0.01L,旗帜材料的无量纲弯曲刚度为E=1×10-4。柔性旗帜结构使用48自由度绝对结点坐标板单元进行离散。并行分块进程数为N=80。

|
图 16 初始状态:均匀来流中的斜置板 Fig.16 Initial configuration: inclined plate in uniform flow |
使用中等规模网格对该问题进行并行计算仿真。流场计算域空间范围为x∈[-12, 48],y∈[-15, 15],z∈[-15, 15],总网格量为240×192×192;均匀区网格区单元尺寸为dh=0.02,均匀区部分网格量为144×96×96;对矩形旗帜使用41×41个边界Lagrange点离散,物面网格边长为dsx=dsy=0.025。
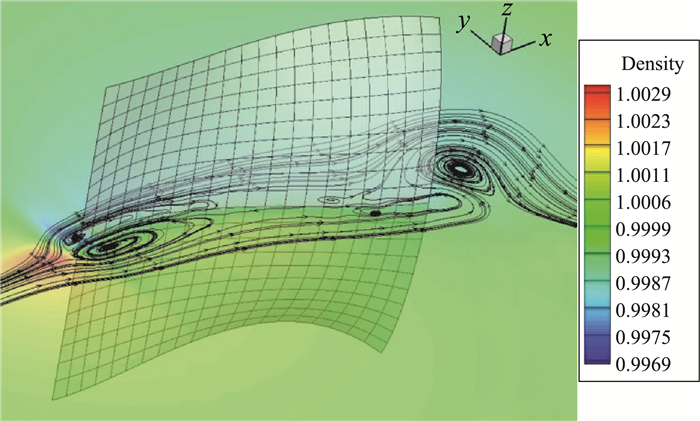
图 17、图 18分别显示了旗帜摆动中的中间截面z=0和展向一侧横截面z=-0.5的流线图。可以看出,不同于二维索流致摆动算例(可视为展向无限长的旗帜摆动问题),三维有限展向的旗帜摆动的流场显示出明显的展向变化和三维效应。

|
图 17 z=-0.5截面:密度云图与流线(t=50.0) Fig.17 Density contour and streamline at z=-0.5 |
|
图 18 z=0截面:密度云图与流线(t=50.0) Fig.18 Density contour and streamline at z=0 (t=50.0) |
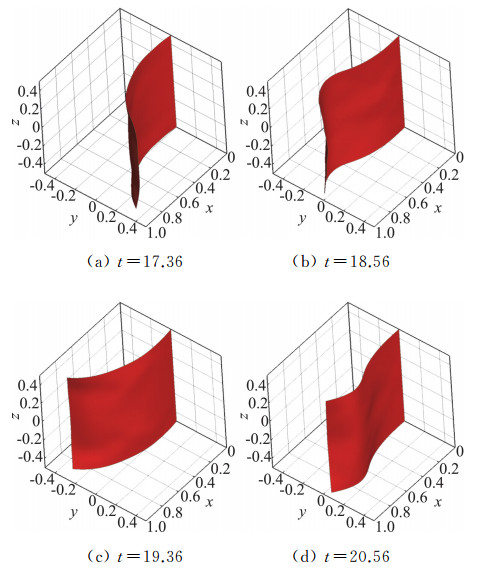
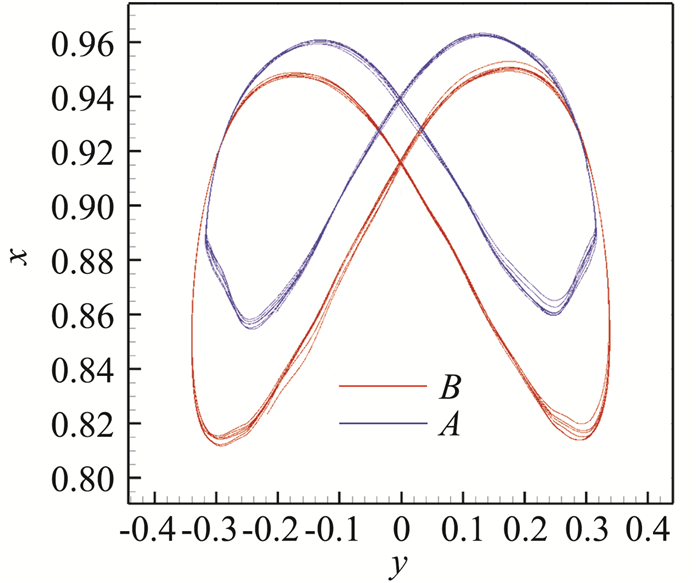
图 19显示了一个周期(t=17.36~21.36)之内,旗帜的四个摆动瞬时构型。t=17.36时,旗帜自由边摆动至y方向极大值,此时旗帜的整体速度达到极小值,并受到旗帜两侧压差产生的-y方向侧向力,该力使旗帜具有向y负方向摆动的趋势;t=18.56时,旗帜处于y中间位置,y方向整体速度绝对值达到极大值,同时由于旗帜构型发生改变,两侧压差力较之前开始反向,变为+y方向;在t=19.36时,旗帜整体-y方向速度在+y压差力作用下减至接近0,该方向压差力在该构型下达到极大;t=20.56时,旗帜整体达到+y方向的极速度,继续运动至图 19(a)构型完成一个完整运动周期。旗帜形成稳定摆动后,其后缘中点B和角点A(见图 16)的y-x方向位移形成了如图 20所示的极限环结构。旗帜摆动的无量纲频率为St=Lf/U=0.252,该值与文献值(Huang[16],St=0.26;Tian[15],St=0.263)相差4%以内。
|
图 19 1个周期内旗帜摆动的动态构型 Fig.19 Flag configuration in a time period |
|
图 20 旗帜后缘点A/B的xy方向振动极限环 Fig.20 Limit cycle of point A/B at the afteredge of flag |
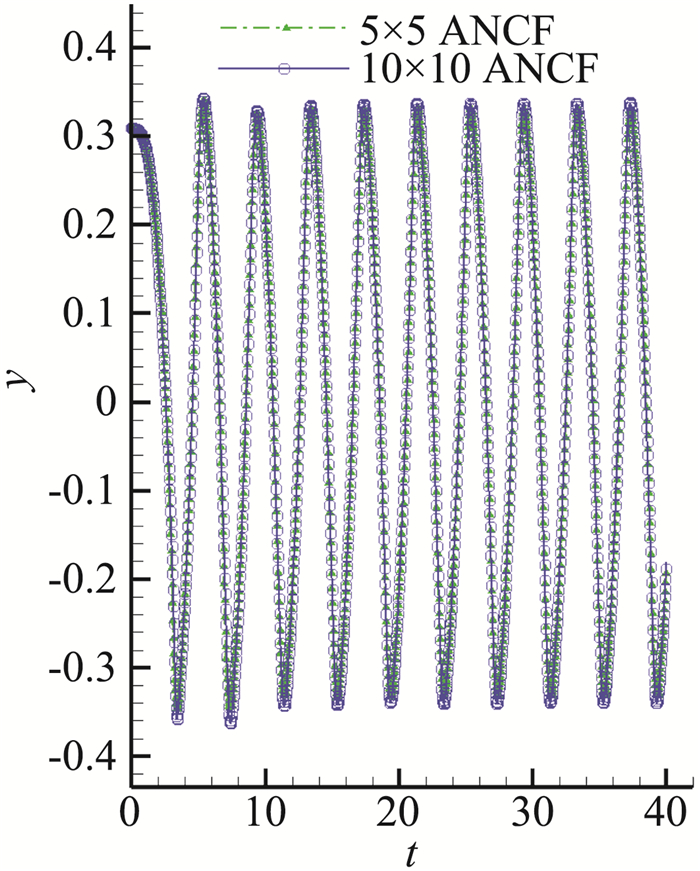
图 21给出了在相同的背景网格中,不同结构离散单元数得到的后缘点的y方向位移-时间曲线。对5×5 ANCF单元和10×10 ANCF单元描述的旗帜结构,二者结果吻合,说明结构单元离散数达到了网格收敛。
|
图 21 后缘点B的位移-时间曲线(5×5, 10×10ANCF单元) Fig.21 y displacement-t curve of B at flag afteredge for different ANCF discrete element scales |
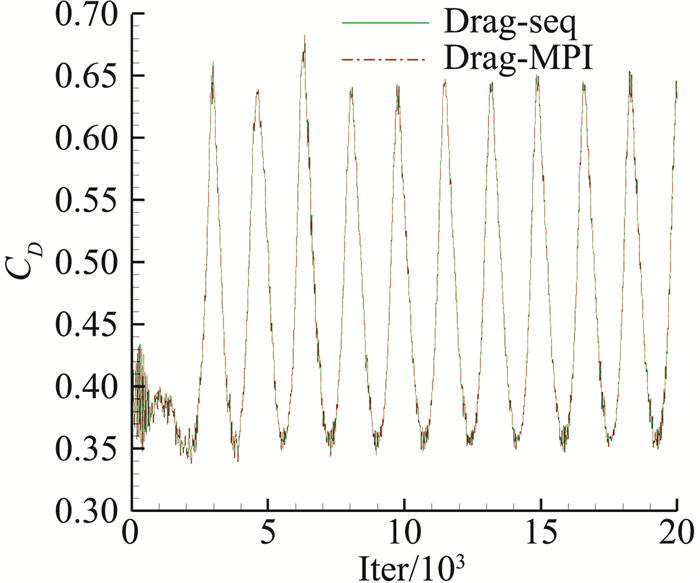
图 22给出了动态物面计算中,串行IB-LBFS计算与并行计算得到的的旗帜阻力系数-时间曲线。两条曲线重合,表明IB-LBFS并行化程序与串行版本具有良好的一致性。
|
图 22 旗帜阻力系数-时间曲线:串行与并行 Fig.22 Drag coefficient-time curve: comparison between serial and parallel computation |
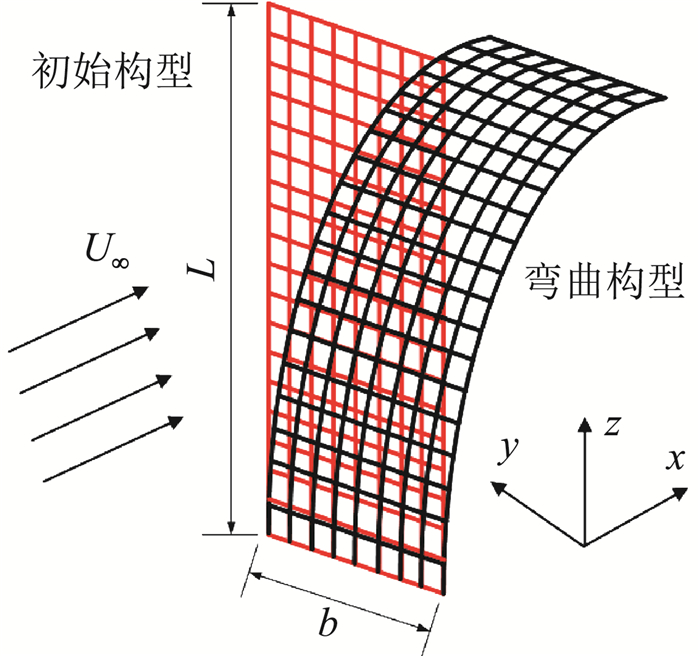
一端固支于地面的弹性板在与其垂直方向的均匀来流中,流体载荷将使其产生弯曲变形,并在板的周围和流动后方形成绕流结构。这一模型与Luhar和Nepf[17]在研究藻类植物在水中的姿态构型中所建立的模型相似。该流固耦合系统示意图如图 23所示。
|
图 23 三维来流中的固支板 Fig.23 Clamped plate in three dimensional uniform flow |
来流参数为:均匀来流无量纲速度U0=0.1,雷诺数Re=1600。板初始状态的无量纲几何参数为:宽度为b=1,高度L=5b,厚度h=0.2b;板密度为ρs,固体与流体的密度比为ρ*=ρs/ρf=0.678,无量纲杨氏模量为E*=E/ρfU02=19 054.9,泊松比νs=0.4,板受到的浮力方向沿z正方向,其无量纲值为fb*=0.036 975。计算并行进程数为128,网格均匀区单元尺寸为dh=0.04;全局计算域尺寸为x∈[-20, 120], y∈[-40, 40], z∈[-40, 40],总网格规模为400×250×200;板表面使用11×51个Lagrange节点模拟,考虑到该板具有一定的薄板特性,在物面边界中忽略板的厚度。在结构离散中,使用2×10个绝对节点坐标板单元对该弹性板进行描述。
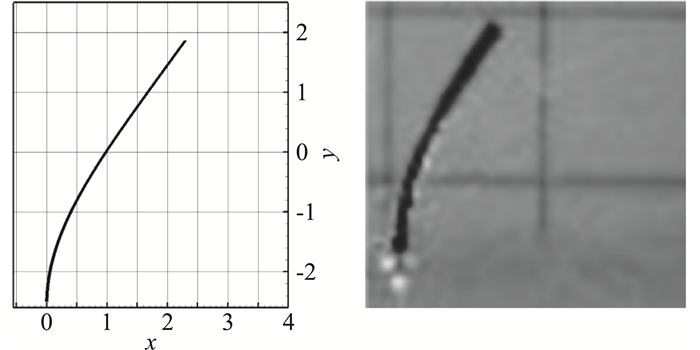
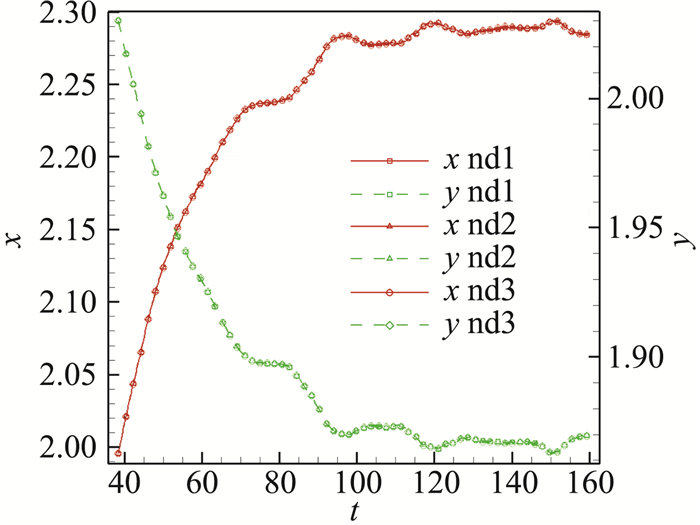
给定板受到系数为C=50的结构Rayleigh阻尼力,弯板在均匀来流流场作用下开始逐渐弯曲,并最终使板弹性力与流体载荷力达到平衡,最终收敛于某一稳定构型。图 24给出了该稳定构型的侧向投影与Nepf[17]试验图像的比较。图 25给出了弯板顶端边界角点(nd1,nd3)和中点(nd2)在x方向(来流方向)和y方向(浮力方向)的位移-时间曲线,t>120 s后构型基本达到收敛位置。板端点在垂直方向的无量纲位移为Δy/b=0.63(文献[17]中Δy=0.59),水平位移为Δx/b=2.28(文献[17]中Δx=2.14),误差分别为6.8%和6.5%。造成这一误差的主要原因在于,本算例中未考虑板的实际厚度,在同样的弹性模量下,所计算的弯曲刚度小于有限厚度情况弯曲刚度,这造成计算位移略微偏大。
|
图 24 弯曲板稳定构型与Nepf[17]实验结构对比 Fig.24 Steady configuration of the clamped plate compared with the experiment result from Nepf[17] |
|
图 25 柔性板上边界端点和中点的y-x方向位移 Fig.25 Upper boundary points of flexible plate y-x displacement |
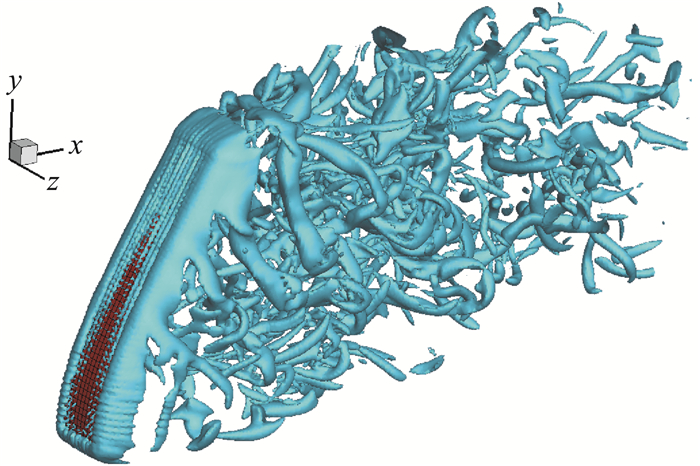
图 26显示了固支弹性板的弯曲稳定收敛构型下,其三维绕流的涡量等值面结构(|w|=0.05)。在给定的雷诺数下,弯板后流动显示出复杂的涡结构条带系统,其三维效应和相应的分离流动结构值得进一步分析。
|
图 26 弯曲板稳定构型的弯板绕流涡量等值面(|w|=0.05) Fig.26 Vortex isosurface of the steady configuration of the clamped plate (|w|=0.05) |
本文提出了浸润边界-格子波尔兹曼通量求解器加速优化算法,并发展了IB-LBFS的并行算法,构建了基于绝对节点坐标板单元的柔性结构动力学求解器,结合IB-LBFS搭建了流固耦合计算平台,并使用多个算例验证了基于IB-LBFS方法的大变形柔性结构流固耦合求解器的并行仿真能力。结果表明:
(1) 本文提出将绝对基于绝对结点坐标法(ANCF)的柔性多体动力学框架与格子玻尔兹曼求解器相结合,构成一种新型的流固耦合数值模拟方法。该方法可显著提高定物面/动态物面迭代计算效率,进一步提高了IB-LBFS解决较大规模网格问题的能力,特别适用于复杂约束柔性体系统的大变形流固耦合数值模拟与仿真。
(2) 在当前的流固耦合动态计算中,仍然采用时间松耦合迭代法,为了增大计算时间步长并减小总计算量,可进一步发展柔性体流固耦合隐式迭代算法。并可通过构建更多的绝对节点坐标单元和其他结构单元,实现复杂的工程结构的柔性体流固耦合计算。
| [1] |
吴江浩, 周超. 仿生微型飞行器悬停飞行的空气动力学研究[J]. 空气动力学学报, 2018, 36(1): 64-79. WU J H, ZHOU C. Review on aerodynamics of bionic micro air vehicle in hovering flight[J]. Acta Aerodynamica Sinica, 2018, 36(01): 64-79. DOI:10.7638/kqdlxxb-2017.0174 (in Chinese) |
| [2] |
苑宗敬, 韩佳坤, 陈刚. 低雷诺数下展弦比对仿生拍动翼推进性能的影响研究[J]. 空气动力学学报, 2018, 36(1): 156-162. YUAN Z J, HAN J K, CHEN G. Investigation on the influence of aspect ratio on the thrust performance of bionic motion wing under low Reynolds number[J]. Acta Aerodynamica Sinica, 2018, 36(01): 156-162. DOI:10.7638/kqdlxxb-2017.0147 (in Chinese) |
| [3] |
GUO Z L, SHU C. Lattice Boltzmann method and its application in engineering[M]. Singapore: World Scientific Publishing Co. Pte.Ltd, 2013.
|
| [4] |
SHU C, LIU N, CHEW Y T. A novel immersed boundary velocity correction-lattice Boltzmann method and its application to simulate flow past a circular cylinder[J]. Journal of Computational Physics, 2007, 226: 1607-1622. DOI:10.1016/j.jcp.2007.06.002 |
| [5] |
WU J, SHU C, ZHAO N. Flow control of a circular cylinder by using an attached flexible filament[J]. Physics of Fluids, 2014, 26(103601): 1-22. |
| [6] |
SHU C, WANG Y, YANG L M, et al. Lattice Boltzmann flux solver, an efficient approach for numerical simulation of fluid flows[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2014, 31: 1-15. |
| [7] |
WANG Y, SHU C, TEO C J. Development of LBGK and incompressible LBGK-based lattice Boltzmann flux solvers for simulation of incompressible flows[J]. International Journal for Numerical Methods in Fluids, 2014, 75: 344-364. DOI:10.1002/fld.3897 |
| [8] |
WANG Y, SHU C, TEO C J. Thermal lattice Boltzmann flux solver and its applications for simulation of incompressible thermal flows[J]. Computers and Fluids, 2014, 94: 98-111. DOI:10.1016/j.compfluid.2014.02.006 |
| [9] |
WANG Y, SHU C, TEO C J, et al. An efficient immersed boundary-lattice Boltzmann flux solver for simulation of 3D incompressible flows with complex geometry[J]. Computers and Fluids, 2016, 124: 54-66. DOI:10.1016/j.compfluid.2015.10.009 |
| [10] |
WU J, SHU C. Implicit velocity correction-based immersed boundary-lattice Boltzmann method and its applications[J]. Journal of Computational Physics, 2009, 228: 1963-1979. DOI:10.1016/j.jcp.2008.11.019 |
| [11] |
WANG Y, SHU C, TEO C J, et al. An immersed boundary-lattice Boltzmann flux solver and its applications to fluid-structure interaction problems[J]. Journal of Fluids and Structures, 2015, 54: 440-465. DOI:10.1016/j.jfluidstructs.2014.12.003 |
| [12] |
SHABANA A A. Definition of the slopes and the finite element absolute nodal coordinate formulation[J]. Multibody System Dynamics, 1997, 1(3): 339-348. |
| [13] |
GERSTMAYR J, HIROYUKI S, AKI M. Review on the absolute nodal coordinate formulation for large deformation analysis of multibody systems[J]. Journal of Computational and Nonlinear Dynamics, 2013, 8(031016): 1-12. |
| [14] |
DUFVA K, SHABANA A A. Analysis of thin plate structures using the absolute nodal coordinate formulation[J]. Proc Inst Mech Eng, Part K:J Multi-body Dyn, 2005, 219(4): 345-355. |
| [15] |
TIAN F B, DAI H, LUO H X, et al. Fluid-structure interaction involving large deformations 3D simulations and applications to biological systems[J]. Journal of Computational Physics, 2014, 258: 451-469. DOI:10.1016/j.jcp.2013.10.047 |
| [16] |
HUANG W X, SUNG H J. Three-dimensional simulation of a flapping flag in a uniform flow[J]. J Fluid Mech, 2010, 653: 301-336. DOI:10.1017/S0022112010000248 |
| [17] |
LUHAR M, NEPF M H. Flow-induced reconfiguration of buoyant and flexible aquatic vegetation[J]. Limnol Oceanogr, 2011, 56: 2003-2017. DOI:10.4319/lo.2011.56.6.2003 |
 2019, Vol. 37
2019, Vol. 37

