从20世纪50年代开始,随着超声速军机的发展,英、法、美、前苏联等国逐渐对超声速民机产生浓厚兴趣。协和号、图144、B2707的研制大大促进了声爆相关理论和方法的发展,这期间声爆理论、预测方法以及声爆最小化方法就已经基本建立起来。然而,协和号声爆初始过压达到2 psf,响度约为107 PLdB[1],只能在大洋上空做超声速飞行。超声速民机研制一度陷入低谷。随后80年代美国重启超声速民机技术研发项目(HSCT),主要参与者是波音和麦道,该项目推进了声爆理论、抑制技术和声爆主观接受度等方面的发展,但是当时的技术成熟度和经费还无法支持研制中型(100~200座)超声速民机,低声爆超声速公务机相对容易实现[2]。协和号的退役并没有打消人们超声速飞行的梦想。NASA在NextGen计划中提出了3代超声速民机的技术要求,即N+1超声速公务机(2015)、N+2小型超声速民机(2020)、N+3中型超声速民机(2030),并于2009年委托波音和洛克希德马丁公司分别进行概念设计研究和关键技术开发[1]。此外,2000年以来还有多个项目开展了地面风洞试验和飞行测试,比如,F-5E声爆形状设定的验证(Shaped Sonic Boom Demonstration, SSBD)[3, 4],F-15B静音锥(Quite Spike)项目[5],这些工作验证了声爆理论、预测方法和最小化方法(sonic boom minimization)的有效性。
近些年来,众多飞机制造公司都在积极地开展各自的超声速民机,特别是超声速公务机的概念研究[6]。最近,洛克希德马丁公司正在开展X-59 QueSST项目[7],除了要验证低声爆技术,还将建立声爆及居民对声爆的反应数据,为民机在陆地上空超声速飞行提供立法依据。在概念设计以及远景规划中, 广为人知的声爆标准是NASA在3代超声速民机中提出的70PLdB标准,已有的工作表明,超声速民机设计要达到此声爆标准,难度仍然很大。困难来自于低声爆构型设计中一些相互矛盾、相互制约的因素,比如,机体容积和细长体外形、低速起降和高速巡航的气动性能、低阻构型与低声爆构型等等。这些问题是超声速民机特有的,相比于亚声速民机,设计难度和工作量显著增加。因此,超声速民机的设计工作非常需要理论方法的指导,特别是在概念设计中需要有快速有效的计算方法。
在超声速民机概念设计阶段,关于声爆计算的理论方法寥寥可数,标准声爆理论和声爆最小化方法是最重要的两个理论方法。如果有一个初始构型,在给定的约束条件下可以通过构型参数优化设计来寻得一个最低的声爆,这是正向设计,但初始构型对优化解影响很大,有些构型即使经过优化也可能达不到预期的声爆设计要求。当前比较成熟的方法是反向设计的方法,即在初始构型基础上,采用中场声爆最小化方法,即JSGD理论[2],确定等效飞机截面积,以此为约束迭代得到飞机构型,中场声爆最小化方法基于Whitham的声爆修正线性理论[8-9],因此该方法假定近场非线性较弱。尽管标准声爆理论和中场声爆最小化方法有弱非线性假定的局限,但是这两个理论方法分别给出了诠释声爆现象、减小声爆策略的数学公式,并且在应用计算中简单快速。它们是超声速民机概念设计中基本的理论和方法,在理论上具有重要意义,在概念设计中也有实用价值,因此,我们需要对其有全面深入的认识。本文主要对这两个理论方法及应用进行了评述和展望。
1 声爆的理论和预测方法 1.1 Whitham修正线性理论及标准声爆理论Whitham修正线性理论[8-9]不仅是标准声爆理论及预测方法的基础,而且也是中场声爆最小化方法的基础。因此,本节先对该理论做一个概述。在Whitham的修正线性理论基础上,20世纪60、70年代形成了标准的声爆理论[10],随后为了描述机动飞行以及大气边界层中声波的复杂变化,声爆理论进一步被细化和完善,并形成了在概念设计中应用的声爆预测方法。修正的线性声爆预测理论,虽有局限性,但快速有效,拓展后可处理许多实际复杂的情况,在多学科多目标优化概念设计中很有用。
Whitham的修正线性理论有两个表述,一个基于飞机坐标系[8],另一个基于地面坐标系[9]。下面分别简要介绍。在飞机坐标系下,针对均匀大气中的无升力细长旋成体,Whitham (1952)修正线性理论的主要步骤是:首先求出小扰动线化势流方程的解(式1),定义F函数(式2),它给出了扰动解与旋成体横截面面积的关系。在同一半径r处,声压与F函数成正比,声压形状与F函数形状相似。然后修正声速,因为小扰动下声速是常数,特征线是平行的直线,不能形成激波,因此需要修正。Whitham的做法是假设经过旋成体轴向一点的近似特征线(直线)上的解是过该同一点的准确特征线(曲线)上的解。这个修正的解并不是原非线性方程的精确解,但是结果表明这样的处理可以较好地描述弱非线性效应[10-11]。最后,激波的切线方向假设为两条相交特征线的角平分线,旋成体头部某区域内所有正过压形成了N波的头激波,即对应的特征线汇聚,扰动叠加求得头激波强度(式3)。详细推导还可参见中文文献[12]。
| $ \frac{{\delta p\left( {\xi ,r} \right)}}{{{p_0}}} = M_0^2{\beta ^{ - 1/2}}F\left( \xi \right){r^{ - 1/2}} $ | (1) |
| $ F\left( y \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int\limits_0^y {\frac{{S''\left( \xi \right){\rm{d}}\xi }}{{\sqrt {y - \xi } }}} $ | (2) |
| $ \frac{{\Delta p}}{{{p_0}}} = {\left( {2\beta } \right)^{1/4}}\frac{\gamma }{{{{\left( {\gamma + 1} \right)}^{1/2}}}}{\left[ {\int_0^{{y_0}} {F\left( y \right){\rm{d}}y} } \right]^{1/2}}{r^{ - 3/4}} $ | (3) |
Walkden[13]借用超声速面积律(area rule)的波阻分析方法将上述Whitham的理论推广到翼身组合升力构型的情形。将F函数中S换成等效横截面面积Se,Se=SV+SL,体积贡献的横截面面积(SV)与升力贡献的横截面面积(SL)之和,这相当于将飞机等效为一个旋成体。体积贡献的横截面面积(SV)由该处与马赫锥相切的平面切出的截面在轴向投影而得到,这与超声速面积律中的处理是一致的。
对于在均匀大气中匀速飞行的情形,采用上述Whitham的理论[8]可以方便求得远场地面上N波(通常还要乘以地面反射系数1.9~2.0),而对于非均匀大气或机动飞行的情形,上述方法很麻烦。简便的方法是采用地面坐标系下的射线寻迹(ray tracing)方法,例如Whitham基于射线的修正线性理论[9],Plotkin[10]称其为Whitham’s Rule。下面简要介绍该理论。
基于射线Whitham重新阐述了修正线性理论并给出相应的计算公式[9]。线性理论的解可给出一阶精度的波幅,但是声波的形状(或射线到达时间,或特征线位置)仅是零阶精度,为了获得一致的一阶精度,需要修正声波的传播速度即声速,或者说,尽管声速变化很小以及由此导致声波的形状改变很小,但传播足够远的距离后,声波的形状改变会很大甚至产生激波,因此需要修正声速以描述波的非线性变形。在地面坐标系下,无风情形的声波过压为式(4),与式(1)形式上相同,由于采用不同坐标系,它们的自变量不同。
| $ \frac{{\delta p}}{{{p_0}}} = \frac{{F\left( \tau \right)}}{{\sqrt B }} $ | (4) |
| $ \tau = t - \int_0^s {\frac{{{\rm{d}}s}}{a}} $ | (5) |
式中,t是波前到达s处的时间,τ是波前的相位,s是波前沿着声线传播的距离,B是s的函数,反映幅值的变化。如果是非均匀大气,式(5)中声速a需替换为a0+δa+δu,进一步可得:
| $ \tau = t - \int_0^s {\frac{{{\rm{d}}s}}{{{a_0}}}} + F\left( \tau \right){\mathit{\Lambda}} \left( s \right) $ | (6) |
其中
| $ \frac{{\delta p}}{{{p_0}}} = \frac{{F\left( {\tau - F\left( \tau \right){\mathit{\Lambda}}\left( s \right)} \right)}}{{\sqrt B }} $ | (7) |
式(7)表明相位为τ的波前到达s处的提前时间是F(τ)Λ(s)。
非线性变形的压强信号上每点提前F(τ)Λ(s),激波位置由面积平衡(area balance)确定(图 1),这指的是激波位置将声压信号划分成面积相等的两部分。这等价于两条相交特征线的角平分线即是激波的切线方向,因为线化的激波速度等于该激波前后等熵波速度的平均值[10]。
设T(s)是在s处刚好形成激波的波前的相位,由式(6)可得
| $ T\left( s \right) = {t_{{\rm{shock}}}} - \int_0^s {\frac{{{\rm{d}}s}}{{{a_0}}}} + F\left( {T\left( s \right)} \right)\mathit{\Lambda }\left( s \right) $ | (8) |
式中tshock是在s处形成激波的时间,上式对s求导,dtshock/ds即是激波速度的倒数,再由Rankine-Hugoniot关系式的1阶近似可得线化的激波速度Us,可求得
| $ F\left( {T\left( s \right)} \right) = {\left[ {2\int_0^{T\left( s \right)} {F\left( t \right){\rm{d}}t} } \right]^{1/2}}{\left[ {\mathit{\Lambda }\left( s \right)} \right]^{ - 1/2}} $ | (9) |
上式给出激波后的F函数,因此也就给出了激波后过压,即
| $ \frac{{\Delta p}}{{{p_0}}} = \frac{{F\left( {T\left( s \right)} \right)}}{{\sqrt B }} $ | (10) |
激波位置可通过麻烦的迭代计算得到,Middleton[15]和Hayes[16]分别给出了一般性的算法。特例,在远场形成N波,此时T(s)→τ0,这里F(τ0)=0。
前面讨论了基于射线的修正线性理论,下面简要介绍射线寻迹法。假设大气声速a0和密度ρ0是变化的,声压信号的波长远小于大气梯度的长度尺度,无风速情形下由声压信号波动方程可以推导得出,
| $ \nabla \cdot \left( {\frac{{{P^2}}}{{{\rho _0}{a_0}}}\mathit{\boldsymbol{n}}} \right) = 0 $ | (11) |
式中n是射线单位方向向量,与波前函数正交,其中ρ0a0是声阻抗,
| $ P{\left( {\frac{A}{{{\rho _0}{a_0}}}} \right)^{1/2}} = {\rm{constant}}\left( {{\rm{Blokhintzev}}\;不变量} \right) $ | (12) |
其中A是射线管面积。数值计算时要考虑每个微小的射线管面积。
Plotkin[10]总结利用射线求解声爆的标准过程是:第1步,根据线化的面积律计算飞机的初始声源信号,由此得到Whitham的F函数(声源确定);第2步,初始的某一射线的方位由飞机的位置和航迹确定,随着时间推进计算该射线的方位及射线管面积,根据Blokhintzev不变量,由近场声压幅值求出中场(或远场)某处声压幅值,此处声波信号的形状仍与近场声波信号形状相同,只是幅值改变(声压传播);第3步,计算每点的提前量F(τ)Λ(s),出现多值点时,采用面积平衡确定激波位置,然后由激波后过压公式计算激波强度(计算激波)。上述标准声爆预测计算流程概况为图 2。
1.2 声爆预测方法评述声爆预测方法一般由两部分组成,一部分是声源的计算,另一部分是声信号的传播。每一部分都有若干种处理方法,由此形成各种声爆预测方法。如果以声信号传播算法不同来区别,主要的声爆预测方法有以下四种。一是标准的声爆预测方法,如上节图 2所示,它以F函数为核心,先由飞机几何及飞行参数,结合面积律求出F函数,即得到声源,然后利用射线寻迹,由声压信号非线性变形计算激波位置,由激波后F函数得到声爆。在该方法的基础上,计及特殊飞行状态而形成的软件有,ARAP[16];TRAP[17]。第二种是Thomas(1972)提出的波形参数法(waveform parameter method)[18],它不以F函数为核心,而是直接处理声压信号,即把声压信号分段,用若干参数描述,计算每段信号的传播得到声爆。该方法不依赖F函数,可以利用CFD或实验得到近场声压。因此,波形参数法适用性更广,在许多项目中得到应用。例如该方法被Plotkin拓展到处理汇聚的声爆,形成了FOBOOM[19],并被美国空军应用为BOOMAP2;Plotkin进一步开发了SBORT[20],计算速度提升了1-2个量级,并被美国空军应用为BOOMAP3; Plotkin在FOBOOM和SBORT基础上为美国空军开发了PCBoom3[21],该软件发展到PCBoom6.6[22]。第三种方法也不依赖于F函数,而是采用非线性Burgers方程计算声压的演化传播,并在方程中加入吸收项、分子弛豫项、大气分层项等,这称为增广(Augmented) Burgers方程。例如Rallabhandi[23]为NASA开发了sBOOM,其中压强信号传播采用了增广Burgers方程。第四种方法采用Khokhlov-Zabolotskaya-Kuznetsov (KZK)方程[24-27],相比于增广Burgers方程,增加考虑了衍射、轴向/横向对流等三维效应的影响,KZK方程是三维的,计算量更大。
第一种方法无论声源计算还是声压信号传播都以F函数为核心,这意味着非线性较强时会使计算准确性大打折扣,但是该方法计算效率高,在非线性较弱时可以得到比较准确的结果。后三种方法的模型复杂性依次增加,计算量也逐渐增大,但是这三种方法不依赖F函数,适用于非线性较强的情形,可从更准确的近场声压出发计算声爆。
国内学者应用波形参数法的较多[28-31],为了计及更复杂的大气影响,也开始有研究增广Burgers方程的工作[32]。
经过近60年的发展,国外已经有成熟的声爆预测方法和软件以及开展了系统的风洞实验和飞行验证试验[14, 33]。具有一定准确度、高效率的声爆预测方法是概念设计阶段必不可少的。我们不仅要掌握已有声爆预测方法的原理,更要着重调研相关的风洞实验和飞行试验结果,经过校验的预测方法才能更好地应用于概念设计。
2 声爆最小化方法及应用范例 2.1 声爆最小化方法的代表——JSGD理论在前述标准声爆理论基础上,20世纪60、70年代发展了声爆最小化方法,现在也称为Jones-Seebass-George-Darden理论(JSGD或SGD理论)[1]。Rallabhandi和Plotkin等[34-36]进一步发展了该理论。声爆最小化方法构成了当前低声爆构型概念设计的基础。下面简要介绍声爆最小化方法及其发展。
对于足够光滑细长体型的飞机,产生的等熵压缩波在远场最终汇聚形成N波。Jones[37]证明了远场的激波强度的下限对应于飞机头部钝化,相应的F(x=0)为Delta函数,这样的近场信号很快就形成N波,根据式(3),激波强度按照r-3/4衰减,快于如式(1)按照r-1/2衰减的柱波。McLean[38]指出在爬升阶段,声信号达到地面时还没有形成N波。随后许多研究者指出甚至在巡航阶段,足够光滑细长的大型飞机,其声信号达到地面时可能也没有形成N波。Hayes[39]指出在真实大气中,特征线相比于均匀大气的情形汇聚得更慢。这样,中场信号就可能出现在地面处(所谓中场信号,通常位于数倍飞机长度距离之外,其形状依赖于飞机构形并随离开飞机的距离变化而改变;远场信号形状不再随离开飞机的距离变化而改变)。如果地面处为中场信号,则还含有F函数的信息,设计合适的F函数,即相应地改变飞机形状,就可以有效减小地面处声爆。对于中场信号Seebass[40]和George[41]指出头激波强度的下限同样要求F(x=0)为Delta函数。George和Seebass[42-43]发展了一个完整的理论来使头激波和尾激波最小化,这个理论成为声爆最小化方法的基础。
这里先只考虑地面信号(实际为中场信号时)的头激波[41],以一简单情形为例来说明。如果要使地面处最大过压最小化,就要重新定义F函数,F(y)=F1(y)+F2(y),其中F1=δ(y),Delta函数(即Jones的F函数),F2是添加的部分,对应AEy0O(图 3),AE段F2为常数,由式(2)表明此段S″e=0,即此段等效横截面面积Se=常数,因此这一段过压也为常数(由式(1)可知)。在给定体积和升力的前提下,添加F2(AEy0O),意味着要相应减小F1的面积,因此就减小了地面处头激波强度,即减小了最大过压Ps0,在地面形成平顶型(flat-top)信号(图 3)。

|
图 3 F函数及对应的平顶型信号 Fig.3 F function and pressure signature of flat-top type |
AE段F2也可以不为常数,而是线性增长(图 4),此部分对应着扰动波的压缩,只要在地面(实际为中场)该部分的压缩不形成激波,此时对应有一个从头激波Ps到最大过压Pmax的提升时间τ,在地面形成斜坡型(ramp)信号(图 4),通过调节F2使头激波最小。

|
图 4 F函数及对应的斜坡型信号 Fig.4 F function and pressure signature of ramp type |
飞机头部钝化可使该构型的声爆最小,但是此时头部弓形激波导致的激波阻力很大,相比较,细尖的头部在近场只产生等熵压缩波,此时阻力小,但是远场压缩波汇聚成激波,声爆大。为了兼顾阻力和声爆,Darden[44-45]拓展了前述Seebass-George声爆最小化理论[42-43],去除了其中头部钝化限制(文献中简称SGD理论或JSGD理论)。此时F函数表示成
| $ \begin{array}{l} F\left( y \right) = 2yH/{y_f}\;\;\;\;\;\left( {0 \le y \le {y_f}/2} \right)\\ F\left( y \right) = C\left( {2y/{y_f} - 1} \right) - H\left( {2y/{y_f} - 2} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{y_f}/2 \le y \le {y_f}} \right)\\ F\left( y \right) = B\left( {y - {y_f}} \right) + C\;\;\;\left( {{y_f} \le y \le \lambda } \right)\\ F\left( y \right) = B\left( {y - {y_f}} \right) + D\;\;\;\left( {\lambda \le y \le l} \right) \end{array} $ | (13) |
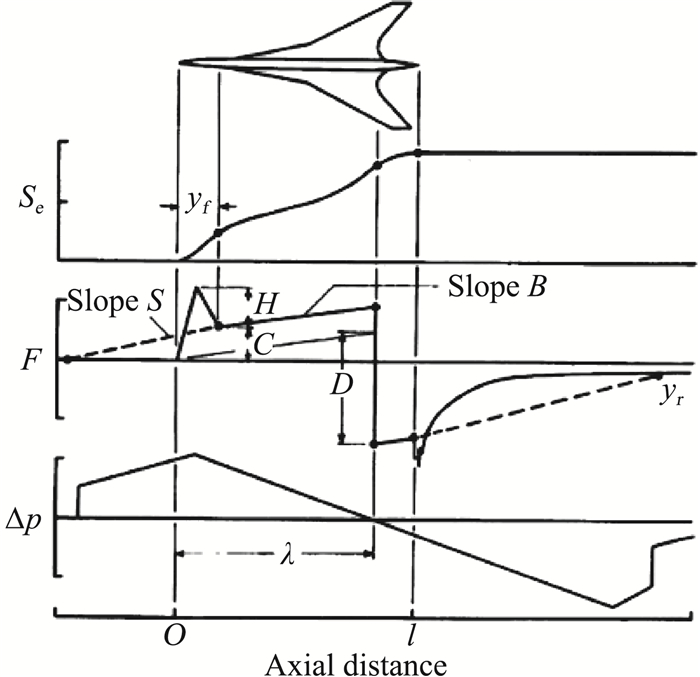
F函数在头部不再是Delta函数,而换成尖锥状(spike)函数(图 5),去除了钝化限制。图 5中,H是尖锥的高度,yf是尖锥宽度或前部面积平衡点,yr是后部面积平衡点,λ是F函数小于零的起始点轴向坐标,l是飞机等效长度。由声爆最小化计算出F函数,然后就得到等效截面面积分布Se:
| $ {S_e}\left( l \right) = 4\int_0^l {F\left( y \right)\sqrt {l - y} {\rm{d}}y} $ | (14) |
|
图 5 Darden的F函数及对应的有效横截面和ramp型信号 Fig.5 Darden's F function and pressure signature (picture from Darden[44]) |
F(y>l)可以采用Petty[46]的方法(假定尾流面积为常数)给出。
当头部很钝,面积分布有无穷大梯度,F函数是Delta函数,即yf=0时激波强度最小。由式(3)可知头激波强度与F函数曲线下方(F>0)的面积成正比。随着yf增加,F函数尖峰下的面积增加,激波强度也就增加了。例如,某型飞机Δp(yf/l=0.2)是Δp(yf/l=0)的1.2倍左右[45]。
利用JSGD理论的设计过程是通过设计合适的F函数,即以F函数中的参数作为优化变量,使地面信号满足设定的平顶型或斜坡型,由得到F函数计算出等效截面面积Se分布,以Se为约束迭代计算出外形。
前述F函数在表示后部信号时存在局限性,因为飞机后部有发动机及尾翼,比较复杂,文献[34-36]改进了F函数,峰值不再固定在yf/2处,F函数中的几个坡度细分为更多段,增加设计灵活性,以适应同时满足声爆信号参数及其它性能参数,特别是使响度最小。Rallabhandi[47, 34]提出一种高效的两步伪反设计优化方法(bilevel pseudoinverse optimization),第一步,设计变量是改进的F函数中的参数,地面信号响度最小为优化目标,用遗传算法得到优化的等效截面面积Se分布;第二步,设计变量是外形参数,以前一步得到Se分布为优化目标,用遗传算法计算出优化的外形参数。
飞机等效截面的改变对地面信号影响很大,如果要对比低保真度和高保真度两种设计方法,这两种方法都需要基于准确的外形数据以便比较[47, 48]。Colonno和Alonso[49]在前述工作基础上研究了输入参数不确定性对地面信号不确定性的影响。
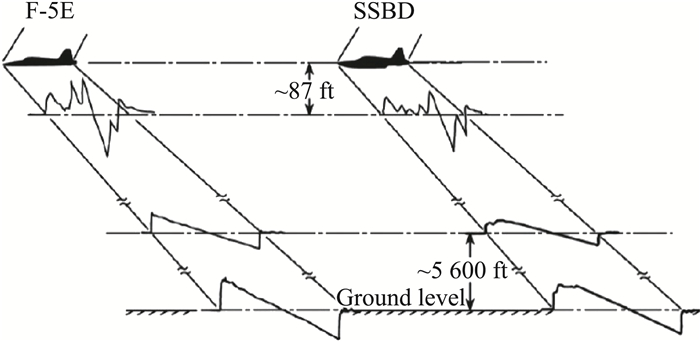
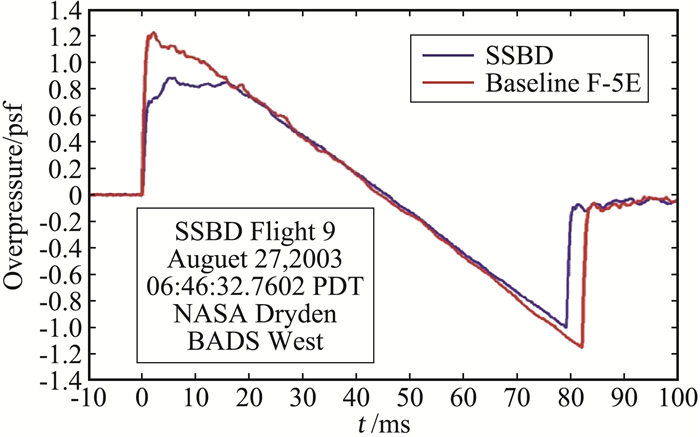
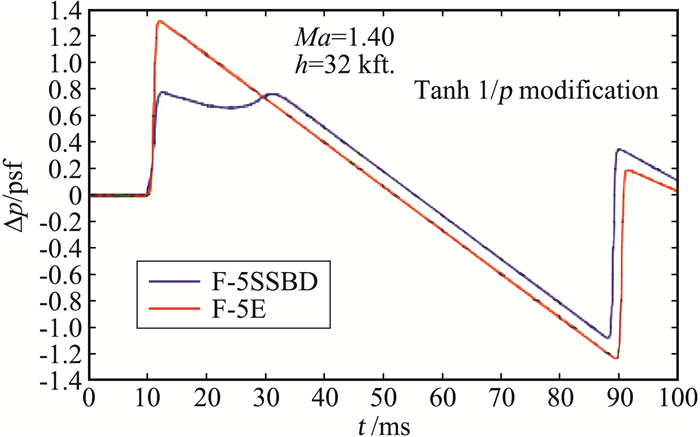
2.2 JSGD理论应用范例以JSGD理论为代表的声爆最小化方法通过设计合适的F函数,可设定声爆形状(shaped sonic boom or shaped boom),并在一定约束条件下使声爆尽可能小。这里列举两个典型的应用JSGD理论的例子。第一个例子是AFRL/NASA以F-5E为飞行平台开展的声爆形状设定的验证(Shaped Sonic Boom Demonstration, SSBD)[3-4]。SSBD目标是验证源于JSGD理论的低音爆飞机外形设计方法,采用前体修型的F-5E进行飞行验证[4]。F-5E SSBD外形的特点:前体钝化,飞机前体长度增加,发动机进气口和机翼距离前端更远。在近场,钝化的头部形成较强的弓形激波,后面跟随着一些较弱的激波,这些弱激波的速度低于弓形激波的,而且它们间隔较远,它们在到达地面时还未汇聚,由此减小声爆,参见图 6。F-5E的声爆初始过压约为1.3psf,响度约为102 PLdB,声爆水平很高,依据JSGD理论前体修型的F-5E SSBD实现了平顶型地面信号,初始过压降到0.7 psf左右(图 7)。飞行验证试验表明地面声爆信号是可以计算预测的(图 8的理论计算结果与图 7的飞行实验地面测试结果非常接近),同时,表明了利用JSGD理论修改飞机外形实现低声爆设计是可行的。F-5E等效截面中容积占比大大高于低音爆构型(比如HSCT),因此,F-5E SSBD前部修型改变非常大以实现较为合适的地面信号。这说明JSGD理论非常依赖于初始构型,如果初始构型太差,就很难进一步降低声爆水平,因为基于JSGD理论的几何修型还要受到其它约束条件的限制。
|
图 6 F-5E和F-5E SSBD的压强信号演化 Fig.6 Pressure signatures of F-5E and SSBD (picture from Maglieri[14]) |
|
图 7 F-5E和F-5E-SSBD飞行测试的地面压强信号 Fig.7 Ground pressure signatures of F-5E and SSBD from flight test(picture from Pawlowski[4]) |
|
图 8 F-5E和F-5E-SSBD理论计算的地面压强信号 Fig.8 Ground pressure signatures of F-5E and SSBD from simulations(picture from Pawlowski[4]) |
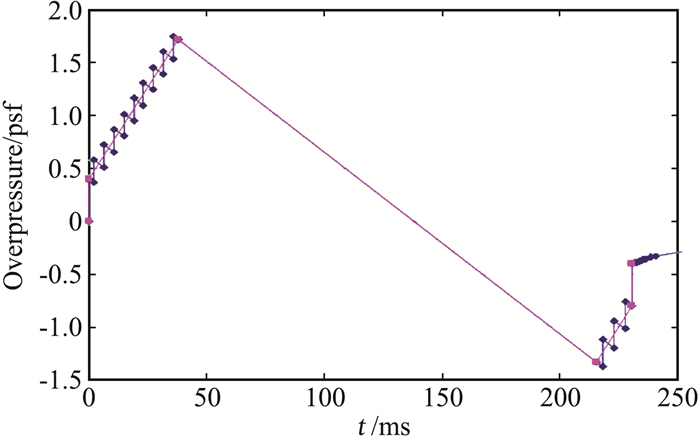
第二个例子来自洛马的N+2小型超声速民机验证项目。首先要提一下,在对公众声爆接受度的研究中,Leatherwood等[50-51]发现声爆的频谱特性更重要,采用感觉噪声级比单纯用声爆初始过压、最大过压、提升时间等参数更可靠。因此,洛马研究团队为了使响度最小化,设定了一种由多个小激波构成的斜坡型声爆信号(multi-shock ramp signature),见图 9,它比图 4所示的斜坡型信号复杂,通过调整激波间隔时间,在声压等效的情况下,可以得到更小的响度[52]。
|
图 9 斜坡型和等效的多激波斜坡型压强信号 Fig.9 Ramp and equivalent multi-shock signatures (picture from Morgenstern[52]) |
洛马N+2第1阶段和第2阶段都应用了JSGD理论,第2阶段是以第1阶段的LM1021为初始构型,但是只采用JSGD理论,在飞行轨迹外(off-track) ±40°处声爆信号没有明显改善。这是因为初始构型LM1021机翼和V型尾翼之间的膨胀波强度难以减弱,对应升力有较大的间断。由此可见,JSGD理论受到初始构型的约束,难以进一步改善声爆信号。因此,洛马对LM1021的后体重新设计得到LM1044。洛马N+2第2阶段LM1044的结果表明,整个声爆毯(巡航开始阶段)最大声爆小于85PLdB,平均声爆比第1阶段LM1021降低了4PLdB[53]。计及大气吸收和分子弛豫情况下,LM1044巡航全程平均响度79PLdB,若再计及湍流影响,大致为74PLdB,这仍然未达到NASA N+2代超声速民机70PLdB目标。实现NASA 3代超声速民机的声爆指标是一个具有相当挑战性的工作。洛马两个阶段的工作表明,声爆最小化方法的应用效果受制于初始的布局构型,当应用该方法达不到设计目标时,不得不重新考虑初始的布局构型设计。初始布局构型设计相当关键。
JSGD理论用到Whitham的修正线化理论,只在1.2 < Ma < 3范围有效,而在跨声速0.9 < Ma < 1.15范围近场高度非线性(声速线对外形敏感),当Ma>3时近场也有了明显的非线性现象(出现强激波),这些非线性情形(尽管仍是小扰动)通常需要用CFD计算。由于这些非线性,声爆最小化方法,由地面信号计算其所对应的等效面积分布就没有唯一性,这时需要采用迭代的方法[54-55]。
对于小扰动但有明显非线性或大扰动强非线性的情形,上述声爆最小化方法不适用,此时可采用近场压强信号最小化方法,即近场(一般在3-4倍参考长度处)的压强场通过求解可压的Euler方程得到,也可以通过风洞实验测得,采用遗传算法对飞机外形进行优化,优化目标是近场激波强度达到最小[56, 57],近场信号到地面的传播是求解增广Burgers方程。如果采用的是风洞模型的测试数据或该模型的CFD计算数据,则需要考虑从小尺度模型到全尺寸的变换,然后才可由传播算法计算出全尺寸飞行器的地面声爆。
国内一些学者在上述方面也开展了工作,比如,冯晓强等[58]应用JSGD理论尝试设计了一种超声速客机。冯晓强等[59]应用了改进的JSGD理论,采用遗传算法,以超压值和有效容积为优化目标。乔建领等[60]研究了一种代理优化方法在低音爆设计中的应用,表明其效率高于遗传算法,优化结果好于梯度法。
声爆最小化方法的物理思想是,在机头保持一个足够强的弓形激波,后面跟随的较弱的激波追不上前面的弓形激波,不会产生汇聚,但是这个头部的弓形激波较强,也不利于进一步减小声爆。为了进一步减小头部激波同时防止激波汇聚,湾流公司(Gulfstream Aerospace)开发了创新性的静音锥技术(Quite SpikeTM),在飞机头部加装静音锥(可伸缩、非轴对称、略向下偏离重心水平线),静音锥每一级的膨胀波使下一级的激波变弱,弱激波互相平行,同时机头处的激波也减弱了,这样就不会在远场汇聚成强激波。在F-15B Quite Spike项目中静音锥安装在F-15B上进行了飞行试验以验证静音锥结构系统的可行性,并测量了近场压强信号以验证CFD计算结果[61-62]。加装静音锥还有一个好处,保证飞机前部有足够的容积,这是低声爆公务机设计难点,因为减小头部激波通常意味着要减小机身前部的等效截面面积。Howe[63]针对湾流公司QSJ构型的远场计算结果是,2级的静音锥可以将地面头激波从0.4 psf(无静音锥)降到0.15psf。国内沈沉等[64]也开展了静音锥的数值研究工作。
综上,基于JSGD理论的低声爆设计方法是可行的,在某一基准构形下,通过JSGD理论设计合适的F函数可以使声爆进一步减小,但无法给出可能存在的更低声爆外形,而通过外形布局的巧妙设计,比如湾流公司的静音锥,洛马的LM1044,就获得了更低的声爆。还有一些未经过充分验证的非常规布局,比如,类似于Busemann的上下双翼构型[65],利用激波和膨胀波之间的干扰以减弱激波强度。更多的通过外形布局设计减小声爆的构想可参考Maglieri的综述文章[14]。
3 总结与展望本文先介绍了Whitham修正线性理论的两种表述的主要思想和公式,这是标准声爆理论和声爆最小化方法的基础,然后评述了在概念设计中声爆预测的几种方法及应用,接着介绍了低声爆构型概念设计的重要方法——声爆最小化方法,以及该方法应用的两个典型例子。
1) 标准声爆理论中的F函数建立了飞机横截面积与声压以及声爆之间的关联,声爆最小化方法给出了设计合适的F函数以达到尽可能小的声爆的策略。已有工作表明声爆理论和最小化方法是有效的。
2) 声爆最小化方法的应用效果受制于初始的布局构型,当应用该方法不能达到设计目标时,也许不得不尝试修改初始的布局构型,甚至多次修型迭代。初始布局构型的设计非常关键。
当前超声速民机有一些主要的设计目标,在概念设计中存在着特有的难以兼顾的矛盾,这大大增加了设计难度和工作量。解决途径是发展专门针对超声速民机的多学科多目标优化设计方法,其中,标准声爆理论和最小化方法是组成该设计方法的重要基石。声爆最小化方法是针对声爆这个唯一目标的,实际应用中仅仅依靠声爆最小化方法通常难以满足设计要求,亟需进一步研究可以有效地兼顾声爆/阻力等多目标参数的理论和方法。
| [1] |
MORGENSTERN J M, et al. Advanced concept studies for supersonic commercial transports entering service in 2030-35[C]//28th AIAA Applied Aerodynamics Conference, June 2010, Chicago, Illinois, AIAA-2010-5114.
|
| [2] |
SEEBASS R, ARGROW B. Sonic boom minimization revisited[C]//Proceedings of the 2nd Theoretical Fluid Mechanics Meeting, AIAA, Reston, VA, June 1998, AIAA-98-2956.
|
| [3] |
PLOTKIN K J, et al. Ground measurements of a shaped sonic boom[C]//10th AIAA/CEAS Aeroacoustics Conference, AIAA-2004-2923.
|
| [4] |
PAWLOWSKI J W, et al. Origins and overview of the shaped sonic boom demonstration program[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, January 2005, Reno, Nevada, AIAA-2005-5.
|
| [5] |
COWART R, et al. An overview of the gulfstream/NASA quiet spikeTM flight test program[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Jan. 2008, Reno, Nevada, AIAA-2008-123.
|
| [6] |
SUN YC, SMITH H. Review and prospect of supersonic business jet design[J]. Progress in Aerospace Sciences, 2017, 90: 12-38. DOI:10.1016/j.paerosci.2016.12.003 |
| [7] | |
| [8] |
WHITHAM G B. The flow pattern of a supersonic projectile[J]. Communications on Pure and Applied Math, 1952, 3: 301-348. |
| [9] |
WHITHAM G B. On the propagation of weak shock waves[J]. Journal of Fluid Mechanics, 1956, 1: 290-318. DOI:10.1017/S0022112056000172 |
| [10] |
PLOTKIN K J. Review of sonic boom theory[C]//AIAA 12th Aeroacoustics Conference, AIAA-1989-1105.
|
| [11] |
杨训仁, 陈宇. 大气声学(第二版)[M]. 北京: 科学出版社, 2007. YANG X R, CHEN Y. Atmosphere acoustics[M]. Beijing: Science Press, 2007. (in Chinese) |
| [12] |
张强. 气动声学基础[M]. 北京: 国防工业出版社, 2012. ZHANG Q. Fundamentals of aerodynamic acoustics[M]. Beijing: Defense Industry Press, 2012. (in Chinese) |
| [13] |
WALKDEN F. The shock pattern of a wing-body combination, far from the flight path[J]. Aero Quarterly, 1958, Ⅰ: 164-194. |
| [14] |
MAGLIERI D J, et al. Sonic boom six decades of research[R]. NASA/SP-2014-622, 2014.
|
| [15] |
MIDDLETON D, CARLSON H W. A numerical method for calculating near-field sonic boom pressure signatures[R]. NASA-TN-D-3082, 1965.
|
| [16] |
HAYES W D, et al. Sonic boom propagation in a stratified atmosphere with computer program[R]. 1968, NASA CR-1299.
|
| [17] |
TAYLOR A D. The TRAPS sonic boom program[R]. NOAA TM ERL-87, 1980.
|
| [18] |
THOMAS C L. Extrapolation of sonic boom pressure signatures by the waveform parameter method[R]. NASA TN D-6832, 1972.
|
| [19] |
PLOTKIN K J. Focus boom footprints for various air force supersonic operations[R]. Wyle Research Report WR 85-22, 1985.
|
| [20] |
PLOTKIN K J. A rapid method for the computation of sonic booms[C]//15th AIAA Aeroacoustics Conference, October 1993, Long Beach, CA, AIAA-1993-4433.
|
| [21] |
PLOTKIN K J, et al. USAF single-event sonic boom prediction model: PCBoom3[R]. N95-14889, 1995.
|
| [22] |
PAGE J A, PLOTKIN K J, WILMER C. PCBoom Version 6.6 technical reference and user manual[R]. Wyle, Rept. WR-10-10, 2010.
|
| [23] |
RALLABHANDIS K. Sonic boom adjoint methodology and its applications[C]//29th AIAA Applied Aerodynamics Conference, June 2011, Honolulu, Hawaii, AIAA-2011-3497.
|
| [24] |
LEE Y. Numerical solution of the KZK equation for pulsed finite amplitude sound beams in thermoviscous fluids[D]. Ph. D. dissertation, The University of Texas at Austin, 1993.
|
| [25] |
PINTON G F, TRAHEY G E. Shock wave propagation with the KZK equation[C]//IEEE Ultrasonic Symposium, P2L-6, October 2006.
|
| [26] |
TAKENO J, et al. Analysis of sonic boom propagation based on the KZK equation[C]//53rd AIAA Aerospace Sciences Meeting, January 2015, Kissimmee, Florida, AIAA-2015-0745.
|
| [27] |
陈鹏, 李晓东. 基于Khokhlov-Zabolotskaya-Kuznetsov方程的声爆频域预测法[J]. 航空动力学报, 2010, 25(2): 359-365. CHEN P, LI X D. Frequency domain method for predicting sonic boom propagation based on Khokhlov-Zabolotskaya-Kuznetsov equation[J]. Journal of Aerospace Power, 2010, 25(2): 359-365. (in Chinese) |
| [28] |
冯晓强, 李占科, 宋笔锋, 等. 基于混合网格的声爆/气动一体化设计方法研究[J]. 空气动力学学报, 2014, 32(1): 30-37. FENG X Q, LI Z K, SHOU B F, et al. Optimization of sonic boom and aerodynamic based on structured/unstructured hybrid grid[J]. Acta Aerodynamica Sinica, 2014, 32(1): 30-37. (in Chinese) |
| [29] |
LENG Y, QIAN Z S. Sonic boom signature prediction and analysis for a type of hypersonic long-range civil vehicle[C]//21st AIAA International Space Planes and Hypersonics Technologies Conference, March 2017, Xiamen, China, AIAA-2017-2244.
|
| [30] |
王刚, 马博平, 雷知锦, 等. 典型标模音爆的数值预测与分析[J]. 航空学报, 2018, 39(1): 121458. WANG G, MA B P, LEI Z J, et al. Simulation and analysis for sonic boom on several benchmark cases[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 121458. (in Chinese) |
| [31] |
郝璇, 苏诚, 刘芳, 等. 超声速飞行器低声爆气动布局优化设计研究[J]. 空气动力学学报, 2018, 36(2): 327-333. HAO X, SHU C, LIU F, et al. Optimization design research on low sonic boom configuration for supersonic transport[J]. Acta Aerodynamica Sinica, 2018, 36(2): 327-333. DOI:10.7638/kqdlxxb-2016.0047 (in Chinese) |
| [32] |
张绎典, 黄江涛, 高正红. 基于增广Burgers方程的音爆远场计算及应用[J]. 航空学报, 2018, 39(7): 122039. ZHANG Y D, HUANG J T, GAO Z H, et al. Far field simulation and applications of sonic boom based on augmented Burgers equation[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 122039. (in Chinese) |
| [33] |
朱自强, 兰世隆. 超声速民机和降低声爆研究[J]. 航空学报, 2015, 36(8): 2507-2528. ZHU Z Q, LAN S L, et al. Study of supersonic commercial transport and reduction of sonic boom[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2507-2528. (in Chinese) |
| [34] |
RALLABHANDIS K, MAVRIS D N. Sonic boom minimization using inverse design and probabilistic acoustic propagation[J]. Journal of Aircraft, 2006, 43(6): 1815-1828. DOI:10.2514/1.20457 |
| [35] |
PLOTKIN K J, RALLABHANDIS K, LI W. Generalized formulation and extension of sonic boom minimization theory for front and aft shaping[C]//47th AIAA Aerospace Sciences Meeting, January 2009, Orlando, Florida, AIAA-2009-1052.
|
| [36] |
PLOTKIN K J. Sonic boom shaping in three dimensions[C]//15th AIAA/CEAS Aeroacoustics Conference, May 2009, Miami, Florida, AIAA-2009-3387.
|
| [37] |
JONES L B. Lower bounds for sonic bangs[J]. Journal of Royal Aeronautical Society, 1961, 65: 1-4. DOI:10.1017/S0001924000063545 |
| [38] |
MCLEAN F E. Some Non-Asymptotic effects on the sonic boom of large airplanes[R]. NASA TN D-2877, June 1965.
|
| [39] |
HAYES W D. Brief review of the basic theory. Sonic boom research[R]. SEEBASS A R(ed.), NASA SP-147, 1967.
|
| [40] |
SEEBASS R. Sonic boom theory[J]. Journal of Aircraft, 1969, 6(3): 177-184. DOI:10.2514/3.44032 |
| [41] |
GEORGE A R. Lower bounds for sonic booms in a midfield[J]. AIAA Journal, 1969, 7(8): 1542-1545. DOI:10.2514/3.5429 |
| [42] |
GEORGE A R, SEEBASS R. Sonic boom minimization including both front and rear shocks[J]. AIAA Journal, 1971, 9(10): 2091-2093. DOI:10.2514/3.6478 |
| [43] |
SEEBASS R, GEORGE A R. Sonic boom minimization[J]. Journal of the Acoustical Society of America, 1972, 51(2C): 686-694. DOI:10.1121/1.1912902 |
| [44] |
DARDEN C M. Sonic boom theory:its status in prediction and minimization[J]. Journal of Aircraft, 1977, 14(6): 569-576. DOI:10.2514/3.58822 |
| [45] |
DARDEN C M. Sonic boom minimization with nose-bluntness relaxation[R]. NASA Langley Research Center, TP-1348, Hampton, VA, Sept. 1979.
|
| [46] |
PETTY J S. Lower bounds for sonic boom considering the negative overpressure region[J]. Journal of Aircraft, 1970, 7(4): 375-377. DOI:10.2514/3.44182 |
| [47] |
RALLABHANDIS K, MAVRIS D N. Sonic boom minimization using improved linearized tools and probabilistic propagation[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, January 2005, Reno, Nevada, AIAA-2005-1019.
|
| [48] |
RALLABHANDIS K, MAVRIS D N. Aircraft geometry design and optimization for sonic boom reduction[J]. Journal of Aircraft, 2007, 44(1): 35-47. DOI:10.2514/1.20456 |
| [49] |
COLONNO M R, ALONSO J J. Sonic boom minimization revisited: the robustness of optimal low-boom designs[C]//13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, September 2010, Fort Worth, Texas, AIAA-2010-9364.
|
| [50] |
LEATHERWOOD J D, SULLIVAN B M. Effect of sonic boom asymmetry on subjective loudness[R]. NASA TM-107708, 1992.
|
| [51] |
LEATHERWOOD J D, et al. Summary of recent NASA studies of human response to sonic booms[J]. Journal of Acoustic Society American, 2002, 111(1): 586-598. DOI:10.1121/1.1371767 |
| [52] |
MORGENSTERN J, et al. Optimum signature shaping for low sonic boom[C]//30th Applied Aerodynamics Conference, June 2012, AIAA-2012-3218.
|
| [53] |
MORGENSTERN J, et al. Overview of sonic boom reduction efforts on the Lockheed Martin N+2 supersonic validations program[C]//32nd AIAA Applied Aerodynamics Conference, June 2014, Atlanta, GA, AIAA-2014-2138.
|
| [54] |
DARDEN C M, et al. Status of sonic boom methodology and understanding[R]. 1989, NASA CP-3027.
|
| [55] |
DARDEN C M. Limitations of linear theory for sonic boom calculations[J]. Journal of Aircraft, 1993, 30(3): 309-314. DOI:10.2514/3.46335 |
| [56] |
LI J H et al. Shape optimization of supersonic bodies to reduce sonic boom signature[C]//34th AIAA Applied Aerodynamics Conference, June 2016, Washington, D. C., AIAA-2016-3432.
|
| [57] |
LI J H et al. Prediction, minimization and propagation of sonic boom from supersonic bodies[C]//55th AIAA Aerospace Sciences Meeting, January 2017, Grapevine, Texas, AIAA-2017-277.
|
| [58] |
冯晓强, 李占科, 宋笔锋. 超声速客机低音爆布局反设计技术研究[J]. 航空学报, 2011, 32(11): 1980-1986. FENG X Q, LI Z K, SHOU B F, et al. A research on inverse design method of a lower sonic boom supersonic aircraft configuration[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 1980-1986. (in Chinese) |
| [59] |
冯晓强, 宋笔锋, 李占科, 等. 超声速飞机低声爆布局混合优化方法研究[J]. 航空学报, 2013, 34(8): 1768-1777. FENG X Q, SHOU B F, LI Z K, et al. Hybrid optimization approach research for low sonic boom supersonic aircraft configuration[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1768-1777. (in Chinese) |
| [60] |
乔建领, 韩忠华, 宋文萍. 基于代理模型的高效全局低音爆优化设计方法[J]. 航空学报, 2018, 39(5): 121736. QIAO J L, HAN Z H, SHOU W P, et al. An efficient surrogate-based global optimization for low sonic boom design[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 121736. (in Chinese) |
| [61] |
COWART R, et al. An overview of the Gulfstream/NASA Quiet SpikeTM flight test program[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Jan 2008, Reno, Nevada, AIAA-2008-123.
|
| [62] |
HOWE D C, et al. Quiet SpikeTM Near field flight test pressure measurements with computational fluid dynamics comparison[C]//46th AIAA Aerospace Sciences Meeting and Exhibit, Jan 2008, Reno, Nevada, AIAA 2008-128.
|
| [63] |
HOWE D C, et al. Improved sonic boom minimization with extendable nose spike[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, 2005, Reno, Nevada, AIAA-2005-1014.
|
| [64] |
沈沉, 周华. 细长杆降低超声速客机气动噪声的数值分析[J]. 空气动力学学报, 2012, 30(1): 39-45. SHEN C, ZHOU H. Numerical analysis of slender rod noise reduction of supersonic passenger aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(1): 39-45. DOI:10.3969/j.issn.0258-1825.2012.01.007 (in Chinese) |
| [65] |
UTSUMI Y, OBAYASHI S. Design of supersonic biplane aircraft concerning sonic boom minimization[C]//28th AIAA Applied Aerodynamics Conference 28 June-1 July 2010, Chicago, Illinois, AIAA-2010-4962.
|
 2019, Vol. 37
2019, Vol. 37



