2. 西北工业大学 航空学院 气动与多学科优化设计研究所, 西安 710072
2. Institute of Aerodynamic and Multidisciplinary Design Optimization, School of Aeronautics, Northwestern Polytechnical University, Xi'an 710071, China
从近期国际航空科学技术的发展来看,尽管高亚声速客机获得了极大成功,但随着日益增长的航空运输需求,飞行时间过长严重降低了远距离飞行旅客的舒适性和旅行效率,迫切需要发展飞行速度更快的客机。因此,超声速客机成为未来民机发展的重点方向之一。
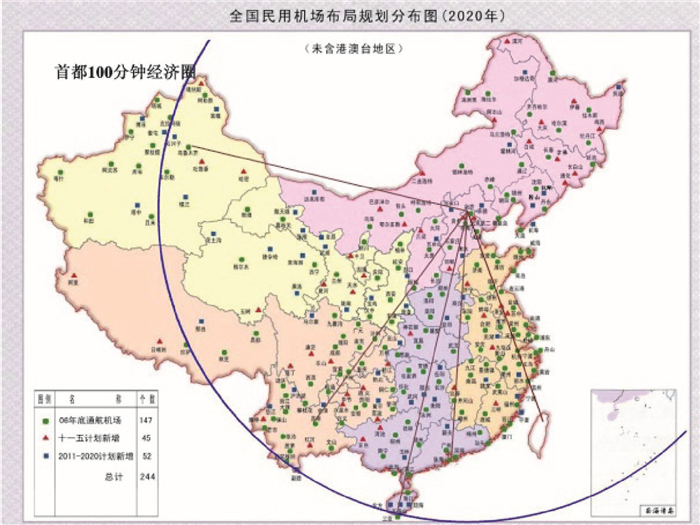
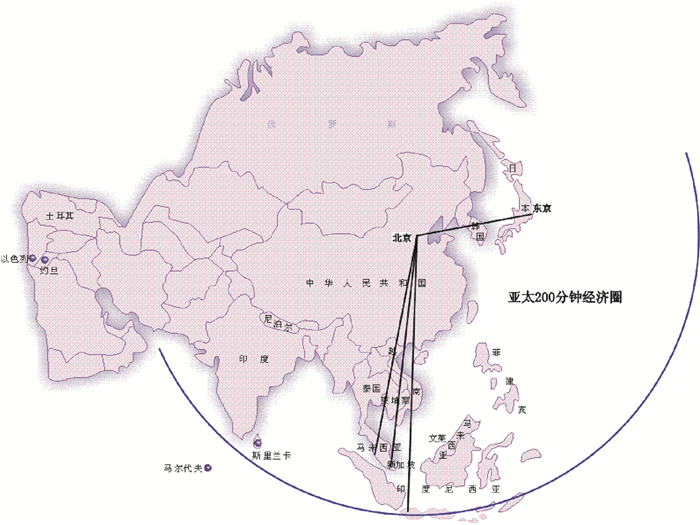
更快的旅行速度是人类永恒的追求。在民用航空领域,超声速客机的作用类似于公路系统中的“高速公路”、铁路系统中的“高铁”。相比于传统亚声速民机,超声速客机能够成倍地缩短飞行时间,可大幅提高旅行效率。以巡航马赫数为2的超声速客机为例,相同飞行距离下能比现有亚声速客机节省一半以上的时间。更快的旅行速度能够促进世界各国在经济、政治、文化等领域的交流与合作。以中国为例,超声速客机可大幅度缩短旅行时间,有利于形成首都100分钟经济圈(图 1),显著改善国内旅客的出行效率。随着中国与东盟各国、周边国家经济交流的不断深入,考虑到未来东盟经济贸易一体化趋势的不断发展,利用超声速客机打造亚太地区200分钟经济圈(图 2),加强同东南亚和中国周边各国的交往,对于进一步促进我国经济可持续发展具有重大的现实意义。另外,发展超声速客机可以极大促进我国同世界各国在经济文化等领域的交流与合作,形成“全球一日经济圈”。例如从北京到华盛顿,乘坐高亚声速客机需要约15小时,而乘坐超声速客机可以减少到6个小时,旅行效率大大提高。
|
图 1 首都100分钟经济圈示意图 Fig.1 Sketch of 100 minutes economic circle around Beijing |
|
图 2 亚太200分钟经济圈示意图 Fig.2 Sketch of Asian-Pacific economic circle within 200 minutes |
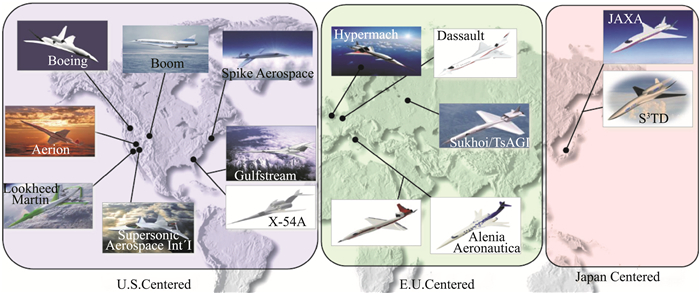
超声速客机的研制开始于20世纪中后期。20世纪60年代,美国、英法和前苏联就分别论证了超声速客机的可行性,并启动了第一代超声速客机研究计划。20世纪70年代,“协和”号、“图 144”分别投入商业运营[1]。但是,由于其严重的声爆问题(“协和”号巡航阶段的地面声爆可达108 PLdB)以及耗油率高、安全性差等问题,最终导致了以“协和”号为代表的第一代超声速客机商业运营的失败[2]。20世纪90年代前后,各国在吸取第一代超声速客机失败教训的基础上,提出了各自的第二代超声速客机研究计划,其中最具代表性的是美国的HSCT(High Speed Civil Transport)计划[3],但这些计划仅仅停留在方案设计阶段并未付诸制造。21世纪以来,随着航空科学技术的快速进步,世界各国均掀起了新一代环保型超声速客机的研究热潮。美国、欧洲和日本分别针对这些关键问题制定了一系列研究计划(如图 3),包括HSR(High Speed Research)计划[4]、QSP(Quiet Supersonic Platform)计划[4]、NEXST计划[5]、“N+3”计划[6]等。以美国为例,NASA在过去15年内至少投入18亿美元的经费来开展新一代超声速客机技术的研究。此外,以波音公司和洛克希德-马丁公司为代表的飞机制造商也在超声速客机研究方面有大量投入。根据NASA制定的“N+3”计划,在10年内美国将研制出可投入商业运营的小型超声速公务客机,在20年左右时间将研制出100-300座的大型超声速客机(如表 1所示)。由表 1可知,新一代超声速客机在地面声爆强度、氮氧化物排放、耗油率、载客量等方面都有十分严格的要求。
|
图 3 美国、欧洲和日本关于超声速客机的研究进展[7] Fig.3 Research progress of supersonic transports by USA, Europe and Japan[7] |
| 表 1 NASA“N+3”计划中各阶段超声速客机的技术指标要求[6] Table 1 Technical indicators of supersonic transport aircrafts in different phases of NASA's N+3 program[6] |
|
|
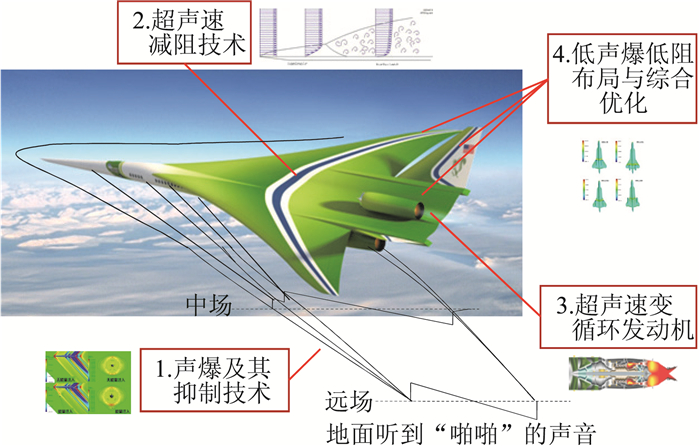
通过大量文献的调研和详细数据分析,特别是从国外这些主要研究计划的深入分析,认为新一代环保型超声速客机相比于其他种类飞机具有一些独特的性能要求,因此首要需要突破如下四大关键技术:(1)声爆预测及其抑制技术;(2)超声速减阻技术;(3)超声速变循环发动机技术;(4)低声爆低阻布局与综合优化技术。图 4给出了各关键技术与超声速客机的对应关系示意图。本文主要对这四个方面的关键技术进行综述,对研究现状进行分析,并进一步介绍西北工业大学超声速客机研究中心在新一代超声速客机关键技术方面的研究进展。
|
图 4 新一代环保型超声速客机研制所面临的四大关键技术瓶颈 Fig.4 Key technologies of the next-generation environmentally friendly supersonic transports |
声爆是由飞行器在超声速飞行时产生的激波和膨胀波系在大气中演化并传播到地面引起的。地面声爆强度与机体周围的激波膨胀波分布、传播时的大气条件有着密切关系。较强的地面声爆会严重影响生态环境和人类正常的生活工作,严重时甚至破坏建筑物。以“协和”号超声速客机为例,其巡航时的地面声爆高达108 PLdB,因而被美国、马来西亚等多个国家禁止在陆地上空作超声速飞行。这极大地限制了超声速客机运营航路规划,削弱了市场竞争力。据了解,国际民航组织明确指出,超声速客机的地面声爆强度必须降低至可接受的标准,才允许在大陆上空超声速飞行。虽然民航组织还未给出具体的指标要求,但NASA的“N+3”计划要求是声爆水平不超过70 PLdB,而目前国际先进水平只能达到80~85 PLdB。声爆每降低1个分贝,都意味着声能量的显著降低。要达到这个要求,在技术上的差距十分显著,新一代环保型超声速客机研制面临巨大挑战。因此,声爆及其抑制技术应该是其最先需要突破的核心关键技术。
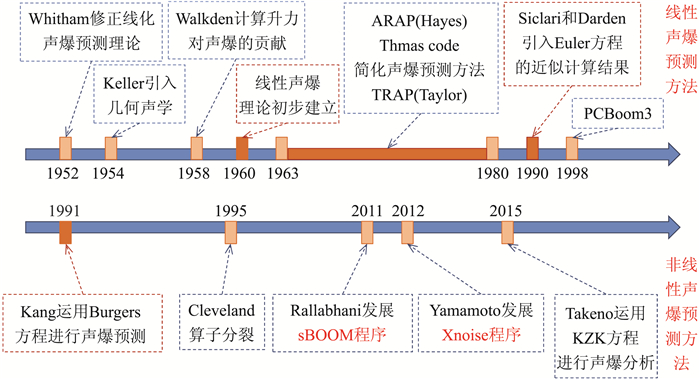
对远场声爆强度的准确预测,是评估和降低声爆水平的前提。从20世纪50年代开始,国际上针对声爆预测开展了系统性研究(如图 5),发展了多种方法(各方法的优缺点如表 2所示),开发了一系列预测程序。其中,近场CFD计算与增广Burgers方程相结合的方法,由于能够比较准确计算激波上升时间、且计算量相对较小,逐渐成为高精度声爆预测的最主要方法。目前,基于增广Burgers方程的声爆传播计算,已经能够考虑分子弛豫、热粘吸收、大气分层、几何声学、风梯度、经典非线性等效应对声爆的影响。除上述效应外,大气湍流对声爆传播的影响也受到重视。2015年,日本Takeno等[22]用统计学方法将大气边界层内的阵风湍流影响加入到KZK(Khokhlove-Zabolotskaya- Kuznetsov)方程中,开展了考虑大气湍流影响的声爆预测研究。在国内,从公开发表的文献看,我国对声爆预测方面的研究开始于2009年[23-24],西北工业大学和北京航空航天大学是最早开展声爆研究的单位。虽然起步较晚,但目前也取得了较大进展。近几年来,国内在近场声爆CFD计算与基于增广Burgers方程的远场声爆预测方面进展迅速。西北工业大学[25-27]、中国空气动力研究与发展中心[27]、航空工业空气动力研究院[28-30]、中国航空研究院[31]、中国商飞公司北京民用飞机技术研究中心[32]等多家单位都开展了相关研究,发展了一系列声爆的近、远场预测方法,并针对AIAA声爆预测研讨会发布的标模进行了计算研究。
|
图 5 国际上关于声爆预测理论与方法研究的发展历程(含代表性的预测软件或程序) Fig.5 Development history of sonic-boom prediction theory and methods (including representative prediction software or codes) |
| 表 2 现有声爆预测方法及其优缺点 Table 2 Strength and weakness of existing sonic-boom prediction methods |
|
|
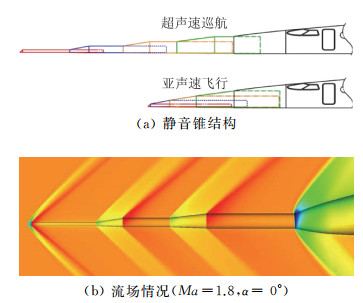
在对声爆预测理论和方法开展研究的同时,声爆抑制技术的研究也在同步进行。声爆抑制技术主要分两类:主动抑制技术和被动抑制技术。主动抑制技术中,以能量注入技术为代表。Zaidi[33-34]通过激光脉冲的方式向超声速流场中注入能量,改变了原本的激波结构,避免飞机各部件产生的激波相互叠加和干扰,实现了降低远场声爆强度的目的。被动抑制技术中,以静音锥技术为代表,湾流公司[35-36]提出通过在机头安装若干可伸缩的圆锥体和圆柱体,能够使机头原本较强的弓形激波变为若干道弱激波,并避免声爆传播过程中出现激波的叠加和干扰,从而达到延长远场声爆上升时间、降低声爆强度的目的。如图 6为静音锥的结构及其近场流场情况。在国内,针对声爆抑制技术的研究也主要集中在能量注入和低声爆静音锥技术方面[37-39],探索了相关参数对声爆抑制效果的影响规律。
|
图 6 静音锥构型及其流场情况[40-41] Fig.6 Configuration of a low-boom quiet spike and corresponding flow field [40-41] |
超声速减阻技术是提高超声速客机经济性的主要手段,是新一代环保型超声速客机的另一个关键技术。与亚声速飞行不同,超声速飞行时激波不可避免,因此降低激波阻力和摩擦阻力成为减阻的重点。
激波是将飞行器超声速飞行时的部分能量以压缩空气做功的形式传递到大气中,其强度与飞机的等效截面积分布密切相关。目前,减小激波阻力主要是通过优化飞机的等效截面积分布或采用消波技术来实现。优化飞机等效截面积来降低激波阻力,主要根据超声速面积率,即等效截面积变化平缓的飞机其激波阻力较小。而消波技术主要基于斜激波和膨胀波理论,以Busemann双层翼技术[42-45]为代表(图 7),利用两翼型之间的激波干涉与反射效应来达到消除或降低激波阻力的目的。但目前该技术需要解决在非设计点存在的流动“雍塞”等问题。国内,中国航天空气动力技术研究院[46]和西北工业大学[47]分别开展了Busemann双翼的相关研究。

|
图 7 Licher双层翼布局与激波抑制技术[42-45] Fig.7 Licher biplane configuration and shock wave control technology[42-45] |
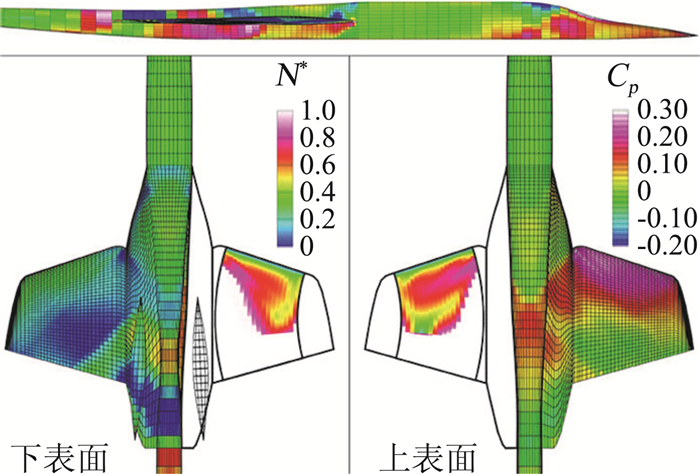
除激波阻力外,超声速巡航时的摩擦阻力也不容忽视。研究表明,超声速客机的摩阻仍然占总阻力的20%~40%,而采用自然层流技术有可能实现5%~10%的减阻效果,具有巨大的潜力。美国[48-50]、欧洲[51-52]、日本[53-55]均开展了大量超声速层流减阻技术的研究,目前已应用于部分型号设计。例如Aerion公司的AS2[50](图 8),通过对机翼、机翼与机身结合部进行优化设计,实现了大范围超声速自然层流,从而显著降低了巡航阶段的摩擦阻力。相比之下,国内目前尚未见到关于超声速层流翼型和机翼设计方面的研究报道。
|
图 8 Aerion公司AS2超声速公务机的自然层流机翼设计[50] Fig.8 Natural-laminar-flow wing designed for supersonic business jet AS2 of Aerion[50] |
性能优良的航空发动机是超声速客机能够持续以高燃油效率进行超声速巡航的保证,是新一代环保型超声速客机实现经济性和环保性的重要支撑。虽然“协和”和“图-144”都投入了市场运营,但由于其发动机的耗油率高、噪声大、氮氧化物的排放量大等问题,造成客机经济性差、环保不达标,再加上其他原因最终导致其退出历史舞台[2]。新一代环保型超声速客机应该克服上述缺点,其发动机应该在亚声速和超声速飞行时都具有良好的经济性和推重比。目前,广泛应用于亚声速飞行的大涵道比涡扇发动机无法用于超声速飞行,而小涵道比涡扇或涡喷发动机,在起飞阶段噪声较大、亚声速飞行时耗油率偏高、污染物的排放量较多。因此,为缓解亚声速飞行和超声速巡航的动力矛盾,需要发展能够兼顾两者优势的发动机,将其作为新一代超声速客机的动力装置。而变循环发动机(variable-cycle engine, VCE)由于具有能够兼顾亚声速巡航低油耗和超声速巡航高推重比的优点,受到了广泛关注,成为发展新一代环保型超声速客机的关键技术之一。
伴随着各种超声速客机的研究计划,国外变循环发动机的研制得到了长足进步。从20世纪70年代开始,通用电气公司(GE)就研制了从YJ101第一代变循环验证机到GE21、GE33(即后来的YF120,如图 9)变循环发动机[56]。罗罗公司在20世纪80年代也提出了变循环发动机方案,但并未投入实际应用[57]。NASA在关于“N+3”代超声速客机的研究计划[58]中,已经将超声速变循环发动机技术作为推进系统研究的重要内容。
在国内,与航空发动机技术相关的各科研院所和高校都非常重视变循环发动机的研究。沈阳发动机设计研究所[59]、北京航空航天大学[60]、西北工业大学[61]、南京航空航天大学[62]和空军工程大学[63]等纷纷开展了不同层次的分析与设计研究。但目前在公开发表的文献中,还没有关于变循环发动机验证机的报道。
1.4 低声爆低阻布局及综合优化技术的国内外研究进展低声爆低阻布局及综合优化技术,是发展新一代环保型超声速客机的又一关键技术。从近期国际航空科学技术的发展趋势分析,由于超声速客机的特殊性,特别是声爆这一问题的出现,常规布局无法同时满足低声爆和低阻的苛刻设计要求,急需发展新的布局设计理念和设计方法以获得满足要求的布局。从声爆来源来看,声爆是飞机对周围空气的压缩引起的,如何在兼顾气动性能的情况下控制气流的压缩形式以使远场声爆达到最小,成为研究的重点。目前,国内外主要采用等效截面积分布的反设计方法(SGD)和声爆/气动综合优化设计方法来实现气动与声爆的权衡。
SGD方法是在20世纪70年代由Seebass、George和Darden[64-65]在线化声爆预测理论的基础上提出并完善的。由于声爆F函数[10]包含了飞行器作为声源的特性,通过优化声爆F函数的分布形式可以使远场声爆强度降低。然后,在此基础上,根据F函数与飞机等效截面积分布的对应关系,获得超声速客机的等效截面积分布。最后,通过调整飞机的外形参数来获得最优的等效截面积分布。该方法在20世纪末的HSCT计划及本世纪以来的新一代超声速客机计划中仍有大量应用[3]。
近年来,随着高效数值优化算法、高精度声爆预测以及计算流体力学的飞速发展,声爆/气动综合优化设计在超声速客机精细化设计的研究中得到了重视。其中,高效优化算法主要为基于Adjoint的梯度方法和运用类似机器学习技术的代理优化方法;高精度声爆预测主要采用近场CFD计算与远场基于增广Burgers方程传播相结合的方法;高精度气动分析主要采用基于高分辨率、低耗散雷诺平均Navier-Stokes(RANS)方程的求解器。例如,2014年Rallabhandi[66]运用基于增广Burgers方程的伴随方法实现了超声速公务机的优化设计。2018年Kirz[67]运用代理优化方法开展了美国AIAA声爆预测研讨会标模的低声爆优化设计研究。
针对超声速客机的低声爆和低阻要求,国际上提出了一系列新概念布局,以大幅度改善飞机的声爆特性。例如美国SAI的QSST[68]、美国N+X代超声速客机方案[6]、日本小型SST[69]、俄罗斯S-21[70]、法国Trijet超声速公务机[70]、迈阿密大学查戈成教授提出的双向飞翼布局[71]等,部分外形如图 10所示。值得关注的是,美国BOOM公司2016年完成了BOOM Airliner设计[72],现已完成低声爆验证机XB-1的风洞试验,下一步准备进行试飞验证,并计划2023年投入市场运营。2017年,Sun等[73]对当今主要超声速公务机的布局和设计方法进行了较全面的综述。2018年,NASA和洛马公司完成了低声爆验证机X-59 QueSST的设计和风洞试验[74]。

|
图 10 国际上一些低声爆、低阻超声速客机布局的研究进展概况 Fig.10 Recent progress of low-boom and low-drag configurations for supersonic transport |
在国内,各研究院所和高校也都相继开展了低阻低声爆布局和声爆/气动综合优化设计方法的研究,尤其是在最近几年取得了较大进展。在低声爆优化设计方面,西北工业大学发展了基于代理模型的高效优化设计方法[75]和基于本征正交分解与增广Burgers方程的低声爆反设计方法[76],为降低远场声爆强度提供了新思路。中国航天空气动力技术研究院[77]基于遗传算法和超声速线化理论及波形参数法,开展了某公务机的低声爆优化设计,并对气动性能进行了评估。中国空气动力研究与发展中心[78]推导出流场/声爆的耦合伴随方程,并开展了超声速公务机的低声爆优化设计研究。中国航空研究院[79]开发了超声速民机的低声爆优化设计平台,并采用标模进行了优化设计验证。
针对前文梳理的关键技术,下文将西北工业大学的研究进展进行比较详细的介绍。西北工业大学是国内最早从事声爆研究的单位之一,也是比较系统化地开展超声速客机关键技术研究的单位之一。因此,对西北工业大学过去10年研究工作的总结和梳理,对于国内相关领域的研究具有参考意义。
2 西北工业大学超声速客机研究中心研究进展西北工业大学自2009年起,比较系统地开展了关于声爆预测理论方法、声爆抑制、超声速客机布局与优化设计、以及超声速层流减阻技术等研究。2016年,瞄准超声速客机技术的发展前沿,依托翼型/叶栅空气动力学国家级重点实验室和飞行器设计国家重点学科,重新梳理了超声速客机关键技术的研究方向,并组建了超声速客机研究中心(下文简称“中心”)。下文将对中心研究进展进行介绍。
2.1 声爆预测理论和方法研究进展根据超声速客机从概念设计到详细设计阶段对声爆预测的不同需求,中心发展了快速预测方法和高精度预测方法。快速预测方法包括简化声爆预测方法和声爆修正线化预测理论;高精度预测方法主要是近场CFD计算与远场传播方法(波形参数法和增广Burgers方程)相结合的方法。
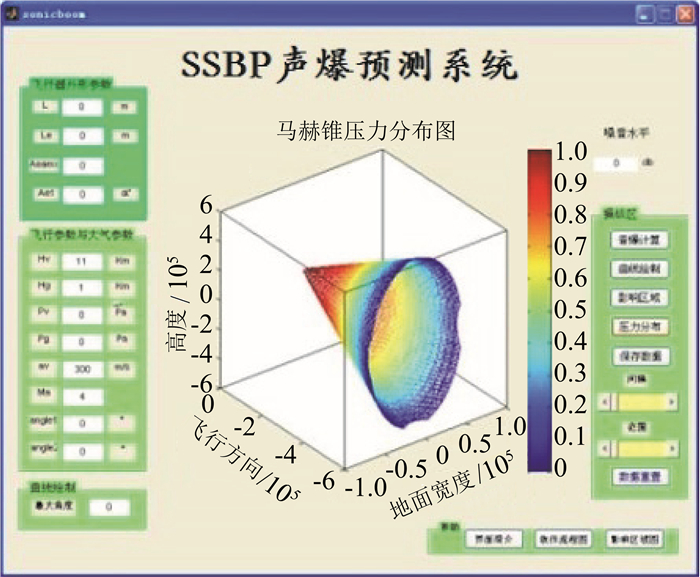
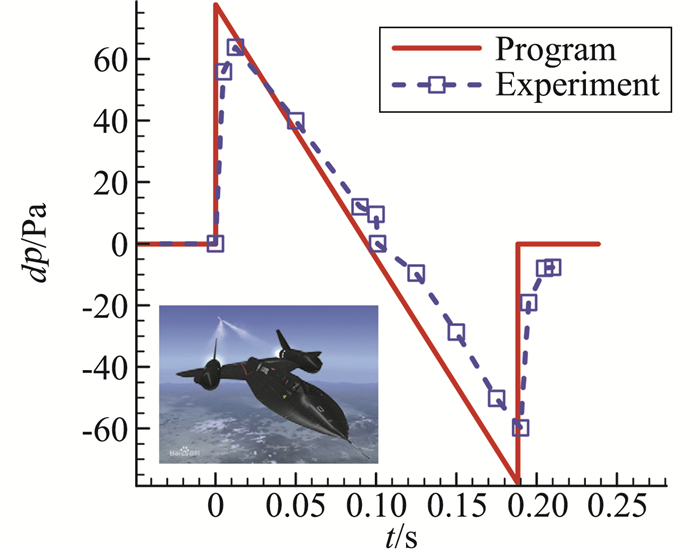
基于简化预测方法,中心发展了简化声爆预测系统“SSBP”[24](如图 11),并针对典型超声速飞机开展了声爆特性研究。以SR-71为例,在巡航马赫数为1.5、飞行高度为14.6 km的情况下,飞机正下方的计算的“N型波”与试验值对比如图 12所示。计算结果能够初步反映“N型波”的形态,在过压量级上与试验值能够良好符合。
|
图 11 所开发的SSBP简化声爆预测系统[24] Fig.11 Sonic-boom prediction system based on simplified prediction method (SSBP)[24] |
|
图 12 简化声爆预测结果与试验值的对比[24] Fig.12 Comparison of predicted sonic boom by SSBP with flight test data[24] |
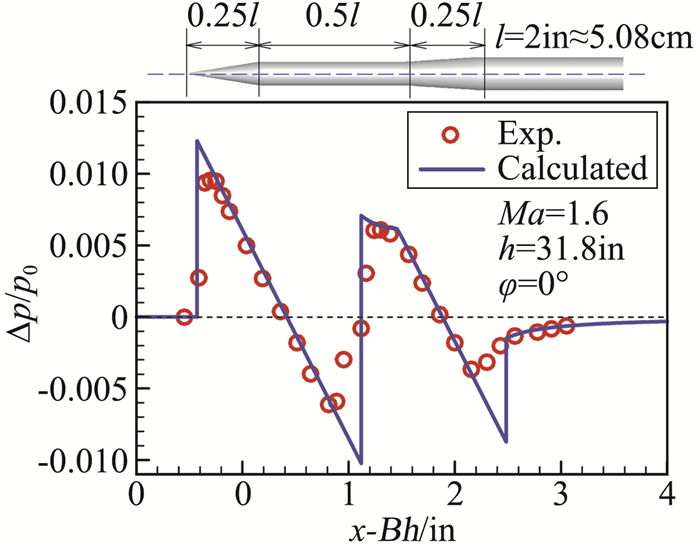
基于Whitham修正线化声爆预测理论,本中心发展了修正线化理论计算近场和远场声爆波形的预测方法。针对尖锥体标模,使用修正线化理论预测方法计算了在Ma1.41、模型正下方10倍模型长度位置的近场声爆信号。图 13给出了尖锥标模外形级和近场压强信号与实验值的对比,可知计算结果与实验值符合较好。
|
图 13 基于Whitham理论计算的压强信号与实验比较[80] Fig.13 Comparison of predicted sonic boom based on Whitham's theory with experimental data[80] |
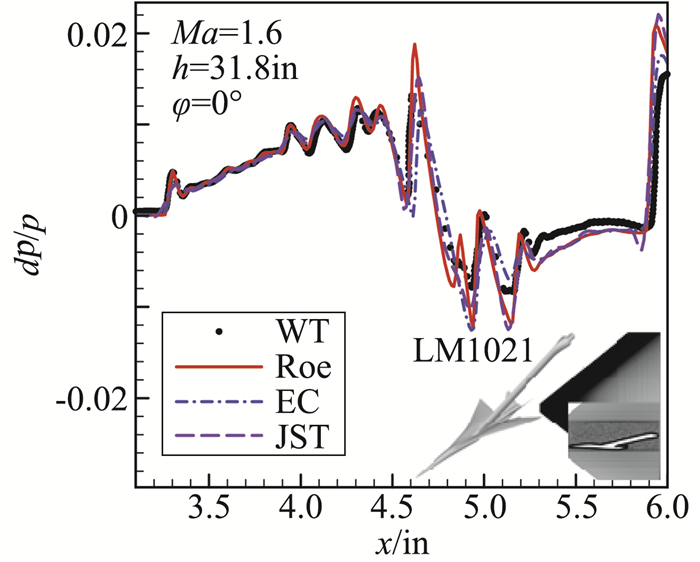
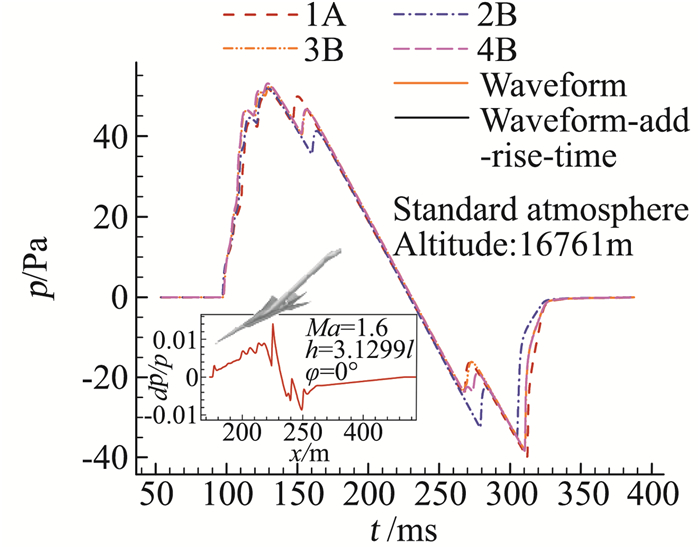
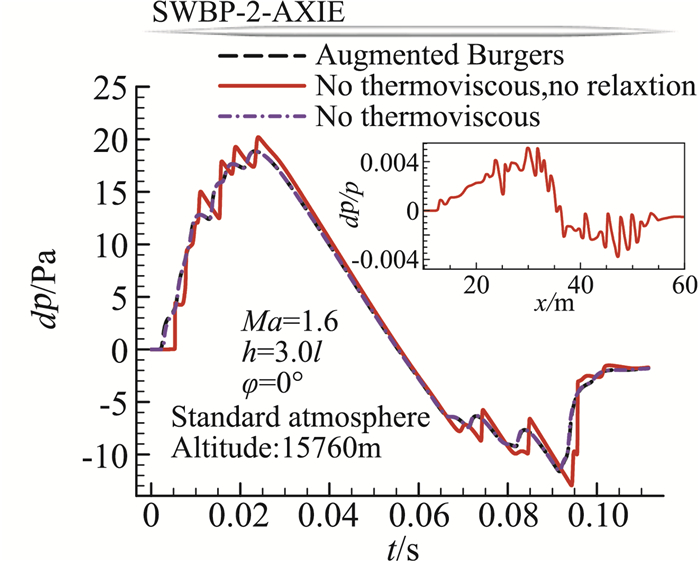
在高精度声爆预测方法方面,中心最近发展了一套近场高精度CFD数值模拟与远场传播方法相结合的方法。在近场声爆CFD计算方面,研究团队发展了能够高精度捕捉空间流场中激波膨胀波系的非结构网格求解器“HUNS3D”[80]。该CFD求解器具有熵相容EC格式、E-CUSP格式等多种空间离散格式。基于该求解器,开展了不同离散格式对近场压强信号计算结果的影响研究[81-83],如图 14所示。在远场传播方法方面,基于波形参数法发展了远场声爆预测方法[84],并采用经验公式添加了激波的上升时间,开发了“FL-BOOM”程序[85]。图 15为运用波形参数法对LM-1021标模的近场压强信号进行传播得到的远场波形,通过对比可知计算结果与SBWP-1(AIAA第一届声爆预测研讨会)提供的结果符合良好;基于增广Burgers方程传播的计算,发展了考虑分子弛豫、热粘吸收、大气分层、风梯度、几何声学、非线性等效应的声爆预测程序“bBoom”,研究了各个效应对远场波形的影响,以及风对声爆影响域的影响规律,如图 16所示。
|
图 14 不同空间离散格式计算的结果与风洞试验对比[81-83] Fig.14 Comparison of computed near-field pressure signals using different spatial discretization schemes with experimental data[81-83] |
|
图 15 由波形参数法得到的远场波形信号与SBPW2大会结果对比[80] Fig.15 Comparison of different far-field waveforms using waveform-parameter method with result of SBPW2[80] |
|
图 16 增广Burgurs方程中不同效应对远场波形的影响(bBoom程序) Fig.16 Comparison of far-field waveforms based on Burgers equation solutions considering different effects(bBoom code) |
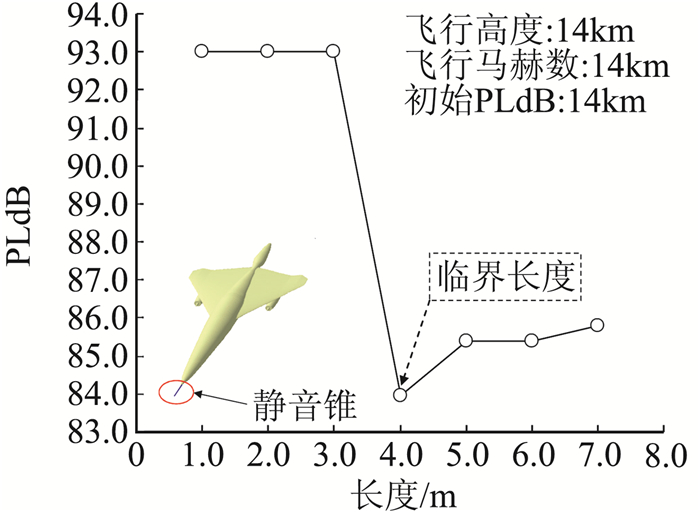
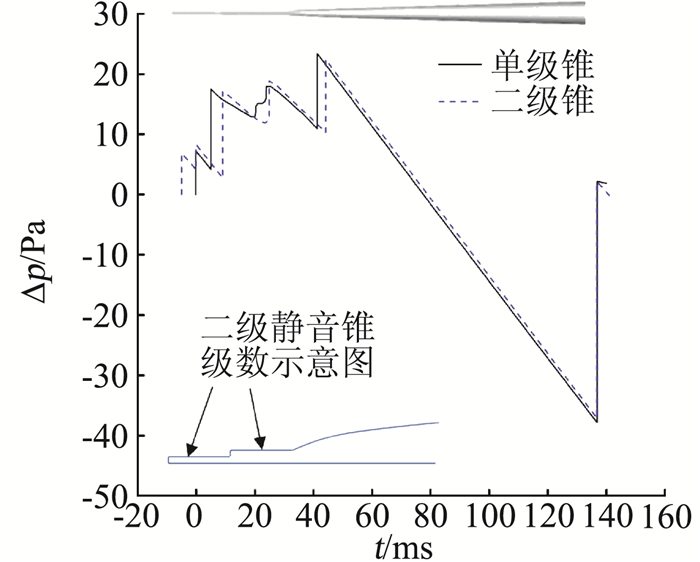
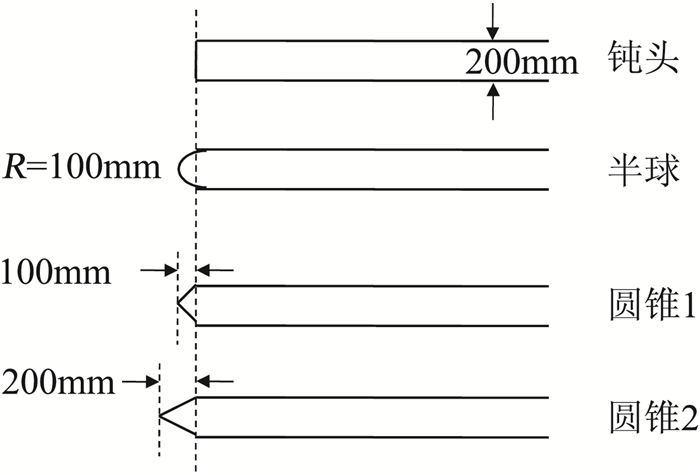
针对低声爆静音锥抑制技术,中心尝试开展了静音锥的长度、级数和头部形状对声爆抑制效果的影响规律研究[85-86]。图 17给出了不同长度静音锥的声爆抑制效果。研究表明,静音锥只有在其长度大于某一临界值时才具有显著的声爆抑制效果;当长度小于这一临界值时,静音锥产生的激波在传播过程中会与机头的强弓形激波合并,无法起到声爆抑制的作用。针对静音锥级数的研究表明,以二级静音锥和一级静音锥对比为例(如图 18),二级静音锥的初始过压和最大过压相对较小,声爆的持续时间更长,更具有低声爆的特征。针对静音锥的头部形状研究如图 19、图 20和表 3所示,结果表明不同头部形状的静音锥对声爆抑制的效果差异不大,但对静音锥的驻点温度及阻力系数有较大影响。
|
图 17 不同长度静音锥的声爆抑制效果 Fig.17 Sonic-boom reduction effects of quiet spikes with different length |
|
图 18 不同级数的静音锥对远场声爆波形的影响 Fig.18 Influences of different number of series of quiet spikes on far-field sonic-boom waveform |
|
图 19 不同头部形状的静音锥示意图 Fig.19 Sketch of quiet spikes with different noses |

|
图 20 不同头部形状的静音锥对应的近场压强信号 Fig.20 Comparison of near-field pressure signals of aircraft with quiet spikes featuring different noses |
| 表 3 不同头部形状的静音锥对声爆特性、驻点温度、阻力系数的影响 Table 3 Influences of quiet spikes with different nose shapes on sonic boom, stagnation temperature and drag coefficient of supersonic transport aircraft |
|
|
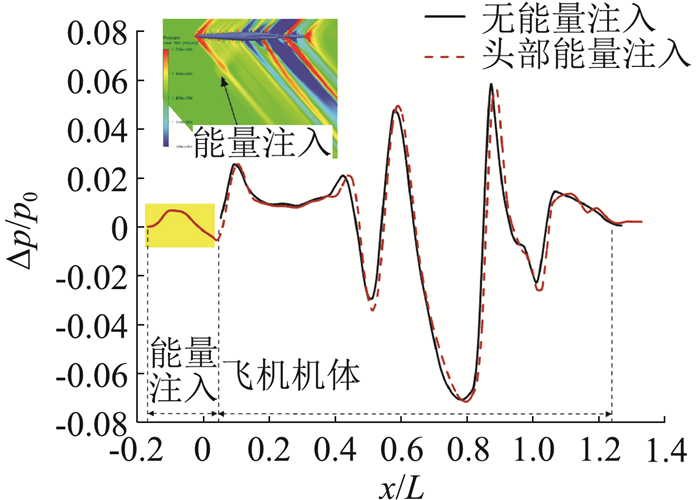
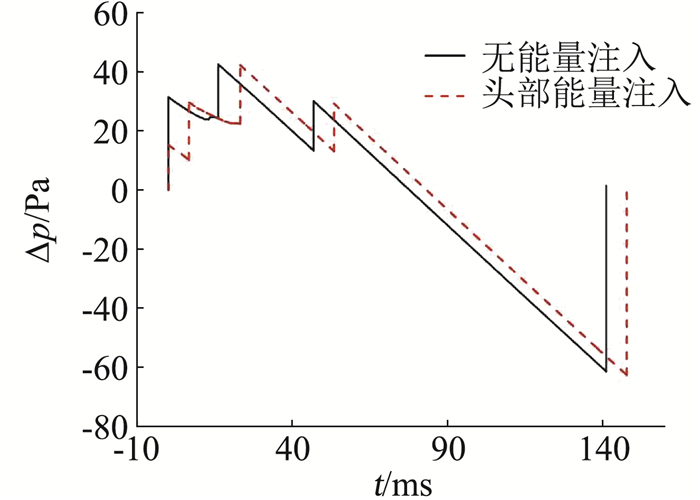
除此之外,中心还探索了能量注入法降低声爆强度的机理,分析了注入位置、注入量、注入点数等对声爆、阻力特性的影响规律[85-88]。利用热阻塞模型分析得出,通过向流场中注入能量可以产生类似静音锥的效果(如图 21和图 22所示)。与静音锥不同的是,该方法是通过向流场中主动注入能量改变原本的激波结构,避免激波的叠加和干扰。多点能量注入与多级静音锥类似,能够通过延长远场声爆的持续时间、减小初始过压值和最大过压值来达到降低声爆强度的目的。
|
图 21 机头下方能量注入前后的近场压强分布对比 Fig.21 Comparison of near-field pressure signals with and without energy injection under the nose |
|
图 22 机头下方能量注入对远场波形的影响 Fig.22 Influence of energy injection under the nose on far-field sonic-boom waveform |
中心在该方面的研究主要分为三个方面:低声爆布局反设计方法、高效全局的低声爆布局优化设计方法和低声爆、低阻新概念布局。
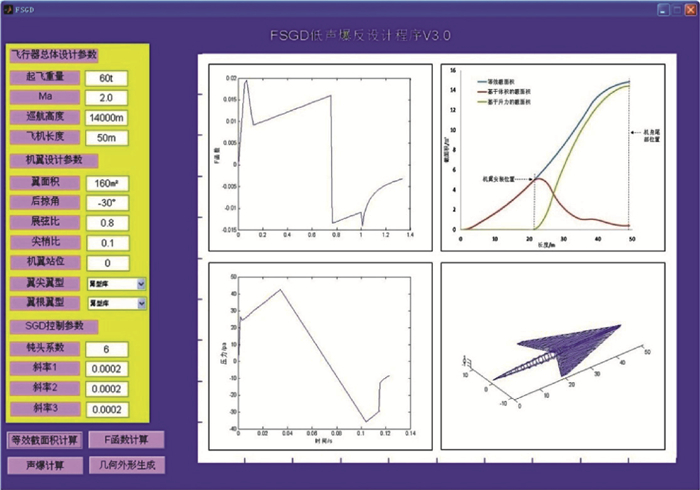
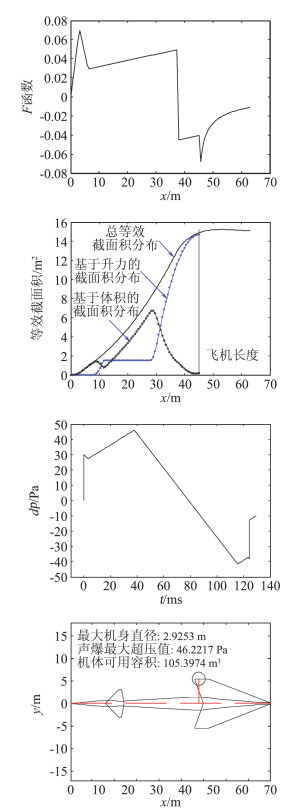
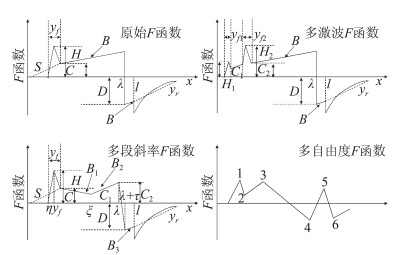
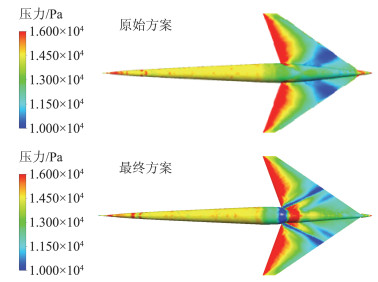
在低声爆反设计方法方面,发展了基于SGD方法的低声爆外形反设计方法[90]和基于CFD的低声爆反设计方法[91],开发了基于SGD的快速低声爆布局反设计程序“FSGD”(如图 23)[85-92]。基于FSGD程序,开展了钝头系数、声爆F函数斜率、飞机长度等SGD方法中关键控制参数对远场波形的影响研究。针对传统SGD方法存在的声爆与气动难以协调的问题,发展了几种改进型的SGD方法(如图 24)。在一种多段斜率F函数反设计方法的基础上,提出了新的声爆F函数表达式,并应用于低声爆布局方案设计(如图 25)。基于CFD的低声爆反设计方法是将远场波形对应的近场压强信号作为目标,运用CFD技术求解空间流场中近场压强信号,通过优化手段调整外形参数,来改变近场压强,并最终使其满足低声爆要求。图 26给出了低声爆设计前后两种方案的物面压力云图对比。
|
图 24 SGD反设计方法改进前后对应的F-函数[85, 92-93] Fig.24 Original F-function and improved functions of inverse design method SGD for supersonic transports[85, 92-93] |
|
图 26 基于CFD的低声爆反射设计前后两种方案的物面压力云图对比[85, 92-93] Fig.26 Comparison of wall pressure distributions of original configuration and new configuration designed using SGD method[85, 92-93] |
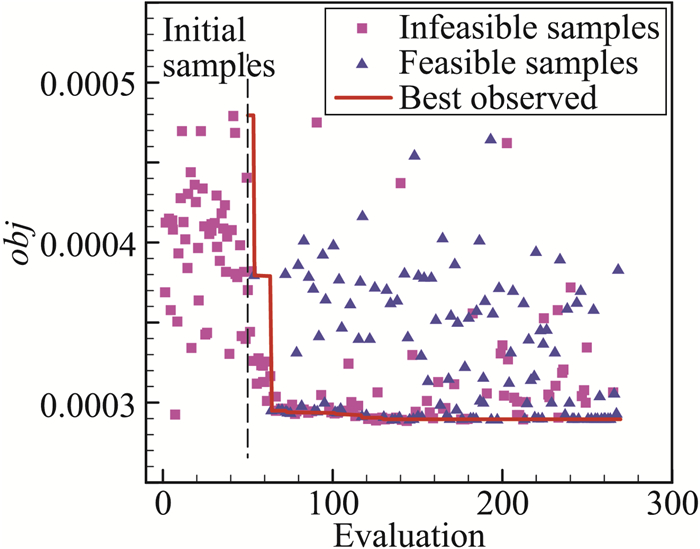
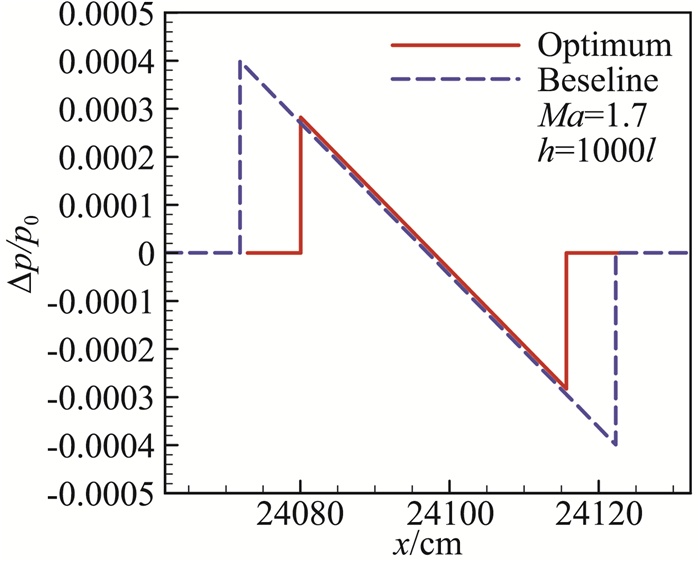
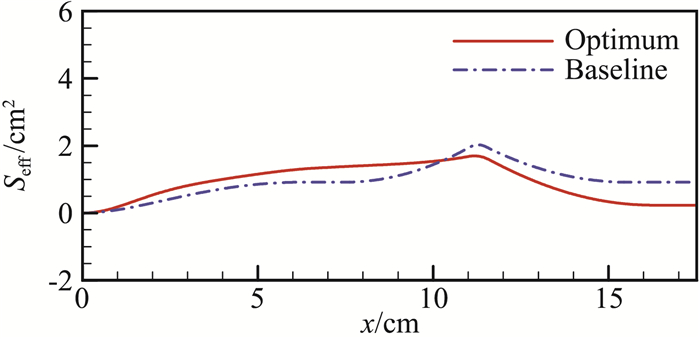
在高效全局的低声爆优化设计方法研究方面,团队发展了一套基于代理模型的高效全局多目标多约束优化算法和程序“SurroOpt”[94-102],并发展了基于代理优化算法的一种具有全局优化能力的高效低声爆优化设计方法[75],其流程如图 27所示。通过简单圆锥体模型的低声爆优化设计实例,对比分析了该方法与遗传算法、梯度优化的优化效率和优化结果。结果表明,该方法的效率相比于遗传算法能够提高2个量级,优化结果相比于梯度优化更具有全局性。之后,将该方法运用于SBPW-1提供的翼身组合体标模的低声爆优化设计中,将远场声爆N型波的过压峰值减少了27.4%(如图 28-图 33所示),结果表明该方法在复杂外形低声爆优化设计中具有很好的应用潜力。
|
图 33 优化前后等效截面积分布对比[75] Fig.33 Comparison of effective cross-section distribution between baseline and optimum[75] |
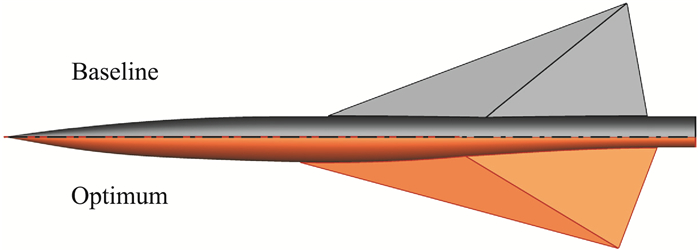
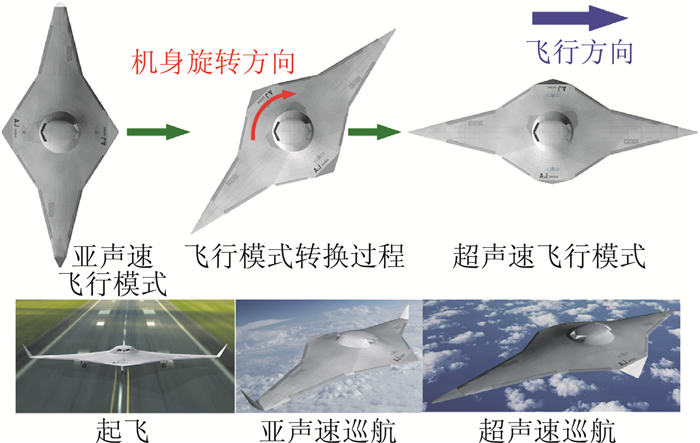
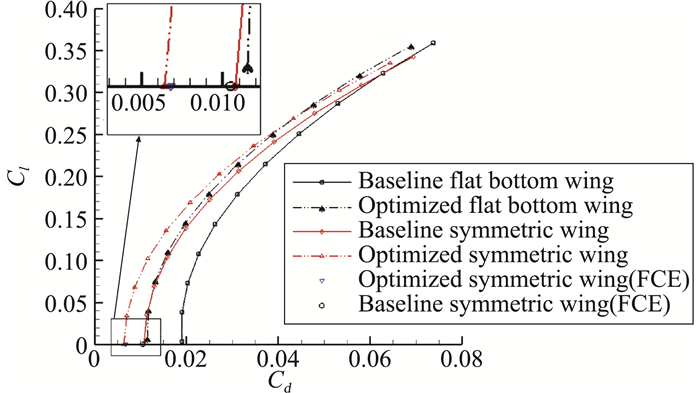
在低声爆低阻新概念布局方面,为兼顾低声爆和高气动性能的要求,团队基于查戈成教授提出的可用于超声速客机的双向飞翼布局概念研究了一种超声速客机新概念布局[103-110]。双向飞翼布局以大展弦比状态进行起飞和着陆,而在超声速巡航飞行时,飞翼水平旋转90°,以小展弦比状态进行超声速飞行,如图 34。针对飞翼的阻力特性,基于FCE算法开展了全机气动性能优化,如图 35和图 36所示。在兼顾起飞着陆和巡航阶段性能的情况下,可以通过设计升力分布,获得满足低声爆要求的等效截面积分布。
|
图 34 双向飞翼布局在起飞着陆、亚声速飞行、超声速巡航构型转换 Fig.34 Transformation of supersonic bi-direction flying wing vehicle between take-off, landing, subsonic flight, and supersonic cruise |

|
图 35 双向飞翼优化前后上表面压力云图 Fig.35 Comparison of upper wall pressure contour between baseline and optimal bi-direction flying wings |
|
图 36 Ma=2.0时双向飞翼优化前后极曲线对比 Fig.36 Comparison of polar curves of bi-direction flying wings at Ma=2.0 between baseline and optimal configuration |
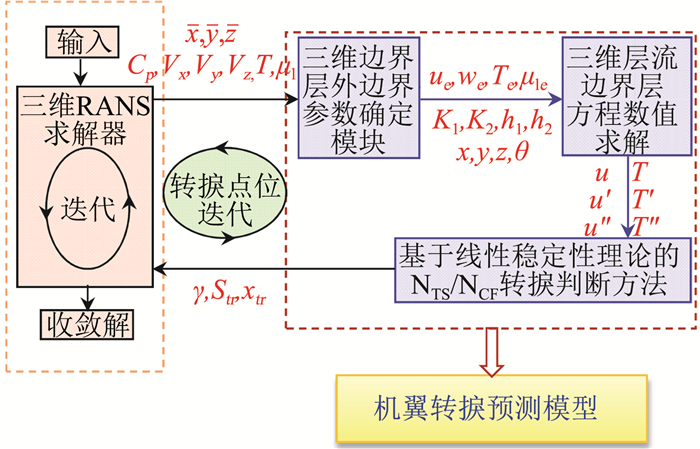
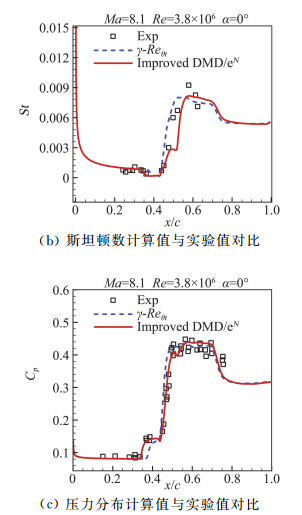
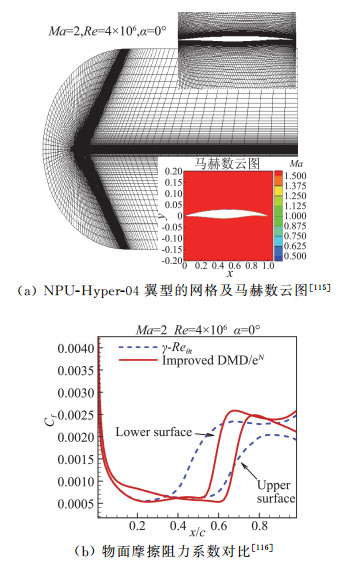
在超声速层流减阻技术方面,团队目前开展了基于DMD/eN方法[111-112]、γ-Reθt的超声速转捩预测方法研究[113],发展了具有转捩预测功能的RANS方程求解器“PMNS3D”[114]。图 37为耦合转捩自动判断的RANS方程求解流程。以高超声速双楔流动为例,在马赫数为8.1、雷诺数为3.8×106和迎角为0°的情况下,对比分析了基于γ-Reθt和基于DMD/eN的转捩预测方法,双楔几何外形和两种方法转捩位置预测结果如图 38所示,结果表明两种方法的计算结果与实验值符合良好。之后,将两种方法应用于自主设计的兼顾跨声速和高超声速流动特性的NPU- Hyper-04翼型中[115],如图 39所示。可以看出两者计算的上表面转捩位置差异较小,但下表面计算结果差异较大,需要开展进一步研究。
|
图 37 耦合转捩自动判断的RANS方程求解器“PMNS3D”流程图 Fig.37 Flowchart of flow solver "PMNS3D" with automatic transition prediction methods |
|
图 38 基于γ-Reθt和基于DMD/eN方法的高超声速双楔流动的转捩预测结果对比 Fig.38 Comparison of hypersonic transition prediction results for a double wedge using γ-Reθt and DMD/eN methods |
|
图 39 基于γ-Reθt和DMD/eN的转捩预测方法计算的物面摩擦阻力系数对比[116] Fig.39 Comparison of friction coefficient distributions obtained by using γ-Reθt and DMD/eN methods |
本文梳理出了发展新一代环保型超声速客机首先需要突破的四大关键技术,并概述了国内外在相关研究领域的研究现状。此外,还比较详细地介绍了西北工业大学近10年来在声爆预测理论与方法、声爆抑制、低声爆低阻外形布局与综合优化设计、超声速层流减阻技术方法的研究进展。
针对发展新一代环保型超声速客机急需突破的关键科学与技术问题,我们认为未来需要重点研究的方向包括(但不仅限于):
1) 发展考虑真实大气条件的远场声爆精细化预测方法。在近场声爆信号的CFD计算方面,研究适用于捕捉空间激波膨胀波系的网格/自适应网格技术、激波捕捉高精度格式和离散方法等。在远场传播方面,研究基于考虑大气旋度、湍流效应的增广Burgers方程的声爆传播方法。同时,为准确验证声爆预测方法的可信度,开展声爆预测方法的验证与确认研究、风洞试验与飞行试验验证技术研究也十分必要。
2) 发展声爆抑制技术和新概念布局设计方法。在声爆抑制方面,研究对飞机气动、结构影响较小的主动或被动声爆抑制技术。在新概念布局设计方面,运用SGD方法、基于CFD的反设计方法或基于本征正交分解的反设计方法研究兼顾气动特性、声爆特性的新概念布局方案。
3) 发展精度高且稳健的超声速转捩预测方法与超声速层流翼型/机翼设计技术。将eN方法、γ-Reθ方法以及DMD方法相结合,发展适用于超声速流动的混合转捩预测模型。
4) 发展激波抑制减阻技术。开展等离子体控制的主动激波抑制技术研究和Licher双层翼波阻抑制技术研究,重点突破双层翼布局中出现的流动“雍塞”等问题。
5) 发展针对复杂超声速客机外形的高效全局的气动/声爆综合优化设计方法。在综合优化过程中,需发展高效的大规模网格的变形方法、高维全局的代理优化理论与方法、多学科优化理论与方法等。
6) 开展满足飞行器全包线推力需求的变循环发动技术研究。研究发动机工作模态的平稳转换技术、高速风扇稳定性技术等。
| [1] |
朱自强, 兰世隆. 超声速民机和降低音爆研究[J]. 航空学报, 2015, 36(8): 2507-2528. ZHU Z Q, LAN S L. Study of supersonic commercial transport and reduction of sonic boom[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(8): 2507-2528. (in Chinese) |
| [2] |
CHUDOBA B, COLEMAN G, OZA A, et al. What price supersonic speed? A design anatomy of supersonic transportation Part 1[J]. Aeronautical Journal, 2008, 112(1129): 141-151. DOI:10.1017/S0001924000002074 |
| [3] |
Douglas Aircraft Company. Study of high-speed civil transports[R]. NASA CR-1989-4235, 1989.
|
| [4] |
PLOTKIN J K, MAGLIERI J D. Sonic boom research: history and future[R]. AIAA 2003-3575, 2003.
|
| [5] |
SAKATA K. Supersonic experimental airplane(NEXST) for next generation SST technology[R]. AIAA 2002-0527, 2002.
|
| [6] |
MORGENSTERN M J, STELMACK M, JHA D P. Advanced concept studies for supersonic commercial transports entering service in 2030-35 (N+3)[R]. AIAA 2010-5114, 2010.
|
| [7] |
JONES T. NASA'squiet supersonic aircraft[R]. EAA AirVenture, 2017.
|
| [8] |
CARLSON H W. Simplified sonic-boom prediction[R]. NASA TP-1978-1122, 1978.
|
| [9] |
PLOTKIN J K. A rapid method for the computation of sonic booms[R]. AIAA 1993-4433, 1993.
|
| [10] |
WHITHAM G B. The flow pattern of a supersonic projectile[J]. Communications on Pure & Applied Mathematics, 1952, 5(3): 301-348. |
| [11] |
WALKDEN F. The shock pattern of a wing-body combination, far from the flight path[J]. Aeronautical Quarterly, 1958, 9(2): 164-194. DOI:10.1017/S0001925900001372 |
| [12] |
GEORGE A R. Reduction of sonic boom by azimuthal redistribution of overpressure[J]. AIAA Journal, 1969, 7(2): 291-298. DOI:10.2514/3.5088 |
| [13] |
HAYES D W, HAEFELI C R, KULSRCD E H. Sonic boom propagation in a stratified atmosphere, with computer program[R]. NASA CR-1969-1299, 1969.
|
| [14] |
YAMASHITA R, SUZUKI K. Full-field sonic boom simulation in real atmosphere[R]. AIAA 2014-2269, 2014.
|
| [15] |
YAMASHITA R, SUZUKI K. Rise time prediction of sonic boom by full-field simulation with thermal nonequilibrium[R]. AIAA-2015-2583, 2015
|
| [16] |
YAMASHITA R, SUZUKI K. Full-field sonic boom simulation in stratified atmosphere[J]. AIAA Journal, 2016, 54(10): 3223-3231. DOI:10.2514/1.J054581 |
| [17] |
CHEUNG S, EDWARDS T, LAWRENCE S. Application of CFD to sonic boom near and midfield prediction[R]. NASA TM-1990-102867, 1990.
|
| [18] |
SICLARI M J, DARDEN C M. An Euler code prediction of near-field to midfield sonic boom pressure signals[R]. AIAA 1990-4000, 1990.
|
| [19] |
THOMAS C L. Extrapolation of sonic boom pressure signals by the waveform parameter method[R]. NASA TN D-1972-6832, 1972.
|
| [20] |
CLEVELAND R O. Propagation of sonic booms through a real, stratified atmosphere[D]. Austin: The University of Texas at Austin, 1995.
|
| [21] |
RALLABHANDI S K. Advanced sonic boom prediction using the augmented Burgers equation[J]. Journal of Aircraft, 2011, 48(4): 1245-1253. DOI:10.2514/1.C031248 |
| [22] |
TAKENO J, MISAKA T, SHIMOYAMA K, et al. Analysis of sonic boom propagation based on the KZK equation[R]. AIAA-2015-0745, 2015.
|
| [23] |
陈鹏, 李晓东. 基于Khokhlov-Zabolotskaya-Kuznetsov方程的声爆频域预测法[J]. 航空动力学报, 2010, 25(2): 359-365. CHEN P, LI X D. Frequency domain method for predicting sonic boom propagation based on Khokhlov-Zabolotskaya-Kuznetsov equation[J]. Journal of Aerospace Power, 2010, 25(2): 359-365. (in Chinese) |
| [24] |
冯晓强, 李占科, 宋笔锋. 超音速客机音爆问题初步研究[J]. 飞行力学, 2010, 28(6): 21-23. FENG X Q, LI Z K, SONG B F. Preliminary analysis on the sonic boom of supersonic aircraft[J]. Flight Dynamics, 2010, 28(6): 21-23. (in Chinese) |
| [25] |
乔建领, 韩忠华, 丁玉临, 等.基于非线性Burgers方程的超声速客机远场声爆预测方法[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-125, 2018.
|
| [26] |
王刚, 马博平, 雷知锦, 等. 典型标模音爆的数值预测与分析[J]. 航空学报, 2018, 39(01): 169-181. WANG G, MA B P, LEI Z J, et al. Simulation and analysis for sonic boom on several benchmark cases[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(01): 169-181. (in Chinese) |
| [27] |
张绎典, 黄江涛, 高正红. 基于增广Burgers方程的音爆远场计算及应用[J]. 航空学报, 2018, 39(7): 122039. ZHANG Y D, HUANG J T, GAO Z H. Far field simulation and applications of sonic boom based on augmented Burgers equation[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 122039. (in Chinese) |
| [28] |
钱战森, 刘忠臣, 冷岩, 等. OS-X0试验飞行器声爆特性测量与数值模拟分析[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-116, 2018.
|
| [29] |
冷岩, 钱战森, 刘中臣.超声速飞行器声爆特性数值模拟预测及影响因素分析[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-121, 2018.
|
| [30] |
刘中臣, 钱战森, 冷岩.声爆近场空间压力分布风洞试验精确测量技术研究[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-120, 2018.
|
| [31] |
徐悦, 宋万强. 典型低音爆构型的音爆计算研究[J]. 航空科学技术, 2016, 27(7): 12-16. XU Y, SONG W Q. Near field sonic boom calculation on typical LSB configurations[J]. Aeronautical Science & Technology, 2016, 27(7): 12-16. (in Chinese) |
| [32] |
霍满, 谭廉华, 林大楷, 等.声爆标模近场计算对远场预测影响研究[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-122, 2018.
|
| [33] |
ZAIDI H S, et al. Influence of upstream pulsed energy deposition on a shockwave strucutre in supersonic flow[R]. AIAA-2002-2073, 2002.
|
| [34] |
ZAIDI H S, SHNEIDER N M, MILES B R. Shock wave mitigation through off body pulsed energy deposition[J]. AIAA Journal, 2004, 42(2): 326-331. DOI:10.2514/1.9097 |
| [35] |
FREUND D, et al. Quiet spikeTM prototype flight test results[R]. AIAA-2007-1178, 2007.
|
| [36] |
HOWE D. Improved sonic boom minimization with extendable nose spike[R]. AIAA-2005-1014, 2005.
|
| [37] |
冯晓强, 宋笔锋, 李占科. 低声爆静音锥设计方法研究[J]. 航空学报, 2013, 34(5): 1009-1017. FENG X Q, SONG B F, LI Z K. Research of low sonic boom quiet splike design method[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1009-1017. (in Chinese) |
| [38] |
沈沉, 周华. 细长杆降低超声速客机气动噪声的数值分析[J]. 空气动力学学报, 2012, 30(1): 39-45. SHEN C, ZHOU H. Numerical analysis of slender-rod-noise-reduction of supersonic passenger aircraft[J]. Acta Aerodynamica Sinica, 2012, 30(1): 39-45. DOI:10.3969/j.issn.0258-1825.2012.01.007 (in Chinese) |
| [39] |
兰世隆.超声速民机音爆抑制技术的研究进展[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-119, 2018.
|
| [40] |
HOWE D, SIMMONS Ⅲ F, FREUND D. Development of the gulfstream quiet spike TM for sonic boom minimization[R]. AIAA-2008-124, 2008.
|
| [41] |
SIMMONS F, FREUND D, SPIVEY N D, et al. Quiet SpikeTM: The design and validation of an extendablenose boom prototype[R]. AIAA-2007-1774, 2007.
|
| [42] |
BUSEMANN A. Aerodynamic lift at supersonic speeds[C]//Proceedings of the Volta Congress. 1935: 315-347.
|
| [43] |
MATSUSHIMA K, MARUYAMA D, KUSUNOSE K. Extension of Busemannbiplane theory to three dimensional wing fuselage configurations[C]//Proceedings of the 27th International Congress of the Aeronautical Sciences. Nice, France: ICAS, 2010.
|
| [44] |
LICHER R M. Optimum two-dimensional multiplanes in supersonic flow, SM-18688[R]. California: Douglass Aircraft Co, 1955.
|
| [45] |
李占科, 张翔宇, 冯晓强, 等. 超声速双层翼翼型的阻力特性研究[J]. 应用力学学报, 2014, 31(04): 483-488+1. LI Z K, ZHANG X Y, FENG X Q, et al. The study on the drag characteristic of supersonic biplane[J]. Chinese Journal of Applied Mechanics, 2014, 31(04): 483-488+1. (in Chinese) |
| [46] |
刘荣健, 白鹏, 黄志澄.基于Busemann双翼机原理的低声爆气动布局研究进展[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-114, 2018.
|
| [47] |
刘奇, 周泽堃, 王刚, 等.二维Busemann双翼开缝减阻研究[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-118, 2018.
|
| [48] |
LYNDE M N, CAMPBELL R L. Expanding the natural laminar flow boundary for supersonic transports[R]. AIAA-2016-4327, 2016.
|
| [49] |
GARZON G A, MATISHECK J R. Supersonic testing of natural laminar flow on sharp leading edge airfoils. recent experiments by Aerion Corporation[R]. AIAA-2012-3258, 2012.
|
| [50] |
STURDZA P. Extensive supersonic natural laminar flow on the Aerion business jet[R]. AIAA-2007-685, 2007.
|
| [51] |
IULIANO E, DONELLI R, QUAGLIARELLA D, et al. Natural laminar flow design of a supersonic transport jet wing-body[R]. AIAA-2009-1279, 2009.
|
| [52] |
IULIANO E, QUAGLIARELLA D, DONELLI R, et al. Design of a supersonic natural laminar flow wing-body[J]. Journal of Aircraft, 2011, 48(4): 1147-1162. DOI:10.2514/1.C031039 |
| [53] |
TOKUGAWA N, KWAK D Y, YOSHIDA K, et al. Transition measurement of natural laminar flow wing on supersonic experimental airplane NEXST-1[J]. Journal of Aircraft, 2008, 45(5): 1495-1504. DOI:10.2514/1.33596 |
| [54] |
ISHIKAWA H, TOKUGAWA N, UEDA Y, et al. Natural laminar flow wing design of supersonic transport at high Reynolds number condition[C]//29th Congress of the International Council of the Aeronautical Sciences, St. Petersburg, Russia, 2014.
|
| [55] |
ISHIKAWA H, UEDA Y, TOKUGAWA N. Natural laminar flow Wing design for a low-boom supersonic aircraft[R]. AIAA-2017-1860, 2017.
|
| [56] |
周红.变循环发动机特性分析及其与飞机一体化设计研究[D].西安: 西北工业大学, 2016: 3-20. ZHOU H. Investigation on the variable cycle engine characteristics and integration design with aircraft[D]. Xi'an: Northwestern Polytechnical University, 2016: 3-20. (in Chinese) |
| [57] |
GRÖNSTEDT U T J, PILIDIS P. Control optimization of the transient performance of the selective bleed variable cycle engine during mode transition[J]. Journal of Engineering for Gas Turbines and Power, 2002, 124(1): 75-81. |
| [58] |
MORGENSTERN J, NORSTRUD N, MARC S, et al. Final report for the advanced concept studies for supersonic commercial transports entering service in the 2030 to 2035 period, N+3 supersonic program[R]. NASA CR-2010-216796, 2010.
|
| [59] |
胡松岩. 变几何涡轮及其设计特点[J]. 航空发动机, 1996, 3(1): 21-26. |
| [60] |
刘智刚, 方祥军, 刘思永, 等. 某变循环发动机超声涡轮设计与分析[J]. 航空动力学报, 2010, 25(9): 2103-2110. LIU Z G, FANG X J, LIU S Y, et al. Design and analysis of HP-turbine for variablecycle engine[J]. Journal of Aerospace Power, 2010, 25(9): 2103-2110. (in Chinese) |
| [61] |
谢振伟.变循环发动机建模与分布式控制研究[D].西安: 西北工业大学, 2016: 8-9. XIE Z W. Research on modeling and distributed control of variable cycle engine[D]. Xi'an: Northwestern Polytechnical University, 2016: 8-9. (in Chinese) |
| [62] |
苟学中.变循环发动机建模及控制规律研究[D].南京: 南京航空航天大学, 2011: 1-55.
|
| [63] |
骆广琦, 李游, 刘琨, 等. 变循环发动机组合变几何调节方案[J]. 航空动力学报, 2014, 29(10): 2273-2278. LUO G Q, LI Y, LIU K, et al. Combined variable geometry regulation schemes for variable cycle engine[J]. Journal of Aerospace Power, 2014, 29(10): 2273-2278. (in Chinese) |
| [64] |
SEEBASS A R, GEORGE A R. Sonic-boom minimization[J]. Journal of the Acoustical Society of America, 1971, 51(49): 72-72. |
| [65] |
DARDEN C M. Sonic-boom minimization with nose-bluntness relaxation[R]. NASA TP-1979-1348, 1979.
|
| [66] |
RALLABHANDI S K. Application of adjoint methodology to supersonic aircraft design using reversed equivalent areas[J]. Journal of Aircraft, 2014, 51(6): 1873-1882. DOI:10.2514/1.C032518 |
| [67] |
KIRZ J. Surrogate based shape optimization of a low boom axisymmetric body[R]. AIAA-2018-2849, 2018.
|
| [68] |
MICHAEL P. Putting a 'Q' into supersonic flight[J]. Professional Pilot, 2007, 41(9): 58-62. |
| [69] |
SAKATA K. Japan's supersonic technology and business jet perspectives[R]. AIAA-2013-0021, 2013.
|
| [70] |
CHUDOBA B, OZA A, ROBERTS K, et al. What price supersonic speed?-an applied market research case study-part 2[J]. The Aeronautical Journal, 2008, 112(1130): 219-231. DOI:10.1017/S0001924000002165 |
| [71] |
ZHA G C, IM H, ESPINAL D. Toward zero sonic-boom and high efficiency supersonic flight, Part Ⅰ: a novel concept of supersonic bi-directional flying wing[R]. AIAA-2010-1013, 2010.
|
| [72] |
WIKIPEDIA. Boom technology[EB/OL]. (2018-7-11)[2018-7-11]. https://www.flyingmag.com/boom-supersonic-passenger-aircraft-emerges.
|
| [73] |
SUN Y, SMITH H. Review and prospect of supersonic business jet design[J]. Progress in Aerospace Sciences, 2017, 90: 12-38. DOI:10.1016/j.paerosci.2016.12.003 |
| [74] |
LILLIAN IPSON. NASA's ExperimentalSupersonic Aircraft Now Known as X-59 QueSST[EB/OL]. (2018-7-5)[2018-7-5] https://www.nasa.gov/aero/nasa-experimental-supersonic-aircraft-x-59-quesst
|
| [75] |
乔建领, 韩忠华, 宋文萍. 基于代理模型的高效全局低音爆优化设计方法[J]. 航空学报, 2018, 39(5): 121736. QIAO J L, HAN Z H, SONG W P. An efficient surrogate-based global optimization for low sonic boom design[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(5): 121736. (in Chinese) |
| [76] |
张绎典, 黄江涛, 高正红.基于本征正交分解和增广Burgers方程的低声爆外形反设计方法[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-117, 2018.
|
| [77] |
郝璇, 苏诚, 刘芳, 等. 超声速飞行器低声爆气动布局优化设计研究[J]. 空气动力学学报, 2018, 36(2): 327-333. HAO X, SU C, LIU F, et al. Optimization design research on low sonic boom configuration for supersonic transport[J]. Acta Aerodynamica Sinica, 2018, 36(2): 327-333. DOI:10.7638/kqdlxxb-2016.0047 (in Chinese) |
| [78] |
黄江涛, 张绎典, 高正红, 等. 基于流场/声爆耦合伴随方程的超声速公务机声爆优化[J]. 航空学报, 2019, 40(5): 122505. HUANG J T, ZHANG Y D, GAO Z H, et al. Sonic boom optimization of supersonic jet based on flow/sonic boom coupled adjoint equations[J]. Acta Aeronauticaet Astronautica Sinica, 2019, 40(5): 122505. (in Chinese) |
| [79] |
王宇航, 徐悦.基于主观评价模型的超音速民机低音爆设计平台开发[C]//首届空气动力学大会, 绵阳: 中国空气动力学会, CARS-04-2018-123, 2018.
|
| [80] |
MA B, WANG G, REN J, et al. Near field sonic boom analysis with HUNS3D solver[R]. AIAA-2017-0038, 2017.
|
| [81] |
王刚, 马博平, 雷知锦, 等. 典型标模音爆的数值预测与分析[J]. 航空学报, 2018, 39(1): 164-176. WANG G, MA B P, LEI Z J, et al. Simulation and analysis for sonic boom on several benchmark cases[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(1): 164-176. (in Chinese) |
| [82] |
王刚, 马博平, 雷知锦, 等.网格对声爆近场预测的影响的数值研究[C]//第十七届全国计算流体力学会议.中国, 杭州: 2017: 46-58.
|
| [83] |
MA B P, WANG G, REN J, et al. Near-field sonic-boom prediction and analysis with hybrid grid Navier-Stokes solver[J]. Journal of Aircraft, 2018, 55(5): 1890-1904. DOI:10.2514/1.C034659 |
| [84] |
冯晓强.声爆计算方法研究及在超声速客机设计的应用[D].西安: 西北工业大学, 2012: 9-15. FENG X Q. The research of sonic boom prediction method and application in supersonic aircraft design[D]. Xi'an: Northwestern Polytechnical University, 2012. (in Chinese) |
| [85] |
冯晓强.超声速客机低声爆机理及设计方法研究[D].西安: 西北工业大学, 2014: 15-47. FENG X Q. The research of low sonic boom mechanism and design method of supersonic aircraft[D]. Xi'an: Northwestern Polytechnical University, 2014. (in Chinese) |
| [86] |
冯晓强, 宋笔锋, 李占科. 低声爆静音锥设计方法研究[J]. 航空学报, 2013, 34(5): 1009-1017. FENG X Q, SONG B F, LI Z K. Research of low sonic boom quiet spike design method[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1009-1017. (in Chinese) |
| [87] |
雷知锦, 马博平, 王刚, 等.机头静音锥对超声速民机降低声爆效果的影响[C]//第十七届全国计算流体力学会议.中国, 杭州: 2017. 189-201.
|
| [88] |
李占科, 彭中良, 徐合良. 静音锥对超声速客机声爆水平的影响[J]. 航空工程进展, 2013, 4(03): 346-351. LI Z K, PENG Z L, XU H L. Effect of the quiet spike on sonic boom of the supersonic airliner[J]. Advances in Aeronautical Science and Engineering, 2013, 4(03): 346-351. DOI:10.3969/j.issn.1674-8190.2013.03.014 (in Chinese) |
| [89] |
FENG X Q, LI Z K, SANG J H, et al. Optimization of sonic boom suppression by off-body energy deposition[C]//Applied Mechanics and Materials. Trans Tech Publications, 2014, 477: 7-13.
|
| [90] |
冯晓强, 李占科, 宋笔锋. 超声速客机低音爆布局反设计技术研究[J]. 航空学报, 2011, 32(11): 1980-1986. FENG X Q, LI Z K, SONG B F. A research on inverse design method of a lower sonic boom supersonic aircraft configuration[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(11): 1980-1986. (in Chinese) |
| [91] |
冯晓强, 李占科, 宋笔锋, 等. 基于混合网格的声爆/气动一体化设计方法研究[J]. 空气动力学学报, 2014, 32(1): 30-37. FENG X Q, LI Z K, SONG B F, et al. Optimization of sonicboom and aerodynamic based on structured/unstructured hybrid grid[J]. Acta Aerodynamica Sinica, 2014, 32(1): 30-37. (in Chinese) |
| [92] |
FENG X Q, LI Z K, SONG B F. Research of low boom and low drag supersonic aircraft design[J]. Chinese Journal of Aeronautics, 2014, 27(3): 531-541. DOI:10.1016/j.cja.2014.04.004 |
| [93] |
冯晓强, 宋笔锋, 李占科, 等. 超声速飞机低声爆布局混合优化方法研究[J]. 航空学报, 2013, 34(8): 1768-1777. FENG X Q, SONG B F, LI Z K, et al. Hybrid optimization approach research for low sonic boom supersonic aircraft configuration[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1768-1777. (in Chinese) |
| [94] |
韩忠华. Kriging模型及代理优化算法研究进展[J]. 航空学报, 2016, 37(11): 3197-3225. HAN Z H. Kriging surrogate model and its application to design optimization:a review of recent progress[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3197-3225. (in Chinese) |
| [95] |
HAN Z H. SurroOpt: a generic surrogate-based optimization code for aerodynamic and multidisciplinary design[C]//Proceedings of ICAS 2016, paper no. 2016_0281, Daejeon, Korea, 2016.
|
| [96] |
HAN Z H, ZHANG K S. Surrogate-based optimization. Real-World Applications of Genetic Algorithms[M]//Dr. Olympia Roeva (Ed.), ISBN: 978-953-51-0146-8, InTech, 2012: 343-362.
|
| [97] |
HAN Z H, CHEN J, ZHANG K S, et al. Aerodynamic shape optimization of natural-laminar-flow wing using surrogate-based approach[J]. AIAA Journal, 2018, 56(7): 2579-2593. DOI:10.2514/1.J056661 |
| [98] |
LIU J, SONG W P, HAN Z H, et al. Efficient aerodynamic shape optimization of transonic wings using a parallel infilling strategy and surrogate models[J]. Structural and Multidisciplinary Optimization, 2017, 55(3): 925-943. DOI:10.1007/s00158-016-1546-7 |
| [99] |
HAN Z H, ZHANG Y, SONG C X, et al. Weighted gradient-enhanced kriging for high-dimensional surrogate modeling and design optimization[J]. AIAA Journal, 2017, 55(12): 4330-4346. DOI:10.2514/1.J055842 |
| [100] |
HAN Z H, GOERTZ S, ZIMMERMANN R. Improving variable-fidelity surrogate modeling via gradient-enhanced kriging and a generalized hybrid bridge function[J]. Aerospace Science and technology, 2013, 25: pp. 177-189. DOI:10.1016/j.ast.2012.01.006 |
| [101] |
HAN Z H, ZIMMERMANN R, GOERTZ S. An alternative cokriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(5): 1205-1210. DOI:10.2514/1.J051243 |
| [102] |
HAN Z H, GOERTZ S. Hierarchical kriging model for variable-fidelity surrogate modeling[J]. AIAA Journal, 2012, 50(9): 1285-1296. |
| [103] |
BERGER C, CARMONA K, ESPINAL D, et al. Supersonic bi-directional flying wing configuration with low sonic boom and high aerodynamic efficiency[R]. AIAA-2011-3663, 2011.
|
| [104] |
GUAN X H. Supersonic bi-directional flying wing wave drag optimization based on alternative form of CST method[C]//Applied Mechanics and Materials. Trans Tech Publications, 2014, 477: 240-245.
|
| [105] |
李占科, 张旭, 冯晓强, 等. 双向飞翼超声速客机激波阻力和声爆研究[J]. 西北工业大学学报, 2014, 32(04): 517-522. LI Z K, ZHANG X, FENG X Q, et al. Study on drag and sonic boom of supersonic bi-directional flying wing[J]. Journal of Northwestern Polytechnical University, 2014, 32(04): 517-522. DOI:10.3969/j.issn.1000-2758.2014.04.008 (in Chinese) |
| [106] |
关晓辉, 宋笔锋, 李占科. 两种超声速翼身激波阻力优化方法对比研究[J]. 航空学报, 2013, 34(11): 2510-2519. GUAN X H, SONG B F, LI Z K. Comparative study of two supersonic wing-body wave drag optimization methods[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(11): 2510-2519. (in Chinese) |
| [107] |
GUAN X H, SONG B F, LI Z K. Extended far-field composite element supersonic wing body wave drag optimization method[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1036-1045. |
| [108] |
GUAN X H. Supersonic wing-body two-level wave drag optimization using extended far-field composite-element methodology[J]. AIAA Journal, 2014, 52(5): 981-990. DOI:10.2514/1.J052305 |
| [109] |
关晓辉.超声速客机气动外形参数化方法研究[D].西安: 西北工业大学, 2012: 79-88. GUAN X H. The research on shape parameterization of supersonic civil transport[D]. Xi'an: Northwestern Polytechnical University, 2012: 79-88. (in Chinese) |
| [110] |
关晓辉.超声速客机外形参数化与激波阻力优化研究[D].西安: 西北工业大学, 2014: 99-113. GUAN X H. Research on shape parameterization and wave drag optimization of supersonic civil transport[D]. Xi'an: Northwestern Polytechnical University, 2014: 99-133. (in Chinese) |
| [111] |
韩忠华, 王绍楠, 韩莉. 一种基于动模态分解的翼型流动转捩预测新方法[J]. 航空学报, 2017, 38(1): 120034. HAN Z H, WANG S N, HAN L. A novel method for automatic transition prediction of flows over airfoils based on dynamic mode decomposition[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 120034. (in Chinese) |
| [112] |
WU M M, HAN Z H, WANG S N, et al. A DMD-based automatic transition prediction method for flows over airfoils[R]. AIAA 2017-4303, 2017.
|
| [113] |
宋文萍, 吴猛猛, 朱震, 等. 面向层流减阻设计的转捩预测方法研究[J]. 空气动力学学报, 2018, 36(2): 213-228. SONG W P, WU M M, ZHU Z, et al. Transition prediction methods towards significant drag reduction via laminar flow technology[J]. Acta Aerodynamica Sinica, 2018, 36(2): 213-228. DOI:10.7638/kqdlxxb-2018.0035 (in Chinese) |
| [114] |
韩忠华.旋翼绕流的高效数值计算方法及主动流动控制研究[D].西安: 西北工业大学, 2007: 67-68. HAN Z H. Efficient method for simulation of viscous flows past helicopter rotors and active flow control[D]. Xi'an: Northwestern Polytechnical University, 2007: 67-68. (in Chinese) |
| [115] |
孙祥程, 韩忠华, 柳斐, 等. 高超声速飞行器宽速域翼型/机翼设计与分析[J]. 航空学报, 2018, 39(6): 121737. SUN X C, HAN Z H, LIU F, et al. Design and analysis of hypersonic vehicle airfoil/wing at wide-range Mach numbers[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(6): 121737. (in Chinese) |
| [116] |
吴猛猛.基于DMD的流动稳定性分析及超声速边界层转捩预测方法[D].西安: 西北工业大学, 2018: 53-60. WU M M. Flow stability analysis based on DMD and transition prediction for supersonic boundary layer[D]. Xi'an: Northwestern Polytechnical University, 2018: 53-60. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37