飞翼布局无人机由于其较大的升阻比以及较优秀的隐身特性,是高空长航时无人机的一种理想选择[1-2]。飞翼布局无人机大多采用涡轮喷气发动机或者涡轮风扇发动机,为保证无人机的隐身特性,一般采取进排气一体化外形设计[3-4]。而无人机尾喷管的喷流会对外流场产生一定的影响,进而改变无人机的气动特性[5]。由于飞翼布局无人机纵向稳定性较弱,航向处于中立稳定[6],精细研究发动机喷流对无人机操稳特性的影响规律具有较大的意义。
现阶段获取喷流影响量的手段有风洞试验和数值计算。对于典型战机,由于其展弦比较小,考虑国内主要风洞的尺寸和试验模型的堵塞度,可以进行风洞试验[7-8];但对于飞翼布局无人机,由于其大展弦比的外形特点,考虑模型堵塞度缩比后,模型内部空间不足,测量部件安装空间不够,导致试验精度差等问题,无法精细刻画无人机进排气对气动特性的影响规律。
随着计算流体力学的发展,数值模拟越来越多应用在无人机气动特性研究及流动控制中[9]。为精细刻画喷流对飞翼布局无人机气动特性的影响规律,本文利用CFD技术,研究了喷流带来的尾部外形破坏,以及喷流效应对无人机气动特性的影响规律。
1 数值模拟方法 1.1 控制方程本文通过求解Reynolds平均N-S方程,守恒形式[9]为:
| $ \begin{array}{l}{\frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x_{i}}\left(\rho u_{i}\right)=0} \\ {\frac{\partial}{\partial t}\left(\rho u_{i}\right)+\frac{\partial}{\partial x_{j}}\left(\rho u_{i} u_{j}\right)=-\frac{\partial p}{\partial x_{i}}+\frac{\partial \tau_{i j}}{\partial x_{j}}} \\ {\frac{\partial e}{\partial t}+\frac{\partial}{\partial x_{j}}\left(u_{j} e\right)=\frac{\partial}{\partial x_{j}}\left(-u_{j} p+u_{i} \tau_{i j}+q_{i}\right)}\end{array} $ | (1) |
需要指出的是,式中,
模型中更具体的各参数的意义以及模型验证详见文献[10]。为了使式(1)封闭,需要对式(1)中的雷诺应力做出各种假设。从对模式处理的出发点不同,一般可将湍流模式分为雷诺应力模型和涡粘性模型两类,受计算条件的约束,雷诺应力模型计算量巨大,使其应用范围受到限制,在工程湍流问题中广泛应用的是涡粘性模型[11]。本文选取Menter SST[12]湍流模型进行计算[13]。
1.2 数值离散方法采用有限体积法求解Reynolds平均可压缩N-S方程和模型输运方程;无粘通量采用Roe的FDS格式[14],并通过限制器[15]来抑制振荡;粘性通量采用二阶中心差分格式;时间推进采用LU-SGS (Lower-Upper Symmetric Gauss-Seidel)隐式方法。
2 计算模型网格及边界条件本文所采用的计算模型如图 1所示内外流一体化的飞翼布局无人机模型,无人机翼展13 m,平均气动弦长3.12 m,下文重点分析Ma0.2、Ma0.4、Ma0.6下无人机的气动特性。

|
图 1 计算模型 Fig.1 Computational model |
本文对无喷流外形(基准外形)和喷流外形进行结构化网格生成,研究喷流对无人机气动特性的影响量。图 2给出了无人机尾喷管处的网格,其中红色部分为基准外形,黑色部分为喷流外形。网格生成中保证壁面法向网格满足y-plus小于1。

|
图 2 计算网格示意图 Fig.2 Computational grid |
计算域远场采用远场边界条件,壁面采用无滑移壁面,发动机出口设置为压力出口边界,给定出口边界的总压和总温。
3 计算模型验证本文中的基准无人机模型(无进排气系统)曾在高低速风洞中进行过风洞试验,为校核本文采用的计算方法和湍流模型的精度,本文计算了图 2中的基准模型所对应的风洞试验状态,并与该模型在高低速风洞试验中的试验结果进行对比。
低速试验中,模型缩比为1:5;高速试验中,模型缩比为1:12;计算来流Ma分别为0.2和0.6,基于单位长度的雷诺数分别为4.78×106和2.77×106。风洞试验数据经过了支架干扰修正。图 3-图 5给出了Ma0.2和Ma0.6下,无人机CFD计算结果与试验结果的对比。
|
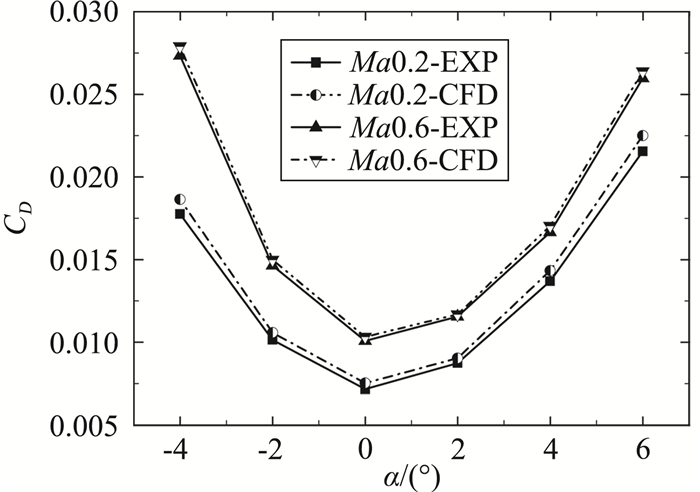
图 3 计算与试验阻力系数对比 Fig.3 Comparison of drag coefficient between computation and experiment |
|
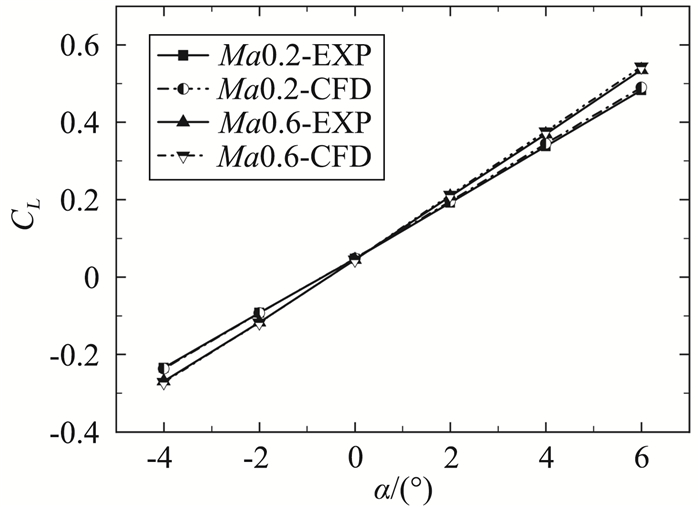
图 4 计算与试验升力系数对比 Fig.4 Comparison of lift coefficient between computation and experiment |
|
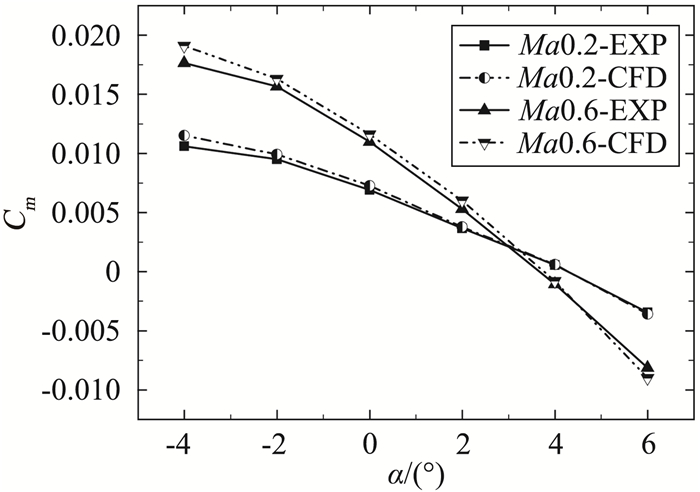
图 5 计算与试验俯仰力矩系数对比 Fig.5 Comparison of pitch moment between computation and experiment |
可以看到,本文计算方法下获取的无人机气动特性与风洞试验结果吻合良好。Ma0.2时,阻力系数约有5%左右的差异,升力系数吻合良好,俯仰力矩系数与试验相差约4%左右;Ma0.6时,阻力系数差异约在2%左右,升力系数差异很小,俯仰力矩系数差异约为1.5%左右,CFD计算结果与试验对比验证了本文计算方法的精度。
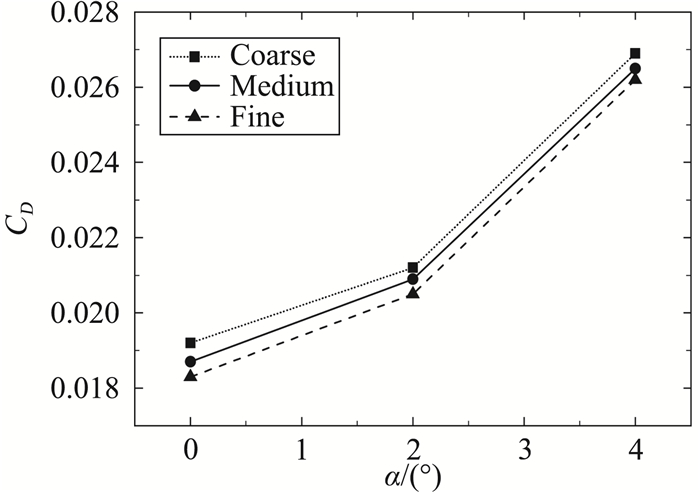
4 网格无关性验证为确保计算方法的正确性,并衡量网格因素对计算结果的影响,本文参考文献[16], 通过三套不同尺度的网格量,对进排气系统外形进行网格无关性研究。对无人机半模型进行网格划分,在保证壁面法向网格满足y-plus小于1的前提下,生成粗网格(1100万)、中等网格(2400万)、密网格(23500万)三套网格。对Ma 0.6下,20 km高空条件进行数值仿真。图 6-图 8给出了三套网格下,阻力系数、升力系数以及俯仰力矩系数对比。
|
图 6 不同网格尺度下阻力系数对比 Fig.6 Comparison of drag coefficient at different grids |
|
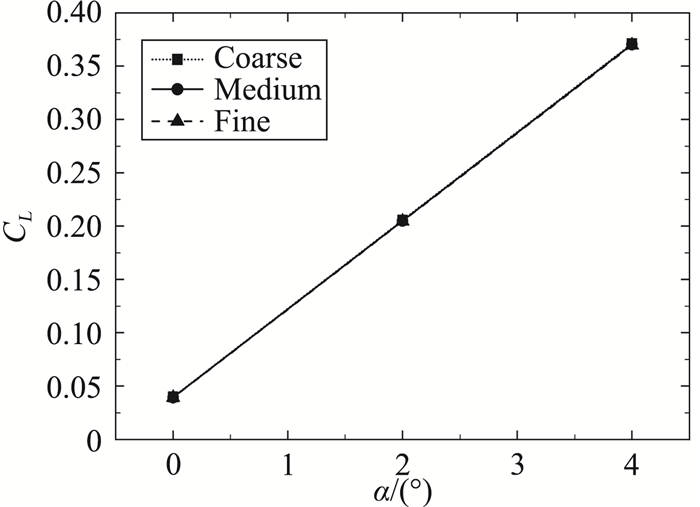
图 7 不同网格尺度升力系数对比 Fig.7 Comparison of lift coefficient at different grids |
|
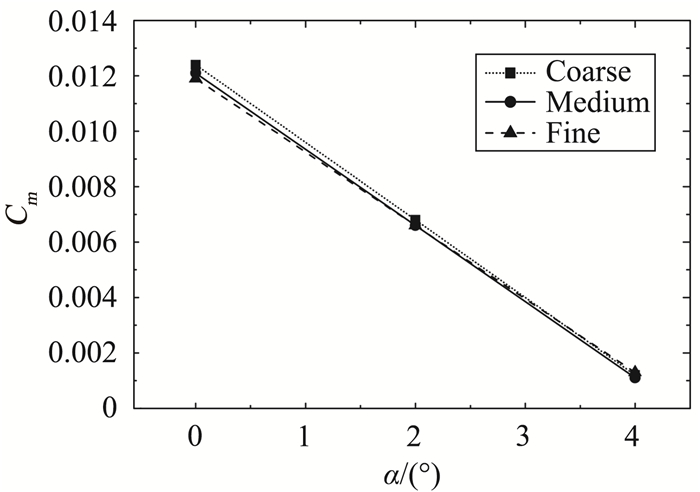
图 8 不同网格尺度俯仰力矩系数对比 Fig.8 Comparison of pitch moment at different grids |
从图 6-图 8可以看到,三种网格尺度下升力系数的差别很小;阻力系数略有平移,网格越密阻力系数越小;网格尺度主要影响俯仰力矩系数的斜率,网格量越大,俯仰力矩斜率越小,但整体变化并不大。
虽然中等量网格得到的阻力系数与密网格得到的结果略有差距,但无量纲量相差仅0.0003,考虑到本文需要获取的是喷流影响量以及网格量过大带来的计算成本,因此后续采取中等网格进行数值计算。
5 外形变化对无人机气动特性影响在飞翼布局无人机设计阶段,无人机气动布局设计、优化一般采用无进排气部件的模型进行优化设计。实际飞行中由于发动机进排气需要,无人机机体外形会发生相应破坏,进而对无人机气动特性产生一定影响。在研究飞翼布局无人机喷流影响量时,喷流状态相比基准外形气动特性的变化包含两部分:一部分是模型变化带来的影响;一部分是喷流效应带来的影响。本文首先研究喷流模型与基准模型下气动特性对比。
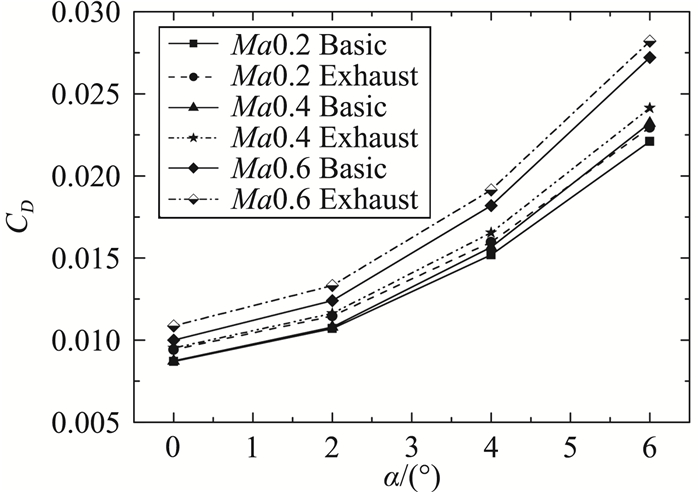
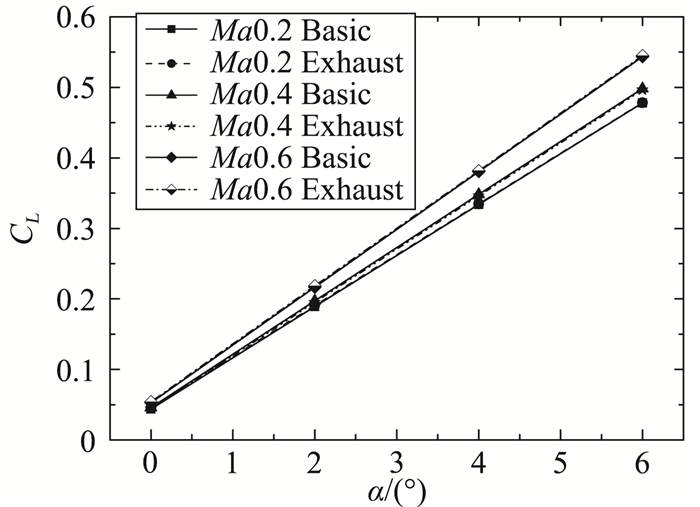
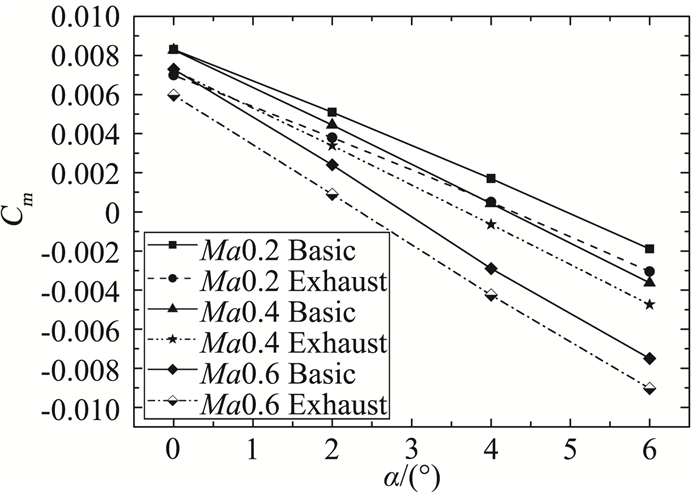
图 9-图 11给出了喷流模型和基准模型之间由于模型差异带来的气动力差异。可以看到,不同Ma数下,喷流模型的阻力系数较基准外形略大6%~9%左右;升力系数变化不大;俯仰力矩系数向下平移约0.012,无人机升阻比下降近5%~8%。外形产生的变化对无人机气动特性影响较大。
|
图 9 喷流模型与基准外形阻力系数对比 Fig.9 Comparison of drag coefficient between basic model and exhaust model |
|
图 10 喷流模型与基准外形升力系数对比 Fig.10 Comparison of lift coefficient between basic model and exhaust model |
|
图 11 喷流模型与基准外形俯仰力矩系数对比 Fig.11 Comparison of pitch moment between basic model and exhaust model |
由于不同马赫数、不同迎角下,外形变化对无人机气动特性的影响相似,因此下面以Ma0.6零度迎角下的流场进行分析。图 12-图 15给出了基准外形和喷流外形下,无人机壁面和对称面的压力系数分布。
|
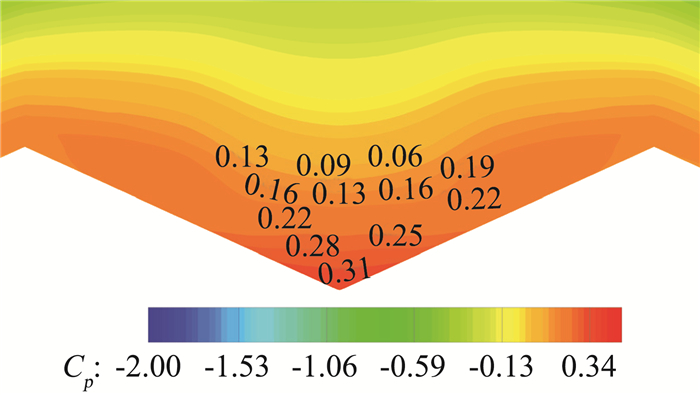
图 12 基准模型尾部压力云图 Fig.12 Pressure contour on the tail of the basic model |
|
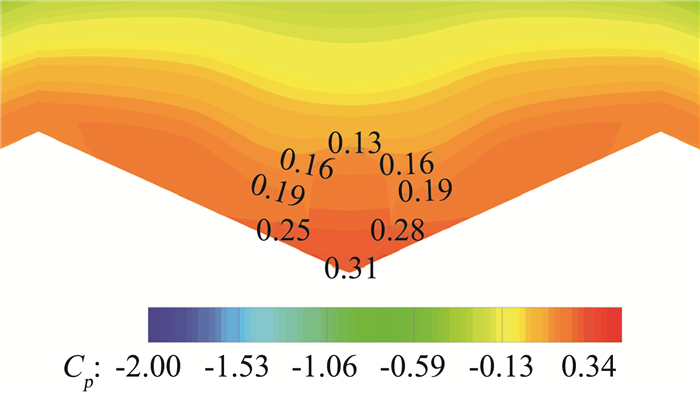
图 13 喷流外形尾部压力云图 Fig.13 Pressure contour on the tail of the exhaust model |
|
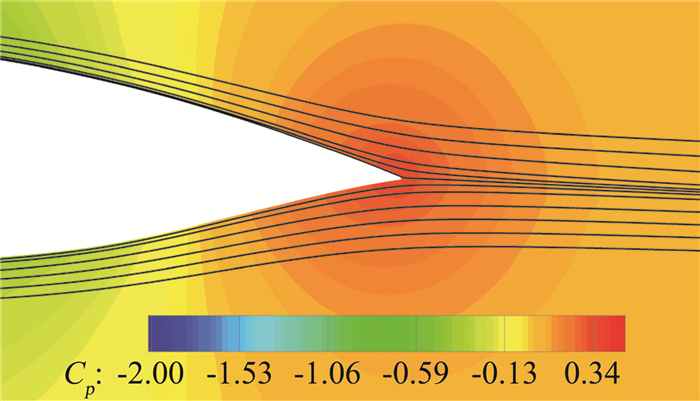
图 14 基准外形对称面压力系数云图 Fig.14 Pressure contour on the symmetry of the basic model |
|
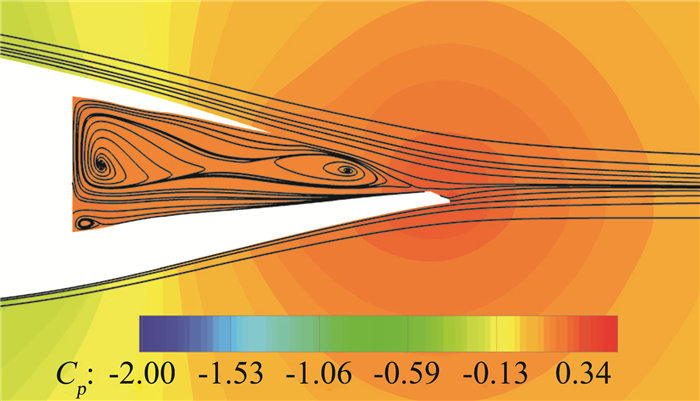
图 15 喷流模型对称面压力系数云图 Fig.15 Pressure contour on the symmetry of the exhaust model |
从图 12和图 13可以看到,无人机整体压力云图分布基本相同,但基准构型在尾喷管出口处为高压区域。该区域的高压在阻力方向表现为“推力”的形式,对于喷流模型该“推力”消失就表现出图 9中阻力系数增大的效果;由于升力贡献面远大于喷管面积,因此外形改变对升力系数影响不大;而该位置的高压对无人机贡献抬头力矩,因此喷流模型下该抬头力矩消失,表现出图 11中的的特性。通过该区域压力系数均值与喷管面积进行核算,可确定无人机气动特性发生变化是由于该部位的变化带来的。
6 喷流效应对无人机气动特性影响选取两种来流条件下三种不同喷流落压比[17]进行数值计算,来流参数按照标准大气参数设置,计算状态如下表 1所示。
| 表 1 计算状态表 Table 1 Computational conditions |
|
|
在工程应用中,动力系统一般只考虑发动机喷流所产生的阻力系数,不考虑喷流产生的升力系数进和俯仰力矩系数,因此本文中的阻力系数扣除尾喷管的阻力系数,对升力系数和俯仰力矩系数则不扣除尾喷管部件。
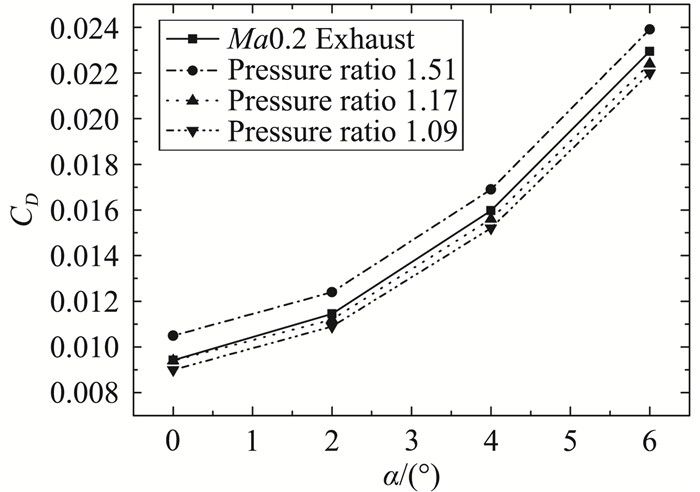
6.1 Ma 0.2喷流效应分析图 16-图 18给出了Ma0.2时无人机喷流效应对气动特性的影响规律。可以看到,落压比P0/P∞=1.51时,喷流使无人机阻力系数略微增加,落压比P0/P∞=1.17及1.09时,喷流使无人机阻力系数减小。综合认为,由于涡扇发动机喷流落压比较小时,喷流效应并不明显。当落压比相对较大(P0/P∞=1.51)时,喷流的引射效应占主导作用,阻力系数相对喷流模型增加;当落压比较小时喷流体积效应占主导作用,尾部产生高压作用相当于“推力”,因此使无人机阻力系数减小。
|
图 16 来流Ma0.2时阻力系数喷流效应 Fig.16 Effect of exhaust on drag coefficient (Ma=0.2) |
|
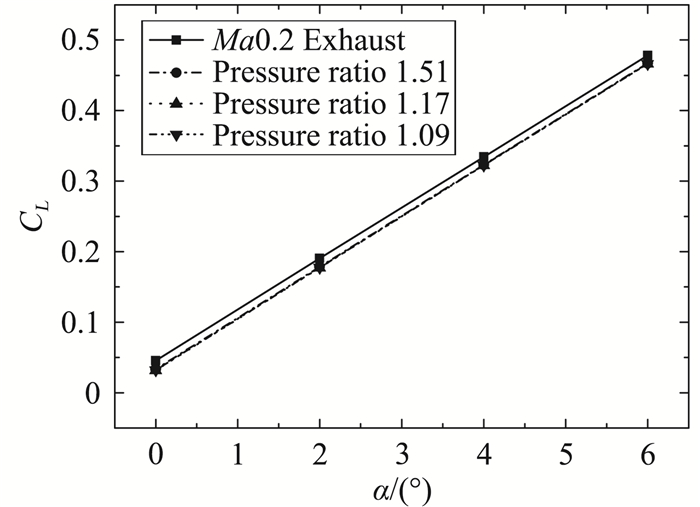
图 17 来流Ma0.2时升力系数喷流效应 Fig.17 Effect of exhaust on lift coefficient (Ma=0.2) |
|
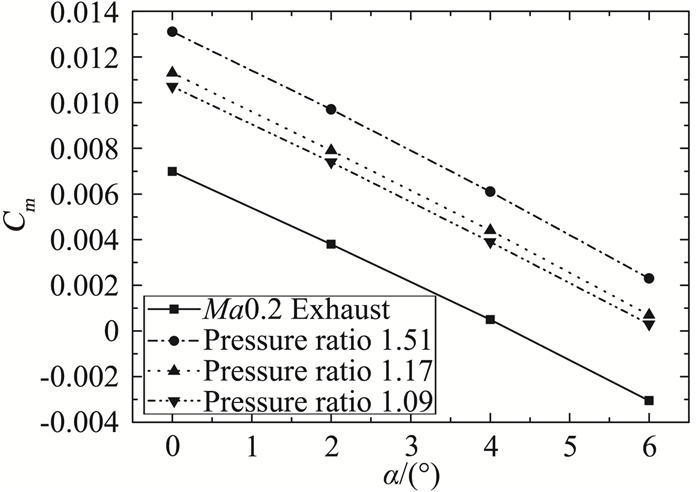
图 18 来流Ma0.2时俯仰力矩系数喷流效应 Fig.18 Effect of exhaust on pitch moment coefficient (Ma=0.2) |
另外,喷流使无人机升力系数略微减小;喷流效应使无人机产生较大抬头力矩,抬头力矩随落压比的增加而增加。这主要是由于飞翼布局无人机特殊的非对称、非圆喷管造成的。并且无人机的纵向静稳定度发生变化,纵向静稳定度从喷流外形(无喷流)的-6.61%改变为-7.10%、-6.95%、-6.82%(随落压比减小排列)。
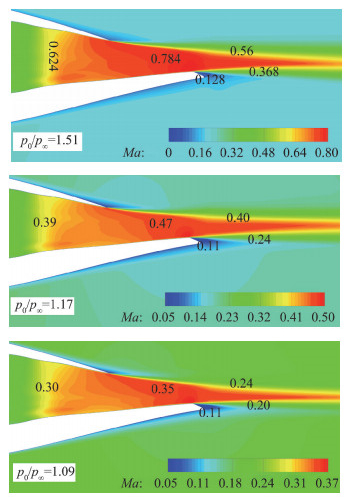
图 19给出了Ma0.2,0°迎角下不同落压比时尾喷管处的马赫云图。可以看到,不同落压比下喷口马赫云图的形态基本不变,但出口马赫数差异较大:喷流落压比越大,出口马赫数越高。
|
图 19 来流Ma0.2不同落压比喷管出口马赫云图(0°迎角) Fig.19 Mach contour on the tail of the exhaust model at different nozzle pressure ratios (angle of attack=0°, Ma=0.2) |
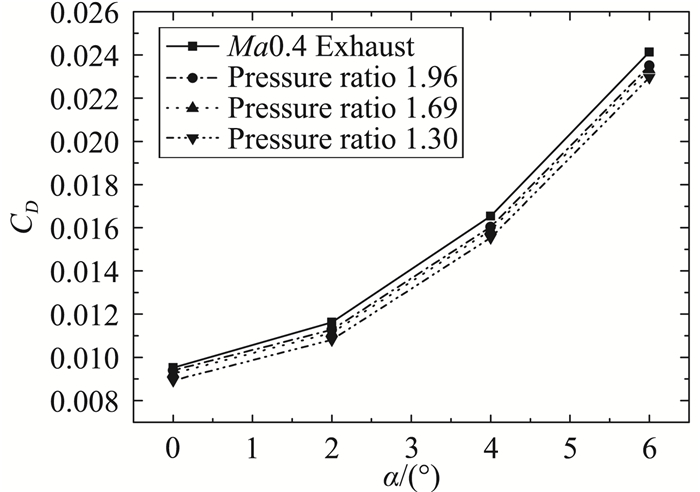
图 20-图 22给出了Ma0.4时无人机喷流效应对气动特性的影响规律。可以看到,与Ma0.2不同,Ma0.4时,不同落压比均使无人机阻力系数减小,落压比越小,减小量越大,这主要是由于喷流体积效应占主导地位。
|
图 20 来流Ma0.4时阻力系数喷流效应 Fig.20 Effect of exhaust on drag coefficient (Ma=0.4) |
|
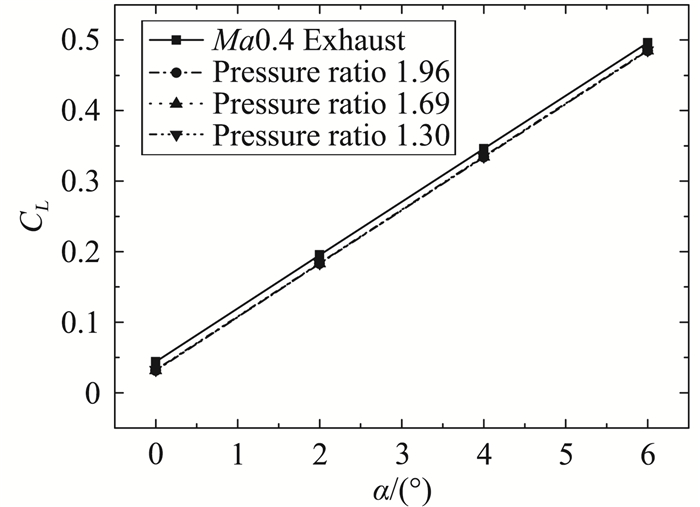
图 21 来流Ma0.4时升力系数喷流效应 Fig.21 Effect of exhaust on lift coefficient (Ma=0.4) |
|
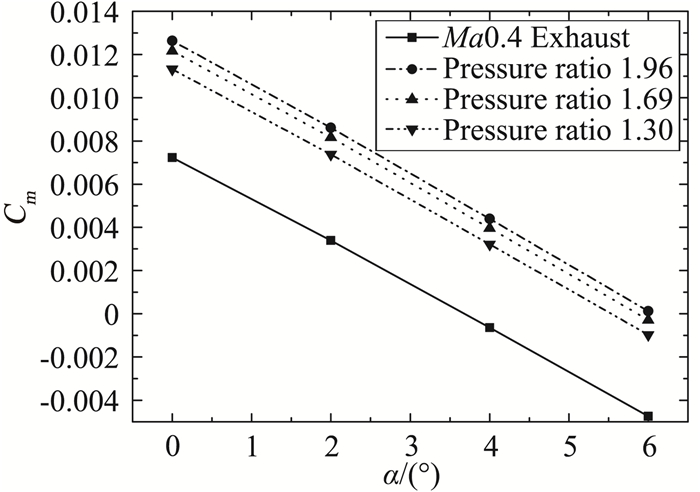
图 22 来流Ma0.4时俯仰力矩系数喷流效应 Fig.22 Effect of exhaust on pitch moment coefficient (Ma=0.4) |
Ma0.4时喷流同样给无人机施加抬头力矩,并且使无人机的纵向静稳定度发生变化,纵向静稳定度从喷流外形(无喷流)的-7.55%改变为-7.87%、-7.83%、-7.73%(随落压比减小排列)。
图 23给出了不同落压比下,喷管出口处的马赫云图。可以看到,不同落压比下出口马赫云图形态一致,出口马赫数随落压比有一定的变化。
|
图 23 来流Ma0.4不同落压比喷管出口马赫云图(0°迎角) Fig.23 Mach contour on the tail of the exhaust model at different nozzle pressure ratios (angle of attack=0°, Ma=0.4) |
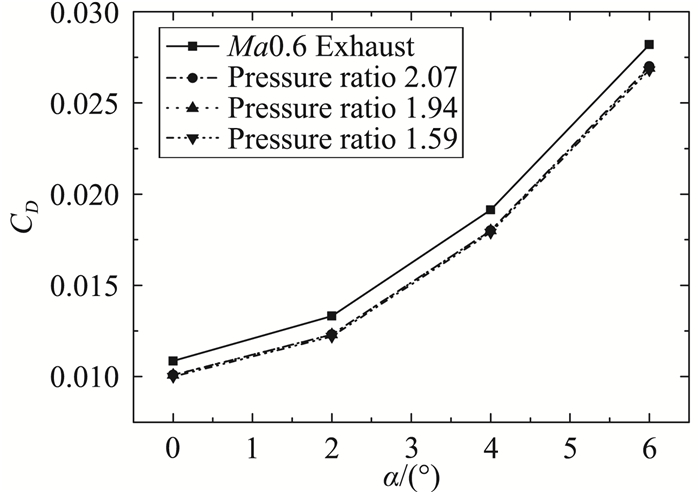
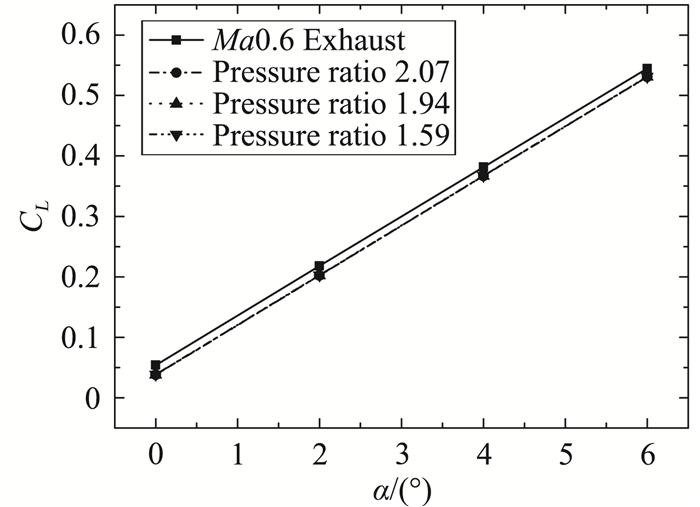
图 24-图 26给出了Ma0.6时无人机喷流效应对气动特性的影响规律。可以看到,与Ma0.2不同,Ma0.6时,不同落压比均使无人机阻力系数减小,落压比越小,减小量越大,这主要是由于喷流体积效应占主导地位;升力系数与俯仰力矩系数与Ma0.2相同,但Ma0.6下落压比的影响量明显较小。
|
图 24 来流Ma0.6时阻力系数喷流效应 Fig.24 Effect of engine exhaust on drag coefficient (Ma=0.6) |
|
图 25 来流Ma0.6时升力系数喷流效应 Fig.25 Effect of engine exhaust on lift coefficient (Ma=0.6) |
|
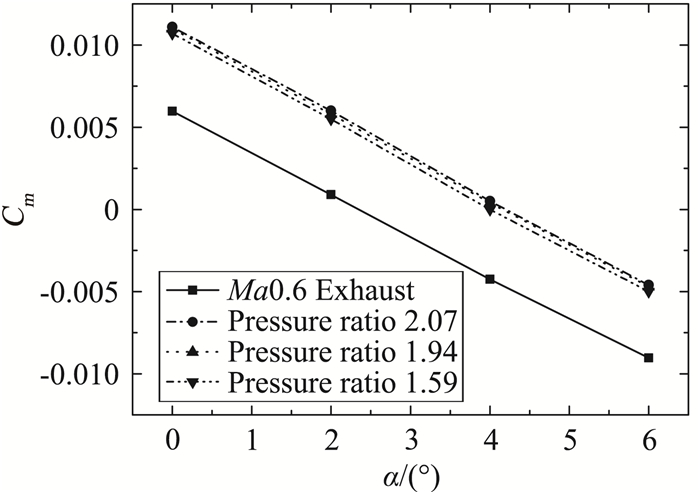
图 26 来流Ma0.6时俯仰力矩系数喷流效应 Fig.26 Effect of engine exhaust on pitch moment coefficient (Ma=0.6) |
Ma0.6时喷流同样给无人机施加抬头力矩,并且使无人机的纵向静稳定度发生变化,纵向静稳定度从喷流外形(无喷流)的-8.71%改变为-9.08%。
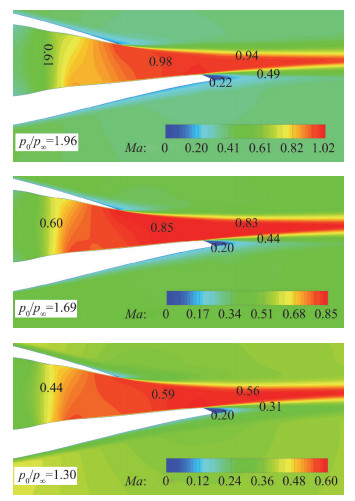
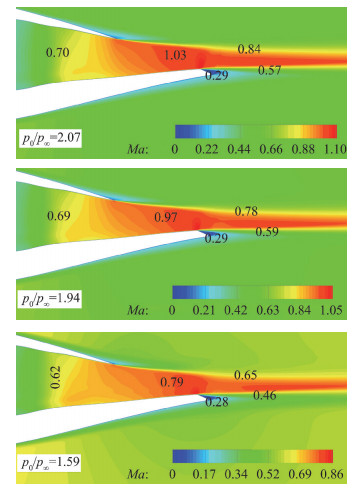
图 27给出了不同落压比下,喷管出口处的马赫云图。可以看到,不同落压比下出口马赫云图形态一致,并且出口马赫数随落压比的变化与前文所述一致。
|
图 27 来流Ma0.6不同落压比喷管出口马赫云图(0°迎角) Fig.27 Mach contour on the tail of the exhaust model at different nozzle pressure ratios (angle of attack=0°, Ma=0.6) |
最后,下面三表给出了三个Ma数下,基准外形、喷流外形以及不同落压比时无人机升阻比的变化。可以看到,不同Ma时无人机基准外形最大升阻比达到21.97、22.22、20.92,喷流外形(无喷流)时升阻比最小,有喷流时升阻比略微增加,但仍小于基准外形。
| 表 2 来流Ma=0.2时不同外形、不同落压比时升阻比对比 Table 2 Comparison of L/D in different nozzle pressure ratios and different models (the coming flow Ma=0.2) |
|
|
| 表 3 来流Ma=0.4时不同外形、不同落压比时升阻比对比 Table 3 Comparison of L/D in different nozzle pressure ratios and different models (the coming flow Ma=0.4) |
|
|
| 表 4 来流Ma=0.6时不同外形、不同落压比升阻比对比 Table 4 Comparison of L/D in different nozzle pressure ratios and different models (the coming flow Ma=0.6) |
|
|
本文通过雷诺平均N-S方程数值模拟方法,研究了喷流对典型飞翼布局无人机气动特性的影响规律,研究结果表明:
1) 喷流导致飞翼布局无人机外形发生变化,该外形的变化对无人机气动特性有一定的影响,使无人机阻力系数增加约6%~9%,并使俯仰力矩系数下移;
2) 扣除尾喷管的阻力系数,喷流效应对无人机升力系数影响较小;对阻力系数的影响主要取决于喷流落压比:当落压比较小时,喷流体积效应起主导作用,使无人机阻力系数减小;反之喷流引射作用占主导作用,使无人机阻力系数增加。另外,喷流效应给无人机附加抬头力矩;
3) 总体来看,相对设计阶段的基准外形,发动机喷流给无人机带来的气动影响有:无人机最大升阻比最大减小量为2,使无人机纵向静稳定度略微增加0.3%~0.4%,并给无人机附加抬头力矩。
| [1] |
余永刚, 黄勇, 周铸, 等. 飞翼布局气动外形设计[J]. 空气动力学学报, 2017, 35(6): 832-836. YU Y G, HUANG Y, ZHOU Z, et al. Aerodynamic design of a flying-wing aircraft[J]. Acta Aerodynamic Sinica, 2017, 35(6): 832-836. DOI:10.7638/kqdlxxb-2015.0163 (in Chinese) |
| [2] |
MIALAN B, FOL T. Aerodynamic optimization of subsonic flying wing configurations. AIAA 2002-2931[R]. Reston: AIAA, 2002.
|
| [3] |
张乐, 周洲, 许晓平, 等. 飞翼无人机保形进排气系统动力数值模拟与流场特性分析[J]. 西北工业大学学报, 2015, 33(3): 353-360. ZHANG L, ZHOU Z, XU X P, et al. Numerical simulation of power and flow field characteristics of conformal intake and exhaustfor flying wing unmanned aerial vehicle[J]. Journal of Northwestern Polytechnical University, 2015, 33(3): 353-360. DOI:10.3969/j.issn.1000-2758.2015.03.001 (in Chinese) |
| [4] |
谭兆光, 陈迎春. 机体/动力装置一体化分析中的动力影响效应数值模拟[J]. 航空动力学报, 2009, 8(8): 1766-1772. TAN Z G, CHEN Y C. Numerical simulation method for the powered effects in airframe/propulsion integration analysis[J]. Journal of Aerospace Power, 2009, 8(8): 1766-1772. (in Chinese) |
| [5] |
郁新华, 陶于金, 师小娟. 进排气效应对飞翼布局无人机气动特性的影响[J]. 飞行力学, 2011, 29(5): 18-21. YU X H, TAO Y J, SHI X J. Effect of engine air intake and exhaust on the aerodynamic performance of the UAV[J]. Flight Dynamics, 2011, 29(5): 18-21. (in Chinese) |
| [6] |
李进涛.飞翼式高空长航时无人机飞行品质特性研究[D].西安: 西北工业大学, 2007. LI J T. Research of th flying wing flight quality in high altitude and long endurance unmanned aerial vehicle[D]. Xi'an: Northwest Polytechnical University, 2007. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1034718 |
| [7] |
黄烁桥, 申功炘, ROBERT KONRATH, 等. 喷流对飞机尾流涡影响的试验研究[J]. 航空学报, 2010, 31(5): 899-908. HUANG S Q, SHEN G X, ROBERT KONRATH, et al. Experimental investigation of influence of jets on aircraft wake vortices[J]. Acta Aeronautica et Astronutica Sinica, 2010, 31(5): 899-908. (in Chinese) |
| [8] |
李周复. 风洞特种实验技术[M]. 北京: 航空工业出版社, 2010: 153-184. LI Z F. Wind tunnel experiment technology[M]. Beijing: Aviation Industry Press, 2010: 153-184. (in Chinese) |
| [9] |
MAHMOOD G M, SMITH D R.Proportional aerodynamic control of a UAV wing model using synthetic jets[R]. AIAA 2007-3851, 2007.
|
| [10] |
DAVID C WILCOX. Turbulence modeling for CFD[M]. Third edition. California: DCW Industries Inc, 2006: 243-249.
|
| [11] |
阎超. 计算流体力学方法与应用[M]. 北京: 北京航空航天大学出版社, 2006: 221-223. YAN C. Computational methods and application[M]. Beijing: Beihang university press, 2006: 221-223. (in Chinese) |
| [12] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering application[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [13] |
张翔, 阎超. 高超声速热流计算湍流模型性能评估[J]. 北京航空航天大学学报, 2015, 41(2): 337-342. ZHANG X, YAN C. Property evaluation on turbulence models calculation in hypersonic heat transfer simulation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 337-342. (in Chinese) |
| [14] |
ROE P L. Approximate Riemann solvers' parameter vectors and difference schemes[J]. Comp Phys, 1982, 170: 507-512. |
| [15] |
VAN LEER B. Towards the ultimate conservation different schemeV:a second-order sequal to Godunov's methods[J]. Journal of Computational Physics, 2004, 201(1): 238-260. DOI:10.1016/j.jcp.2004.05.015 |
| [16] |
王运涛, 孙岩, 王光学, 等. DLR-F6翼身组合体的高阶精度数值模拟[J]. 航空学报, 2015, 36(9): 2923-2929. WANG Y T, SUN Y, WANG G X, et al. High-order accuracy numerical simulation of DLR-F6 wing-body configuration[J]. Acta Aeronautica et Astronutica Sinica, 2015, 36(9): 2923-2929. (in Chinese) |
| [17] |
范杰川. 风洞试验手册[M]. 北京: 航空工业出版社, 2002: 369-374. FAN J C. Handbook of wind tunnel test[M]. Beijing: Aviation Industry Press, 2002: 369-374. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


