2. 中国空气动力研究与发展中心 计算空气动力研究所, 绵阳 621000;
3. 中国运载火箭技术研究院, 北京 100076
2. Computational Aerodynamics Institute of China Aerodynamics Research and Development Center, Mianyang 621000, China;
3. China Academy of Launch Vehicle Technology, Beijing 100076, China
高速飞行器舱内热环境、航空发动机和火箭发动机燃烧室承热能力的有效预测,一方面取决于飞行器表面热流和燃烧室壁面热流的准确模拟,另一方面也取决于防隔热材料热物性参数的准确确定。目前,工程上确定材料热传导系数的方法大多假设材料的热传导系数为常数或是随温度变化的已知函数,采用稳态法、激光法、灵敏度法等方法进行参数辨识[1-8]。对于热传导系数随温度变化规律未知的情况,文献[9-12]将材料的热传导系数值按温度区间分段离散,并通过材料内部或边界温度场的测量结果采用折半法、复变量求导法、遗传算法等方法来辨识出各温度段的热传导系数值。但是,在工程实际应用中发现,由于辨识问题是数学上的不适定问题,当测量误差较大或是计算数学模型和真实物理模型存在一定差异时,在辨识结果中可能会出现比较大的数值振荡,甚至出现某些温度下热传导系数值小于0的非物理情况。因此,有必要在辨识过程中对热传导系数值引入一些物理约束,例如,热传导系数值应大于0;对碳纤维增强树脂基这一类防隔热材料而言,材料的热传导系数值随温度增加而增加等。同时,在实际工程应用中,使用内置的热电偶直接测量低热导率材料内部温度时,热电偶的传热能力远高于材料会导致材料测点附近的温度场发生显著变化,测得温度往往低于实际温度。例如文献[13]在利用热电偶测量燃烧固体温度时,分析了热电偶传热导致的温度损失。为保证在防热系统设计时留有较充足的设计余量,工程上通常要求温度较高时的温度计算预测结果能略高于温度实测值。因此,本文在辨识材料热传导系数的遗传算法基础上进一步考虑上述这些物理约束和工程约束,建立了考虑约束的材料热传导系数辨识方法,并进行了算例考核分析。
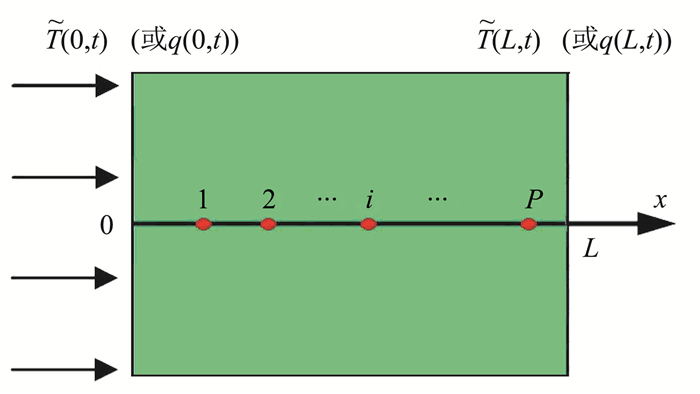
1 辨识材料热传导系数的数学模型确定材料热传导系数的实验原理图如图 1所示,假设上下边界为绝热边界条件后,传热问题可以简化为一维传热问题。假设在材料左右边界可以进行温度和热流的测量,在材料内部可以进行温度的测量,则当边界条件和观测条件为以下两种情况时,可以进行材料热传导系数的辨识:
|
图 1 辨识材料热传导系数示意图 Fig.1 Sketch of thermal conductivity estimation |
1) 没有材料内部测点温度测量的情况:此时在左右边界分别给定温度或热流测量结果作为边界条件,同时将其中一个边界上除边界条件状态量外的另一状态量作为观测量。
2) 材料内部进行了测点温度测量的情况:此时在左右边界分别给定温度或热流测量结果作为边界条件,将内部测点的温度作为观测条件。
不失一般性,本文针对第二种情况进行分析,即在材料左右边界给定温度边界条件,在材料内部选取一个或多个测点进行温度测量后来对材料的热物性参数进行辨识。此时的传热方程为:
| $ \rho c_{p} \frac{\partial T}{\partial t}=\frac{\partial}{\partial x}\left[k(T) \frac{\partial T}{\partial x}\right] $ | (1) |
边界条件:x=0:T=T(0, t);x=L:T=T(L, t);
初始条件:t=0:T=T0;
观测方程:
其中,ρ为材料密度,cp为材料比热,
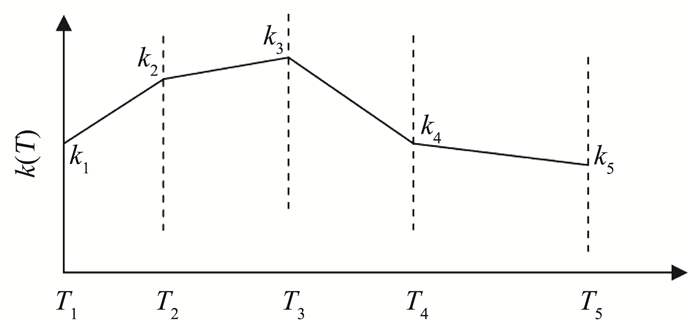
式(1)中的热传导系数值是温度的函数,若函数形式未知,则可将温度的可能取值范围分段,热传导系数值在各段取线性函数,如图 2。设在整个温度区间取M个节点,对应温度为Ti(i=1, M),则k(T)可写为:
|
图 2 随温度变化热传导系数示意图 Fig.2 Sketch of temperature-dependant thermal conductivity |
| $ k(T) = \sum\limits_{i = 1}^M {{k_i}} {\varphi _i}(T) $ | (2) |
且:
| $ \begin{array}{l} {\varphi _i} = \left\{ {\begin{array}{*{20}{l}} {\left( {T - {T_{i - 1}}} \right)/\left( {{T_i} - {T_{i - 1}}} \right);T \in \left[ {{T_{i - 1}}, {T_i}} \right]}\\ {\left( {{T_{i + 1}} - T} \right)/\left( {{T_{i + 1}} - {T_i}} \right);T \in \left[ {{T_i}, {T_{i + 1}}} \right]}\\ {0;\quad {\rm{ other }}} \end{array}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(i = 2, M - 1);\\ {\varphi _M} = \left\{ {\begin{array}{*{20}{l}} {\left( {T - {T_{M - 1}}} \right)/\left( {{T_M} - {T_{M - 1}}} \right);T \in \left[ {{T_{M - 1}}, {T_M}} \right]}\\ {0;\quad {\rm{ other }}} \end{array}} \right.。\end{array} $ |
可见,如果给定热传导系数在各温度区间内的值ki(i=1, M),则可以采用有限控制体积法[1]来进行热传导正问题的数值求解。然而就逆问题而言,热传导系数k(T)未知,需要由观测方程式(2)中的信息来辨识,因此该逆问题可转化为求合适的k(T)使如下目标函数达极小的优化问题:
| $ \begin{array}{*{20}{l}} {J(k(T)) = }\\ {\int\limits_{t = 0}^t {\sum\limits_{i = 1}^P {\left\{ {{{\left[ {T\left( {{x_i}, t, k(T)} \right) - \tilde T\left( {{x_i}, t} \right)} \right]}^2}{w_i}} \right\}} } {\rm{d}}t} \end{array} $ | (3) |
其中,t=[0, tf]表示温度测量的时间段,wi为各测点温度偏差在目标函数中占的权值。由于k针对温度区间进行了离散,因此式(3)中的函数优化问题转化为了针对参数ki(i=1, N)的参数优化问题,下面介绍其优化策略。
2 辨识材料热传导系数的遗传算法对于上述优化问题,可以采用的优化方法主要分为两类:一类是梯度类优化算法,如最速下降法和共轭梯度法;另一类是遗传算法。由于梯度类优化算法对初值选取比较敏感,尤其是当M值较大(即温度区间分段较密)时,优化计算易于陷入局部极值。因此,本文优化计算采用具有较强鲁棒性和全局优化能力的遗传算法[14]。其基本思路是随机生成一个由待优化参数组合构成个体的种群,计算所有个体对应的目标函数,并转换为适应值F的形式,如:
| $ F=1/J ~~~或 ~~~ F=a-J (a是一较大的正数) $ | (4) |
以使最小的目标函数对应于最大的适应值,再通过适当的选择、复制、进化机制,使适应值较大的个体能在优化过程中被保留并不断进化,类似于生物界中的“适者生存”,这样经过若干代进化后最终得到的适应值最大的个体即为优化问题的最优解。对于材料热传导系数的辨识,J为式(3)中的形式,其具体算法如下:
(1) 首先是编码,可以采用二进制编码或十进制编码,将待优化参数ki (i=1, M)分别对应成二进制数或十进制浮点数序列,组合在一起形成个体的染色体;
(2) 初始化:利用随机方法产生N个个体,形成初始种群,利用每个个体对应的ki (i=1, M)进行热传导正问题计算,利用式(3)和式(4)得到各个体的J和适应值;
(3) 个体选择、复制操作:对初始种群,根据适应值决定的概率分布,采用轮盘赌选择法来重新生成N个个体;
(4) 对步骤(3)生成的N个个体进行单点交叉、均匀变异操作,产生新的种群;
(5) 对新种群中的N个体进行热传导正问题计算,找出新种群中适应值最大的个体,判断计算是否收敛,若收敛,则停止,否则返回步骤(3)。
下面给出两个算例,第一个算例对热传导系数为常值,左端受常值热流Q右端绝热的一维平板传热问题进行分析,这一问题的边界温度和内点温度都存在解析解,以这些解析解加上标准差为σ的白噪声作为测量值,对热传导系数进行辨识。当L=1,cp=1,Q=1,测点取在x=0.5时分析了三种情况,一是σ=0,即不考虑测量噪声;二是σ取为x=0.5处最大温度的1%;三是σ取为x=0.5处最大温度的5%。表 1中给出了辨识结果,从表中可以看到,即使在测量噪声比较大的情况下,辨识结果与给定值较为符合。这一结果表明热传导正问题的计算方法和遗传算法本身都是有效的。
| 表 1 热传导系数的真值和辨识结果 Table 1 Exact and estimated values of const thermal conductivity |
|
|
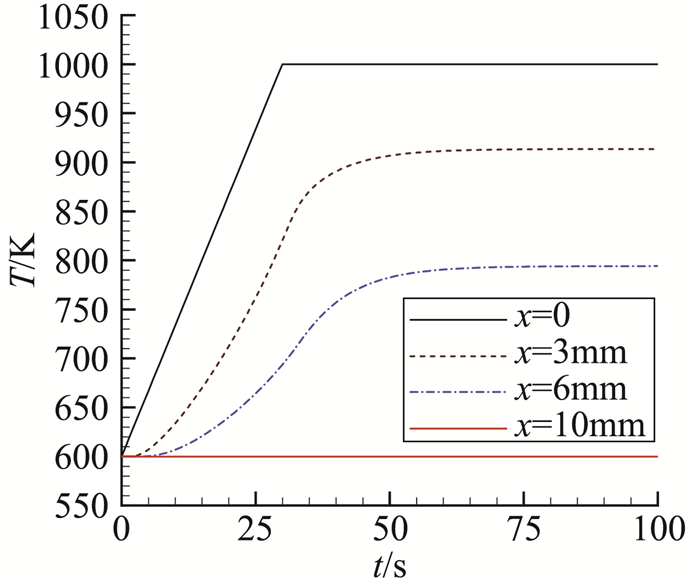
第二个算例的参数设置为:材料的ρ=1000 kg/m3,cp=1000 J/kg·K,L=0.01 m,T0=600 K,材料左右边界的温度条件如图 3中“x=0”, “x=10mm”示,两个测点分别位于x=3 mm和x=6 mm位置。设材料热传导系数随温度变化的函数为式(2)中的形式,Ti和ki给定值列于表 2的前两行。由此可计算出两个测点的温度历程,如图 3中“x=3 mm”和“x=6 mm”。
|
图 3 温度边界条件及测点温度 Fig.3 Temperatures of boundary condition and measurement points |
| 表 2 材料热传导系数随温度变化的函数及辨识结果 Table 2 Specified temperature-dependant thermal conductivity and estimation results |
|
|
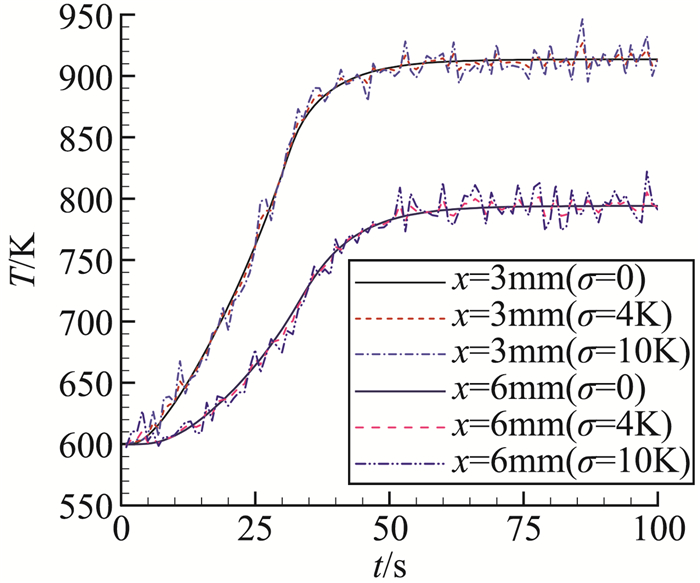
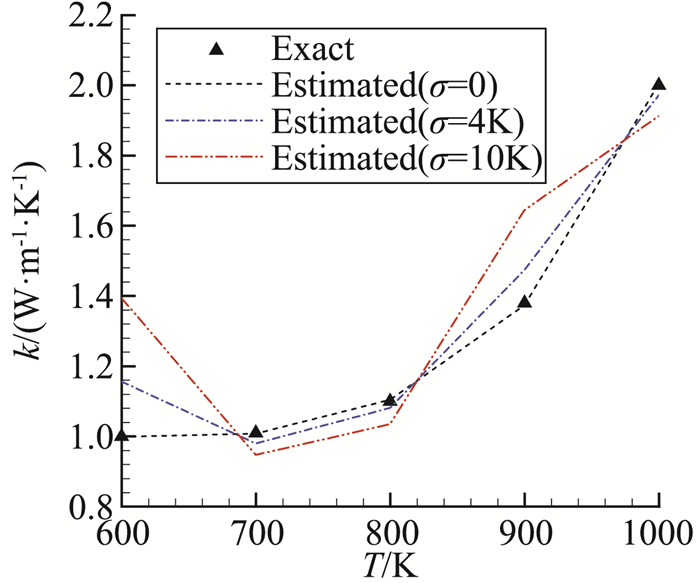
下面分析逆问题,将两个测点温度计算值分别叠加标准差σ=0、4 K和10 K的白噪声来做为测量值(示于图 4),采用遗传算法来对ki(i=1, 5)进行辨识,其中σ=0表示不叠加白噪声,用于验证算法。遗传算法采用二进制编码,种群样本数取为50,交叉概率为0.8,变异概率为0.05。表 2和图 5中给出了此时的辨识结果,从结果中可以看到:
|
图 4 考虑测量噪声后的测点温度值 Fig.4 Temperatures with measurement noise |
|
图 5 热传导系数辨识结果 Fig.5 Estimated value of thermal conductivity |
(1) 当σ=0时,辨识结果和给定值符合较好,相对误差 < 5‰,验证了辨识方法的有效性。
(2) 考虑测量噪声后,辨识结果与给定值有较大偏差,辨识结果中出现了比较大的数值振荡,对应较低温度的k1值大于k2、k3和k4值,与真实物理情况存在一定差异。因此,下面考虑在辨识算法中加入约束来进行计算分析。
3 考虑物理约束的热传导系数辨识算法首先在辨识算法中考虑一项物理约束即碳纤维增强树脂基复合材料的热传导系数值随温度增加不减小。对于上面约束条件的施加方法,考虑如下两种方法。
3.1 辨识增量的方法这一方法的基本思想是从某个ki(如k2)开始,不辨识热传导系数的绝对量,而是辨识其增量:
| $ \Delta k_{i}=k_{i}-k_{i-1}, \Delta k_{i} \geqslant 0 \quad(i=2, M) $ | (5) |
并且将增量值的取值范围限定为大于或等于0的数,这样就保证了从k2开始即满足“热传导系数随温度增加而不减”的约束条件。
3.2 罚函数方法由于材料的热传导系数值随温度增加不减小,这就相当于对辨识结果施加了如下约束:
| $ \begin{array}{l}对于{k_{m}, m \in[1, M-1]}, \\有 {k_{n} \geqslant k_{m}, n \in[m+1, M]}\end{array} $ | (6) |
为了在遗传算法中引入此约束,需要采用罚函数的方法[15],其基本思想是:在进化过程中,若种群中某样本个体对应的优化变量不满足上述约束,则在其目标函数值上增加一正值作为“惩罚”,从而减小其适应值,使其在后期的交叉选择过程中被选中的概率减小;而其它满足约束的样本个体则不施加这一“惩罚”,在后期的交叉选择过程中被选中的概率较大;这样不断进化,可得到既有较大适应值又满足约束的样本作为辨识结果。
对应到遗传算法的实际计算中,样本目标函数的计算公式需要由式(3)变为下式:
| $ \begin{aligned} J(\vec{k}) &=\int\limits_{t=0}^{t f} \sum\limits_{i=1}^{P}\left\{\left[T\left(x_{i}, t, k_{i}\right)-\widetilde{T}\left(x_{i}, t\right)\right]^{2} w_{i}\right\} \mathrm{d} t \\ &+\varepsilon \cdot \sum\limits_{m=1}^{M-1}\left(\sum\limits_{n=m+1}^{M} \max \left(k_{m}-k_{n}, 0\right)\right) \end{aligned} $ | (7) |
其中ε为罚因子,ε值的选取对辨识结果有较大影响,当ε值较小时,罚函数的作用未充分显现;而当ε值较大时,在优化计算早期会出现很多样本都因不满足约束而被淘汰的情况,影响优化计算效率,因此实际使用中需要根据优化结果是否满足约束的情况来对ε值进行调整。
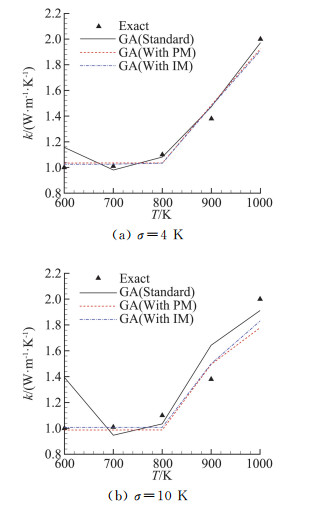
3.3 算例与结果分析对应第2节中算例考虑测量噪声的情况,分别采用辨识增量的方法和罚函数方法来进行辨识计算,辨识增量的方法中,5个优化变量为:k1,Δk2,Δk3,Δk4,Δk5;罚函数方法中优化变量仍为ki(i=1, 5),罚因子ε值取为100。表 2和图 6中的“GA(With IM)”和“GA(With PM)”给出了此时的辨识结果。从结果中可以看到:
|
图 6 考虑约束情况下的热传导系数辨识结果 Fig.6 Estimated value of thermal conductivity with constraints taken into account |
(1) 在两组不同测量噪声水平下的辨识结果都满足热传导系数值大于0和热传导系数值随温度增加不减小的约束条件,上节所建立的算法是有效的。
(2) 在两组不同测量噪声水平下,随着测量误差的增加,辨识结果与给定值的偏差增大,但整体来看,辨识结果与给定值基本符合,在温度测量标准差σ=10 K情况(对x=6mm测点而言,该标准差近似对应于温升的6%)下,辨识结果与给定值的偏差小于10%。
(3) 两种考虑约束的算法得出的辨识结果基本一致,但从方法构建上来看,辨识增量的方法推导较为简便,没有自由参数;而罚函数方法中罚因子ε值的选取有一定的经验成分。
4 工程应用约束的实现下面进一步讨论工程实际应用中“温度较高时计算温度计算预测结果能略高于温度实测值”这一约束的实现。以第三节中的辨识增量的方法为基础,将待辨识参数记为
| $ \begin{array}{l} J\left( {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \theta } } \right) = \\ \sum\limits_{l = 1}^N {\sum\limits_{i = 1}^P {\left\{ {{{\left[ {T\left( {{x_i}, {t_l}, \vec \theta } \right) - \tilde T\left( {{x_i}, {t_l}} \right)} \right]}^2}{w_i}{\varepsilon _{il}} + {\eta _{il}}} \right\}} } ;\\ {\varepsilon _{il}} = \left\{ {\begin{array}{*{20}{l}} {{G_1};T\left( {{x_i}, {t_l}, \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \theta } } \right)}&{ < \tilde T\left( {{x_i}, {t_l}} \right)且\tilde T\left( {{x_i}, {t_l}} \right) > {T_C}}\\ {1;\;\;\;\;{\rm{otherwise}}}&{\rm{ }} \end{array}} \right.;\\ {\eta _{il}} = \left\{ {\begin{array}{*{20}{l}} {{G_2};T\left( {{x_i}, {t_l}, \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \theta } } \right)}&{ < \tilde T\left( {{x_i}, {t_l}} \right)且\tilde T\left( {{x_i}, {t_l}} \right) > {T_C}}\\ {0;\;\;\;\;{\rm{otherwise}}}&{\rm{ }} \end{array}} \right. \end{array} $ | (8) |
其中,N为时间方向上的离散点数;εil和ηil均为罚因子;TC为需要施加约束的温度阈值,即温度超过TC后才需要施加“计算预测结果略高于实测值”的约束;G1、G2为大于1的正数。
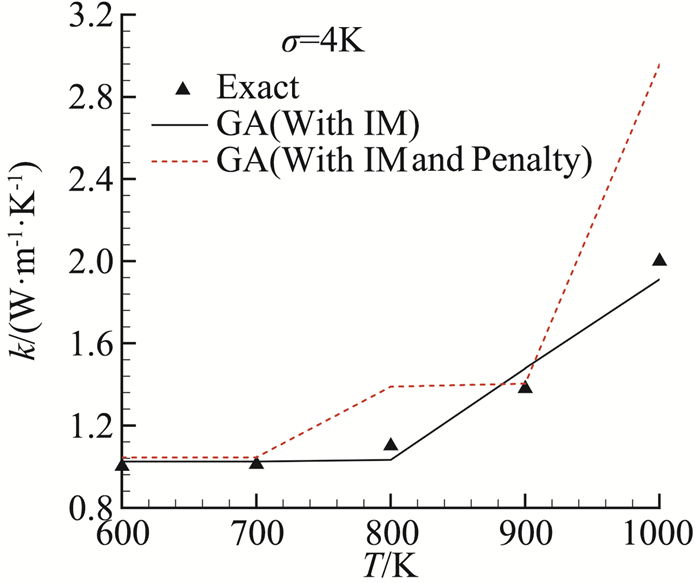
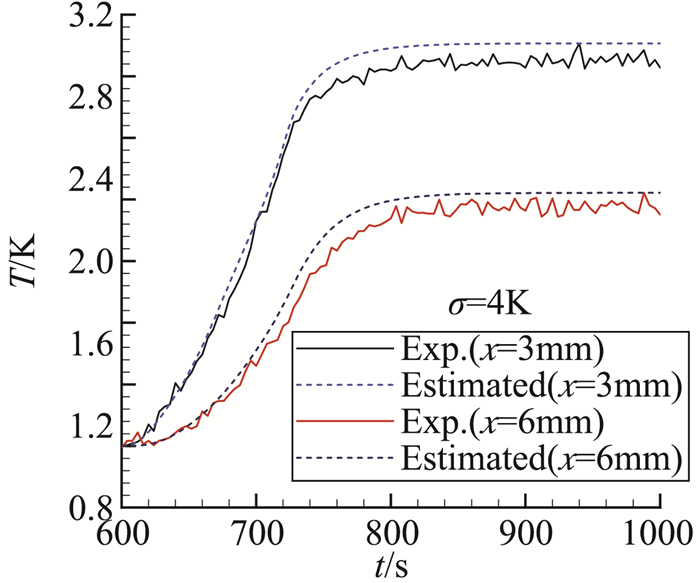
采用这一算法对第2节中考虑σ=4 K测量噪声的算例进行计算,取TC=700 K,G1=10000,G2=500,此时辨识出的结果如表 2的最后一行和图 7中的“GA(With IM and Penalty)”示,图 8给出了利用这一辨识结果计算出的测点温度。从中可以看到:温度为700 K和1000 K的热传导系数辨识结果显著高于给定值而温度为800 K的热传导系数辨识结果稍低于给定值,这使得利用辨识结果计算出的温度值大于测量值,满足工程约束要求。
|
图 7 热传导系数辨识结果 Fig.7 Estimated value of thermal conductivity |
|
图 8 测点温度值对比 Fig.8 Comparison of temperatures at measurement points |
本文通过辨识增量和引入罚函数的方法,在辨识材料热传导系数的遗传算法中实现了一项物理约束:材料热传导系数值随温度增加不减小,和一项工程应用约束:温度较高时的仿真计算结果应高于实测值。算例计算结果表明:辨识计算结果与真值整体符合较好,考虑约束后,在测量噪声较大的情况下,热传导系数辨识结果中没有出现非物理的振荡;测点温度计算预测结果在高温条件下达到了高于实测值的设计条件。辨识方法是有效的,在工程实际中有良好的应用前景,目前已在某型飞行器防热材料的热物性参数地面标定试验中得到了初步的工程应用,下步将针对方法中罚因子的合理选取开展进一步的深入分析。
| [1] |
BECK J V, BLACKWELL B, Jr CLAIR C R S. Inverse heat conduction-ill-posed problems[M]. John Wiley&Sons. New York, 1985.
|
| [2] |
OZISIK M N, ORLANDE H R B. Inverse heat transfer-fundamentals and applications[M]. New York: Taylor&Francis, 2000.
|
| [3] |
杨晨, Ulrich Gross. 基于热传导逆问题方法预测材料热物性参数[J]. 化工学报, 2005, 56(12): 2415-2420. YANG C, ULRICH G. Estimation of thermal properties based on inverse heat conduction method[J]. Journal of Chemical Industry and Engineering, 2005, 56(12): 2415-2420. DOI:10.3321/j.issn:0438-1157.2005.12.027 (in Chinese) |
| [4] |
王登刚, 刘迎曦, 李守巨, 等. 识别材料导热系数和导温系数的温度场逆分析[J]. 上海理工大学学报, 2001, 23(3): 233-237. WANG D G, LIU Y X, LI S J, et al. Inverse heat conduction problem for identifying thermal conductivity and thermal diffusivity simultaneously[J]. J University of Shanghai for Science and Technology, 2001, 23(3): 233-237. DOI:10.3969/j.issn.1007-6735.2001.03.012 (in Chinese) |
| [5] |
薛齐文, 杨海天, 杜秀云. 同伦正则化算法求解多宗量瞬态热传导反问题[J]. 计算物理, 2006, 23(2): 151-157. XUE Q W, YANG H T, DU X Y. An inverse heat conduction problem with multi-variables in a transient state with a homotopic regularization method[J]. Chinese Journal of Computational Physics, 2006, 23(2): 151-157. DOI:10.3969/j.issn.1001-246X.2006.02.005 (in Chinese) |
| [6] |
薛齐文, 魏伟, 杨海天. 多宗量瞬态热传导反演识别[J]. 固体力学学报, 2009, 30(1): 65-69. XUE Q W, WEI W, YANG H T. Parameters identification of inverse heat conduction problems in transient state with multi-variables[J]. Chinese Journal of Solid Mechanics, 2009, 30(1): 65-69. (in Chinese) |
| [7] |
姜贵庆, 马淑雅. 防热涂层材料热防护性能预测[J]. 空气动力学学报, 2004, 22(1): 24-28. JIANG G Q, MA S Y. The prediction of thermal protection performance for coating material[J]. Acta Aerodynamica Sinica, 2004, 22(1): 24-28. DOI:10.3969/j.issn.0258-1825.2004.01.005 (in Chinese) |
| [8] |
钱炜祺, 蔡金狮. 用灵敏度法辨识热传导系数及热流参数[J]. 空气动力学学报, 1998, 16(2): 226-231. QIAN W Q, CAI J S. Parameter estimation of heat conduction coefficient and heat flux by sensitivity method[J]. Acta Aerodynamica Sinica, 1998, 16(2): 226-231. (in Chinese) |
| [9] |
赵晓琳.多孔介质有效导热系数的算法研究[D].辽宁: 大连理工大学, 2009. ZHAO X L. The research of effective conductivity in porous media[D]. Liaoning: Dalian University of Technology (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10141-2009116601.htm |
| [10] |
周焕林, 徐兴盛, 李秀丽, 等. 反演二维瞬态热传导问题随温度变化的导热系数[J]. 应用数学和力学, 2014, 35(12): 1341-1351. ZHOU H L, XU X S, LI X L, et al. Identification of temperature-dependent thermal conductivity for 2-D transient heat conduction problems[J]. Applied Mathematics and Mechanics, 2014, 35(12): 1341-1351. DOI:10.3879/j.issn.1000-0887.2014.12.006 (in Chinese) |
| [11] |
唐中华, 钱国红, 钱炜祺. 材料热传导系数随温度变化函数的反演方法[J]. 计算力学学报, 2011, 28(3): 377-382. TANG Z H, QIAN G H, QIAN W Q. Estimation of temperature-dependent function thermal conductivity for a material[J]. Chinese Journal of Computational Mechanics, 2011, 28(3): 377-382. (in Chinese) |
| [12] |
周宇, 钱炜祺, 何开锋, 等. 同时反演材料热传导系数和比热的算法[J]. 计算物理, 2011, 28(5): 719-724. ZHOU Y, QIAN W Q, HE K F, et al. Estimating temperature-dependent thermal conductivity and specific heat simultaneously[J]. Chinese Journal of Computational Physics, 2011, 28(5): 719-724. DOI:10.3969/j.issn.1001-246X.2011.05.012 (in Chinese) |
| [13] |
ISHIHARA, A. Burning surface temperature measured with a thermocouple[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA 2003-5086, 2003. https://arc.aiaa.org/doi/abs/10.2514/6.2003-5086
|
| [14] |
周明, 孙树栋. 遗传算法原理及应用[M]. 北京: 国防工业出版社, 1999. ZHOU M, SUN S D. Principle and application of genetic algorithms[M]. Beijing: National Defense Industry Press, 1999. (in Chinese) |
| [15] |
KRAMER O, SCHLACHTER U, SPRECKELS V. An adaptive penalty function with meta-modeling for constrained problems[C]//Proceedings of 2013 IEEE Congress on Evolutionary Computation, June20-23, Cancun, Mexico. pp. 1350-1354, 2013. https://ieeexplore.ieee.org/document/6557721/
|
 2019, Vol. 37
2019, Vol. 37


