2. 中国科学院大学 工程科学学院, 北京 100049;
3. 中国科学院力学研究所 高温气体动力学国家重点实验室, 北京 100190
2. School of Engineering Science, University of Chinese Academy of Sciences, Beijing 100049, China;
3. LHD, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
在数值模拟复杂流体流动问题中, 特别是在研究非定常多尺度流动的细微结构及其机理时, 高精度格式比低精度格式更能准确地捕捉各种小尺度量,特别像湍流、旋涡、气动声学等流动问题。因而,近年来高精度低耗散数值方法的研究越来越受到重视。对于可压缩复杂流动的精细模拟,除了需要高精度、低耗散地分辨小尺度流动细节,还需要对激波进行捕捉,并尽量避免数值振荡。1994年,Liu等对ENO格式进行了改进[1],提出了WENO(Weighted Essential Non-Oscillatory)格式,WENO格式成为目前应用最广泛的激波捕捉格式。随即,Jiang和Shu对该方法进一步改进[2],提出了新的光滑度量因子,使得WENO格式的精度进一步得到提高。数值试验表明,Jiang和Shu的WENO格式具有较强的鲁棒性,因而被广泛地使用。此后,人们对WENO格式进行着一系列测试、评估和改进[3-7]。在国内,高精度激波捕捉格式的构造也得到了广泛的重视。邓小刚等[8-9]构造了高精度加权紧致格式WCNS和高精度耗散加权紧致格式DWCNS。张涵信等[10]基于三阶ENN格式,引入加权函数,构造了一种具有四阶或五阶精度的WENN高阶格式。傅德薰、马延文先后提出了耗散比拟法[11]和群速度控制方法[12],以及三阶和五阶精度的迎风紧致格式以及超紧致格式[13]。任玉新等[14]提出了色散最优耗散可调的高分辨率线性格式。李新亮、何志伟等[15-16]提出非线性谱分析优化的保单调格式和群速度控制方法。
一般而言,低耗散特性及强激波捕捉能力不容易兼顾。因而近年来发展出了混合格式(Hybrid schemes),即将两种格式混合使用,在间断或大梯度区采用强鲁棒的激波捕捉格式,而在相对光滑区采取无耗散的中心格式或低耗散的线性格式。Pirozzoli[17]运用光滑识别器作为判据,在光滑区使用紧致格式而在非光滑区使用WENO格式,从而较好实现了分辨小尺度波与捕捉激波的效果。Ren等使用了加权思想[5],将WENO格式与紧致格式混合使用,避免了两种格式之间的“硬切换”,从而起到了更好的效果。
本文的主要工作就是基于WENO格式中的光滑因子,构建一种新型的加权函数,并在此基础上将经典的7阶WENO格式和8阶中心格式组合成混合格式,实现数值耗散的自适应控制,构造出一种自适应低耗散的数值格式。通过对格式进行非线性色散、耗散特性分析,对比研究格式在不同波数下的色散和耗散特性,并经若干一维和二维算例数值验证新格式对流场间断及小尺度波的捕捉能力,以期为可压缩湍流的数值模拟提供一种新的方法。
1 数值方法 1.1 数值格式构造方法使用Jiang等提出的WENO7格式[2]为通量插值形式,本文使用原始变量重构形式。WENO7格式[18]为:
| $ {H_{j + 1/2}} = \sum\limits_{k = 0}^3 {{\omega _k}} H_{j + 1/2}^{(k)} $ | (1) |
| $ H_{j + 1/2}^{(k)} = \sum\limits_{k = 0}^3 {a_l^{(k)}} {f_{j + k - 3 + l}} $ | (2) |
其中:Hj+1/2(k)为模板各给出的通量,ωk为各个模板对应的非线性权值,相应的表达式为:
| $ \begin{aligned} \omega_{k} &=\frac{\alpha_{k}}{\alpha_{0}+\alpha_{1}+\alpha_{2}+\alpha_{3}} \\ \alpha_{k} &=\frac{C_{k}}{\left(\varepsilon+\beta_{k}\right)^{p}}, p=2, \varepsilon=10^{-5} \sim 10^{-7} \end{aligned} $ | (3) |
根据Taylor级数展开式容易给出光滑区域的理想加权因子:
| $ C_{0}=\frac{1}{35}, C_{1}=\frac{12}{35}, C_{2}=\frac{18}{35}, C_{3}=\frac{4}{35} $ | (4) |
光滑度量因子βk的表达式为:
| $ \beta_{k}=f_{k}^{\prime 2}+\frac{13}{12} f_{k}^{\prime \prime 2}+\frac{1043}{960} f_{k}^{\prime \prime \prime 2}+\frac{1}{12} f_{k}^{\prime} f_{k}^{\prime \prime \prime} $ | (5) |
其中:
八阶中心格式的数值通量表达式为:
| $ \begin{aligned} F_{j}=& \frac{1}{840}\left[672\left(f_{j+1}-f_{j-1}\right)-168\left(f_{j+2}-f_{j-2}\right)+\right.\\ &\left.32\left(f_{j+3}-f_{j-3}\right)-3\left(f_{j+4}-f_{j-4}\right)\right] \end{aligned} $ | (6) |
半点格式的表达式为:
| $ \begin{aligned} F_{j+1 / 2} &=\frac{1}{840}\left[533\left(f_{j}+f_{j+1}\right)-139\left(f_{j-1}+f_{j+2}\right)+\right.\\ 29( &\left.\left.f_{j-2}+f_{j+3}\right)-3\left(f_{j-3}+f_{j+4}\right)\right] \end{aligned} $ | (7) |
由于WENO格式的耗散相对较大,而中心格式无耗散,因此本文的目的是将两种格式进行混合,从而构造出一种低耗散的数值格式。基于这一思想,在此引入加权函数σ,格式变为:
| $ F_{j+1 / 2}=\sigma H_{j+1 / 2}+(1-\sigma) F_{j+1 / 2}^{C D 8} $ | (8) |
为实现对该混合格式数值耗散的自适应控制,本文建立起加权因子σ与光滑度量因子βk的关系。根据βk在光滑区时很小,而在间断区相对较大这一特点,本文在此构造σ与βk的关系式为:
| $ \sigma=\arctan \left(n \cdot \beta^{2}\right) /\left(\frac{\pi}{2}\right) $ | (9) |
这里β=min{|βk|}, n根据不同的算例取相应的值。一般对于马赫数较高或者振荡比较剧烈的问题,需要格式有足够的耗散来抑制振荡,此时n的取值将会有所增加,以此来保证赋予WENO格式一个较大的权重,这样混合格式也将会有足够的耗散来抑制非物理振荡,从而能达到更好的计算效果。例如在RT不稳定性计算中取n=103,而在马赫数相对较高的激波-密度波干扰问题中取n=5×103。
在流场光滑区域βk很小,当βk趋于0时,σ也趋于0,此时格式为近似八阶中心格式,将具有很低的耗散;在流场非光滑区域βk值相对较大,此时σ趋于1,因此格式将会保留足够的耗散来抑制非物理振荡。这样,该格式将会具有中心格式与WENO格式共同的特点。
1.2 数值格式误差分析采用Fourier精度分析法[19]分析该空间离散格式,所得到的修正波数的虚部Ki和实部Kr分别表示数值格式的色散和耗散效应, α为波数。从图 1中可以看出,本文H-WENO7-CD8格式的色散误差要比经典的WENO7更小,而WENO格式在高波数区存在较大的耗散误差,其耗散也在高波数区也比WENO7要小,原因是H-WENO7-CD8格式是通过经典的WENO7格式与中心格式加权组合而成,而中心格式无耗散。这就在一定程度上降低了新格式的耗散。
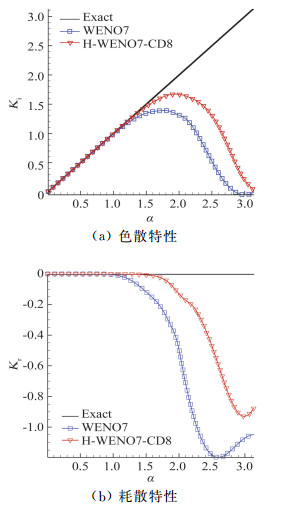
|
图 1 两种不同格式的色散(a)和耗散(b)特性 Fig.1 Spectral properties of two different schemes |
该问题为一个马赫数为3的运动激波和正弦密度波相互干扰,使用各空间离散格式模拟一维激波-密度脉动干涉算例[20],以测试数值方法对小尺度结构的分辨能力。该控制方程为一维的Euler方程组,初始条件为:
| $ \left[\begin{array}{l}{\rho} \\ {u} \\ {p}\end{array}\right]_{\mathrm{L}}=\left[\begin{array}{l}{3.857143} \\ {2.629369} \\ {10.333333}\end{array}\right] $ | (10) |
| $ \left[\begin{array}{l}{\rho} \\ {u} \\ {p}\end{array}\right]_{\mathrm{R}}=\left[\begin{array}{c}{1+0.2 \sin (5 x)} \\ {0} \\ {1}\end{array}\right] $ | (11) |
以x=1处为左右侧分界点,最终结果在区间x=[0, 10]上进行计算,结束时间为t=1.8。网格点数为N,由于该问题不存在解析解,因此选用N=4001时的结果作为参考的精确解(Exact),采用Runge-Kutta方法进行时间推进,通量分裂使用Steger-Warming分裂,使用局部特征分解。
图 2给出了WENO7格式和H-WENO7-CD8格式的计算结果。可以看出,WENO格式和新格式均能较好地捕捉x=7.4处的间断以及x=5.5左侧的密度波动,但在该网格数下WENO7得到的幅值明显偏小;而H-WENO7-CD8格式不但能得到与精确解符合更好的波形,而且幅值也更接近精确解,因此新格式比WENO7对流场间断及脉动具有更强的分辨率。
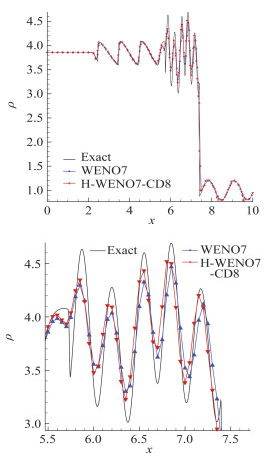
|
图 2 Shu-Osher问题,t=1.8时刻的密度分布, N=201 Fig.2 Density distribution of the 1D shock/turbulence interaction at t=1.8, N=201 |
Rayleigh-Taylor(RT)不稳定性问题[19]是当两种密度不同的流体界面有微小的扰动,且由于某种原因从重流体到轻流体的方向产生加速度时, 在这两种流体的界面上就会出现不稳定性。RT不稳定性包含很多细致结构,以此用来测试数值格式分辨率。其计算条件设置如下[19]:计算域为[0, 0.25] × [0, 1];初始时刻,轻重流体的交界面位于y=0.5处,密度ρ=2的流体位于界面之下,密度ρ=1的流体位于界面之上。初始场为:
| $ \left\{\begin{array}{l}{\rho=2} \\ {u=0} \\ {v=-0.025 c \cdot \cos (8 \pi x)} \\ {p=2 y+1, \quad 0 \leqslant y \leqslant 0.5}\end{array}\right. $ | (12) |
| $ \left\{\begin{array}{l}{\rho=1} \\ {u=0} \\ {v=-0.025 c \cdot \cos (8 \pi x)} \\ {p=y+1.5, \quad 0.5 \leqslant y \leqslant 1}\end{array}\right. $ | (13) |
其中:声速
| $ \frac{\partial U}{\partial t}+\frac{\partial F_{1}(U)}{\partial x}+\frac{\partial F_{2}(U)}{\partial x}=S $ | (14) |
源项的表达式为S=(0, ρ, 0, ρv)T。计算最终时间t=1.95。
图 3分别给出了WENO7和H-WENO7-CD8两种不同格式在网格60×240和240×960上计算得到的数值结果。从图 3中可以看出,在网格60×240上不同的格式捕捉到的流动结构和相关文献基本保持一致,密度大的流体沿中轴线流入密度小的流体,中轴线两侧形成了若干小尺度的涡结构,两种格式均能保证质量守恒,而新格式在此粗网格上能分辨出更多的小尺度结构。网格加密到240×960之后,新格式捕捉到的小尺度涡结构仍然要比WENO7要多,这就表明了在复杂结构的数值计算中,H-WENO7-CD8格式拥有更高的数值结构分辨率。
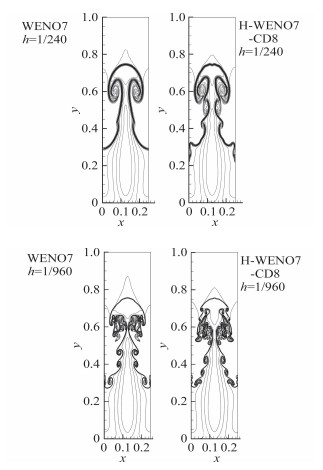
|
图 3 RT不稳定性密度分布 Fig.3 Rayleigh-Taylor instability: density profile |
这是一个入射角为60°的马赫数为10的激波的双马赫反射问题[21]。具体求解设置为:计算区域[0, 0] × [4, 1],下边界y=0,平板前缘位于x=0.1667处,一直延伸到x=4前,从x=0到x=0.1667给定波后条件;平板处采用波后壁面条件;上边界各点的值由马赫数为10的激波的精确运动来确定。计算最终时间为t=0.2。
由于中心格式无耗散,而在双马赫反射的计算中需要数值格式有足够的耗散,因此需要设定一个开关函数,在间断区时,要给予WENO格式足够的权重,在此961×241的密网格的计算中,限制式(9)中的σ≥0.94,这样就可以有效的防止发散。
图 4给出了在网格数相同情况下, 采用不同格式所计算得到的密度等值线及其在接触间断和马赫杆附近的放大图(a:WENO7;b:H-WENO7-CD8),可以看出,两种格式均能很好的捕捉到该问题基本的流动特征,如马赫杆、激波和滑移线。另外通过比较两幅局部放大图可以清楚地看到,H-WENO7-CD8格式能分辨出更多的近壁面结构,更清晰的捕捉到了滑移线的卷曲现象和小尺度的涡,表明新格式对于小尺度结构具有良好的分辨能力,具有较高的分辨率。
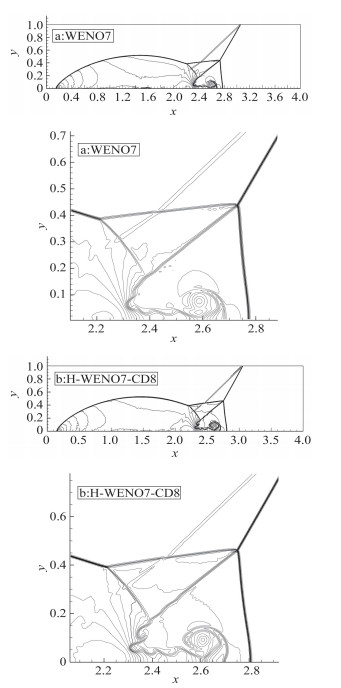
|
图 4 密度分布, 网格点数961×241, 30条等值线, 从ρ=1.731到ρ=20.92 Fig.4 Density contours of the Double Mach Reflection problem, 961×241 grid |
本文通过新型加权函数将经典的WENO格式和中心格式结合起来,利用光滑度量因子设定中心格式和WENO格式上的混合权重,实现了对格式数值耗散的自适应控制,构造出一种自适应低耗散的数值格式。通过对一维激波密度脉动干涉问题和二维的瑞利-泰勒不稳定性问题和双马赫问题进行数值模拟,结果表明新的格式在继承了原WENO格式良好的激波捕捉特性的同时,具有更低的耗散,对小尺度结构更高的分辨率,并且有较好的稳定性,这也为可压缩湍流的高分辨率数值模拟提供了一种新的备选方法。此外,本文构造格式是在均匀网格上推导的,这也是目前大多数高精度差分格式的做法。在实际应用中,对于曲面非光滑网格,格式会产生几何诱导误差,几何守恒问题对计算格式的精度和稳定性都有较大的影响,将在今后的工作中考虑格式的几何守恒律问题。
致谢: 本项目得到国家自然科学基金(Nos.11472010, 91441103,11372330, 11472278)、国家重点研发计划(2016YFA0401200)、科学挑战专题项目(JCKY2016212A501)以及民用飞机专项科研(MJ-2015-F-028)的资助。感谢中国科学院力学研究所的傅德薰、马延文研究员对本研究的帮助。感谢国家超级计算天津中心以及国家超级计算广州中心提供计算机时。
| [1] |
LIU X D, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115(1): 200-212. DOI:10.1006/jcph.1994.1187 |
| [2] |
JIANG G S, SHU C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126(1): 202-228. DOI:10.1006/jcph.1996.0130 |
| [3] |
MARTÍ M P, TAYLOR E M, WU M, et al. A bandwidth-optimized WENO scheme for the effective direct numerical simulation of compressible turbulence[J]. Journal of Computational Physics, 2006, 220(1): 270-289. DOI:10.1016/j.jcp.2006.05.009 |
| [4] |
CASTRO M, COSTA B, DON W S. High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws[J]. Journal of Computational Physics, 2011, 230(5): 1766-1792. DOI:10.1016/j.jcp.2010.11.028 |
| [5] |
REN Y X, LIU M E, ZHANG H X. A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics, 2003, 192(2): 365-386. DOI:10.1016/j.jcp.2003.07.006 |
| [6] |
武从海, 赵宁, 田琳琳. 一种改进的紧致WENO混合格式[J]. 空气动力学学报, 2013, 31(4): 477-481. WU C H, ZHAO N, TIAN L L. An improvement hybrid compact-WENO scheme[J]. Acta Aerodynamica Sinica, 2013, 31(4): 477-481. (in Chinese) |
| [7] |
张树海, 李沁, 张来平, 等. 中国CFD史[J]. 空气动力学学报, 2016, 34(2): 157-174. ZHANG S H, LI Q, ZHANG L P, et al. The history of CFD in China[J]. Acta Aerodynamica Sinica, 2016, 34(2): 157-174. DOI:10.7638/kqdlxxb-2016.0001 (in Chinese) |
| [8] |
DENG X G, MAO M L. Weighted compact high-order nonlinear schemes for the Euler equations[C]//Computational Fluid Dynamics Conference. 2006. https://arc.aiaa.org/doi/abs/10.2514/6.1997-1941
|
| [9] |
DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44. DOI:10.1006/jcph.2000.6594 |
| [10] |
张涵信, 贺国宏, 张雷. 高精度差分求解气动方程的几个问题[J]. 空气动力学学报, 1993, 11(4): 347-356. ZHANG H X, HE G H, ZHANG L. Some important for high order accurate difference solving gas dynamics equations[J]. Acta Aerodynamica Sinica, 1993, 11(4): 347-356. (in Chinese) |
| [11] |
马延文, 傅德薰. 计算空气动力学中一个新的激波捕捉法-耗散比拟法[J]. 中国科学:数学, 1992, 35(3): 263-271. MA Y W, FU D X. A new method to capture shock wave in computing aerodynamic-dissipation analogy method[J]. Scientia Sinica Mathematics, 1992, 35(3): 263-271. (in Chinese) |
| [12] |
MA Y W, FU D X. Fourth order accurate compact scheme with group velocity control (GVC)[J]. Science China Mathematics, 2001, 44(9): 1197-1204. DOI:10.1007/BF02877439 |
| [13] |
MA Y W, FU D X. Super compact finite difference method (SCFDM) with arbitrarily high accuracy[J]. Computational Fluid Dynamics, 1996, 5(2): 259-276. |
| [14] |
SUN Z S, REN Y X, CÉDRIC LARRICQ. A class of finite difference schemes with low dispersion and controllable dissipation for DNS of compressible turbulence[J]. Journal of Computational Physics, 2011, 230(12): 4616-4635. DOI:10.1016/j.jcp.2011.02.038 |
| [15] |
LI X L, LENG Y, HE Z W. Optimized sixth-order monotonicity-preserving scheme by nonlinear spectral analysis[J]. International Journal for Numerical Methods in Fluids, 2013, 73(6): 560-577. DOI:10.1002/fld.3812 |
| [16] |
HE Z W, ZHANG Y S, GAO F J, et al. An improved accurate monotonicity-preserving scheme for the Euler equations[J]. Computers & Fluids, 2016, 140: 1-10. |
| [17] |
PIROZZOLI S. Conservative hybrid compact-WENO schemes for shock-turbulence interaction[J]. Journal of Computational Physics, 2002, 178(1): 81-117. DOI:10.1006/jcph.2002.7021 |
| [18] |
傅德薰, 马延文, 李新亮, 等. 可压缩湍流直接数值模拟[M]. 北京: 科学出版社, 2010: 178-181. FU D X, MA Y W, LI X L, et al. Direct numerical simulation of compressible turbulence[M]. Beijing: Science Press, 2010: 178-181. (in Chinese) |
| [19] |
冷岩.高分辨率数值方法研究及飞行器CFD软件开发[D].北京: 中国科学院大学, 2012. LENG Y. High-resolution numerical schemes and aircraft CFD software development[D]. Beijing: University of Chinese Academy of Sciences, 2012. http://dspace.imech.ac.cn/handle/311007/46343?mode=full&submit_simple=Show+full+item+record |
| [20] |
SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1987, 83(1): 32-78. |
| [21] |
SHI J, ZHANG Y T, SHU C W. Resolution of high order WENO schemes for complicated flow structures[J]. Journal of Computational Physics, 2003, 186(2): 690-696. DOI:10.1016/S0021-9991(03)00094-9 |
 2019, Vol. 37
2019, Vol. 37


