广泛存在于航空航天、风工程等空气动力学领域的钝体绕流问题通常为无序、非线性、多尺度的湍流分离运动,在使用数值模拟方法(CFD)对其进行分析计算时,湍流的求解成为影响CFD计算精度的瓶颈问题[1]。在诸多的湍流模型中,兼顾计算精度与资源消耗的RANS/LES混合方法受到人们的青睐[2],混合模型在近壁区及远场使用RANS模型,而在分离区及尾迹区切换为更合理的类LES滤波模型,极大地提高了计算精度,且资源消耗远小于LES仅略大于RANS。近年来,不同学者发展了种类繁多的混合方法,其中包括DES(Detached Eddy Simulation)方法[3]、SAS(Scale Adaptive Simulation)方法[4-7]、PANS(Partially Averaged Navier-Stokes)方法[8]、PITM(Partially Integrated Transport Model)方法、LNS(Limited Numerical Scales)方法等。其中DES方法是最早出现的混合方法,经过一系列改进(DDES、IDDES)已发展较为成熟[9-13];SAS模型为能够解析宽频非定常湍流脉动而对计算网格依赖较小的新一代非定常湍流预测方法(URANS),通过加入参照当地流动的冯卡门(von Karman)长度尺度Lvk, 合理地释放更多流场信息[14-15];PANS模型同样是最近发展的一种RANS-DNS桥接模型,模型构造相对简单,通过加入模化湍动能比例参数fk调整湍流的模化量来调整湍流求解尺度[16];DES模型的提出者Spalart在2000年时曾预测,2045年左右计算机的计算能力才能满足利用LES解决90%的湍流问题,因此,在现阶段,验证与发展RANS/LES方法仍是非常必要的[17-18]。
钝体绕流中的圆柱绕流计算模型简单,同时又包含如湍流壁面、剪切层失稳、流动分离、周期性涡脱落等丰富的流动现象,是考察湍流模型计算性能的标准算例。Re=3900的圆柱绕流是典型的亚临界雷诺数流动,流动结构复杂且耗费资源较少,人们对该雷诺数的圆柱绕流进行了大量的实验[19-22]及数值研究[23-29],有可靠丰富的数据可供参考。本文选用SAS模型及两种变fk构造函数的PANS模型计算了Re=3900的圆柱绕流流场,并重点从流场特征捕捉、气动力特性计算、涡黏性控制等方面对SAS模型及PANS模型进行了比较,通过对比标准网格与加密网格后的计算结果,比较了两类混合方法对网格的适应性,并探讨了两类混合模型的尺度函数对流场的调控机制。
1 计算模型及数值方法 1.1 控制方程控制方程为三维N-S方程,在一般计算坐标系(τ, ξ, η, ζ)下的守恒形式为:
| $ \frac{\partial \overline{\omega}}{\partial \tau}+\frac{\partial\left(\overline{F}-\overline{F}_{V}\right)}{\partial \xi}+\frac{\partial\left(\overline{G}-\overline{G}_{V}\right)}{\partial \eta}+\frac{\partial\left(\overline{H}-\overline{H}_{V}\right)}{\partial \zeta}=0 $ | (1) |
式中:ω为守恒变量,F、G、H为无粘通量,FV、GV、HV为黏性通量,各物理量的具体表述参见文献[1]。
1.2 湍流模型 1.2.1 SST-k-ω模型SST模型由标准k-ω模型与k-ε模型混合修改而成,该模型兼顾了k-ω模型的近壁性能及k-ε模型的远场准确性,SST模型中湍动能k和比耗散率ω的输运方程可表示如下:
| $ \begin{array}{c}{\frac{\partial \rho k}{\partial t}+\nabla \cdot(\rho U k)=P_{k}-\beta^{*} \rho k \omega+} \\ {\nabla \cdot\left[\left(\mu+\sigma_{k} \mu_{t}\right) \nabla k\right]}\end{array} $ | (2) |
| $ \begin{array}{l}{\frac{\partial \rho \omega}{\partial t}+\nabla \cdot(\rho U \omega)=\frac{\alpha}{v_{t}} P_{k}-\beta \rho \omega^{2}+} \\ {\nabla \cdot\left[\left(\mu+\sigma_{\omega t} \mu_{t}\right) \nabla \omega\right]+\left(1-F_{1}\right) \frac{2 \rho \sigma_{\omega 2}}{\omega} \nabla k \nabla \omega}\end{array} $ | (3) |
式中模型参数σk、α、β、σω、σω2均由对应的k-ω模型参数φ1和k-ε模型参数φ2通过一定函数计算得到,其对应的函数关系为:
| $ \varphi=F_{1} \varphi_{1}+\left(1-F_{1}\right) \varphi_{2} $ | (4) |
SST模型中湍动黏度μt可表示为:
| $ \mu_{t}=\frac{\alpha_{1} \rho k}{\max \left(\alpha_{1} \omega, S F_{2}\right)} $ | (5) |
式中S为应变率张量Sij的模(
尺度自适应SAS(Scale-Adaptive Simulation)模型是一种较新的创新型湍流模型,它通过在湍流模型中加入刻画当地流动拓扑的von Karman长度尺度Lvk来作为湍流模型的第二长度尺度[6]。基于SST模型的SAS模型构造方法为在式(3)SST模型的ω方程中加入发挥自适应作用的源项QSAS,其定义式为:
| $ Q_{\mathrm{SAS}} =\\ \max \left[\rho \xi \kappa S^{2}\left(\frac{L}{L_{v k}}\right)^{2}-C \cdot \frac{2 \rho k}{\sigma_{\varphi}} \max \left(\frac{|\nabla \omega|^{2}}{\omega^{2}}, \frac{|\nabla k|^{2}}{k^{2}}\right), 0\right] $ | (6) |
式中,湍流尺度
由式(6)可以看出:在SAS模型中出现了由一阶及二阶速度导数决定的长度尺度项Lvk,该长度尺度基于当地流动而与网格尺度无关,在湍流边界层内,Lvk能模化惯性子区所有湍流脉动,同时,在非稳态区域Lvk能根据当地网格分辨的湍流涡动态调整RANS长度尺度。在SAS模型中,湍动黏度μt仍按照式(5)计算。
1.2.3 SST-PANS模型本文中所用PANS模型同样是基于SST模型修改而成[8],其原理是在SST模型中引入两个模型控制参数fk和fω:
| $ f_{k}=\frac{k_{u}}{k}, \quad f_{w}=\frac{\omega_{u}}{\omega} $ | (7) |
式中:fk为模化湍动能与总的湍动能之比,fω是模化比耗散率与总的比耗散率的比值。如果假定fk和fω是不随时间和空间变化的常数,则k和ω的输运方程(2)、(3)变为:
| $ \begin{array}{l}{\frac{\partial \rho k_{u}}{\partial t}+\nabla \cdot\left(\rho U k_{u}\right)=P_{k u}-\beta^{*} \rho k_{u} \omega_{u}+} \\ {\nabla \cdot\left[\left(\mu+\sigma_{k u} \mu_{t u}\right) \nabla k_{u}\right]}\end{array} $ | (8) |
| $ \begin{array}{l}{\frac{\partial \rho \omega_{u}}{\partial t}+\nabla \cdot\left(\rho U \omega_{u}\right)=\frac{\partial}{v_{t u}} P_{k u}-\beta_{u} \rho \omega_{u}^{2}+} \\ {\nabla \cdot\left[\left(\mu+\sigma \omega_{u} \mu_{t u}\right) \nabla \omega_{u}\right]+} \\ {\quad\left(1-F_{1}\right) \frac{2 \rho \sigma_{\omega 2 u}}{\omega_{u}} \nabla k_{u} \nabla \omega_{u}}\end{array} $ | (9) |
将式(8)、(9)与式(2)、(3)对比可以发现在PANS模型中主要是模型参数发生了变化,PANS模型中模型参数σku、σωu、σω2u、β表示为:
| $ \begin{array}{l}{\sigma_{k u}=\sigma_{k} \frac{f_{\omega}}{f_{k}}, \sigma_{\omega u}=\sigma_{\omega} \frac{f_{\omega}}{f_{k}}, \sigma_{\omega 2 u}=\sigma_{\omega 2} \frac{f_{\omega}}{f_{k}}} \\ {\beta_{u}=\alpha \beta^{*}-\frac{\partial \beta^{*}}{f_{\omega}}+\frac{\beta}{f_{\omega}}, f_{\omega}=\frac{f_{\varepsilon}}{f_{k}}, f_{\varepsilon}=\frac{\varepsilon_{u}}{\varepsilon}}\end{array} $ | (10) |
通过以上变化,将SST模型转变为SST-PANS模型,由k、ε、ω的关系可得式(10)中fω与fk和fε的关系,在SST-PANS模型中,fε一般取为1,这样PANS中的参数可以表示为fk的函数。通过调节fk的值(1-0),改变模化的湍动能与比耗散率的比值,从而实现RANS-DNS的转化。这时湍动黏度μtu变为:
| $ \mu_{t u}=\frac{\alpha_{1} \rho k u}{\max \left(\alpha_{1} \omega u, S F_{2}\right)} $ | (11) |
在早期PANS模型的应用中,fk通常被设置为空间常数,通过计算发现对于整个流场很难确定合适统一的fk值。对于复杂的分离流动问题,计算时分离区与尾迹区需要较小的fk值(fk < 1)释放湍流信息,而近壁区与远场区采用RANS模型(fk=1)更合理,因此近年来人们逐渐尝试用适当的函数来计算fk分布,本文选取其中两种相对简单、计算相对稳定的变fk函数来进行对比。
(a) 类DES型fk函数[31-32]。该函数参考DES模型中模型尺度的构造方法,将fk表示为网格尺度Δ与湍流尺度Lu的函数:
| $ f_{k}=\min \left[C_{\mathrm{PANS}}\left(\Delta / L_{u}\right)^{\frac{2}{3}}, 1\right]\\{L_u} = k_u^{\frac{1}{2}}/{\beta ^*}{\omega _u}, \Delta = \max (\Delta x, \Delta y, \Delta z) $ | (12) |
式中模型常数CPANS取0.3。用该函数进行计算时,在分离区与尾迹区,网格尺度要小于湍流尺度,因此fk < 1;在壁面及远场区域,网格尺度大于湍流尺度,因此fk=1。文中将使用类DES型fk分布函数的PANS模型称为PANS(des)模型。
(b) Tanh型fk函数[33]。在该函数中,fk可表示为:
| $ \begin{array}{*{20}{l}} {{f_k} = \{ 1 + \tanh [2\pi (\mathit{\Lambda } - 0.5)]\} /2}\\ {\mathit{\Lambda } = 1/\left( {1 + {\lambda ^{4/3}}} \right), \lambda = {L_u}/\Delta } \end{array} $ | (13) |
对比式(12)与式(13)可知,Tanh型fk函数由湍流尺度、网格尺度及tanh函数修改而成,tanh函数的取值范围为(-1, 1),这样根据流动与网格关系得到不同位置的fk取值范围为(0, 1)。文中将使用Tanh型fk函数的PANS模型称为PANS(tanh)模型。
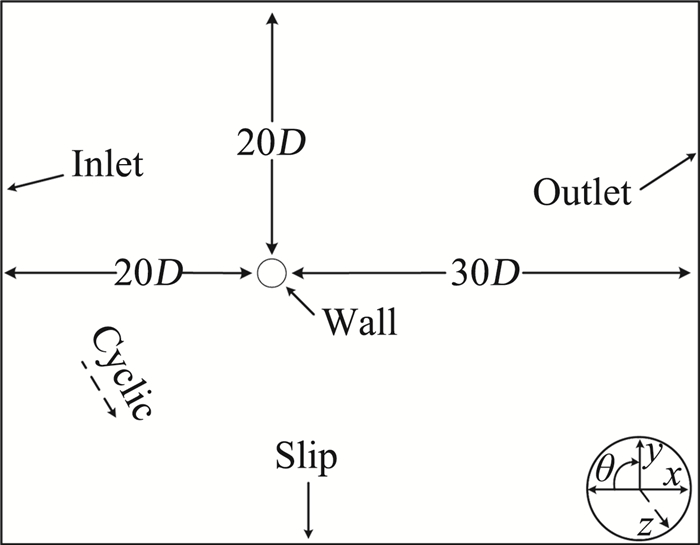
2 计算模型及数值方法 2.1 计算域、网格及边界设置文中圆柱绕流计算雷诺数为Re=3900(基于圆柱直径D与远场来流速度U∞),图 1为计算域及边界条件示意图。为减小上游来流对计算的影响并使尾迹区流动充分发展,上游来流区域(x方向)及横向区域(y方向)延展至20D,下游计算区域设置为30D。根据近尾迹区流向结构的展向波长设置计算域展向长度(z方向)为πD[2]。圆柱体设置为无滑移壁面,上游入口流动各物理量由无扰动自由来流条件给定,下游出口设置为无反射边界,计算域的上下界面设置为自由滑移壁面,计算域的前后边界设置为周期边界。文中坐标系设置如图 1右下角所示,轴向从上游到下游方向为x正方向,坐标系符合右手螺旋法则,横向为y方向,展向为z方向,方位角从上游圆柱前驻点为0°开始,顺时针旋转为壁面方位角θ的正方向,下游背风点为180°。
|
图 1 计算域及边界条件 Fig.1 Computational domain and boundary conditions |
图 2为圆柱绕流的局部网格示意,计算网格为分块结构化网格。为了保证计算精度, 在壁面附近及尾迹分离区域对网格进行适当加密,壁面第一层网格高度为0.002D,保证壁面y+ < 1。为了探讨不同模型的尺度函数对网格的敏感性,文中设置了两套计算网格,其中标准网格保证近壁增长率为1.06,分离区网格固定为0.1D;加密网格为保证近壁增长率为1.04,分离区网格固定为0.05D。参考文献[24, 25]中的网格设置见表 1。

|
图 2 圆柱绕流局部网格 Fig.2 Computational grid for the cylinder |
| 表 1 计算网格 Table 1 Computational grids |
|
|
文中对所求方程组空间离散采用有限体积法(FVM),对流项中速度项的离散采用三阶限制(TVD)中心差分格式,湍流项离散采用二阶限制中心差分格式,梯度项及黏性项的离散采用四阶中心差分格式,压力与速度耦合选用PISO算法。为了保证计算的收敛性及稳定性,时间项离散采用二阶隐式后退欧拉(Backward)格式,并采用自适应时间步长方法[24],时间步长设置为库朗数(Courant number)小于0.5,并且保证在一个涡脱落周期内包含近500个时间步。
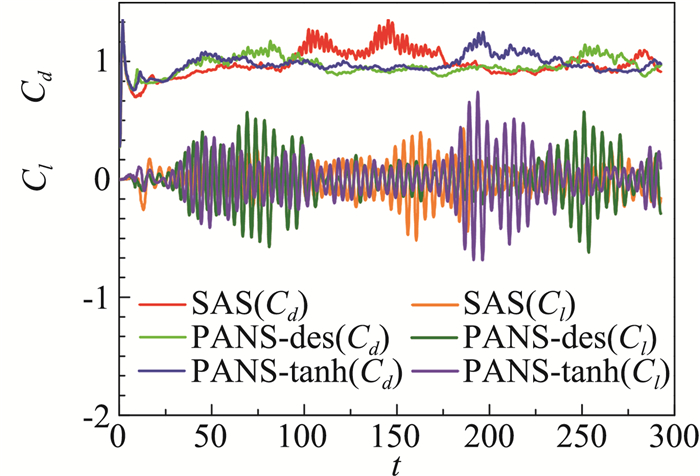
3 计算结果分析 3.1 数据采集及流场宏观结构文中分别计算了SST、SAS、PANS(des)、PANS(tanh)模型的圆柱绕流流场。周期性涡脱落是该计算雷诺数下的显著特征。为了获得合理的统计数据,根据Franke等[34]的研究结果,圆柱绕流的统计周期应大于40个脱落周期。因此参照文献[34, 25],本文中总的计算时间约为60个涡脱落周期, 在对非定常结果的统计时去掉前10个脱落周期,将后50个周期内的统计数据作为有效数据进行模型的对比。计算结果进行时间与空间平均。图 3中给出了以标准网格计算结果为例的圆柱绕流升力系数(Cl)、阻力系数(Cd)的时程(U∞/D无量纲化)变化曲线。可以看出Re=3900时的升力幅值已不再稳定,但仍呈现出周期性变化趋势,同时阻力系数表现出强烈的脉动现象,并在一平均值附近上下摆动。
|
图 3 升力、阻力系数随时间变化及升力频谱 Fig.3 Time history of lift Cl, drag Cd coefficients |
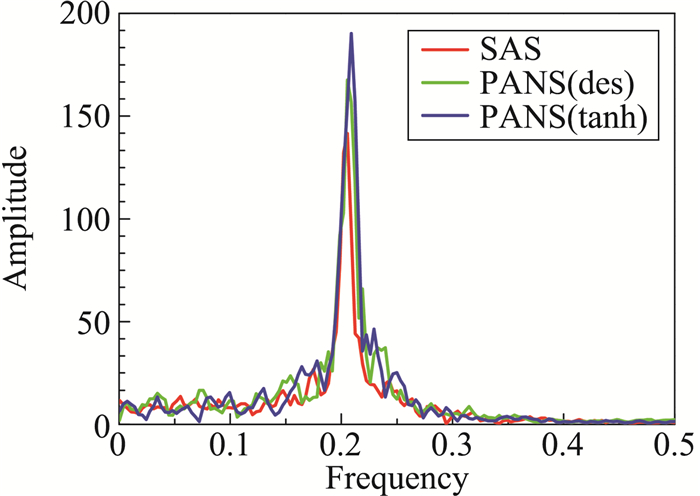
图 4中给出了由升力系数时程曲线经过傅里叶变换(FFT)获得的涡脱落频率功率谱,由此可以计算涡脱落频率f及斯特劳哈数St(St=fD/U∞)。各模型阻力系数(Cd)及斯特劳哈数St见表 2。
|
图 4 升力频谱 Fig.4 Spectra of lift |
| 表 2 圆柱绕流平均积分量对比 Table 2 Summary of the mean integrated quantities for the cylinder flow |
|
|
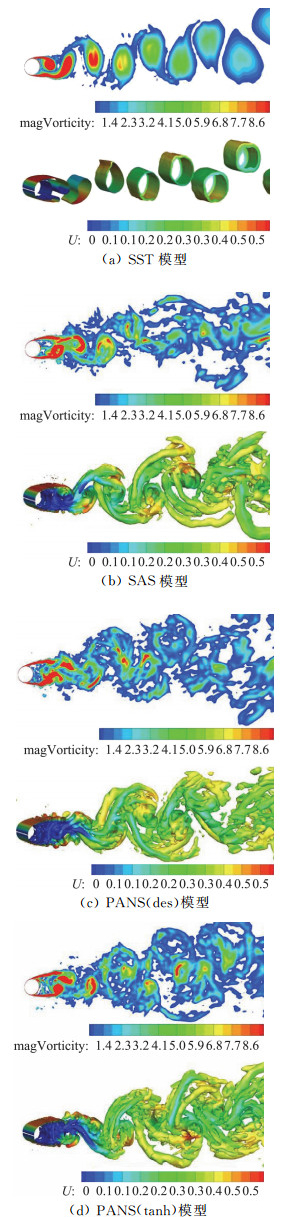
图 5为四种模型基于标准网格计算得到的圆柱绕流流场二维瞬时(t=300)涡量分布及用轴向速度染色的三维Q分布,对比可知:由于RANS模型湍流黏性较大,抹去了很多重要的流场细节,计算结果只捕捉到大尺度的脱落涡结构,Q图也只先显示出近似二维的流动结构,这说明RANS模型基本上没有求解小尺度流动的能力;SAS模型及PANS模型均捕捉到丰富的流动结构,二维涡量及三维Q值均显示出复杂的周期性涡脱落现象。分析三者的Q图可清晰地发现附着于壁面的二维层流剪切层及分离区流向与展向相嵌套的三维无序涡体结构。SAS模型与PANS模型均允许形成湍流谱,表现出预期的类似LES模型的求解小尺度运动的能力。同时,仔细对比SAS模型与PANS模型的结果可以看出,PANS模型能捕捉到比SAS模型更丰富的湍流结构。
|
图 5 不同模型计算得到的流场瞬时涡量与Q值图(t=300) Fig.5 Instantaneous vorticity and Q of different models(t=300) |
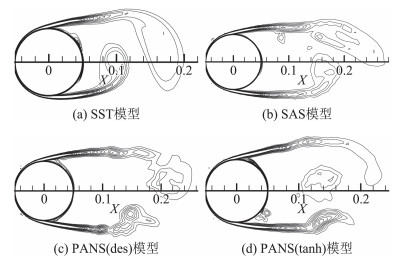
由实验及以往计算结果[23]可知,圆柱绕流壁面剪切层的发展对外界影响因素非常敏感,微小外部干扰很容易造成边界层的提前分离,使得剪切层变短,进而影响回流区及整个流场的测量或计算结果。图 6为用涡量等值线表示的标准网格条件下四种模型的瞬时(t=300)剪切层,通过对比可知剪切层长度关系为:SAS>PANS(des)>PANS(tanh)>SST。
|
图 6 不同模型瞬时分离剪切层示意图(t=300) Fig.6 Instantaneous separating shear layers of different models(t=300) |
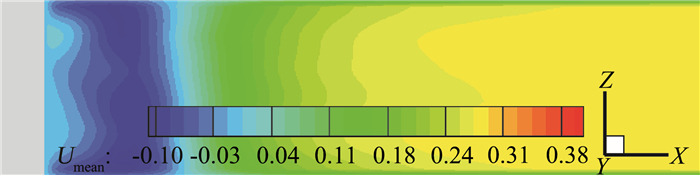
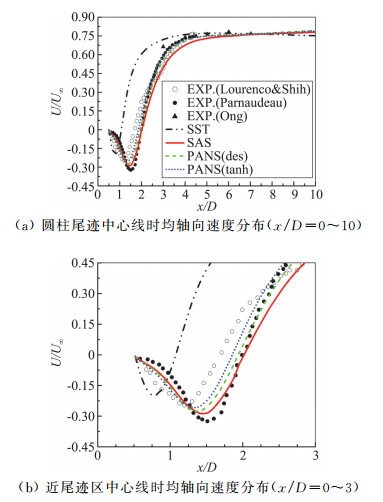
图 7为以SAS模型为例的y=0平面轴向速度时均图,可以清晰地看出在圆柱近尾迹区域形成一个流速与来流相反的区域,即圆柱绕流的回流区。图 8为圆柱下游尾迹区中心线上时均轴向速度分布。由图可知,圆柱背风点处速度为0,速度为逐渐增大的负值,到达回流区中心时速度负值最大。背风点与空间流动的再附点即流向速度恢复到0的点之间的距离即为回流区长度(Lr/D)。四种模型均模拟出了圆柱后的速度分区,但彼此间差别较大,特别是对回流区的模拟。图 8(b)图是对回流区中心线时均轴向速度的放大图。首先需要说明的是用空心圆圈表示的实验数据是Lourenco & Shih(1993)用PIV测量获得[20],用实心圆表示的实验数据是Parnaudeau等(2008)同样用PIV测量获得[21],可以看到两者实验测得的回流区长度差别较大。最近几年的文献也出现了与Parnaudeau实验接近或与Lourenco实验接近的两种数值计算结果,有意思的是Kravchenko等(2000)在用B-Spline伽辽金方法对Re=3900进行的LES数值计算中[23],最先发现了数值结果与Lourenco实验数据在回流区与近尾迹区速度型的差别。Kravchenko计算的回流区长度大于Lourenco实验值,其当时推测可能有外加扰动导致Lourenco实验中圆柱壁面剪切层过早分离,造成剪切层变短,进而影响回流区长度。Parnaudeau实验数据在回流区及速度型方面均验证了Kravchenko的数值计算结果。由于实验时间较晚,实验方法更先进、严谨,本文中我们认为Parnaudeau的实验值是更可信的。分析图 8(b)可知,SST模型计算的圆柱回流区长度误差较大,SAS与PANS计算的回流区长度关系为SAS>PANS(des)>PANS(tanh)。三种模型计算的回流区区域位于两个实验值之间,与Parnaudeau实验值仍存在一定误差,其中SAS模型与Parnaudeau实验最接近。以上结论与图 6中得出的剪切层长度结论也是一致的。
|
图 7 y=0平面轴向速度时均分布 Fig.7 Mean streamwise velocity along the y=0 surface |
|
图 8 圆柱尾迹中心线上时均轴向速度分布 Fig.8 Mean streamwise velocity along the wake center line |
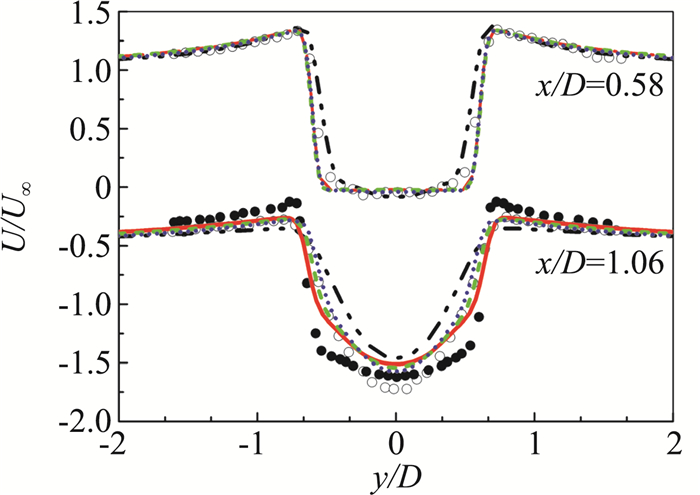
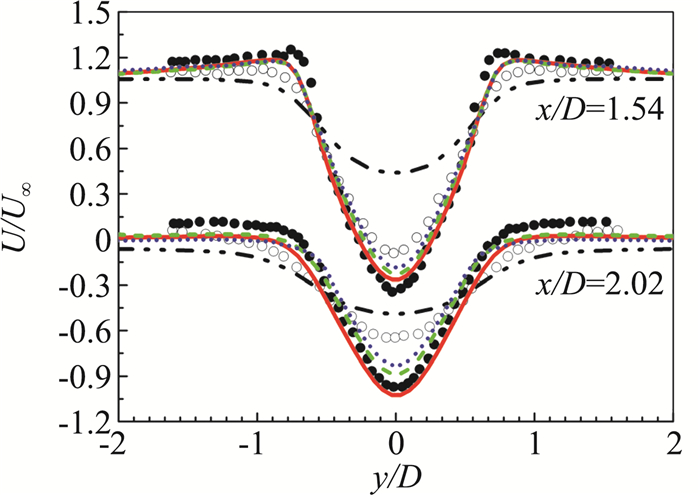
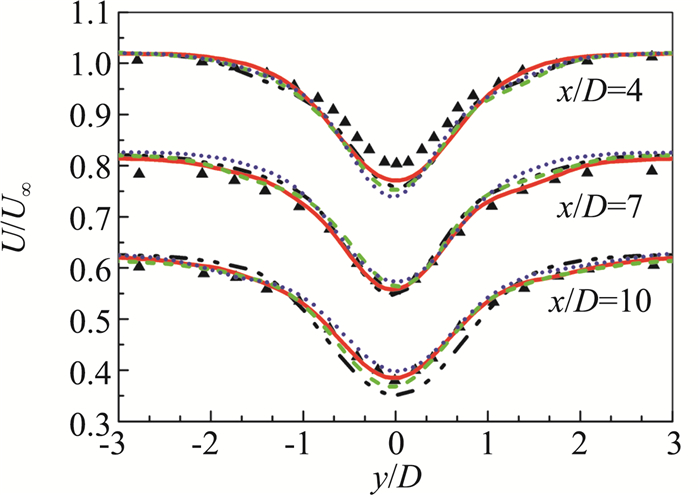
图 9~图 11为圆柱绕流下游不同截面处的时均轴向速度分布(图例见图 8)。可以看到轴向速度流型从近尾迹区到远尾迹区由U型向V型转变,结合前部分析可知,剪切层过早分离同样会导致速度型的过早转变,图中两种实验值的对比也说明了这一点。图 9近壁x/D=0.58时,四种模型的速度型均为U型,彼此差别不大,而到回流区x/D=1.06时,四种模型出现差别,SST模型为完全的V型,SAS模型与两种PANS模型同样没有计算出更加正确的U型,而是介于U型与V型之间,其中SAS模型与Parnaudeau实验得到的U型更接近,同时PANS(des)要稍好于PANS(tanh);在近尾迹回流区后部x/D=1.54、2.02位置处,除了SST没有计算出正确的速度型,SAS模型与两种PANS模型的计算结果只是速度峰值与实验值存在一定误差,整体均与实验值吻合较好;在远尾迹区x/D=4、7、10位置处,四种模型计算的速度型均较好,速度峰值与实验存在较小误差。以上分析说明近尾迹区域特别是回流区流动较为复杂、敏感,计算控制更困难,同时远尾迹区受近壁区影响较小,使得远尾迹区计算误差小于近尾迹区。
|
图 9 不同截面的平均轴向速度分布(x/D=0.58,1.06) Fig.9 Mean streamwise velocity at different surfaces (x/D=0.58, 1.06) |
|
图 10 不同截面的平均轴向速度分布(x/D=1.54,2.02) Fig.10 Mean streamwise velocity at different surfaces (x/D=1.54, 2.02) |
|
图 11 不同截面的平均轴向速度分布(x/D=4,7,10) Fig.11 Mean streamwise velocity at different surfaces (x/D=4, 7, 10) |
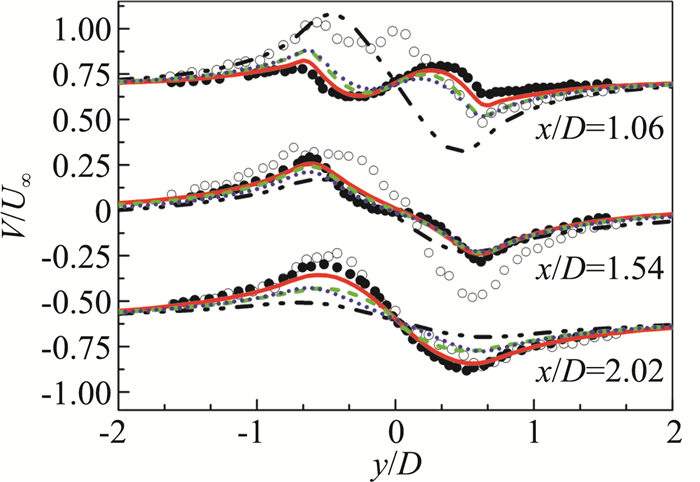
图 12为圆柱绕流下游近尾迹回流区附近不同截面处的时均横向速度分布(图例见图 8)。由x/D=1.06处的时均横向速度与实验值可以看到,SAS与两种PANS模型得到的速度型均与Parnaudeau实验值较吻合,与SST模型比较显示出较高的计算精度。x/D=1.54、2.02处的对比结果可以看出四种模型在速度型与峰值上均存在一定误差,与轴向速度计算结果类似。
|
图 12 不同截面的平均横向速度分布(x/D=1.06,1.54,2.02) Fig.12 Mean cross-flow velocity at different surface (x/D=1.06, 1.54, 2.02) |
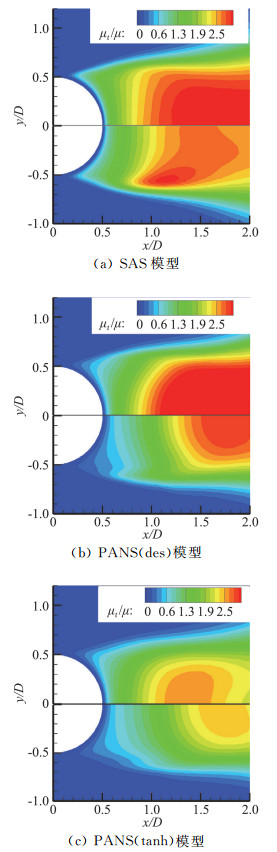
根据混合模型的构造原理可知,其湍流尺度求解能力是基于对涡黏性的控制作用。图 13为三种混合模型计算的圆柱绕流时均湍动黏度μt/μ(湍动黏度与来流黏度之比)分布,上部为标准网格计算结果,下部为加密网格计算结果。仅从数值来看,SAS模型与两种PANS模型的湍动黏度分布关系为SAS>PANS(des)>PANS(tanh)。PANS模型所求湍动黏度要小于SAS模型,这也解释了图 4中PANS模型对流场的捕捉要好于SAS模型。但需要注意的是,较低的湍动黏度不一定获得较准确的数值计算结果。由文中气动力的比较可知,SAS模型要好于PANS模型。通过比较网格加密后的湍流黏度可知,两种PANS模型在近壁网格密集区域出现了湍流黏度较低的区域,这是由于PANS模型的fk构造函数仍是由当地湍流尺度和网格尺度来控制,在近壁网格较密的条件下,PANS模型显现出类似DES模型对网格敏感的缺点,这时近壁RANS区域被破坏,而网格尺度还没有小到能够进行大涡模拟的程度。
|
图 13 时均湍流黏度比(μt/μ)分布(标准网格:上,加密网格:下) Fig.13 Time-averaged distributions of μt/μ (baseline grid: top, fine grid: bottom) |
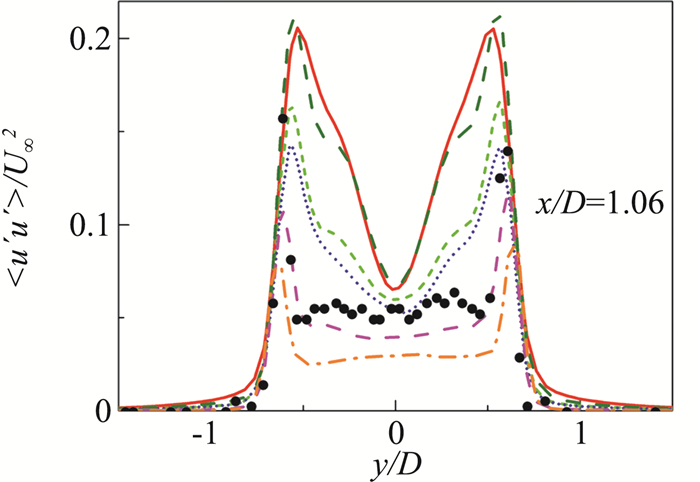
图 14为三种混合模型在不同网格条件下计算的局部(x/D=1.06)时均轴向雷诺应力分布(图例见图 15)。可以看到SAS模型及两种PANS模型计算的雷诺应力与实验值均有较大差距,这可能是由于涡黏性模型的内在缺陷造成的。我们在此关注不同的模型在不同网格条件下的计算差异。可以看到SAS模型在标准网格与加密网格条件下均高估了雷诺应力值,但两种网格下的计算结果差别不大;两种PANS模型对不同的网格表现出相似的规律,在加密网格时雷诺应力均出现了明显的降低,结合图 13中的黏度分布可知,由于近壁区域网格的加密,湍流黏度降低,导致模化的雷诺应力减少,同时有没有求解足够的雷诺应力,导致了雷诺应力不足现象的发生,这也验证了PANS构造函数对网格较敏感的缺陷。同时两种PANS模型函数比较可以看出,PANS(des)模型计算的雷诺应力及气动力分布要稍优于PANS(tanh)模型,这也说明了PANS(tanh)模型构造函数对网格的敏感程度要大于PANS(des)模型的构造函数。
|
图 14 局部时均轴向雷诺应力分布 Fig.14 Time-averaged distributions of streamwise Reynolds stress |
|
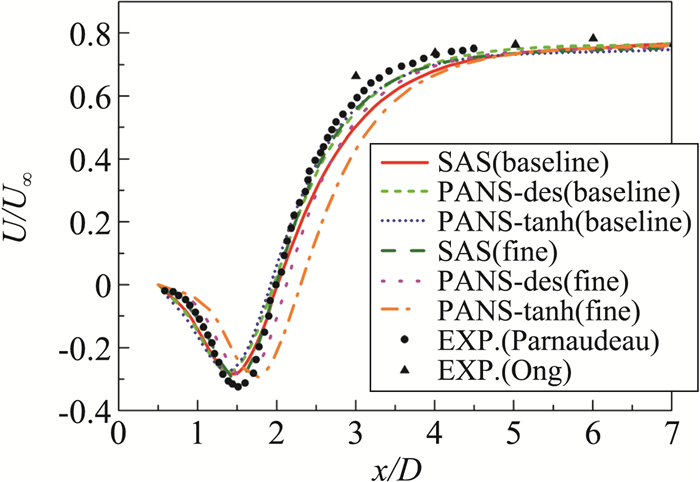
图 15 时均轴向速度分布 Fig.15 Time-averaged distributions of streamwise velocity |
图 15为三种模型在不同网格条件下的时均轴向速度分布对比。结合前文分析可知,SAS模型网格独立性较好,标准网格与加密网格下的计算结果没有体现出太大差别,且由于对剪切层的计算更准确,计算得到的回流区大小更接近实验值。两种PANS模型由于对网格较敏感,在加密网格时延缓了剪切层的转捩,导致回流区变长。这在PANS(tanh)模型的计算结果中表现更明显。
3.4 积分统计量比较表 2为四种模型计算的圆柱绕流平均积分统计量与相关实验值及数值结果对比。可以看到在与剪切层运动密切相关的参数中,普通网格下SAS与两种PANS模型均取得了与实验值较吻合的回流区长度(Lr/D)计算结果,与构造相对完善的LES-THE、SA-IDDES、V2-f- DES模型的计算结果也是相近的,其中SAS模型的计算结果与实验值最接近;加密网格时,两种PANS模型均过大地预测了回流区长度。在阻力系数(Cd)及分离角(θSep)的计算中,在标准网格下三种混合模型计算误差均较小,Cd满足实验值的0.98±0.05区间,在加密网格时,SAS模型的计算结果变化不大,两种PANS模型获得了较小的分离角及阻力系数。在其余的比较项中,可以看到四种模型对圆柱尾迹旋涡脱落频率的计算及壁面压力的计算均较准确,所计算的斯特劳哈数(St)与背风点压力系数(-Cpb)差别不大。对于SST模型,由于其构造模化了所有的湍流量,导致重要的流场细节被抹平,其计算的阻力系数、背风点压力系数、回流区长度、分离角均存在较大误差。同时可以看到两种网格条件下PANS(des)计算结果稍好于PANS(tanh)。比较文献[25]中两种fk为常数的PANS模型计算结果可以看出,fk=0.1时,流场fk值已处于较低水平,但计算的回流区长度要小于本文变fk计算结果,而fk=0.3时的计算结果误差已较大,这说明了变fk在流场计算中更合理,同时也说明了流场对fk值是比较敏感的。
3.5 混合模型调控机制比较由前述分析可知,SAS及PANS等涡黏性混合模型均能通过降低流场湍动黏度来求解更多湍流尺度,但SAS及PANS对求解尺度的调控机制是完全不同的。由前文模型构造我们可知,SAS模型中引入了von Karman长度尺度Lvk,通过当地湍流尺度L与Lvk的比例关系来控制ω输运方程中源项QSAS的生成量,因此SAS模型在分离区是通过L/Lvk的调控作用来增大ω的值,从而降低湍动黏度的值;PANS模型是通过加入一个fk参数来调控流场可解/不可解湍流量的比例,fk值越小,可解尺度就释放的越多,文中PANS模型使用了两种变fk函数,其核心是当地湍流尺度与网格尺度的比例关系,两者都是通过减小ω方程中耗散项的量,从而使求解的ω值增大,进而使湍动黏度减小。
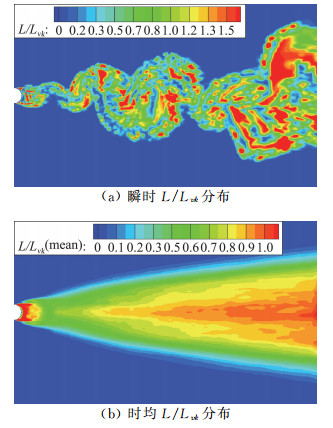
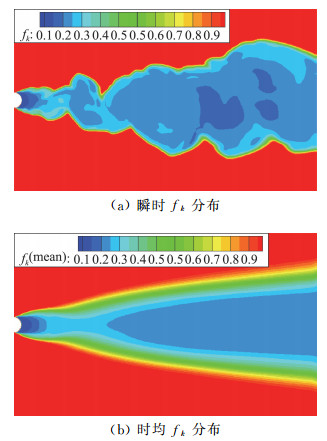
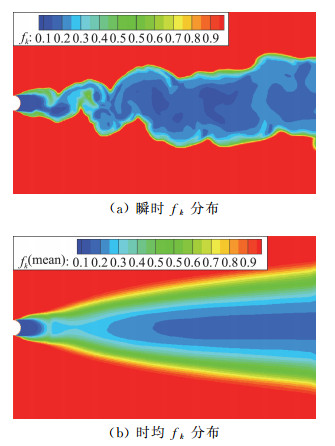
图 16为SAS模型计算的瞬时及时均L/Lvk分布。可以看到在尾迹分离区L/Lvk的值较大,而在远场区L/Lvk基本为0。图 17和图 18是两种变fk的PANS模型计算得到的瞬时及时均fk分布,可以看到在分离区fk的值处在较低水平,而在远场范围fk=1湍流信息均被模化。通过比较两类模型中对涡黏度起关键调控作用的L/Lvk与fk分布可以看出,立足于当地流动、对网格无依赖的SAS模型局部分辨率更高,可以反映出流场结构的无序与丰富状态。PANS模型中网格尺度的关联性使得其局部分辨率降低,且计算结果对网格及计算初值设置非常敏感。从以上来看,SAS模型对流场涡黏性的调控机制是有优势的。
|
图 16 SAS模型计算的瞬时及时均L/Lvk分布 Fig.16 Time-averaged and instantaneous distributions of L/Lvk for SAS |
|
图 17 PANS(des)模型计算得到的瞬时及时均fk分布 Fig.17 Time-averaged and instantaneous distributions of fk for PANS(des) |
|
图 18 PANS(tanh)模型计算得到的瞬时及时均fk分布 Fig.18 Time-averaged and instantaneous distributions of fk for PANS(tanh) |
对比图 17和图 18,显示了PANS模型的两种函数计算的fk分布差别不大,在近尾迹区fk均处在较低水平,这有效地调整了流场的求解尺度。同时可以看到PANS(des)模型相比PANS(tanh)模型在近尾迹区的分辨率更高,其在回流区后部及远尾迹区的fk值要稍小于后者。分析两种模型的构造可知,PANS(des)模型fk函数构造相对简单,但其对流场的调控作用更加直接和灵敏,而PANS(tanh)模型中fk函数中借助tanh函数,tanh函数整体从-1~1变化,这使得函数的整体灵敏度下降,从而影响fk的分布。同时图 13中可以看到PANS(des)的湍动黏度稍高于PANS(tanh),其获得的气动力分布也稍好于后者。这也说明了两种变fk函数比较,类DES的fk调控函数更好一些,计算的湍流耗散也更合理。
4 结论本文以Re=3900的圆柱绕流作为算例比较了SAS、PANS(des)、PANS(tanh)湍流模型在大分离流动中的计算能力,主要从流场特征捕捉、气动力特性计算、流场涡黏性控制等方面对所用湍流模型进行了比较,并通过不同的网格计算条件对比了不同模型调控函数的网格敏感性。计算结果表明:三种混合模型均具有求解三维小尺度涡运动的能力,并能较完整地展现出亚临界雷诺数下圆柱绕流层流剪切层形成、发展、失稳、分离,在下游近尾迹区形成回流区直至远尾迹区形成剪切分离区的过程。同时,通过对比计算结果得到以下结论:
1) 在对湍流结构的显示方面,PANS模型相比SAS模型能捕捉到更丰富的湍流结构,两类模型对流场气动力的计算均存在一定误差,回流区计算误差要大于远尾迹区,三种模型气动力计算与实验吻合关系为SAS>PANS(des)>PANS(tanh)。
2) SAS模型Lvk尺度立足当地流动,局部流场分辨度更高,调控作用更强;PANS模型对网格设置较敏感。两类模型相比,SAS模型的流场信息调控模式更优秀,获得的流动涡黏性更合理。
3) 两种PANS模型中,类DES可变fk分布函数构造相对简单,所得fk分布更准确;借助tanh函数的fk分布函数调节灵敏度较低,计算得到的尾迹区fk值偏低,对流场调控作用稍差。
| [1] |
吴子牛. 计算流体力学基本原理[M]. 北京: 科学出版社, 2003. WU Z N. Basic principle of computational fluid dynamics[M]. Beijing: Science Press, 2003. (in Chinese) |
| [2] |
张兆顺, 崔桂香, 徐春晓. 湍流大涡数值模拟的理论和应用[M]. 北京: 清华大学出版社, 2008. ZHANG Z S, CUI G X, XU C X. Theory and application of LES modeling[M]. Peking: Tsinghua University Press, 2008. (in Chinese) |
| [3] |
SPALART P R. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41(1): 203-229. |
| [4] |
MENTER F R, KUNTZ M, BENDER R. A scale-adaptive simulation model for turbulent flow predictions. AIAA-2003-767[R]. Reston: AIAA, 2003.
|
| [5] |
MENTER F R, EGOROV Y. A scale-adaptive simulation model using two-Equation models. AIAA-2005-1095[R]. Reston: AIAA, 2005.
|
| [6] |
MENTOR F R, EGOROV Y. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 1:theory and model description[J]. Flow, Turbulence and Combustion, 2010, 85(1): 113-138. DOI:10.1007/s10494-010-9264-5 |
| [7] |
EGOROV Y, MENTOR F R. The scale-adaptive simulation method for unsteady turbulent flow predictions. Part 2:application to complex flows[J]. Flow, Turbulence and Combustion, 2010, 85(1): 139-165. DOI:10.1007/s10494-010-9265-4 |
| [8] |
GIRIMAJI. Partially-averaged Navier-Stokes model for turbulence: implementation and validation. AIAA-2005-2502[R]. Reston: AIAA, 2005.
|
| [9] |
SPALART P R. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical & Computational Fluid Dynamics, 2006, 20(3): 181-195. |
| [10] |
XIAO Z X, CHEN H X, ZHANG Y F. Study of delayed-detached eddy simulation with weakly nonlinear turbulence model[J]. Journal of Aircraft, 2006, 43(5): 1377-1385. DOI:10.2514/1.20127 |
| [11] |
XIAO L H, XIAO Z X, DUAN Z W, et al. Improved-delayed-detached-eddy simulation of cavity-induced transition in hypersonic boundary layer[J]. International Journal of Heat and Fluid Flow, 2015, 51: 138-150. DOI:10.1016/j.ijheatfluidflow.2014.10.007 |
| [12] |
XIAO Z X, LIU J, LUO K Y, et al. Investigation of flows around a rundimentary landing gear with advanced detached-eddy-simulation approaches[J]. AIAA Journal, 2013, 51(1): 107-125. DOI:10.2514/1.J051598 |
| [13] |
肖志祥, 罗堃宇, 刘健. 宽速域RANS-LES混合方法的发展及应用[J]. 空气动力学学报, 2017, 35(3): 338-353. XIAO Z X, LUO K Y, LIU J. Developments and applications of hybrid RANS-LES methods for wide-speed-range flows[J]. Acta Aerodynamica Sinica, 2017, 35(3): 338-353. DOI:10.7638/kqdlxxb-2017.0048 (in Chinese) |
| [14] |
杜磊, 宁方飞. 高亚临界雷诺数圆柱绕流的尺度自适应模拟[J]. 力学学报, 2014, 46(4): 487-496. DU L, NING F F. Scale adaptive simulation of flows around a circular cylinder at high sub-critical Reynolds number[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 487-496. (in Chinese) |
| [15] |
白俊强, 王晨, 张扬. 一种基于冯卡门尺度的湍流模式在模拟稳态和非稳态流动问题中的应用[J]. 工程力学, 2014, 31(11): 39-45. BAI J Q, WANG C, ZHANG Y. Application of a turbulence model based on von Karman length scale in steady and unsteady flow simulation[J]. Engineering Mechanics, 2014, 31(11): 39-45. (in Chinese) |
| [16] |
杜若凡, 阎超, 罗大海. PANS方法在双圆柱绕流数值模拟中的性能分析[J]. 北京航空航天大学学报, 2015, 41(8): 1374-1380. DU R F, YAN C, LUO D H. Assessment of PANS method for simulation of flow around tandem cylinders[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1374-1380. (in Chinese) |
| [17] |
徐晶磊, 高歌, 杨炎. 基于当地流动结构的RANS/LES混合模型[J]. 航空学报, 2014, 35(11): 2992-2999. XU J L, GAO G, YANG Y A. RANS/LES hybrid model based on local flow structure[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2992-2999. (in Chinese) |
| [18] |
刘周, 杨云军, 周伟江, 等. 基于RANS-LES混合方法的翼型大迎角非定常分离流动研究[J]. 航空学报, 2014, 35(2): 372-380. LIU Z, YANG Y J, ZHOU W J, et al. Study of unsteady separation flow around airfoil at high angle of attack using hybrid RANS-LES method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 372-380. (in Chinese) |
| [19] |
NORBERG C. Effects of Reynolds number and a low-intensity free-stream turbulence on the flow around a circular cylinder[M]. Publication No. 87/2, Sweden: Department of Applied Thermodynamics and Fluid Mechanics, Chalmers University of Technology, 1987.
|
| [20] |
LOURENCO L M, SHIH C. Characteristics of the plane turbulent near wake of a circular cylinder: a particle image velocimetry study[Z]. (Private Communication), 1993.
|
| [21] |
PARNAUDEAU. Experimental and numerical studies of the flow over a circular cylinder at Reynolds number 3900[J]. Physics of Fluids, 2008, 20(8): 1-14. |
| [22] |
ONG, WALLACE. The velocity field of the turbulent very near wake of a circular cylinder[J]. Experiments in Fluids, 1996, 20: 441-453. DOI:10.1007/BF00189383 |
| [23] |
KRAVCHENKO, MOIN. Numerical studies of flow over a circular cylinder at ReD=3900[J]. Physics of Fluids, 2000, 12(2): 403-417. |
| [24] |
LYSENKO. Large-eddy simulation of the flow over a circular cylinder at Reynolds number 3900 using the OpenFoamToolbox[J]. Flow Turbulence Combust, 2012, 89: 491-518. DOI:10.1007/s10494-012-9405-0 |
| [25] |
LUO D H. Comparative assessment of PANS and DES for simulation of flow past a circular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 134: 65-77. DOI:10.1016/j.jweia.2014.08.014 |
| [26] |
ALESSANDRO. Detached-eddy simulations of the flow over a cylinder at Re=3900 using OpenFoam[J]. Computers and Fluids, 2016, 136: 152-169. DOI:10.1016/j.compfluid.2016.05.031 |
| [27] |
JEE K, SHARIFF K. Detached-eddy simulation based on the V2-f model[J]. International Journal of Heat & Fluid Flow, 2014, 46: 84-101. |
| [28] |
KIM. Large eddy simulation of turbulent flow past a circular cylinder in subcritical regime. AIAA-2006-1418[R]. Reston: AIAA, 2006.
|
| [29] |
唐虎, 常楠士. 亚临界圆柱绕流的DES方法比较[J]. 航空学报, 2017, 38(3): 120294. TANG H, CHANG S N. Comparison of detached eddy simulation schemes on a subcritical flow around circular cylinder[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 120294. (in Chinese) |
| [30] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [31] |
LAKSHMIPATHY, TOGITI. Assessment of alternative formulations for the specific-dissipation rate in RANS and variable-resolution turbulence models. AIAA-2011-3978[R]. Reston: AIAA, 2011.
|
| [32] |
DAVISON. The PANS k-ε model in a zonal hybrid RANS-LES formulation[J]. International Journal of Heat & Fluid Flow, 2014, 46: 112-126. |
| [33] |
ELMILIGUI. Numerical study of flow past a circular cylinder using RANS, Hybrid RANS/LES and PANS Formulations. AIAA-2004-495[R]. Reston: AIAA, 2004.
|
| [34] |
FRANKE. Large eddy simulation of the flow past a circular cylinder at Re=3900[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(10): 1191-1206. DOI:10.1016/S0167-6105(02)00232-5 |
 2019, Vol. 37
2019, Vol. 37


