2. 中国科学院 深圳先进技术研究院, 深圳 518000
2. Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen 518000, China
自20世纪初莱特兄弟成功试飞第一架飞机以来,飞行器的发展如火如荼。气动外形设计作为飞行器设计的“先行官”,具有举足轻重的作用。随着科技的进步,气动设计经历了从机械式到信息化的转变。20世纪前半叶,气动设计都是通过手工修形设计得到,其严重依赖于设计人员的经验,设计周期很长。20世纪中叶以来,计算流体力学(Computational Fluid Dynamics, CFD)应运而生,CFD结合CAD(Computational Aid Design)技术,已经可以进行半自动化的飞行器气动外形设计。但CFD分析仍是一个比较耗时的过程,在飞行器设计中需要反复调用CFD分析模块,计算量很大。
机器学习技术则提供了另一种解决手段,它通过计算手段,利用经验或已有数据改善系统自身的性能。在气动设计中,给定若干外形和性能样本集,数据代理模型可以自动训练、建立性能仿真模型,并快速评估仿真模型性能。目前应用比较成熟的机器模型包括二项式响应面、Kriging以及神经网络[1]等。2006年,多伦多大学的Hinton[2]首次提出“深度学习”概念——使用多隐层神经网络提高数据识别精度。2012年,Hilton跟他的学生Krizhevsky合作建立深层卷积神经网络,并在ImageNet视觉竞赛中取得第一名[3]。2016年3月,AlphaGo横空出世,通过卷积神经网络提高搜索树的选择和剪枝,战胜了围棋世界冠军李世石,引爆了“人工智能”时代[4]。
从目前的研究资料来看,气动外形设计中的机器学习技术还处于比较初级的阶段。以神经网络模型为例,美国NASA AMES研究中心、加拿大科学院空气动力研究所等,研究过发动机叶片翼型优化[5]和跨声速飞行器外形优化[6]等课题,但大都以单隐层或有限隐层的神经网络、径向基神经网络等简单模型为主,使用以卷积神经网络为代表的深度学习模型很少。这可能有几个原因:气动数据少,发展时间短,问题性质复杂。但深度学习效果强大、市场广阔,应用到气动外形设计中的潜力是不言而喻的,有些学者已经先行探索,比如陈海等[7]使用卷积神经网络,以翼型图像为输入预测了翼型的气动系数。
本文以乘波体为设计背景探索深度学习技术在气动代理模型中的应用。从乘波体外形出发,根据三维流场乘波体设计方法提取设计变量,评估气动力性能,生成大规模数据集。选择深度残差网络(Residual Neural Network, ResNet),测试气动性能预测精度,并探索了基于图片识别的模型构建。
1 数据和方法 1.1 乘波体设计与性能评估大数据是深度学习发展的基石之一(另两个为硬件平台和算法)。只有在海量数据基础上,深度学习才能真正发挥威力,比如AlphaGo,其模型训练使用的棋盘数据达3×107之多。
现阶段由于风洞实验、数值模拟和飞行实验的成本和效率,气动外形性能数据量有限,且完整性与确定性较差,建立气动大数据并不容易。本文的研究重点是机器学习模型的预测精度,暂不考虑气动数据的精确性,因此以一类简单的外形“乘波体”为例,开发设计方法并快速预估性能,大量生成可供测试的数据。本文使用基于激波装配法的乘波体设计方法[8],结合基于多重网格的快速搜索技术,实现了三维流场乘波体的快速生成。
乘波体使用椭圆钝锥激波流场作为设计流场,设计状态为Ma=5、H=30 km。设计过程如图 1(a),可简述如下:取一条空间曲线作为FCT (Flow Capture Tube),将其沿水平方向投影到激波曲面,投影线就是乘波体的前缘线;从前缘线出发追踪流线,即可得到乘波体下表面,上表面一般是自由流面。FCT是乘波体设计中的主要设计变量,曲线有多种方法可以进行参数化表示,本文选择一种常用且高效的参数化方法B样条作为几何表达工具[9]。如图 1(a)所示,在FCT上取31个点,布置流线,向后追踪流线得到图 1(b)的乘波外形。
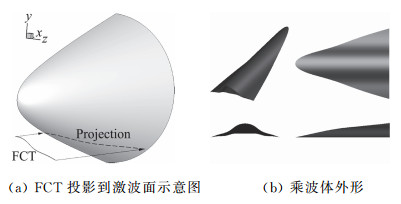
|
图 1 三维流场乘波体设计示意图 Fig.1 Waverider design with 3D flow field |
追踪流线得到的乘波体外形中保存有流场信息,可以使用流线积分法预估得到乘波体的无黏气动性能,计算非常迅速。图 1(a)所示的乘波体生成与性能预测的总耗时约0.3 s,生成的外形图 1(b)升阻比预估为7.8(不考虑底阻),容积率0.134,与CFD计算的性能误差不超过5%。
乘波体设计结合流线积分法可以快速计算飞行器的气动性能,为三维流场乘波体的气动数据的大规模生成奠定了基础。其设计参数为B样条表达FCT的控制点,固定z坐标均匀分布,设计变量为6个y坐标。性能数据参数为5个:升力系数CL、阻力系数CD、纵向压心位置CF、平面投影面积S、容积V。所以单条数据为6个设计变量到5个性能评估数据的映射。
1.2 拉丁超立方采样机器模型的训练需要一定量由输入设计变量到输出响应值的数据集。而在设计空间中合理选取样本点,对是否可以获取有效信息非常重要,这一过程叫做实验设计。目前常用的实验设计方法包括均匀实验设计、正交实验设计、D-最优实验设计等。
拉丁超立方采样(Latin Hypercube Sampling,LHS)是一种比较流行的现代实验设计方法,已获得广泛应用。其选取样本点的方法如下所示:
| $ x_{j}^{(i)}=\frac{\varepsilon_{j}^{(i)}+U_{j}^{(i)}}{N} $ | (1) |
其中j为设计变量的维数,i为样本序号,最大为N。ε为0, 1, ..., N-1的独立随机数列,有N!种排列,决定xj(i)所在的子区间;U是[0, 1]之间的随机数,决定xj(i)在子区域的具体位置。
LHS的采样在任一维上都有个数与样本数量相同的子区间,每个子区间有且仅有1个样本;样本在每个子区间内随机选取,因此LHS方法可以保证一定的均匀性。图 2展示了三维变量在给定范围内分别选择1000和10 000的采样点示意图,可以看到,在大样本情况下LHS采样可以保持比较均匀。

|
图 2 拉丁超立方采样效果图 Fig.2 Samples using LHS method |
在1.1节的乘波体设计中,6个设计变量的变化范围均定为[-25, -5],经过验证,设计空间均可行。深度学习模型的一大特点是适合于海量数据的特征提取,因此生成十万条数据作为样本集。表 1给出任选3个样本数据的形式,包括6个设计参数和对应的5个性能参数。
| 表 1 采样的数据示意 Table 1 Data of three samples |
|
|
伴随人工智能时代发展迅速的深度模型中,目前应用最广泛的是卷积神经网络(Convolutional Neural Network, CNN),已经在计算机视觉、语音识别等领域取得了突破性成果。CNN通过卷积与池化操作,将低层特征逐层组合成抽象的高层属性类别,结构复杂,参数数目多,具有良好的识别性。
为了进一步提升模型能力,设计具有深层次的网络是非常自然的想法,深度对于模型带来的性能提升最为显著。最近几年神经网络的层数提高很快,以ImageNet竞赛中表现出色的卷积神经网络为例:2012年,AlexNet[10],8层网络;2014年,VGGNet[11],16层;2014年,GoogleNet[12],22层。
但训练深层次的神经网络非常困难,很多情况下由于训练不到位,单纯把Layer堆积起来的深层网络效果反而不如较浅的网络好。深度残差神经网络(Residual Neural Network, ResNet)解决了这一问题。ResNet由微软亚洲研究院何凯明研究员于2015年的ImageNet图像识别竞赛中首次使用,将卷积神经网络层数提高到惊人的100层。ResNet在2015年ImageNet的图像检测和定位领域均获得第一名,显示了强大的能力。2016年,ResNet获得图像识别领域顶级会议CVPR最佳论文奖[13]。
ResNet在普通深度卷积网络的基础上增加跨层拟合训练残差,在训练每层时除了使用目标函数梯度外,还增加残差梯度,有效防止了深度模型训练时梯度随深度增加而消失的问题,从而使模型的准确率得到很大提升。深度残差网络的核心是残差单元,通过使用残差单元,可以构建极深的神经网络。
如图 3(a)所示,残差单元的具体阐述如下[13]:假设某段神经网络的输入是x,期望输出是H(x),将输入x传到输出时,需要学习的目标是H(x)。ResNet则改变学习目标,不再学习完整的输出H(x),而只学习输出和输入的差别H(x)-x,即残差F(x)=H(x)-x。何凯明通过实验证明,优化F(x)比优化H(x)容易得多。x通过旁路支线将输入直接连到后面层,使得后面层可以直接学习残差,这种结构被称为短链接,可以跳过2层、3层或更多层,直接执行协同映射, 如图 3(b)所示。残差单元的数学定义为:
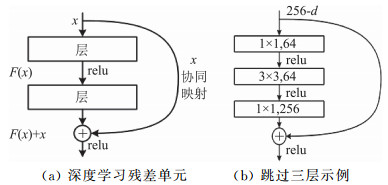
|
图 3 ResNet残差单元结构图 Fig.3 View of the ResNet unit block |
| $ x_{l+1}=f\left(x_{l}+F\left(x_{l}, W_{t}\right)\right) $ | (2) |
其中,xl和xl+1分别为第l个残差单元的输入和输出;f是激活函数,一般为修正线性单元(rectified linear unit, relu), relu=max{0, x}; F为残差;W为卷积核。残差训练的重要突破在于重构学习过程,引入一条捷径,使训练过程中底层误差可以通过捷径向上一层传播,减弱了层数过多造成的梯度消失现象,很大程度上解决了层级与准确度之间的矛盾。
2 基于数据的性能预测本文构建了10层ResNet,由9个卷积层和一个全连接层组成,实现工具Caffe[14]。采用动量梯度下降算法,其权值初始学习率设置为0.01, 动量值0.98, 批大小128,权值衰减0.0005,保留层保留率为0.8,最大训练迭代次数40 000次,以上参数定义可参考文献[15]。使用的计算平台配置为CPU: Intel Xeon(R) CPU E5-2690 2.60 GHz; GPU: GeForce GTX TITAN X (×1)。
数据为100 000个LHS方法选取的样本集,其中90 000个为训练样本,10 000个为验证样本,总训练时间为45 min。
定义测试数据的平均绝对误差
| 表 2 不同模型的测试精度 Table 2 Test precision of surrogate models |
|
|
为了说明ResNet的预测能力,本文对比了两个经典的浅层学习模型:随机森林和普通前馈神经网络(Neural Network, NN)。
随机森林(Random Forests, RF)是一种简单快速的集成学习模型,它是并行式集成学习方法Bagging模型的一种改型,实现如下:首先通过自主采样法得到T个样本集,基于每个采样集训练基学习器,并行处理,得到Bagging模型[16]。在Bagging模型的基础上,进一步引入随机属性选择,通过模型属性扰动,提高辨别能力。随机森林简单易实现、计算开销小,在很多现实任务中表现出了强大的性能,被誉为“代表集成学习技术最高水平的方法”。
本文构建了个体学习器数目为100的随机森林,计算平台配置为CPU: Intel Xeon(R) CPU E5-2690 2.60 GHz,采用MATLAB实现。90 000条样本为训练数据,10 000条为测试数据,训练时间300 s。误差分布如表 2第2行所示,可以看到气动力系数的精度较高,但投影面积和容积的识别精度较低。
另一模型为双隐层神经网络,输入层神经元6个,第一隐层8个,第二隐层2个,输出层1个。隐层神经元激励函数为双曲正切函数,输出层为线性输出,计算平台配置同随机森林。针对5个参数分别设计和训练了5个NN,均使用误差逆传播(error Back Propagation, BP)算法训练,其中样本集中90%为训练数据,10%为验证数据,单个神经网络的训练时间约为25 min,模型的总训练时间为2 h左右。
NN模型的测试精度如表 2第3行所示。综合这3个模型的精度,可以看到对于5个气动性能参数,ResNet的预测精度均是最高的。相应的,ResNet深度学习模型的深层次导致参数数量多、训练时计算量消耗较大,在使用了一块GeForce Titan GPU加速计算的情况下,训练时间45 min,相比随机森林的5 min长得多。但一旦训练完毕,使用模型对数据进行预估的速度很快,基本可达1000次/秒,满足效率要求。
3 基于图像识别的性能预测第2节中使用的样本数据集给出了数据到数据的映射。但一方面,飞行器的参数化是一项比较复杂的工作,难以保证参数化模型的精度;第二,深度学习模型在图片识别领域最为成熟,应用最广,单纯数据到数据的映射难以充分挖掘现阶段人工智能的优势。
本文提出另外一个气动性能预测思路:直接将飞行器外形转化为二维图片,建立图片数据集,再训练深度学习模型预测性能。这是一种比较直观的做法,可以省略外形参数化步骤,同时更为方便应用成熟的图片识别深度学习技术。在具体操作中,选定投影平面,将飞行器按照部件分开,例如机身、机翼、尾翼、发动机短舱等,将各部件投影到投影平面,形成二维图像,其中每个像素点的颜色代表图像对应位置的高度或厚度,这样每个飞行器外形就可以分解为对应的几个二维图片。
乘波体外形较为简单,可以分为上下两个表面部件,投影到俯视图平面,每个像素点的灰度值代表此点相对于参考平面的z坐标位置。因为乘波体的上表面都是自由流面,包含信息较少,其前缘足以充分表达,所以仅保留下表面图像即可。图 4给出样本集中两个外形下表面的投影图,固定头部顶点位置,采样图像大小均为200×500像素,总共建立100 000图片到数据的映射作为图片样本集。

|
图 4 两个采样乘波体的下表面映射图像 Fig.4 Figures of two waverider lower surfaces |
仍然使用10层ResNet进行训练,计算平台机器配置为CPU: Intel(R) Xeon(R) CPU E5-2690 2.60 GHz;GPU: GeForce GTX TITAN X(×4)。训练时间24.5 h。
表 3给出了气动性能的预测精度。从测试结果看,基于图片数据集的测试精度比基于数据的测试精度低,这可能是因为图片数据的维数(200×500个像素点)大幅增加,影响了深度学习模型的训练精度。但相比飞行器参数化得到的数据,此方法实现更为容易,有望推广到升力体、翼身融合体或工程外形之中。
| 表 3 基于图片数据集的测试精度 Table 3 Test precision of ResNet based on picture data set |
|
|
本文以乘波体气动外形数据为例,研究了深度学习模型在气动性能预测中的应用,结论如下:
(1) 人工智能深度学习需要大量的数据,乘波体外形相对简单,生成外形效率高,比较适合这类研究探索;拉丁超立方采样是比较有效的实验设计方法,具有较好的均匀性。
(2) 对比于传统机器学习模型,深度残差神经网络ResNet通过多层的非线性变换,预测精度更高,证实了其作为飞行器气动数据代理模型的有效性。
(3) 鉴于现有深度学习模型都以图片或语音为应用场景,本文利用飞行器图片作为输入,使用ResNet建立图片与气动指标的非线性映射,实现了飞行器的非参数化性能预测。
| [1] |
高正红, 王超. 飞行器气动外形设计方法研究与进展[J]. 空气动力学学报, 2017, 35(4): 516-528. GAO Z H, WANG C. Aerodynamic shape design method for aircraft:status and trends[J]. Acta Aerodynamica Sinica, 2017, 35(4): 516-528. DOI:10.7638/kqdlxxb-2017.0058 (in Chinese) |
| [2] |
HILTON G E. OSINDERO S, THE Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. http://cn.bing.com/academic/profile?id=17d47c184b5c67d42650a0aa38117d73&encoded=0&v=paper_preview&mkt=zh-cn
|
| [3] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. Imagenet classification with deep convolutional neural networks[C]//Proceedings of Advances in Neural Information Processing System. South lake Tahoe, USA: Curran Associates Press, 2012: 1097-1105. https://dl.acm.org/citation.cfm?id=2999257
|
| [4] |
SILVER D, HUANG A, MADDISON C, et al. Mastering the game of Go with deep neural networks and tree search[J]. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 |
| [5] |
HOYLE N, BRESSLOFF N W, KEANE A J. Design optimization of a two-dimensional subsonic engine air intake[J]. AIAA Journal, 2006, 44: 2672-2681. DOI:10.2514/1.16123 |
| [6] |
PATNAIK S N, CORONEOS R M. A subsonic aircraft design optimization with neural network and regression approximators[R]. AIAA 2004-4606, 2004. http://arc.aiaa.org/doi/abs/10.2514/1.11113
|
| [7] |
陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294-299. CHEN H, QIAN W Q, HE L. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294-299. DOI:10.7638/kqdlxxb-2017.0098 (in Chinese) |
| [8] |
陈冰雁, 刘传振, 纪楚群. 基于激波装配法的乘波体设计与分析[J]. 空气动力学学报, 2017, 35(3): 421-428. CHEN B Y, LIU C Z, JI C Q. Waverider design and analysis based on shock-fitting method[J]. Acta Aerodynamica Sinica, 2017, 35(3): 421-428. DOI:10.7638/kqdlxxb-2017.0039 (in Chinese) |
| [9] |
LES PIEGL, WAYNE TILLER. The NURBS book (second edition)[M]. USA: Springer-Verlag, 1995: 32-84.
|
| [10] |
KRIZHEVSKY ALEX, SUTSKEVER I, HINTON G. Image-Net classification with deep convolutional neural networks[J]. Communications of the ACM, 2017, 6(6): 84-90. |
| [11] |
SIMONYAN K, ZISSERMAN A. Very deep convolutional networks for large scale image recognition[C]//International Conference on Learning Representations. San Diego, USA, 2015. https://arxiv.org/abs/1409.1556
|
| [12] |
CHRISTIAN S, LIU W, JIA Y, et al. Going deeper with convolutions[C]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, USA, 2015. https://arxiv.org/abs/1409.4842
|
| [13] |
HE K M, ZHANG X, REN S Q, et al. Deep residual learning for image recognition[R]//IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, USA, 2015. https://arxiv.org/abs/1512.03385
|
| [14] |
JIA Y Q, SHELHAMER E, DONALHUE J, et al. Caffe: convolutional architecture for fast feature embedding[C]//Proceedings of the ACM International Conference on Multimedia. Glasgow, UK, 2014. https://arxiv.org/pdf/1408.5093.pdf
|
| [15] |
HE K M, ZHANG X, KOMODAKIS N. Delving deep into rectifiers: surpassing human-level performance on imagenet classification[C]//IEEE International Conference on Computer Vision. Santiago, Chile, 2015. https://arxiv.org/abs/1502.01852
|
| [16] |
BREIMAN L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
 2019, Vol. 37
2019, Vol. 37


