气动力建模是飞行器工程中确定总体设计参数、飞行轨迹、操纵性与稳定性等的重要基础,模型精度直接影响控制效果和仿真可信度。高速飞行器的气动力受飞行高度、速度、舵干扰等多种因素耦合影响,非线性强。传统气动力设计通常采用基于数据表的多元插值方法,以工程估算、数值计算、风洞试验等手段,给出特定格式的标称气动力数据表,在进行控制设计、飞行仿真时,多元插值获得飞行中任意点的气动力参数,这种方法的局限性是,数据表的格式要求严格,多元插值计算量大,多来源冗余数据利用困难。飞行试验是不同于地面预测的气动力数据来源,精度相对较高。然而,飞行试验的气动力数据是一些沿弹道的离散点,很难转换成类似于地面预测的标称气动力数据表。如何有效利用飞行试验数据是一个难题。
在飞行力学领域,气动力建模已经开展了多年的研究。气动力模型发展了两种形式,分别为数学表达式类和智能学习类。
(1) 传统数学表达式形式。即根据气动力的物理特性、统计规律等,利用数学方法获得的气动力与飞行状态、控制输入等参数之间的数学关系式,如非线性代数模型、傅立叶级数模型、积分方程模型等[1]。对于数学表达式形式的气动特性建模,比较适合于状态范围变化较小的局部气动力建模,比如特定高度、速度、攻角等条件下的线性/定常气动力建模。对于空域、速域、飞行姿态和控制面偏转范围变化都比较大,且气动布局复杂的飞行器, 气动力与飞行高度、速度、迎角、侧滑角、角速率、舵偏角等参数之间的关系呈现高度非线性,传统数学类模型气动建模方法很难给出全局都误差很小的准确描述。
(2) 人工智能形式。即根据计算机模拟人的某些思维过程和智能行为的有关理论,通过对大量气动力数据的机器学习,建立气动力模型,如神经网络、模糊逻辑、支持向量机[2]等。基于人工智能的神经网络方法,能够逼近任意非线性,是理想的非线性建模方法。基于机器学习的气动建模方法已经在翼型气动建模[2]、直升机气动建模[4]和飞机大迎角气动建模[5]等方面成功应用。张瑞民等[6]采用BP神经网络对飞机大迎角动态气动特性进行了建模。龚正等[7]基于结构自适应神经网络对飞行器纵向大振幅强迫振荡试验气动力进行了建模探索。史志伟等[8]讨论了径向基神经网络在飞机大迎角大振幅风洞试验中建模的应用。付军泉和史志伟等[8]讨论了循环神经网络在飞机非定常气动力建模中的应用。王博斌[10]基于RBF神经网络开展了翼面大幅振动时域非线性气动建模。王文正等[11]采用聚类分析方法对飞行试验数据进行了初步气动数据挖掘分析。朱莉和高正红[12]采用BP神经网络对翼型的气动特性建模和翼型设计进行了探索。陈海和钱炜祺等[13]研究了深度神经网络对翼型气动力的建模应用。目前基于神经网络的气动建模研究多基于风洞动态试验或CFD动态计算结果,目标多是对大攻角非线性气动特性的局部描述,但在实际飞行试验中,建立的模型很难反映整个弹道的气动特性,因此很难直接应用于飞行仿真研究。对于高速飞行试验,还需要针对飞行高度、速度、攻角、侧滑角、角速率、舵偏角等空域、速域、状态范围变化都比较大的情况,进行机器学习类气动力建模方法的应用探索。
本文利用多次飞行仿真的气动力数据作为研究数据,运用人工BP神经网络,建立高速飞行器全弹道的非线性气动力模型,并验证建模方法的可行性。BP神经网络是最常用的机器学习方法之一[14],它具有良好的学习能力及非线性拟合能力,是处理非线性函数逼近的有效方法。李锋等指出[15],在地面试验不完全相似模拟的情况下,有必要通过飞行试验手段进行气动模型的验证与确认。本文基于机器学习方法建立的气动模型具有高精度拟合、能充分反映飞行器飞行空域内完全模拟真实飞行的特点,对于高速飞行器的飞行试验气动数据挖掘和地面气动数据库的修正具有应用价值。
1 机器学习气动建模方法 1.1 气动力建模一般形式气动力模型是表征飞行器的气动力/力矩与飞行状态、控制输入等参数之间关系的函数。通常可表做一般形式:
| $ C_{i}=f\left(H, M a, \alpha, \beta, \omega_{x}, \omega_{y}, \omega_{z}, \delta_{e}, \delta_{r}, \delta_{a}, \cdots\right) $ | (1) |
式中,H、Ma、α、β分别为高度、马赫数、攻角、侧滑角;ωx、ωy、ωz分别为滚转、偏航和俯仰角速度;δe、δr、δa分别为升降舵、方向舵和副翼舵偏角,共10个参数。特别地,本文以Ci(i=A、N、Z、mx、my、mz)表示三轴气动力/力矩系数,反映了飞行器飞行力学特性。
1.2 气动力建模机器学习算法针对人工BP神经网络,给出气动力建模的机器学习算法。人工BP神经网络的机器学习算法是误差反向传递的,其核心思想是把一组输入问题的解转化为一个非线性优化问题,以优化算法对迭代权值进行计算,加入隐层神经元个数,从而得到更加精确的解。
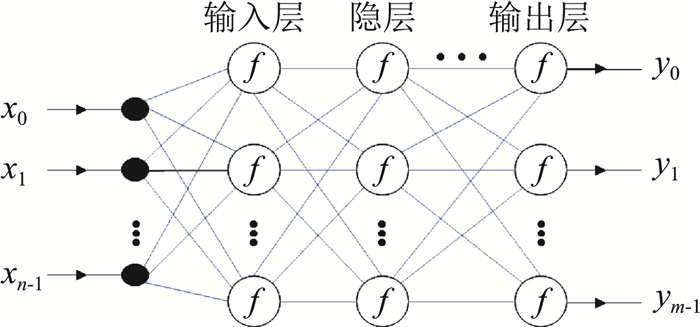
网络结构或拓扑分三层:输入层、隐含层和输出层(图 1)。一般的,对于高速飞行器气动力模型,神经网络的输入层为高度、马赫数、攻角、侧滑角、角速度、舵偏角;输出层为三轴气动力系数和力矩系数。在进行神经网络训练时,信号是从输入层传递到隐层,然后到输出层,每一层的输出作为下一层的输入;误差从输出层反向传播,经隐层传播至输入层。
|
图 1 BP神经网络的结构 Fig.1 BP neural networks structure |
以求解非线性最小二乘问题的Levenberg-Marquardt(LM)算法作为权值的迭代更新算法[16],它既有Gauss-Newton法的局部收敛性,又有梯度下降法的全局特性[17]。它的训练函数在训练次数和准确度方面,明显优于共轭梯度法。以机器学习中常用的S形函数作为神经网络各隐含层的激活函数,比如逻辑函数:
| $ f\left(x_{i}\right)=\frac{1}{1+\mathrm{e}^{-x_{i}}} $ | (2) |
该函数单调且一阶可微,输出映射限于(0, 1)之间,是优化稳定的。不足之处是容易出现梯度消失,导致训练困难,输出也不以0为中心。
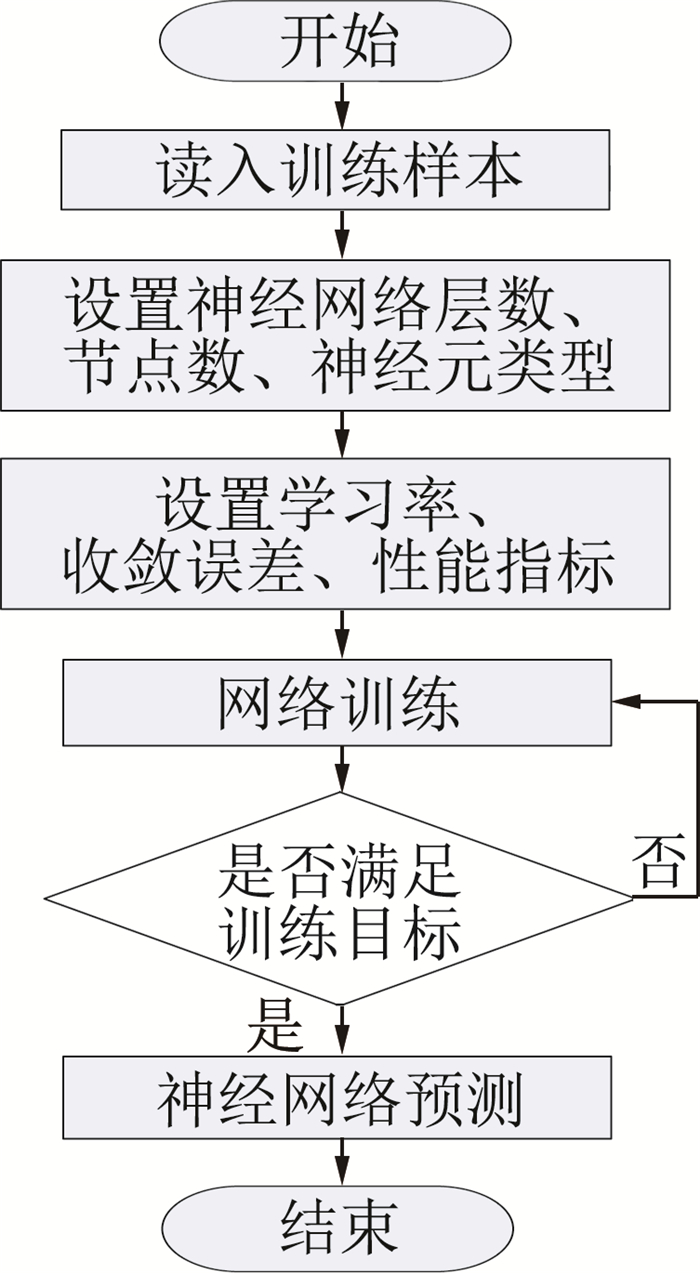
基于BP神经网络的气动力建模算法流程如图 2所示,模型训练完成且满足精度要求以后,即可用于飞行器的总体设计、飞行控制等。模型检验的主要依据是样本的拟合误差,为了避免分母中力矩系数为0时出现奇异值,取作模型输出与样本数据偏差的平方和与样本数据的平方和之比作为评判指标,定义为平均相对误差:
|
图 2 气动力建模计算流程 Fig.2 Aerodynamic modeling algorithm flow chart |
| $ E=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(C_{{\text { net}}i}-C_{f i}\right)^{2}}{\sum\limits_{i=1}^{n} C_{f i}^{2}}} $ | (3) |
式中,Cneti是神经网络预测的气动系数,Cfi是训练的原始气动系数。
在机器学习领域,人工BP神经网络包含2个重要的超参数——神经网络层数和隐含层神经元个数。它们被用于控制神经网络的结构和拓扑,在配置神经网络时,必须确定合适值。隐层及神经元过少,拟合误差大;神经元过多,模型计算效率低[18]。为了清晰表述,根据机器学习领域的一般惯例,考虑到气动建模10个输入的情况,下面针对神经网络结构层数和各层神经元个数进行讨论。
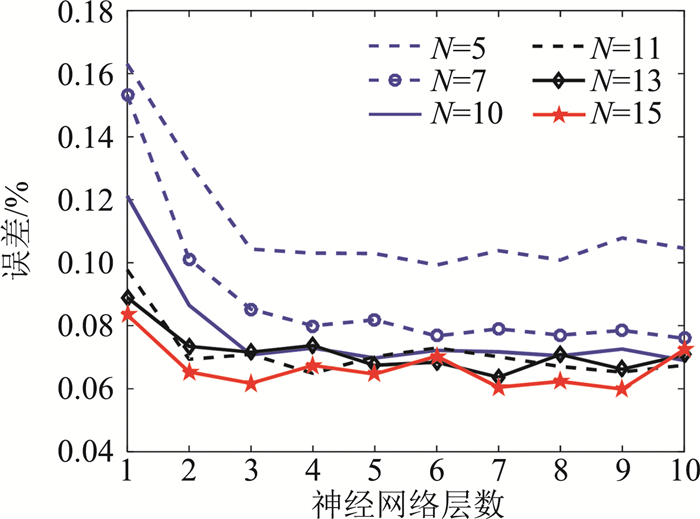
1.3 神经网络层数为了选择合适的网络层数,首先分析网络层数对拟合误差的影响。对单次飞行仿真的气动样本进行训练,样本点数为7801,气动数据为随高度、马赫数、攻角、侧滑角、舵偏、角速度变化的气动力和力矩系数。针对10个输入参数1个输出参数的情况,即单气动参数建模的情况,每层神经元的个数都分别取值为5、7、10、11、13、15,通过设置不同的隐层数,计算不同网络层数的拟合误差(见图 3)。从图 3可以看出,当每层神经元的个数取值为5和7时,拟合误差较大;随着每层神经元个数的增多,拟合精度提高;当神经元数增加到10以上时,随神经元数提高,拟合精度增加不再明显,且拟合误差随网络层数大致呈下降趋势,当网络层数大于3以后,下降趋势变缓。可以认为,当隐层网络层数大于3以后,通过增加网络层数来提高计算精度的效果已并不明显。因此,本文选择采用包含3个隐层的BP神经网络建模。
|
图 3 不同神经网络隐层数下的拟合误差 Fig.3 Fitting pecision with different layer numbers of neural networks |
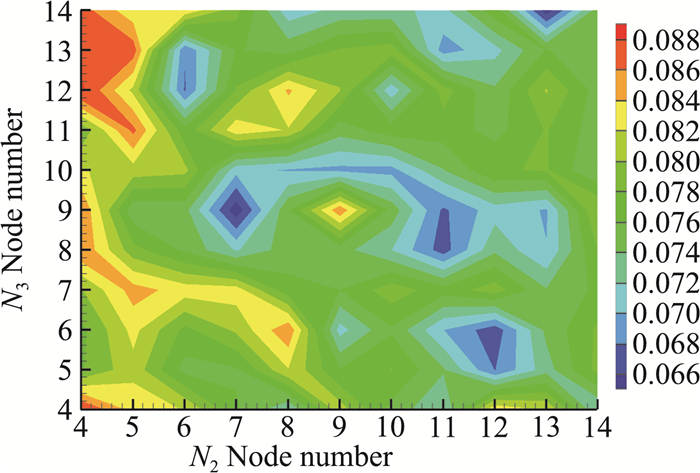
考察不同隐层神经元数对拟合误差的影响。神经网络隐层数取为3,其中,第一层神经元数为设定10,第2隐含层和第3层隐层的神经元个数在4~14范围内任意取值。图 4给出了拟合误差等值云图,横坐标为第2隐层神经元数,纵坐标为第3隐层神经元数。可以看出,第2隐含层和第3隐层存在多个神经元个数组合达到拟合误差极小值。若计入第1隐含层,达到拟合误差最小值的神经元数组合是(10, 7, 9),即第1~3隐含层的神经元个数分别为10、7、9。
|
图 4 神经网络隐层神经元数对拟合误差的影响 Fig.4 Fitting pecision with different hidden layer node numbers of neural networks |
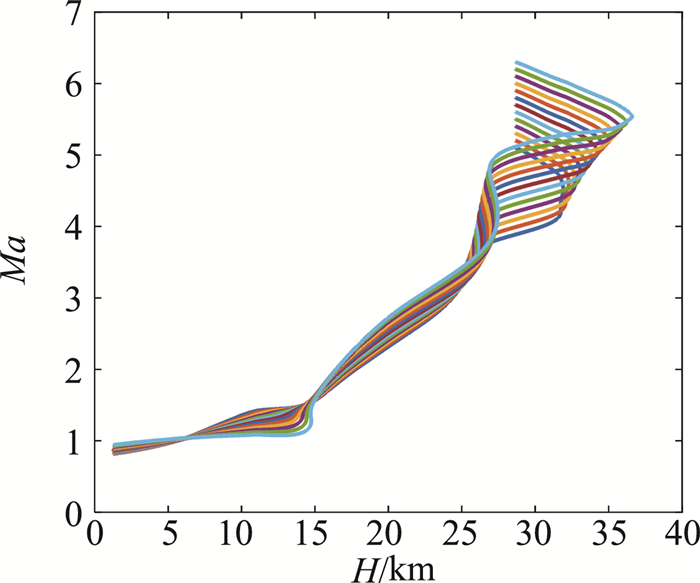
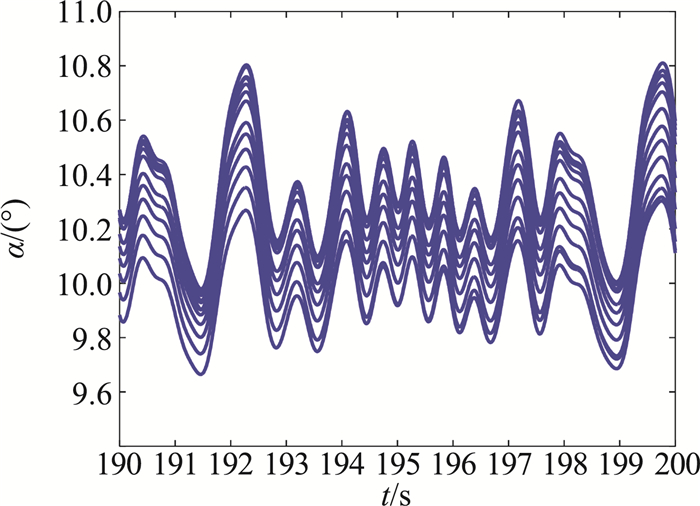
以某试验飞行器为例,仿真计算得到13条弹道数据,通过气动力参数辨识生成气动力建模的样本数据(如图 5所示)。弹道的高度范围0~38 km,马赫数为0.8~6.3,攻角范围-2°~12°,侧滑角范围-2°~2°,三通道具有全程激励的舵偏角,以保证全程具有可进行气动参数辨识的气动力矩。为了更好地进行气动力矩参数的辨识,采用文献[18]的方法设计了三通道最优的正弦组合波激励信号,该信号的优点是能够覆盖较宽的频率范围,对基准弹道的扰动较小,且能够三通道同时持续激励。图 6是飞行攻角的激励效果曲线,各条弹道的攻角幅值都在1°左右,效果良好。为了模拟真实的飞行试验情况,在飞行仿真数据中加入了误差和噪声。
|
图 5 训练样本高度-速度图 Fig.5 Height versus velocity in training samples |
|
图 6 攻角激励效果曲线 Fig.6 Angle of attack incentive effect |
利用含有误差和噪声的飞行仿真数据,采用文献[20]的气动力参数估计方法,得到飞行器的气动力系数、力矩系数、攻角、侧滑角等气动参数。在气动参数估计前,需要对含有误差和噪声的飞行仿真数据进行预处理,并利用弹道、姿态、角速度、加速度等数据进行误差估计和数据重建,以尽可能地消除各种随机误差和噪声。经预处理和数据重建后,各参数之间具有很好的相容性,可以根据飞行动力学方程和几何关系,直接辨识气动参数。
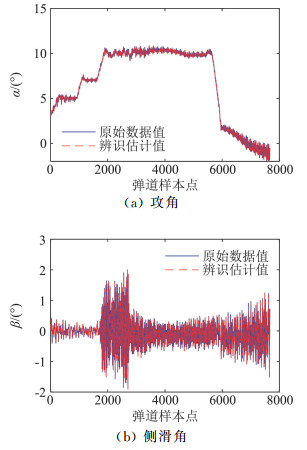
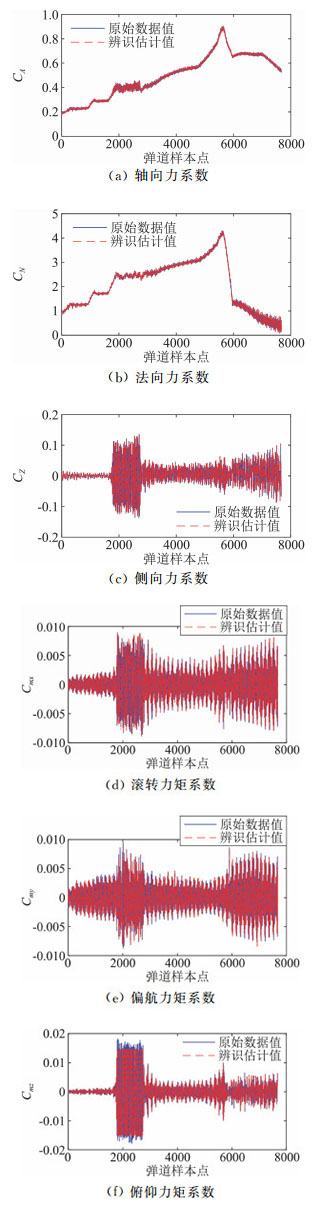
图 7和图 8分别给出了某一条弹道攻角、侧滑角、气动力和力矩系数的估计结果,作为随后的气动建模的输入样本数据。
|
图 7 攻角和侧滑角的估计结果 Fig.7 Identification results of attack angle and sideslip angle |
|
图 8 气动力和力矩系数估计结果 Fig.8 Compare of origin aerodynamic and identification |
基于某飞行器飞行仿真数据,建立人工BP神经网络气动力模型。神经网络输入层和输出层设置如前文所述,设定为5层结构,第1层为输入层,第2~ 4层为隐层,第5层为输出层,神经元个数组合为(10, 10, 7, 9, 1)。输入层的参数有10个,依次为高度、马赫数、攻角、侧滑角、滚转角速度、偏航角速度、俯仰角速度、升降舵偏角、副翼舵偏角和方向舵偏角。输出层为单输出,每个模型单独设置。算例中,建立6个气动参数模型,分别为轴向力系数CA、法向力系数CN、侧向力系数CZ、滚转力矩系数Cmx、偏航力矩系数Cmy、俯仰力矩系数Cmz。考虑到训练的效率,学习率参数设置为0.2,训练的收敛目标值为1×10-8,最大训练次数4000次。
2.4 建模结果及精度确认将13条弹道的气动数据作为建模样本输入,样本点数为97 693,建立了一个气动模型。为了检验方法的有效性,又另外仿真了4条不参与建模的弹道。其中2条弹道在参与训练的样本数据覆盖的高度、速度、姿态、控制范围之内,初始弹道初始马赫数分别为5.45和6.0,用于检验模型的预测能力。另2条在训练样本状态范围之外,初始马赫数分别为4.9和6.5,用于检测模型的外推能力。
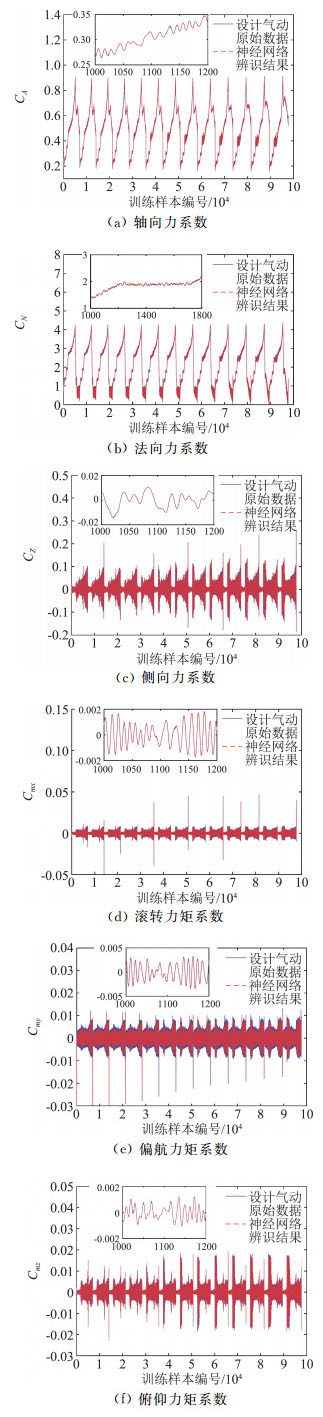
2.4.1 样本拟合情况基于神经网络的气动预测结果与13条弹道的原始气动数据进行了对比,训练初始弹道的马赫数范围为5.1~6.3。同训练数据的对比结果见图 9,预测精度情况见表 1。从结果可以看出,曲线一致性较好,最大误差仅为0.23%,建立的模型能够很好地拟合高度非线性的气动力数据。
|
图 9 13条弹道气动的预测结果 Fig.9 Aerodynamic prediction results of 13 trajectory data |
| 表 1 全部样本的拟合精度(单位:%) Table 1 Fitting accuracy of total sample (unit: %) |
|
|
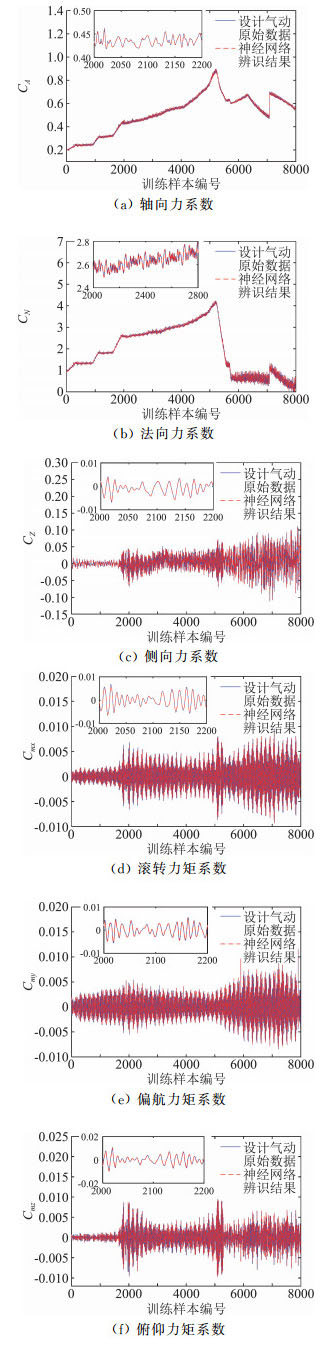
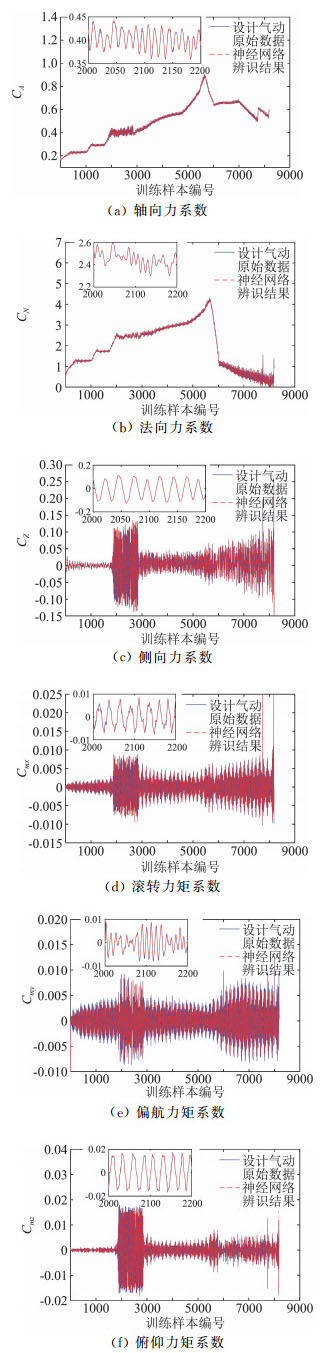
对未参与建模的两条弹道进行了气动预测,计算的初始马赫数分别为5.45和6.0,考察气动模型对训练样本状态范围内的预测能力。预测结果和原始气动数据的对比见图 10和图 11,预测精度结果见表 2。从结果可以看出,最大误差为0.27%,说明在训练样本状态范围内,具有很好的预测能力。
|
图 10 气动模型对单条弹道的预测结果之一 Fig.10 Aerodynamic predictionof inner trajectory |
|
图 11 气动模型对单条弹道的预测结果之二 Fig.11 Another aerodynamic prediction results of inner trajectory |
| 表 2 对样本范围内弹道的预测精度(单位:%) Table 2 Fitting accuracy of inner trajectory (unit: %) |
|
|
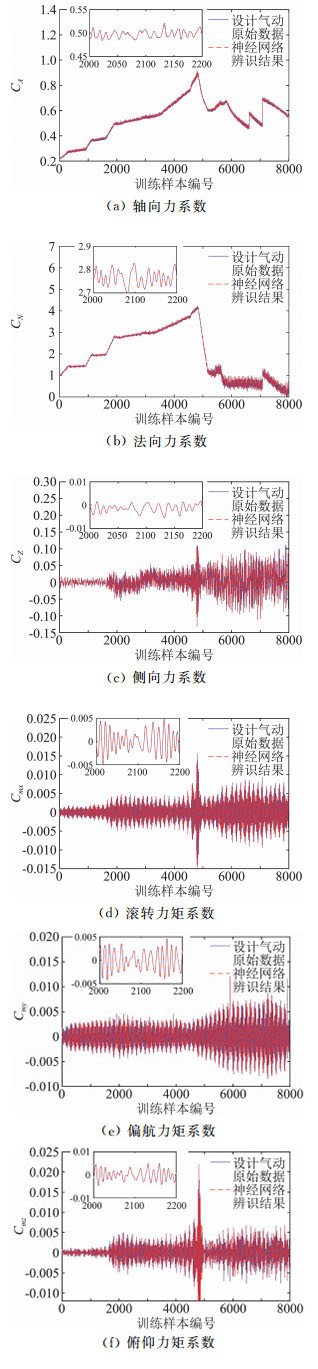
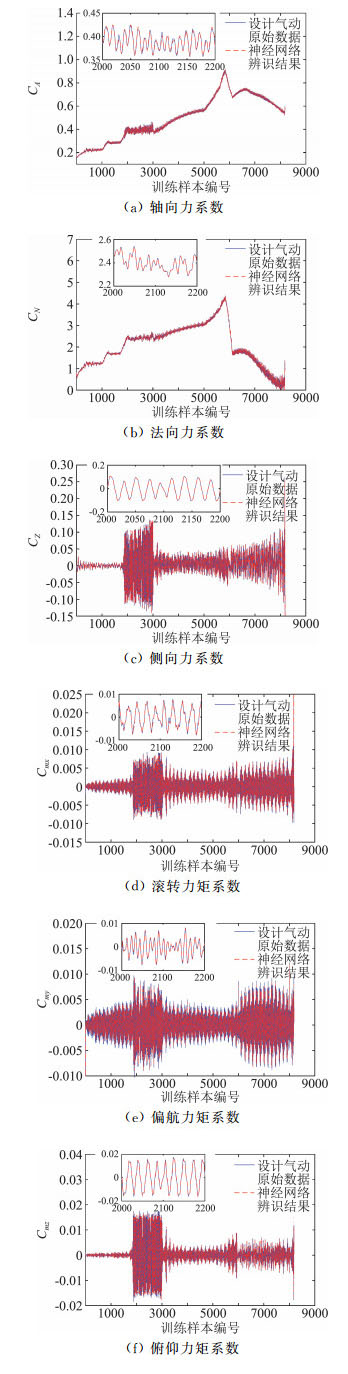
预测的两条弹道初始马赫数在训练样本状态范围之外,分别为4.9和6.5,略超出训练值的范围。目的是考查计算结果对相邻状态的外推能力。预测结果和原始气动数据的对比见图 12和图 13,预测精度见表 3。从结果可以看出,最大误差为0.54%,预测精度较好,但是低于样本状态范围内的预测精度值。
|
图 12 气动模型对样本外弹道的预测结果一 Fig.12 An aerodynamic prediction of outer trajectory |
|
图 13 气动模型对样本外弹道的预测结果二 Fig.13 Anothre aerodynamic prediction of outer trajectory |
| 表 3 对样本范围外的单弹道的预测精(单位: %) Table 3 Fitting accuracy of outer trajectory (unit:%) |
|
|
利用某飞行器飞行仿真弹道数据的气动辨识结果作为训练样本,通过对13条弹道气动数据的气动建模,得到了六分量的大空域、宽速域的非线性气动力模型,并对模型的预测精度和外推能力进行了分析。通过建模计算和分析,得到如下结论:
1) BP神经网络层数和隐层神经元个数两个参数值影响气动模型精度。根据高度、速度、攻角、侧滑角、角速率和舵偏角等10个输入情况下的气动建模算例,得到了1%以内的建模精度的局部最优的结构参数,即(10, 10, 7, 9, 1)。
2) 该机器学习方法建立的气动模型,对13条弹道的10种输入条件下、强非线性气动力数据样本具有很好的拟合效果,建模误差小于1%,并且对样本外的小范围状态具有一定的外推性,但最大外推边界还有待进一步研究。
3) 基于BP神经网络的气动建模方法,满足飞行器大空域、宽速域、姿态和舵偏等多元强耦合、非线性特性的逼近拟合需求,为进行气动试验的验证与确认、气动数据挖据等开辟了新的技术途径。
4) 该方法可快速融合大量的飞行试验数据、风洞试验数据和理论计算数据,可以用于飞行器地面设计气动数据库修正、飞行仿真以及飞行器总体性能分析。
| [1] |
蔡金狮. 飞行器系统辨识[M]. 宇航出版社, 1995. CAI J S. System identification for flight vehicles[M]. China Astronautic Publishing House, 1995. (in Chinese) |
| [2] |
吴辰, 姚宏, 彭兴钊, 等. 支持向量回归机在飞机气动力建模中的应用[J]. 计算机仿真, 2013, 30(10): 128-132. WU C, YAO H, PENG X Z, et al. Application of support vector regression for aerodynamic modeling[J]. Computer Simulation, 2013, 30(10): 128-132. DOI:10.3969/j.issn.1006-9348.2013.10.030 (in Chinese) |
| [3] |
刘玲君, 周越, 高振勋. 基于神经网络的翼型气动力计算和反设计方法[J]. 气体物理, 2018, 3(5): 41-47. LIU L J, ZHOU Y, GAO Z X. Aerodynamic force calculation and inverse design for airfoil based on neural network[J]. Physics of Gas, 2018, 3(5): 41-47. (in Chinese) |
| [4] |
ALI P, PIETER A. Deep learning helicopter dynamic models[C]//IEEE International Conference on Robotics and Automation. Washington, USA: 2015: 3223-3230. https://people.eecs.berkeley.edu/~pabbeel/papers/2015-ICRA-deep-learning-heli.pdf
|
| [5] |
汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建摸研究进展[J]. 航空学报, 2016, 37(8): 2331-2347. WANG Q, QIAN W Q, DING D. A review of unsteady aerodynamic modeling of aircraft at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347. (in Chinese) |
| [6] |
张瑞民, 张石玉, 赵俊波. 基于神经网络的非定常气动力建模研究[J]. 计算机仿真, 2017, 34(2): 106-110. ZHANG R M, ZHANG S Y, ZHAO J B. The research of neural network in modeling of unsready aerodynamics[J]. Computer Simulation, 2017, 34(2): 106-110. DOI:10.3969/j.issn.1006-9348.2017.02.024 (in Chinese) |
| [7] |
龚正, 沈宏良. 非定常气动力的结构自适应神经网络建模方法[J]. 飞行力学, 2007, 25(4): 13-16. GONG Z, SHEN H L. Structure self-adapting ANN method in modeling of unsteady aerodynamics[J]. Flight Dynamics, 2007, 25(4): 13-16. DOI:10.3969/j.issn.1002-0853.2007.04.004 (in Chinese) |
| [8] |
史志伟, 王峥华, 李俊成. 径向基神经网络在非线性非定常气动力建模中的应用研究[J]. 空气动力学学报, 2012, 30(1): 108-119. SHI Z W, WANG Z H, LI J C. The research of RBFNN in modeling of nonlinear unsteady aerodynamics[J]. Acta Aerodynamica Sinica, 2012, 30(1): 108-119. DOI:10.3969/j.issn.0258-1825.2012.01.019 (in Chinese) |
| [9] |
付军泉, 史志伟, 陈坤, 等. 基于EKF的实时循环神经网络在非定常气动力建模中的应用[J]. 空气动力学学报, 2018, 36(4): 658-663. FU J Q, SHI Z W, CHEN K, et al. Applications of real-time recurrent neural network based on extended Kalman filter in unsteady aerodynamics modeling[J]. Acta Aerodynamica Sinica, 2018, 36(4): 658-663. DOI:10.7638/kqdlxxb-2016.0131 (in Chinese) |
| [10] |
王博斌, 张伟伟, 叶正寅. 基于神经网络模型的动态非线性气动力辨识方法[J]. 航空学报, 2010, 31(7): 1379-1388. WANG B B, ZHANG W W, YE Z Y. Unsteady nonlinear aerodynamics indentification based on neural network model[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(7): 1379-1388. (in Chinese) |
| [11] |
王文正, 郑鹍鹏, 陈功, 等. 数据挖掘技术在飞行试验数据分析和气动参数辨识中的应用研究[J]. 空气动力学学报, 2016, 34(6): 778-782. WANG W Z, ZHENG K P, CHEN G, et al. Application research of data-mining method to flight test data analysis and aerodynamic parameter identification[J]. Acta Aerodynamica Sinica, 2016, 34(6): 778-782. DOI:10.7638/kqdlxxb-2015.0032 (in Chinese) |
| [12] |
朱莉, 高正红. 基于神经网络的翼型优化设计方法研究[J]. 航空计算技术, 2007, 37(3): 33-36. ZHU L, GAO Z H. Aerodynamic optimization design of aerfoi based on neural networks[J]. Aeronautica Computing Technique, 2007, 37(3): 33-36. DOI:10.3969/j.issn.1671-654X.2007.03.010 (in Chinese) |
| [13] |
陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294-299. CHEN H, QIAN W Q, HE L. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294-299. DOI:10.7638/kqdlxxb-2017.0098 (in Chinese) |
| [14] |
陈广强, 王贵东, 陈冰雁, 等. 高超声速飞行器FADS算法研究[J]. 飞机设计, 2015, 35(6): 1-7. CHEN G Q, WANG G D, CHEN B Y, et al. Study of flush air data system algorithms for hypersonic vehicle[J]. Aircraft Design, 2015, 35(6): 1-7. (in Chinese) |
| [15] |
李锋, 杨武兵, 王强, 等. 高超声速气动试验模拟现状与面临的新挑战[J]. 气体物理, 2016, 1(2): 1-9. LI F, YANG W B, WANG Q, et al. Status of ground test for hypersonic aerodynamics and its new challenge[J]. Physics of Gases, 2016, 1(2): 1-9. (in Chinese) |
| [16] |
LEVENBERG K. A method for the solution of certain nonlinear problems in least squares[J]. Quarterly of Applied Mathematics, 1944(2): 164-168. |
| [17] |
MARQUARDT D. An algorithm for least-squares estimation of nonlinear parameters[J]. SIAM Journal on Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [18] |
刘金琨. 智能控制[M]. 北京: 电子工业出版社, 2009. LIU J K. Intelligent control[M]. BeiJing: Publishing House of Electronics Industry, 2009. (in Chinese) |
| [19] |
王贵东.航天飞行器气动参数辨识研究[D].中国航天空气动力技术研究院, 2010. WANG G D. Study on aerodynamic parameter identification for aerospace vehicle[D]. China Academy of Aerospace Aerodynamics, 2010. (in Chinese) |
| [20] |
王贵东, 崔尔杰, 陈则霖. 喷流控制飞行器气动参数辨识方法[J]. 空气动力学学报, 2011, 29(4): 433-438. WANG G D, CUI E J, CHEN Z X. Study on aerodynamic parameter identification method for aircraft with jet thruster control[J]. Acta Aerodynamica Sinica, 2011, 29(4): 433-438. DOI:10.3969/j.issn.0258-1825.2011.04.006 (in Chinese) |
| [21] |
KIRKPATRICK K, Jr MAY J, VALASEKZ J. Aircraft system identification using artificial neural networks[R]. AIAA 2013-0878. https://arc.aiaa.org/doi/abs/10.2514/6.2013-878
|
 2019, Vol. 37
2019, Vol. 37


