2. 空气动力学国家重点实验室, 绵阳 621000;
3. 软件新技术与产业化协同创新中心, 南京 210023;
4. 中国航空工业空气动力研究院, 沈阳 110034;
5. 南京航空航天大学 航空学院, 南京 210016
2. State Key Laboratory of Aerodynamics, Mianyang 621000, China;
3. Collaborative Innovation Center of Novel Software Technology and Industrialization, Nanjing 210023, China;
4. AVIC Aerodynamics Research Institute, Shenyang 110034, China;
5. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
风洞是能人工产生和控制气流,以模拟飞行器或物体周围气体流动,并可量度气流对物体的作用以及观察物理现象的一种管道实验设备,它是进行空气动力实验最常用、最有效的工具之一[1]。在进行风洞实验时,保持风洞实验段马赫数的稳定,以测量飞行器在不同迎角下的气动性能,对于研制高性能飞行器具有重要意义。为了获得准确的实验数据,阶梯变迎角实验模式被广泛应用在风洞实验中。阶梯变迎角模式基于迎角的变化范围间歇地改变迎角以保持马赫数的稳定,但这种方式只能获得少量特定迎角处的实验数据,实验效率不高,而且在每一个迎角处都要等待马赫数稳定后再测量相应的气动性能,这样就不可避免地延长了实验时间,造成较高的能源消耗,对于风洞这种高耗能设备来说是不经济的。连续变迎角实验模式具有更高的实验效率和较低的运行成本,并且可以获得更密集的实验数据,这些优点促使风洞实验方式开始从阶梯变迎角向连续变迎角方式转变。但与此同时, 连续变迎角实验模式的快速时变特性也给风洞马赫数的控制带来了新的挑战,需要研究新的控制算法与策略。
传统的PID(Proportion Integral Differential)控制算法及其改进形式在阶梯变迎角实验过程中可以很好地满足风洞马赫数的控制要求。文献[2]利用神经网络对PID控制参数进行在线实时整定,通过仿真实验证明了该方法可以使马赫数控制更加稳定、迅速。文献[3]针对跨超声速风洞马赫数范围较宽的特点,采用了分段控制的思想,在不同的马赫数范围内,将模糊控制跟PID控制结合,利用模糊控制的快速性与PID控制的稳定性实现了整个马赫数范围内的快速稳定控制。由于风洞的主体是一个环形管道,控制量(如压缩机转速)与被控量(实验段马赫数)在实际物理位置上存在一定的距离,导致控制量的变化不能直接作用于被控量,所以在进行连续变迎角实验时存在一定的延迟,当迎角变化的速度超过0.1°/s时,仅仅使用PID控制或其改进算法无法满足马赫数控制精度达到±0.001的要求。
针对PID控制算法存在的缺陷,近年来出现了很多基于预测的控制方法,这些方法统称为模型预测控制(Model Predictive Control,MPC)算法[4]。许多研究者已经通过仿真实验证明,使用模型预测控制可以很好地对连续变迎角实验模式下的马赫数进行控制。文献[5]使用统一模型预测控制对阿姆斯特丹航空航天实验室拥有的高速风洞进行马赫数控制,实验结果表明该控制方法与传统PID控制算法相比,抗迎角扰动能力提高4倍并且马赫数的控制性能提高30%~60%。文献[6]出于马赫数高精度控制的考虑,选取稳定段总压和实验段静压作为被控量,设计了基于迎角补偿的模型预测控制器,使马赫数的控制精度达到了大飞机研制要求。但是模型预测控制方法需要在线求解约束优化问题,计算量大,只适用于具有高性能计算机的环境[7]。
中国航空工业空气动力研究院的0.6 m×0.6 m连续式跨声速风洞将压缩机转速作为控制马赫数稳定的唯一驱动方式。为了解决PID控制方法在连续变迎角实验模式下存在的缺陷,同时尽可能节约能源,其目前主要采用前馈控制与PID反馈控制结合的策略。前馈部分的设计需要先通过固定转速,连续变化迎角,得到迎角与实际马赫数的关系曲线;然后再通过固定迎角,增加转速,得到转速与实际马赫数的关系曲线;最后通过这两条曲线得到前馈系数,即转速变化量与迎角变化量的比值,这样就可以根据迎角变化量提前对转速进行补偿。但是这种方式存在两个明显缺点:1)为了得到前馈系数需要进行两次实验,增加了实验次数;2)不同迎角下,转速与实际马赫数的关系曲线是存在一定差别的,导致前馈系数计算不准确。
针对这两个缺点,本文采用高斯过程回归(Gaussian Process Regression,GPR)直接对不同马赫数下的实验数据进行建模,在其他条件一定的情况下,将迎角、实际马赫数、实验段截面积作为模型输入,压缩机转速作为模型输出,直接预测给定马赫数前提下不同迎角对应的压缩机转速。根据预测得到的转速值,提前对压缩机转速进行调节,可以减轻PID控制的调节压力,从而提高连续变迎角实验方式下的马赫数控制精度。这种直接从实验数据中学习规律的方法减少了实验次数,并且避免了近似计算造成的误差。另外,GPR输出的预测值置信度可以指导新增实验数据的获取,以进一步保证马赫数控制精度。
1 高斯过程回归(GPR)GPR是基于贝叶斯理论和统计学习理论发展起来的一种全新的机器学习方法,适于处理小样本、非线性等复杂问题[8]。GPR不需要显式的指定目标函数的具体形式,只需假设其服从某个指定均值函数和协方差函数的高斯过程,目标函数的后验分布是通过拟合训练数据自动学习得到的,所以它属于非参数模型[9-10]。相较于其他常用的参数模型,比如神经网络、支持向量回归、多项式回归等,GPR具有容易训练、超参数自适应获取以及预测结果具有概率意义等优点,并且已经在许多领域得到了成功应用[11-13]。
1.1 预测高斯过程是一个随机变量的集合,并且其中任意有限数量随机变量的联合分布为多元高斯分布。从函数空间的角度出发,高斯过程可以看作定义在函数f(x)上的一个分布,它的性质完全由均值函数和协方差函数确定:
| $ m(\boldsymbol{x})=\boldsymbol{E}[f(\boldsymbol{x})] $ | (1) |
| $ k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\boldsymbol{E}\left[(f(\boldsymbol{x})-m(\boldsymbol{x}))\left(f\left(\boldsymbol{x}^{\prime}\right)-m\left(\boldsymbol{x}^{\prime}\right)\right)\right] $ | (2) |
| $ f(\boldsymbol{x}) \sim G P\left(m(\boldsymbol{x}), k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)\right) $ | (3) |
式中,x,x′∈Rd, 为d维输入向量,m(x)为均值函数,k(x, x′)为协方差函数。
假设训练集为{(xi, yi)|i=1, …, n },针对回归问题,考虑如下模型:
| $ \boldsymbol{y}_{i}=f\left(\boldsymbol{x}_{i}\right)+\varepsilon $ | (4) |
式中,ε~N(0, σnoise2)为高斯噪声,xi为第i个输入向量,yi为相应加入噪声的观测值。为了计算方便,通常将yi进行中心化处理,然后将均值设为0,此时所有观测值组成的列向量y= [y1, y2, …, yn]T的先验概率分布为:
| $ \boldsymbol{y} \sim N\left({\bf{0}}, \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})+\sigma_{\mathrm{noise}}^{2} {\boldsymbol{I}}_{n}\right) $ | (5) |
式中,X为特征矩阵,其中每一行表示一个输入向量;K(X, X) =Kn=(kij)为n×n阶对称正定协方差矩阵,矩阵元素kij=k(xi, xj),使用xi与xj之间的距离来度量yi和yj之间的相关性;In为n阶单位矩阵。
对于给定的测试样本x*,其对应的预测值f*与观测值y的联合先验分布为:
| $ \left[\begin{array}{l}{ \mathit{\boldsymbol{y}}} \\ {f_*}\end{array}\right] \sim N\left({\bf{0}}, \left[\begin{array}{cc}{\boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})+\sigma_{\mathrm{noise}}^{2} \boldsymbol{I}_{n}} & {\boldsymbol{K}\left(\boldsymbol{X}, \boldsymbol{x}_{*}\right)} \\ {\boldsymbol{K}\left(\boldsymbol{x}_{*}, \boldsymbol{X}\right)} & {\boldsymbol{K}\left(\boldsymbol{x}_{*}, \boldsymbol{x}_{*}\right)}\end{array}\right]\right) $ | (6) |
其中,K(x*, X)=K(X, x*)T为测试样本与训练集之间的1×n阶的协方差矩阵;K(x*, x*)为测试样本之间的协方差矩阵。
根据式(6),并且通过一定的矩阵运算,可以得到预测值f*的条件概率分布为:
| $ f_{*} | \boldsymbol{X}, \boldsymbol{y}, \boldsymbol{x}_{*} \sim N\left(\overline{f}_{*}, \operatorname{cov}\left(f_{*}\right)\right) $ | (7) |
其中,
| $ \overline{f}_{*}=\boldsymbol{K}\left(\boldsymbol{x}_{*}, \boldsymbol{X}\right)\left[\boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})+\sigma_{\mathrm{noise}}^{2} \boldsymbol{I}_{n}\right]^{-1} \boldsymbol{y} $ | (8) |
| $ \begin{array}{l}{\operatorname{cov}\left(f_{*}\right)=\boldsymbol{K}(\boldsymbol{x}, \boldsymbol{x}, )-} \\ {\quad \boldsymbol{K}(\boldsymbol{x}, \boldsymbol{X}) \times\left[\boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})+\boldsymbol{I}_{n}\right]^{-1} \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{x}_* )}\end{array} $ | (9) |
最终,我们将式(8)作为测试样本的预测值,式(9)表示预测的方差,用来衡量该预测的不确定性。
1.2 训练GPR的训练其实是选择合适的协方差函数以及确定其最优超参数的过程[8]。不同的协方差函数确定了在该高斯过程先验下目标函数可能具有的性质。比如,周期协方差函数表示目标函数具有周期性;平方指数协方差函数表示目标函数具有无穷阶导数,即处处光滑;线性协方差函数表示目标函数是线性的[14]。在实际应用中,使用最广泛的为平方指数协方差函数,具体形式如下:
| $ k\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\sigma_{f}^{2} \exp \left(-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right)^{\mathrm{T}} \boldsymbol{S}^{-1}\left(\boldsymbol{x}-\boldsymbol{x}^{\prime}\right)\right) $ | (10) |
式中,σf2为信号方差,S=dig(l2),l为输入向量各个维度的带宽,这些参数称为平方指数协方差函数的超参数。每种不同的协方差函数都存在一些像σf2和l这样的超参数,超参数的取值决定了协方差函数的具体形状,同时也决定了从高斯过程中所采样函数的特征。假设一个协方差函数的超参数集合为θ={θi}i=1m,m为超参数的个数,一般通过极大似然法来确定θ的最优值。
首先根据多元高斯分布的边际属性可得观测值y的边缘概率分布:
| $ p(\boldsymbol{y} | \boldsymbol{X})=N\left({\bf{0}}, \boldsymbol{K}(\boldsymbol{X}, \boldsymbol{X})+\sigma_{\mathrm{noise}}^{2} \boldsymbol{I}_{n}\right) $ | (11) |
式(11)一般称作边际似然。通过式(11)可以得到训练集的负对数边际似然函数为:
| $ \begin{aligned} L(\theta) &=-\ln p(\boldsymbol{y} | \boldsymbol{X}) \\ &=\frac{1}{2} \boldsymbol{y}^{\mathrm{T}} \boldsymbol{C}^{-1} \boldsymbol{y}+\frac{1}{2} \ln |\boldsymbol{C}|+\frac{n}{2} \ln 2 \pi \end{aligned} $ | (12) |
其中C=Kn+σnoise2In,| C |为矩阵C的行列式。所以GPR模型的优化目标为:
| $ \theta^{*}=\arg \min _{\theta} L(\theta) $ | (13) |
计算L(θ)关于各个超参数θi的偏导数,然后采用共轭梯度下降法、牛顿法等优化方法对超参数进行迭代更新以最小化L(θ)。最后将优化后的超参数θ*代入式(8)和式(9)就可以得到测试样本x*最终的预测值f*和方差cov(f*)。
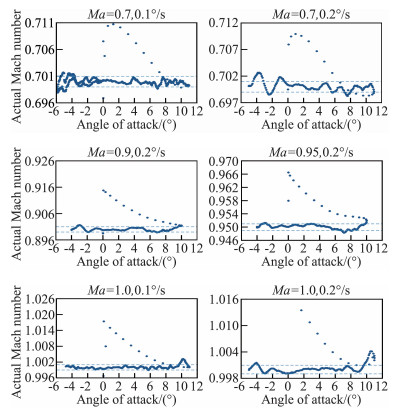
2 实验设计 2.1 数据预处理使用J7标模在连续变迎角实验模式下得到的数据进行建模,其中迎角变化范围为-5°~11°。在实际实验过程中,由于迎角回零操作或者其他一些复杂因素的影响可能会产生一些异常数据,这些异常数据会严重影响建模的准确性,所以在建模前需要将这些数据进行删除。删除前与删除后的数据分别如图 1、图 2所示,图中的虚线表示马赫数±0.001误差带。
|
图 1 包含异常点的数据 Fig.1 Data with outliers |

|
图 2 清洗后的数据 Fig.2 Cleaned data |
原始实验数据中,为了检验连续变迎角实验方式下角速度对马赫数控制精度的影响,在某些马赫数条件下可能测量了两组实验数据,其迎角变化速度分别为0.1°/s和0.2°/s,但是由于角速度不影响迎角、实时马赫数、实验段截面积和压缩机转速之间的关系,同时也为了保证不同马赫数下的数据量尽量均衡,所以对于这种情况只取角速度为0.1°/s的数据进行建模。在进行实际风洞实验时,不同范围的马赫数条件下,实验段截面积也可能会做相应的调整。本文使用的数据中,马赫数0.85以上(包括马赫数0.85)条件下的截面积是马赫数0.85以下的7/6倍,所以我们以马赫数0.85为界,其以下的截面积设为1 m2,以上的截面积设为7/6 m2(由于最终输入模型的数据是经过标准化的,所以这样设置是合理的)。经过处理后的数据集的特征分布直方图如图 3所示。

|
图 3 特征分布直方图 Fig.3 Feature distribution histogram |
由图 3可知,不同特征之间的量级是不一样的,而GPR主要采用基于梯度的优化算法进行训练。为了加快梯度下降的速度,并且使得算法可以更好地逼近最优解,提高预测精度[15],所以在将数据输入模型之前,还需要对每一个特征进行标准化处理,标准化公式如下所示:
| $ \tilde{x}_{j}^{i}=\frac{x_{j}^{i}-\mu_{j}}{\sigma_{j}} $ | (14) |
式中,xji表示第i个样本的第j个特征,μj为第j个特征的均值,σj是第j个特征的标准差,
GPR模型中的超参数可以通过最大化训练数据的边际似然函数获得,但是一般情况下边际似然函数都是关于超参数的非凸函数,在使用基于梯度的优化算法进行求解时,如果超参数的初值选取不当,算法很可能会收敛到局部最优解。为了解决该问题,采用最大边际似然法进行初始超参数的选择,具体的步骤如下:
① 从特定的超参数先验P(θ)中随机选择一个超参数θ0;
② 将θ0作为初始值,使用共轭梯度下降算法最小化负对数边际似然函数,经过m次迭代,得到优化后的超参数θm;
③ 重复①、② M次,从M个初始超参数中选择使负对数边际似然达到最小的作为最终的初始超参数。
文献[16]通过大量的实验得出结论:尽管超参数先验分布对协方差函数最终优化得到的超参数取值有较大影响,但是对GPR模型最终的预测精度影响甚微。所以在实际应用中选择比较简单、常见的概率分布作为超参数的先验分布即可,比如标准高斯分布、合适范围内的均匀分布等。
本文最终选择标准高斯分布作为超参数的先验分布,从中随机采样20次,得到20组不同的初始超参数。对于每组超参数使用共轭梯度下降算法进行500次迭代优化,从中选取使负对数边际似然最小的取值作为最终的初始超参数。
2.3 协方差函数的选择正如1.2节所述,协方差函数对GPR模型至关重要,因为它包含了我们对于目标函数特性的假设。当我们对目标函数的先验知识比较充足时,可以准确地选择合适的协方差函数来解释数据中的结构。但是通常情况下,我们并不清楚目标函数的一些显著特征。式(10)所示的平方指数协方差函数的超参数数量较少且具有可解释性,而且已有理论证明,“当训练数据足够多时,平方指数协方差函数有能力学得任意的连续函数”[17]。所以当我们对目标函数的先验知识不足时,为了不引入错误的先验知识并且保证预测的准确性,可以使用平方指数协方差函数来对数据进行解释。下文将使用平方指数协方差函数的GPR模型称为标准高斯过程回归(Standard Gaussian Process Regression,S-GPR)。
S-GPR假设目标函数具有如下形式:
| $ y=f\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \cdots, \boldsymbol{x}_{D}\right) $ | (15) |
式中x1, x2, …, xD表示输入向量的各个维度。最终的函数输出y同时取决于输入向量的所有维度,这使得S-GPR对于远离训练样本的数据预测效果很差。
为了解决该问题,本文使用加性高斯过程回归(Additive Gaussian Process Regression,Add-GPR)[18]来对风洞实验数据进行建模。Add-GPR使用加性协方差函数,其可以看作广义加性模型(Generalized Additive Model,GAM)[19]与S-GPR的推广。具体的,为输入向量的每一个维度分配一个基本的协方差函数,并且定义不同阶的加性协方差函数以全面考虑特征之间的交互作用。不同阶的协方差函数定义如下:
| $ \tilde{k}_{1}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\sigma_{1}^{2} \sum\limits_{i=1}^{D} k_{i}\left(x_{i}, x_{i}^{\prime}\right) $ | (16) |
| $ \tilde{k}_{2}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\sigma_{2}^{2} \sum\limits_{i=1}^{D} \sum\limits_{j=i+1}^{D} k_{i}\left(x_{i}, x_{i}^{\prime}\right) k_{j}\left(x_{j}, x_{j}^{\prime}\right) $ | (17) |
| $ \tilde{k}_{n}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\sigma_{n}^{2} \sum\limits_{1 \leqslant i_{1}<i_{2}<\cdots<i_{n} \leqslant D} \quad \prod\limits_{d=1}^{n} k_{i d}\left(x_{i d}, x_{i d}^{\prime}\right) $ | (18) |
其中,D为输入向量的维度,
| $ k_{\text { add }}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\sum\limits_{i=1}^{D} \tilde{k}_{i}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right) $ | (19) |
易知,当只考虑特征之间的一阶交互时,Add-GPR等价于GAM;如果只考虑特征之间的D阶交互,并且将基本协方差函数设为平方指数协方差函数,则Add-GPR就退化为S-GPR。
由于平方指数协方差函数的良好性质,所以本文将其作为迎角、实时马赫数、实验段截面积三个输入维度的基本协方差函数,并且使用式(19)所示的完整加性协方差函数(此时D=3)作为GPR最终的协方差函数对实验数据进行建模。
3 实验结果及分析经过数据清洗后,得到在马赫数0.6、0.7、0.75、0.8、0.85、0.9、0.95、1.0、1.05、1.1条件下,迎角连续变化时的10组控制数据,总样本个数为2578。其中输入向量在特征空间的分布情况如图 4所示。
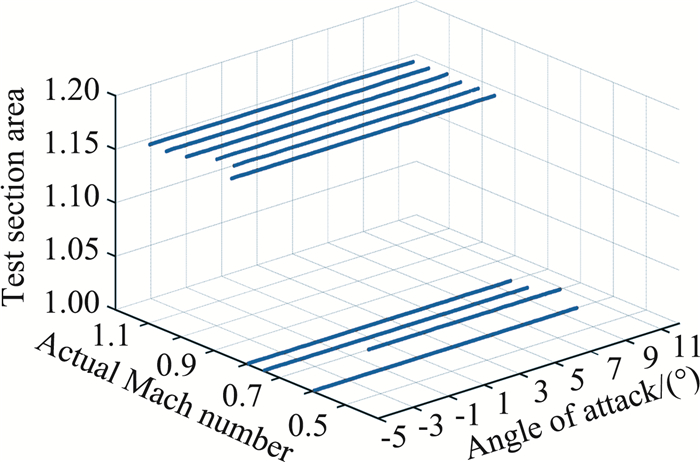
|
图 4 输入向量散点图 Fig.4 Scatter plot of input vector |
图 4中的每组数据的实际马赫数都在相应的马赫数条件附近波动。以马赫数0.75条件下的数据为例,实际马赫数的波动情况如图 5所示。
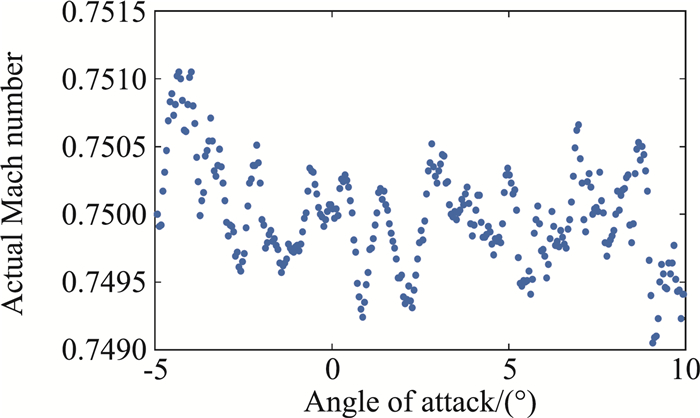
|
图 5 实际马赫数散点图 Fig.5 Scatter plot of actual Mach numbers |
实验将从两个角度说明Add-GPR对风洞实验数据进行建模的有效性, 并且提出了基于高斯过程回归的马赫数控制策略。
3.1 随机划分数据集使用机器学习算法执行预测任务有一个基本的假设,即训练数据与测试数据是独立同分布的。基于这个假设我们将2578个样本随机打乱,使用常用的机器学习模型分别进行5折交叉验证,最终得到预测结果的RMSE(Root Mean Square Error)如表 1所示。其中,RMSE的计算公式为:
| 表 1 预测结果对比 Table 1 Comparison of prediction results |
|
|
| $ \delta_{\mathrm{RMSE}}=\sqrt{\sum\limits_{i=1}^{m} \frac{\left(y_{i}-\hat{y}_{i}\right)^{2}}{m}} $ | (20) |
式中,m为测试集样本数量,yi为样本的真实输出,
由表 1可以看出,Add-GPR每一次交叉验证的预测精度都要高于其他常用的回归模型,同时GPR的预测效果也比其他模型的预测精度要好。这是因为神经网络、SVR和多项式回归属于参数化模型[9],参数化模型需要对目标函数的形式做有限参数的假设,函数形式确定了,则模型的复杂度也就相应确定了。但是选择合适的目标函数的形式是一项十分困难的任务,如果目标函数的形式不符合数据的真实分布,则预测效果会变得很差。相比之下,GPR属于非参数模型,其复杂度随着样本数量的增加而增加,不需要人为做相应的假设,所以GPR模型更加灵活,预测精度更高[10]。
连续式跨声速风洞在连续变迎角模式下,马赫数控制要达到±0.001的精度,则压缩机输出转速与目标转速之间的误差应该在±2 r/min之内。图 6为Add-GPR 5折交叉验证实验中,测试集实际转速与预测转速之间的绝对误差分布直方图。从图 6中可以看出,绝对误差基本都分布在2 r/min之内,可以满足连续变迎角方式下的马赫数控制要求。
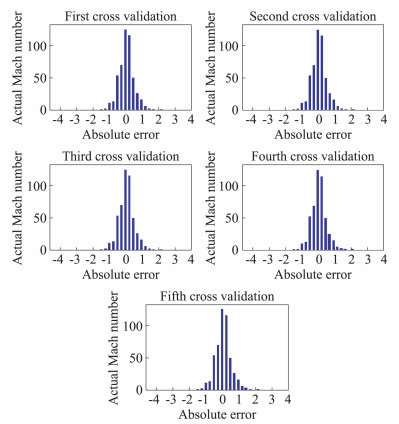
|
图 6 绝对误差直方图 Fig.6 Absolute error histogram |
一个好的预测模型应该对于远离训练集的样本依然有很好的预测能力。但是随机划分数据集时,虽然测试样本对于模型来说是未见的,但其相对于训练集的距离是比较近的。为了进一步说明Add-GPR对风洞数据的建模能力,我们采用分组划分数据集的方式产生训练集跟测试集。由于在3.1节实验中,S-GPR与Add-GPR的预测效果最好,所以本节只对这两种方法进行比较。
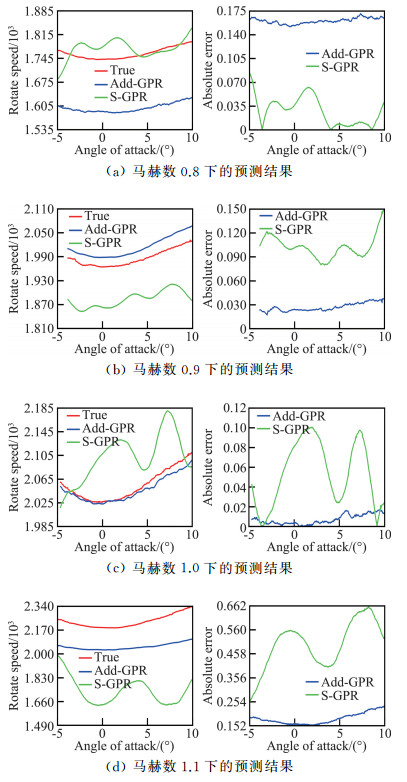
由图 4可知,共有10组在不同马赫数条件下测得的数据,我们以其中9组作为训练集,剩余1组作为测试集共进行了4次实验,每次实验分别将马赫数0.8、0.9、1.0、1.1条件下的数据作为测试集,最终得到的转速预测曲线如图 7所示。
|
图 7 转速预测曲线 Fig.7 Predictive curve of rotational speed |
图 7中,左图为不同马赫数下Add-GPR与S-GPR的预测转速曲线,右图为两者预测的绝对误差。可以看出,S-GPR的预测曲线跟真实的转速曲线相差很大,而Add-GPR的预测虽然跟真实曲线也存在一定的差距,但是各个攻角处预测的绝对误差趋于稳定,这说明Add-GPR预测曲线与真实曲线的变化趋势是基本一致的。实验结果显示,马赫数1.1条件下的预测相对来说比较差,这主要是因为马赫数大于1.1的条件下是没有实验数据的,所以建模时只能利用马赫数小于1.1一侧的数据信息,而其他马赫数条件的两侧都存在数据,可以利用的信息更多。
接下来将说明基于所提出的控制策略,只需预测转速曲线与真实转速曲线的变化趋势一致,就可以满足马赫数控制的要求。
3.3 控制策略在连续变迎角实验过程中,如果我们要控制某一马赫数稳定,只需将要固定的马赫数、连续变化的迎角以及实验段截面积输入训练好的模型,就可以提前得到不同迎角下,为了保持马赫数稳定,压缩机应该输出的转速。此时t时刻产生的总控制信号为:
| $ U(t)=U_{f f}(t)+U_{f b}(t) $ | (21) |
其中,
| $ U_{f f}(t)=S(\alpha(t+\tau))-S(\alpha(t+\tau-1)) $ | (22) |
| $ \begin{aligned} U_{f b}(t)=& K_{P} e(t)+K_{L} \sum\limits_{j=0}^{t} e(j)+\\ & K_{D}[e(t)-e(t-1)] \end{aligned} $ | (23) |
式(21)~式(23)中,Uff为前馈控制部分的输出信号,α(t+τ)为t+τ时刻的迎角,S(α(t+τ))为该迎角下保持马赫数稳定所需要的压缩机转速;Ufb为PID反馈控制的输出信号,τ为PID控制算法的延迟时间,其中前馈部分先于PID反馈τ时间进行控制。
由式(22)可知,只要预测曲线与真实曲线的变化趋势一致,那么前馈部分输出的信号就是相同的,即使预测转速与真实转速之间存在偏差,也不影响最终的控制效果。前馈部分预测的越准确,马赫数在PID反馈控制的延迟时间内产生的偏移就越小,此时通过PID反馈控制就可以达到马赫数的控制精度要求。
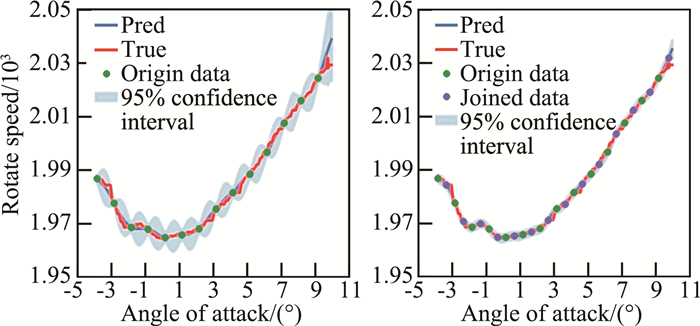
训练数据很多时,我们可以得到比较准确的压缩机转速预测曲线。但是很多情况下,我们在某一马赫数条件下只能得到有限的实验数据,此时预测结果可能无法达到连续变迎角模式下的马赫数控制精度要求。由于GPR模型是一种概率模型,它可以得到预测结果的方差,以评估预测结果的置信度,所以当控制精度不足时,可以根据预测方差来改善预测精度。在预测方差比较大的区域有针对性地增加实验数据来提高预测的精度,这种有目的的改善可以使用较少的数据达到很好的预测结果。我们以马赫数0.9条件下的数据为例来说明该方法的有效性。实验结果如图 8所示。
|
图 8 提高预测精度 Fig.8 Improving predictive accuracy |
图 8中,红色曲线表示真实的转速曲线,蓝色曲线表示预测结果,阴影部分为预测值95%的置信区间。左图为只有14个样本点的实验结果,右图是在左图预测结果不确定性最大的区域额外加入14个训练样本后的实验结果。可以发现右图转速曲线的预测结果有一定改善,并且预测结果的置信度得到了显著提高,因而PID反馈控制的精度得到了保证。
4 结论本文提出了一种基于GPR的前馈控制与PID反馈控制结合的控制策略,该策略可以提高连续变迎角实验模式下的马赫数控制精度, 并且具有简单、节能等优点。前馈部分将迎角、实际马赫数和风洞实验段截面积作为Add-GPR的输入来预测压缩机转速曲线,通过实验证明了Add-GPR对风洞实验数据建模的有效性。同时利用GPR输出的预测结果的置信度, 可以指导新增实验数据的获取,以进一步提高马赫数控制精度。由于风洞实验条件的限制,本文只考虑了3个因素对压缩机转速的影响,而且其中截面积只有两种不同的取值,这其实限制了模型泛化能力[20]。如果实验条件允许,可以采集多组不同工况下的实验数据,并且加入其他因素作为模型的输入,比如温度、压强等,这些措施都可以提高转速曲线的预测精度,进而使马赫数的控制更加稳定。
| [1] |
李周复. 风洞实验手册[M]. 北京: 航空工业出版社, 2015. LI Z F. Handbook of wind tunnel test[M]. Beijing: Aviation Industry Press, 2015. (in Chinese) |
| [2] |
王凯文.神经网络PID控制在FD12风洞亚跨流场校测中的应用[D].哈尔滨工程大学, 2011. WANG K W. Application of neural network PID control in measured sub-flow field calibration of FD12 wind tunnel[D]. Harbin Engineering University, 2011.(in Chinese) 神经网络PID控制在FD12风洞亚跨流场校测中的应用 |
| [3] |
LUO Y, XING S, SONG W, et al. Fuzzy and PID compound control of mach number for 0.6 meters supersonic wind tunnel[C]//Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC) 2011. IEEE, 2011: 3992-3995. https://www.infona.pl/resource/bwmeta1.element.ieee-art-000006009954
|
| [4] |
CAMACHO D E F, BORDONS D C. Model predictive control[J]. International Journal of Robust & Nonlinear Control, 2007, 18(8): 799-799. |
| [5] |
SOETERBOEK R A M, PELS A F, VERBRUGGEN H B, et al. A predictive controller for the Mach number in a transonic wind tunnel[J]. IEEE Control Systems, 2002, 11(1): 63-72. |
| [6] |
袁平, 易凡, 肖宇航, 等. 面向迎角变化的风洞流场模型预测控制器[J]. 控制与决策, 2018, 33(6): 1026-1032. YUAN P, YI F, XIAO Y H, et al. Wind tunnel flow field model predictive controller for angle of attack variation[J]. Journal of Control and Decision, 2018, 33(6): 1026-1032. (in Chinese) |
| [7] |
YUGENG X I, DEWEI L I, LIN S, et al. Model predictive control-Status and challenges[J]. Acta Automatica Sinica, 2013, 39(3): 222-236. DOI:10.1016/S1874-1029(13)60024-5 |
| [8] |
RASMUSSEN C E, WILLIAMS C K I. Gaussian process for machine learning[M]. MIT Press, 2006: 106-107.
|
| [9] |
MURPHY K P. Machine learning:A probabilistic perspective[M]. MIT Press, 2012.
|
| [10] |
GHAHRAMANI Z. Probabilistic machine learning and artificial intelligence[J]. Nature, 2015, 521(7553): 452. DOI:10.1038/nature14541 |
| [11] |
RICHARDSON R R, OSBORNE M A, HOWEY D A. Gaussian process regression for forecasting battery state of health[J]. Journal of Power Sources, 2017, 357: 209-219. DOI:10.1016/j.jpowsour.2017.05.004 |
| [12] |
PILON B H A, MURILLOFUENTES J J, COSTA J P C L D, et al. Predictive analytics in business intelligence systems via Gaussian processes for regression[C]//International Joint Conference on Knowledge Discovery, 2015. https://link.springer.com/chapter/10.1007/978-3-319-52758-1_23
|
| [13] |
DEISENROTH M P, FOX D, RASMUSSEN C E. Gaussian processes for data-efficient learning in robotics and control[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2015, 37(2): 408-423. |
| [14] |
DUVENAUD D. Automatic model construction with Gaussian processes[D]. University of Cambridge, 2014. https://www.repository.cam.ac.uk/handle/1810/247281
|
| [15] |
KUMARSINGH B, VERMA K, THOKE A S. Investigations on impact of feature normalization techniques on classifier's performance in breast tumor classification[J]. International Journal of Computer Applications, 2015, 116(19): 11-15. DOI:10.5120/20443-2793 |
| [16] |
CHEN Z, BO W. How priors of initial hyperparameters affect Gaussian process regression models[J]. Neurocomputing, 2017, 275: 1702-1701. |
| [17] |
MICCHELLI C A, XU Y, ZHANG H. Universal kernels[J]. Journal of Machine Learning Research, 2006, 7: 2651-2667. |
| [18] |
DUVENAUD D, NICKISCH H, RASMUSSEN C E. Additive Gaussian processes[J]. Neural Information Processing Systems, 2012, 226-234. |
| [19] |
HASTIE T J, TIBSHIRANI R J. Generalized additive models[J]. Statistical Science, 1986, 1(3): 297-318. DOI:10.1214/ss/1177013604 |
| [20] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016. ZHOU Z H. Machine learning[M]. Beijing: Tsinghua University Press, 2016. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


