气动数据建模是飞行器飞行性能仿真评估的基础。对于飞机、导弹等飞行器,其常规飞行包线内的气动特性通常是马赫数、总迎角、滚转角及三个等效舵偏角的六维函数,如果要通过计算和风洞试验手段来得到整个飞行包线范围内的气动特性,需要的试验和计算量十分巨大。当迎角比较小时,可以进行简化,建立以线化空气动力系数(导数)为基础的数学模型来得到不同马赫数、不同迎角、不同舵偏角下的气动特性。而现代飞行器的机动性越来越大,迎角和舵偏角变化范围更宽,舵与舵之间会存在较强的干扰,此时不能再沿用线性导数模型,需要根据典型试验结果,如风洞试验或高精度的数值计算结果,来建立起多变量非线性的气动特性数学模型。如果进一步考虑流动非定常效应,数学模型中还需进一步考虑角速率、迎角变化率等影响,参数空间将进一步增大。即
飞行器的气动特性建模主要有两大类方法:一类是基于机理建模的方法,如多项式模型、基于几何对称关系的三角函数模型、微分/积分方程模型等,比较典型的例子是大迎角非定常气动力的微分方程模型[2-7]。另一类方法是基于人工智能的“黑箱”建模方法,如决策树方法、BP神经网络、RBF神经网络建模方法、模糊逻辑建模方法、Kriging方法及高斯过程法等[8-11],其基本思想是建立决策树、神经网络等输入-输出之间的映射模型,通过训练样本数据的学习,对模型的结构、权值参数进行调整,使其对数据具有最佳的拟合及预测效果,因而该方法也通常称为机器学习方法。相比较而言,基于机器学习的建模方法对非线性数据的拟合能力通常优于机理建模方法,但泛化能力较弱,而机理建模方法中的模型各项都有一定的物理意义,具有较好的普适性。近年来,深度学习方法研究取得了重大进展,该方法也是机器学习方法,目前已在流体力学和气动特性建模中得到了初步应用[12]。为加以区分,BP神经网络、RBF神经网络建模方法、Kriging方法等通常称为浅层学习方法。本文采用三类建模方法——分类与回归树方法、浅层学习方法和深度学习方法,对典型案例的气动数据进行了建模计算,并对这几类建模方法的优势和不足进行了比较分析。
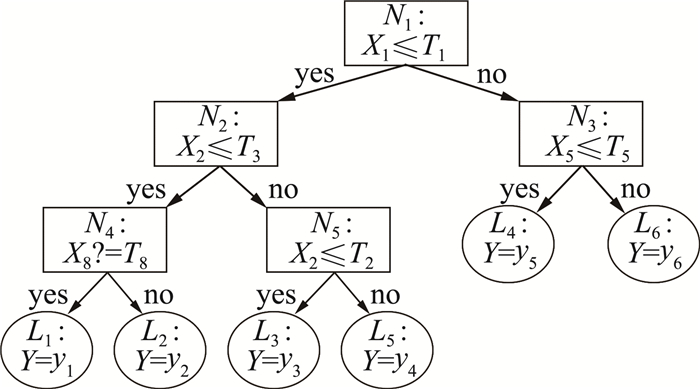
1 分类与回归树方法 1.1 基本思想分类与回归树(Classification and Regression Tree Method,CART)方法是一种决策树方法,也是一种非常有趣并且十分有效的非参数分类和回归方法,是以实例为基础,利用已知的多变量数据构建预测准则,再根据其他变量值进行预测的方法[13]。该方法采用了与传统统计学完全不同的二叉决策树的形式来构建预测准则,其决策树的主要结构如图 1所示,其基本思想是根据样本各变量值Xi与阈值Ti的比较进行分化,构建起二叉树,树的叶子结点Li代表的就是预测值,其中,分化的优劣及阈值Ti的选取由它产生的子结点值的离散程度来确定。决策树的最终构建包含两个过程:建树和剪枝。建树就是通过部分的训练样本数据建立起决策树,直到每一个叶子结点都对应样本点为止。剪枝的过程则是通过剩余的训练样本数据,对已经构建的决策树进行结点的增减,使得决策树在分类性能上能够达到最优。该方法目前在航空科学研究领域已得到了应用[14-15]。
|
图 1 CART方法中的决策树示例 Fig.1 Decision tree in CART method |
考虑如图 2所示的轴对称火箭,采用DATCOM软件[16],计算马赫数M=1.5、总迎角α=6°情况下三个舵面都偏转时的轴向力,作为实测数据进行建模。数据共有216组舵面组合,对应滚转舵偏δx= 0°, 5°, 10°;偏航舵偏δy=-15°, -10°, -5°, 0°, 5°, 10°, 15°, 20°;俯仰舵偏δz=-20°, -15°, -10°, -5°, 0°, 5°, 10°, 15°, 20°的全组合。同时由于每组舵面组合取了8个不同的滚转角ϕ=-135°, -45°, 0°, 22.5°, 45°, 67.5°, 90°, 180°。因而共计216×8=1728个状态数据点。文献[17]中基于均匀性原则从1728组数据中选出50个状态点作为训练样本点,采用正交最小二乘法(OLS)进行建模,对其余1678个状态点进行预测,得到了比较好的结果。
|
图 2 典型轴对称火箭 Fig.2 Typical axisymmetric rocket |
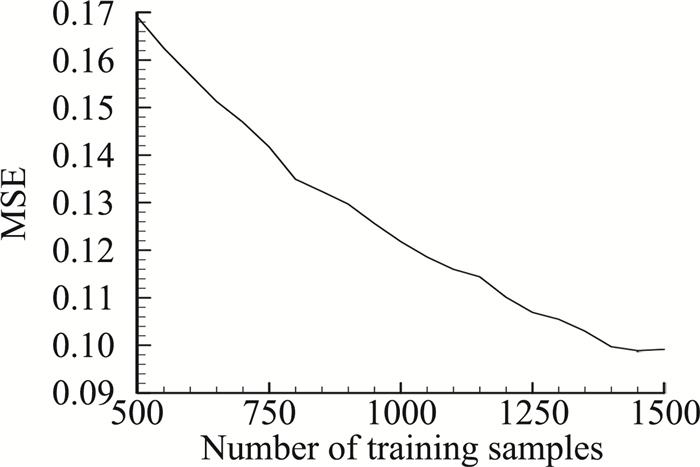
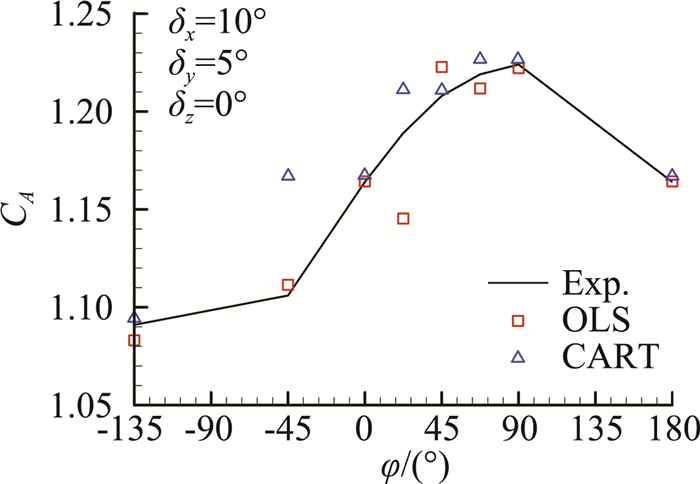
对这一算例考虑CART建模方法,首先分析了训练样本数对建模效果的影响。图 3中给出了不同训练样本数情况下CART模型对所有1728组样本的预测结果,可以看到,随着训练样本点的增加,预测结果的均方差逐步减小。图 4中的“CART”给出了训练样本数为250时建立的CART模型对一组舵偏组合状态的预测结果,及其与正交最小二乘建模结果的比较。从图 4中可以看到该建模方法是可行的。
|
图 3 训练样本数对预测均方差影响 Fig.3 Influence of training samples number on modelling result |
|
图 4 建模预测结果对比 Fig.4 Comparison of model prediction results |
在函数逼近领域,早先最普遍采用的神经网络是BP网络,它是一种是多层前馈神经网络,因网络训练采用误差反向传播(Back-Propagation,BP)学习算法而得名。近年来,随着径向基函数(Radial Basis Function,RBF)神经网络的提出和发展,为函数逼近提供了一种更有效的方法,它在逼近能力、分类能力、学习速度等方面均优于BP网络[18]。
RBF网络是一种三层前向神经网络:输入层由信号源节点组成;第二层为隐层,隐单元的个数由所描述的问题而定,隐层采用径向基函数作为网络的激励函数;第三层为输出层,采用线性激励函数。
设一个多输入多输出的RBF网络有m个输入节点、n个隐层节点、p个输出节点。RBF网络的输出为:
| $ \hat{y}_{k}=\sum\limits_{j=1}^{n} w_{j k} R_{j}(\boldsymbol{x}) $ | (1) |
式中,x为输入向量;
| $ R_{j}( \mathit{\boldsymbol{x}})=\exp \left(-\frac{\left\| \mathit{\boldsymbol{x}}- \mathit{\boldsymbol{c}}_{j}\right\|^{2}}{\sigma_{j}}\right) $ | (2) |
式中cj为第j个径向基函数的中心;σj为与第j个径向基函数宽度相关的变量;‖·‖为L2范数,表示x与cj的欧拉距离。径向基函数的输出位于区间(0, 1)内,输入与中心向量的距离越近,则基函数的输出越大。对于给定的输入x,只有靠近中心部分才被激活。
2.2 Kriging建模方法Kriging模型是从采矿和地理统计学应用中发展起来的一种响应面函数模型,是在已知近似函数的基础上添加了局部的“扰动”来拟合样本点[19]。该方法实际上是高斯过程建模方法(Gaussian Process,GP)的特例。高斯过程定义为一系列随机变量的集合,且其中任意两个随机变量间都满足联合高斯分布。高斯过程建模方法核心思想是将训练样本视为高斯随机过程,当系统有新输入时,高斯过程方法对输出的预测值是一个符合高斯分布的随机变量。高斯过程建模需要确定均值函数、协方差函数中的未知参数,这些未知参数被统称为超参数,通常基于贝叶斯原理来确定[20]。
Kriging建模的具体方法如下[19]:设训练样本的自变量x为n维向量,ns个样本输出构成的输出向量为y,则其近似函数模型为:
| $ \hat{\boldsymbol{y}}=\beta+\boldsymbol{r}^{\mathrm{T}}(\boldsymbol{x}) \boldsymbol{R}^{-1}(\boldsymbol{y}-\boldsymbol{f} \beta) $ | (3) |
其中
| $ \boldsymbol{r}^{\mathrm{T}}(x)=\left[R\left(\boldsymbol{x}, \boldsymbol{x}^{1}\right), R\left(\boldsymbol{x}, \boldsymbol{x}^{2}\right), \ldots, R\left(\boldsymbol{x}, \boldsymbol{x}^{n s}\right)\right]^{\mathrm{T}};\\R\left( \mathit{\boldsymbol{x}}^{i}, \mathit{\boldsymbol{x}}^{j}\right)=\exp \left[-\sum\limits_{k=1}^{n} \theta_{k}\left|x_{k}^{i}-x_{k}^{j}\right|^{2}\right] $ | (4) |
这里,x的上标表示样本点序号,下标表示矢量的分量;R(xi, xj)是任意两个样本点xi和xj的互相关函数;参数θk即为超参数。
由式(3)可得出
| $ \hat{\beta}=\left(\boldsymbol{f}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{f}\right)^{-1} \boldsymbol{f}^{\mathrm{T}} \boldsymbol{R}^{-1} \boldsymbol{y} $ | (5) |
方差的估计值
| $ \hat{\sigma}^{2}=\left[(\boldsymbol{y}-\boldsymbol{f} \hat{\beta})^{\mathrm{T}} \boldsymbol{R}^{-1}(\boldsymbol{y}-\boldsymbol{f} \hat{\beta})\right] / n_{s} $ | (6) |
而参数θk的最大似然估计则由下式给出:
| $ \underset{{{\theta }_{k}}>0}{\mathop{\max \varPhi \left( {{\theta }_{k}} \right)}}\,=-\frac{1}{2}\left[ {{n}_{s}}\ln \left( {{{\hat{\sigma }}}^{2}} \right)+\ln |\mathit{\boldsymbol{{R}}}| \right] $ | (7) |
其中,
| $ y_{\mathrm{pre}}=\hat{\beta}+\boldsymbol{r}^{\mathrm{T}}\left(\boldsymbol{x}_{\mathrm{pre}}\right) \boldsymbol{R}^{-1}(\boldsymbol{y}-\boldsymbol{f} \hat{\beta}) $ | (8) |
式中rT(xpre)利用式(4)计算。
为提高Kriging模型的泛化能力,可通过交叉校验的方法来对模型中的超参数进行优化。交叉校验的基本思想是从所有样本点中依次选取不同的样本点进行建模后,对剩余样本点进行预测,计算其均方预测误差。然后基于均方预测误差最小化的原则对超参数θk进行优化,以舍一交叉校验为例,其均方预测误差如下式(9)。
| $ \min E\left(\theta_{k}\right)=\frac{1}{n_{s}} \sum\limits_{i=1}^{n_{s}}\left[e^{\left(n_{n}-i\right)}\right]^{2}\\ e^{\left(n_{s}-i\right)}=y^{i}-y_{\mathrm{pre}}^{\left(n_{s}-i\right)}\left(\boldsymbol{x}^{i}\right) $ | (9) |
其中e(ns-i)表示建模数据不包含(xi, yi)时,利用其余ns-1个样本点建模结果对xi的预测误差。
2.3 支持向量机SVM方法支持向量机(Support Vector Machines, SVM)是在统计学习理论的基础上发展起来的新型算法,由V. Vapnik等在20世纪90年代提出,建立在严密的统计学理论基础上,引入了结构风险最小化原则,具有较好的泛化能力。该模型的基本思想是在线性可分情况下构建最优分类超平面,获得支持向量, 然后以支持向量的核展开表示模型,从而达到模型的稀疏表示。对于非线性问题,则是将原问题映射到一个高维特征空间,然后在特征空问中进行线性运算[21-22]。最小二乘支持向量机(Least Square SVM)是标准SVM的一个变形,是将标准支持向量机算法中的不等式约束化为等式约束得到的。由此,求解二次优化问题转化成解一次线性方程组,使收敛速度更快,计算的复杂性降低。具体算法为:
给定N个训练样本{ xi, yi},其中xi∈Rn为n维的训练样本输入,yi∈R为训练样本输出。其目标函数为:
| $ \begin{array}{l}{\min J( \mathit{\boldsymbol{w}}, \mathit{\boldsymbol{\xi}})=\frac{1}{2} \mathit{\boldsymbol{w}}^{\mathrm{T}} \mathit{\boldsymbol{w}}+\frac{\gamma}{2} \sum\limits_{i=1}^{N} \xi_{i}^{2}} \\ {\text { s.t. } y_{i}\left(\mathit{\boldsymbol{w}}^{\mathrm{T}} \mathit{\boldsymbol{g}}\left(\mathit{\boldsymbol{x}}_{i}\right)+b\right)=1-\xi_{i}, i=1, \ldots, N}\end{array} $ | (10) |
式中,w为l维权重矢量,g (x)是将x从输入空间映射到特征空间的函数,ξi是xi的松弛系数,b为偏置项,γ是边际系数。
将上述目标函数增广为拉格朗日函数形式后,对各变量求偏导并令其偏导数为0,可将求解的优化问题转化为求解如下线性方程组,即:
| $ \left[\begin{array}{cc}{0} & { \mathit{\boldsymbol{l}}^{\mathrm{T}}} \\ { \mathit{\boldsymbol{l}}^{\mathrm{T}}} & {\boldsymbol{\varOmega}+\frac{1}{\gamma} \boldsymbol{I}}\end{array}\right]\left[\begin{array}{l}{b} \\ {\boldsymbol{\alpha}}\end{array}\right]=\left[\begin{array}{l}{0} \\ {\boldsymbol{y}}\end{array}\right] $ | (11) |
其中,l =[1, 1, …, 1]T;y =[y1, y2, …, yN]T;α =[α1, α2, …, αN]T;I为单位矩阵;Ω为核函数矩阵,矩阵元素Ωij=f(xi, xj),f(·)为满足Mercer条件的对称正定核函数,通常取为:
f(xi, xj) = exp(-‖ xi - xj ‖2/δ),δ为核半径。
由式(11)解出b和α后,LS-SVM的回归函数为:
| $ y(\boldsymbol{x})=\sum\limits_{i=1}^{N} \alpha_{i} f\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right)+b $ | (12) |
上述模型中有两个超参数——正则化参数γ和核半径δ,需要通过交叉校验等方法来确定[23]。
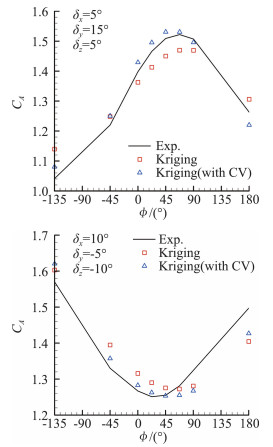
2.4 算例 2.4.1 火箭气动特性建模沿用1.2节中的算例,将基于均匀性原则选取的50个状态点作为训练样本点,采用Kriging建模方法进行建模,对其余1678个状态点进行预测,预测的均方误差为0.1924。进一步针对50个建模样本采用舍一交叉校验方法来优化超参数,对其余1678个状态点进行预测,可得出均方误差为0.1219。图 5中给出了两组典型舵偏状态下的建模预测结果对比。其中“Kriging”表示标准Kriging模型建模结果,“Kriging(with CV)”表示通过交叉校验方法优化超参数后的建模结果。可以看到,对这一气动建模问题能采用Kriging模型进行建模,且通过交叉校验可提高模型的泛化能力。
|
图 5 Kriging模型建模预测结果 Fig.5 Prediction results of Kriging model |
以NASA阿姆斯研究中心7 ft×10 ft低速风洞中开展的展弦比λ=2尖前缘三角翼俯仰振荡动态试验[24]为研究对象。迎角变化历程为:
| $ \alpha(\tau)=45^{\circ}+45^{\circ} \sin (k \tau) $ | (13) |
τ是无量纲时间,τ=t(V/ c);减缩频率k=0.01、0.02、0.03、0.04。俯仰力矩参考轴在77%bA处。分别采用Kriging模型、RBF神经网络模型和SVM支持向量机模型进行建模,模型的输入都取为迎角的时间历程:α(τ)、α(τ-8)、α(τ-16)、α(τ-24)、α(τ-32),输出为τ时刻的纵向气动系数。
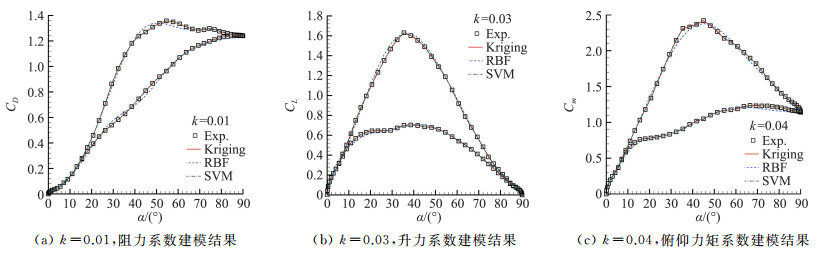
首先用静态试验数据和减缩频率k=0.01、0.03、0.04的大振幅振动试验数据训练Kriging模型、RBF神经网络模型和SVM支持向量机模型。不同减缩频率下的不同气动系数训练结果与试验数据的比较示于图 6,图中“Kriging”对应Kriging模型,“RBF”对应RBF神经网络模型,“SVM”对应SVM支持向量机模型,“Exp.”对应风洞试验数据。由图 6可见,训练结果与试验数据拟合得较好。
|
图 6 建模结果对比 Fig.6 Comparison of modeling results |
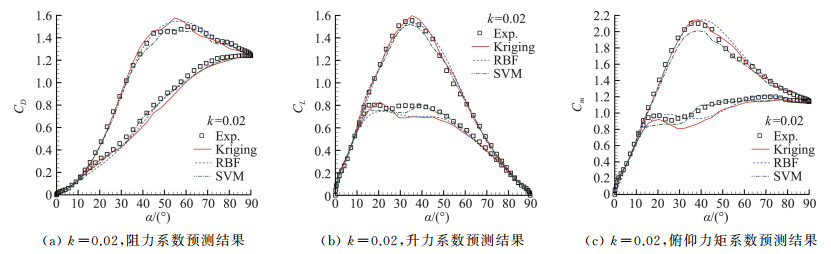
再用训练后的模型参数预测缩减频率k=0.02的工况。不同模型的预测结果与试验数据比较示于图 7,具体的预测误差值示于表 1。从图表中看出,预测结果与试验数据也符合较好。其中,由于SVM进行了交叉校验,一定程度上提升了模型的泛化能力,使得SVM的预测结果略优于Kriging模型和RBF神经网络模型。
|
图 7 预测结果对比 Fig.7 Comparison of model prediction results |
| 表 1 k=0.02工况的不同模型预测误差 Table 1 Comparison of prediction error for different model for k=0.02 case |
|
|
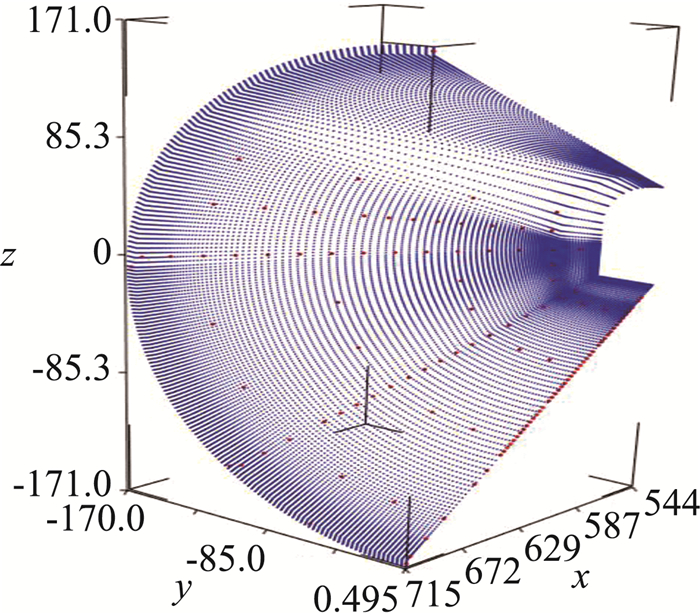
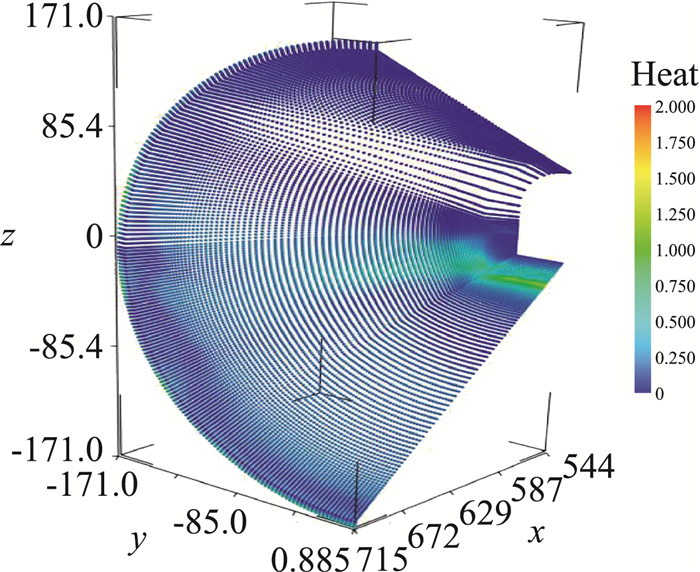
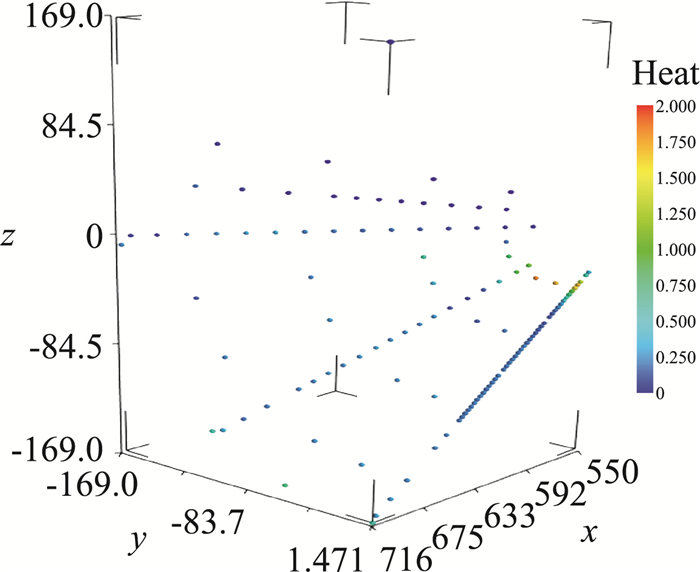
以某飞行器的表面热流数据为例,对数值计算获得的连续分布热环境和风洞试验点热流值进行融合。要求融合后的结果在风洞试验点位置处同测量结果一致,对CFD数值仿真网格点处的值进行适当的修正,融合后的结果能够在整体上体现试验结果的数据特性。图 8是所有气动热数据样本点的位置,其中32 922个蓝色点为CFD网格点,计算数据如图 9所示,118红色点位置为风洞试验测量点,试验数据如图 10示。
|
图 8 数据采集点 Fig.8 Data sampling points |
|
图 9 数值计算数据 Fig.9 Data of CFD |
|
图 10 风洞试验数据 Fig.10 Wind tunnel test data |
数据融合过程中需要建立风洞试验数据和CFD计算数据的差量模型,并使用差量模型对CFD网格点处的值进行修正。由于Kriging模型具有准确拟合建模数据点的特性,因此被用于建立差量模型。另外,由于风洞试验点位置与CFD网格点并非完全对应,因此对每个风洞试验点,选取附近的CFD数据点利用RBF方法进行插值。之所以采用RBF方法是由于实验表明在数据较少时,RBF建模效率比Kriging更高,且建模精度相当。
由此可得气动热数据融合方法:(1)针对每一个风洞试验点,若有与之对应的CFD数据点,则直接使用,否则,选取附近少量CFD数据,使用RBF方法建立插值模型,并计算相应的值; (2)计算风洞试验数据和CFD计算数据的差量,并使用Kriging方法建立差量模型; (3)使用Kriging模型对所有的CFD数据点进行修正,得到融合结果。
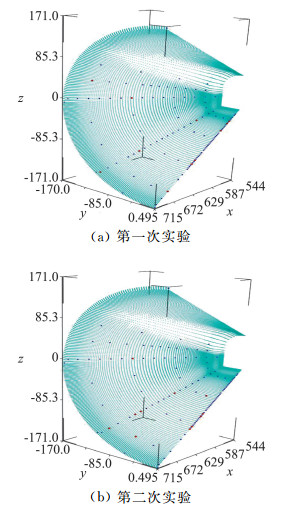
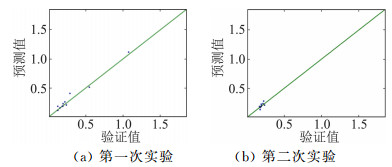
为了验证本文所提方法的有效性,随机选取10%的风洞试验数据作为预测验证数据,其余90%的数据作为样本数据与CFD计算数据一起构建融合模型。实验进行了两次,图 11(a)和图 11(b)的红色点是两次实验随机选取的10%风洞试验数据在空间的分布情况。图 12(a)和图 12(b)是验证结果对比,其中横坐标表示用于验证的风洞试验数据的真实值,纵坐标表示在这些验证位置通过融合模型计算得到的预测值。第一次和第二次实验验证的均方根误差分别为0.04782和0.02762。由图 12和均方根误差可知预测数据与验证数据基本一致,说明模型达到了数据融合的目的。
|
图 11 两次实验验证数据分布图 Fig.11 The positions of validation data for two experimental cases |
|
图 12 预测数据与验证数据对比 Fig.12 Comparison of validation data and prediction |
通过上述机器学习模型算例分析,可以看到,几种方法都能对气动数据进行较好的建模。但几种模型也有各自的特点和优缺点,如表 2所示。
| 表 2 几种建模方法比较 Table 2 Comparison of modeling methods |
|
|
(1) Kriging建模方法可对训练样本完全拟合,RBF神经网络方法和SVM支持向量机方法则不要求训练样本完全拟合。
(2) Kriging建模方法、RBF神经网络方法和SVM支持向量机方法都可以通过交叉校验优化超参数来提高模型的泛化能力。对Kriging模型而言,超参数是θk;对RBF模型而言,超参数是隐层节点数;对SVM模型而言,超参数是γ和δ。CART方法则对训练样本量有较高要求,建模结果的精度和模型的泛化能力随训练样本数增加而提高。
(3) Kriging方法、RBF神经网络方法和SVM支持向量机方法都需要对样本数据进行大量的矩阵运算,但RBF神经网络方法的矩阵维数取决于隐层节点数,而Kriging方法和SVM支持向量机方法的矩阵维数取决于样本点数,当样本点数较多时,矩阵运算的计算资源要求会增加,计算效率和计算精度会下降。因此,Kriging方法和SVM支持向量机方法中的建模样本点数不宜过多,在普通个人微机上一般不超过2000个样本点,具体数量视微机性能而定,而RBF神经网络方法则对样本点数无特殊限制。CART建模方法中没有矩阵运算,且样本点越多,建模效果越好,但随着样本点的增加,逻辑判断运算量较大。
3 气动特性建模的深度学习方法前面的浅层学习方法存在两方面问题,一是需要人为提取输入特征参数,二是泛化能力有所不足。深度神经网络通过增加隐层层数,一方面使得模型能更有效地表征非线性函数的丰富特征;另一方面则通过层与层之间的无监督学习,实现特征的逐级提取,可较好地克服浅层学习方法存在的不足。但是,随着网络层数的增加,如果采用传统的神经网络训练方法会出现三个问题,一是“梯度消失”现象;二是优化易于陷入局部最优值;三是如果网络全连接的话,会带来网络权值参数数目的几何增长。因此,在深度神经网络训练方法中,使用自下而上非监督学习与自上而下监督学习结合的方法,对训练数据特征提取后再进行网络权值调整,解决了“梯度消失”和陷入局部最优的问题;同时基于局部感知和权值共享,则大幅减少了待优化网络权值数[25-26]。
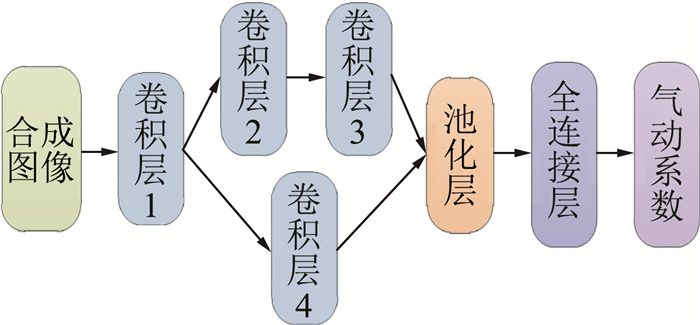
近年来,随着计算资源的增强和大数据的兴起,以深度神经网络为代表的深度学习方法在图像与语音识别、语义理解、智能控制等方面得到了广泛应用,并逐步与空气动力学研究结合[27-33]。文献[33]将深度神经网络模型用于气动特性建模,基于CNN模型对翼型气动系数进行了预测,但该方法只能处理给定马赫数和迎角的情况,没有将流动条件作为输入,限制了其使用范围。为了在输入中引入流动条件,文献[34]中利用迎角度数对翼型图像进行旋转,利用马赫数对图像颜色进行改变,构造了一幅人工图像,作为预测模型的输入。本节提出另一种方法,将流动条件参数组成一个向量,认为该向量是一幅分辨率为1×nfc的图像,其中nfc为流动条件的参数个数。通过双三次插值,将该向量的分辨率调整为同翼型图像一致,与翼型图像一起构成“合成图像”,即2个二维矩阵,作为预测模型的输入。同时,由于翼型图像与流动参数向量对应图像的特征丰富程度不同,选用如图 13所示的有向无环图(Directed Acyclic Graph,DAG)深度神经网络[35],该网络结构在卷积层1后分为两个支路,能较好地处理图像特征相差较大的情况,提高预测精度[11]。其训练和测试方法与常规CNN预测模型类似。具体的网络参数设置:图像分辨率为85×85;卷积层1选取卷积核大小为8×8,卷积核数量为40,步长为1;卷积层2选取卷积核大小为5×5,卷积核数量为80,步长为1;卷积层3选取卷积核大小为5×5,卷积核数量为120,步长为2;卷积层4选取卷积核大小为2×2,卷积核数量为120,步长为2;所有卷积层所用到的非线性激励函数均选取为ReLU函数;池化区域大小为2×2,步长为2,即相邻池化区域不重叠,选择的池化方法为最大池化法。
|
图 13 DAG模型结构 Fig.13 Model structure of DAG network |
算例中用到的翼型为NACA0012翼型叠加扰动函数后的变形体,共300个;流动条件中迎角取值为2°、6°、9°、12°和15°,马赫数取值为0.1、0.3和0.6,雷诺数固定为6.5×106;翼型形状和流动条件任意组合,共构成翼型数据样本4200组。图 14中给出了随机选取的8个翼型图像。图 15给出了3个迎角和马赫数组成的向量[6, 0.3]、[9, 0.6]、[12, 0.1]乘以放大倍数后变为[102, 127.5]、[153, 255]、[204, 42.5],视为三张图片将分辨率调整为85×85后的图像。

|
图 14 任意8个翼型图像(翼型厚度放大10倍) Fig.14 Eight random selected airfoils (thickness amplified 10 times) |

|
图 15 任意3个由迎角和马赫数构成的图像 Fig.15 Pictures corresponding to three sets of angle of attack and Mach number |
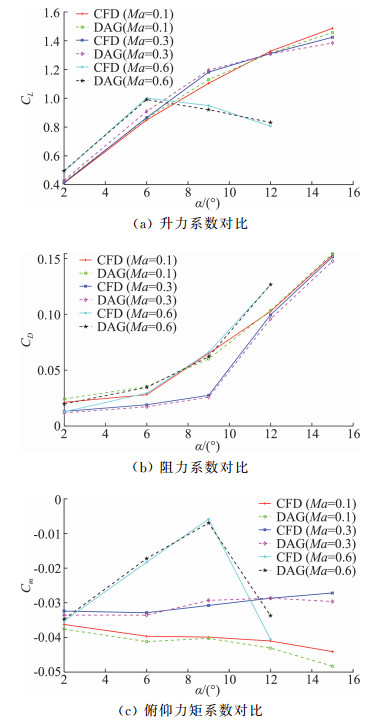
将这4200组样本的顺序打乱,随机选择3360组翼型图像和对应的流动条件作为训练样本,将气动系数作为期望值,对预测模型进行训练;剩下的840组翼型数据作为测试样本,对预测模型进行测试。结果显示,840组翼型升力系数、阻力系数、俯仰力矩系数预测结果的标准差绝对值分别为0.0418、0.0049和0.0042,相对值分别为4.38%、7.23%和12.73%。随机给出一个翼型在不同迎角和马赫数下CFD计算气动系数和预测气动系数的对比如图 16所示。图 16中,“CFD”表示通过CFD计算得到的气动系数,“DAG”表示通过模型预测得到的气动系数,α表示迎角。从图 16中可以看出,本文建立的预测模型能够比较准确地对3个气动系数进行预测。
|
图 16 CFD计算和预测气动系数对比 Fig.16 Comparison of CFD and model prediction results |
在此需要指出的是,深度学习模型虽然从建模便捷性和泛化能力等方面看优于浅层学习模型,但也存在不足,还需要进一步的改进完善:一是对训练数据量的要求较高;二是模型中超参数,如网络层数、隐层节点数的选取,较为困难,这些超参数的选取对建模结果有直接影响;三是所提取特征的可解释性较弱。
4 小结本文对气动特性“黑箱”建模的三类机器学习方法——分类与回归树方法、浅层学习方法和深度学习方法, 进行了算法说明与分析应用。将分类与回归树方法、Kriging建模方法、RBF神经网络方法及SVM支持向量机方法分别应用于火箭气动特性建模、三角翼大迎角非定常气动特性建模、气动热试验数据融合。结果显示浅层学习方法可通过交叉校验对模型中的超参数进行优化来提高泛化能力;Kriging建模方法和SVM支持向量机方法的训练样本数受矩阵运算限制较大。CART方法对训练样本量有较高要求,但其建模结果的精度和模型的泛化能力随训练样本数增加而提高。
同时,将流动条件参数组成向量,再映射为图像,与翼型图像构成“合成图像”,建立了以翼型几何图像、来流马赫数、迎角为输入,翼型气动特性为输出的DAG深度神经网络模型,得到了比较好的预测效果,拓展了气动特性深度学习建模方法的使用范围。
从上述对浅层学习和深度学习模型的分析应用看,浅层学习在模型结构简洁性、计算效率和建模数据量方面有优势,而深度学习模型在泛化能力、特征自动提取方面有优势。因此,后续可考虑将两种建模方法结合起来开展研究。例如,提高深度学习模型的可解释性,分析其提取特征的物理含义并将这些特征作为浅层学习的输入,使浅层学习模型在较少数据量的情况下也能具有较强的泛化能力。
| [1] |
GRAUER J A, MORELLI E A. A generic nonlinear aerodynamic model for aircraft[R]. AIAA 2014-0542. https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140011902.pdf
|
| [2] |
GOMAN M, KHRABROV A. State space representation of aerodynamic characteristics of an aircraft at high angles of attack[R]. AIAA 1992-4651. https://arc.aiaa.org/doi/abs/10.2514/3.46618
|
| [3] |
汪清, 钱炜祺, 丁娣. 飞机大迎角非定常气动力建模研究进展[J]. 航空学报, 2016, 37(8): 2331-2347. WANG Q, QIAN W Q, DING D. A review of unsteady aerodynamic modeling of aircrafts at high angles of attack[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2331-2347. (in Chinese) |
| [4] |
黄达, 郑万祥. 基于风洞试验的非定常气动力微分方程建模方法[J]. 南京航空航天大学学报, 2014, 46(4): 599-602. HUANG D, ZHENG W X. Unsteady aerodynamic modeling method using differential equations based on wind tunnel test[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(4): 599-602. DOI:10.3969/j.issn.1005-2615.2014.04.017 (in Chinese) |
| [5] |
何开锋, 王文正, 钱炜祺. 根据风洞试验结果建立有尾翼导弹数学模型[J]. 流体力学实验与测量, 2004, 18(4): 62-66. HE K F, WANG W Z, QIAN W Q. Mathematic modeling for the missile aerodynamics with tail-wing according to wind-tunnel test results[J]. Experiments and Measurements in Fluid Dynamics, 2004, 18(4): 62-66. DOI:10.3969/j.issn.1672-9897.2004.04.014 (in Chinese) |
| [6] |
何开锋, 钱炜祺, 张勇, 等. 偏最小二乘法在气动数据建模中的应用[J]. 宇航学报, 2014, 35(3): 277-282. HE K F, QIAN W Q, ZHANG Y, et al. Application of partial least squares regression method in modeling of aerodynamic data[J]. Journal of Astronautics, 2014, 35(3): 277-282. DOI:10.3873/j.issn.1000-1328.2014.03.005 (in Chinese) |
| [7] |
傅建明. 喷流姿控战术导弹三维气动力数学模型[J]. 上海航天, 2005(4): 13-18. FU J M. Three dimensional aerodynamic mathematical model for tactical missiles with jet steering[J]. Aerospace Shanghai, 2005(4): 13-18. DOI:10.3969/j.issn.1006-1630.2005.04.004 (in Chinese) |
| [8] |
SANTOS M C, MATTOS B S, GIRARDI R M. Aerodynamic coefficient prediction of airfoils using neural networks[R]. AIAA 2008-0887, 2008. https://arc.aiaa.org/doi/10.2514/6.2008-887
|
| [9] |
WANG Z J, LAN C E, BRANDON J M. Fuzzy logic modeling of lateral-directional unsteady aerodynamics[R]. AIAA 99-4012.
|
| [10] |
史志伟, 明晓. 基于模糊聚类的模糊神经网络在非定常气动力建模中的应用[J]. 空气动力学学报, 2005, 23(1): 21-24. SHI Z W, MING X. The application of FNN in unsteady aerodynamics modeling based on fuzzy clustering[J]. Acta Aerodynamica Sinica, 2005, 23(1): 21-24. DOI:10.3969/j.issn.0258-1825.2005.01.005 (in Chinese) |
| [11] |
刘新亮, 张昆仑, 郭波. 高斯过程元模型建模方法及在火箭弹气动分析中应用[J]. 固体火箭技术, 2010, 33(5): 486-490. LIU X L, ZHANG K L, GUO B. Research on Gaussian process surrogate model and its application to rocket aerodynamic analysis[J]. Journal of Solid Rocket Technology, 2010, 33(5): 486-490. DOI:10.3969/j.issn.1006-2793.2010.05.002 (in Chinese) |
| [12] |
张天姣, 钱炜祺, 周宇, 等. 人工智能与空气动力学结合的初步思考[J]. 航空工程进展, 2019, 10(1): 1-11. ZHANG T J, QIAN W Q, ZHOU Y, et al. Preliminary Thoughts on the combination of artificial intelligence and aerodynamics[J]. Advances in Aeronautical Science and Engineering, 2019, 10(1): 1-11. (in Chinese) |
| [13] |
张松林. CART-分类与回归树方法介绍[J]. 火山地质与矿产, 1997, 18(1): 67-75. ZHANG S L. An introduction to the methodology of CART-Classification and regression trees[J]. Volcanology& Mineral Resources, 1997, 18(1): 67-75. (in Chinese) |
| [14] |
CHATI Y S, BALAKRISHNAN H. Statistic modeling of aircraft engine fuel flow rate[R]. ICAS-2016-0619. http://www.mit.edu/~hamsa/pubs/ChatiBalakrishnanICAS2016.pdf
|
| [15] |
杨俊.气动数据挖掘、建模方法初步研究[D].四川绵阳: 中国空气动力研究与发展中心, 2016. YANG J. Preliminary study of methods using in modeling and data mining for aerodynamic data[D]. Mianyang: China Aerodynamics Research and Development Center, 2016. (in Chinese) |
| [16] |
AUMAN L. Missile DATCOM user's manual-2008 revision[R]. AFRL-RB-WP-TR-2009-3015, 2008.
|
| [17] |
QIAN W Q, YANG J, ZHOU Y. A comparative study of mathematical modeling methods for rocket aerodynamic data[C]//7th European Conference For Aeronautics And Space Sciences. Milan, Italy, EUCASS-100, 2017.
|
| [18] |
SU W, GAO Z H, ZUO Y T. Application of RBF neural network ensemble to aerodynamic optimization[R]. AIAA 2008-0154.
|
| [19] |
SIMPSON T W, et al. Kriging models for global approximation in simulation-based multidisciplinary design optimization[J]. AIAA Journal, 2001, 39(12): 2233-2241. DOI:10.2514/2.1234 |
| [20] |
RASMUSSEN C E, WILLIAMS C K I. Gaussian process for machine learning[M]. Cambridge: The MIT Press, 2006.
|
| [21] |
ANDRÉS E, SALCEDO-SANZ S, MONGE F, et al. Efficient aerodynamic design through evolutionary programming and support vector[J]. Expert Systems with Applications, 2012, 39(12): 10700-10708. DOI:10.1016/j.eswa.2012.02.197 |
| [22] |
WANG Q, QIAN W Q, HE K F. Unsteady aerodynamic modeling at high angles of attack using support vector machines[J]. Chinese Journal of Aeronautics, 2015, 28(3): 659-668. DOI:10.1016/j.cja.2015.03.010 |
| [23] |
王克奇, 杨少春, 戴天虹, 等. 采用遗传算法优化最小二乘支持向量机参数的方法[J]. 计算机应用与软件, 2009, 26(7): 109-111. WANG K Q, YANG S C, DAI T H, et al. Method of optimizing parameter of least squares support vector machines by genetic algorithm[J]. Computer Application and Software, 2009, 26(7): 109-111. DOI:10.3969/j.issn.1000-386X.2009.07.037 (in Chinese) |
| [24] |
JARRAH M A, ASHLEY H. Impact of flow unsteadiness on maneuvers and loads of agile aircraft[R]. AIAA 89-1282. https://arc.aiaa.org/doi/abs/10.2514/6.1989-1282
|
| [25] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [26] |
尹宝才, 王文通, 王立春. 深度学习研究综述[J]. 北京工业大学学报, 2015, 41(1): 48-59. YIN B C, WANG W T, WANG L C. Review of deep learning[J]. Journal of Beijing University of Technology, 2015, 41(1): 48-59. (in Chinese) |
| [27] |
KUTZ J N. Deep learning in fluid dynamics[J]. Journal of Fluid Mechanics, 2017, 814: 1-4. DOI:10.1017/jfm.2016.803 |
| [28] |
LING J, KURZAWSKI A, TEMPLETON J. Reynolds averaged turbulence modeling using deep neural networks with embedded invariance[J]. Journal of Fluid Mechanics, 2016, 807: 155-166. DOI:10.1017/jfm.2016.615 |
| [29] |
GUO X X, LI W, LORIO F. Convolutional neural networks for steady flow approximation[C]//ACM SigKDD International Conference. San Francisco, CA, 2016: 481-490. https://dl.acm.org/citation.cfm?id=2939738
|
| [30] |
HUANG J J, DUAN L, WANG J X, et al. High-mach-number turbulence modeling using machine learning and direct numerical simulation database[R]. AIAA 2017-0315.
|
| [31] |
XIAO H, WU J L, WANG J X, et al. Physics informed machine learning for predictive turbulence modeling: Progress and perspectives[R]. AIAA 2017-1712.
|
| [32] |
YILMAZ E, GERMAN B. A convolutional neural network approach to training predictors for airfoil performance[R]. AIAA 2017-3660.
|
| [33] |
陈海, 钱炜祺, 何磊. 基于深度学习的翼型气动系数预测[J]. 空气动力学学报, 2018, 36(2): 294-299. CHEN H, QIAN W Q, HE L. Aerodynamic coefficient prediction of airfoils based on deep learning[J]. Acta Aerodynamica Sinica, 2018, 36(2): 294-299. DOI:10.7638/kqdlxxb-2017.0098 (in Chinese) |
| [34] |
ZHANG Y, SUNG W J, MAVRIS D N. Application of convolutional neural network to predict airfoil lift coefficient[R]. AIAA 2018-1903.
|
| [35] |
YANG S, RAMANAN D. Multi-scale recognition with DAG-CNNs[C]//2015 IEEE Intenational Conference on Computer Vision. IEEE, 2015: 1215-1223. https://www.cv-foundation.org/openaccess/content_iccv_2015/papers/Yang_Multi-Scale_Recognition_With_ICCV_2015_paper.pdf
|
 2019, Vol. 37
2019, Vol. 37


