下击暴流是雷暴天气中引起近地面短时灾害性大风的强下沉气流[1]。按照水平影响范围的大小,下击暴流分为宏下击暴流和微下击暴流,微下击暴流在雷雨天气发生的概率可达60~70%[2]。下击暴流在世界范围内造成了大量工程结构物的破坏,尤其是导致输电线塔结构的倒塌[3]。此外,下击暴流引起的低空风切变对飞机的起飞和降落带来巨大威胁,是引发飞机低空飞行事故的主要原因之一[4]。
作为结构抗风设计的重要依据,风剖面特征是下击暴流研究的重要关注点之一。目前国内外学者通过现场实测、理论研究、物理实验和数值模拟等多种研究方法对下击暴流的风剖面特征开展了相关研究[5-6]。Fujita[7]依据实测资料指出下击暴流竖直风剖面的最大风速值位于50~100 m。Kim和Hangan[8]进行了下击暴流的定常和非定常风场的计算流体力学(Computational Fluid Dynamics,CFD)数值模拟,研究了下击暴流的竖直和径向风剖面特征。Sengupta和Sarkar[9]基于实验和CFD数值模拟方法研究了下击暴流在光滑地面下的稳态风场特性。Mason等[10-11]基于CFD方法研究了理想轴对称下击暴流风场和风剖面特征。国内学者瞿伟廉、吉柏锋[12-13]、汤卓等[14]、李朝等[15]、王超等[16]采用CFD方法研究了下击暴流的风场和风剖面特征。陈勇等[17-18]采用实验和CFD方法研究了下击暴流的风场特征并据此提出了下击暴流风速模型。邹鑫等[19]结合实验和大涡模拟的结果,提出了沿径向变化的径向风速剖面模型和分区域的竖向风速剖面模型。
上述工作对于下击暴流风剖面特性研究起到了非常重要的作用,但是在这些工作大都基于光滑地面假定。自然界中地面粗糙状况普遍存在,且表现出具体的粗糙特征。而由于地面粗糙度的不同,来流在近地面的风速剖面形状和特点,会表现出不同于流经光滑地面的特点。基于上述原因,本文将建立考虑地面粗糙度的下击暴流风场模型,研究地面粗糙度对下击暴流近地面风场特性的影响,特别是对下击暴流竖直和径向风剖面特征的影响。
1 下击暴流风场模型 1.1 地面粗糙度地面粗糙度是大气边界层气象学中反映下垫面特征的重要指标,是影响大气边界层内风速剖面的重要参数。通常采用粗糙度长度z0描述地面粗糙度,它是指大气边界层近地面风速值向下递减至0时的所在高度。任一水平区域的粗糙度长度可表示为[20]:
| $ z_{0}=\frac{h s}{2 A} $ | (1) |
式中:z0为该水平区域的粗糙度长度,m;h为该水平区域内的平均粗糙元素高度,m;s为该水平区域内的粗糙元素平均迎风面积,m2;A为该水平区域内的平均单个粗糙元素所占的水平投影面积,m2。
在我国现行的建筑结构荷载规范[21]中,地貌类别依地面粗糙度分为A、B、C、D四类。美国[22]和澳大利亚/新西兰[23]规范对地貌类别的划分标准基本一致,并且都将地貌类别划分为四类。其中澳大利亚规范中对各类地形对应的粗糙长度z0进行了明确的划分(如表 1所示),本文采用该粗糙长度划分进行地面粗糙参数的标定。
尽管在气象尺度中,下击暴流已属于极小尺度的天气现象。但是要在实验室中模拟这种天气现象仍然存在较大难度,因为原型尺度很大,所以实验都是采用极小的几何缩尺比。因此,要在当前下击暴流实验中,模拟不同地面粗糙状况是很难实现的。
在计算流体力学中考虑地面的粗糙状况对计算域内流场的影响,需要考虑近地面的流动特征。在近壁面附近,流动受壁面影响,雷诺数很小,大多数湍流模型在近壁面附近不适用,通常采用壁面函数或壁面模型方法求解近壁面区域流动。相比于壁面模型方法对近壁面网格的高分辨率要求,壁面函数法采用半经验公式将近壁面物理量与湍流核心区的求解变量联系起来,可充分节约计算资源。壁面函数法中近壁面流速可表示为[24]:
| $ \frac{u_{p} u^{*}}{\tau_{\omega} / \rho}=\frac{1}{\kappa} \ln \left(E \frac{\rho u^{*} y_{p}}{\mu}\right)-\Delta B $ | (2) |
式中:
| $ \Delta B = \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {0, }&{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;K_S^ + \le 2.25} \end{array}\\ \frac{1}{\kappa }\ln \left( {\frac{{K_S^ + - 2.25}}{{87.75}} + {C_S}K_S^ + } \right) \cdot \\ \;\;\sin \left( {0.4258\left( {\ln K_S^ + - 0.81} \right)} \right), \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2.25 < K_S^ + \le 90\\ \begin{array}{*{20}{c}} {\frac{1}{\kappa }\ln \left( {1 + {C_S}K_S^ + } \right), }&{\;\;\;\;\;\;\;\;\;\;\;\;K_S^ + > 90} \end{array} \end{array} \right. $ | (3) |
式中:KS+=ρu*KS/μ,KS是粗糙高度,CS是粗糙常数。
地貌粗糙类型中粗糙长度和计算流体力学壁面函数法中粗糙高度的关系,不同的计算流体力学软件有不同的定义方法。Blocken等[25]根据壁面粗糙度影响函数式(3)和ANSYS-Fluent中基于均匀粗糙元建立的壁面函数法提出在ANSYS-Fluent中实际地貌粗糙长度和壁面函数法中粗糙高度的换算关系为:
| $ K_{S, {\rm A B L}}=9.793 y_{0} / C_{S} $ | (4) |
式中KS, ABL为粗糙高度;y0为大气边界层中的地面粗糙长度;CS为粗糙常数。
需要指出的是,式(4)中的粗糙高度的计算,是通过调整均匀粗糙元的高度及分布密度来实现对自然界地面不同粗糙类型的模拟。Blocken和Person[26]通过对某体育馆周围风场对比研究, 验证了式(4)在CFD模拟实际地面粗糙状况中的适用性。地面粗糙长度通过用户自定义功能(User Defined Function, UDF)编写程序调整ANSYS-Fluent壁面函数模型中的均匀粗糙元高度及分布密度,使其满足式(4)中不同地面粗糙长度。
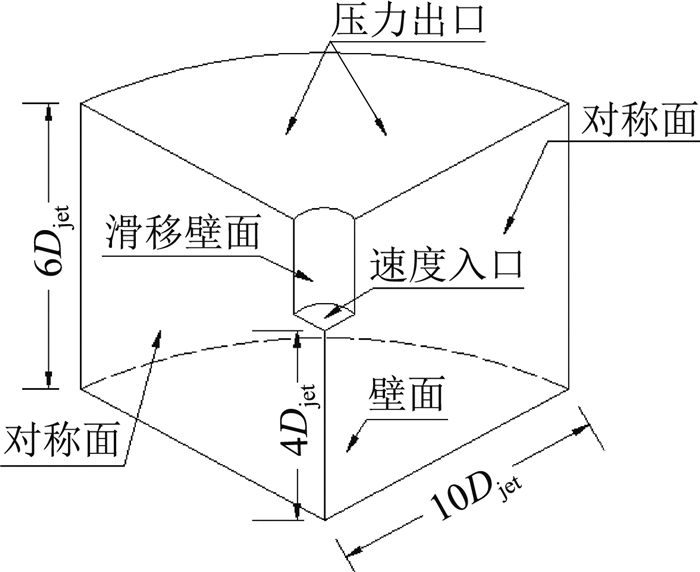
1.2 计算模型本文选择冲击射流模型作为下击暴流的计算风场模型。近年来,大量基于冲击射流模型开展的下击暴流物理实验结果也表明该计算风场模型同实测数据吻合较好[9-10]。实际上,下击暴流的发生、发展和消亡时间短,具有强非平稳特征。尽管下击暴流冲击地面前后的风场变化剧烈,但在沿径向扩展后仍然会形成特定的稳定边界层结构。因此,本文采用稳态数值模拟方法来考察地面粗糙度对下击暴流沿径向扩展后的风场影响。主要模型参数包括:计算入口位置到地面的距离为Hjet=4Djet,初始出流直径Djet=600 m,初始出流速度Vjet=18 m/s。计算域和网格分别如图 1和图 2所示。
|
图 1 计算域示意图 Fig.1 Schematic diagram of computational domain |
|
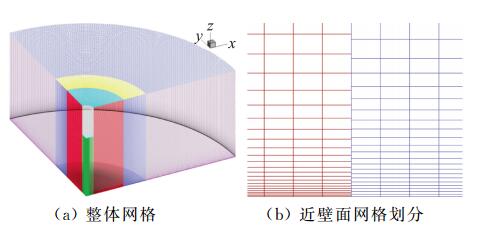
图 2 计算网格 Fig.2 Computational mesh |
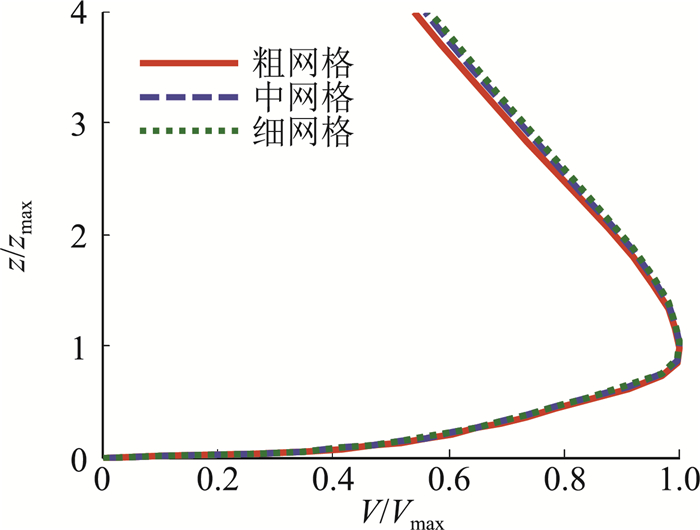
下击暴流计算模型为足尺模型,考虑到数值模拟的计算负担和主要关心的区域,在距离风暴中心0.5Djet、1.5Djet和4.0Djet处将计算域进行分块划分网格(图 2(a)),通过内部面边界条件连接相邻计算域形成非一致网格(图 2(b))。四块计算域近壁面的首层网格高度分别为0.1 m、0.25 m、0.5 m和0.75 m,网格最大长宽比分别为60、52、42和105,粗糙元高度分别为0.05 m、0.125 m、0.25 m和0.375 m。总网格数为15 287 724。为考察网格依赖性,对比了采用同样的网格划分方案的粗网格(网格数11 736 808)、中网格(网格数15 287 724)和细网格(网格数17 911 800)三种网格方案下,相同粗糙高度zo=0.2 m情况下同一径向位置处(r=1.5Djet)的风剖面,如图 3所示。
|
图 3 计算网格依赖性检验 Fig.3 Computational grid dependency test |
计算边界条件如表 2所示。计算模型对应的下击暴流风场为三维不可压缩湍流流动。采用剪切应力运输SST k-ω湍流模型,其控制方程见文献[24]。SST k-ω湍流模型的优势在于它综合了标准k-ω模型对于近壁面区域计算的优点和k-ε模型对于远场区域计算的优点,同时,在湍流黏性公式中考虑了湍流剪切应力的影响。利用ANSYS-Fluent完成对控制方程的求解。压力和速度场的耦合采用SIMPLE算法,求解参数为默认的缺省值。采用二阶迎风格式对动量、压力、湍动能和湍流耗散率进行求解。
| 表 2 计算边界条件 Table 2 Computational boundary conditions |
|
|
为验证下击暴流的CFD数值模拟方法,在浙江大学风洞进行了下击暴流的实验。下击暴流的实验装置包括下击暴流模拟段、流场测试段和测试系统三部分构成,如图 4所示。下击暴流实验初始条件为:初始出流直径Djet=0.4 m,初始出流速度Vjet=6 m/s,计算入口位置到地面的距离为Hjet=1.2 m。

|
图 4 下击暴流实验装置 Fig.4 Equipment for downburst experiment |
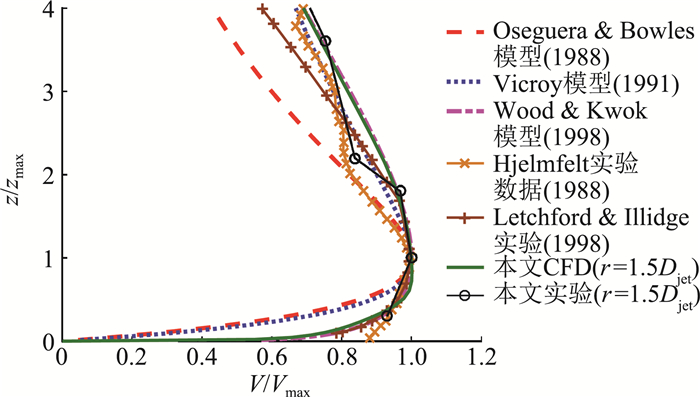
为检验数值模拟结果,选取CFD模拟结果和实验结果,与下击暴流风剖面模型[27-29]、实验[30]和实测结果[31]进行比较(图 5),其中CFD模拟结果选取地面粗糙长度为zo =0.002 m,距离风暴中心径向距离为r=1.5Djet的风剖面。从图 5中可以看出,下击暴流CFD数值模拟的风剖面与实验结果、风剖面模型以及实测的风剖面基本特征相吻合。
|
图 5 下击暴流的风剖面验证 Fig.5 Wind profile validation of downburst |
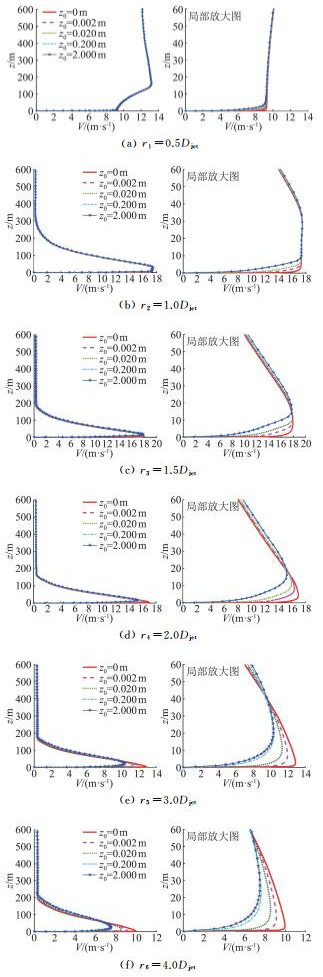
下击暴流的竖直风剖面与大气边界层近地风的风剖面一样,用来表征风速沿高度的变化规律。为了考察地面粗糙度对下击暴流竖直风剖面的影响,选取6个距离风暴中心的径向位置,分别为r1=0.5Djet、r2=1.0Djet、r3=1.5Djet、r4=2.0Djet、r5=3.0Djet和r6=4.0Djet的竖向风剖面如图 6所示。
|
图 6 下击暴流竖直风剖面 Fig.6 Vertical wind profiles of downburst |
从图 6可以看出,r1=0.5Djet处,各类地貌下的风速剖面基本重合,各个曲线最大风速值及其所在的高度也趋近相等。r2=1.0Djet处,10 m高度以下,随着粗糙长度的增加,风剖面的上升趋势越缓;10 m高度以上,速度剖面趋于重合。r3=1.5Djet处,地面粗糙度对风剖面的影响更加显著,随着粗糙长度的增加,速度曲线的最大风速值略有减小,但最大风速所在的高度明显增大,第3类和第4类地貌下的速度曲线基本重合。r4=2.0Djet处,随着粗糙长度的增加,速度曲线的最大风速值减小,最大风速所在的高度增大。可以看出,随着径向距离的增加,地面粗糙度对风剖面的影响愈加显著。在r5=3.0Djet处,光滑壁面条件下风剖面的最大风速值vmax=12.851 m/s,最大值所在高度为zmax=3.053 m,然而在第4类地貌条件下,风速剖面的最大风速vmax=10.331 m/s,所在高度为zmax=22.799 m;最大风速值vmax降低了19.61%,最大风速所在高度zmax增加了6.47倍。在r6=4.0Djet处,光滑壁面条件下风剖面的最大风速值vmax=9.969 m/s,最大值所在高度zmax=3.481 m,而在第4类地貌条件下,风速剖面的最大风速为vmax=7.509 m/s,所在高度zmax=26.962 m;最大风速值vmax降低了24.68%,最大风速所在高度zmax增加了6.75倍。
对比图 6中不同径向位置的风剖面可知:在风暴中心附近(r≤1.0Djet),地面粗糙度对于风剖面的影响较小;但在1.0Djet < r≤2.0Djet,地面粗糙度对风剖面开始产生较为明显的影响;r≥2.0Djet,地面粗糙度对风剖面的影响非常显著。
分析其原因,在距离风暴中心较近的位置处,下沉气流刚刚冲击地面形成近地风,地面粗糙度的影响并未显现;在距离风暴中心较远的位置处,随着下沉气流冲击地面后形成的近地风在沿径向发展的过程中经过粗糙的地面,产生能量耗散效应,地面粗糙度对于风剖面的影响才逐渐变得显著,且不同地貌下的竖直风剖面产生较大差异。
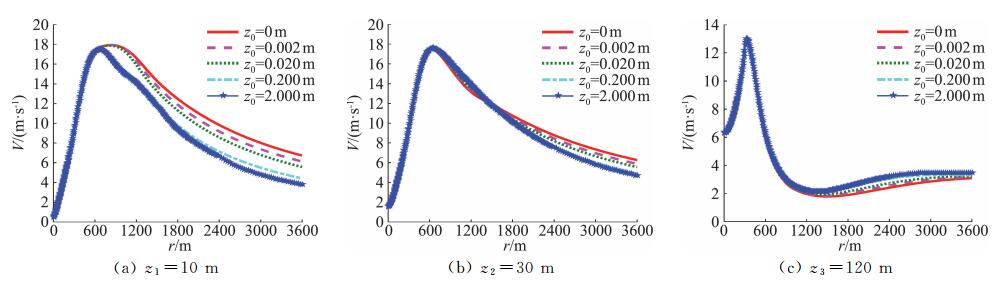
2.2 径向风剖面下击暴流的径向风剖面表征下击暴流的风速沿径向距离的变化规律。为了考察地面粗糙度对下击暴流径向风剖面的影响,选取距地面分别为z1=10 m、z2=30 m和z3=120 m三个高度位置的径向风剖面,如图 7所示。
|
图 7 下击暴流径向风剖面 Fig.7 Radial wind profiles of downburst |
从图 7中可以看出,在z1=10 m高度,地面粗糙度对下击暴流径向风剖面影响显著,随着地面粗糙长度的增加,沿径向发展的方向,下击暴流的风速从最大风速值下降更迅速,而且影响范围广;z2=30 m和z3=120 m高度,地面粗糙度对风剖面的影响主要体现在远离风暴中心的区域,随着地面粗糙长度的增加,沿径向发展的方向,下击暴流的风速逐步降低。
需要注意的是,在远离风暴中心的区域,下击暴流的风速值已经从最大风速逐步下降到较小的幅值范围。但考虑到下击暴流的最大风速在近地面高度产生,当遭遇强下击暴流时,在距离风暴中心较远的径向位置下击暴流引起的近地面强风仍然具有很大的威胁和破坏性。在下击暴流形成后并沿径向扩散过程中,不能因下击暴流存在自然衰减过程而忽视地面粗糙度对风场特征的影响。
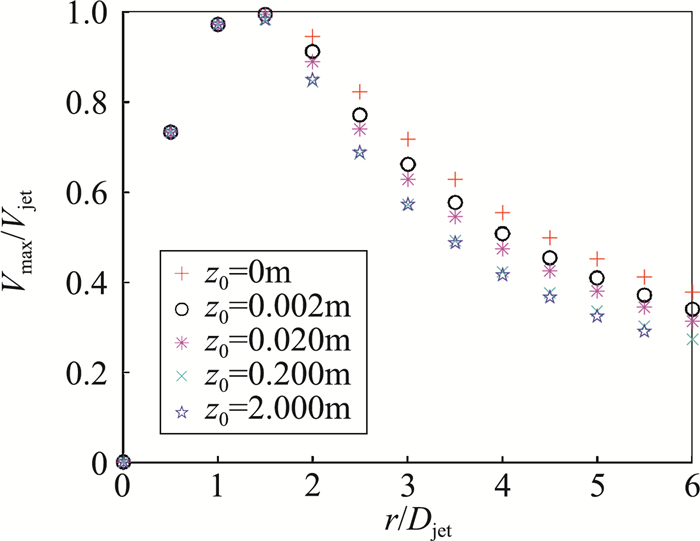
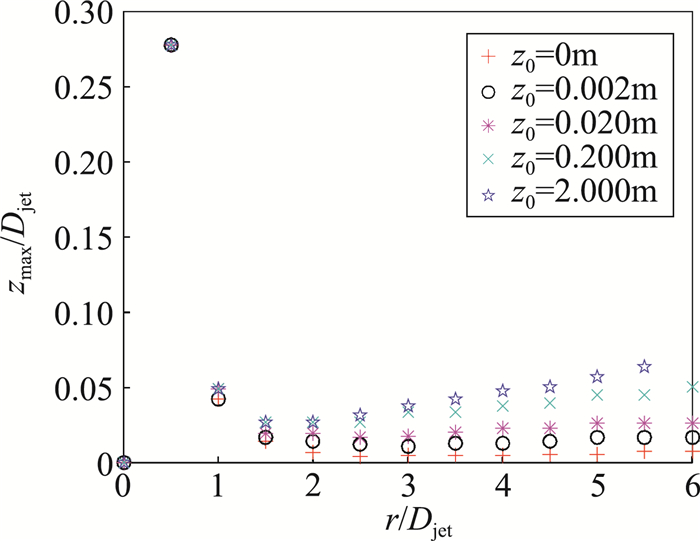
2.3 最大水平风速除了风剖面的形态特征,最大风速值也是风剖面特性中的重要特征参数之一。图 8和图 9分别是不同地面粗糙类别下各径向位置下击暴流水平风速最大值及其所在高度。
|
图 8 最大水平风速值 Fig.8 Maximal radial wind velocity value |
|
图 9 最大水平风速所在高度 Fig.9 Heights with maximal radial wind velocity |
从图 8和图 9中可以看到,在下击暴流风暴中心附近(r≤1.0Djet),各径向位置的最大风速值和最大风速所在高度都基本不受地面粗糙度影响。随着径向位置远离风暴中心,地面粗糙度的影响愈加显著。随着地面粗糙长度的增加,各径向位置的最大风速值逐渐下降,而最大风速所在高度逐步上升。
结合下击暴流的竖直风剖面的分布特点(见图 6),下击暴流的风速在近地面区域达到最大值,在这个高度范围内地面粗糙度对于风剖面的影响显著。因此,地面粗糙度对下击暴流风剖面特征的影响不能忽略,需要在积累更多研究数据特别是实测数据的基础上,在风剖面模型中考虑地面粗糙度的修正。
3 结论(1) 在距离风暴中心较近的位置(r≤1.0Djet),下沉气流刚刚冲击地面形成近地风,地面粗糙度的影响并未显现,各径向位置的最大风速值和最大风速所在高度都基本不受地面粗糙度影响;随着下沉气流冲击地面后形成的近地风在沿着径向发展,地面粗糙度对于风剖面的影响变得显著,不同地面粗糙度下的竖直风剖面存在较大差异;
(2) 在近地面高度,地面粗糙度对下击暴流径向风剖面影响显著,随着地面粗糙长度的增加,下击暴流的风速下降迅速,且影响范围大;随着高度增加,地面粗糙度对风剖面的影响主要体现在远离风暴中心的区域;
(3) 下击暴流的风速在近地面区域达到最大值,在这个高度范围内地面粗糙度对于风剖面的影响显著。地面粗糙度对下击暴流风剖面特征的影响不能忽略,需要在下击暴流风剖面模型中考虑地面粗糙度的修正。
| [1] |
FUJITA T T. Manual of downburst identification for project NIMROD[R]. SMRP-RP-156. NASA-CR-156953, 1978.
|
| [2] |
PROCTOR F H. Numerical simulations of an isolated microburst. Part Ⅱ:Sensitivity experimentst[J]. Journal of Atmospheric Sciences, 1989, 46(14): 2143-2165. DOI:10.1175/1520-0469(1989)046<2143:NSOAIM>2.0.CO;2 |
| [3] |
DEMPSEY D, WHITE H. Winds wreak havoc on lines[J]. Transmission and Distribution World, 1996, 48(6): 32-37. |
| [4] |
SHEN J, PARKS E K, BACH R E. Comprehensive analysis of two downburst-related aircraft accidents[J]. Journal of aircraft, 1996, 33(5): 924-930. DOI:10.2514/3.47037 |
| [5] |
LETCHFORD C W, MANS C, CHAY M T. Thunderstorms-their importance in wind engineering, a case for the next generation wind tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12-15): 1415-1433. DOI:10.1016/S0167-6105(02)00262-3 |
| [6] |
瞿伟廉, 吉柏锋. 下击暴流的形成与扩散及其对输电线塔的灾害作用[M]. 科学出版社, 2013. QU W L, JI B F. Formation and diffusion of downburst and its disaster effects on transmission tower[M]. 2013. (in Chinese) |
| [7] |
FUJITA T T. Tornadoes and downbursts in the context generalized planetary scales[J]. Journal of Atmospheric Science, 1981, 38(8): 1511-1534. DOI:10.1175/1520-0469(1981)038<1511:TADITC>2.0.CO;2 |
| [8] |
KIM J D, HANGAN H. Numerical simulations of impinging jets with application to downbursts[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(4): 279-298. DOI:10.1016/j.jweia.2006.07.002 |
| [9] |
SENGUPTA A, SARKAR P P. Experimental measurement and numerical simulation of an impinging jet with application to thunderstorm microburst winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(3): 345-365. DOI:10.1016/j.jweia.2007.09.001 |
| [10] |
MASON M S, WOOD G S, FLETCHER D F. Impinging jet simulation of stationary down burst flow over topography[J]. Wind and Structures, an International Journal, 2007, 10(5): 437-462. DOI:10.12989/was.2007.10.5.437 |
| [11] |
MASON M S, WOOD G S, FLETCHER D F. Numerical simulation of downburst winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2009, 97(11-12): 523-539. DOI:10.1016/j.jweia.2009.07.010 |
| [12] |
吉柏锋, 瞿伟廉. 下击暴流作用下高层建筑物表面风压分布特性[J]. 华中科技大学学报(自然科学版), 2012, 40(9): 89-94. JI B F, QU W L. Mean wind pressure distribution characteristics on tall building under downburst[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(9): 89-94. (in Chinese) |
| [13] |
吉柏锋, 瞿伟廉, 王翼飞, 等. 下击暴流竖直风剖面的时变特征[J]. 武汉理工大学学报, 2013, 35(10): 92-97. JI B F, QU W L, WANG Y F, et al. Study on time varying characteristics of downburst vertical wind profile[J]. Journal of Wuhan University of Technology, 2013, 35(10): 92-97. DOI:10.3963/j.issn.1671-4431.2013.10.018 (in Chinese) |
| [14] |
汤卓, 吕令毅. 雷暴冲击风荷载的大涡模拟[J]. 空气动力学学报, 2011, 29(1): 47-51. TANG Z, LV L Y. Large eddy simulation of downburst wind load[J]. Acta Aerodynamica Sinica, 2011, 29(1): 47-51. DOI:10.3969/j.issn.0258-1825.2011.01.008 (in Chinese) |
| [15] |
LI C, LI Q S, XIAO Y Q, et al. A revised empirical model and CFD simulations for 3D axisymmetric steady-state flows of downbursts and impinging jets[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 102: 48-68. DOI:10.1016/j.jweia.2011.12.004 |
| [16] |
王超, 汪之松, 李正良. 冲击射流与壁面射流风剖面特征比较和影响因素参数化分析[J]. 工程力学, 2015, 32(11): 86-93. WANG C, WANG Z S, LI Z L. Comparison and parametric analysis of wind profile characteristics of impinging jet and wall jet[J]. Engineering Mechanics, 2015, 32(11): 86-93. DOI:10.6052/j.issn.1000-4750.2014.04.0294 (in Chinese) |
| [17] |
陈勇, 彭志伟, 楼文娟, 等. 冲击风稳态流场CFD模拟及三维风速经验模型研究[J]. 计算力学学报, 2010, 27(3): 428-434. CHEN Y, PENG Z W, LOU W J, et al. CFD simulations of steady downbursts and 3D wind velocity empirical models[J]. Chinese Journal of Computational Mechanics, 2010, 27(3): 428-434. (in Chinese) |
| [18] |
陈勇, 柳国光, 徐挺, 等. 运动雷暴冲击风水平风速时程分析及现象模型[J]. 同济大学学报:自然科学版, 2012, 40(1): 22-26. CHEN Y, LIU G G, XU T, et al. Time histories of horizontal wind velocity of moving thunderstorms and phenomenological model[J]. Journal of Tongji University (Natural Science), 2012, 40(1): 22-26. (in Chinese) |
| [19] |
邹鑫, 汪之松, 李正良. 稳态雷暴冲击风风速剖面模型研究[J]. 振动与冲击, 2016, 35(15): 74-79. ZOU X, WANG Z Z, LI Z L. Wind velocity profile model of steady thunderstorm downburst[J]. Journal of Vibration and Shock, 2016, 35(15): 74-79. (in Chinese) |
| [20] |
邓院昌, 刘沙, 余志, 等. 实际地形风场CFD模拟中粗糙度的影响分析[J]. 太阳能学报, 2010, 31(12): 1645-1648. DENG Y C, LIU S, YU Z, et al. Effect of roughness on CFD wind field simulation over natural terrain[J]. Acta Energiae Solaris Sinica, 2010, 31(12): 1645-1648. (in Chinese) |
| [21] |
GB 50009-2012.建筑结构荷载规范[S]. 2012-10-01. GB 50009-2012. Building Structure Load Specification[S]. 2012-10-01. (in Chinese) |
| [22] |
ANSI/ASCE7-10. Minimum design loads for buildings and other structures[S]. 2010-01-01.
|
| [23] |
AS/NZS 1170.2: 2002. Structural design actions, Part 2: Wind actions[S]. 2002-01-01.
|
| [24] |
Fluent 14. 0 User's guide[M]. ANSYS FLUENT Inc, 2011.
|
| [25] |
BLOCKEN B, STATHOPOULOS T, CARMELIET J. CFD simulation of the atmospheric boundary layer:Wall function problems[J]. Atmospheric Environment, 2007, 41(2): 238-252. DOI:10.1016/j.atmosenv.2006.08.019 |
| [26] |
BLOCKEN B, PERSOON J. Pedestrian wind comfort around a large football stadium in an urban environment:CFD simulation, validation and application of the new Dutch wind nuisance standard[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2009, 97(5): 255-270. |
| [27] |
OSEGUERA R M, BOWLES R L. A simple analytic 3-dimensional downburst model based on boundary layer stagnation flow[R]. NASA TM-100632, 1988.
|
| [28] |
VICROY D D. A simple, analytical, asymmetric microburst model for downdraft estimation[R]. NASA TM-104053, 1991.
|
| [29] |
WOOD G S, KWOK K C S. An empirically derived estimate for the mean velocity profile of a thunderstorm downburst[C]//Proceedings of 7th Australian Wind Engineering Society Workshop, Melbourne: Australian Wind Engineering Society, 1998.
|
| [30] |
LETCHFORD C, ILLIDGE G C. Turbulence and topographic effects in simulated thunderstorm downdrafts by wind tunnel jet[C]//Proceedings of 10th International Conference on Wind Engineering, Copenhagen: The International Association for Wind Engineering, 1999.
|
| [31] |
HJELMFELT M R. Structure and life cycle of microburst outflows observed in Colorado[J]. Journal of Applied Meteorology, 1988, 27(8): 900-927. DOI:10.1175/1520-0450(1988)027<0900:SALCOM>2.0.CO;2 |
 2019, Vol. 37
2019, Vol. 37

