2. 大连理工大学 工程力学系, 大连 116024
2. Department of Engineering Mechanics, Dalian University of Technology, Dalian 116024, China
流体微团加速到超声速以后无法感知到达之前遇到的空间物体,只能在物体前通过急剧压缩的激波才能把速度降下来。因此,激波是可压缩流动的基本特征。早期计算流体力学(CFD)的算法无法模拟这一现象,直到1954年Lax提出处理包含有间断流动问题的弱解理论后[1-2],国内外众多科学家开始研究在计算过程中能自动分辨出激波的算法,提出TVD、NND、ENO、WENO等具有里程碑意义的激波捕捉格式[3],解决了航天航空等领域很多工程模拟问题,极大提高了CFD地位,使其发展为一个重要的学科分支。尽管建立这些格式时考虑了激波间断,但是本质上还是1950年von Neumann提出的把间断描述成流动参数连续变化过渡区的思路[4],构造出来的格式存在以下难以克服的理论困境。
数值计算的离散格式是对偏微分方程的近似,按照CFD收敛性理论,数值解随着网格尺度减小趋向理论解,CFD追求的极限是方程的理论解,原则上说对于方程不能描述的流动现象,数值解和实验值不具有可比性。海平面环境下马赫数小于10的激波厚度大约1×10-8 m,流体在这么小的空间内受到剧烈压缩,暂且不说准确模拟所需要的网格尺度及其带来的计算量,从连续介质假设出发建立的N-S方程是否适用于激波模拟也存在争议,因为Stoke假设(3λ+2μ=0)不再成立[5],计算时需要对体积膨胀黏性系数λ进行修正才能得到与实验相符的激波内部温度[6]。从事稀薄气体动力学研究的学者认为激波内部结构涉及到热力学非平衡,连续介质假设本身就不成立,“从理论上说,Navier-Stokes方程不能用来描述激波结构的[7]”。无黏流体力学把激波表示成间断,两侧参数和运动速度满足兰金-许贡纽(Rankine-Hugoniot, R-H)关系式,这是迄今为止几乎很少有争议的理论。所谓间断在数学上就是在同一空间位置对应至少两组(激波前后)流体变量,在多维情况下可能更多,例如二维马赫反射三岔点有四组流体变量。很多基于弱解理论构造的激波捕捉格式考虑了间断,但是用参数连续变化的思路描述激波注定不可能计算出真正的数学间断,捕捉到的激波主要是现象模拟。
按照上述观点,常规N-S方程及其理论解不能用来描述激波内部物理现象,那么基于离散格式的数值解至少在过渡区内没有物理意义,采用Euler方程产生的后果是无法评价过渡区内数值解的精度(激波前后参数相差很大),激波捕捉格式对于激波相交等现象更是无能为力。
20世纪60年代Moretti等人将激波装配方法和Lax-Wendroff格式结合,在CDC 600型计算机上进行,总耗时为360 s,给出了超声速钝头体问题的数值解,2002年Moretti回顾从业36年来CFD领域模拟激波的进展,针对超声速钝头体绕流比较了捕捉法和装配法计算结果,认为准确模拟激波还需要发展装配法[8-9]。对于50年前提出的装配法,文献[10]的评价具有代表性——“激波装配法具有计算精度高、物理概念清晰等优点,但是计算过程复杂、计算量大,并且必须事先知道激波的大概位置。一般来说,激波装配法仅适用于那些激波比较简单而事先可以估计激波形状和位置的定常流动问题。”
造成计算复杂的主要原因是求解过程中激波运动和变形。装配法减少了网格量,造成计算量大的原因是激波及其相交点等空间网格点需要判别、标记或特殊处理,增加代码编写复杂性和并行计算难度。随着CFD网格技术发展,这些难点也得到缓解。国外文献把最早Moretti提出的称为边界激波装配法,仅能处理形状较为规则和位移不大的脱体激波。后来Richtmyer等人[11]提出了浮动激波装配方法,在静止网格基础上嵌入R-H关系式,允许激波在背景网格上滑动,解决了内部激波装配难题。近年来Zhong等人将这种方法和高精度有限差分格式相结合有效提高内部光滑流场的计算精度,成功应用于许多高超声速流动的求解中[12-13]。基于结构网格的边界激波装配法和浮动激波装配法在模拟激波相交和马赫反射等复杂波系结构时面临一定困难。Paciorri和Bonfigolioli等人[14-16]采用非结构网格技术和局部网格重构提出了激波阵面追踪法,记录激波在背景网格上的位置,对激波附近的背景网格进行挖洞,然后再利用Delanay方法在洞内重构以激波阵面分界的新网格,时间推进过程中根据R-H关系式得到新的激波位置,重新判别、挖洞和填补背景网格。这种算法不需要考虑网格节点之间的连接关系,也就减少了对于特殊点进行处理的麻烦,增加了代码的普适性,但是在激波边界节点对应的网格单元只能采用一阶插值,像常用的多块重叠网格技术一样存在插值引起的精度降低问题。其次,不允许激波在一个时间步内跨越多个网格节点,通常选择足够小的时间步长,因而对计算效率有所影响。上述这3类装配法时间推进过程中需要判别激波位置,增加了计算量,而且激波前后网格数目是变化的,不利于并行计算。2015年刘君等人[17]提出了基于非结构动网格的激波(间断)装配方法,从能够描述网格变形的任意拉格朗日-欧拉坐标系(Arbitrary Lagrangian-Eulerian, ALE)下的控制方程出发,得到激波位置及其两侧的参数后,装配的激波就变成了一个移动边界,对于存在内部激波的计算域则变成类似于拼接网格的多个分区,激波运动由上下游参数驱动,采用成熟的动网格技术[18]进行移动和变形。与Paciorri及Bonfigolioli的装配法相比,在保留非结构网格的优点外,新的装配法不需要在每一步对计算网格进行挖洞重构,避免了插值误差,易于并行计算,并且时间步长不受限制。采用这种算法模拟了内部存在正规反射和马赫反射等复杂激波结构的算例[19-21],从效果看,较好地解决了传统装配法遇到的“计算过程复杂、计算量大”问题。
为了突破“激波装配法仅适用于那些激波比较简单而事先可以估计激波形状和位置的定常流动问题”的限制,刘君等人提出了在采用捕捉法计算的流场基础上辨识并装配主要激波结构、计算过程中自动装配内部细致结构和新生激波的解决思路。在技术途径上提出了新的数据结构,在激波边界通量计算时,如果采用Roe、van Leer、AUSM等格式就是捕捉法,如果采用R-H关系式就是装配法,实现两种方法之间任意转换。按照上述思路,为了解决装配法的应用难题,亟需发展激波、接触间断等流场特征结构的辨识算法。
目前,常用的激波辨识算法主要有三种[22]:第一种根据最大变量梯度确定激波面,该方法实现简单,但需要设置合适的过滤器才能消除错误的结果;第二种为法向马赫数法[24],该方法认为在激波面上流动的法向马赫数等于1,该方法与第一种方法相比适用性更强,但也需要设置适当的过滤器才能获得良好结果,且难以用于探测接触间断;第三种为基于特征线理论的方法[25-26],该方法与前两种方法相比更精确、更有效,但实施过程复杂且计算量大。
综上所述,这些激波辨识算法难以在复杂三维问题中广泛应用,且上述算法辨识出的激波通常为具有一定宽度的激波带,难以直接用于装配法。因此,需要发展新的辨识算法来推动激波装配法实用化进程。
本文提出了一种光源射线法,该方法可将捕捉法中探测到的具有一定宽度的激波带拟合成一系列离散线段(二维)或三角形面片(三维),利用曲线/曲面拟合算法进一步将其拟合成连续的曲线/曲面。该曲线/曲面可作为激波装配法中的激波面,并且可根据计算需要对其进行任意形式的网格划分。为便于表述,先用二维模型的实际操作过程进行原理说明,然后简单介绍三维推广过程,并展示实际工程问题的辨识结果。
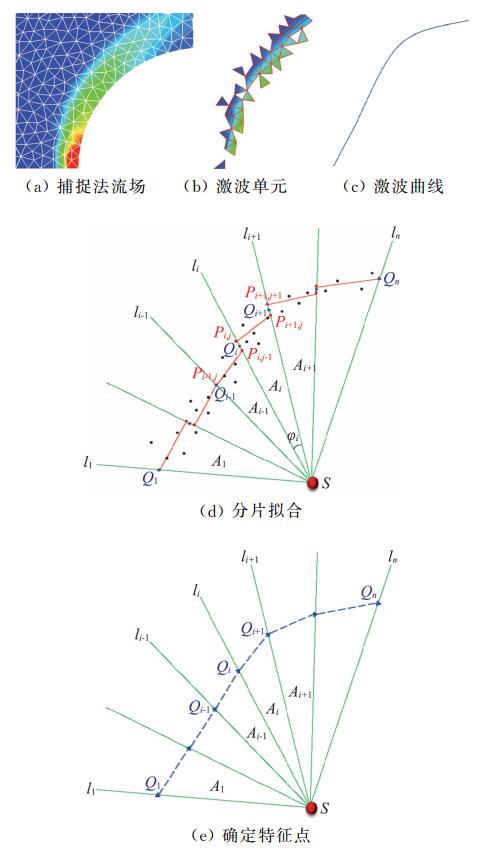
1 流场结构辨识算法 1.1 二维辨识算法流程算法的基本实现过程为:首先,通过流动特征探测技术辨识出符合流动特征要求的单元。如图 1(a)为超声速钝体扰流的流场结构,图 1(b)为利用激波探测技术在上述流场中辨识出的激波单元。上述激波单元的格心或格点构成集合T。其次,在钝体内部空间设置光源点S,设定角度间隔φ1… φi… φn-1,从光源处发射出来的n条光线l1… li… ln将空间分割为n-1个子区域,射线li和li+1构成区域Ai的边界,φi为射线li和li+1夹角,如图 1(d)所示。单个区域Ai内的所有离散点构成子集Ti,满足T=
|
图 1 光源射线法示意图 Fig.1 Sketch of source-rays method |
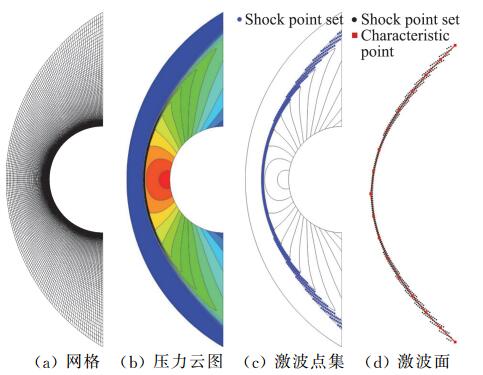
针对二维超声速钝头体绕流问题,采用1.1节所述方法进行激波面辨识。算例中,空气来流马赫数Ma=5.0、无量纲密度ρ=1、无量纲温度T=1,来流攻角为0°。钝头体中心位置坐标为(0, 0),钝头体半径为0.0254。网格为160×100的四边形网格,其中沿钝头体法向的节点数为100。计算网格和捕捉法流场压力云图分别如图 2(a)和图 2(b)所示。
|
图 2 基于压力梯度的激波辨识结果 Fig.2 Shock wave surface extraction based on pressure gradient |
考虑到很多高精度格式的限制器选择压力梯度来进行调节,在此也将其作为激波特征参数来探测脱体激波。对于捕捉法得到的压力场,用格林公式计算出每个网格单元的压力梯度矢量。作为间断面,激波厚度理论上处于分子自由程大小这一数量级,其两侧压力的梯度值为无穷大。但是,在捕捉法数值计算中,激波表现为带状分布的过渡区且具有较大压力梯度。对于不同的问题以及不同的计算网格,激波带上的压力梯度值都有所不同。因此,难以通过一个固定的压力梯度值将激波带提取出来。本文为了准确获得激波点集的分布,首先计算出流场中的最大压力梯度值|∇p|max,然后针对不同问题设置相应的阈值系数k,压力梯度阈值|∇p|thre=k|∇p|max,所有满足条件|∇p|≥|∇p|thre的单元格心点构成激波点集T。Case1取阈值系数k=0.1,获得离散点集,如图 2(c)所示。针对上述激波离散点集,采用光源射线法进行曲线拟合。光源S位置固定在(x, y)=(0.1, 0)处,相邻两条射线间的夹角取常值φi=4.5°。辨识出的结果如图 2(d)所示,从图中可以看出辨识出的激波曲线与捕捉法流场中的激波点集T吻合度很高,能准确描述激波形状,对激波曲线重新进行网格离散即可作为激波边界直接用于激波装配法。
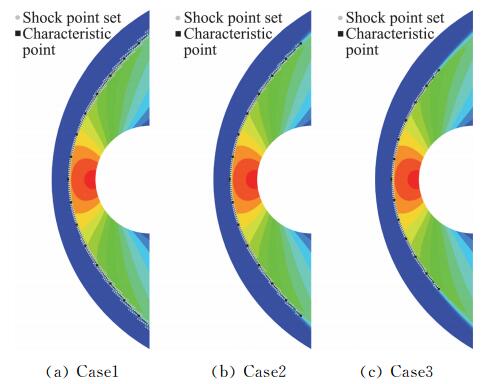
离散点集的分布取决于所选择参数和阈值,为了比较不同压力梯度阈值下所辨识出的激波曲线,在捕捉法流场的基础上另外补充两个辨识状态:Case2取k=0.2,Case3取k=0.3。得到的点集及其最终辨识出来的脱体激波曲线如图 3所示。从3个状态的辨识结果可以看出,不同的压力梯度条件下所获取的离散点集有所不同,导致最终辨识出的激波曲线长度有所区别,但三条激波曲线都能与捕捉法流场中激波的位置和形状保持一致,将其作为激波装配法中的激波边界可快速得到收敛解。得到初始激波位置以后的装配法计算方法和过程参见文献[17, 19-21],这里不再赘述。
|
图 3 不同压力梯度阈值下的脱体激波辨识结果比较 Fig.3 Comparison of shock surface extraction results under different pressure gradient thresholds |
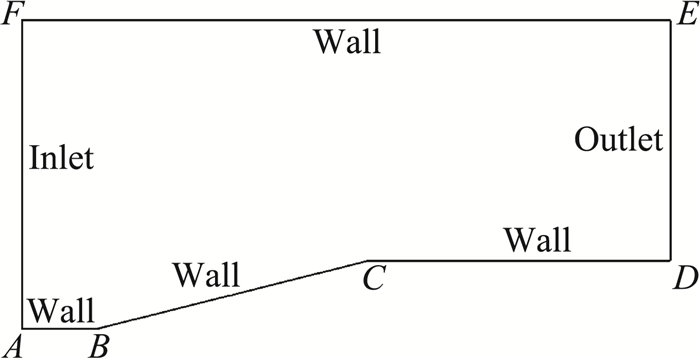
对波系更为复杂的马赫反射问题进行数值模拟,计算区域及边界条件如图 4所示。边长为LAF=0.4、LAB=0.1、LDE=0.312、LEF=0.85,斜楔BC倾角为14°;边界AF为超声速入口、DE为超声速出口,其余为滑移壁。计算网格为300×218的四边形网格,其中入口和出口边界上的网格节点数为300。来流马赫数Ma=1.9,攻角为0°。
|
图 4 计算域 Fig.4 Calculation domain |
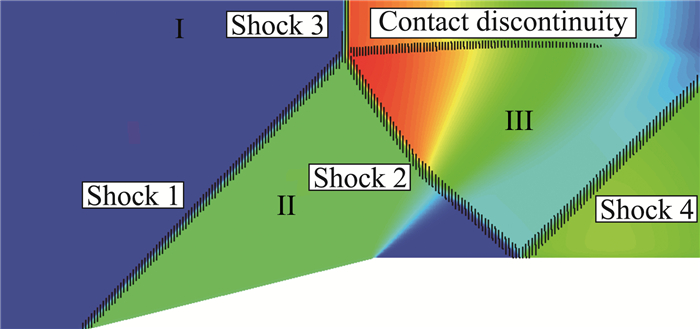
由于斜楔BC的偏转作用,自由来流在点B处产生一道入射激波(Shock1);激波达到壁面FE处时发生马赫反射,产生一道反射激波(Shock2)和一条马赫杆(Shock3);反射激波在壁面CD处再次发生反射,产生第二道反射激波(Shock4)。流场稳定后的密度云图以及波系结构如图 5所示。采用激波及接触间断探测方法可从流场中获得主要的四条激波点集和一条接触间断点集分布。为了检验不同的探测方法对最终结果的影响,激波点集采用密度梯度作为参考量进行探测,接触间断点集由密度梯度和压力梯度共同决定。同样,先计算出全场最大密度梯度值|∇ρ|max和最大压力梯度|∇p|max。激波探测的密度梯度阈值|∇ρ|threS=kρS|∇ρ|max,所有满足|∇ρ|≥|∇ρ|threS的单元节点构成激波点集,这里取kpS=0.03。接触间断单元由密度梯度和压力梯度共同决定,满足密度梯度较大且压力梯度较小,即|∇ρ|≥|∇ρ|threc、|∇p|≤|∇p|threc,其中|∇ρ|threc=kρc|∇ρ|max、|∇p|threc|=kpc|∇p|max。所有满足该条件的单元节点构成曲线拟合所需的接触间断点集。这里取kρc=0.05、kpc=0.035,其中在不同密度梯度阈值|∇ρ|threc下辨识出的接触间断长度有一定区别,但位置和形状基本一致。激波和接触间断离散点集分布如图 5所示。
|
图 5 捕捉法密度云图及间断点集分布 Fig.5 Density contours and discontinuity point set distribution under shock-capturing schemes |
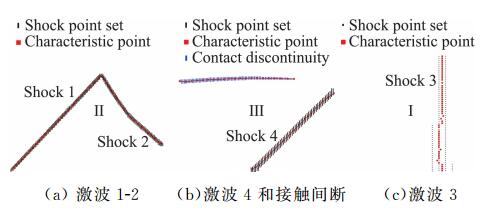
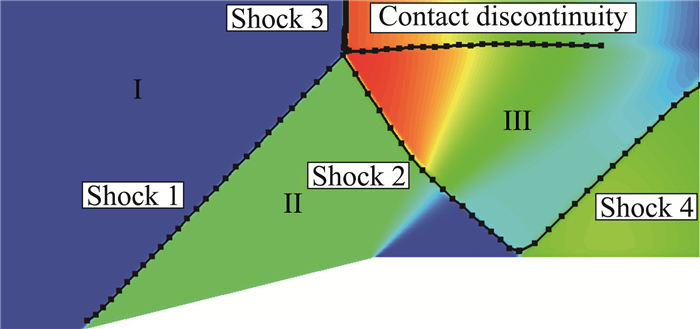
获得离散点集后,通过在区域内合理布置光源可拟合出每条激波和接触间断曲线。首先在Ⅱ区设置一个光源,光源发出等间距射线,采用上文光源射线法可辨识出表征激波1和激波2的曲线,如图 6(a)所示。同理,在Ⅲ区布置光源可辨识出激波4和接触间断曲线,如图 6(b)所示。在I区设置光源可辨识出马赫杆曲线,如图 6(c)所示。所有曲线的最终辨识结果与流场密度云图的比较如图 7所示。可以看出,辨识出的曲线与采用捕捉法获得的波系结构高度吻合,直接用于装配法有助于快速得到收敛解。得到初始激波位置以后的装配法计算方法和过程参见文献[17, 19-21],后文也会有简单介绍,这里不再赘述。
|
图 6 激波和接触间断辨识过程 Fig.6 Shock wave and contact discontinuity surface extraction process |
|
图 7 激波及接触间断辨识结果与流场比较 Fig.7 Comparison between feature surface extraction result and flow field structure |
值得注意的是,这里光源的位置分布并不唯一,可采用不同的分布方式达到相似的效果,比如可先在Ⅰ区设置光源同时拟合出激波1和激波3曲线,再在Ⅲ区设置光源得到激波2、激波4和接触间断曲线。
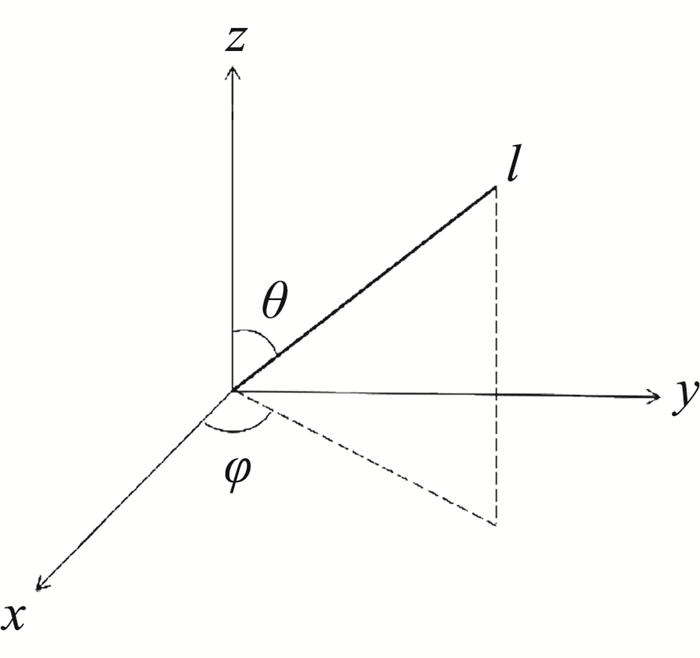
2 三维实现 2.1 三维辨识算法流程三维问题的辨识过程与二维类似,首先通过流场探测技术获取捕捉法流场中相应流动特征的离散点集,然后在离散点集的基础上利用光源射线法进行特征曲面的拟合。三维问题中射线l的方向在直角坐标系中由两个角度决定,分别为与z轴的夹角θ以及l在xy平面内的投影与x轴的夹角φ,如图 8所示。通过给定一系列角度{θi, φi},离散点集T所在的空间区域A被射线集{li}分割成n个子区域。每个子区域Ap由三条射线li、lj和lk构成,满足
|
图 8 射线方向示意图 Fig.8 Ray direction |
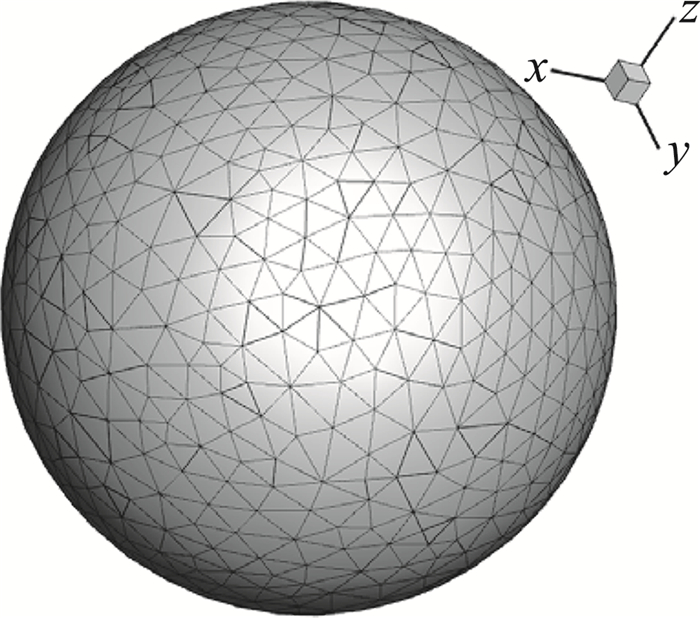
本文通过引入单位球可确定各射线之间的连接关系,如图 9所示。对半径为1的球面进行三角形离散,获得一系列三角形面片,各顶点连接关系确定,且三角形面片满足连续且不相交条件。
|
图 9 单位球 Fig.9 Unit sphere |
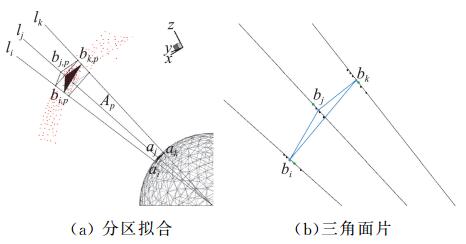
将单位球的球心作为光源S,球心与单位球上三角形面片的三个顶点ai、aj、ak的连线li、lj、lk构成一个子区域Ap,如图 10(a)所示。若Ap内离散点的个数不小于3,则对Ap内所有离散点进行平面拟合,拟合出的平面与三条射线的交点分别为bi, p、bj, p和bk, p;若该子区域内离散点的个数小于3,则跳过该区域。所有区域拟合完成后,每条射线li与不同子区域内的拟合平面形成若干交点。将各射线li上的交点取平均值获得特征点bi,则各子区域Ap的三条射线边界上的特征点bi、bj和bk构成目标三角形面片,如图 10(b)所示。最终,整个离散点集T被拟合成一系列连续的三角形面片,三角形面片顶点的连接关系由单位球确定。可对上述三角形面片构成的空间曲面重新进行网格划分,获得可用于装配法的激波面网格。
|
图 10 子区域内三角形面片拟合过程 Fig.10 Triangular fitting process in sub-region |
通过以下两个算例验证本文辨识算法在三维问题中的有效性。
算例一:对三维半椭球面进行辨识。椭球面方程为
| $ \left\{\begin{array}{l}{x=a \sin \theta \cos \varphi} \\ {y=b \sin \theta \cos \varphi} \\ {z=c \cos \theta}\end{array}\right. $ |
在椭球面附近随机生成100 000个点作为离散点集,随机点坐标B(x′, y′, z′)满足:
| $ \left\{\begin{array}{l}{x^{\prime}=a^{\prime} \cos \theta^{\prime} \cos \varphi^{\prime}} \\ {y^{\prime}=b^{\prime} \cos \theta^{\prime} \sin \varphi^{\prime}} \\ {z^{\prime}=c^{\prime} \sin \theta^{\prime}}\end{array}\right. $ |
其中,
| $ \left\{\begin{array}{l}{a^{\prime}=(0.97+0.06 k) a} \\ {b^{\prime}=(0.97+0.06 l) b} \\ {c^{\prime}=(0.97+0.06 m) c} \\ {\varphi^{\prime}=\alpha_{1}+i\left(\alpha_{2}-\alpha_{1}\right), \quad 0 \leqslant \alpha_{1}, \quad \beta_{2} \leqslant 2 \pi} \\ {\theta^{\prime}=\beta_{1}+j\left(\beta_{2}-\beta_{1}\right), \quad 0 \leqslant \beta_{1}, \quad \beta_{2} \leqslant 0.5 \pi}\end{array}\right. $ |
式中,i、j、k、l、m为区间[0, 1]内的随机数。
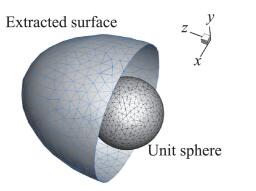
获得的离散点集如图 11所示。单位球共有736个节点、1468个三角形单元(如图 9),球心位置坐标为(0, 0, 0)。单位球位置及椭球面辨识结果如图 12所示。从结果可以看出,辨识出的曲面光滑完整且形状与离散点分布形状一致。

|
图 11 椭球随机点集 Fig.11 Random point set of ellipsoid |
|
图 12 单位球及拟合结果 Fig.12 Unit sphere and the extracted surface of ellipsoid |
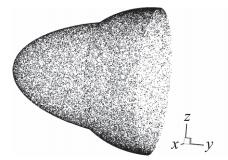
算例二:对三维双椭球面进行拟合。椭球面一满足方程
|
图 13 双椭球随机点集 Fig.13 Random point set of double-ellipsoid |
|
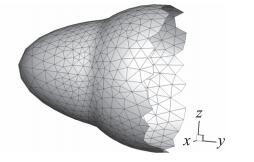
图 14 双椭球面拟合结果 Fig.14 Extracted surface of double-ellipsoid |
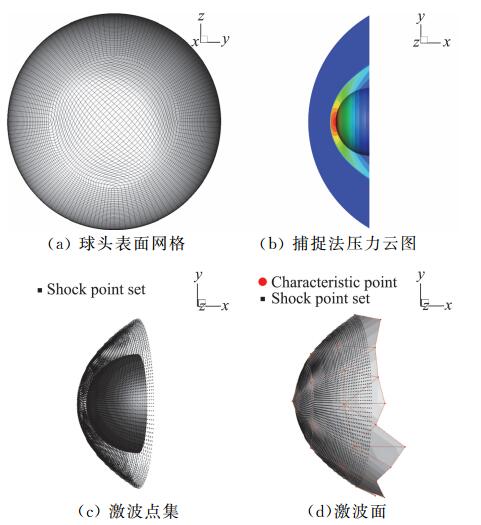
对三维超声速球头绕流进行模拟,来流马赫数Ma=5.0, 无量纲密度ρ=1.0, 无量纲温度T=1.0,来流攻角和侧滑角均为0°。球头的球心位置坐标为(0, 0, 0),球头半径为0.0254。计算网格共有508 365个的六面体单元,球面网格如图 15(a)所示。图 15(b)为流场压力云图,图 15(c)为根据流场压力梯度获得的激波带离散点集。算例中,压力梯度阈值系数k=0.05离散点为满足|∇p|≥|∇p|thre的所有单元节点,共有23 640个。单位球共包含1734个节点,3464个三角形面片,球心坐标为(2, 0, 0)。最终辨识出的激波面如图 15(d)所示,除了边缘附近外的其他区域辨识结果与离散点集吻合较好,将边缘位置稍作处理即可作为初始激波面用于激波装配法。对于不同的初始位置的激波,最终收敛解相同,故本例不再展示装配法的计算过程,计算方法参见文献[17, 19-21]。
|
图 15 三维超声速球头绕流激波辨识过程 Fig.15 Shock wave surface extraction process of 3D blunt body flow |
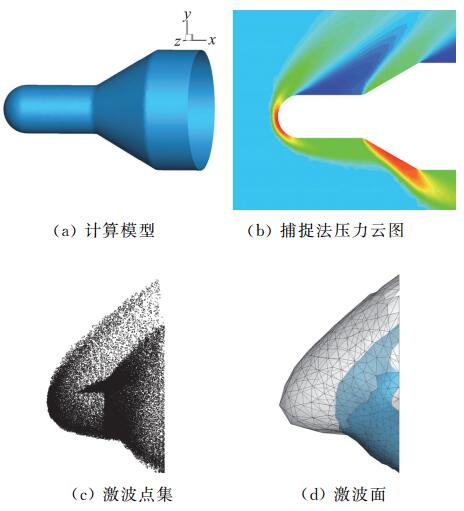
在球头绕流算例的基础上,对波系较为复杂的球柱锥组合体外形进行模拟,检验特征面提取方法处理三维复杂问题的能力。计算模型如图 16(a)所示,来流马赫数Ma=4.04,来流攻角为20°。波系结构如图 16(b)所示,在最外层形成一道弓形激波,在锥裙与柱体的结合处形成一个内嵌激波。探测出的激波点集和提取出的激波面分别如图 16(c)和图 16(d)所示。
|
图 16 球柱锥组合体绕流激波辨识过程 Fig.16 Shock wave surface extraction process of cylinder with a hemispherical nose and a conical flow |
利用上述方法获得初始激波面后,将其作为激波边界用于激波装配法,进行流动数值模拟,考查所述激波辨识方法在实际使用中的效果。
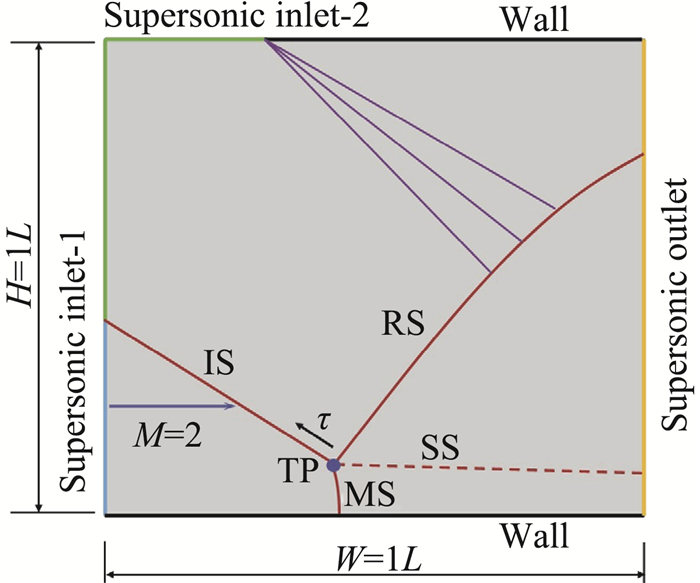
对于定常激波装配法,初始激波位置及形状会影响计算的收敛过程,但最终的收敛结果都相同。因此,本节直接采用文献[19]算例的部分结果说明激波装配法与捕捉法的区别。该算例为具有复杂波系结构的马赫反射问题,来流马赫数2.0,偏转角δ=14°。计算区域为L×L的正方形,边界上网格节点均匀分布,节点间距为0.01L,内部区域为三角形网格,单元数为22 429。流场波系结构及边界条件如图 17所示,入射激波IS和反射激波RS、马赫杆MS交于三波点TP,SS为接触间断。
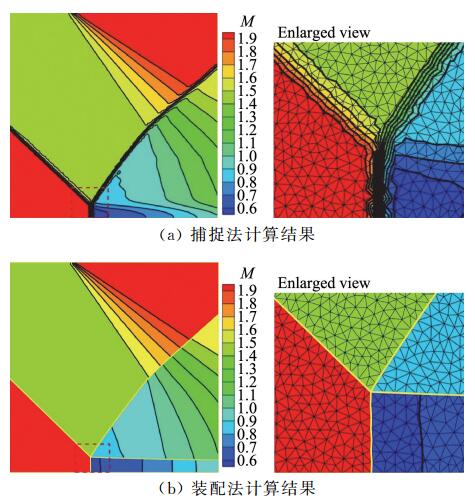
首先采用激波捕捉法获得初始流场,在此基础上采用本文辨识算法辨识出激波及接触间断的位置和形状,将其作为装配法的初始间断面,结合R-H关系式进行装配法流场计算。得到初始激波位置以后的计算过程参见文献[19],计算结果完全一致。下面给出部分结果,如图 18所示,其中图 18(a)为采用捕捉法的计算结果,图 18(b)为采用装配法的计算结果。从图中可以看出,捕捉法流场中激波附近出现等值线的扭曲和震荡,且激波呈带状分布,具有很宽的过渡区。与此相比,采用装配法所获得的流场中各区域之间界线分明,激波是一个没有宽度的界面,激波两侧变量值严格满足R-H关系式。
|
图 18 装配法与捕捉法计算结果对比(马赫数云图)[19] Fig.18 Comparison between shock-capturing solution and shock-fitting solution[19] |
通常对于具有一定“厚度”的空间点集,采用传统的拟合方法难以将其拟合成形状一致的光滑曲面,本文提出的光源射线法很好地解决了此类问题。
对于从捕捉法流场中获取的具有一定“厚度”的激波带和接触间断带,采用该方法进行空间曲面拟合后可作为激波装配法中的初始间断面。尤其对于具有复杂波系结构的流场,该方法提供了一种装配初始流场的途径。本文详细介绍了该算法在二维问题中的实现过程,并将其成功推广应用于三维问题。算例结果表明,辨识出的激波曲面整体上与捕捉法流场中激波带分布相吻合,但是三维问题中激波曲面边缘附近的辨识效果有待进一步提高。对于复杂工程问题,往往存在较为复杂的三维波系结构,间断面的提取过程更为困难和繁琐,该方法还需进一步完善。
对于传统激波装配法,在初始激波面给定后需要经过若干步迭代才能收敛到准确的形状和位置。尤其对于三维问题,收敛过程更加漫长,甚至出现难以收敛的情况。采用本文方法可提供较为准确的初始激波,有助于缩短收敛过程。
本文所提方法除了用于激波装配法外,未来还可应用于自适应网格算法。根据不同的流动特征可拟合出相应的空间曲面,进而可以任意调整该曲面附近区域的网格分布,达到网格根据流动特征自动调整的目的。
| [1] |
LAX P D. Weak solutions of nonlinear hyperbolic equations and their numerical computation[J]. Communications on Pure and Applied Mathematics, 1954, 7(1): 159-193. DOI:10.1002/(ISSN)1097-0312 |
| [2] |
LAX P, WENDROFF B. Systems of conservation laws[J]. Communications on Pure and Applied mathematics, 1960, 13(2): 217-237. DOI:10.1002/(ISSN)1097-0312 |
| [3] |
张涵信, 沈孟育. 计算流体力学-差分格式原理和应用[M]. 北京: 国防工业出版社, 2003. ZHANG H X, SHEN M Y. Computational fluid dynamics-theory and application of difference scheme[M]. Beijing: National Defense Industry Press, 2003. (in Chinese) |
| [4] |
VON NEUMANN J, RICHTMYER R D. A method for the numerical calculation of hydrodynamic shocks[J]. Journal of Applied Physics, 1950, 21(3): 232-237. DOI:10.1063/1.1699639 |
| [5] |
KUNDU P K. Fluid mechanics[M]. San Diego: Academic Press, 1990.
|
| [6] |
赵学瑞, 廖其奠. 黏性流体力学[M]. 北京: 机械工业出版社, 1983. ZHAO X R, LIAO Q D. Viscous fluid mechanics[M]. Beijing: China Machine Press, 1983. (in Chinese) |
| [7] |
吴其芬, 陈伟芳, 等. 稀薄气体动力学[M]. 湖南长沙: 国防科技大学出版社, 2004. WU Q F, CHEN W F. Rarefied gas dynamics[M]. Changsha: National University of Defense Technology Press, 2004. (in Chinese) |
| [8] |
ABBETT M, MORETTI G. A time-dependent computational method for blunt body flows[J]. AIAA Journal, 1966, 4(12): 2136-2141. DOI:10.2514/3.3867 |
| [9] |
MORETTI G. Thirty-six years of shock fitting[J]. Computers & Fluids, 2002, 31(4): 719-723. |
| [10] |
张德良. 计算流体力学教程[M]. 北京: 高等教育出版社, 2010. ZHANG D L. A Course in Computational Fluid Dynamics[M]. Beijing: Higher Education Press, 2010. (in Chinese) |
| [11] |
RICHTMYER R D, MORTON K W. Difference methods for initial-value problems[M]. New York: Interscience Publisher, 1967.
|
| [12] |
RAWAT P S, ZHONG X L. On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions[J]. Journal of Computational Physics, 2010, 229(19): 6744-6780. DOI:10.1016/j.jcp.2010.05.021 |
| [13] |
PRAKASH A, PARSONS N, WANG X, et al. High-order shock-fitting methods for direct numerical simulation of hypersonic flow withchemical and thermal nonequilibrium[J]. Journal of Computational Physics, 2011, 230(23): 8474-8507. DOI:10.1016/j.jcp.2011.08.001 |
| [14] |
PACIORRI R, BONFIGLIOLI A. A shock-fitting technique for 2D unstructured grids[J]. Computers & Fluids, 2009, 38(3): 715-726. |
| [15] |
PACIORRI R, BONFIGLIOLI A. Shock interaction computations on unstructured, two-dimensional grids using a shock-fitting technique[J]. Journal of Computational Physics, 2011, 230(8): 3155-3177. DOI:10.1016/j.jcp.2011.01.018 |
| [16] |
BONFIGLIOLI A, GROTTADAUREA M, PACIORRI R, et al. An unstructured, three-dimensional, shock-fitting solver for hypersonic flows[J]. Computers & Fluids, 2013, 73: 162-174. |
| [17] |
刘君, 邹东阳, 徐春光. 基于非结构动网格的非定常激波装配法[J]. 空气动力学学报, 2015, 33(1): 10-16. LIU J, ZOU D Y, XU C G. An unsteady shock-fitting technique based on unstructured moving grids[J]. Acta Aerodynamica Sinica, 2015, 33(1): 10-16. DOI:10.7638/kqdlxxb-2014.0109 (in Chinese) |
| [18] |
刘君, 徐春光, 白晓征. 有限体积方法和非结构动网格[M]. 北京: 科学出版社, 2016. LIU J, XU C G, BAI X Z. Finite volume methods and unstructured dynamic meshes[M]. Beijing: Science Press, 2016. (in Chinese) |
| [19] |
ZOU D, XU C, DONG H, et al. A shock-fitting technique for cell-centered finite volume methods on unstructured dynamic meshes[J]. Journal of Computational Physics, 2017, 345: 866-882. DOI:10.1016/j.jcp.2017.05.047 |
| [20] |
刘君, 邹东阳, 董海波. 动态间断装配法模拟斜激波壁面反射[J]. 航空学报, 2016, 37(3): 836-846. LIU J, ZOU D Y, DONG H B. A moving discontinuity fitting technique to simulate shock waves impinged on a straight wall[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 836-846. (in Chinese) |
| [21] |
刘君, 邹东阳, 董海波. 基于非结构变形网格的间断装配法原理[J]. 气体物理, 2017(1): 13-20. LIU J, ZOU D Y, DONG H B. Principle of new discontinuity fitting technique based on unstructured moving grid[J]. Physics of Gases, 2017(1): 13-20. (in Chinese) |
| [22] |
WU Z N, XU Y Z, WANG W B, et al. Review of shock wave detection method in CFD post-processing[J]. Chinese Journal of Aeronautics, 2013, 26(3): 501-513. DOI:10.1016/j.cja.2013.05.001 |
| [23] |
PAGENDARM H G, SEITZ B. An algorithm for detection and visualization of discontinuities in scientific data fields applied to flow data with shock waves[J]. Scientific Visualization:Advanced Software Techniques, 1993, 161-177. |
| [24] |
LOVELY D, HAIMES R. Shock detection from computational fluid dynamics results[C]//14th Computational Fluid Dynamics Conference. 1999: 3285. https://www.researchgate.net/publication/2581120_Shock_Detection_from_Computational_Fluid_Dynamics_Results
|
| [25] |
KANAMORI M, SUZUKI K. Shock wave detection in two-dimensional flow based on the theory of characteristics from CFD data[J]. Journal of Computational Physics, 2011, 230(8): 3085-3092. DOI:10.1016/j.jcp.2011.01.007 |
| [26] |
KANAMORI M, SUZUKI K. Shock wave detection based on the theory of characteristics for CFD results[C]//20th AIAA Computational Fluid Dynamics Conference. Honolulu, Hawaii, 2011. https://www.researchgate.net/publication/268474447_Shock_Wave_Detection_based_on_the_Theory_of_Characteristics_for_CFD_Results
|
 2019, Vol. 37
2019, Vol. 37