流动不稳定性被认为是流体力学的重要关键科学问题之一,在自然界和工程实际中广泛存在,得到了学术界的普遍重视。对于一个处于稳定状态的流体动力系统,其受到的外力、惯性力和黏性应力等相互平衡。当这些作用力受到某些扰动的影响时,便会产生不稳定性现象。其中一个典型的例子是柱状射流破碎(Barreo & Loscertales[1]; Eggers & Villermau[2]),如日常生活中的水龙头出水、人工喷泉、消防水枪喷流等,都是从小孔射出一股水射流因流动不稳定性形成水滴的简单过程。近年来随着日益增长的实际需求,液-液、气-液等更复杂的复合结构射流破碎问题被不断提出。比如在高速气流作用下聚焦微量流体的流动聚焦技术,能够形成多层微细射流并破碎成壳核结构的微纳胶囊,在生命科学、材料科学、农业、食品加工等领域具有重要应用价值(司廷等[3])。在这些问题中,不同条件下所产生的流动现象往往差别较大,究其原因在于射流破碎的不稳定性机理发生了变化[4]。早在19世纪中后期和20世纪初,Helmholtz[5-6]、Kelvin[7-9]、Rayleigh[10-11]、Reynolds[12-13]和Taylor[14-15]和Weber等[16]就已经对不同流动现象所涉及的不稳定性问题进行阐述和研究,并利用数学方法开展深入的流体动力学机理分析。经过一个多世纪的发展,射流破碎相关的不稳定性理论体系正在逐渐完善,能够准确预测实验中发现的一些现象(尹协远 & 孙德军[17])。但是,不同于质点或刚体运动学、动力学等经典力学问题的常微分方程表述形式,流体动力学问题往往是基于Navier-Stokes方程,并由偏微分形式给出相应的边界条件,这一差别使得流动不稳定性问题的求解难度陡升,也使得不稳定性理论在实际应用中存在一定的局限性。
物理学以实验为基础,但只有在成功运用数学之后才能真正完善。因此,给出一定数学形式的表述将有助于理解不稳定性的概念。根据微分方程的稳定性理论,基本流在t0时刻受到干扰而偏离无扰动时的初始状态x0(t)。扰动后的状态x(t; t0, x0)满足扰动条件下的微分方程,扰动幅度为‖x-x0‖,其中“‖ ‖”代表物理量的范数。如果对于任意常数ε>0,都存在常数δ=δ(ε, t0),使得只要初始扰动幅度‖x(t0; t0, x0)- x0‖ < δ,则对于任意的t>t0都有‖x(t; t0, x0)- x0(t)‖ < ε,表示受到有界幅值扰动后的基本流场输出的响应幅值有界,称此时基本流动为稳定的。其中x既可以是速度u,也可以是压力p,这些物理量都满足Navier-Stokes方程组以及边界条件。前述不稳定性定义中,当δ与时间无关时称为一致稳定的。如果扰动响应幅值保持不变,基本流动为临界稳定的(或称中性稳定)。如果存在ε>0,使得对于任意的小量δ=δ(ε, t0),初始扰动‖x(t0; t0, x0)- x0 (t0)‖ < δ时,都存在t>t0使得‖x(t; t0, x0)-x0(t)‖>ε,即不论初始扰动有多小,经过足够长时间后输出响应均被放大,则称基本流对扰动为不稳定的。上面定义中给出的是Liapunov意义下的稳定性或不稳定性[19],在此定义下,稳定是个局部的概念(全局不稳定性除外),且只有在同步意义下才能够就稳定与否进行讨论(即在相同时刻下比较零解和扰动解的差距),不稳定性涉及的时间域是无穷的。可见,不稳定性理论主要考察小振幅扰动在无扰动基本流上的响应[4, 17, 20]。
线性不稳定性分析方法能够将射流破碎这样的物理问题转化为数学问题进行求解,也就是基于实验条件建立简化的物理模型,在基本流动中引入小振幅扰动,考察小扰动在时间、空间或时空中的响应。如果引入的小扰动不断增长,流场最终发展成另外一种状态,流场就是不稳定的;反之,如果流场最终恢复到原始状态,流场就是稳定的。对于射流破碎问题,Rayleigh[10-11]最早建立了真空中半无限长的无黏液体圆柱模型,引入正则模方法建立线性化小扰动控制方程进行求解[17],获得了液体射流破碎的不稳定模态,并进一步预测了射流表面的扰动波长。不稳定性分析结果发现,只有波长大于射流周长的扰动随时间增长,扰动增长率最快的扰动波长约是射流周长的1.437倍10-11]。在此基础上,Weber[16]研究了液体黏性对射流不稳定性的影响,发现射流的黏性增大时,最不稳定扰动的波长也增大。这些工作都是在时间模式下开展的,时间模式反映的是扰动幅值随时间的演化,在空间上是周期性的。除此之外,不稳定性理论还包括时空模式和空间模式,时空模式下扰动的幅值同时随时间和空间变化,而空间模式反映的是扰动幅值随空间的演化。Keller等[21]进行了半无限长射流的空间和时空不稳定性研究,预测了射流的破碎长度,Leib & Goldstein[22]进一步考虑了流体黏性的影响,之后Lin & Kang[23]又考虑了周围气体的物理属性,建立了两相流体射流模型。到了20世纪80年代后,随着计算机技术的迅速发展,研究射流破碎的物理模型考虑了更全面的过程参数,射流破碎的不稳定性分析方法也从无黏到有黏、均匀基本流到真实流动、单一作用到多场耦合[24-25]、局部不稳定性到全局不稳定性[26-27]、线性到弱非线性甚至非线性等不断发展,相应的流动机理也得到了更加深入和广泛的研究。
目前绝大部分情况下遇到的射流问题,其特征尺度都在数百纳米以上,因此相应的流动仍然符合连续性介质假设,可以采用流体力学Navier-Stokes方程进行求解。此类问题涉及了不同的物理参量和作用力项,在求解过程中要逐一考虑。在理论建模时,有时可以忽略黏性力项的影响,从而使问题大大简化;而在实际流动中,人们往往要关注黏性力的作用,因为黏性力对扰动能量具有耗散作用,是连通机械能和内能的桥梁。当黏性力足够大时,任何有界流动都趋向稳定。此外在使流体扰动趋稳的同时,黏性也具有扩散作用,能够使某些流动(如平行剪切流)变得更加不稳定。表面(或界面)张力也具有类似的双重作用,一方面能够阻止流体表面积增加,另一方面也能释放液体表面能,使得射流更容易破碎成液滴。在研究射流不稳定性过程中,往往将衡量黏性作用和表面张力作用的雷诺数Re和韦伯数We作为重点研究对象。此外,在具有温度场梯度的射流问题中,温度差也具有双重作用:一方面会诱使液体内部表面张力凸显,引发热对流;另一方面热传导会减小温度差异,使流动趋稳[24-25]。这样的双重作用在物理界似乎十分普遍,又例如流动的固定边界在一定程度上能够抑制扰动的发展,所以边界相互靠近能使流动趋稳;但趋稳效应并不是绝对的,边界附近往往存在附面层,附面层中强剪切向外扩散会造成流动失稳。实际流动中,这些作用机理并不只有一个在起作用,往往会耦合在一起,不稳定性理论研究的重要目的就是要理解不同过程参数的作用机制,探索每种参数的失稳或趋稳效应,并获得不同模态转换以及能够起主导作用的因素,揭示流动不稳定性的物理规律和内在机理。
线性不稳定性分析方法能够有效地研究柱状射流及复合射流破碎问题,时至今日,相关领域已经取得了丰富的研究进展。本文重点回顾了柱状射流和复合射流的局部线性不稳定性分析方法的主要内容和具体步骤,旨在表明如何运用数学原理解决相关的物理问题,为实际应用提供重要的指导。
1 小扰动法和正则模法人们对射流破碎的观察和研究由来已久。早在近两个世纪前,Bidone 1823年就研究了不同形状小孔产生射流的形状;Savart 1833年发现射流会转变成液滴,并对射流施加周期性震荡在射流表面获得了固定频率的扰动,获得了射流-液滴的转变规律;Plateau 1843年进一步发现受表面张力作用,长波的扰动可减少射流的表面积。而对射流不稳定性的理论研究最早可以追溯到19世纪70年代,Rayleigh[10-11]利用线性不稳定性理论开展了真空中无黏液体射流破碎问题的理论研究,发现表面张力抵抗惯性力能够促使射流失稳破碎。这些因表面张力波的曲张以及收缩导致的液柱破碎,现在将之称为Rayleigh模式。在这种模式下,表面张力对圆柱液体射流的破碎起到了主要作用,破碎后形成的液滴尺寸与射流喷孔半径为同一量级。之后的研究发现,在Rayleigh模式之外还有另一种不稳定性模式称之为Taylor模式。在Taylor模式下,流体界面上的压力以及剪切力的大小不同使液体破碎成细小的雾滴,流体之间的作用力对射流破碎起主导作用[28]。一般而言,低速液体射流对应Rayleigh模式下的射流,这种情况下的射流线性和非线性研究相对较多,与之相对的是高速射流,惯性力占据绝对优势,外层流体速度也增大,流体之间的相互作用已十分突出,在这种模式下射流不稳定性问题变得十分复杂。
整体上,小扰动法和正则模法是线性不稳定性理论的主要处理方法。流体力学问题涉及的非线性偏微分方程往往无法直接获得解析解,因而许多情况下不得不借助近似方法推导精确解的近似解析表达式,其中,小扰动方法是摄动法的一种,能够求解近似解。采用摄动法处理非线性方程时,如果非线性项是高阶小量,可以将其略掉以作初步近似,使非线性问题变成线性问题。线性问题能更方便地求出解析解,将线性问题的解析解作为非线性问题解析解的零阶近似,再将非线性问题的通解表达成它的零阶近似解和一个摄动解之和,然后代入原定解问题中,略去更高阶小量可获得关于摄动解的线性定解问题,求解这个定解问题将得到原定解问题的一级近似。按照此方法进行下去,能够得到各级的近似解。这种求近似解的方法就称为摄动法。在处理不稳定性问题的过程中,通常只需一级近似,这就是小扰动法。直接求解小扰动线化方程的初边值问题能够得到扰动随时间完整的演化过程,然而小扰动线化方程仍然为偏微分方程,处理起来相对困难,目前常用的求解方法是模态展开法,即正则模法。能够使用正则模法的前提是基本流具有对称性。正则模法又分为时间、时空和空间模式,以前者为例,假设基本流只随空间演化(系数与时间t无关,基本流定常),由分离变量法和Laplace变换知识可将扰动展开成幂级数形式,每个分量满足相同的线性系统(相同的控制方程和边界条件),称为一个模态。当流动稳定时,所有的扰动模态都必须是稳定的;当流动不稳定时,这些扰动模态中至少有一个是不稳定的[4, 17-19, 29]。
小扰动法和正则模法使原问题的求解大大简化,然而能够求得解析解的例子仍然有限,特别是在考虑有黏问题时,利用Navier-Stokes方程无法得到解析形式的色散关系,一般需要采用数值方法计算求解[30-33]。常用的数值方法包括有限差分法、打靶法和正交函数法等,其中正交函数法中涉及了一种基于光滑函数逼近的谱方法,因其精度高、速度快、收敛性好被普遍采用[34-37]。此外,尽管Rayleigh的理论研究工作距今已有一个多世纪,但其处理不稳定性问题的研究方法一直被采纳,成为射流破碎机理研究的最有利工具之一[26-30]。在此之后各式各样的射流类型被提出,特别是电雾化、流动聚焦、电流动聚焦[38]等的出现使得射流不稳定性理论面临着一些挑战,但是采用小扰动法以及正则模法研究新型射流问题仍能得出许多重要结论,与实验现象吻合。
2 线性不稳定性分析方法的主要步骤近年来,经学者们不断完善,射流破碎的不稳定性研究已经形成了相应的理论体系,尤以线性不稳定性分析方法最为成熟。通常条件下,纯粹的射流问题可以直接基于Navier-Stokes方程进行求解。当涉及力、热、电、磁等耦合条件时,控制方程和边界条件将要进行相应的变化。本节将对线性不稳定性分析方法的研究步骤逐一进行阐述,主要关注纯粹的柱状射流和复合射流破碎问题,并对带电射流、热射流等问题作简要介绍。
2.1 模型建立在不稳定性理论研究中,完全依照实际情况建立物理模型进行求解是最可靠的,但是往往由于边界条件或材料属性复杂,使得对物理问题的直接建模和求解变得艰难而繁琐。为此,可以通过对物理问题的综合分析,对物理模型进行简化,在不改变物理规律和物理本质基础上,开展深入且系统的研究。
在射流形成和破碎过程中,射流表面或界面上的扰动振幅不断增长,最终切断射流并使射流末端的流体分离出去,形成孤立的液滴。从不稳定性角度考虑,局部的小扰动经历足够长的时间或者足够远的距离之后,最终都会发展成较大的扰动,从而引起射流的破碎。射流的破碎是必然的,也说明该流动是不稳定的。为了开展线性不稳定性分析,首先要建立理想状态下半无限长的射流模型,射流表面扰动发展方向沿流动方向。比如最简单的空气中单轴液体射流的破碎问题,可以建立一个无扰动时的半无限长液体圆柱模型,周围介质为静止的空气,存在一个气-液界面,在界面附近气体和液体的流动情况可以视具体问题进行求解或简化。同样道理,对于多层结构的复合射流,可以类似地建立无扰动时的半无限长复合圆柱模型。
除了柱状射流或复合射流的几何结构,在实际计算中还需要考虑更多因素,可以通过进一步的假设或者简化达到目的。比如常见的液体射流,驱动液体流出小孔形成射流的压力一般较低,此时液柱可以认为是不可压缩的;而对于一般的低速气体流动,在射流马赫数小于0.3时,可以用不可压缩流动进行分析。在一些射流问题中,涉及的流体多为水、油、酒精、空气等低黏性物质,可视之为牛顿流问题处理;一旦涉及到高分子材料的溶液,射流表现出非牛顿流体的性质,就要建立非牛顿流体模型进行分析求解。在微细射流中,惯性力和表面张力的作用远大于重力,为此忽略重力影响是可行的。流体的黏性假设更接近实际情况,但是会带来复杂的求解过程,而无黏假设能够将问题大大简化,甚至能够获得解析的色散关系,为此在大雷诺数下往往采用无黏假设进行建模。常见的射流研究都是处于常温常压下,流体之间的温度差较小,可以认为流体内部温度定常且均匀分布,黏性耗散产生的热量对温度影响甚微,为此忽略流体之间的温度差异也是合理的;当涉及到高温射流、固体物质熔融态射流、等离子体射流、含颗粒射流、电磁射流等问题时,需要考虑温度梯度、离子态、非牛顿流、流固耦合、多场耦合等条件,可以建立更复杂的物理模型研究其不稳定性。此外在某些具体问题中,还需要考虑更加细致的假设,以期能够理论求解和分析。
2.2 基本方程和边界条件对于柱状射流和复合射流问题,不可压缩流体力学Navier-Stokes方程包括连续性方程以及动量守恒方程,写为:
| $ \nabla \cdot \boldsymbol{u}=0 $ | (1) |
| $ \frac{\partial \boldsymbol{u}}{\partial t}+\boldsymbol{u} \cdot \nabla \boldsymbol{u}=-\frac{1}{\rho} \nabla p+\nu \nabla^{2} \boldsymbol{u}+\boldsymbol{f} $ | (2) |
其中u为速度矢量,在柱坐标系(r, θ, z)中u=(ur, uθ, uz),且u=‖ u‖,p为流体静压,ρ为流体密度,t为时间,ν=μ/ρ为运动黏性系数,μ为动力黏性系数,f为系统受到的外力。对于存在热学条件的热射流问题,需要增加能量守恒方程,一般可以表示为:
| $ \begin{aligned} \frac{\partial}{\partial t}\left(\frac{\rho u^{2}}{2}+\rho \varepsilon\right) &=\\ &-\nabla \cdot\left[\rho \boldsymbol{u} \frac{u^{2}+2 \omega}{2}-\boldsymbol{u} \cdot \boldsymbol{\sigma}^{\prime}-\chi \nabla T\right] \end{aligned} $ | (3) |
其中ω为焓,ε为内能,σ'为黏性应力张量,χ表示热导率为温度T和压强p的函数,∇T表示温度梯度,-χ ∇T表示由热传导引起的热流密度。而对于涉及电场条件的带电射流问题,还需要考虑电学Maxwell方程组,一般可以表示为:
| $ \begin{array}{l}{\nabla \cdot \boldsymbol{D}=q, \nabla \cdot \boldsymbol{B}=0, \nabla \times \boldsymbol{E}=-\frac{\partial \boldsymbol{B}}{\partial t}}, \\ {\nabla \times \boldsymbol{H}=\boldsymbol{J}+\frac{\partial \boldsymbol{D}}{\partial t}}\end{array} $ | (4) |
其中,D、q、B、E、H、J分别为电位移矢量、自由电荷密度、磁感应强度、电场强度、磁场强度、电流密度,在物理量D、B、E、H、J之间存在一定的本构关系。方程(3)中四个关系式依次对应:Gauss定律,磁场是无旋场,Faraday定律(变化的磁场产生电场),电流密度与电场变化都能产生磁场。在一定情况下,这些方程都可以根据实际情况进行简化,便于理论求解和分析。
柱状微细射流和复合射流问题的边界条件分别对应最外层、表/界面以及对称轴三种位置,表/界面上主要是运动学和动力学边界条件,而在最外层和对称轴上,需要考虑主要物理量的有限性。当涉及电射流问题时,需要增加电学边界条件。一般来说,边界条件可以根据具体问题进行简化,并最终表示成在边界上不同物理量之间的关系式。
在无穷远处和对称轴上,射流的速度和压力是有限值:
| $ \boldsymbol{u}<\infty, p<\infty, r=0 $ | (5) |
| $ \boldsymbol{u}<\infty, p<\infty, r \rightarrow \infty $ | (6) |
在表/界面上运动学边界条件:
| $ \frac{\partial F}{\partial t}+\boldsymbol{u} \cdot \nabla F=0 $ | (7) |
其中F为界面方程。在表/界面上动力学边界条件:
| $ \left\|\boldsymbol{T}^{m}+\boldsymbol{T}^{e}\right\| \cdot \boldsymbol{n}=\gamma \nabla \cdot \boldsymbol{n}+(\delta-\boldsymbol{n} \boldsymbol{n}) \nabla \cdot \gamma, $ | (8) |
式中Tm、Te分别为表/界面的水动力学应力张量和电动力学Maxwell张量,n为法向单位矢量,γ为表/界面张力系数,δ为单位矩阵。在实际情况下,还需根据物理模型的具体假设添加相应的边界条件,如考虑黏性时,还需考虑界面速度连续条件等,比如:
| $ \boldsymbol{u}_{1}=\boldsymbol{u}_{2} $ | (9) |
当考虑电射流问题时,往往需要考虑表面上电荷分布qs以及电场切向连续性条件,常可以写为:
| $ \boldsymbol{n} \cdot\|\boldsymbol{D}\|=q_{s}, \boldsymbol{n} \times\|\boldsymbol{E}\|=0 $ | (10) |
分别代表界面上的Gauss定律以及切向电场连续,其具体表达式需要根据模型建立的情况进行展开。
2.3 基态条件在进行不稳定性分析时,必须事先给出流场在未扰动时的基本速度型等条件,称为基态条件。无扰动下的基本速度型u0满足控制方程及边界条件,但由于Navier-Stokes方程及相应边界条件的复杂性,一般很难直接给出基本速度型的准确解。为了处理方便,研究中曾采用过多种简化的基本速度型。
均匀速度型是最简单的一种速度型,往往直接假设每一相流动的速度都是均匀的,能够使问题求解大大简化,缺点在于边界上速度连续性条件会失效(不同流体的速度相同除外),动力学边界条件等也要进行修正[39]。在此基础上改进的Kelvin-Helmholtz (K-H)速度型假设流速在流体内均匀分布,在界面上存在阶跃,是较通用的速度型,尤其是在不考虑流体黏性作用时使用[40]。分段光滑的均匀速度型缝合了K-H速度型在界面处不连续的缺点,比存在阶跃的均匀速度型更接近真实流动。上面几种速度型都是通过直接构造得到,往往和实际流场有一定差距,在处理低黏性流动问题时,也能够获得和实验一致的结论。
黏性作用对基本速度分布具有重要影响。由于射流呈均匀轴对称的圆柱形,基本流速度场一般只考虑轴向分量,常采用“管流”抛物线速度型来近似估计黏性液体射流的速度型[35, 37]。由于液体射流和周围环境介质的界面两侧存在速度差,在黏性作用下,流体界面处存在边界层,也可以采用误差函数[31, 32, 36]或者双曲正切函数估计界面外侧环境流体的速度分布[33]。为了更接近实际情况,学者也试图利用流体力学基本方程和边界条件近似求解基本速度型。Lin[30]利用Navier-Stokes方程推导了竖直圆管中黏性气体包围黏性液体的基本速度型解析表达式;李芳[35]对驱动气体加上约束,得到圆管中黏性气体包围黏性液体的解析表达式。然而,由于黏性流场情况下几乎很难得到解析解,一些数值计算方法被提出,对从毛细管出口到射流破碎整个过程进行模拟。Gordillo[41-42]通过细长体假设,利用边界层方程对高速气流剪切作用下液柱射流中的基本速度型进行数值求解,只要给定初始位置的液体和气体速度分布,即可得到在空间演化的液体射流和驱动气体的基本速度型。在涉及到热、电、磁等复杂条件时,也要考虑基态条件的补充,比如温度场、电场、磁场等,需要根据具体问题给出[43],这里不再赘述。
2.4 线化小扰动法在将射流不稳定性问题归结为微分方程初边值问题后,采用小扰动法将问题进一步转化为线化小扰动方程的初边值问题。将各物理量写成基本解加小扰动形式,扰动后的速度、压力和圆柱射流界面位置表示为:
| $ \boldsymbol{u}=\boldsymbol{u}_{0}+\boldsymbol{u}^{\prime}=\left(u_{0 r}, u_{0 \theta}, u_{0 z}\right)+\left(u_{r}^{\prime}, u_{\theta}^{\prime}, u_{z}^{\prime}\right) $ | (11) |
| $ p=p_{0}+p^{\prime} $ | (12) |
| $ r=R+r^{\prime} $ | (13) |
其中u0、p0、R为流场速度、压力和界面位置的基本解,u′、p′、r′为速度、压力和界面位置的扰动量。在只考虑基本流轴向速度分量的情况下,u0r=0和u0θ=0。将扰动形式的u、p和r代入控制方程及边界条件,基态条件下的控制方程和边界条件自动满足,进一步略去高阶扰动项,可得到小扰动形式的控制方程和边界条件。比如,流体力学Navier-Stokes方程转化为:
| $ \nabla \cdot \boldsymbol{u}^{\prime}=0 $ | (14) |
| $ \rho\left(\frac{\partial \boldsymbol{u}^{\prime}}{\partial t}+\boldsymbol{u}^{\prime} \cdot \nabla \boldsymbol{u}_{0}+\boldsymbol{u}_{0} \cdot \nabla \boldsymbol{u}^{\prime}\right)=-\nabla p^{\prime}+\mu \nabla^{2} \boldsymbol{u}^{\prime} $ | (15) |
相应地,无穷远处和对称轴上流速和压力是有限值:
| $ \boldsymbol{u}^{\prime}<\infty, \quad p^{\prime}<\infty, \quad r=0 $ | (16) |
| $ \boldsymbol{u}^{\prime}<\infty, \quad p^{\prime}<\infty, \quad r \rightarrow \infty $ | (17) |
由于交界面为物质面,满足
| $ -\frac{\partial r^{\prime}}{\partial t}+u_{r}^{\prime}-u_{0 z} \frac{\partial r^{\prime}}{\partial z}=0 $ | (18) |
处理动力学边界条件时比较复杂,需要根据实际情况给出水动力学应力张量的具体表达式,并代入边界条件中进行简化。这里给出法向单位矢量n的具体表述:
| $ \boldsymbol{n}=\left(1, -\frac{1}{r} \frac{\partial r^{\prime}}{\partial \theta}, -\frac{\partial r^{\prime}}{\partial z}\right) $ | (19) |
于是曲率可以表述为:
| $ \nabla \cdot \boldsymbol{n}=\frac{1}{r}-\frac{1}{r^{2}} \frac{\partial^{2} r^{\prime}}{\partial \theta^{2}}-\frac{\partial^{2} r^{\prime}}{\partial z^{2}} $ | (20) |
此外,能量方程、电学方程等也可以类似处理,相应的边界条件也能够根据线化小扰动法逐一给出,将在具体实例中进行介绍。
2.5 无量纲化及无量纲参数为了能够得到普适的结果,需要对控制方程和边界条件无量纲化。这里分别选取特征长度、特征速度、特征时间、特征压力为R、U、R/U、ρU 2,则无量纲化后的物理量为:
| $ \left( {\bar r, \bar z, \overline {{r^\prime }} } \right) = \frac{{\left( {r, z, {r^\prime }} \right)}}{R}, \mathit{\boldsymbol{\bar u}} = \frac{{{\mathit{\boldsymbol{u}}^\prime }}}{U}, \bar t = \frac{{tU}}{R}, \bar p = \frac{{{p^\prime }}}{{\rho {U^2}}} $ | (21) |
将式(21)代入到线化小扰动方程和边界条件,可以得到无量纲化的线化小扰动方程和边界条件,形式上和式(14)式(15)类似。同时可给出主要的无量纲参数如下:
| $ R e=\frac{\rho U R}{\mu}, W_{e}=\frac{\rho U^{2} R}{\gamma}, Q=\frac{\rho_{i}}{\rho}, N=\frac{\mu_{i}}{\mu} $ | (22) |
式中Re为雷诺数,表示惯性力和黏性力之比,We为韦伯数,表示惯性力和表面张力之比,Q为密度比,N为黏性系数比,i代表不同的流动相。
如果涉及多个界面,且含有热、电、磁等条件,将需要进一步考虑表面张力比、比热比、热传导系数比、电导率比、介电常数比,以及其他多个无量纲参数,比如Peclet数(表征射流液体的热特征)、Marangoni数(表征表面张力随温度的变化率)、毛细数(表征黏性力对表面张力的比值)、Ohnesorge数(表征黏性力、惯性力和表面张力的关系)等。通过研究无量纲参数对不稳定性扰动增长的影响,可以直接反映出各过程参数对射流破碎的影响规律,包括液体流量速度、气体压力、电场强度、温度场等外部控制参数以及材料的黏性、表面张力、密度、电导率、热传导系数等物性参数。在具体问题中,可以采取不同的特征尺度,所得到的特征方程和边界条件也不尽相同,无量纲参数也可以相应地进行取舍。
2.6 正则模法由于射流问题的基本流具有对称性,因此可以使用正则模法对线化小扰动方程中的物理量进行Fourier分解,将方程转换成一系列的模态叠加,每个模态都满足线性系统,于是可以分别进行处理。如果某一模态是不稳定的,则相应的局部化初始扰动不仅会运动和传播而且也会随时间或空间增长;每个稳定模态都以其自身的增长率增长,以其自身的相速度运动。稳定的系统要求所有模态均是稳定的,反之只要存在某一不稳定模态,系统就处于不稳定状态。流体力学线化小扰动控制方程中的未知量有u′r、u′θ、u′z、p′,可将扰动速度表达为:
| $ \begin{array}{l}{\boldsymbol{u}^{\prime}(r, \theta, z, t)=\zeta \int\limits_{-\infty}^{+\infty} \mathrm{d} k \sum\limits_{-\infty}^{+\infty} \mathrm{d} \omega\{\overline{\boldsymbol{u}}(k, n, \omega, r)\} \times \Re} \\ {\Re=\mathrm{e}^{\mathrm{i}(n \theta+k z+\omega t)}}\end{array} $ | (23) |
其中n、k分别为周向和轴向扰动波数,ω为时间增长率,ζ是一个常数,u是速度的特征函数。ω的积分围道是Laplace逆变换的Bromwich围道。由于控制方程中的特征函数为径向位置r的函数,独立于θ、z、t,简便起见,可将任一小扰动X′和微小位移r′表示成:
| $ X^{\prime}(r, \theta, z, t)=\overline{X}(r) \Re+\mathrm{c.c} $ | (24) |
| $ r^{\prime}(r, \theta, z, t)=\overline{r} \Re+\mathrm{c.c} $ | (25) |
上式中c.c表示共轭复数,虚根
正则模法可以分为时间模式、时空模式和空间模式。通过假定ω为复数来反映扰动幅值在时间轴上演化的方式为时间模式。由于轴向以及周向无界,为使θ, z→∞时因变量满足扰动有界条件,k和n须为实数,反映了扰动在空间上是周期性的。其中n=0表示轴对称扰动形式,n≠0表示非轴对称扰动形式。为了研究扰动随时间的演化需要假定时间增长率和扰动相速度为复数:ω=ωr+iωi, c=cr+ici。若对某一波数,存在复扰动增长率的虚部ωi < 0或扰动相速度ci < 0,则在此波数下系统对扰动为不稳定的,即:ωi < 0或ci < 0时,射流是不稳定的。在通常情况下,射流和复合射流最终会破碎成液滴,说明射流一直是不稳定的,必然存在ωi < 0或ci < 0,使扰动不断增长。若假定扰动在周向空间和时间上是周期性的,即ω和n为实数,而沿主流方向波数k=kr+iki为复数,则称为空间模式。在某些问题当中,扰动幅值可能同时随时间和空间演化,空间模式稳定性和实验相差较大,此时既不同于时间模式也不同于空间模式,扰动时间增长率ω以及周向波数为n为复数,称为时空模式。时空模式不稳定性分析方法有两种传播模式,一种是扰动只向流动的下游传播,此时称为对流不稳定性;另一种是扰动既向流动的下游传播也向流动的上游传播,称为绝对不稳定性。正则模法的三种模式中,时间不稳定性研究方法相对简单,时空不稳定性理论则更接近实际情况,空间不稳定性也能够获得特定情况下的物理规律,在处理具体问题中可以选择性应用。
2.7 色散关系许多偏微分方程都可以用于描写波动现象,如波动方程utt-b2uxx=0的解为左行波和右行波的叠加:u(x, t)=f(x-bt)+f(x+bt)。任何一个物理量,当其为时间和空间变量的函数时,它的随体微商可以表示为:dV/dt=∂V/∂t+V·∇V,设时间尺度为T,空间尺度L,速度尺度为U。在经典的波的概念中,波是质点振动的传播,振幅a=UT,则微商非定常项与非线性项之比可以用波长与振幅之比表示:
| $ \frac{\partial \boldsymbol{V} / \partial t}{\boldsymbol{V} \cdot \nabla \boldsymbol{V}}=\frac{U / T}{U^{2} / L}=\frac{L}{U T}=\frac{L}{a} $ | (26) |
当a远小于L时,非线性项可以忽略,此时的波称为线性波(小振幅波),否则非线性项必须考虑,此时为非线性波,常见的波多为弱非线性波。
利用正则模法将控制方程及边界条件转化为求解关于k、n、ω的特征值关系G(ω, k, n)=0,称为色散关系。将基本波解(也称平面波解)u(r, t)=Uei(K·r+ωt)代入线性偏微分方程后,线性偏微分方程与线性波的色散关系形成一一对应:给定线性偏微分方程可以用正则模法求出相应色散关系,由某个色散关系也能反解出对应的线性偏微分方程。线性波的色散方程为G(ω, K)=0,非线性波的色散关系相比线性波的色散关系更为复杂,角频率ω不仅与波数K有关还与振幅a相关。基本波解中ξ=K·r+ωt表示位相,当ξ为常数时得ω=Ω(K),相速度c=ωK/|K|2为波的传播速度,群速度νg=∂ω/∂K是能量的传播速度,物理问题中的波动现象往往是周期和波长都很大的长波包络周期和波长均很小的小波,长波和小波群以群速度运动,短波以相速度运动。当ω为实数且νg≠c时,波传播过程中能量将重新分布,这种现象称为波的色散,相应的波称为色散波;νg=c时波的能量以同样的速度随波前进,能量将不再重新分布,此时的波称为非色散波。当ω为复数时,相应的波称为扩散波动,如热传导方程;反之ω为实数时为非扩散波动。扩散波动存在不稳定模态,如果不稳定模态的群速度νg全不等于零,扰动虽然会随着扰动中心运动到很远的上游或者下游,然而对于某一固定点而言,该点扰动仍然很小,这种不稳定性称为对流不稳定性;如果存在某一不稳定模态其群速度为0,那么在某些固定点上扰动将会增长,这种不稳定性称为绝对不稳定性。对于非扩散波动,若ω(k)为k的非线性实函数,即∂2ω(k)/∂k2≠0,这种非扩散波动称为色散波动,如KDV方程(郭玉翠2008);如果ω(k)为k的线性实函数,即∂2ω(k)/ ∂k2=0,这种非扩散波动为非色散波动,如线性方程ut-βux=0。
通过色散关系能够直观地反映出不同参数的影响规律,因为色散关系可以表述成如下形式:
| $ G(\omega, k, n, W e, R e, Q, N, \cdots)=0 $ | (27) |
在一定条件下(比如无黏、均匀速度型等),方程(27)可以表述成解析形式的表达式,而在其他条件下(比如有黏、非均匀速度型等),往往需要通过数值方法进行分析。总之都可以最终获得扰动时间增长率ω、周向波数n、轴向波数k以及不同控制参数之间确定的关系。
2.8 谱配置法数值方法求解不稳定性问题时,往往是将问题转化为一个广义特征值问题,具体数值方法包括有限差分法、打靶法和正交函数法等[24, 35]。有限差分法较为简便直观,但精度较差;打靶法原理简单,但是不容易求出所有的特征值;而正交函数法通常精度高、速度快。正交函数法又可以分为Galerkin法、Tau法和谱配置法[20]。Tau法是较早采用的方法,但容易产生伪特征值。Galerkin法可以避免伪特征值的出现,但是处理边界条件比较复杂。谱配置法既可以避免伪特征值,又简单易行,目前被广泛使用。谱配置法的主要思想是用光滑函数(一般是正交多项式)逼近方程的解,获得解的近似谱展开式,再根据展开式和原方程求出展开式的系数方程组。采用Legendre多项式作为近似展开式的基函数时,这种谱方法称为Legendre谱配置法,采用Chebyshev多项式作为基函数时,称为Chebyshev谱配置法。
以Chebyshev谱配置法为例,由于Chebyshev多项式Tn(y)=cos(ncos-1(y))定义在区间[-1, 1]上,需要将物理空间[0, 1]转变成计算空间[-1, 1],相应的变换有线性变换r=0.5(1+y)和非线性变换r=0.5[1+tanh(δy)/ tanh(δ)]。将模型当中涉及到的特征函数展开成Chebyshev多项式级数形式,代入到轴对称问题的特征方程和边界条件当中,即得配置方程和边界条件。在流体内部选取合适的配置点后,最终将不稳定性问题转化成广义特征值问题,
| $ \boldsymbol{A} x=\omega \boldsymbol{B} x $ | (28) |
其中x是特征向量,ω为待求特征值,A和B是由控制方程和边界条件构造而来的系数矩阵。至此将微分方程问题最终转化为代数方程问题。求解广义特征值的方法较多,在MATLAB、FORTRAN等程序包中均可获得。
综上所述,利用线性不稳定性分析方法处理射流破碎问题的一般步骤包括:(1)根据实验中涉及的实际条件建立简化的物理模型;(2)根据流动涉及的不同相和交界面,列出控制方程和边界条件;(3)给出基本速度型和其他基态条件;(4)假设基本流动受到小扰动,采用小扰动法线性化基本方程和边界条件,推导出线性偏微分方程组;(5)选取合适的特征参数,对方程进行无量纲化,获得无量纲化的小扰动控制方程和边界条件,以及相应的主要无量纲参数;(6)利用正则模法导出有关特征值和特征函数的特征方程以及相应的边界条件,也就是基于线性问题叠加原理,任意初始扰动可以表示成各种简正波形的叠加,每一种简正波形均因满足线性方程而且可单独处理,从而将线性偏微分方程转化为对每一简正波形的特征值方程;(7)推导出表征扰动增长率、波数以及其他过程参数之间关系的色散关系;(8)最终求解所得到的特征值问题,并进行系统分析,也可以引入实验或数值模拟进行对比研究。值得一提的是,针对不同问题,以上的研究步骤大体相似,但细节会略显不同。
3 射流不稳定性分析实例在生活和工程实际中,我们能够遇到非常多的柱状射流和复合射流问题。比如日常见到的自来水出流,当水龙头阀门稍微打开,能够观察到液滴直接从管口滴落。当阀门继续打开,便能够形成一股水柱从管口流出,沿水柱表面上的扰动在流动下游发展,最终使射流破碎,只是液柱破碎频率较高,我们很难直接分辨射流的破碎过程。Rayleigh[10]不仅实验观测了射流破碎时清晰的界面结构,还利用线性不稳定性分析方法对液体射流破碎机理进行研究,预测了实验中观察的现象。近年来,随着微纳加工技术的发展,微纳尺度流动逐渐兴起,其中基于柱状射流和复合射流技术制备微纳液滴或胶囊,在医学、药学、材料学、化学等诸多领域得到广泛应用。与之相关的基础研究工作也得到广泛重视,特别是利用不稳定性理论对实验进行定性和定量预测,对实际中的过程控制和工程应用起到关键性作用。
在这里,我们首先回顾Rayleigh[10]的早期研究,介绍在简单模型中获得解析形式色散关系的过程,然后按照上述主要步骤,以流动聚焦技术中射流破碎为例介绍线性不稳定性分析方法的具体应用。流动聚焦是一种生成柱状微细射流及复合射流的微纳尺度流动方法,其原理可描述为从毛细管流出的流体在周围高速流体驱动下,经过小孔聚焦后在毛细管孔处形成稳定的锥形,并在锥形的顶端形成一股微细射流,射流在流出小孔外一段距离后破碎成单分散液滴[54]。最近,司廷等对流动聚焦及射流不稳定性的研究成果进行了总结,并给出了不同结构流动聚焦技术中单轴射流、复合射流、带电射流等的生成方法。下面将根据线性不稳定性分析方法的流程,简要回顾不同结构流动聚焦中射流及复合射流破碎的理论研究进展。
3.1 真空中无黏射流破碎Rayleigh[10]利用线性不稳定性理论研究了无黏液体射流的破碎问题。假设液体为无黏不可压缩的牛顿流体,半无限长的液体射流处在真空中,忽略温度变化,假设液体的密度为常数。平衡状态下射流径向、周向基本流速为0:u0r=u0θ=0,轴向流速为:u0z=U,则控制方程和边界条件大大简化。在柱坐标下,线化小扰动控制方程为:
| $ \frac{1}{r} \frac{\partial\left(r u_{r}^{\prime}\right)}{\partial r}+\frac{\partial u_{z}^{\prime}}{\partial z}+\frac{1}{r} \frac{\partial u_{\theta}^{\prime}}{\partial \theta}=0 $ | (29) |
| $ \rho \frac{\partial u_{r}^{\prime}}{\partial t}=-\frac{\partial p^{\prime}}{\partial r}, \frac{\partial u_{\theta}^{\prime}}{\partial t}=-\frac{\partial p^{\prime}}{r \partial \theta}, \frac{\partial u_{z}^{\prime}}{\partial t}=-\frac{\partial p^{\prime}}{\partial z} $ | (30) |
由微分几何知识可知扰动后界面位置为:
| $ \boldsymbol{r}=\left[a+\zeta \mathrm{e}^{\mathrm{i}(n \theta+k z+\omega t)}\right] \boldsymbol{e}_{r}+z \boldsymbol{e}_{z} $ | (31) |
其中er、ez分别为r、z方向的单位矢量,a为未扰动时界面的位置,ζ为界面扰动的幅值。由运动学和动力学边界条件可得:
| $ \begin{array}{l}{\omega^{2} \rho \zeta=k p_{1}} \\ {\left.p^{\prime}\right|_{r=a}=-\frac{\gamma \zeta}{a^{2}}\left(1-n^{2}-k^{2} a^{2}\right) \mathrm{e}^{\mathrm{i}(n \theta+k z)}}\end{array} $ | (32) |
可得∇2p′=0,展开后为:
| $ \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial p^{\prime}}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} p^{\prime}}{\partial \theta^{2}}+\frac{\partial^{2} p^{\prime}}{\partial z^{2}}=0 $ | (33) |
将X=p情况下的式(24)代入式(33)得:
| $ r^{2} \frac{\mathrm{d}^{2} \overline{p}}{\mathrm{d} r^{2}}+r \frac{\mathrm{d} \overline{p}}{\mathrm{d} r}-\left(n^{2}+k^{2} r^{2}\right) \overline{p}=0 $ | (34) |
上式为n阶修正Bessel方程,结合边界条件可得:
| $ {\hat u_r}(r) = \frac{{{\rm{i}}k{p_1}}}{{\omega \rho }}\left[ {{I_{n + 1}}(kr) + \frac{n}{{kr}}{I_n}(kr)} \right] $ | (35) |
最终可得色散关系:
| $ \omega^{2}=-\frac{\sigma}{\rho a^{3}} \frac{k a I_{n}^{\prime}(k a)}{I_{n}(k a)}\left(1-n^{2}-k^{2} a^{2}\right) $ | (36) |
对于任意的n∈N+,满足对于任意的ka使得ω2>0,此时ωi=0,射流处于中性稳定状态;n=0时ka≥1或ka≤-1,ω2≥0,此时ωi=0,射流仍处于中性稳定。上述情况下ω为实数,ωi=0,此时界面不断震荡,但既不增长也不衰减,界面上存在为非扩散色散波动。其中n≠0对应非轴对称扰动,n=0对应轴对称扰动。可见如果扰动为非轴对称的,则射流是稳定的。
当n=0且-1 < ka < 1时, ω2 < 0,可解得一对共轭复数,其中一解ωi < 0,射流处于不稳定状态。可见扰动波长λ=2π/k大于未扰动射流周长2πa情况下的轴对称扰动,射流为不稳定的。在n=0还发现,ω随ka变化而连续变化,|ωi|存在最大值,对应最大扰动增长率和最不稳定状态。通过对方程(36)求ka导数,并令导数等于0,可以得到最快增长扰动对应的波数。Rayleigh认为对不稳定性起主要支配作用的是最大扰动增长率,能够导致射流破碎。扰动增长率ωi为a的函数,当ka=0.697即当λmax=9.02a时,ωi取得最大值
Rayleigh对射流不稳定性的分析是在时间域展开的,但实际中扰动是在时间域和空间域上共同发展演化最终导致射流失稳、破碎。Keller等[21]注意到这个事实,在Rayleigh结果上进一步展开讨论,开展了针对半无限长射流的空间和时空稳定性研究,理论预测了射流的破碎长度。然而上述所有工作中射流均是无黏的,Leib & Goldstein[45]在Keller等工作的基础上研究了表面张力和速度型对黏性射流影响,发现忽略黏性影响后,射流绝对/对流不稳定性转换临界韦伯数Wecrit的值恒为π。实验中射流所处环境流体的流速和密度对射流破碎也有较大影响。Kang & Lin[46]研究了环境气体密度对旋拧射流非轴对称扰动影响。Yuen[47]考虑了射流破碎中的非线性效应,对初始扰动中高频谐波产生卫星滴的现象给出了解释。Drazin[43]认为扰动初始波幅可能并不完全相同,同时不稳定演化过程中(尤其是后期)非线性起着重要作用。此后Lin研究了界面剪切作用对射流不稳定性影响,采用能量积分方法分析和解释了射流破碎机理,发现对流不稳定性状态存在Rayleigh和Taylor两种模式,Rayleigh模式下表面张力主导毛细收缩进而使得射流的产生破碎,剪切力会抑制界面失稳;而Taylor模式下环境气体惯性力以及界面上剪切作用主导射流破碎。也即剪切效应在两种模式下对射流破碎产生的作用是相反的[28, 48-52]。
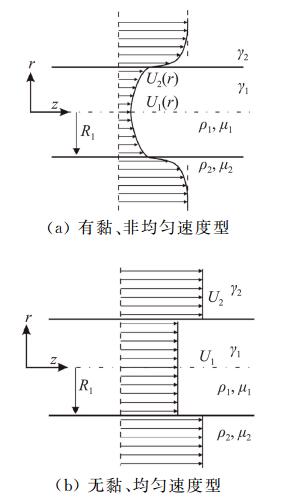
3.2 单轴流动聚焦中射流破碎在典型的单轴流动聚焦实验中[53-68],当锥形始终保持稳定时,小孔出口处的外层驱动流体形成高速气流,内层被驱动液体形成柱状微细射流,周围环境为静止的空气。内部液体射流和外部驱动气流(一般为空气)之间形成明确的界面,流体的黏性作用会使界面处产生边界层。在外部高速气流与周围静止空气之间存在剪切和混合,高速气流的流速在外边界会迅速衰减,并与静止空气相互作用产生旋涡。实验观察发现,小孔直径(数百微米)一般远大于射流直径(数十微米或更小),射流破碎长度一般只有数百微米,而周围静止空气与高速气流剪切形成的旋涡一般在射流破碎的下游较远处才出现,于是可以将周围静止空气对射流的影响忽略不计。此外,驱动气流在小孔出口的扩张角比较小,液体射流的直径也变化不大,于是可以近似认为液体射流和驱动气流都只沿轴向运动,基本流满足轴对称条件。因此,为了便于线性不稳定性分析,可以建立如下近似的物理模型:半径为R1的半无限长的液柱被外半径为R2的半无限长的环形气流包围(R2≫R1,或R2→∞)。进一步,可以合理地假设液体和气体均为不可压缩牛顿流体,密度ρ1和ρ2、黏性系数μ1和μ2、表面张力系数σ等物理属性都不发生变化,并忽略温度的影响。
控制方程可以由式(1)和式(2)给出,边界条件包括对称轴、界面上和最外层三个位置,分别由式(5)~式(9)给出。选取液体射流半径R1、流速U1为特征长度和特征速度,特征时间为R1/U1,特征压力为ρ1U12,无量纲化后的控制方程为:
| $ u_{r i}^{\prime}+\frac{u_{r i}}{r}+\mathrm{i} \alpha u_{z i}=0 $ | (37) |
| $ \begin{array}{*{20}{c}} {u_{zi}^{\prime \prime } + \frac{{u_{zi}^\prime }}{r} - \left[ {{\alpha ^2} + R{e_i}\left( {{\rm{i}}\alpha {U_{zi}} - {\rm{i}}\omega } \right)} \right]{u_{zi}}}\\ { - R{e_i}{v_i}U_{zi}^\prime - {\rm{i}}\alpha R{e_i}{{\left( {\frac{1}{Q}} \right)}^{{\delta _{i2}}}}{p_i} = 0} \end{array} $ | (38) |
| $ \begin{array}{l}{u_{r i}^{\prime \prime}+\frac{u_{r i}^{\prime}}{r}-\left[\frac{1}{r^{2}}+\alpha^{2}+R e_{i}\left(\mathrm{i} \alpha U_{z i}-\mathrm{i} \omega\right)\right] u_{r i}} \\ {\quad-R e_{i}\left(\frac{1}{Q}\right)^{\delta_{i 2}} p_{i}^{\prime}=0}\end{array} $ | (39) |
其中无量纲参数分别为Re1=ρ1U1R1/μ1,Re2=(Q/N) Re1,黏性比N=μ2/μ1,密度比Q=ρ2/ρ1,下标i=1, 2代表内层液体射流和外层气流。
对称轴上流速和压力有限且射流轴对称条件:
| $ u_{r 1}=u_{z 1}^{\prime}=p_{1}^{\prime}=0 $ | (40) |
|
图 1 高速流体驱动作用下单轴射流的简化模型[36] Fig.1 Schematic diagram of simplified model for a single jet in a co-flowing driving fluid[36] |
界面上速度连续条件:
| $ u_{r 1}=u_{r 2}, u_{z 1}+U_{z 1}^{\prime} \eta=u_{z 2}+U_{z 2}^{\prime} \eta $ | (41) |
界面上运动学边界条件:
| $ \mathrm{i} \omega \eta=\mathrm{i} \alpha U_{z i} \eta-u_{r i} $ | (42) |
界面上动力学边界条件:
| $ \mathrm{i} \alpha u_{r 1}+u_{z 1}^{\prime}-N\left(\mathrm{i} \alpha u_{r 2}+u_{z 2}^{\prime}\right)+\left(U_{z 1}^{\prime \prime}-N U_{z 2}^{\prime \prime}\right) \eta=0 $ | (43) |
| $ p_{1}-\frac{2}{R e} u_{r 1}^{\prime}-\left(p_{2}-\frac{2 N}{R e} u_{r 2}^{\prime}\right)+\frac{1}{W e}\left(1-\alpha^{2}\right) \eta=0 $ | (44) |
外边界流速及压力扰动量条件:
| $ u_{r 2}=u_{z 2}^{\prime}=p_{2}^{\prime}=0 $ | (45) |
直接求解流动聚焦的基本流场是非常繁琐的,且得不到解析解[3, 37, 68-69],Si等[36]基于双曲正切函数构建了Uzi(r)=ai tanh[bi(r-1)]+ci这种简化的基本速度型,其中ai、bi和ci为待定系数,需要结合界面处的速度Us、液体剖面斜率K、黏性比N、密度比Q以及液体气体动量比接近1等条件确定。Us主要影响液体基本速度型;界面上剪切力与剖面斜率K成正比,剪切力越大液体和气体射流边界层厚度越小。Us和K对液体、气体速度差几乎无影响。黏性比N和密度比Q主要对气体速度型起作用,黏性比的减小,密度比的增大都能够导致气体边界层厚度的减小、密度比的增大还能够导致液体和气体速度差迅速减小。当液体和气体边界层的厚度趋于0时,双曲正切函数构建的简化基本速度型将会退化为K-H速度型。
鉴于基本速度型为非均匀速度型且控制方程涉及到流体黏性,该问题难以得到解析形式的色散方程,因此可采用Chebyshev谱配制法数值求解不稳定模对应特征值,能够获得最大增长率对应的波数,分析基本速度型、韦伯数、雷诺数、密度比等参数对不稳定模增长率和频率的影响。结果发现相较于界面处的速度Us,界面处液体速度剖面斜率K对流动不稳定性影响较大,较小的K值附近出现长波不稳定性,较大的K值往往引发短波不稳定性,而短波不稳定性越强,形成的液滴就越小,这一结论与Lin & Chen[70]的研究相一致。表面张力对时间增长率有双重影响,在长波区域,表面张力对时间不稳定性有抑制作用,但对扰动波的传播速度无影响;在短波不稳定区域,表面张力既会促进射流失稳,也能够加快扰动波的传播速度。密度比Q主要反映了外部气体密度对射流不稳定性的影响,外部气流密度不同会影响流体之间惯性力大小的不同,所以气体密度越大射流时间不稳定越明显,但对扰动波的传播速度不产生影响。相较而言,黏性的影响更为复杂,黏性较大时Re在较小的值域(< 10)变动时,黏性增大会导致最不稳定增长率和对应的最不稳定波数均变大,但对最不稳定波数影响更为明显,此时扰动波在长波不稳定区域传播较快;惯性力增大使得Re处于10~200时,随着Re变大最大扰动增长率显著变小,对应的最不稳定波数缓慢变大,此时扰动波在短波不稳定区域传播较快。同时,Si等[71]还发现黏性影响相对于惯性力足够小时,由于速度型的作用,黏性不稳定模态并不与无黏K-H不稳定模态吻合,且有黏时的扰动波传播速度均大于无黏时扰动波传播速度。外部气体对气体边界层影响显著,黏性比N=μ2/μ1越小时气体黏性越小,射流时间稳定性影响越明显。此外,时空不稳定性理论被用于成功预测滴模式和射流模式的转换。上述均是轴对称(n=0)模式下的时间不稳定性结果。实验中观察到了呈螺旋型的射流,为此Si等[72]进一步研究了第一类非轴对称(n=1)模型下We对不稳定模的影响,对比了n=0和n=1下We对不稳定性影响的差异,发现理论与实验结果吻合。在理论分析中,最不稳定扰动增长率对时间不稳定性起决定作用,主宰着射流的破碎过程,对应的波数αmax就决定着射流表面扰动波长的大小:
| $ \lambda=\frac{2 \pi R_{1}}{\alpha_{\max }} $ |
Si等(2009)获得了实验参数下最不稳定扰动的波长随着液体流量Ql变化趋势,理论预测与实验结果一致。单轴流动聚焦中射流破碎的线性不稳定性理论研究较多,相关进展可参阅Gañán-Calvo等[73]、司廷等[3]综述论文。
3.3 电流动聚焦中射流破碎电流动聚焦技术源于电雾化和流动聚焦技术[74]。电雾化是将具有一定电导率的液体通入一根毛细金属管,毛细金属管与平板电极之间加载直流电压,在适当的流量和电压作用下,管口处的液体在切向电场力的作用下形成一个稳定的弧形圆锥,并在锥形顶端生成一股稳定的细小射流,射流向下游运动一段长度后破碎成细小的带电微滴[35, 37]。可见流动聚焦和电雾化都是通过外力将液体射流界面拉伸成微细射流,进而破碎成单分子微粒,二者物理机理是相似的。Gañán-Calvo等[59]结合了流动聚焦和电雾化,提出了电流动聚焦:在流动聚焦毛细管口和小孔入口之间锥形区域加载电场,利用电场作用改变锥形结构进而改变射流不稳定性。实验发现小孔附近的锥形显著缩小,诱生的射流变细,获得的液滴直径更小。司廷等[66]2011年另辟蹊径,将电场作用到流动聚焦射流区域,通过直接改变射流不稳定性进而使得雾化更为剧烈,获得的液滴尺度更小。
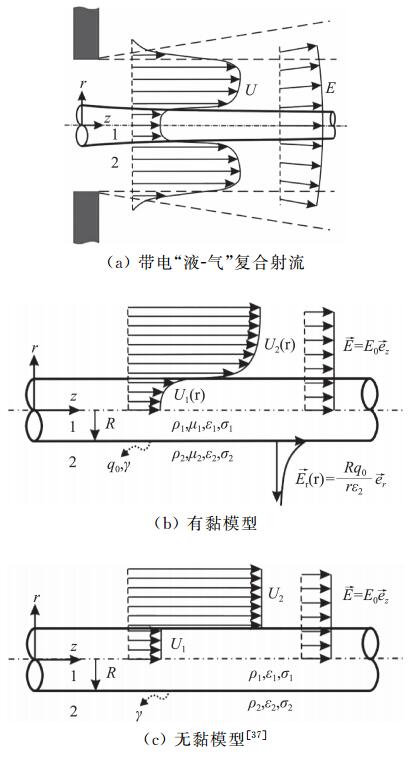
基于电流动聚焦的实验和上述模型,李广滨[37]建立了更为简化的理论模型,如图 2所示,分别研究了有黏和无黏情况下带电“液-气”同轴射流中扰动在时域发展和演化的情况。在分析有黏情况下同轴射流不稳定性时,Li等[69]采用“管流+误差函数”模式构造基本速度型。
|
图 2 电流动聚焦的简化物理模型示意图 Fig.2 Sketch of coflowing liquid-gas jets under the axis electric field at the orifice exit |
与Si等[71]、李芳[35]类似,Li等[64]忽略外剪切层、温度变化以及重力对射流影响,忽略界面上的质量传递,假设内外层流体均为不可压缩黏性牛顿流体,电导率和电容率均为常数。由静电学知识可知,电荷在加载电场的作用下会被松弛到导体界面上,假设液体电松弛时间相当小,以至于在液体射流内部不存在自由电荷。然而界面受到扰动的情况下,电荷的分布情况取决于电松弛时间τe=ε/σ(σ为电导率,ε为介电常数)和水动力学特征时间τF=L/U的相对大小。通过实验发现,水的电松弛时间τe的量级为1×10-6s,水动力学特征时间τF的量级为1×10-4s,于是可得τe/τF的量级为1×10-2。说明扰动情况下射流中的自由电荷有充足的时间松弛到平衡状态[35]。因而可以假设自由电荷只分布在“液-气”交界面上。松弛到界面上的自由电荷在电场诱导的磁场作用下会受到磁场力,为了处理问题的简便,忽略磁场对界面上自由电荷的作用。实验中由于射流出口的存在使得射流区域并不是理想的“平板-平板”电极结构,加载电场呈轴向分量远大于径向分量的发散状,所以还要假设射流处于均匀的轴向电场当中。
单位体积流体受到电场力为fe=∇·Te, 其中Te=εEE-εE2δ/2为Maxwell应力张量,其中ε为介电常数,δ表示Kronecker函数。由自由电荷只分布在两种流体界面上可得fe=0,此时动量方程退化为无体积力的形式。用Maxwell方程组定量地描述电场作用,由于自由电荷只分布在界面上,Maxwell方程组可以简化为∇·Di=0,∇×Ei=0,方程中Ei表示电场强度,Di=εEi为电位移矢量。由于电场强度E无旋,可引入电势函数Ei=-∇Vi,进而能够得到电势Vi的Laplace方程:
| $ \Delta V_{i}=0 $ | (46) |
在柱坐标系特定情形下r=0是控制方程的奇点,然而物理意义上r=0又不是奇点,所有的物理量在r=0处应该为单值、光滑、有界的:
| $ \mathop {\lim }\limits_{r \to 0} \frac{{\partial {\mathit{\boldsymbol{u}}_1}}}{{\partial \theta }} = 0, \mathop {\lim }\limits_{r \to 0} \frac{{\partial p}}{{\partial \theta }} = 0 $ | (47) |
分布在流体界面上的自由电荷,在电场作用下参与界面上力的平衡,所以要对动力学边界条件(8)进行修正:
| $ \begin{array}{l}{\boldsymbol{T}=\boldsymbol{T}^{h}+\boldsymbol{T}^{e}, \boldsymbol{T}^{h}=-p \boldsymbol{\boldsymbol { \delta }}+\mu\left[\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right]} \\ {\boldsymbol{T}^{e}=\varepsilon \boldsymbol{E} \boldsymbol{E}-\varepsilon E^{2} \boldsymbol{\delta} / 2}\end{array} $ | (48) |
电场边界条件包括界面上电场强度切向分量连续条件和Gauss定理:
| $ \left(\boldsymbol{E}_{2}-\boldsymbol{E}_{1}\right) \times \boldsymbol{n}=0, \quad r=R+\eta $ | (49) |
| $ \boldsymbol{n} \cdot\left(\varepsilon_{2} \boldsymbol{E}_{2}-\varepsilon_{1} \boldsymbol{E}_{1}\right)=\boldsymbol{q}_{s}, r=R+\eta $ | (50) |
式中qs为界面电荷密度,满足界面电荷守恒方程:
| $ \begin{array}{l}{\frac{\partial q_{s}}{\partial t}+\boldsymbol{u} \cdot \nabla q_{s}-q_{s} \boldsymbol{n} \cdot(\boldsymbol{n} \cdot \nabla) \boldsymbol{u}} \\ {\quad+\left(\sigma_{2} \boldsymbol{E}_{2}-\sigma_{1} \boldsymbol{E}_{1}\right) \cdot \boldsymbol{n}=0}\end{array} $ | (51) |
在有黏模型中涉及了非均匀速度型,无法得到解析形式的色散关系,采用谱配置方法进行处理。Li等[69]发现:轴对称(n=0)扰动和第一类非轴对称扰动(n=1)对射流稳定性影响最为突出;外部驱动气体惯性力及界面处黏性剪切力能促进射流失稳;表面张力对轴对称扰动具有双重影响,对非轴对称扰动有抑制作用;内层液体黏性不是很大时,增加液体黏性会促进射流失稳,驱动气体黏性的耗散作用能够抑制射流失稳;同时还发现了电欧拉数Eu与界面上初始自由电荷密度Q0对射流稳定性影响相互耦合,这些都与实验现象定性一致。电场力和惯性力的耦合效果能够带来更强的雾化效果和更为细小的液滴,但也给理论和数值研究带来更大的困难:与普通流动聚焦相比,电流动聚焦控制方程需要增加一组电学方程,同时也要增添电场方面的边界条件。然而困难不仅仅及于此,电流动聚焦中电场加载方向和射流结构多样性也给实验和理论带来巨大挑战。如李芳[35]将加载电场分成径向和轴向两个方向,研究了更为新颖的射流结构(同轴射流)的不稳定性。根据毛细管嵌套的数目不同分为单轴流动聚焦和复合流动聚焦;径向电场作用下的同轴流动聚焦研究中,根据射流电导率的不同又分为内驱动和外驱动两种模式等。相关研究亟待开展。
3.4 复合流动聚焦中射流破碎当单轴流动聚焦核心装置中的毛细管不再是单个毛细管,而是两个或多个毛细管形成的复合结构时,就变成复合流动聚焦。因这种结构中多种流体相互耦合,给实验和理论研究带来一定困难,相关研究刚刚起步,目前的报道比较有限。Martín-Banderas等[60]系统介绍了单轴和同轴流动聚焦在制备微颗粒和微胶囊方面的重要应用前景。Si等[75]利用三个嵌套的毛细管组成三轴针头展开了三轴流动聚焦实验,得到了稳定的三轴锥形和三层结构的微胶囊以及三层液体射流的直径尺度律。Si等[76-77]采用“一包二”结构的复合针头,施加外部电场增强锥形稳定性,最终得到了稳定的锥-射流结构和能够长时间保存的多核微胶囊。
复合流动聚焦中射流破碎的线性不稳定性理论研究也具有重要意义。Herrada等[78]通过研究气体驱动下同轴射流不稳定性发现了“滴-射流”模式之间的转换机理,并与实验中“射流-滴”模式与流模式之间转换边界进行了对比。基于同轴流动聚焦实验,李广滨[37]建立了简化的三相“水-油-水”型复合射流模型,针对模型进行了时间不稳定性和时空不稳定性分析,得到了物理参数对射流不稳定性的影响规律及内外界面如何相互耦合作用,给出了“绝对-对流”不稳定性转换关系。李芳[35]系统地研究了同轴带电射流的不稳定性,在无黏不稳定性研究中,得到了解析色散关系,在有黏情况下利用Chebyshev谱配置法求得控制方程解析解。在此基础上,李帅兵等[38]进一步研究了驱动气流对同轴带电射流的不稳定性影响。
在无黏带电复合射流的物理模型建立中,假设流动无旋、不可压,同时忽略流体间温度差异和重力影响,忽略磁场对射流影响,假设内层流体为导体,中间层流体为电介质,两层流体之间界面上无质量传递,无渗透互溶效应,在场强为E0的理想均匀轴向电场作用下,自由电荷均被松弛到内界面上。松弛到界面上的自由电荷有两方面作用,一是能够提供径向电场,破坏理想轴向电场的假设,二是与轴向电场相互作用产生切向电应力,这部分电应力由界面上黏性剪切力抵消,破坏了无黏假设。为此进一步假设界面上自由电荷密度足够小,诱导的径向电场和切向电应力也足够小。
与Si等[71]和Li等[69]的模型假设不同的是,添加的流动无旋的假设更强。无旋下∇×ui=0,引入速度势满足ui=∇φi,又因为无黏流动连续方程为∇·ui=0,可得
| $ \Delta \varphi_{i}=0 $ | (52) |
对应的小扰动形式为Δφi′=0。在圆柱坐标系下展开后为n阶修正Bessel方程,方程及其解形式为:
| $ \frac{\mathrm{d}^{2} \overline{\varphi_{i}}}{\mathrm{d} r^{2}}+\frac{\mathrm{d} \overline{\varphi_{i}}}{r \mathrm{d} r}-\left(k^{2}+\frac{n^{2}}{r^{2}}\right) \overline{\varphi_{i}}=0 $ | (53) |
| $ \overline{\varphi_{i}}=A_{i} I_{n}(k r)+B_{i} K_{n}(k r) $ | (54) |
结合射流速度势在对称轴上的扰动量有限和无穷远处的扰动为0的边界条件φ1′|r→0 < ∞, φ3′|r→0 < ∞可得φ1、φ2、φ3具体表达式。利用ui=∇φi可解出射流速度u1、u2、u3。求出速度具体表达式还需运动学边界条件
| $ u_{i r}^{\prime}=\frac{\partial \eta_{i}}{\partial t}+U_{i z} \frac{\partial \eta_{i}}{\partial z} $ |
其中ηi为离开平衡位置距离。
忽略重力、电场力、磁场力以及黏性力下的动量方程满足:
| $ \rho_{i}\left(\frac{\partial \boldsymbol{u}_{i}}{\partial t}+\boldsymbol{u}_{i} \cdot \nabla \boldsymbol{u}_{i}\right)=-\nabla p_{i} $ |
利用无旋下的Lamb公式:u·∇u=∇(u·u/2)+(∇×u)×u=∇(u·u/2)将动量方程简化为:
| $ \nabla p_{i}=-\rho_{i} \nabla\left(\frac{\partial \varphi_{i}}{\partial t}+\frac{\boldsymbol{u}_{i} \cdot \boldsymbol{u}_{i}}{2}\right) $ | (55) |
由密度定常条件可解得:
| $ p_{i}=-\rho_{i}\left(\frac{\partial \varphi_{i}}{\partial t}+\frac{\boldsymbol{u}_{i} \cdot \boldsymbol{u}_{i}}{2}\right)+\mathrm{const.} $ | (56) |
求解电场时,由于自由电荷只存在于界面上,忽略磁场和体电荷作用下射流内部的Maxwell方程简化为:∇·Di=0,∇×Ei=0。故可引入势函数Vi满足ΔV′i=0,在柱坐标系下此方程为n阶修正Bessel方程,解的形式为:
这里的动力学边界条件为:
| $ \begin{array}{l}{\gamma\left(\nabla \cdot \boldsymbol{n}_{1}\right)=p_{1}-p_{2}+\boldsymbol{n}_{1} \cdot\left(\boldsymbol{T}_{2}^{e}-\boldsymbol{T}_{1}^{e}\right) \cdot \boldsymbol{n}_{1}} \\ {\gamma\left(\nabla \cdot \boldsymbol{n}_{2}\right)=p_{2}-p_{3}+\boldsymbol{n}_{2} \cdot\left(\boldsymbol{T}_{3}^{e}-\boldsymbol{T}_{2}^{*}\right) \cdot \boldsymbol{n}_{2}}\end{array} $ |
其中n为界面上法向单位矢量,T为水动力学张量Th与电应力张量Te之和T=Th+Te。将p1、p2、p3、E1、E2、E3代入动力学边界条件就可得到色散方程(表达式比较复杂,此处省略)。如果不考虑电场作用(略掉色散方程中有关电场的量),则可得不带电同轴射流的色散方程:
| $ \frac{\hat{\eta}_{1}}{\hat{\eta}_{2}}=\frac{\frac{\left(\beta+\mathrm{i} \alpha U_{32}\right)^{2}}{\alpha \Delta_{8}}-\frac{(\beta+\mathrm{i} \alpha)^{2} \Delta_{3}}{\alpha \rho_{32} \Delta_{5}}+\frac{1-n^{2}-\alpha^{2}}{\rho_{32} W e_{2}}}{\frac{(\beta+\mathrm{i} \alpha)^{2} \Delta_{6}}{\alpha \rho_{32} \Delta_{5}}} $ | (57) |
| $ \frac{{{{\hat \eta }_2}}}{{{{\hat \eta }_1}}} = \frac{{\frac{{{{\left( {\beta + {\rm{i}}\alpha {U_{12}}} \right)}^2}}}{{\alpha {\Delta _7}{\Delta _4}}} - \frac{{{{(\beta + {\rm{i}}\alpha )}^2}}}{{\alpha {\rho _{12}}{\Delta _5}}} - \frac{{\frac{{1 - {n^2}}}{{{a^2}}} - {\alpha ^2}}}{{{\Delta _4}W{e_1}{\rho _{12}}}}}}{{ - \frac{{{{(\beta + {\rm{i}}\alpha )}^2}{\Delta _1}}}{{\alpha {\Delta _5}{\Delta _4}{\rho _{12}}}}}} $ | (58) |
式(57)和式(58)分别为界面扰动振幅比的不同表示式,由射流内外层界面上的动力学边界条件代入流速ui和压力pi得到,联立可得色散方程。上述求解过程发现,无旋假设下应用Lamb公式简化动量方程,能够直接简便地求出压力场,避免了求解偏微分方程带来的困难,从而给求得解析解带来方便。最终求得的无量纲化的色散方程,本质上是以无量纲波数α=R2k为自变量,以无量纲复频率β=ωR2/U2为因变量的四次代数方程。在其他参数已知情况下,每给出一无量纲波数,能够得到两组共4个无量纲复频率β。一般而言,每组无量纲复频率中会存在一个β的实部βr>0,对应不稳定模式。在这个问题中,扰动振幅比为一个复数而非实数,也就是说界面波动演化差异不仅仅存在于扰动振幅的大小,而且存在于界面相位角上,表述为:
| $ \hat{\eta}_{1} \hat{\eta}_{2}=\left|\hat{\eta}_{1} / \hat{\eta}_{2}\right| \mathrm{e}^{\mathrm{i}\left(\varphi_{1}-\varphi_{2}\right)} $ | (59) |
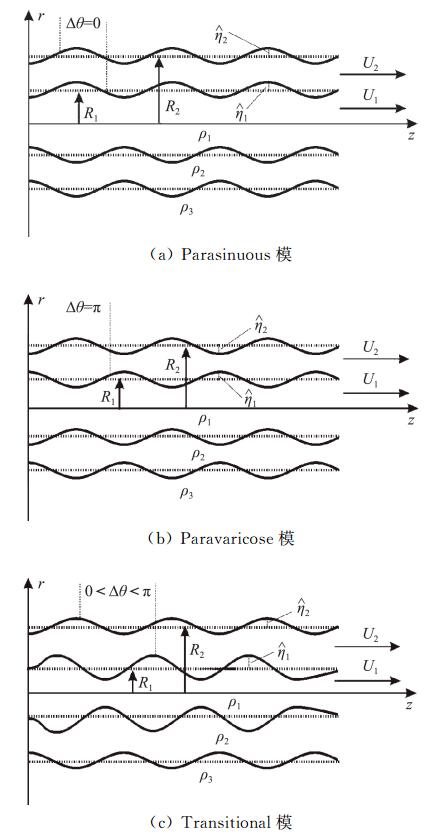
式中(φ1-φ2)表示界面相位差。将不稳定的β连同其他参数代入式(59)中可知不稳定状态对应的界面相位差。φ1-φ2=0表示界面同向运动,φ1-φ2=π表示界面反向运动。平面液膜射流的表面扰动波有对称波和反对称波两种形式[25]。当两个界面发生的变形相位相同时为反对称扰动,当两个界面的变形在相位上相差π时是对称型扰动。然而在同轴射流中发现扰动界面相位差不等于但是接近于0和π,因此通常称之为parasinuous模和paravaricose模。李芳[35]发现还存在一个过渡模,称之为transitional模,一般与parasinuous模相接,位于parasinuous模右端,在transitional模下内外界面相位差随着波数从0变化到π(图 3)。
|
图 3 液体射流和表面波 Fig.3 Schematic of liquid sheet and surface waves |
通过研究电欧拉数Eu、韦伯数We、界面两侧射流流速比U12、U32以及介电常数比ε13、ε23等无量纲参数与射流模态之间的相互影响,发现最不稳定扰动增长率βrmax随着外层气流流速增大而增大,射流由长波不稳定性向短波不稳定性演化。而实验中常通过改变气体压力差Δpg控制气体流速。在研究单轴流动聚焦时Si等[72]发现,气体压力差Δpg对液体射流的形态影响较大,随着Δpg的增大,扰动波长λ不断减小,振幅不断变大。李广滨等[37]研究带电单轴射流以及不带电同轴射流过程中发现,随着Δpg增大,射流内外径减小,液体射流越不稳定,扰动由长波不稳定性向短波不稳定性过渡。此外,表面张力促进射流失稳;轴向电场对射流不稳定性具有双重影响,且存在某一临界值,当加载电场强度小于此临界值时射流不稳定性受到抑制,当加载电场强度超过此临界值时,轴向电场会促进射流失稳。以上结果与已有实验现象相吻合[35-37]。
虽然采用小扰动法和正则模法在研究流动聚焦、电流动聚焦、同轴流动聚焦等问题中取得了一定的研究进展,然而不容否认,这些方法的实施需要采用合理的近似和假设建立物理模型,需要正确处理流场以及电场的边界条件。将来,研究领域需要从时间域拓展到空间或时空域,采用的基本速度型从简单的近似速度型到接近实际的速度型,从线性不稳定性发展到非线性, 从局部不稳定性发展到全局。这些深入的研究能够为复杂射流破碎的机理分析打开广阔的天地。但是,简化模型的优势在于,它能够在确切条件下揭示不稳定性的某些内在机理。例如无黏假设,没有黏性力时流体的惯性力、流体压力和表面张力维持平衡,一个小扰动就可能打破这种微妙的平衡关系,而黏性力的存在一定程度上能够耗散扰动能量使流动稳定化,从而在扰动发生时维持平衡关系的存续。
3.5 其他相关问题工程实际中,许多液体射流与周围气体间往往存在较大的温差,由温差导致的温度扰动会在射流表面产生温度变化[79-80],射流表面的温度变化会导致表面张力变化,产生热毛细力,进而导致液体表面剪切力发生变化。在不同条件下,温度扰动可能加快或者减慢液体射流的破碎过程。Furlani[81]对温度扰动下的黏性牛顿流体射流问题进行了时间线性不稳定性分析,并假设表面张力在液体射流方向周期变化,表面张力与温度关系呈线性变化:
| $ \sigma=\sigma_{0}-\gamma\left(T-T_{0}\right) $ | (60) |
式中T0和T为射流液体的初始温度和终态温度,σ0和σ为对应的表面张力,γ为表面张力随温度的变化率。变化的表面张力产生了Marangoni流动,进而对液体射流破碎成液滴过程产生影响。Xu等[80]在射流温度沿轴向单调增加的假设条件下,研究了温度场扰动下射流不稳定性,发现了毛细力、表面波和热模式三种不稳定模式,计算求得了三种模式中性曲线。Mashayek等[79]研究了对射流施加两种不同温度扰动时,液体与环境传热、液内导热对射流破碎的影响,发现了当温度与射流界面扰动的相位差为0时,温度扰动与界面扰动会相互抵消;相位差为π/2时温度扰动与界面扰动不能相互抵消;射流只受到温度扰动时,射流破碎时间随Bi数增大而增大。
另一个工程实际问题涉及了压力旋流喷嘴,被广泛应用于各种工程喷射系统当中,尤其是航空发动机、船用发动机、燃气轮机以及汽油缸内直喷发动机燃油喷射等领域。此外,喷气净化器、泡沫发生器、食用液体喷雾烘干、涂料喷雾等领域也应用了旋转液体射流的破碎机理,取得了极佳的喷雾效果。李帅兵等[38]研究了轴向速度差异对同轴射流带来的不稳定性影响,然而周向速度差异对射流不稳定性影响还尚待研究。
不容忽视的是,之前的许多理论研究工作为了简化射流的物理模型和理论推导过程,将模型投影到平面二维系统中,研究平面二维扰动下黏性液体射流的不稳定性。而旋转射流不得不考虑射流的三维性质,研究难度将显著增大。上述这些都给不稳定性理论研究带来了机遇和挑战。
值得一提的是,现实生活中几乎所有问题都涉及非线性效应,而线性问题只是一种特例。在本文中,射流破碎时的动力学过程基本上都是一个非线性过程,线性不稳定性分析方法可以描述最优扰动的性质,但却难以刻画出射流从形成到破碎的全部过程。也就是说,通过采用近似的线性模型可以使我们分析出实际问题在某些方面的特性,却很难刻画整个系统的非线性本质。所以线性不稳定性分析方法既是研究非线性问题的基础却又存在先天不足。从这个角度看,线性问题和非线性问题就像数轴上的有理数和无理数一样,测度为零的前者可以无限逼近后者,但是却无法完美精确地刻画后者。实际上,非线性研究更有助于揭示射流破碎问题中的液滴非均匀分布现象以及卫星液滴的形成,这是线性稳定性方法所不能做到的。目前的非线性不稳定性分析主要借助多尺度展开方法推导色散方程,然而这在数学上存在较大难度,需要更深入、更全面的理论推导和分析。
4 结论流动不稳定性是一个很古老但是依然很活跃的研究领域。其中,射流破碎问题的研究由来已久,从Rayleigh[10]算起,至今已经有近一个半世纪的历史。目前,实验观测和数值模拟都是重要的研究方法,而将物理问题转化为数学问题进行定量分析,能够使研究体系达到更趋完善的地步。
线性不稳定性分析方法是流动不稳定性研究的经典方法,而小扰动法和正则模法又是线性不稳定性分析中最为常用的方法。其主要思想是将任意物理量展开成基本解和小扰动的形式,再将小扰动分解为一系列模态的叠加,每个模态都满足线性系统,使得每个模态能够分别处理。正则模方法包括时间、空间和时空不稳定性分析三种模式。其中时间不稳定性研究方法最为简单常用,小扰动在空间上呈现周期性,幅值在时间轴上演化,能够预测最大扰动增长率以及不同过程参数的影响规律。而空间和时空不稳定性方法更接近实际情况,能够预测不稳定模态之间的转换。本文将线性不稳定性分析处理射流破碎过程的研究方法概括为八个部分,并逐一阐述,给出了相应的关键步骤。
在分析射流破碎相关的具体问题时,基于不同假设和近似建立物理模型,小扰动法和正则模法的处理方式也会略有不同。按照线性不稳定性分析方法的处理步骤,本文首先回顾了Rayleigh早期推导的无黏条件下解析形式色散关系的过程,然后以流动聚焦技术为例,系统总结了线性不稳定性分析方法的应用及相关进展。流动聚焦涵盖了宏观和微观两种尺度,涉及了多层流体界面,能够与电场、温度场等耦合,是一个包含了惯性力、表面张力、黏性力、电场力等相互作用的复杂流体力学问题。本文列举了单轴流动聚焦、电流动聚焦和复合流动聚焦三个典型例子,详细介绍了三种情况下如何进行模型假设和方程处理,边界条件设定以及无量纲化,并介绍了黏性、流速比、电场力以及表面张力等对射流不稳定性的影响规律等。这些结果对实际应用具有重要的指导意义。
在未来一段时间内,射流破碎的研究将向广度和深度继续延展。一方面涉及非牛顿流、热不稳定性和电磁场作用的同轴射流及复合射流等复杂问题亟待研究;另一方面,射流在时间、空间和时空域的线性甚至非线性发展,以及从局部到全局不稳定性的理论方法将获得更多关注。
| [1] |
BARRERO A, LOSCERTALES I G, Barrero A, et al. Micro-and nanoparticles via capillary flows[J]. Annual Review of Fluid Mechanics, 2007, 39(1): 89-106. |
| [2] |
EGGERS J, VILLERMAUX E. Physics of liquid jets[J]. Progress in Physics, 2008, 71(3): 036601. DOI:10.1088/0034-4885/71/3/036601 |
| [3] |
司廷, 李广滨, 尹协振. 流动聚焦及射流不稳定性[J]. 力学进展, 2017, 47(1): 178-226. SI T, LI G B, YIN X Z. Flow focusing and jet instability[J]. Advances in Mechanics, 2017, 47(1): 178-226. (in Chinese) |
| [4] |
朗道Л Д, 栗弗席兹E M, 著.流体动力学(第5版)[M].李植, 译.北京: 高等教育出版社, 2013.
|
| [5] |
HELMHOLTZ H Von. Veber discontinuirliche Flüssigkeits-bewegungen[J]. Monats Königl Preuss Akad Wiss Berlin, 1868, 23: 215-228. |
| [6] |
HELMHOLTZ H Von. Die energie der wogen und des windes[J]. Annalen der Physik, 1890, 41(12): 641-662. |
| [7] |
KELVIN L. Hydrokinetic solutions and observations[J]. Phil Mag, 1871(4): 42, 362-77. |
| [8] |
KELVIN L. On the vibrations of a columnar vortex[J]. Phil Mag, 1880(5): 10, 155-68. |
| [9] |
THOMSON S W. LII. On the stability of steady and of periodic fluid motion[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 2009, 23: 459-464. |
| [10] |
RAYLEIGH L. On the capillary phenomenon of jets[J]. Proceedings of the Royal Society of London, 1879, 29: 71-97. DOI:10.1098/rspl.1879.0015 |
| [11] |
RAYLEIGH L. On the instability of jets[J]. Proceedings of the London Mathematical Society, 1878, 10(1): 4-13. |
| [12] |
REYNOLDS O. An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous and of the law of resistance in parallel channel[J]. Philosophical Transactions of the Royal Society, 1883, 35: 84-99. |
| [13] |
REYNOLDS O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion[J]. Philosophical Transactions of the Royal Society of London, Series A, 1895, 186: 123-164. DOI:10.1098/rsta.1895.0004 |
| [14] |
TAYLOR G I. Experiments with rotating fluids[J]. Proceedings of the Royal Society of London, Series A, 1921, 100(703): 114-121. DOI:10.1098/rspa.1921.0075 |
| [15] |
TAYLOR G I. Stability of a viscous liquid contained between two rotating cylinders[J]. Philosophical Transactions of the Royal Society of London, Series A, 1923, 102(223): 289-343. |
| [16] |
WEBER V C. Zum zerfall eines flüssigkeitsstranhles[J]. Z Angew Math Mech, 1931, 11: 136-154. DOI:10.1002/(ISSN)1521-4001 |
| [17] |
尹协远, 孙德军. 旋涡流动的稳定性[M]. 北京: 国防工业出版社, 2003. YIN X Y, SUN D J. Vortex stability[M]. Beijing: National Defense Industry Press, 2003. (in Chinese) |
| [18] |
郭玉翠. 非线性偏微分方程[M]. 北京: 清华大学出版社, 2008. GUO Y C. Nonlinear partial differential equations[M]. Beijing: Tsinghua University Press, 2008. (in Chinese) |
| [19] |
马知恩, 周义仓, 李承治. 常微分方程定性与稳定性方法[M]. 科学出版社, 2015.
|
| [20] |
CANUTO C, HUSSAINI M Y, QUARTERONI A, et al. Spectral methods in fluid dynamics[M]. New York: Springer-Verlag, 1988.
|
| [21] |
KELLER J B, RUBINOW SI, T U Y O. Spatial instability of a jet[J]. Physics of Fluids, 1973, 16(12): 2052-2055. DOI:10.1063/1.1694264 |
| [22] |
LEIB S J, GOLDSTEIN M E. Convective and absolute instability of a viscous jet[J]. Physics of Fluids, 1986, 29(4): 952-954. DOI:10.1063/1.866000 |
| [23] |
LIN S P, KANG D J. Atomization of a liquid jet[J]. Physics of Fluids, 1987, 30(7): 2000-2006. DOI:10.1063/1.866214 |
| [24] |
丁宁.加热条件下液体射流破碎机理的研究[D].天津: 天津大学, 2002.
|
| [25] |
阎凯. 圆环旋转粘性液体射流稳定性及破碎研究[D]. 北京:北京交通大学, 2014. YAN K. Study on stability and breakup of an annular swirling viscous liquid sheet[D]. Beijing: Beijing Jiaotong University, 2014. (in Chinese) |
| [26] |
HUERRE P, MONKEWITZ P A. Local and global instabilities in spatially developing aows[J]. Annual Review of Fluid Mechanics, 1990, 22(1): 473-537. |
| [27] |
YARIN A L, ORON A, ROSENAU P. Capillary instability of thin liquid film on a cylinder[J]. Physics of Fluids A:Fluid Dynamics, 1993, 5(1): 91-98. |
| [28] |
LIN S P, REITZ R D. Drop and spray formation from a liquid jet[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 85-105. |
| [29] |
LASHERAS J C, HOPFINGER E J. Liquid jet instability and atomization in a coaxial gas stream[J]. Annual Review of Fluid Mechanics, 2000, 32(1): 275-308. DOI:10.1146/annurev.fluid.32.1.275 |
| [30] |
LIN Y, ENGVOLD O, WIIK J E. Counterstreaming in a large polar crown filament[J]. Sol Phys, 2003, 216(1-2): 109-120. |
| [31] |
YECKO P, ZALESKI S, FULLANA J M. Viscous modes in two-phase mixing layers[J]. Physics of Fluids, 2002, 14(12): 4115-4122. DOI:10.1063/1.1513987 |
| [32] |
BOECK T, ZALESKI S. Viscous versus inviscid instability of two-phase mixing layers with continuous velocity profile[J]. Physics of Fluids, 2005, 17(3): 032106. DOI:10.1063/1.1862234 |
| [33] |
SEVILLA A, GORDILLO J M, Martínez-Bazán C. The effect of the diameter ratio on the absolute and convective instability of free coflowing jets[J]. Physics of Fluids, 2002, 14(9): 3028-3038. DOI:10.1063/1.1496511 |
| [34] |
苏海容.自由射流界面稳定性的伪谱分析[D].上海: 上海大学, 2003. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y552375
|
| [35] |
李芳.同轴带点射流的稳定性研究[D].合肥: 中国科学技术大学, 2007. LI F. Instability of an electrified coaxial jet[D]. Hefei: University of Science and Technology of China, 2007. (in Chinese) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1210610 |
| [36] |
司廷.流动聚焦的实验和理论研究[D].合肥: 中国科学技术大学, 2009. SI T. Experimental and theoretical investigation on flow focusing[D]. Hefei: University of Science and Technology of China, 2009. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10358-2009110996.htm |
| [37] |
李广滨.复合流动聚焦的实验和理论研究[D].合肥: 中国科学技术大学, 2016. LI G B. Experimental and theoretical investigation on compound flow focusing[D]. Hefei: University of Science and Technology of China, 2016. (in Chinese) http://cdmd.cnki.com.cn/Article/CDMD-10358-1016103170.htm |
| [38] |
李帅兵, 杨睿, 罗喜胜, 等. 气流作用下同轴带电射流的不稳定性研究[J]. 力学学报, 2017, 49(5): 997-1007. LI S B, YANG R, LUO X S, et al. Instability study of an electrified coaxial jet in a coflowing gas stream[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(5): 997-1007. (in Chinese) |
| [39] |
CHAUHAN A, MALDARELLI C, RUMSCHITZKI D S, et al. Temporal and spatial instability of an inviscid compound jet[J]. Rheologica Acta, 1996, 35(6): 567-583. DOI:10.1007/BF00396508 |
| [40] |
LI F, YIN X Y, YIN X Z. Linear instability of a coflowing jet under an axial electric field[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 74:036304, 2006, 74(3 Pt 2): 036304. |
| [41] |
GORDILLO J M, GAÑÁN-CALVO A M, PÉREZ-SABORID M. Monodisperse microbubbling:absolute instabilities in coflowing gas-liquid jets[J]. Physics of Fluids, 2001, 13(12): 3839-3842. DOI:10.1063/1.1416188 |
| [42] |
GORDILLO J M, PÉREZ-SABORID M, GAÑÁN-CALVO A M. Linear stability of co-flowing liquid-gas jets[J]. Journal of Fluid Mechanics, 2001(448): 23-51. |
| [43] |
德拉津P G(英), 雷德W H(美).流体动力稳定性[M].第1版.天津: 宇航出版社, 1990. DRAZIN P G, REID W H. Hydrodynamic stability[J]. Tianjin: China Astronautic Publishing House, 1990. |
| [44] |
KELLER J B, RUBINOW S I, TU Y O. Spatial instability of a jet[J]. Physics of Fluids, 1973, 16(12): 2052. DOI:10.1063/1.1694264 |
| [45] |
LEIB S J, GOLDSTEIN M E. The generation of capillary instabilities on a liquid jet[J]. Journal of Fluid Mechanics, 1986, 168: 479-500. DOI:10.1017/S0022112086000472 |
| [46] |
KANG D J, LIN S P. Breakup of swirling liquid jets[J]. Int J Eng Fluid Mech, 1989, 2: 47-62. |
| [47] |
YUEN M C. Non-linear capillary instability of a liquid jet[J]. Journal of Fluid Mechanics, 1968, 33(1): 151-163. |
| [48] |
LARYEA G N, NO S Y. Development of electrostatic pressure-swirl nozzle for agricultural applications[J]. Journal of Electrostatics, 2003, 57(2): 129-142. DOI:10.1016/S0304-3886(02)00122-5 |
| [49] |
JAYAN N, RAGHUNANDAN B N. A technique for drop size control during throttling of a rocket engine[J]. Atomization & Sprays, 2003, 13(4): 345-356. |
| [50] |
GAUTAM A, WALDREP J C, DENSMORE C L. Aerosol gene therapy[J]. Molecular Biotechnology, 2003, 23(1): 51-60. |
| [51] |
FENN J B, MANN M, MENG C K, et al. Electrospray ionization for mass-spectrometry of large biomolecules[J]. Science, 1989(246): 64-71. |
| [52] |
BERKLAND C, PACK D W, KIM K. Controlling surface nano-structure using flow-limited field-injection electrostatic spraying (FFESS) of poly[J]. Biomaterials, 2004(25): 5649-5658. |
| [53] |
GAÑÁN-CALVO A M. Erratum:cone-jet analytical extension of Taylor's electrostatic solution and the asymptotic universal scaling laws in electrospraying[J]. Physical Review Letters, 1997, 79(2): 217-220. DOI:10.1103/PhysRevLett.79.217 |
| [54] |
GAÑÁN-CALVO A M. Generation of steady liquid microthreads and micron-sized monodisperse sprays in gas streams[J]. Physical Review Letters, 1998, 80(2): 285-288. DOI:10.1103/PhysRevLett.80.285 |
| [55] |
GAÑÁN-CALVO A M, BARRERO A. A novel pneumatic technique to generate steady capillary microjets[J]. Journal of Aerosol Science, 1999, 30(1): 117-125. DOI:10.1016/S0021-8502(98)00029-9 |
| [56] |
GAÑÁN-CALVO A M, GORDILLO J M. Perfectly monodisperse mircobubbling by capillary flow focusing[J]. Physical Review Letters, 2001, 87(27): 274501. DOI:10.1103/PhysRevLett.87.274501 |
| [57] |
GAÑÁN-CALVO A M. Perfectly monodisperse microbubbling by capillary flow focusing:an alternate physical description and universal scaling[J]. Physical Review E, 2004, 69(2): 027301. DOI:10.1103/PhysRevE.69.027301 |
| [58] |
GAÑÁN-CALVO A M. Enhanced liquid atomization:from flow-focusing to flow-blurring[J]. Applied Physics Letters, 2005, 86(21): 214101. DOI:10.1063/1.1931057 |
| [59] |
GAÑÁN-CALVO A M, LÍPEZ-HERRERA J M, RIESCO-CHUECA P. The combination of electrospray and flow focusing[J]. Journal of Fluid Mechanics, 2006, 566: 421-445. DOI:10.1017/S0022112006002102 |
| [60] |
MARTÍN-BANDERAS L, FLORES-MOSQUERA M, RIESCO-CHUECA P, et al. Flow focusing:a versatile technology to produce size-controlled and specific morphology microparticles[J]. Small (Weinheim an der Bergstrasse, Germany), 2005, 1(7): 688-692. DOI:10.1002/(ISSN)1613-6829 |
| [61] |
MARTÍN-BANDERAS L, RODRÍGUEZ-GIL A, CEBOLLA Á, et al. Towards high-throughput production of uniformly encoded microparticles[J]. Adv Mater, 2006, 18: 559-564. DOI:10.1002/(ISSN)1521-4095 |
| [62] |
GAÑÁN-CALVO A M. Electro-flow focusing:the high-conductivity low-viscosity limit[J]. Physical Review Letters, 2007, 98(13): 134503. DOI:10.1103/PhysRevLett.98.134503 |
| [63] |
GAÑÁN-CALVO A M. Absolute instability of a viscous hollow jet[J]. Physical Review E, 2007, 75(2): 027301. DOI:10.1103/PhysRevE.75.027301 |
| [64] |
GAÑÁN-CALVO A M, FERRERA C, MONTANERO J M. Universal size and shape of viscous capillary jets:application to gas-focused microjets[J]. Journal of Fluid Mechanics, 2011, 670: 427-438. DOI:10.1017/S0022112010006476 |
| [65] |
MONTANERO J M, REBOLLO-MUÑOZ N, HERRADA M A, et al. Global stability of the focusing effect of fluid jet flows[J]. Physical Review E, 2011, 83(3): 036309. DOI:10.1103/PhysRevE.83.036309 |
| [66] |
司廷, 尹协振. 流动聚焦研究进展及其应用[J]. 科学通报, 2011, 56(8): 537-546. SI T, YIN X Z. Progress and application of flow focusing[J]. Chinese Sci Bull (Chinese Ver), 2011, 56(8): 537-546. (in Chinese) |
| [67] |
司廷, 刘志勇, 尹协振. 流动聚焦中锥形和射流直径影响因素的实验研究[J]. 实验流体力学, 2008, 22(1): 21-26. SI T, LIU Z Y, YIN X Z. Experiments of effects of flow parameters on cone and jet diameter in flow focusing[J]. Journal of Experiments in Fluid Mechanics, 2008, 22(1): 21-26. DOI:10.3969/j.issn.1672-9897.2008.01.005 (in Chinese) |
| [68] |
李广滨, 司廷, 尹协振. 电场作用下无黏聚焦射流的时间不稳定性研究[J]. 力学学报, 2012, 44: 876-883. Li G B, Si T, Yin X Z. Temporal instability study of inviscid focused jets under an electric field[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44: 876-883. DOI:10.6052/0459-1879-12-032 (in Chinese) |
| [69] |
LI G, LUO X, SI T, et al. Temporal instability of coflowing liquid-gas jets under an electric field[J]. Physics of Fluids, 2014, 26(5): 054101. DOI:10.1063/1.4875109 |
| [70] |
LIN S P, CHEN J N. Role played by the interfacial shear in the instability mechanism of a viscous liquid jet surrounded by a viscous gas in a pipe[J]. Journal of Fluid Mechanics, 1998, 376: 37-51. DOI:10.1017/S0022112098002894 |
| [71] |
SI T, LI F, YIN X Z, et al. Modes in flow focusing and instability of coaxial liquid-gas jets[J]. Journal of Fluid Mechanics, 2009, 629: 1-23. DOI:10.1017/S0022112009006211 |
| [72] |
SI T, LI F, YIN X Z, et al. Spatial instability of coflowing liquid-gas jets in capillary flow focusing[J]. Physics of Fluids, 2010, 22(11): 112105. DOI:10.1063/1.3490066 |
| [73] |
GAÑÁN-CALVO A M, MONTANERO J M, MARTÍN-BANDERAS L, et al. Building functional materials for health care and pharmacy from microfluidic principles and flow focusing[J]. Advanced Drug Delivery Reviews, 2013, 65(11): 1447-1469. |
| [74] |
LI F, YIN X Y, YIN X Z. Instability of a viscous coflowing jet in a radial electric field[J]. Journal of Fluid Mechanics, 2008, 596: 285-311. DOI:10.1017/S0022112007009597 |
| [75] |
SI T, FENG H X, LUO X S, et al. Formation of steady compound cone-jet modes and multilayered droplets in a tri-axial capillary flow focusing device[J]. Microfluidics and Nanofluidics, 2015, 18(5-6): 967-977. DOI:10.1007/s10404-014-1486-8 |
| [76] |
SI T, LI G, WU Q, et al. Optical droplet vaporization of nanoparticle-loaded stimuli-responsive microbubbles[J]. Applied Physics Letters, 2016, 108(11): 111109. DOI:10.1063/1.4944539 |
| [77] |
SI T, YIN C, GAO P, et al. Steady cone-jet mode in compound-fluidic electro-flow focusing for fabricating multicompartment microcapsules[J]. Applied Physics Letters, 2016, 108(2): 021601. DOI:10.1063/1.4939632 |
| [78] |
HERRADA M A, MONTANERO J M, FERRERA C, et al. Analysis of the dripping-jetting transition in compound capillary jets[J]. Journal of Fluid Mechanics, 2010, 649: 523-536. DOI:10.1017/S0022112010000443 |
| [79] |
MASHAYEK F, ASHGRIZ N. Nonlinear instability of liquid jet with thermocapillarity[J]. Journal of Fluid Mechanics, 1995, 283: 97-123. DOI:10.1017/S0022112095002242 |
| [80] |
XU J J, DAVIS S H. Instability of capillary jets with thermocapillarity[J]. Journal of Fluid Mechanics, 1985, 161: 1-25. DOI:10.1017/S0022112085002798 |
| [81] |
FURLANI E P. Temporal instability of viscous liquid microjets with spatially varying surface tension[J]. Journal of Physics A:Mathematical and General, 2005, 38(1): 263-276. DOI:10.1088/0305-4470/38/1/020 |
 2019, Vol. 37
2019, Vol. 37


