计算流体力学(Computational Fluid Dynamics,CFD)作为一项重要的流体分析手段,在近30年间得到了飞速的发展,尤其是在诸如飞行器气动设计等外流问题中,CFD已成为初步设计、详细设计和计算校核的主要方法,与风洞试验一起成为飞行器设计和研发的重要研究手段[1]。目前CFD技术在求解可压缩流动的飞机流场问题中,各类算法、求解器、前处理与后处理软件系统都已趋于成熟;在精细化湍流模拟[2]、气动生血[3]等问题中也有了长足的进步。
在进行飞行器气动设计时,CFD的可信度研究十分必要,也是当前的研究热点,其基本内容和方法就是CFD的验证和确认(verification & validation)[4]。1998年,AIAA发布了世界上第一个关于CFD验证与确认的指南[5]。国际上组织了很多CFD的验证和确认专题研讨会议,比如欧洲的计算空气动力学研究项目ECARP(European Computational Aerodynamics Research Project),该项目的目标是评估各种湍流模型,并对软件系统进行统一的研究[6]。2001年6月至2016年7月期间,AIAA阻力计算的工作小组组织了六次阻力预测会议(Drag Prediction Workshop)[7]。其中DPW2会议选择德国宇航局设计的跨声速民用飞机模型DLR-F6作为实验和CFD的基准模型,其巡航马赫数为0.75,巡航升力系数为0.5,2008年法国的S2MA风洞对DLR-F6进行了风洞试验;DPW4、DPW5、DPW6会议选择CRM(Common Research Model)作为基准模型,由于具有公认的试验数据,并且经过了广泛的验证,CRM模型的计算已成为检验CFD程序对典型跨声速工况预测能力的重要算例。此外,第一届AIAA计算流体力学高升力装置预测会议发布了标准的HILIFTPW-1高升力预测模型[8];中国航空研究院在2012年设计了空气动力学验证模型CAE-AVM风洞模型,该模型在荷兰的DNW-HST跨声速风洞进行了试验测试,一方面验证模型的气动性能,另一方面也对CFD数值计算方法进行校核[9]。
为了评估国内CFD技术状态,为飞行器研制提供技术参考,中国空气动力研究与发展中心(CARDC)开展首届CFD可信度专题研讨会(AeCW-1),并设计了单通道客机CHN-T1标模[10],用于风洞试验和CFD可信度研究。
本文工作结合AeCW-1研讨会的计算任务,研究了SST与SA两种湍流模式在标模计算中的网格收敛性与抖振特性的计算能力;分别从标模的抖振特性、静气弹效应、雷诺数影响方面评估了CFD计算的可信度以及CHN-T1标模的设计气动特性。
1 计算状态与计算方法 1.1 CHN-T1标模简介AeCW-1的计算构型有三种,其中Config.1为“机身-机翼-平尾-垂尾”(BWHV)构型, 是基础构型,具体的参数见表 1,其中Sref为全模的参考面积、Cref为参考弦长、xref/yref/zref为力矩参考点;Config.2在Config.1基础上加上风洞试验的支撑;Config.3在Config.2基础上考虑了机翼的静气弹变形。CHN-T1标模的实验马赫数为0.78,雷诺数为3.3×106,升力系数为0.5。
| 表 1 CHN-T1 BWHV构型参数 Table 1 The parameter of BWHV configuration of CHN-T1 |
|
|
本文涵盖了部分AeCW-1研讨会的计算任务,包括三个计算状态,其中Case 1为网格收敛性研究,采用Config.1构型,同时对比SST与SA湍流模式计算结果;Case 2b与Case2c为抖振特性研究,分别采用Config.2与Config.3构型,并对比SST与SA的计算结果;Case 3为雷诺数的影响研究,采用SST湍流模式计算Config.3构型。具体的计算状态参见表 2及文献[11]。
| 表 2 计算状态 Table 2 Computational State |
|
|
本文计算工作基于开源的CFL3D Version6.7结构网格求解器[12],该求解器由NASA兰利研究中心开发于20世纪90年代,内含多种湍流模式及计算格式,使用MPI进行大规模并行计算。
对标模的计算基于定常RANS的方法,时间离散采用隐式LU-ADI格式依当地时间步长进行推进;空间离散的重构步采用三阶迎风MUSCL格式,其中限制器类型选择iflim=4[12],演化步采用无熵修正的Roe的FDS(Flux Differential Splitting,通量差分裂)格式[13];采用三重网格W循环加速技术;采用自由来流边界进行全湍流计算,湍流模式选取航空领域广泛应用的SST[14]与SA[15]模式。
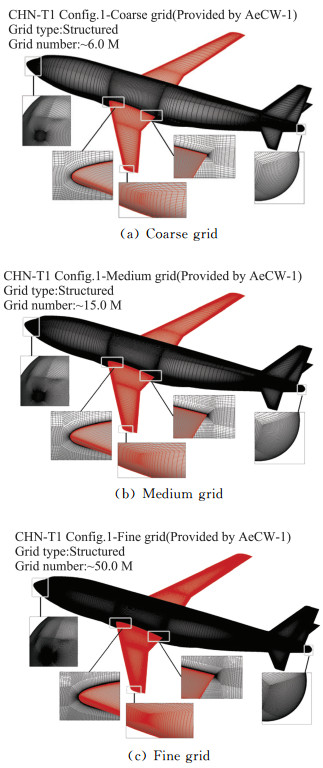
2 网格收敛性研究网格收敛性是评价计算精度及网格质量高低的一种策略,本文采用组委会提供的粗、中、细网格[11]进行网格收敛性研究,三套网格及部件节点分布见图 1。机翼上的网格量对于捕捉激波的影响较大,三套网格在机翼弦向上的网格点数分别为61、81、121;y+的值对于摩擦阻力的计算尤为关键,在不含壁函数的SST与SA湍流模型中,由y+控制的第一层网格高度应在粘性底层以内,以便更好地描述边界层速度型,三套网格y+的值分别约为1.0、0.6、0.4。随着网格的加密,网格间距造成的数值耗散减小,对于机头、机尾等部件的阻力预测更加准确。
|
图 1 粗、中、细三套网格的节点分布情况 Fig.1 Node distribution for coarse, medium and fine grids |
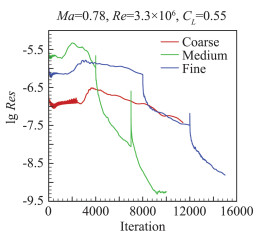
图 2展示了采用SST湍流模型计算得到的密度残差收敛历史,其中粗网格的收敛速度较慢,这是由于在该计算中使用了较小的CFL数以保证计算稳定。
|
图 2 粗、中、细三套网格的残差收敛历史 Fig.2 History of residual in coarse, medium and fine grid |
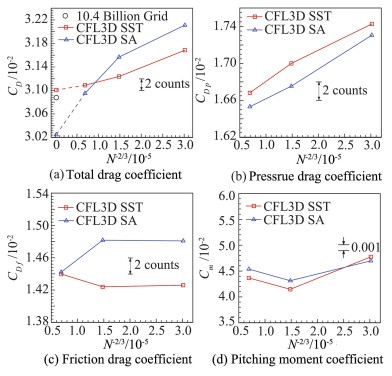
网格收敛性期望得到一条迎角AOA或力系数随横坐标N-2/3/10-5的线性走势,该式中N为网格量。图 3(a)展示了总阻力系数的网格收敛性,发现随着网格的加密,SST与SA计算的阻力值都呈下降趋势,在从粗网格到中网格时两种湍流模式的阻力变化量基本一致,而从中网格到细网格时SA的变化量大于SST。相比之下SST计算的阻力随网格量的变化更接近线性关系,并且利用外插得到的无限密网格上的收敛阻力值与组委会提供的104亿网格参考值[11]较为接近。图 3(b)展示了压差阻力CDp系数的网格收敛性,发现SST与SA都具有较好的收敛特性,并且两者计算的压差阻力较为接近。图 3(c)展示了摩擦阻力CDf的网格收敛性,在粗网格与中网格上SA的预测结果比SST大了约6 counts(1 count=0.0001),而在细网格上两种湍流模式的预测值接近。图 3(d)展示了力矩特性的网格收敛性,力矩特性并没有体现出单调的收敛趋势。总的来说对于组委会提供的网格而言,SST的网格收敛性表现优于SA。
|
图 3 气动力系数的网格收敛性 Fig.3 Grid convergence with aerodynamic coefficients |
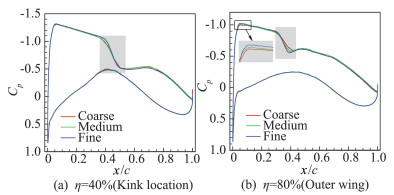
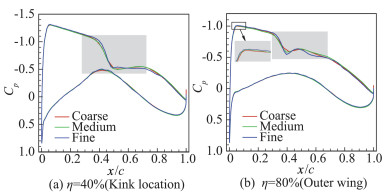
随着网格的加密,数值模拟对于精细流动结构的捕捉能力逐渐增强。图 4、图 5分别展示了SST与SA湍流模式计算η=40%、80%两个展向位置的机翼表面压力系数Cp分布,三套网格计算的压力分布形态基本一致;随着网格的加密,激波位置不变但激波处的压力梯度越来越大;对η=80%位置吸力平台的高度计算:用SST计算从粗到细网格时,平台高度略微抬高,而采用SA模式计算的高度基本一致;采用SA模式计算的细网格下η=80%位置激波后的压力恢复区出现明显抖动。
|
图 4 CHN-T1 Case1: SST计算的截面压力分布的网格收敛性 Fig.4 CHN-T1 Case1 grid convergence with sectional pressure distribution using SST |
|
图 5 CHN-T1 Case1: SA计算的截面压力分布的网格收敛性 Fig.5 CHN-T1 Case1 grid convergence with sectional pressure distribution using SA |
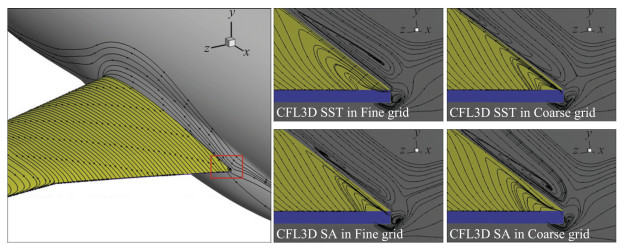
对于翼身结合部位流动现象的模拟是标模计算的一个重点,网格量的大小会影响该处分离流的计算[16]。图 6展示了翼身结合部位置的流线图,发现两种湍流模式在粗网格及细网格上都捕捉到了角隅涡,并且随着网格的加密,分离区的大小几乎不发生变化。
|
图 6 CHN-T1 Case1:翼身结合部的角隅涡 Fig.6 CHN-T1 Case1: horseshoe vortex in wing-body configuration |
综合考量气动力系数以及流动结构的捕捉情况,本文在后续的抖振特性、静气弹效应、雷诺数影响研究中选用中网格进行计算。
3 抖振特性研究超临界机翼在跨声速飞行时可能会产生由激波/附面层相互干扰而引起抖振现象,这将严重影响飞行器的飞行品质与结构寿命[17]。发生抖振时机翼上表面的激波以及其后的分离泡位置变动,属于典型的非定常现象,但是利用定常的RANS计算结合一定判据可以较好的确定飞机的抖振边界[18]。
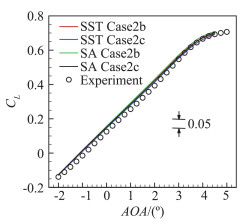
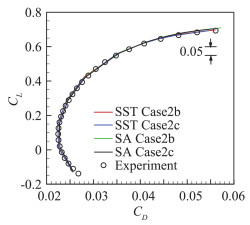
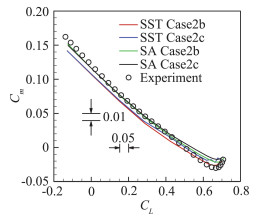
本文计算了在马赫数固定的情况下,随着迎角的不断增大CHN-T1标模逐渐进入抖振的过程。图 7展示了利用SST与SA湍流模式计算得到的升力线,并与风洞实验值[19]对比,发现升力线都在迎角4°后偏离线性走势。图 8展示了极曲线,其计算值与实验值吻合。图 9反映了力矩系数随升力系数的变化,在升力系数小于0.4时SA的计算结果与实验值吻合较好,而升力系数大于0.4时SST的计算结果与实验值吻合的更好。适航规章要求民用运输类飞机在正常使用状态下不得超过抖振发生边界[20],当Cm~CL曲线发生弯折即可判定发生抖振。后续对于抖振状态的流场分析选择SST计算的Case2b。
|
图 7 CHN-T1 Case2b/ Case2c抖振研究:升力线 Fig.7 CHN-T1 Case2b/ Case2c buffet study: lift curve |
|
图 8 CHN-T1 Case2b/ Case2c抖振研究:极曲线 Fig.8 CHN-T1 Case2b/ Case2c buffet study: drag polar |
|
图 9 CHN-T1 Case2b/ Case2c抖振研究:力矩特性线 Fig.9 CHN-T1 Case2b/ Case2c buffet study: pitching moment curve |
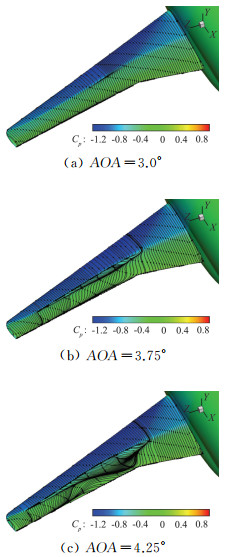
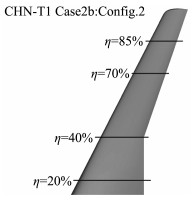
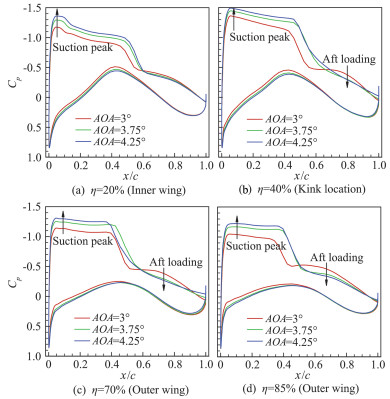
对抖振特性的研究从分离区及激波强度两个方面开展。首先探索分离区的变化,选取迎角为3°、3.75°、4.25°观察机翼表面流线分布,如图 10所示,在迎角3°时机翼表面几乎不出现分离;当迎角增大到3.75°时能明显观察到激波/边界层干扰从而产生的分离,其中分离线的位置紧挨激波位置,再附线的位置约为50%弦长;当迎角到4.25°时机翼表面出现了大面积分离,机翼中部的流线分布较为紊乱,此时已进入了危险的抖振区域。以图 11中4个典型的截面为例分析进入抖振状态的压力分布特点,如图 12所示,发现随着迎角增大,各截面的前缘吸力峰值不断提高,进而导致了激波的增强;外翼段的后加载显著下降,使得进入抖振状态的低头力矩减小,Cm~CL曲线发生弯折,操纵特性变差,在展向η=40%、70%位置处的后缘的压力恢复剧烈,使得边界层更容易出现分离。
|
图 10 进入抖振状态的机翼表面流线 Fig.10 The streamlines on the wing surface in buffet state |
|
图 11 CHN-T1 Config.2机翼展向典型截面位置示意图 Fig.11 CHN-T1 Config.2 typical sections on the wing platform |
|
图 12 CHN-T1 Case2b:典型截面压力分布随迎角的变化 Fig.12 CHN-T1 Case2b: the change of pressure distribution on typical sections with AOA |
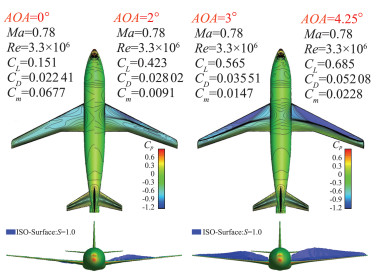
探索抖振状态下激波随迎角的变化,图 13展示了迎角为0°、2°、3°、4.25°时表面压力分布及提取的空间激波,其中激波判据为:
|
图 13 CHN-T1 Case2b:表面压力分布及激波随迎角变化 Fig.13 CHN-T1 Case2b : the change of pressure distribution and shock with AOA |
| $S = \frac{\mathit{\boldsymbol{U}}}{a}\frac{{\nabla \mathit{\boldsymbol{p}}}}{{\left\| {\nabla \mathit{\boldsymbol{p}}} \right\|}} $ | (1) |
式中:U为速度矢量,a为声速,△p为压力梯度矢量,‖▽p‖为压力梯度矢量的二范数,该式表示了无量纲速度在压力梯度方向上的投影,当S≥1.0则认为出现激波[21]。从S=1.0的等值面图中可以发现在0°迎角时机翼上表面无激波出现,而迎角2°时机翼中段出现激波,随着迎角不断增加,激波范围扩展至内外翼段。
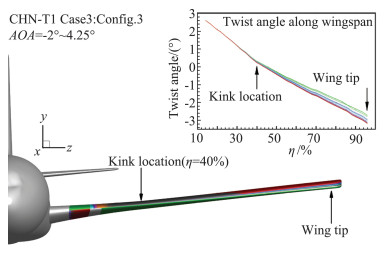
4 静气弹效应研究AeCW-1组委会提供了经过静气动弹性变形的标模构型Config.3,图 14展示了经过静气弹变形后的机翼形变及扭转角沿展向分布的情况,迎角自-2°变化至4.25°时,变形出现在Kink至翼尖区域,变形后外翼段扭转角减小。
|
图 14 CHN-T1 Case3:静气弹变形后的机翼几何变化 Fig.14 CHN-T1 Case3: the geometry of wing after the elastic deformation |
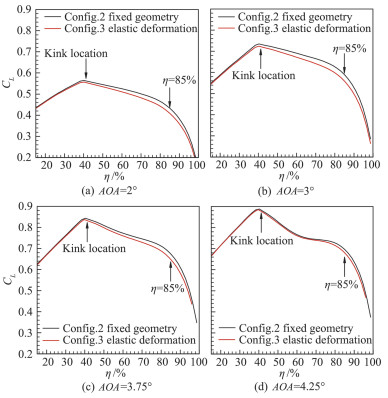
图 15为2°、3°、3.75°、4.25°迎角下静气弹效应对机翼展向升力系数分布的影响,在定迎角计算时,静气弹变形使得整机升力系数有所降低,同时由于Kink以外位置的扭转角减小,在2°、3°、3.75°迎角下变形后的机翼外翼段升力系数明显降低,而进入抖振状态的迎角4.25°下升力系数的变化并不明显。
|
图 15 CHN-T1 Case2b/Case2c:静气弹效应对机翼展向升力系数分布的影响 Fig.15 CHN-T1 Case2b/Case2c: the elastic effect for distribution of lift coefficient in span direction |
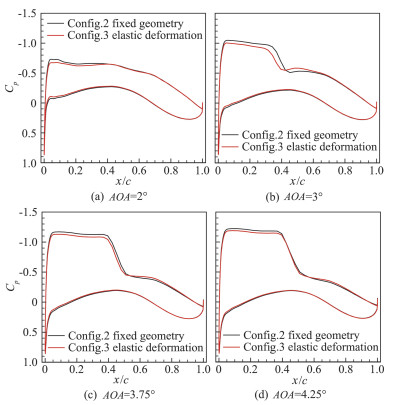
截取机翼展向85%位置(η=85%)研究静气弹效应对压力分布的影响,如图 16所示,在2°、3°、3.75°以及迎角4.25°下,静气弹变形将导致前缘吸力峰、吸力平台下降,从一定程度上削弱了激波。
|
图 16 CHN-T1 Case2b/Case2c: η=85%位置截面压力分布 Fig.16 CHN-T1 Case2b/Case2c: the sectional pressure distribution on η=85% |
雷诺数不同,通常会对转捩点的位置、边界层厚度以及激波位置等产生影响,从而导致飞机气动特性的变化,文献[22]中指出运输机模型的翼型厚度和弯度较大,其所受雷诺数的影响较大。本文以AeCW-1组委会要求的Case 3为例,研究雷诺数对标模气动特性的影响。
表 3展示了Case 3的结果,雷诺数分别取为3.3×106和15.0×106,采用SST湍流模式进行定升力CL=0.5的计算,得到的总阻力与实验的误差在6 counts之内;统计了计算得到的压差阻力与摩擦阻力,发现当雷诺数增加4.5倍后总阻力下降了47.8 counts,其中压差阻力下降了17.1 counts,摩擦阻力下降了29.7 counts。
| 表 3 Case 3结果 Table 3 Computational Results for Case 3 |
|
|
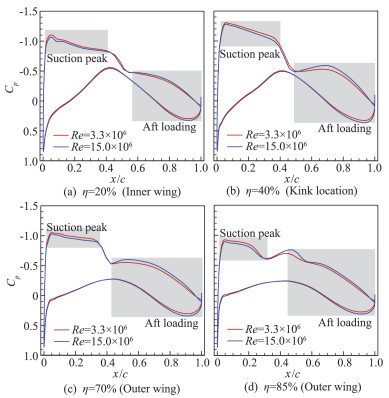
分别对压差阻力和摩擦阻力进行分析。图 17展示了主翼展向η=20%、40%、70%、85%截面的压力分布,发现在大雷诺数下后加载Cp包围的面积增大,同时机翼上表面超声速区的吸力平台有所下降,进而导致了激波强度的减弱、压差阻力减小。
|
图 17 CHN-T1 Case3:不同雷诺数下典型截面的压力分布 Fig.17 CHN-T1 Case3: typical sectional pressure distribution with different Reynolds number |
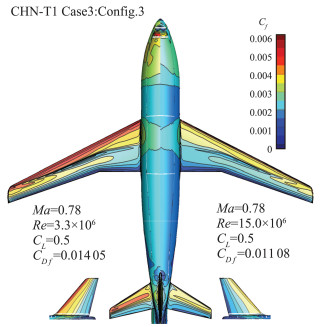
图 18展示了两雷诺数下的壁面摩擦系数(Cf)分布图,不同雷诺数下Cf分布的差别主要体现在机身、主翼、平尾、垂尾的前缘。大雷诺数下前缘的摩擦系数明显下降。
|
图 18 CHN-T1 Case3:不同雷诺数下壁面摩擦系数分布 Fig.18 CHN-T1 Case3: the contour of skin friction coefficient with different Reynolds number |
本文采用结构网格求解器CFL3D计算了CHN-T1标模的典型工况,研究了SST与SA湍流模式在网格收敛性以及抖振特性上的表现,分析了静气弹效应及雷诺数对于标模气动特性的影响,主要结论如下:
(1) 在网格收敛性方面,采用CFL3D的SST模式表现优于SA模式;随着网格加密激波位置不变,激波强度逐渐增大;采用粗网格与细网格同样能够捕捉到翼身结合部的角隅涡。
(2) 对抖振特性的研究,采用SST模式计算的Case2b与实验值吻合最好,CHN-T1标模的抖振源自机翼中段出现的激波/边界层干扰产生的分离,当迎角不断增大时,各截面压力分布的前缘吸力峰值不断提高,导致了激波的增强,外翼段的各截面压力分布后加载下降,使得进入抖振状态的低头力矩减小,Cm~CL曲线发生弯折。
(3) 静气弹效应主要影响了标模Kink位置以外的升力系数沿展向分布,静气弹变形后的机翼外翼段升力系数明显降低,同时该处激波被削弱致使阻力降低。
(4) 雷诺数增大时,标模压差阻力的减小主要来源于压力系数后加载区包围的面积增大以及超声速吸力平台区高度的降低,对于摩擦阻力的影响主要表现在标模各个部件前缘的摩擦系数下降。
| [1] |
王运涛, 王光学, 张玉伦. 采用TRIP2.0软件计算DLR-F6构型的阻力[J]. 空气动力学学报, 2009, 27(01): 108-113. WANG Y T, WANG G X, ZHANF Y L. Drag prediction of DLR-F6 configuration with TRIP2.0 software[J]. Acta Aerodynamica Sinica, 2009, 27(01): 108-113. DOI:10.3969/j.issn.0258-1825.2009.01.020 (in Chinese) |
| [2] |
WANG Z, JIANG C, GAO Z, et al. Prediction for the separation length of two-dimensional sonic injection with high-speed crossflow[J]. AIAA Journal, 2017, 55(3): 1-16. |
| [3] |
ZHANG Y, CHEN H, WANG M, et al. Aeroacoustic prediction of a multi-element airfoil using wall-modeled large-eddy simulation[J]. AIAA Journal, 2017, 55(1): 1-15. DOI:10.2514/1.J055815 |
| [4] |
邓小刚, 宗文刚, 张来平, 等. 计算流体力学中的验证与确认[J]. 力学进展, 2007(02): 279-288. DENG X G, ZONG W G, ZHANG L P, et al. Verification and validation in computational fluid dynamics[J]. Advances in Mechanics, 2007(02): 279-288. DOI:10.3321/j.issn:1000-0992.2007.02.011 (in Chinese) |
| [5] |
STAF A A. AIAA guide for the verification and validation of computational fluid dynamics simulations[M]. American Institute of Aeronautics and Astronautics, 1998.
|
| [6] |
HAASE W, CHAPUT E, LESCHZINER M A. ECARP-European computational aerodynamics research project: validation of CFD codes and assessment of turbulence models[R]. Vieweg & Sohn Verlagsgesellschaft mbH, Germany, 1997.
|
| [7] |
TINOCO E N, BRODERSEN O P, KEYE S, et al. Summary data from the sixth AIAA CFD drag prediction workshop:CRM Cases[J]. Journal of Aircraft, 2017(4): 1-28. |
| [8] |
1st AIAA CFD High Lift Prediction Workshop[EB/OL]. (2009-07-13)[2018-09-20]. https://hiliftpw.larc.nasa.gov/index-workshop1.html
|
| [9] |
赵童.考虑结构重量/变形的超临界机翼气动优化设计[D].北京: 清华大学, 2016: 88-90. ZHAO T. Aerodynamic optimization design of supercritical wing based on structure weight/deformation performance[D]. Beijing: Tsinghua University, 2016: 88-90. (in Chinese) |
| [10] |
余永刚, 周铸, 黄江涛, 等. 单通道客机气动标模CHN-T1设计[J]. 空气动力学学报, 2018, 36(3): 505-513. YU Y G, ZHOU Z, HUANG J T, et al. Aerodynamic design of a standard model CHN-T1 for single-aisle passenger aircraft[J]. Acta Aerodynamica Sinica, 2018, 36(3): 505-513. DOI:10.7638/kqdlxxb-2018.0072 (in Chinese) |
| [11] |
李伟, 王运涛, 洪俊武, 等. 采用TRIP3.0模拟CHN-T1模型气动特性[J]. 空气动力学学报, 2019, 37(2): 272-279. LI W, WANG Y T, HONG J W, et al. Aerodynamic characteristics simulation of CHN-T1 model with TRIP3.0[J]. Acta Aerodynamica Sinica, 2019, 37(2): 272-279. DOI:10.7638/kqdlxxb-2018.0225 (in Chinese) |
| [12] |
NASA Langley Research Center.CFL3D Version 6 Home Page[EB/OL]. (2017-10-7)[2018-09-02]. https: //cfl3d.larc.nasa.gov/
|
| [13] |
Roe P. Approximate Riemannsolvers, parameter vectors, and difference schemes[J]. Journal of Computational physics, 1981, 43(02): 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [14] |
MENTER F, RUMSEY C. Assessment of two-equation turbulence models for transonic flows[R]. AIAA-94-2343, 1994. doi: 10.2514/6.1994-2343
|
| [15] |
SPALART P, ALLMARAS S. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992. doi: 10.2514/6.1992-439
|
| [16] |
张耀冰, 邓有奇, 吴晓军, 等. DLR-F6翼身组合体数值计算[J]. 空气动力学学报, 2011, 29(2): 163-169. ZHANG Y B, DENG Y Q, WU X J, et al. Drag prediction of DLR-F6 using MFlow unstructured mesh solver[J]. Acta Aerodynamica Sinica, 2011, 29(2): 163-169. DOI:10.3969/j.issn.0258-1825.2011.02.006 (in Chinese) |
| [17] |
牟让科, 杨永年. 飞机抖振问题研究进展[J]. 应用力学学报, 2001, 18(z1): 142-150. MU R K, YANG Y N. Advances of studies for the buffet problem of aircraft[J]. Chinese Journal of Applied Mechanics, 2001, 18(z1): 142-150. DOI:10.3969/j.issn.1000-4939.2001.z1.029 (in Chinese) |
| [18] |
KENWAY G K W, MARTINS J R R A. Buffet-onset constraint Formulation for aerodynamic shape optimization[J]. AIAA Journal, 2017, 55(6): 1-18. |
| [19] |
李强, 刘大伟, 许新, 等. CHN-T1标模2.4米风洞气动特性试验研究[J]. 空气动力学学报, 2019, 37(2): 337-344. LI Q, LIU D, XU X, et al. Experimental study of aerodynamic characteristic of CHN-T1 standard model in 2.4m transonic wind tunnel[J]. Acta Aerodynamica Sinica, 2019, 37(2): 337-344. DOI:10.7638/kqdlxxb-2018.0099 (in Chinese) |
| [20] |
顾诵芬, 吴兴世, 杨新军. 运输类飞机的空气动力学设计[M]. 上海: 上海交通大学出版社, 2010: 332.
|
| [21] |
邓烨明.推进/机体一体化中的积分方法研究[D].北京: 清华大学, 2017: 20-22. DENG Y M. Research on integrating method of propulsion/airframe integration[D]. Beijing: Tsinghua University, 2017: 20-22. (in Chinese) |
| [22] |
张培红, 周乃春, 邓有奇, 等. 雷诺数对飞机气动特性的影响研究[J]. 空气动力学学报, 2012, 30(6): 693-698. ZHANG P H, ZHOU N C, DENG Y Q, et al. The effects of Reynolds number on airplane aerodynamic characteristics[J]. Acta Aerodynamica Sinica, 2012, 30(6): 693-698. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


