2. 西安航空学院 飞行器学院, 西安 710077
2. The School of Aircraft, Xi'an Aeronautical University, Xi'an 710077, China
计算流体力学(CFD)和实验流体力学是航空领域特别倚重的两种研究航空器气动特性的手段。实验流体力学方法经典但昂贵,计算流体力学需要实验流体力学技术对计算流体力学程序进行充分的验证与确认。国际上对CFD的验证与确认工作已经进行了很多,如已经完成的六次AIAA阻力预测会议(https://aiaa-dpw.larc.nasa.gov/),三次高升力计算会议(https://hiliftpw.larc.nasa.gov/),用可重复的高水平实验,来验证和确认不同研究机构开发的CFD程序,提供了大量的宝贵经验并为CFD程序的改进提供了非常有价值的参考意见。相关工作在中国并未大规模地、有系统地、多方参与地组织起来,在这个背景下,中国空气动力学会主办的第一届航空CFD可信度研讨会(AeCW-1),以CHN-T1单通道客机标模[1]为研究对象,开展以CFD程序验证和确认为目标的系统研究工作,邀请全国CFD开发者参与进来,标模试验见参考文献[2]。
工程计算上最常用的计算方法是求解雷诺平均Navier-Stokes方程(RANS),湍流行为用湍流模型模拟,如常用的Spalart-Alamars模型(S-A)[3]和Menter[4]开发的SST k-ω两方程模型。两种模型都是基于涡黏性假设构造而成,对湍流非线性特征明显的流动,如旋涡流动、流线弯曲、二次涡等,因超出涡黏性假设成立的范围,模拟能力不足,进而出现了很多针对这些不同流动类型的修正,如Shur等[5]提出的旋涡修正,Mani等[6]提出的流线弯曲修正,Spalart等[7]和Mani等[8]提出的二次本构关系(Quadratic Constitutive Relation,QCR)对S-A模型加入湍流各向异性效应的修正等。以上的修正方法提升了两种常用湍流模型的应用范围,尤其是QCR修正,在第四次AIAA会议[9-11]以后,有QCR修正的湍流模型因对翼身联结处的角涡具有很好的预测能力而大受欢迎。但是,不添加任何修正,天然考虑流线弯曲、湍流各项异性等特点的雷诺应力模型(RSM),由于控制方程数目多、模型构造复杂、计算耗费资源较多、且存在着计算鲁棒性的问题,未得到工业界足够的重视,工程应用较少。对于复杂的外形的工程应用计算,仅见Eisfeld开发的SSG/LRR-ω雷诺应力模型[12-14] (RSM)和Wilcox的Stress-ω模型[15]的有限应用,如NASA的Lee-Rausch等[16]用前述两种RSM模型计算了第二届AIAA高升力会议的构型。目前文献[12]中提出的SSG/LRR-ω雷诺应力模型,对激波诱导分离流动有较好的预测能力,正取得了工业界的重视。一方面,Rumsey等[17]发现,在ONERA M6机翼上,SSG/LRR-ω雷诺应力模型在激波位置和分离区的大小的预测上表现稳健;DLR的Keye等[11]比较了SSG/LRR-ω模型和添加QCR修正的涡黏性模型对翼身结合处的角涡的预测,发现SSG/LRR计算效果和引入QCR的涡黏性模型相当,显示出该湍流模型是一个很有潜力进行工程计算的高级湍流模型;同时,RSM在模型的构造上,主要利用速度一阶导数信息,因此模型对网格的敏感性比k-ω类方法要低,达到网格收敛所需网格数目较少。另一方面,NASA的Rumsey[17]和Dudek[18]等在一些其他的常见流动类型的研究表明,相对于使用对应修正的涡黏性模型,RSM模型并没有明显的压倒性的优势。综上,对RSM的研究和未来发展仍有不少争议,因此NASA的CFD2030远景[19]也提到,需要对RSM模型需进行更充分的研究论证,以进一步开发该模型的潜力。近年来,对雷诺应力模型的开发进展缓慢,但是RSM的工程应用仍在不停发展。Togiti等[20]开发的基于g变量的SSG/LRR雷诺应力模型的变种,具有更好的数值鲁棒性。Nie等[21-22]将RSM和转捩模型耦合,开发出具有自动转捩能力的雷诺应力模型。国内对雷诺应力模型的开发和复杂外形上的计算应用较少。聂胜阳等[23]研究过RSM在ONERA M6机翼上的激波分离流中的预测能力以及聂胜阳等[24]研究RSM在旋涡流动中的预测能力,董义道等[25]对SSG/LRR-ω雷诺应力模型在典型算例和DLR-F6上进行了计算分析,都论证了RSM具有较好的复杂湍流的计算能力。本次CHN-T1模型上的角涡流动很小,因此本文分别使用了标准Spalart-Alamars模型(S-A)和SSG/LRR-ω雷诺应力模型对CHN-T1的所有工况进行计算, 用来考察涡黏性模型和不使用涡黏性假设的雷诺应力模型在CHN-T1运输机标模上的模拟能力,对所得结果进行详细的分析,为湍流模型的开发和应用评估提供参考。
1 计算状态和计算网格AeCW-1研讨会组委会提供的基准非结构网格[26-27],采用Pointwise软件生成。网格生成策略是用block-to-block方法先生成表面网格,然后外推三棱柱。在三棱柱外的空间用阵面推进法填充剩余空间。粗中细网格由block上的点数增加1.414倍得到。粗中细网格的三棱柱层的高度一致。最终的粗网格有230万个网格点,650万网格单元,其中三棱柱有350万;中等网格有595万网格点,1680万网格单元,其中三棱柱有840万;密网格有1725万个网格点,4950万个网格单元,其中三棱柱有2648万。Config1的中等网格和细网格在飞机上的分布如图 1所示。Config2和Config3上的计算网格与Config1的中等网格一致。计算构型的信息和计算状态分别参见表 1和表 2。

|
图 1 case1上中等网格和细网格在机翼机身结合处附近的表面网格分布 Fig.1 Illustration of the grid distribution on medium mesh(left) and fine mesh (right)on the wing-body junction for case1 |
| 表 1 计算构型汇总 Table 1 Summary of the configurations |
|
|
| 表 2 计算状态汇总 Table 2 Summary of the computation settings |
|
|
本文使用自研的基于非结构网格的流场求解器——湍流模型开发平台(UTMDP),对AeCW-1研讨会组委会提供的基准非结构网格进行了计算。流场控制方程为RANS。湍流模型对流项的离散格式为二阶Roe格式;无黏通量的离散格式为中心格式,添加适量的矩阵人工黏性,二阶人工黏性系数为0.5,四阶黏性系数为1/128,不采用墒修正;用多重网格技术加速收敛,LU-SGS隐式时间推进,定常计算,CFL数为5.0,计算分区为24块用于并行计算。
2.2 湍流模型湍流模型选择计算很鲁棒的标准S-A模型和SSG/LRR-ω模型。S-A模型采用去掉转捩控制项的SA-noft2模型,在本文中用S-A简称。SSG/LRR-ω模型若采用通用扩散模型(Generalized Gradient Diffusion Model,GGDH)无法得到稳定的计算结果,所以扩散项采用扩散项模型,即SSG/ LRR-RSM-w2012-SD,在本文中用RSM简称。远场边界条的自由来流湍流度设为0.2%,湍流黏性比设为0.001。计算发现,对于RSM,需要对输运ω的最小值进行一定的限制,以获得稳定的计算结果。SA-noft2模型和SSG/ LRR-RSM-w2012-SD模型的具体信息可以参看NASA Turbulence Model Resource(TMR)[28]。
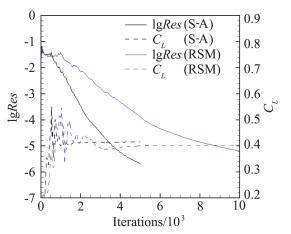
2.3 计算收敛性采用S-A模型计算,在Config1,Config2和Config3构型上都获得了收敛的解。RSM在Config1上可以得到稳定收敛解。如图 2所示,在Config1构型上,即使在密网格计算,使用S-A模型计算5000步后,密度的平均残值的对数可以下降到-6,力系数接近收敛。使用RSM计算则需要更多的迭代步数才能使密度平均残值下降到S-A模型计算5000步后的水平。
|
图 2 在Config1上使用密网格计算2°状态下的收敛历程 Fig.2 Convergence history of the computation using fine mesh at 2° on Config1s |
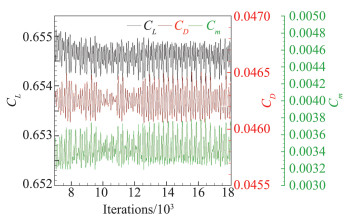
而RSM在有尾支撑的构型上(Config2和Config3),密度平均残值的对数下降到-2之后,就难以进一步下降,力系数震荡。在较小迎角的工况,升阻力系数的变化在1 count以内。当迎角大于3.5°,升阻力系数变化范围扩大,但是升力系数的变化不超过10 counts,阻力系数不超过5 counts,典型的RSM计算的力系数随迭代步数的变化见图 3。此时迎角较大,机翼上出现了激波诱导的较大的分离,飞机处在抖振边界附近,力系数会出现震荡。由于在Config1上RSM可以得到收敛的结果,因此引起Config2和Config3上小迎角状工况的计算仍难以收敛的原因应来源于尾支撑的存在。
|
图 3 4°工况下RSM在Config2上的力系数随迭代步数变化 Fig.3 Force coefficient varies with iteration steps computed by RSM on Config2 at angle of attack 4° |
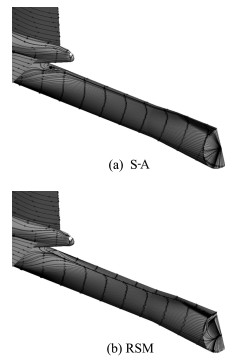
图 4展示了使用S-A和RSM模型计算得到的尾撑上的表面极限流线分布。组委会提供的非结构网格,基于的几何模型是对尾撑进行了截断处理的模型,在尾撑下游的流动出现大分离。S-A模型计算的分离涡是一个稳定的大涡。而RSM解析出更复杂的旋涡结构,进行非定常地脱落,导致计算难以收敛,力系数出现小幅震荡。
|
图 4 Config2上0°工况下S-A和RSM计算的尾撑上的表面极限流线图 Fig.4 Surface skin-friction lines computed by S-A and RSM on Config2 at angle of attack 0° |
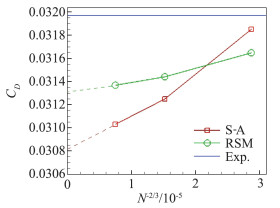
表 3是采用RSM模型和S-A模型对Config1做的网格收敛性研究,参考了文献[2]中的实验结果和文献[29]中的基于104亿网格的RANS计算结果。计算表明,在密网格上仍未达到网格收敛,收敛趋势比较明确, 通过外插到网格尺度为0的值也在表中列出。S-A模型和RSM模型具有相似的网格收敛过程,但RSM模型具有更快的网格收敛趋势,如图 5所示。RSM计算出的定升力迎角和S-A模型计算的定升力迎角有0.1°的差距。和104亿网格计算结果对比发现,RSM模型更接近高密度网格的模拟结果,只是阻力偏大。
|
图 5 定升力条件下的阻力系数随网格单元数目的变化图 Fig.5 Drag coefficient with different grid types and turbulence models for case1 |
| 表 3 Case1上使用S-A模型和RSM的计算结果汇总 Table 3 Summary of results by S-A and RSM |
|
|
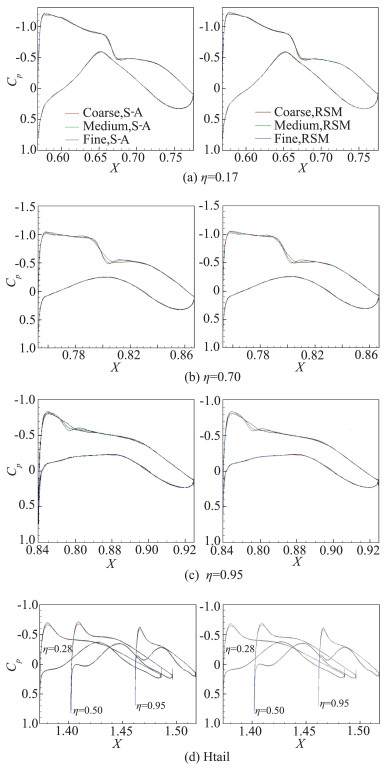
图 6展示的是机翼上部分典型站位的压力分布,取展向站位17%、70%和95%处的机翼以及平尾上3个站位进行比较,左侧为S-A模型在粗中细网格上的计算结果,右侧为RSM计算结果。随着网格密度的增加,激波的分辨率提高,宽度越来越窄, 吸力峰值稍微升高,总体变化幅度很小。在翼梢附近的弱激波,随着网格密度的增加,越来越明显。水平尾翼上的压力吸力峰值随着网格密度增加而小幅增加,其他位置上的压力分布受网格分布的影响很小。
|
图 6 Case1上由S-A和RSM计算的不同展位的压力分布 Fig.6 Pressure distribution at different spanwise locations with S-A and RSM models for Case1 |
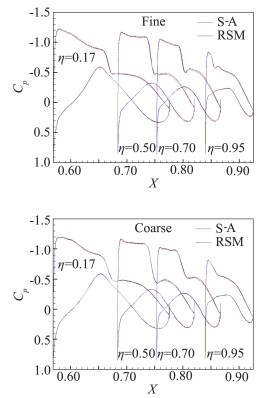
图 7展示的是S-A模型和RSM在粗网格和密网格上计算的压力分布的比较。主要的区别是:在上表面,RSM计算的激波位置较靠近上游,在激波位置的上游,RSM计算的负压大于S-A,在激波下游,RSM计算的负压小于S-A模型的计算结果;在下表面的机翼后加载区域,RSM计算的负压小于S-A模型的计算结果。这些细微差别不随网格密度增加而改变,表明这些差别来源于湍流模型本身对湍流分布和强度的解析不同所致。
|
图 7 S-A和RSM在粗网格和密网格上的计算结果对比 Fig.7 Pressure coefficients calculated by coarse and fine meshes with S-A and RSM models for Case1 |
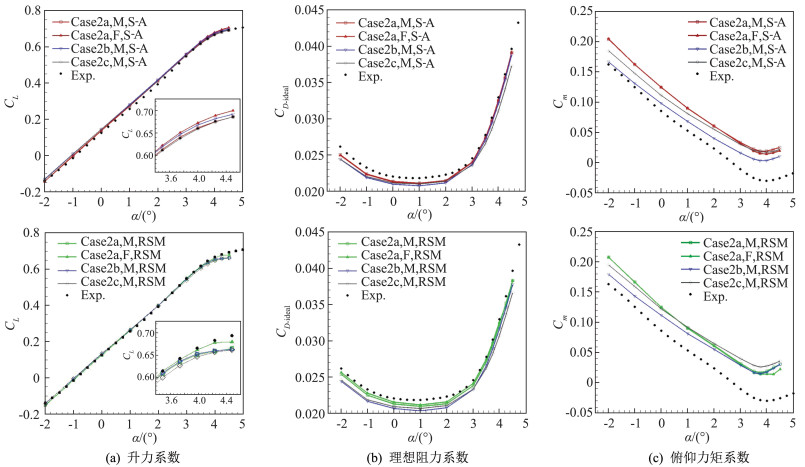
抖振特性的计算研究包含对Config1、Config2和Config3三种构型的计算研究。由于在网格收敛性研究中发现,中等网格上的计算结果和密网格上的计算结果有些微细小差别,但是在抖振边界附近,流动中出现较多复杂分离湍流结构,因此对Case2a的计算,除了按要求在中等网格上进行了计算,还增加了在密网格上的计算分析,用来研究在抖振边界附近工况下网格的影响。图 8使用S-A模型和RSM计算的力系数随迎角的变化图。对升力系数而言,S-A模型在Config1、Config2和Config3上计算的升力系数较实验数据都稍微偏大一些。Config2和Config3考虑了尾撑效应,计算的升力系数在线性区更大一些,在非线性区,Config3上计算的升力系数更接近实验数据。对Config1构型使用中等网格的计算,升力系数在线性区和非线性区上没有明显区别。在非线性区,中等网格上的计算结果更接近实验数据,密网格上计算的升力系数明显偏大。对RSM而言,在不同构型上计算的升力系数都很接近实验数据。主要差别在非线性区,Config1上计算的升力系数最大,Config3上计算的升力系数最小,都明显小于实验数据。但是Config1上使用密网格计算的升力系数更接近实验数据。对理想阻力系数来说,所有构型上计算的阻力系数都小于实验观测。Config1上计算的阻力系数明显高于Config2和Config3;RSM计算结果和实验值的差距大于S-A模型计算的差距;在Config1上的S-A模型和RSM计算的阻力系数更接近实验数据。而俯仰力矩系数的计算,S-A模型和RSM的计算结果都和实验数据差别较大。在Config1构型上,当迎角小于3.75°时,网格密度影响不大,只有高于3.75°时,密网格上计算的俯仰力矩系数略小于中等网格上的计算结果;Config2上的计算结果和实验数据的偏差最小;在较大迎角的工况,考虑了尾撑效应和机翼静气弹变形的Config3构型,其上计算的俯仰力矩系数和实验数据的差别大于没有考虑机翼静气弹变形的Config2,且RSM在Config3上计算的俯仰力矩系数在较大迎角时,产生的偏差甚至大于在Config1上的结果;在Config2和Config3上,RSM计算的结果都较S-A模型计算的结果偏离实验数据。
|
图 8 S-A模型和RSM计算的升力,理想阻力(CD_ideal=CD-CL/(2πAR))和俯仰力矩系数随迎角的变化 Fig.8 CL, CD_ideal and Cm vs. angle of attack computed by S-A and RSM models for Case2 |
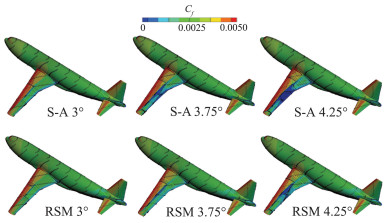
S-A和RSM模型在同一构型上,计算出的流动现象有一些差别。当迎角小于3.5°时,机翼上没有激波诱导的分离;迎角大于3.5°时,出现激波诱导分离,且分离区随迎角增加而增大。当迎角增加到4.5°时,机翼中段出现了大范围的激波分离流。RSM计算的激波诱导分离小于S-A模型计算结果,分离区也小于S-A模型计算结果。图 9展示了S-A模型和RSM模型在Config1上计算的摩阻系数分布,计算工况从左到右分别是迎角为3°、3.75°和4.25°。在3.75°工况上,RSM计算的激波诱导分离明显小于S-A模型的计算结果。随着迎角的增大,分离区扩大,RSM计算的分离区始终小于S-A计算的分离区。
|
图 9 S-A和RSM表面摩阻分布和表面极限流线 Fig.9 Surface skin-friction coefficient and stream lines computed by S-A and RSM modelss |
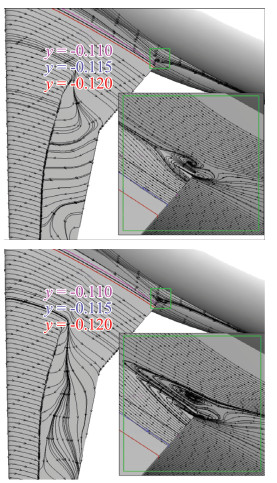
CHN-T1标模使用的机身限制了翼根处的角涡的发展,角涡大小有限。随着迎角的增加,翼根处的角涡增大。图 10显示的是S-A模型和RSM计算的翼根处角涡在4.25°时细节的比较, RSM计算的角涡较大一些,网格加密后,角涡增大,但是相对机翼尺度而言,角涡一直很小,对气动特性的影响可忽略。
|
图 10 Case2a在中等网格是由S-A和RSM计算的角涡 Fig.10 Wing root trailing edge separation bubble computed by S-A and RSM models for Case2a |
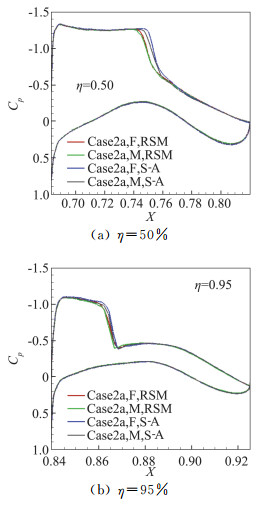
图 11是Config1构型上机翼展向50%和95%站位处计算的压力分布比较,分别使用中等网格和密网格,计算工况是3.75°。可以看出,S-A模型计算的激波位置靠后,RSM计算的激波靠前。在翼梢附近,RSM计算的激波位置仍稍微在上游。网格加密对激波位置无影响,激波随着网格加密宽度变窄。
|
图 11 3.75°工况下50%和95%展向站位的压力分布 Fig.11 Pressure distribution at 50% and 95% spanwise locations and angle of attack 3.75° for Case2 |
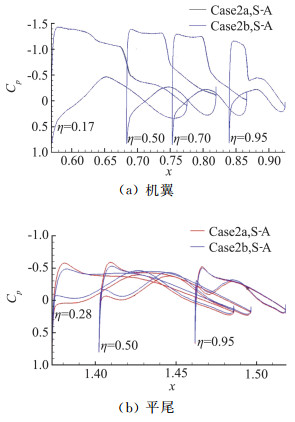
由于S-A和RSM在CHN-T1标模上计算的现象,除了诱导分离区的大小有明显差别外,其他的现象都和接近。因此研究尾撑效应影响的时候,只展示S-A模型的的计算结果。图 12展示了机翼和平尾部分站位上的压力分布的比较。可以看出,在机翼上,压力分布几乎完全一致,尾撑不影响机翼上的流动。但在平尾上,压力分布出现较大的差别,表现为Config2上平尾的上下压力差变小,吸力峰值下降,越靠近平尾翼根尾撑的影响越大。CHN-T1构型的平尾产生负的升力,贡献给抬头力矩。由于平尾的上下压力差变小,平尾对抬头力矩的贡献变小,因而计算的总的俯仰力矩系数降低。计算的结果和Config1相比,更接近实验数据。
|
图 12 4.25°工况下Case2a和Case2b上机翼和平尾上典型站位的压力分布 Fig.12 Pressure distribution at angle of attack 4.25°on wing and htail for Case2a and Case2b |
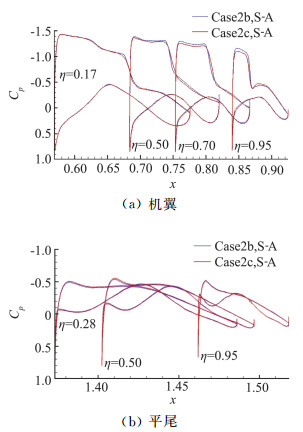
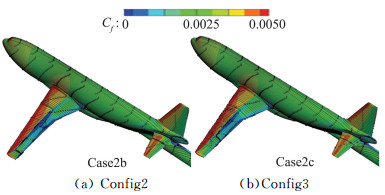
将有尾撑的Config2和Config3比较,发现考虑机翼静气弹变形的Config3构型上,机翼压力分布出现较大的变化,如图 13(a)所示。静气弹变形带来了激波前吸力下降,激波后移,越靠近翼梢越明显。而平尾上的压力分布受静气弹影响较小,吸力峰值微微增加,上下压力差变大。而由于吸力下降,激波变弱,激波诱导的分离也变小,如图 14所示,在3.75°工况下,Config3上激波诱导的分离区明显变小。
|
图 13 4.25°工况下Case2b和Case2c上机翼和平尾上典型站位的压力分布 Fig.13 Pressure distribution at angle of attack 4.25° on wing and htail for Case2b and Case2c |
|
图 14 Case2b和Case2c上S-A计算的3.75°的表面摩阻系数和表面极限流线分布 Fig.14 Surface skin-friction coefficient and streamlines computed by S-A on Config2 and Config3 at angle of attack 3.75° |
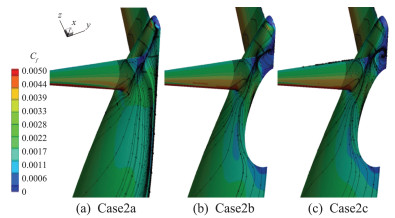
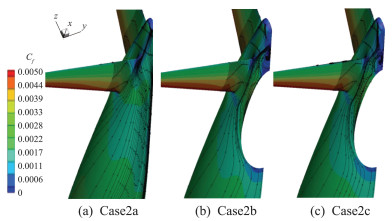
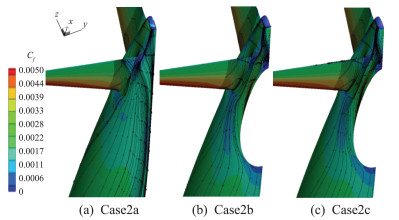
机翼前缘附近吸力下降,会引起俯仰力矩系数下降。而平尾上的上下压力差产生的负升力稍微增加,图 13 4.25°工况下Case2b和Case2c上机翼和平尾上典型站位的压力分布Fig. 13 Pressure distribution at angle of attack 4.25°on wing and htail for Case2b and Case2c 图 14 Case2b和Case2c上S-A计算的3.75°的表面摩阻系数和表面极限流线分布Fig. 14 Surface skin-friction coefficient and streamlines computed by S-A on Config2 and Config3 at angle of attack 3.75°带来总的俯仰力矩系数的增加。然而,计算的力矩系数,如图 8(c)所示,俯仰力矩系数因静气弹效应而增加。导致这一现象的原因是尾撑和静气弹效应对机身尾部作用所引起的俯仰力矩的变化更复杂。图 15展示在三种构型上的机身尾部,由S-A模型计算的表面流线分布和表面摩擦系数在-2°工况的分布。可以看出,因为尾撑的存在,机身尾部上的流动出现显著的变化,形成一个低速旋涡。低速旋涡在考虑静气弹效应的Config3上变小,位置向上游移动。由于静气弹效应,流过机翼的气流被机翼上表面加速的程度稍微下降,被加速的气流从水平尾翼下流过尾撑,引起尾撑和机身间的旋涡因注入能量下降而旋涡尺度和位置都发生了变化。该旋涡位置和能量的变化,因距俯仰力矩参考点较远,带来俯仰力矩的较大变化。由RSM计算的结果也有同样的现象,如图 16所示。只是RSM计算的旋涡要小很多。随着迎角的增加,如图 17和18,低速旋涡的尺寸缩小。对于考虑静气弹效应,计算的力矩系数反而比Config2上更大,迎角越大,和实验数据的差距越大。由于CHN-T1标模的尾撑相对尺寸较大,安装位置离平尾很近,带来平尾上压力分布显著变化,引起俯仰力矩的变化;同时,尾撑对机尾上流动的影响更复杂,诱导出一个分离旋涡,耦合静气弹效应,引起上游来流能量下降,从而导致旋涡位置变化和机尾上的压力分布变化,进而带来俯仰力矩系数的改变。综合考虑S-A和RSM在Config2和Config3上计算的力矩系数和流动现象,可以得出,S-A模型计算出的平尾和机身和尾撑结合处的旋涡更大,可能更接近实验现象。
|
图 15 S-A计算的Case2a、Case2b和Case2c在-2°工况下表面摩阻和极限流线分布 Fig.15 Surface skin-friction coefficient and streamlines caluated by S-A model at angle of attack -2° for Case2a, Case2b and Case2c |

|
图 16 RSM计算的Case2a、Case2b和Case2c在-2°工况下表面摩阻和极限流线分布 Fig.16 Surface skin-friction coefficient and streamlines caluated by RSM model at angle of attack -2° for Case2a, Case2b and Case2c |
|
图 17 S-A计算的Case2a、Case2b和Case2c在4.25°工况下表面摩阻和极限流线分布 Fig.17 Surface skin-friction coefficient and streamlines caluated by S-A model at angle of attack 4.25° for Case2a, Case2b and Case2c |
|
图 18 RSM计算的Case2a、Case2b和Case2c在4.25°工况下表面摩阻和极限流线分布 Fig.18 Surface skin-friction coefficient and streamlines caluated by RSM model at angle of attack 4.25° for Case2a, Case2b and Case2c |
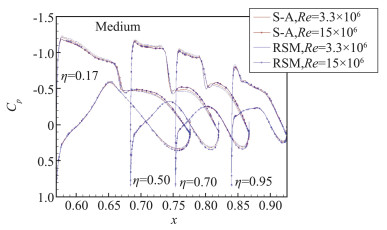
表 4展示的是计算的雷诺数对运输机标模的影响。在低雷诺数时,达到CL=0.5的迎角比高雷诺数工况所需迎角高约0.25°。高雷诺数下的阻力系数明显小于低雷诺数,主要是黏性阻力大幅下降。使用S-A模型和RSM计算的定升力系数下的阻力系数和所需迎角在高雷诺数时更接近一致,表明黏性作用在高雷诺数工况时影响下降。总体而言,高雷诺数时S-A计算结果更接近实验测量,低雷诺数时RSM计算结果更接近。图 19展示的是机翼上典型站位的压力分布的比较:高雷诺数时吸力峰值下降,但是机翼后加载翼段上的负压增加。因此高雷诺数时带来的力矩系数小于低雷诺数。
|
图 19 Case3上机翼部分站位的压力分布 Fig.19 Pressure distributions on the wing for Case3 |
| 表 4 Case3上S-A计算结果汇总 Table 4 Summary of the computations with S-A model for Case3 |
|
|
对本文重要的结论梳理如下:
(1) 对计算收敛性研究发现:S-A模型在所有构型上都具有更好的收敛性,而RSM仅在无尾撑的构型上,收敛性好,在其他构型上计算的力系数出现小幅震荡。引起力系数震荡的主要原因是组委会提供的非结构网格基于的几何模型,其尾撑沿中间某一横截面截断, RSM在横断面后计算出复杂的非定常的旋涡系统,引起力系数的震荡。
(2) 基于Config1构型的定升力系数网格收敛性研究表明:S-A和RSM模型都能趋向于网格收敛。RSM计算的定升力阻力系数更接近实验数据,所需迎角也接近实测数据,比S-A更快趋向于网格收敛。但是计算的力矩系数和实测数据差距明显。使用S-A模型和RSM计算的压力分布很接近;两种湍流模型计算的吸力峰值随网格密度增加而微微增加;在最密的网格上,都可以分辨出翼梢附近的弱激波。
(3) 对Config1构型的计算表明:RSM计算的激波位置比S-A模型计算的位置更靠近上游,激波引起的分离区较S-A模型计算的小,且不随网格密度增加而改变。
(4) 对抖振特性的计算表明:在Config1,Config2和Config3上S-A和RSM计算出的升阻力系数和主要流动现象都很接近。较小的差别体现在:所有构型上,S-A计算的升力系数较实验数据稍微大,RSM计算的升力系数更接近实验数据,在考虑尾撑效应和静气弹效应后,计算阻力系数偏小。计算力矩系数和实验数据的偏差,在考虑尾撑效应后改善;但是考虑静气弹效应后,力矩系数的偏差再一次增加。主要原因是尾撑和机尾的相互作用复杂,是复杂湍流问题,并且计算用的网格在此区域可能不够密,准确捕捉机尾上的复杂湍流现象是一大难点.
(5) 对雷诺数效应研究表明:当雷诺数从Re=3.3×106增加Re=15×106,S-A模型和RSM计算的结果趋于一致,阻力下降,俯仰力矩系数也下降。
对本次CHN-T1标模进行实验研究发现,尾撑所引起的效应带来的干扰较大,流动现象复杂,使得数值模拟很难再现实验结果,因此在未来类似构型的实验,应适当改进尾撑与机身的连接方式,减少尾撑对机尾区域流动的影响。
| [1] |
余永刚, 周铸, 黄江涛, 等. 单通道客机气动标模CHN-T1设计[J]. 空气动力学学报, 2018, 36(3): 505-513. YU Y G, ZHOU Z, HUANG J T, et al. Aerodynamic design of a standard model CHN-T1 for single-aisle passenger aircraft[J]. Acta Aerodynamica Sinica, 2018, 36(3): 505-513. DOI:10.7638/kqdlxxb-2018.0072 (in Chinese) |
| [2] |
李强, 刘大伟, 许新, 等. CHN-T1标模2.4米风洞气动特性试验研究[J]. 空气动力学学报, 2019, 37(2): 337-344. LI Q, LIU D, XU X, et al. Experimental study of aerodynamic characteristic of CHN-T1 standard model in 2.4m transonic wind tunnel[J]. Acta Aerodynamica Sinica, 2019, 37(2): 337-344. DOI:10.7638/kqdlxxb-2018.0099LIQ, (in Chinese) |
| [3] |
SPALART P, ALLMARA S. One-equation turbulence model for aerodynamic flows[C]. 30th Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, AIAA 1992-439, 1992.
|
| [4] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [5] |
SHUR M L, STRELETS M K, TRAVIN A K, et al. Turbulence modeling in rotating and curved channels:assessing the spalart-shur correction[J]. AIAA Journal, 2000, 38(5): 784-792. DOI:10.2514/2.1058 |
| [6] |
MANI M, LADD J A, BOWER W W. Rotation and curvature correction assessment for one and two-equation turbulence models[J]. Journal of Aircraft, 2004, 41(2): 268-273. DOI:10.2514/1.9321 |
| [7] |
SPALART P R. Strategies for turbulence modeling and simulation[J]. International Journal of Heat and Fluid Flow, 2000, 21(3): 252-263. DOI:10.1016/S0142-727X(00)00007-2 |
| [8] |
MANI M, BABCOCK D A, WINKLER C M, et al. Predictions of a supersonic turbulent flow in a square duct[C]. 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA 2013-0860, January 2013.
|
| [9] |
YAMAMOTO K, TABAKA K, MURAYAMA M. Comparison study of drag prediction for the 4th CFD drag prediction workshop using structured and unstructured mesh methods[C]. 28th AIAA Applied Aerodynamics Conference, AIAA 2010-4222, June 2010.
|
| [10] |
YAMAMOTO K, TANAKA K, MURAYAMA M. Effect of a nonlinear constitutive relation for turbulence modeling on predicting flow separation at wing-body juncture of transonic commercial aircraft[C]. 30th AIAA Applied Aerodynamics Conference, AIAA 2012-2895, June 2012.
|
| [11] |
KEYE S, TOGITI V, EISFELD B, et al. Investigation of fluid-structure-coupling and turbulence model effects on the DLR results of the fifth AIAA CFD drag prediction workshop[C]. 31st AIAA Applied Aerodynamics Conference, AIAA 2013-2509, June 2013.
|
| [12] |
EISFELD B. Implementation of Reynolds stress models into the DLR-FLOWer code[R]. Institutsbericht, DLR-IB 124-2004/31, Report of the Institute of Aerodynamics and Flow Technology, Braunschweig, ISSN 1614-7790, 2004.
|
| [13] |
CECORA R D, EISFELD B, PROBST A, et al. Differential Reynolds stress modeling for aeronautics[J]. AIAA Journal, 2015, 53(3): 739-755. DOI:10.2514/1.J053250 |
| [14] |
EISFELD B, BRODERSEN O. Advanced turbulence modeling and stress analysis for the DLR-F6 configuration[C]. 23rd AIAA Applied Aerodynamics Conference, AIAA 2005-4727, June 2005.
|
| [15] |
WILCOX D C. Turbulence modeling for CFD[M]. 3rd ed., DCW Industries, Inc., 2006.
|
| [16] |
LEE-RAUSCH E M, RUMSEY C L, EISFELD B. Application of a full Reynolds stress model to high lift flows[C]. 46th AIAA Fluid Dynamics Conference. AIAA 2016-3944, June 2016.
|
| [17] |
RUMSEY C L. Application of Reynolds stress models to separated aerodynamic flows[M]. Differential Reynolds Stress Modeling for Separating Flows in Industrial Aerodynamics. Springer International Publishing, 2015: 19-37.
|
| [18] |
DUDEK J, CARLSON J R. Evaluation of full Reynolds stress turbulence models in Fun3D[C]. AIAA Aerospace Sciences Meeting. 2017.
|
| [19] |
SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD vision 2030 study: a path to revolutionary computational aerosciences[R]. NASA CR-2014-218178, 2014.
|
| [20] |
TOGITI V K. EISFELD B. Assessment of g-equation formulation for a second-moment Reynolds stress turbulence model (Invited)[C]. 22nd AIAA Computational Fluid Dynamics Conference, AIAA 2015-2925, June 2015.
|
| [21] |
NIE S Y, KRIEMMELBEIN N, KRUMBEIN A, et al. Coupling of a Reynolds stress model with the γ-Reθt transition model[J]. AIAA Journal, 2018, 56(1): 146-157. DOI:10.2514/1.J056167 |
| [22] |
NIE S Y, KRIMMELBEIN N, KRUMBEIN A, et al. Extension of a Reynolds-stress-based transition transport model for crossflow transition[J]. Journal of Aircraft, 2018, 55)(4): 1641-1654. |
| [23] |
聂胜阳, 高正红, 黄江涛. EARSM和DRSM在亚音速旋涡流动中的应用[J]. 应用力学学报, 2011, 28(6): 602-607. NIE S Y, GAO Z H, HUANG J T. Application of EARSM and DRSM in subsonic vortex flow[J]. Chinese Journal of Applied Mechanics, 2011, 28(6): 602-607. (in Chinese) |
| [24] |
聂胜阳, 高正红, 黄江涛. 微分雷诺应力模型在激波分离流中的应用[J]. 空气动力学学报, 2012, 30(1): 52-56. NIE S Y, GAO Z H, HUANG J T. Differential Reynolds stress model for shock & separated flow[J]. Acta Aerodynamica Sinica, 2012, 30(1): 52-56. DOI:10.3969/j.issn.0258-1825.2012.01.009 (in Chinese) |
| [25] |
董义道, 王东方, 王光学, 等. 雷诺应力模型的初步应用[J]. 国防科技大学学报, 2016, 38(4): 46-53. DONG Y D, WANG D F, WANG G X, et al. Preliminary application of Reynbolds stress model[J]. Journal of National University of Defense Technology, 2016, 38(4): 46-53. (in Chinese) |
| [26] |
王年华, 常兴华, 赵钟, 等. 基于HyperFLOW平台的客机标模CHN-T1气动性能预测及可信度研究[J]. 空气动力学学报, 2019, 37(2): 301-309. WANG N H, CHANG X H, ZHAO Z, et al. Aerodynamic performance prediction and credibility study of the transport model CHN-T1 based on HyperFLOW solver[J]. Acta Aerodynamica Sinica, 2019, 37(2): 301-309. DOI:10.7638/kqdlxxb-2018.0183WANGNH, (in Chinese) |
| [27] |
张耀冰, 唐静, 陈江涛, 等. 基于非结构混合网格的CHN-T1标模气动特性预测[J]. 空气动力学学报, 2019, 37(2): 262-271. ZHANG Y B, TANG J, CHEN J T, et al. Aerodynamic characteristics prediction of CHN-T1 standard model with unstructured grid[J]. Acta Aerodynamica Sinica, 2019, 37(2): 262-271. DOI:10.7638/kqdlxxb-2018.0201 (in Chinese) |
| [28] |
RUMSEY C L. Turbulence modeling resource[EB/OL].[2018-10-06]. http://turbmodels.larc.nasa.gov
|
| [29] |
李伟, 王运涛, 洪俊武, 等. 采用TRIP3.0模拟CHN-T1模型气动特性[J]. 空气动力学学报, 2019, 37(2): 272-279. LI W, WANG Y T, HONG J W, et al. Aerodynamic characteristics simulation of CHN-T1 model with TRIP3.0[J]. Acta Aerodynamica Sinica, 2019, 37(2): 272-279. DOI:10.7638/kqdlxxb-2018.0225 (in Chinese) |
 2019, Vol. 37
2019, Vol. 37

