大型运输机的研究是关系我国国民经济发展和科学技术进步的一项重大课题。近年来,基于雷诺平均Navier-Stokes方程(RANS)的计算流体力学(CFD)数值模拟技术已被大量应用于大型运输机全机构型的气动性能评估和气动外形设计中[1-2]。为了获得更真实可靠的气动性能数据,往往需要对考虑发动机短舱/挂架等部件在内的全机复杂构型进行数值模拟,这对全机几何建模、网格划分、湍流模型、求解格式都提出了非常高的要求[3]。其中,如何有效处理大型运输机复杂的物面边界,生成高质量的计算网格并开展高精度计算成为研究重点。对于大型运输机复杂外形而言,生成高质量的贴体结构网格相对比较困难,也比较费时。相较之下,非结构网格更适用于处理复杂外形,网格生成效率更高。长久以来,众多气动工作者一直致力于高精度非结构网格求解器的发展与验证。因此,基于非结构网格求解器开展针对大型运输机复杂构型的RANS数值模拟技术的验证与确认工作[4-8],对于评估当前CFD发展水平,促进相关流动机理的研究和非结构网格求解器的发展均具有重要意义,对于开展精细化气动设计工作也可积累一定的经验。
针对大型运输机构型,目前国外已开展了多项CFD可信度评估的研讨会,其中最具代表性的包括美国AIAA(American Institute of Aeronautics and Astronautics)组织的6次CFD阻力预测研讨会(DPW Ⅰ~DPW Ⅵ)[4, 9-13]、3次CFD高升力构型预测研讨会(HiLiftPW-1~HiLiftPW-3)[5, 14-15],以及欧盟资助的2期欧洲高升力构型计划(EUROLIFT Ⅰ~EUROLIFT Ⅱ)[16]。这些研讨会提供一系列气动标模及计算网格[4-7],如DLR-F4、DLR-F6、DLR-F11、CRM、HL-CRM等,邀请世界范围或欧盟内部的空气动力学研究机构共同参与CFD的验证和评估工作。众多研究者对包括网格生成、气动力预测、气弹影响、风洞试验等在内的工作进行统一的研究确认[4-7],为CFD技术的下一步发展明确方向。有资料显示,参加2009年DPW Ⅳ研讨会的17个研究机构所提供的28组Case 1A数值模拟结果中,有17组结果采用了非结构网格。而参加2016年DPW Ⅵ研讨会的25个研究机构提供的48组Case 1的数值模拟结果中,使用非结构网格的高达32组[4]。对于HiLiftPW系列会议而言,由于包含了增升装置后外形更为复杂,因此非结构网格的优势和主导地位愈加明显[5]。
在国内,中国空气动力学学会曾在2009年-2013年间组织了2届航空CFD可信度开放式专题研讨活动(HiCFD Ⅰ~HiCFD Ⅱ),用以评估国内的CFD技术发展现状,为国产大飞机的研制提供技术参考[4]。但由于国内缺少成熟的大型运输机标模,研讨会未能成系列地稳步开展,CFD的验证和确认工作陷入了瓶颈期。同时,目前国内对于结构网格求解器的研究比较成熟,而非结构网格技术还有待进一步研究。
在此背景下,中国空气动力研究与发展中心计算空气动力研究所联合中国航空研究院、西北工业大学、中国商用飞机有限公司上海飞机设计研究院、中国空气动力研究与发展中心高速空气动力研究所、中山大学国家超级计算广州中心等五家单位联合组织了第一届航空可信度研讨会(the 1st Aeronautics CFD Credibility Workshop, AeCW-1),规定了Case 1~3三组验证算例,并发布了自主设计的大型运输机标模CHN-T1[17],进一步促进国内CFD验证和确认工作的稳步开展,评估CFD当前技术状态,探索CFD的发展方向,为飞行器研制提供更有力的技术支撑。
本文主要针对AeCW-1组委会发布的CHN-T1标模,采用基于RANS方程的非结构求解器TNS对其气动性能进行计算和分析,以评估TNS对大型运输机复杂外形气动计算的可信度。本文工作主要包括:1)巡航性能计算。研究网格量和湍流模型等因素对计算结果的影响,为复杂构型非结构网格的CFD求解工作提供了参考;2)抖振性能计算。分别计算干净构型、带尾撑构型以及考虑机翼静气弹变形构型的气动特性曲线,研究尾撑装置和静气弹变形对气动特性计算结果的影响。通过将计算结果与组委会发布的风洞试验值[18]进行对比,全面考察TNS流动求解器的精度与可靠性。
1 计算构型和计算网格 1.1 计算构型2018年4月,AeCW-1组委会发布了自主设计的大型运输机标模CHN-T1,填补了我国大型运输机计算标模的空白,促进了国内CFD验证与确认工作的稳步开展[17]。此次计算的CHN-T1标模为机身+机翼+平尾+垂尾构型(Body Wing Htail Vtail, BWHV),不带发动机短舱和挂架。
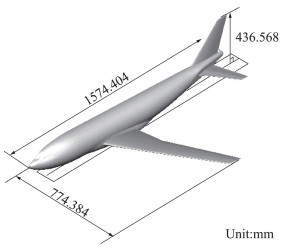
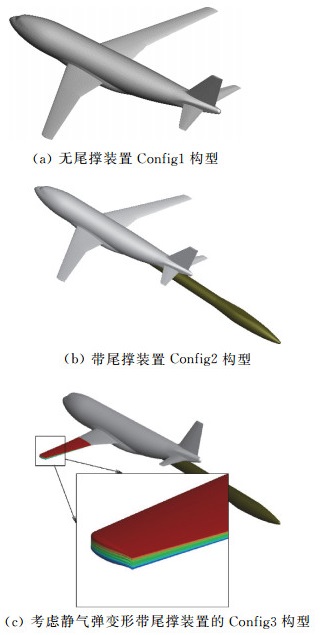
CHN-T1标模的外形如图 1所示,采用类似波音737、空客A320、C919等单通道窄体飞机的布局形式,即下单翼形式的超临界机翼和平尾、单立尾布局[17]。其巡航马赫数为0.78,巡航升力系数为0.5,风洞试验中模型缩比为0.052,具体的几何参数如表 1所示。为研究风洞试验构型对计算结果的影响,组委会提供了标模的三种构型:无尾撑风洞试验构型Config1(图 2(a))、有尾撑风洞试验构型Config2(图 2(b))、以及考虑机翼静气弹变形的有尾撑构型Config3(图 2(c))。本文将采用非结构网格求解器TNS,对三种构型的巡航气动特性及跨声速抖振特性进行计算,并研究网格量和湍流模型对计算结果的影响。
|
图 1 CHN-T1大型运输机外形(机身+机翼+平尾+立尾) Fig.1 Body-wing-htail-vtail configuration of CHN-T1 models |
|
图 2 CHN-T1标模计算构型展示 Fig.2 Different computational configurations of CHN-T1 model |
| 表 1 CHN-T1标模几何参数表 Table 1 Geometric parameters of CHN-T1 models |
|
|
针对巡航状态下Config1构型的气动特性计算,采用组委会提供的粗、中、细3套非结构网格[19-20]进行网格收敛性研究,网格的基本参数见表 2。Config1构型的跨声速抖振特性计算将采用其中的非结构中等网格,图 3为Config1构型的非结构中等网格及其表面网格示意图。针对Config2构型的跨声速抖振特性计算同样采用组委会提供的非结构网格,如图 4所示。针对考虑静气弹变形Config3构型的气动计算,采用组委会提供的非结构网格,图 5为2°迎角下的网格示意图。
|
图 3 组委会提供的Config1构型非结构中等网格示意图 Fig.3 Unstructured computational mesh of Config1 provided by AeCW-1 organizing committee (medium size) |
|
图 4 组委会提供的Config2构型非结构网格示意图 Fig.4 Unstructured computational mesh of Config2 provided by AeCW-1 organizing committees |
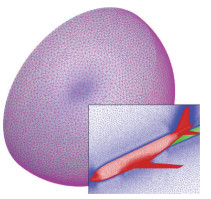
|
图 5 组委会提供的Config3构型非结构网格(迎角为2°) Fig.5 Unstructured computational mesh of Config3 provided by AeCW-1 organizing committee (α=2°) |
| 表 2 非结构计算网格说明 Table 2 Description of unstructured computational meshes |
|
|
TNS是一套基于混合网格技术的RANS方程in-house求解器。它采用有限体积法来离散NS方程,并包含多种无粘通量项离散格式,如JST中心格式、Roe格式、AUSM类格式等。时间推进格式有隐式LU-SGS和显式Runge-Kutta法。此外TNS还采用了多重网格和并行计算技术,适用于可压缩和不可压缩、定常和非定常流动问题的求解。
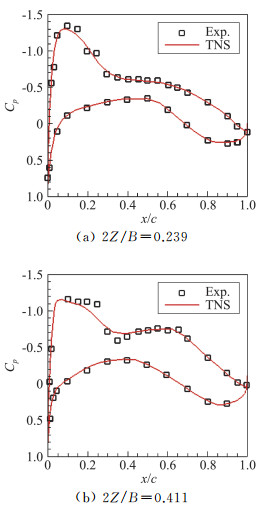
在计算全机复杂构型之前,对TNS求解器的精度进行了初步验证。针对DLR-F6翼身组合体,采用AIAA阻力预测大会DPW提供的六面体结构网格,网格量约为800万。计算状态为Ma=0.75, Re=3.0×106, CL=0.5。图 6给出了采用TNS计算获得的两个典型站位处剖面压力分布与试验结果的对比。可以看出,采用TNS求解器获得的剖面压力分布与试验结果吻合较好,且能较准确地捕捉激波位置,初步验证了TNS求解器的可靠性。
|
图 6 采用TNS求解器计算DLR-F6翼身组合体的剖面压力分布与试验结果对比 Fig.6 Comparison of computed pressure distributions by using TNS and experimental data for DLR-F6 wing-body configuration (Ma=0.75, Re=3.0×106, CL=0.5) |
采用非结构网格求解器TNS对巡航状态下的Config1构型进行数值模拟,并与风洞试验值进行对比。同时还研究了网格量和湍流模型对巡航状态气动力系数计算结果的影响。数值模拟时,空间离散采用JST中心格式,二阶人工粘性系数为1/2,四阶人工粘性系数为1/64;时间推进采用LU-SGS隐式格式,CFL数取2。采用全湍流计算,湍流模型为Spalart-Allmaras一方程模型。为了加速收敛,采用了多重网格技术(3重V型循环)。
3.1 网格收敛性研究针对Config1构型选取不同网格量进行气动计算。选取1.2节所述的3套非结构网格,定升力(CL=0.500(±0.001))计算,以研究阻力、迎角随网格量的收敛性。计算状态为:Ma=0.78, Re=3.3×106, T=300 K。
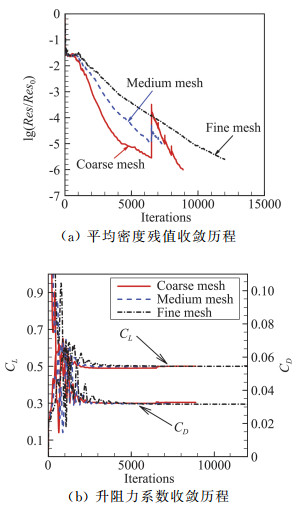
图 7为采用TNS求解器对粗、中、细三套非结构网格进行定升力计算的残值和升阻力系数收敛历程。定升力计算时迭代6500步后开始调整迎角。其中,细网格的初始迎角为2.58°,收敛迎角为2.566°,两者差异较小,因此残值收敛曲线较为光滑。
|
图 7 粗、中、细三套非结构网格定升力计算收敛历程 Fig.7 Convergence histories of residual and force coefficients using coarse, medium and fine meshes (fixed CL=0.5) |
图 8为计算得到的阻力系数、定升力时的迎角随网格量的变化曲线。从图中可以看到随着网格量的增大,中等网格与细网格之间阻力系数的变化量小于5 cts(counts, 阻力单元, cts为缩写),迎角的变化量小于0.045°。但从阻力系数随网格量的变化情况来看,针对本文采用的求解器,目前的三套网格还未达到完全收敛。图中还给出了将阻力系数和迎角外插到网格尺度为零时的结果,阻力系数的外插结果为312.2cts,迎角的外插结果为2.541°,与组委会采用百亿级网格计算的结果[21]相比,阻力系数值与试验值更接近,但迎角差别更大。

|
图 8 阻力系数和定升力计算迎角随网格量的变化曲线 Fig.8 Variation of drag and angle of attack with respect to mesh size (fixed CL=0.5) (Ma=0.78, Re=3.3×106, CL=0.5000) |
表 3给出在升力系数CL=0.5下,采用粗、中、细3套网格得到的Config1构型的阻力系数CD(包括压差阻力系数CDp,摩擦阻力系数CDf)和俯仰力矩系数Cm,升阻比CL/CD。从中可以看出,当固定升力系数CL=0.5(±0.001)时,随着网格量的增加,TNS计算收敛后得到的迎角逐渐减小,阻力系数减小,升阻比增大,力矩系数增大。从总阻力的分解上看,3套网格计算得到的摩擦阻力比较接近,而压差阻力变化比较明显,这也是导致总阻力差别较大的原因。同时,表 3也给出了巡航状态下的试验数据,该试验数据来自中国空气动力研究与发展中心的FL-26风洞,由组委会提供[18]。将计算值与试验值对比可知,计算所得迎角与阻力系数和试验值吻合较好,但力矩系数吻合较差。
| 表 3 不同网格量下TNS计算Config1构型所得巡航气动特性与试验值对比 Table 3 Comparison of computed aerodynamic performances by TNS using meshes of different sizes |
|
|
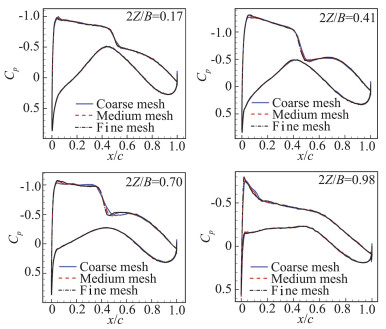
图 9给出了在不同网格量下计算得到的机翼17%、41%、70%、98%站位处剖面压力分布曲线。从图中可以看到,在机翼下表面,采用不同网格量得到的压力分布具有较好的一致性。而在机翼的上表面,网格量对不同站位处剖面压力分布的影响主要体现在预测的激波位置上,中等网格和细网格预测的激波位置较为一致,而粗网格预测的激波比较靠后,同时粗网格的前缘负压峰相比于中等网格和细网格略小一些。
|
图 9 不同网格量下计算所得机翼展向17%、41%、70%、98%站位处剖面压力分布曲线对比 Fig.9 Comparison of computed pressure distributions using different meshes of varying resolution at 17%, 41%, 70%, 98% span-wise stations |
除了采用TNS对3套非结构网格进行了计算外,本文也采用开源软件SU2[22]和商业软件Fluent对同样3套非结构网格进行了求解,其中,SU2计算时空间离散采用JST中心格式,二阶人工粘性系数为0.5,四阶人工粘性系数为0.2,时间推进采用LU-SGS隐式格式,CFL数取10;采用全湍流计算,湍流模型为SA模型;采用单重网格计算。Fluent计算时空间离散采用Roe格式;时间推进格式采用LU-SGS格式,采用自适应CFL数,起始为5,最大为50;采用全湍流计算,湍流模型为SA模型;为了加速收敛,采用了代数多重网格技术(3重F型循环)。计算结果如表 4所示,可以看到,相同网格采用不同求解器所得的计算结果存在一定的差异。不同RANS求解器的计算效率对比如表 5所示,这里需要说明的是,TNS是在课题组的“曙光”高性能服务器上运行的,而SU2和Fluent的计算则是在“天河一号”超级计算机上完成的。
| 表 4 不同RANS求解器计算结果对比 Table 4 Comparison of computed aerodynamic performances calculated by using different RANS solvers |
|
|
| 表 5 不同RANS求解器计算效率对比 Table 5 Comparison of efficiencies of different RANS solvers |
|
|
为研究不同的湍流模型对巡航气动性能计算结果的影响,本小节采用SA湍流模型和SST湍流模型对Config1构型的巡航状态进行计算。计算状态为:Ma=0.78, Re=3.3×106, T=300 K, CL=0.500(±0.001) 计算网格为粗、中、细3套非结构网格。
表 6给出了固定升力系数CL=0.5下,分别采用SA和SST湍流模型,对粗、中、细3套非结构网格计算得到的阻力系数CD、俯仰力矩系数CM和升阻比CL/CD。由表可知,给定升力系数,在同等网格量的条件下,采用SA湍流模型计算的迎角小于SST湍流模型的计算结果。随着网格量的增加,采用SA和SST湍流模型计算的阻力系数都逐渐减小。在粗网格和中等网格下,SA湍流模型计算的阻力系数略大于SST的结果。从阻力分解来看,SA计算的压差阻力较小,摩擦阻力较大。
| 表 6 采用两种湍流模型计算Config1构型所得巡航气动特性对比 Table 6 Comparison of computed aerodynamic performances by using TNS with different turbulence models |
|
|
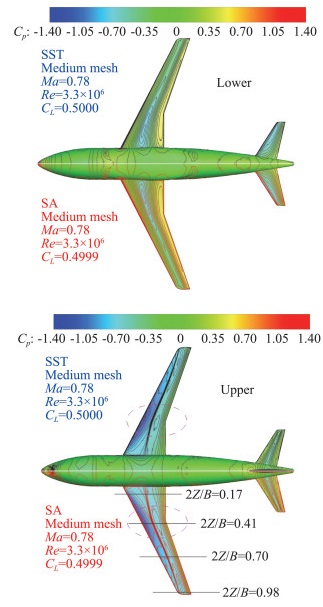
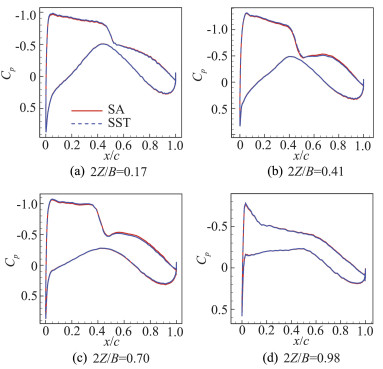
为了寻找SA和SST两种湍流模型的计算阻力系数存在一定差异的具体原因,以中等非结构网格的计算结果为例,给出两种湍流模型下TNS计算的物面压力云图对比和机翼典型站位处(17%、41%、70%和98%)的剖面压力分布对比,如图 10和图 11所示。由图可知,采用两种湍流模型时,计算结果在机翼中段的压力分布存在较大差异。在机翼上表面,激波之前采用SST湍流模型计算的压力系数相比于SA结果较低,激波之后前者计算的压力系数高于后者,因此采用SST湍流模型计算的激波更强,波阻更大。
|
图 10 两种湍流模型下TNS计算的物面压力云图 Fig.10 Comparison of pressure contours obtained by TNS with different turbulence models |
|
图 11 两种湍流模型下TNS计算所得机翼展向17%、41%、70%、98%站位处剖面压力分布曲线对比 Fig.11 Comparison of pressure distributions using different turbulence models at 17%, 41%, 70%, 98% span-wise stations |
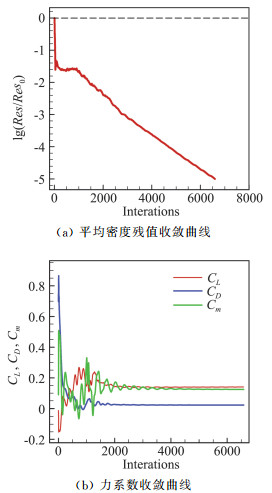
本节针对标模的跨声速抖振特性进行计算,即在固定的马赫数和雷诺数条件下,模拟气动特性随迎角的变化规律,计算状态为Ma=0.78, Re =3.3×106, T=300 K, α=-2.0°、-1.0°、0°、1.0°、2.0°、3.0°、3.5°、3.75°、4.0°、4.25°、4.50°。采用TNS分别对无尾撑风洞试验构型Config1、有尾撑风洞试验构型Config2以及考虑机翼静气弹变形的有尾撑构型Config3进行计算,考察尾撑装置和机翼静气弹变形对气动特性计算结果的影响。计算网格采用1.2节的非结构中等网格,求解器参数设置与上一节相同,流场收敛标准为控制方程的平均密度残值下降5个量级。图 12为Config1构型在迎角0°下采用TNS计算得到的平均密度残值收敛曲线及力系数收敛曲线。可以看到,当残值下降5个量级时,升力系数、阻力系数和力矩系数均已水平,无明显变化,可认为力系数已达到收敛。
|
图 12 Config1构型残值及力系数收敛历程 Fig.12 Convergence histories of residual and force coefficients for Config1 (Ma=0.78, Re=3.3×106, α=0°) |
图 13为3种构型计算得到的气动特性曲线。可以看到,3种构型的气动特性变化趋势基本一致。与试验值相比,计算得到的阻力系数均位于风洞试验值的误差带内,如图 13(b),验证了所采用的TNS非结构网格求解器的精度。同时,将图 13(b)和(c)中巡航状态(CL=0.5)附近的气动特性放大来看,考虑机翼静气弹变形后的Config3构型要比Config1和Config2构型计算的气动特性更贴近于试验值,这也反映出计算构型应尽可能地贴近实际飞行构型,以增加数值模拟的可信度。表 7给出了巡航升力附近(迎角α=3°时) Config1、Config2和Config3三种构型的气动力系数计算结果与试验值的比较, 可以看到, 考虑机翼静气弹变形及尾撑装置影响的Config3构型所得的升力系数和阻力系数值更接近试验值。但三种构型的力矩系数均与试验值吻合较差。

|
图 13 三种构型的气动特性曲线与试验值对比 Fig.13 Comparison of computed aerodynamic characteristics with experimental data for three different configurations |
| 表 7 巡航升力附近(α=3°)三种构型力系数计算结果对比 Table 7 Comparison of computed aerodynamic performances of three configurations at α=3° |
|
|
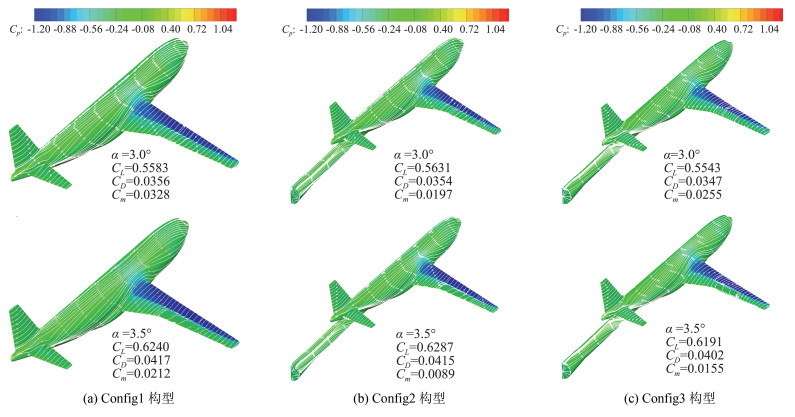
由图 14中的表面极限流线可知,随着迎角的增大,在3.5°迎角时,机翼中段开始出现激波诱导附面层分离,从而导致升力曲线进入非线性段,同时阻力迅速增大,升阻比降低。值得注意的是,Config1构型和Config2构型的分离流动均从机翼中部外翼段流向内翼段,而考虑静气弹变形的Config3构型,分离流动从中部内翼段向外翼段扩张。
|
图 14 三种构型的表面极限流线 Fig.14 Streamlines on the upper surface of three different configurations |
对比各构型的剖面压力分布,以迎角α=3.5°为例,如图 15所示,在三种不同构型的机翼和平尾上截取相同站位处的剖面压力分布进行比较。可以看到,风洞内部的尾撑装置对机翼压力分布影响较小,但对平尾的压力分布影响较大。而在考虑机翼静气弹变形后,机翼不同站位处的压力分布受到明显影响,尤其是在翼尖站位处,静气弹变形较大,压力分布差异显著,激波位置前移且前缘负压下降。但静气弹变形对平尾压力分布的影响较小。

|
图 15 三种构型机翼和平尾不同站位处压力分布对比 Fig.15 Comparison of pressure distributions of wing and tail at different span-wise stations for three different configurations (Ma=0.78, Re=3.3×106, α=3.5°) |
本文针对AeCW-1组委会发布的大型运输机标模CHN-T1开展了非结构网格求解器TNS对气动特性计算可信度的确认研究。针对无尾撑风洞试验构型Config1进行了巡航特性计算,并研究了网格量和湍流模型等因素对数值模拟结果的影响。同时,还针对Config1、有尾撑风洞试验构型Config2及考虑机翼静气弹变形的有尾撑构型Config3进行了跨声速抖振特性计算,考察了支架干扰和静气弹变形对气动特性的影响。本文研究所得的几点结论如下:
(1) 针对CHN-T1标模的巡航升阻比和跨声速抖振特性,非结构网格求解器TNS计算结果与试验值吻合良好,计算的阻力值完全位于试验误差带内,表明该求解器对复杂外形的气动性能计算具有较高的可信度。
(2) 采用不同的网格量和不同湍流模型,巡航气动性能计算结果会有一定的差异。定升力情况下,计算的巡航阻力系数随网格量增大而单调减小;SA和SST湍流模型预测的巡航数阻力系数差别较小(对于细网格,其差别小于1个阻力单元)。
(3) 有无尾撑装置对机翼压力分布计算结果影响较小,但对平尾的压力分布影响较大,因而对力矩系数计算结果影响较大。
(4) 考虑机翼静气弹变形后,计算结果与风洞试验值更加吻合。机翼的压力分布有明显变化,在翼尖站位处变化尤为显著,激波位置前移且前缘负压峰值更低。
致谢: 此项工作是在国家超级计算天津中心的“天河一号”超级计算机上完成,感谢“天河一号”的大力支持。
| [1] |
高正红, 王超. 飞行器气动外形设计方法研究与进展[J]. 空气动力学学报, 2017, 35(4): 516-528. GAO Z H, WANG C. Aerodynamic shape design methods for aircraft:status and trends[J]. Acta Aerodynamica Sinica, 2017, 35(4): 516-528. DOI:10.7638/kqdlxxb-2018.0058 (in Chinese) |
| [2] |
熊俊涛, 乔志德, 韩忠华. 基于Navier-Stokes方程跨声速翼型和机翼气动优化设计[J]. 空气动力学学报, 2007, 25(1): 29-33. XIONG J T, QIAO Z D, HAN Z H. Aerodynamic optimization design of transonic airfoil and wing based on Navier-Stokes equations[J]. Acta Aerodynamica Sinica, 2007, 25(1): 29-33. DOI:10.3969/j.issn.0258-1825.2007.01.006 (in Chinese) |
| [3] |
王运涛. DPW Ⅳ~DPW Ⅵ数值模拟技术综述[J]. 航空学报, 2018, 39(4): 021836. WANG Y T. An overview of DPW Ⅳ~DPW Ⅳ numerical simulation technology[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4): 021836. (in Chinese) |
| [4] |
王运涛. HiLiftPW-1~HiLiftPW-3数值模拟技术综述[J]. 航空学报, 2018, 39(7): 021997. WANG Y T. An overview of HiLiftPW-1 to HiLiftPW-3 numerical simulation technologies[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 021997. (in Chinese) |
| [5] |
王运涛, 孙岩, 王光学, 等. DLR-F6翼身组合体的高阶精度数值模拟[J]. 航空学报, 2015, 36(9): 2923-2929. WANG Y T, SUN Y, WANG G X, et al. High-order accuracy numerical simulation of DLR-F6 wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2923-2929. (in Chinese) |
| [6] |
王运涛, 孟德虹, 孙岩, 等. DLR-F6/FX2B翼身组合体构型高阶精度数值模拟[J]. 航空学报, 2016, 37(2): 484-490. WANG Y T, MENG D H, SUN Y, et al. High-order accuracy numerical simulation of DLR-F6/FX2B wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 484-490. (in Chinese) |
| [7] |
SLOTNICK J, KHODADOUST A, ALONSO J, et al. CFD Vision 2030 Study: A path to revolutionary computational aerosciences: NASA/CR-2014-218178[R]. Washington, D C: NASA, 2014.
|
| [8] |
王刚, 叶正寅. 三维非结构混合网格生成与N-S方程求解[J]. 航空学报, 2003, 24(5): 385-390. WANG G, YE Z Y. Generation of three dimensional mixed and unstructured grids and its application in solving Navier-Stokes equations[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(5): 385-390. DOI:10.3321/j.issn:1000-6893.2003.05.001 (in Chinese) |
| [9] |
ROY C J. Summary of data from the Sixth AIAA CFD drag prediction workshop: Case 1 code verification[C]. 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, AIAA 2017-1206.
|
| [10] |
ABDOL-HAMID K S, CARLSON J, RUMSEY C L, et al. DPW-6results using FUN3D with focus on k-kL-MEAH2015 turbulence model[C]. 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, AIAA 2017-0962.
|
| [11] |
MICHAL T R, BABCOCK D, KAMENETSKIY D S, et al. Comparison of fixed and adaptive unstructured grid results for drag prediction workshop 6[C]. 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, AIAA 2017-0961.
|
| [12] |
TINOCO E N, BRODERSEN O, KEYE S, et al. Summary of data from the sixth AIAA CFD drag prediction workshop: CRM Cases 2 to 5[C]. 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, AIAA 2017-1208.
|
| [13] |
DERLAGA J M, MORRISON J H. Statistical analysis of CFD solutions from the sixth AIAA drag prediction workshop[C]. 55th AIAA Aerospace Sciences Meeting, AIAA SciTech Forum, AIAA 2017-1209.
|
| [14] |
SLOTNICK J, HANNON J, CHAFFIN M. Overview of the 1st AIAA CFD high lift prediction workshop[C]. AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. 2013.
|
| [15] |
BALIN R, JANSENK E. A comparison of RANS, URANS, and DDES for high lift systems from HiLiftPW-3[C]. 2018 AIAA Aerospace Sciences Meeting, AIAA 2018-1254.
|
| [16] |
ELIASSON P, CATALANO P, PAPE M C L, et al. Improved CFD predictions for high lift flows in the European project EUROLIFT Ⅱ[C]. 25th AIAA Applied Aerodynamics Conference, DLR, AIAA 2007-4303.
|
| [17] |
余永刚, 周铸, 黄江涛, 等. 单通道客机气动标模CHN-T1设计[J]. 空气动力学学报, 2018, 36(3): 505-513. YU Y G, ZHOU Z, HUANG J T, et al. Aerodynamic design of a standard model CHN-T1 for single-aisle passenger aircraft[J]. Acta Aerodynamica Sinica, 2018, 36(3): 505-513. DOI:10.7638/kqdlxxb-2018.0072 (in Chinese) |
| [18] |
李强, 刘大伟, 许新, 等. CHN-T1标模2.4米风洞气动特性试验研究[J]. 空气动力学学报, 2019, 37(2): 337-344. LI Q, LIU D, XU X, et al. Experimental study of aerodynamic characteristic of CHN-T1 standard model in 2.4 m transonic wind tunnel[J]. Acta Aerodynamica Sinica, 2019, 37(2): 337-344. DOI:10.7638/kqdlxxb-2018.0099 (in Chinese) |
| [19] |
王年华, 常兴华, 赵钟, 等. 基于HyperFLOW平台的客机标模CHN-T1气动性能预测及可信度研究[J]. 空气动力学学报, 2019, 37(2): 301-309. WANG N H, CHANG X H, ZHAO Z, et al. Aerodynamic performance prediction and credibility study of the transport model CHN-T1 based on HyperFLOW solver[J]. Acta Aerodynamica Sinica, 2019, 37(2): 301-309. DOI:10.7638/kqdlxxb-2018.0183 (in Chinese) |
| [20] |
张耀冰, 唐静, 陈江涛, 等. 基于非结构混合网格的CHN-T1标模气动特性预测[J]. 空气动力学学报, 2019, 37(2): 262-271. ZHANG Y B, TANG J, CHEN J T, et al. Aerodynamic characteristics prediction of CHN-T1 standard model with unstructured grid[J]. Acta Aerodynamica Sinica, 2019, 37(2): 262-271. DOI:10.7638/kqdlxxb-2018.0201 (in Chinese) |
| [21] |
李伟, 王运涛, 洪俊武, 等. 采用TRIP3.0模拟CHN-T1模型气动特性[J]. 空气动力学学报, 2019, 37(2): 272-279. LI W, WANG Y T, Hong J W, et al. Aerodynamic characteristics simulation of CHN-T1 model with TRIP3.0[J]. Acta Aerodynamica Sinica, 2019, 37(2): 272-279. DOI:10.7638/kqdlxxb-2018.0225 (in Chinese) |
| [22] |
ECIBINIB T D, PALACIOS F, COPELAND S R, et al. SU2:An open-source suife for multiphysics simulation and design[J]. AIAA J, 2015, 54(3): 1-19. |
 2019, Vol. 37
2019, Vol. 37


