随着计算流体力学技术在航空领域的广泛应用,计算的验证、确认与可信度问题成为CFD继续深入应用时不可回避的问题之一[1-2]。学术界对CFD可信度问题的研究源自上世纪90年代计算机技术的飞速发展,并逐渐形成了以复现标模气动力数据或流场特征为主要手段的风洞试验能力和CFD模拟能力相互确认方法[3],以此评估当前CFD方法在求解复杂气动问题时的能力,其核心目标是实现准确的巡航阻力预测,这也是当前工业飞机设计领域对雷诺平均Navier-Stokes(RANS)方法的主要需求。以客机为例,参考影响力较为广泛的历届AIAA阻力预测会议(Drag Prediction Workshop, DPW)[4-5]可以发现,随着RANS方法的日趋成熟,其研究内容已不再局限于气动力预测,还延伸出了分离流动预测、湍流模型适用性、收敛解的网格生成要求等主题,其中网格的发展和使用始终都是不可忽视的关键研究课题。
从第三届阻力预测会议开始,嵌套网格(Chimera Grids)就已作为标准网格的一部分对外发布[6-7]。可见伴随着结构和非结构网格的讨论,融合了贴体网格和笛卡尔网格优势的嵌套网格已经成为降低网格生成难度,优化网格拓扑结构并平衡网格量,同时获得精确气动力预测值的策略之一。本文的工作即在讨论结构化嵌套网格结合传统CFD方法对于跨声速客机构型的气动力预测能力,评估嵌套网格相比于传统对接网格的优劣,验证相关求解器的可信度,为今后相关研究提供参考。
由于嵌套网格并非AeCW-1的标准网格,遵循组委会“网格生成指南”自主研制了规模以3.3倍增长的稀-中等-密-极密四套结构化嵌套网格系列,并采用近年开源的NASA CFL3D求解器和自研OFS3D求解器开展了网格收敛性和抖振特性研究,并与组委会对接网格结果进行了对比研究。
1 CHN-T1气动标模CHN-T1(China-Transport 1)[3]是由中国空气动力研究与发展中心(CARDC)研发的用于风洞试验和CFD可信度确认的、具有窄体机身-超临界机翼等几何特征的单通道客机标模。设计全机外形(BWHVNP)包含机身、机翼、平尾、垂尾、短舱、挂架及起落架整流包等部件。
为了突出流场主要特点,此次AeCW-1采用简化的计算模型,基础研究构型为“机身-机翼-平尾-垂尾”构型(BWHV,即Config.1)。该构型自2013年以来经过了全面的风洞试验,气动力和流场数据可靠。为模拟风洞干扰,带支撑构型(Config.2)也是研究构型之一,用于支撑、静气弹变形和雷诺数影响的计算。表 1列出了风洞试验模型及本文计算采用的主要参数。
| 表 1 BWHV风洞试验构型主要参数 Table 1 Primary parameters of BWHV configuration |
|
|
目前,如何进行分区界面的计算信息传递是CFD网格技术的核心,主要的处理方式包括对接(1-1 Blocking)、拼接(Patching)和嵌套等。其中,嵌套网格方法[8]具备灵活的分区策略,各部分通过彼此的交错、重叠区域进行信息传递,从根本上降低了网格拓扑的生成难度,不但实现了网格量的合理分配,而且能够更好地保证物面网格和空间体网格的正交性;此外在处理有活动部件的气动外形(如直升机旋翼)时,嵌套网格具有天然优势。这些也使得嵌套网格方法成为越来越多的商用和自研求解器包含的基础功能之一。
参照网格收敛性对网格规模的要求,首先采用自下而上的网格生成策略对BWHV构型生成中等密度网格,再按相同比例系数在空间三个方向分别进行加密或稀疏得到四套密度不同的网格系列。
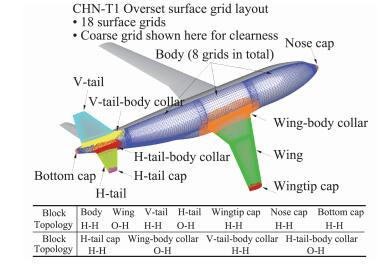
2.1 中等网格采用Pointwise软件生成了如图 1所示物面网格。全机共分为20个网格块(18块贴体空间网格+2块远场网格),图中表格给出了各块贴体空间网格的拓扑结构。考虑到流动在翼面两端都有较强的三维效应,所以将翼根和翼梢处的物面网格均沿展向截去,分别用翼根套环(Collar)和翼尖帽(Cap)网格填充,避免在可能的复杂流动区域进行边界插值操作。此外,与DPW会议所采用的机身网格一体化生成策略(图 2)不同,为了避免机身网格“浸入”翼面内部,降低挖洞难度,本文对机身物面网格采用分块生成策略,这样可以自主控制翼身连接处各块网格的边界,便于进行网格边界插值。
|
图 1 CHN-T1 BWHV构型表面嵌套网格分布 Fig.1 Overset surface grid layout for BWHV configurations of CHN-T1 |

|
图 2 DPW机身一体化嵌套网格生成策略 Fig.2 Compact strategy for wing-body grid generation adopted by DPW series |
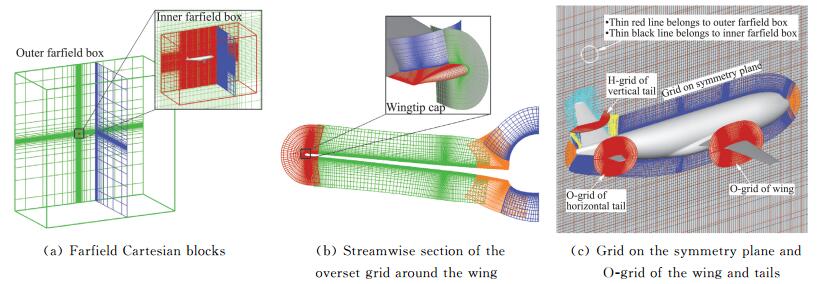
对于机身以及各个翼面的物面网格,首先采用超限插值(TFI)方法生成代数网格,再利用Thomas-Middlecoff方法对其进行椭圆型方程迭代,直至最大残值降至5×10-6量级;而机头、机尾、翼尖和翼身连接处物面网格通过求解双曲型方程推进得到;贴体空间网格则通过沿物面法向推进求解双曲型方程得到。以上方法可保证物面附近网格较好的正交性和较高的整体网格质量。远场网格分为内层和外层两块,均为直角笛卡尔网格。为了更好的进行网格装配,内层网格在机体附近进行了适当加密,加密标准是网格间距略小于贴体空间网格的最外层。图 3展示了几处典型的局部网格形态。
|
图 3 典型区域网格形态 Fig.3 Grid configuration at typical regions |
为了进行网格收敛性研究,以中等密度网格为基础,在各个方向进行加密或加粗进而得到密网格、特密网格和稀网格,加密或加粗系数分别为1.5和0.75。图 4给出了机头、翼身套环和主翼单块物面网格疏密情况对比,其中i、j、k分别对应三个维度的网格点数,而“×M”(Medium)和“×F”(Fine)分别代表相应维度点数及该块网格量与中等网格或密网格对应值的倍数关系。值得注意的是,各套网格的翼身套环(collar)存在一定差别:该块机身网格由双曲型方程推进求解得到,无法精确保证推出距离;而机翼网格截取自wing网格块,由于不同网格的网格间距差别较大,为了满足网格点倍数的要求,导致网格在机翼和机身处的推出距离不同。

|
图 4 网格序列局部对比 Fig.4 Comparison of local surface grid |
表 2给出了上述自研嵌套网格系列与DPW-IV会议标模CRM翼身-平尾构型嵌套网格[7]的参数对比,可见自研嵌套网格参数与DPW及AeCW-1组委会中等结构化对接网格相近。
| 表 2 CHN-T1 BWHV构型网格序列与DPW-IV CRM翼身-平尾构型网格序列参数对比 Table 2 Grid comparison of CHN-T1 BWHV configuration and DPW-IV CRM wing-body-tail configuration |
|
|
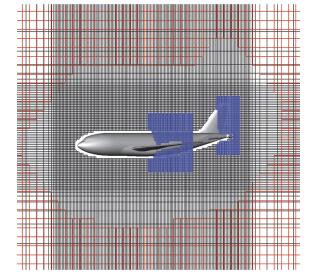
嵌套网格生成之后,要对网格进行挖洞和插值,合称网格装配(Grid Assembly)。挖洞使得“浸入”物面内部的网格单元从计算域中移除,常见方法有洞映射(Hole Map)方法[9]和射线(X-ray)求交法[10]等,插值使得未赋予特殊边界条件的网格块边界单元获得流场信息,常见方法有模板游走法(Stencil Walking) [11-12]、反变换法(Inverse Map)[13]和自适应叉树法(Alternating Digital Tree,ADT)[14]等。本文利用射线求交法及反变换方法进行网格装配。在进行网格挖洞时,由于采用了机身网格分块生成策略,因此只需要对远场笛卡尔网格进行挖洞。为了保证洞边界网格单元大小匹配,使用洞面优化技术,将机体表面一定距离之内的远场网格点均作为洞点挖去。挖洞结果如图 5所示。
|
图 5 挖洞后网格形态 Fig.5 Grid after hole cutting |
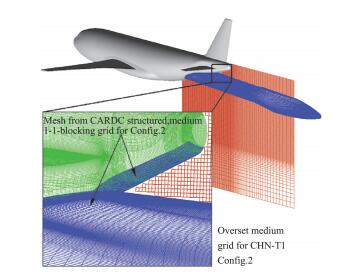
由于支撑与后体机身夹角过小,很难利用双曲型方程生成空间贴体网格,故采用截取对接网格的方法生成。支撑网格及局部细节如图 6所示。首先移植组委会中等结构化对接网格对应位置处的部分贴体网格至缝隙处(细节图中蓝色网格),再生成一块笛卡尔网格填补剩余空间(细节图中红色网格)。其余位置拓扑及网格均与基础构型保持一致,该网格简记为M2网格。
|
图 6 带支撑构型支撑处网格 Fig.6 Grid details around the support of Config.2 |
考虑静气弹变形的Case2c在带支撑构型的基础上增加了机翼变形。但本文暂未实现自动化的网格变形技术,故未针对Case2c生成嵌套网格。下文仅采用CFL3D在组委会提供的各迎角对接网格上进行了数值评估,以讨论静气弹变形的影响。
3 求解器与计算平台 3.1 求解器CFL3D结构化网格求解器[15]由NASA Langley研究中心于20世纪80年代初开始开发,并于2017年在GitHub上开源。CFL3D在有限体积框架下求解三维可压缩非定常RANS方程,能够处理结构化对接、拼接和嵌套网格,有多种湍流模型可供选择。
OFS3D结构化嵌套网格求解器由课题组自主研发,具有二维/三维,定常/非定常,薄层近似/完全N-S方程求解能力,目前已植入了多种空间离散格式及时间推进格式,同样拥有多种常用湍流模型可以调用。
为保证计算结果的可比性,两种求解器均调用SA和SST k-ω湍流模型进行数值模拟。RANS方程对流项和压强项采用二阶迎风Roe格式求解(不加熵修正),并统一采用完全N-S形式和二阶中心差分格式处理粘性项,时间推进格式选用隐式近似因式分解方法。多重网格技术用于加速收敛,CFL数因求解器和网格不同,采用2.0~5.0之间的值,事实证明稳定性和收敛性良好。为论述简洁,两求解器分别简记为“C”和“O”。
3.2 计算平台两种求解器均采用Openmpi-v1.8进行并行编译及计算,并在课题组自建高性能集群上运行。集群搭载主频3.3 GHz的Intel志强系列CPU,运行环境为64位Linux,计算能力约为14 Tflops。
计算效率方面,由于CFL3D不具备网格自动再分区策略,难以实现负载平衡,仅能调用20个线程,计算效率较低。而OFS3D可根据计算总线程数和网格进行自动网格再分,从而实现负载平衡及高加速比。表 3给出了中等网格下调用相同计算资源(20线程)且达到相近收敛阶时两程序计算效率的对比(单位:s),可见若增加计算资源,OFS3D计算效率还将提高,优势更加明显。
| 表 3 BWHV风洞试验构型主要参数 Table 3 Primary parameters of BWHV configuration |
|
|
由于计算资源和篇幅的限制,主要对基础构型的网格收敛性和抖振特性进行重点研究,同时对模型支撑干扰和静气弹影响进行初步计算分析,具体计算状态见表 4。CFL3D由于计算效率较低,暂未完成SA模型特密网格的计算,对于SST模型也仅完成了中等网格的计算。
| 表 4 本文计算状态 Table 4 Simulation conditionsof present cases |
|
|
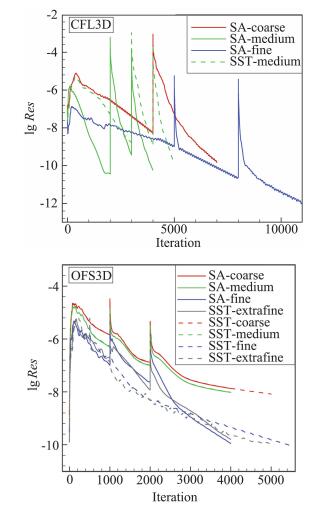
采用Richardson外插方法[6]进行气动力系数收敛性研究。该方法要求在网格系列参数等效的情况下进行定升力计算,且各套网格的残差收敛到相同的量级。但由于计算资源有限,不同密度网格很难收敛到相同量级,故本文通过力系数波动大小来判断是否达到可接受的收敛状态,具体的即升力系数≤±10-3,阻力系数≤±10-4,俯仰力矩系数≤±10-3。图 7给出了不同求解器进行网格收敛性计算时密度残差平均值的收敛曲线。如果求解器具备二阶精度,当以网格单元数的-2/3次幂(-1/3次幂代表网格尺度,平方对应二阶精度)为横坐标,预测值为纵坐标时,若得到一条直线,则可定性说明求解器和求解方法整体满足精度且具备较好的收敛性,且可通过外插得到网格收敛时的结果。参考AIAA阻力预测会议的处理方式[6-7],采用最密的两套网格计算结果进行外插。
|
图 7 两种求解器密度残差收敛历史 Fig.7 Convergence history of density residual by two different solvers |
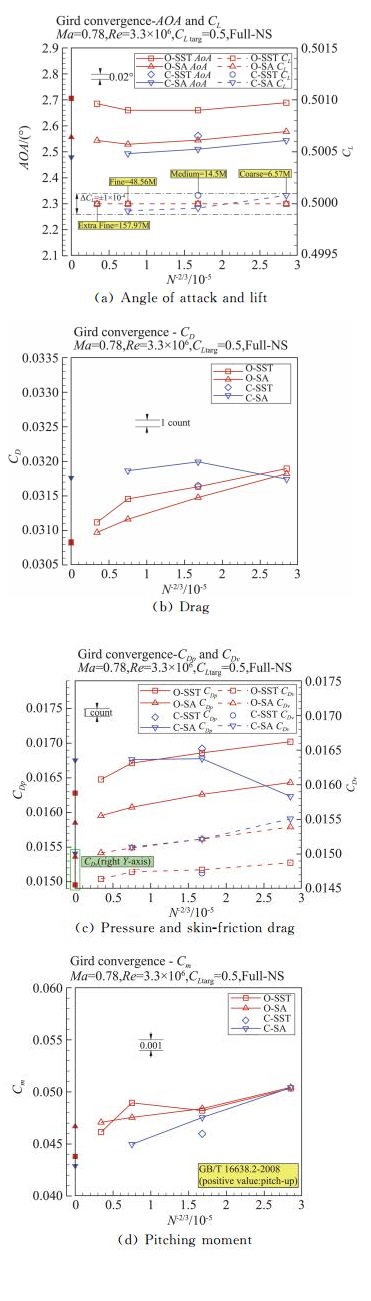
图 8分别给出了迎角、总阻力、阻力分量系数和俯仰力矩系数的收敛性和插值结果。可见,在升力系数满足收敛要求的情况下:(1) OFS3D求解器对各个气动系数的预测均表现出了较好的线性特征,除了迎角和俯仰力矩系数在较密网格上的微小拐折,且采用两种湍流模型时的总阻力插值点基本重合;(2) CFL3D采用SA模型预测的迎角和俯仰力矩系数收敛性较好,但阻力线性度较差,其稀网格的明显误差主要来源于压差阻力,而采用SST模型时,总阻力和阻力分量与OFS3D-SST结果基本一致;(3)对于OFS3D迎角和俯仰力矩系数的转折,这可能与远离力矩中心的微小分离流动对密网格较敏感有关;(4)基于本文的嵌套网格序列,SST湍流模型的收敛性整体上不如SA湍流模型。
|
图 8 CHN-T1 BWHV构型网格收敛性结果:气动特性 Fig.8 Grid-convergence study for CHN-T1 BWHV: aerodynamic characteristics |
表 5给出了各个气动系数的Richardson外插结果。为与对接网格对比,采用CFL3D求解器进行了组委会结构化对接网格的计算及外插(表中“C(1-1)”列)。采用CARDC TRIP 3.0求解器104亿结构对接网格(N-2/3×105值已达0.02)70000步计算结果[16]进行对比可以发现:(1)整体上看,OFS3D求解器两种湍流模型的外插结果更接近百亿规模网格的计算结果,表现出了较好的一致性和收敛性;(2)基于嵌套网格的CFL3D-SA外插迎角、阻力和俯仰力矩系数与百亿网格解差别稍大,阻力系数误差约3%,但更接近试验阻力系数0.03197;(3)基于对接网格的CFL3D-SST也获得了较好的收敛状态,各气动系数与百亿网格解较接近;(4)除OFS3D-SA,各结果俯仰力矩系数较百亿网格解普遍偏小。整体上看,本文生成的网格序列对于收敛性研究是合适的,采用的求解器也具有较高的可靠性。
| 表 5 CHN-T1 BWHV构型Richardson外插结果 Table 5 Richardson extrapolation of BWHV configuration |
|
|
由于本文网格序列完全由手动方式分别生成,考虑到局部网格质量和网格装配精度等因素,各规模网格的参数并不完全等效,加之收敛量级存在差别,以上因素均会对网格收敛性曲线的单调性产生一定影响。
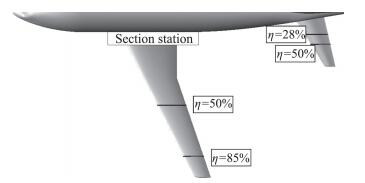
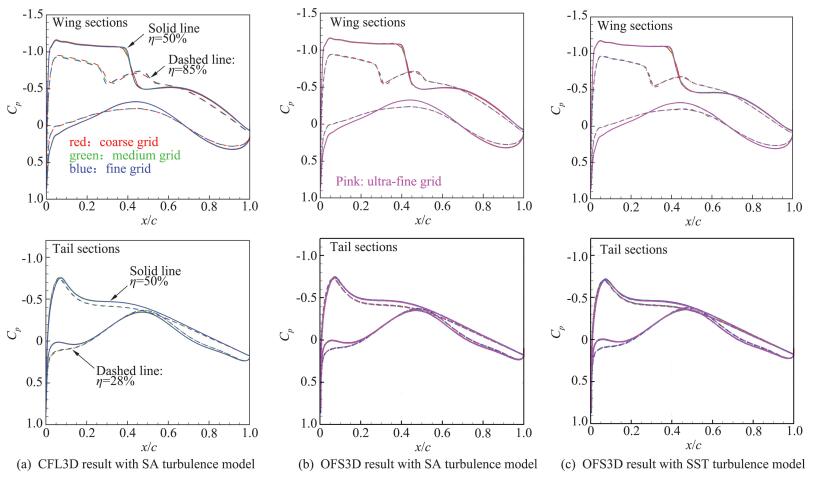
4.1.2 翼面压力分布分别截取机翼和平尾各两个站位(图 9)的压力分布,其随网格密度增加的变化趋势如图 10所示。对于同一求解器、同一湍流模型来说,不同规模网格的差别仅当翼面存在较强激波时(机翼50%)表现得较为明显,随着网格密度的增大,激波厚度逐渐减小。这一趋势在CFL3D求解器上表现得较为明显,而OFS3D变化较小,且密网格和极密网格的计算结果几乎没有变化。
|
图 9 CHN-T1 BWHV构型机翼尾翼站位示意 Fig.9 Section stations of CHN-T1 BWHV wing and tail |
|
图 10 CHN-T1 BWHV构型网格收敛性研究:截面压力分布 Fig.10 CHN-T1 BWHV grid-convergence study: sectional pressure distribution |
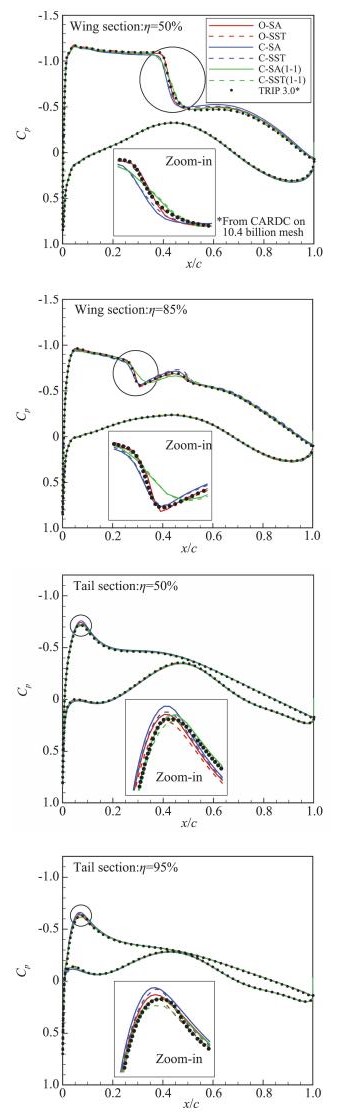
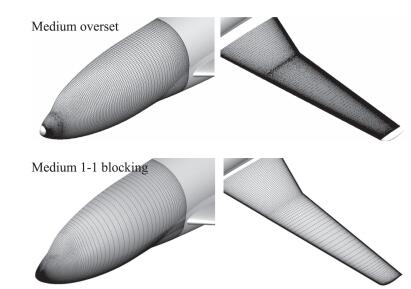
图 11给出了中等嵌套和对接网格上,不同求解器、不同湍流模型得到的截面压力分布对比。仍以TRIP 3.0求解器104亿结构网格计算结果为参照。可以看出,同一求解器在相同网格类型下两种湍流模型得到的压力分布相近(SST相较于SA预测的激波位置稍靠前、前缘吸力峰稍高),也即主要差别来源于求解器和网格类型。对于嵌套网格,CFL3D相较于OFS3D预测的激波位置更靠前、厚度更大,同时前缘吸力峰也更高,OFS3D预测结果与百亿网格解吻合较好。而对接网格的激波分辨率要明显低于嵌套网格,85%机翼截面处的弱激波抹平严重,这也正是嵌套网格相较于对接网格的优势之一。如图 12所示,由于嵌套网格不存在近场密网格向远场辐射的问题,在网格量相当时,嵌套网格可将更多的单元分布于机头、机翼等关键位置和流动复杂处,大大提高了局部流场的分辨率。由压力分布对比可见,中等规模嵌套网格能够满足求解器后续研究需求,但中等规模对接网格在激波处的网格密度稍显不足。
|
图 11 中等网格CHN-T1 BWHV构型截面压力分布对比 Fig.11 Comparison of CHN-T1 BWHV sectional pressure distribution in medium grid |
|
图 12 中等嵌套和对接网格局部分布对比 Fig.12 Comparison of local grid distribution in medium overset and 1-1 blocking grid |
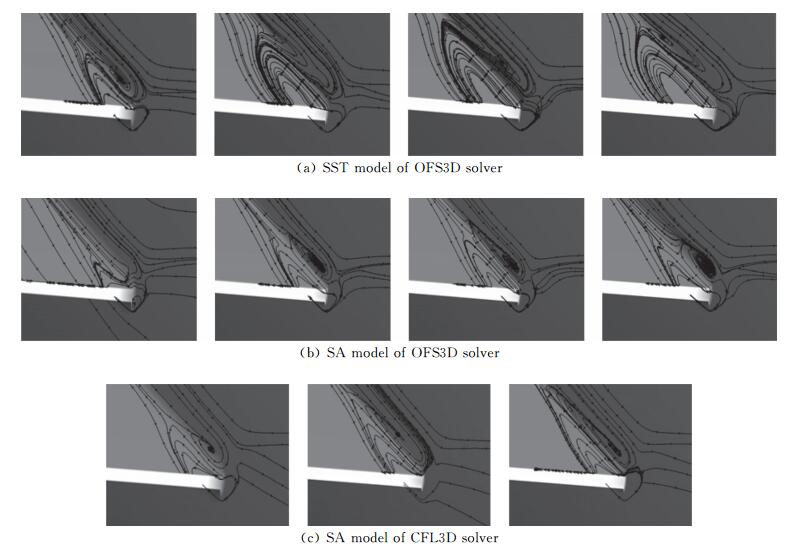
跨声速客机构型的一个典型流动特征就是容易在机翼翼根后缘和机身之间出现分离泡,准确再现这个区域的流动特征也成为了历届DPW会议的主题之一[6-7]。CHN-T1标模在设计时考虑了翼根整流[3],因此在风洞试验中未见明显的分离流动,分离区明显小于DLR-F6翼身组合体构型[6]。图 13给出了该区域的计算表面流线图,从左至右分别为嵌套网格的C/M/F/E-F网格计算结果。可见相对于模型整体尺寸,分离泡尺度很小(约2~9倍后缘厚度)。从稀网格到中等网格,分离在展向和流向有明显扩大,随后在更密的网格上基本趋于稳定。特别地,OFS3D-SST的分离区在密网格上仍有明显扩展,并在特密网格上有所收缩,这也导致了其俯仰力矩在密网格上的拐折(图 8(d))。对于同一规模的网格,CFL3D-SA的分离区在流向大于OFS3D-SA;OFS3D-SST的分离区在流向和展向均明显大于OFS3D-SA的计算结果。
|
图 13 CHN-T1 BWHV构型网格收敛性结果:翼身分离泡 Fig.13 CHN-T1 BWHV grid-convergence study: wing-body separation bubble |
开展各构型气动特性随迎角变化的计算,不但易与风洞试验结果直接对比,掌握支撑、气弹变形等对气动特性的影响程度,进一步评估求解器的可信度,还可以检验设计抖振边界,反向校核风洞试验的准确性。经过网格收敛性研究,本节计算结果均采用中等规模网格获得。试验数据来自文献[17]。
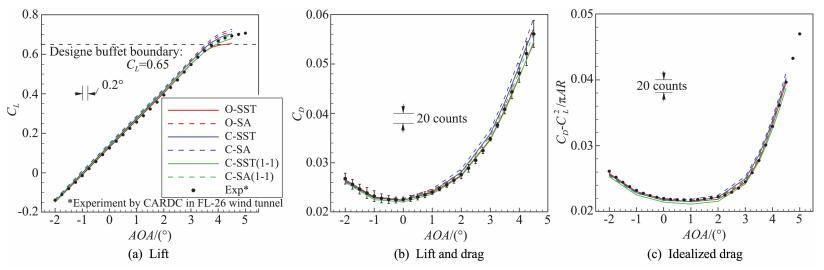
4.2.1 基础构型气动特性图 14给出了升阻力系数和理想阻力系数与试验数据的对比。可以发现,各求解器得到的升力线斜率与试验值吻合较好,并且较理想地复现了非线性段起始区域;OFS3D虽然在线性段与试验值最为吻合,但最大升力系数明显偏低。从试验数据和数值模拟结果可以判断,CHN-T1标模的抖振边界大于1.5倍巡航升力系数(即0.65),达到设计状态[3]。
|
图 14 CHN-T1 BWHV构型气动特性:升阻力 Fig.14 Aerodynamic characteristics of CHN-T1 BWHV: lift and drag |
除嵌套网格CFL3D-SA外,其余求解器和湍流模型得到的阻力系数基本全部落在了试验误差带内,而各预测值与理想阻力系数试验值均吻合较好。整体来看,SA模型得到的最大升力系数和阻力系数均较SST模型大。
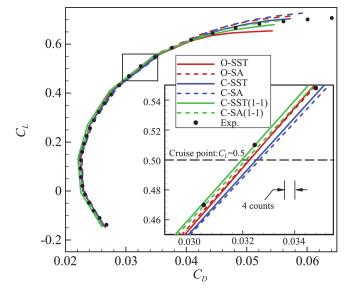
图 15给出了升阻极曲线与试验数据的对比。各预测值基本聚集在试验结果附近,仅在迎角较大时差别稍大。从设计点附近的结果可以看出,各预测值均与试验值吻合较好,相互之间的最大差别在8counts以内,其中OFS3D和对接网格CFL3D的结果与试验值最为接近。
|
图 15 CHN-T1 BWHV构型气动特性:升阻极曲线 Fig.15 Aerodynamic characteristics of CHN-T1 BWHV: drag polar |
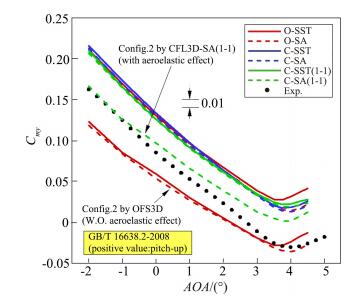
虽然基础构型升阻特性预测结果较为理想,但由于没有考虑模型支撑及静气弹变形的影响,俯仰力矩特性与试验数据相差较大。为此,分别采用OFS3D在嵌套网格上对带支撑构型,以及CFL3D在对接网格上对考虑静气弹变形的带支撑构型进行评估。图 16给出了三种构型的各组预测结果。可见,对于BWHV构型,各组结果重合度较好,但相比试验值明显偏大;采用考虑静气弹变形的带支撑构型在小迎角范围内能够得到更准确的俯仰力矩特性,但迎角大于3°后与试验值仍存在较大差距,而仅考虑支撑干扰的构型在此迎角范围的预测值与试验值则较为吻合。有关模型支撑和静气弹变形的影响仍需开展进一步的计算研究。
|
图 16 CHN-T1气动特性:俯仰力矩 Fig.16 Aerodynamic characteristics of CHN-T1: pitching moment |
嵌套网格相比于对接网格简化了拓扑划分难度,不存在近场密网格的远场辐射问题。对于跨声速运输机构型,能够将更多的网格布置于机头、机翼等关键部位,提高激波等复杂流场结构的分辨率,同时保持计算可靠性。本文自研的嵌套网格系列能够满足网格收敛性研究的需求,但网格系列的构造方式仍有待改进,如何自动化地实现网格布点及密度调整是今后研究的重点,这样不但能够确保网格参数等效,还可以提高网格生成质量和效率。经过计算分析,对于超临界运输机构型的数值模拟,初步得到以下结论:
(1) 气动力和力矩系数在网格系列上存在斜率明显的收敛曲线,较大规模的网格不但能够得到更接近收敛的气动特性预测值,翼面等关键部位较小的网格尺度还能有效提高前缘吸力峰、激波和分离区的分辨率。
(2) 自研OFS3D求解器前后处理和计算效率较高,具备较好的嵌套网格收敛性和可靠性。而CFL3D嵌套网格功能和工具相对缺乏,计算效率较低。同时,嵌套网格CFL3D-SA计算结果并不理想,其嵌套网格计算能力有待进一步验证。
(3) 初步分析表明,湍流模型对压力分布、分离区大小和最大升力系数等的预测有一定影响,对分离区大小影响较大。更深入的湍流模型精度和可信度比较还需要进一步的计算分析。
(4) 对于采用常规测力方法的风洞试验,数值模拟时有必要考虑模型支撑和机翼静气弹变形的影响,这对于获得准确的力矩特性十分必要。
致谢: 感谢清华大学航空航天学院李浩然同学提供的组委会结构密网格CFL3D求解器计算结果。西安理工大学土木建筑工程学院聂胜阳老师在标模计算过程中与作者进行了积极讨论,在此一并致谢!
| [1] |
OBERKAMPFA W L, TRUCANOB T G. Verification and validation in computational fluid dynamics[J]. Progress in Aerospace Sciences, 2002, 38: 209-272. DOI:10.1016/S0376-0421(02)00005-2 |
| [2] |
LI L, BAI W, LIANG Y H. Recent Efforts for Credible CFD Simulations in China[J]. Modelling and Simulation in Engineering, 2011, 861272. |
| [3] |
余永刚, 周铸, 黄江涛, 等. 单通道客机气动标模CHN-T1设计[J]. 空气动力学学报, 2018, 36(3): 505-513. YU Y G, ZHOU Z, HUANG J T, et al. Aerodynamic design of a standard model CHN-T1 for single-aisle passenger aircraft[J]. Acta Aerodynamica Sinica, 2018, 36(3): 505-513. DOI:10.7638/kqdlxxb-2018.0072 (in Chinese) |
| [4] |
阎超, 席柯, 袁武, 等. DPW系列会议述评与思考[J]. 力学进展, 2011, 41(6): 776-784. YAN C, XI K, YUAN W, et al. Review of the drag prediction workshop series[J]. Advances in Mechanics, 2011, 41(6): 776-784. (in Chinese) |
| [5] |
王运涛. DPW IV~DPW VI数值模拟技术综述[J]. 航空学报, 2018, 39(4): 021836. WANG Y T. An overview of DPW IV~DPW VI numerical simulation technology[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(4): 021836. (in Chinese) |
| [6] |
SCLAFANI A J, VASSBERG J C, HARRISON N A, et al. CFL3D/OVERFLOW results for DLR-F6 wing/body and drag prediction workshop wing[J]. Journal of Aircraft, 2008, 45(3): 762-780. DOI:10.2514/1.30571 |
| [7] |
SCLAFANI A J, DEHAAN M A, VASSBERG J C, et al. Drag prediction for the common research model using CFL3D and OVERFLOW[J]. Journal of Aircraft, 2014, 51(4): 1101-1117. DOI:10.2514/1.C032571 |
| [8] |
BENEK J A, STEGER J L, DOUGHERTY F C, et al. Chimera: a grid-embedding technique[R]. AEDC-TR-85-64, 1986.
|
| [9] |
CHIU I T, MEAKIN R. On automating domain connectivity for overset grids[R]. AIAA-95-0854, 1995.
|
| [10] |
LABOZZETTA W F, GATZKE T D, ELLISON S, et al. MACGS-towards the complete grid generation system[R]. AIAA-94-1923, 1994.
|
| [11] |
NIRSCHL H, DWYER H A, DENK V. A chimera grid scheme for the calculation of particle flows[R]. AIAA-94-0519, 1994.
|
| [12] |
STEGER J L, DOUGHERTY F C, BENEK J A. A chimera grid scheme[C]//GHIA K N. Advances in Grid Generation. New York: ASME FED, 1983, 5: 59-69.
|
| [13] |
MEAKIN R L. A new method for establishing intergrid communication among systems of overset grids[R]. AIAA-91-1586, 1991.
|
| [14] |
BONET J, PERAIRE J. An alternating digital tree (ADT) algorithm for 3D geometric searching and intersection problems[J]. International Journal for Numerical Methods in Engineering, 2010, 31(1): 1-17. |
| [15] |
KRIST S L, BIEDRON R T, RUMSEY C L. CFL3D User's Manual (Ver. 5.0)[R]. 2nd ed. The NASA Langley Research Center; 1998. Report No.: NASA/TM-1998-208444. Also the CFL3D Version 6 Home Page[R/OL]. Hampton, VA: the NASA Langley Research Center, (2017-07-10).[2018-09-25]. Available from: https://cfl3d.larc.nasa.gov/
|
| [16] |
李伟, 王运涛, 洪俊武, 等. 采用TRIP3.0模拟CHN-T1模型气动特性[J]. 空气动力学学报, 2019, 37(2): 272-279. LI W, WANG Y T, HONG J W, et al. Aerodynamic characteristics simulation of CHN-T1 model with TRIP3.0[J]. Acta Aerodynamica Sinica, 2019, 37(2): 272-279. DOI:10.7638/kqdlxxb-2018.0225 (in Chinese) |
| [17] |
李强, 刘大伟, 许新, 等. CHN-T1标模2.4米风洞气动特性试验研究[J]. 空气动力学学报, 2019, 37(2): 337-344. LI Q, LIU D W, XU X, et al. Experimental study of CHN-T1 standard model aerodynamic characteristic in 2.4 m transonic wind tunnel[J]. Acta Aerodynamica Sinica, 2019, 37(2): 337-344. DOI:10.7638/kqdlxxb-2018.0099 (in Chinese) |
 2019, Vol. 37
2019, Vol. 37


