2. 华北水利水电大学 土木与交通学院, 郑州 450045;
3. 海南大学 土木与建筑工程学院, 海口 570228
2. School of Civil Engineering and Transportation, North China University of Water Resources and Electric Power, Zhengzhou 450045, China;
3. College of Civil Engineering and Architecture, Hainan University, Haikou 570228, China
受来流湍流的影响,处于大气边界层中的桥梁都会受到抖振力的作用。抖振力与来流的脉动风特性、静力三分力系数、气动导纳函数等有关。气动导纳作为联系脉动风与抖振力的传递函数,其准确性对于桥梁抖振具有重要的意义。
针对于桁架桥,Davenport[1]用速度互相关来计算阻力气动导纳,而升力气动导纳采用基于势流理论推导得到的Sears函数。对于流线型的断面,在没有试验结果的前提下,Sears函数经常被采用。随着试验技术的进步,大量的研究者借助于风洞试验进行气动导纳的研究。但是风洞试验方法通常存在湍流积分尺度明显偏小,低频成份显著不足[2-3],难以得到任意目标风场,可重复性差等问题。
在风场效应可以线性叠加的情况下,气动导纳可以利用阶跃响应函数得到。在机翼理论里,Wagner[4]和Küssner[5]通过考察机翼姿态的阶跃变化、以及穿过半无限阵风场的气动力行为,分别得到了Wagner函数和Küssner函数,用以描述机翼所受到的气动力随时间的演化。通过Fourier变化,Garrick[6]证明了Wagner函数和频域里描述气动自激力的Theodorsen函数互成Fourier变换对。同样Küssner函数和Sears函数也成Fourier变换对。因此,如果能得到Wagner函数和Küssner函数,通过Fourier变换就可以得到Theodorsen函数和Sears函数。Caracoglia和Jones[7]最早设计了一套装置识别得到不同断面的Wagner函数。而Küssner函数的试验识别,由于无法得到理想的阶跃风场,至今还没有在风洞试验里实现过。
至今为止,CFD已经广泛应用于桥梁抗风实践中。但与CFD在静风力系数[8-9]、涡激振动[10-11]、颤振导数识别[9, 12]等方面的广泛应用相比较,气动导纳的数值研究却鲜有报道。Hejlesen等[13]利用离散涡方法,识别了四种桥梁断面的气动导纳函数;唐煜等[14]基于雷诺平均方法,在简谐来流中识别了平板断面和箱梁断面的气动导纳;Bruno等[15]利用阶跃函数的方法计算了机翼断面和箱梁断面的气动力随时间演化的曲线并识别得出各自的气动导纳函数;张伟峰等[16-17]在简谐来流与湍流中利用CFD研究了桥梁断面气动导纳与湍流参数的关系,对数值计算结果与风洞试验结果进行了比较。
风洞试验中存在的问题,可在合理的CFD模拟中克服,从而有望提高气动导纳的识别精度。但气动导纳的CFD识别研究尚处于起步阶段,不同识别方法的计算策略、适应性、计算精度等问题尚没有研究者进行研究。本文基于前期研究成果,对三种气动导纳数值识别方法的计算策略、适应性等问题进行研究。
本文采用二维SST k-ω湍流模型,首先研究了简谐脉动流、湍流和竖向阶跃流在计算域内的传播特性和数值计算方法,然后在这三种来流下分别计算了平板断面和箱梁断面的非定常气动力,并识别得出各自的气动导纳函数和阶跃响应函数,最后分析比较了不同方法的适应性以及计算效率。本文三种气动导纳数值识别方法的研究,对提高气动导纳数值识别精度以及工程应用具有很好的参考价值。
1 气动导纳识别方法概述 1.1 简谐脉动流识别方法处于二维脉动风场中的桥梁断面,受到的抖振力的频域表达式为[18]:
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_b}\left( \omega \right) = \frac{1}{2}\rho UB{{\mathit{\boldsymbol{\bar C}}}_{{\rm{ae}}}}V'\left( \omega \right)\\ {{\mathit{\boldsymbol{\bar C}}}_{{\rm{ae}}}} = \left[ {\begin{array}{*{20}{c}} {2{C_D}{\chi _{Du}}\left( K \right)}&{\left( {{{C'}_D} - {C_L}} \right){\chi _{Dw}}\left( K \right)}\\ {2{C_L}{\chi _{Lu}}\left( K \right)}&{\left( {{{C'}_L} + {C_D}} \right){\chi _{Lw}}\left( K \right)}\\ {2B{C_m}{\chi _{mu}}\left( K \right)}&{B{{C'}_m}{\chi _{mw}}\left( K \right)} \end{array}} \right] \end{array} $ | (1) |
其中:Fb(ω)=[Fx(ω) Fz(ω) Mθ(ω)]T为抖振力矢量;V′(ω)=[u(ω) w(ω)]为脉动风速矢量,u(ω)、w(ω)分别为顺风向和横风向的脉动速度分量的频域表示;Cae为气动力系数矩阵;CD、CL、Cm为静力三分力系数;C′D、C′L、C′m为三分力系数关于攻角的导数;χjg(j=D,L,m; g=u,w)为复气动导纳函数;B为断面的宽度;K=ωB/U为用圆频率表示的无量纲折算频率。
当仅考虑竖向脉动风作用时,由式(1)可以得到升力的功率谱密度:
| $ {S_L} = {\left( {\frac{1}{2}\rho UB} \right)^2}{\left( {{{C'}_L} + {C_D}} \right)^2}{\left| {{\chi _{Lw}}} \right|^2}{S_w} $ | (2) |
其中:Sw为竖向脉动风的功率谱密度,|χLw|2为气动导纳模的平方。
根据式(2)可以得到|χLw|2的表达式:
| $ {\left| {{\chi _{Lw}}} \right|^2} = \frac{{{S_L}}}{{{{\left( {\frac{1}{2}\rho UB} \right)}^2}{{\left( {{{C'}_L} + {C_D}} \right)}^2}{S_w}}} $ | (3) |
当考虑机翼断面在竖向脉动风下的作用时,|χLw|2即Sears气动导纳函数,可以近似表示为[19]:
| $ {\left| {{\chi _s}\left( k \right)} \right|^2} = \frac{1}{{1 + {\rm{ \mathsf{ π} }}K}} $ | (4) |
通过在来流中给定单一频率的竖向简谐脉动,在得到了断面的气动力时程后,就可以根据公式(3)识别出气动导纳。该法识别结果具有较好的平滑性,但一次只可以识别出一个频率点的气动导纳。
1.2 湍流识别方法对于湍流,由于水平脉动风的影响,无法直接从式(1)中得到气动导纳。这里我们采用互谱识别方法[20]。升力的自功率谱密度为:
| $ \begin{array}{*{20}{c}} {{S_L} = {{\left( {\frac{1}{2}\rho UB} \right)}^2}\left[ {4C_L^2{{\left| {{\chi _{Lu}}} \right|}^2}{S_u} + } \right.}\\ {\left. {{{\left( {{{C'}_L} + {C_D}} \right)}^2}{{\left| {{\chi _{Lw}}} \right|}^2}{S_w}} \right]} \end{array} $ | (5) |
升力关于水平向及竖向脉动风的互功率谱为:
| $ \begin{array}{*{20}{c}} {{S_{Lu}} = {{\left( {\frac{1}{2}\rho UB} \right)}^2}\left[ {4C_L^2{\chi _{Lu}}{S_u} + } \right.}\\ {\left. {{{\left( {{{C'}_L} + {C_D}} \right)}^2}{\chi _{Lw}}{S_{wu}}} \right]} \end{array} $ | (6) |
| $ \begin{array}{*{20}{c}} {{S_{Lw}} = {{\left( {\frac{1}{2}\rho UB} \right)}^2}\left[ {4C_L^2{\chi _{Lu}}{S_{uw}} + } \right.}\\ {\left. {{{\left( {{{C'}_L} + {C_D}} \right)}^2}{\chi _{Lw}}{S_w}} \right]} \end{array} $ | (7) |
由此可以得到升力的气动导纳:
| $ {\chi _{Lu}} = \frac{{{S_w}{S_{Lu}} - {S_{wu}}{S_{Lw}}}}{{\rho UB{C_L}\left( {{S_u}{S_w} - {S_{wu}}{S_{uw}}} \right)}} $ | (8) |
| $ {\chi _{Lw}} = \frac{{{S_u}{S_{Lw}} - {S_{uw}}{S_{Lu}}}}{{\frac{1}{2}\rho UB\left( {{{C'}_L} + {C_D}} \right)\left( {{S_u}{S_w} - {S_{uw}}{S_{wu}}} \right)}} $ | (9) |
其中:SLu、SLw为升力关于水平和竖向脉动风的互功率谱;Suw、Swu为水平脉动风和竖向脉动风的互谱。
相比于简谐脉动流方法,湍流识别方法可以一次性得到所有频率范围内的气动导纳函数。但是,该法在某一频率点的识别精度严重依赖于该频率的信号强度,识别结果的平滑性很差,应用前需要进行处理。本文仅讨论竖向脉动风关于升力的气动导纳,其它气动导纳可以采用相同的方法进行研究。
1.3 Küssner识别方法以水平速度U飞行的机翼,穿过幅值为w0的竖向阶跃阵风时,Küssner得到了其气动力随时间演变的公式[5]:
| $ L\left( s \right) = \frac{1}{2}\rho {U_2}B\left( {2{\rm{ \mathsf{ π} }}} \right)\frac{{{w_0}}}{U}\psi \left( s \right) $ | (10) |
其中:s=2tU/B为无量纲时间,ψ(s)为Küssner函数,可以近似表示为[21]:
| $ \psi \left( s \right) = 1 - 0.5{{\rm{e}}^{ - 0.13s}} - 0.5{{\rm{e}}^{ - s}} $ | (11) |
在线性叠加原理成立的前提下,利用杜哈梅积分,任意分布的竖向脉动风w(s)引起的气动升力可以表示为:
| $ L\left( s \right) = \frac{1}{2}\rho UB{{C'}_L}\int_{ - \infty }^s {\psi \left( {s - \sigma } \right)w'\left( \sigma \right){\rm{d}}\sigma } $ | (12) |
对上式进行变量替换,利用分部积分可以得到:
| $ L\left( s \right) = \frac{1}{2}\rho UB{{C'}_L}\left[ {\psi \left( 0 \right)w\left( s \right) + \int_0^\infty {\psi '\left( \sigma \right)w\left( {s - \sigma } \right){\rm{d}}\sigma } } \right] $ | (13) |
求出上式的功率谱密度,并与式(2)相比较,可以得到阶跃函数ψ与气动导纳的关系:
| $ {\left| {{\chi _{Lw}}} \right|^2} = \left[ {\psi \left( 0 \right) + \overline {\psi '} \left( K \right)} \right]\left[ {\psi \left( 0 \right) + {{\overline {\psi '} }^ * }\left( K \right)} \right] $ | (14) |
其中:
数值计算在商业软件ANSYS FLUENT 15.0中进行。湍流模型选用基于RANS的二维SST k-ω湍流模型。
数值模拟断面非定常气动力的第一步是对计算域内来流的演变特性进行研究,确定合适的离散格式、网格尺寸、时间步等参数以保证来流的主要特征在计算域内准确传播。对于湍流来说来流的主要特征有湍流度、积分尺度、功率谱密度等。对于简谐脉动来流来说,需要保证来流的幅值在计算域内维持不变。而对于竖向阶跃流来说,需要保证来流的阶跃特性在计算域内维持不变。下面分别讨论离散格式、网格尺寸、时间步等参数对来流在计算域中传播的影响。
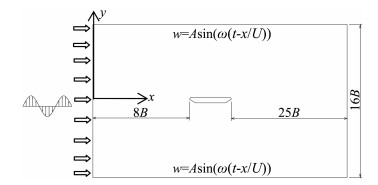
2.1 正弦脉动流在计算域中的传播对于简谐脉动来流,计算域的左侧入口采用速度入口边界条件,u不随时间变化,w为正弦脉动;计算域的上下边界同样采用速度入口,w既是时间的函数也是空间的函数;出口采用压强出口边界条件[16](如图 1所示)。
|
图 1 计算域及边界条件 Fig.1 Computational domain and boundary conditions |
为保障简谐波在计算域内有效传播,应在一个波长内有足够多数量的网格,即:
| $ \lambda = N\Delta x $ | (15) |
其中:Δx为网格尺寸大小,N为一个波长内的网格数量。
由折算频率k=fB/U及式(15),可得到网格尺寸Δx的表达式:
| $ \Delta x = \frac{B}{{Nk}} $ | (16) |
根据唐煜等[14]的研究,当N≥80时可以满足相邻两波峰间幅值的对数衰减率δ=In(Ai+1/Ai) ≤ 0.003。其中Ai+1、Ai分别为相邻两波峰间的幅值。
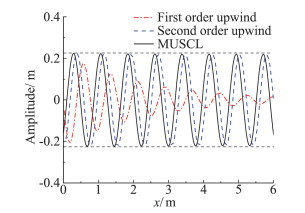
为了研究对流项离散格式对简谐脉动波在计算域内传播的影响,分别采用三种不同的对流项离散格式,扩散项统一采用二阶中心差分。从图 2可以看出,一阶迎风格式由于截断误差的首项包含有二阶导数,会导致较大的数值耗散,使得简谐脉动波的幅值变小。相比较而言,二阶迎风格式由于截断误差的首项为三阶导数,因此它引起的数值耗散就远远小于一阶迎风格式。三阶MUSCL(Monotone Upstream-Centrered Schemes for Conservation Laws)格式的数值耗散最小,简谐脉动在整个计算域内的衰减基本可以忽略不计。所以,对流项的离散选择MUSCL格式。
|
图 2 对流项离散格式对脉动幅值的影响 Fig.2 Influence of the interpolation schemes of the convection terms on the amplitude of the fluctuating wind |
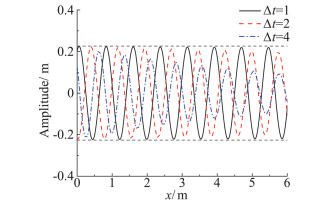
时间项的离散统一采用二阶隐式格式,图 3为无量纲时间步Δt=dt·U/B对简谐脉动幅值的影响。可以看出,随着无量纲时间步的减小,脉动幅值的衰减率也迅速减小。当无量纲时间取1时,基本可以满足计算要求。
|
图 3 无量纲时间步对脉动幅值的影响 Fig.3 Influence of the time step on the amplitude of the fluctuating wind |
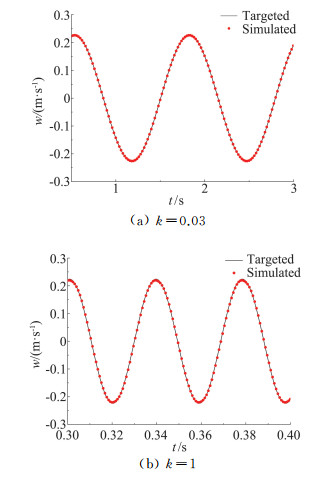
确定了数值计算参数以后,图 4分别计算了无断面计算域中,断面中心位置处折算频率k=0.03和k=1时速度时程与目标值的比较。可以看到,在低折算频率和高折算频率下模拟值与目标值均吻合良好,说明采用以上的数值设置可以保证来流的幅值特性。
|
图 4 无障碍流场中坐标(x,y)=(8B,0)处竖向速度时程 Fig.4 Vertical sinusoidal gust obtained at (x, y)=(8B, 0) in the absence of body sections |
入口采用速度进口边界条件。入口边界处的脉动速度,采用Davidson[22]等人提出的人工谱合成方法。选取Karman谱作为目标风谱,竖向脉动风的湍流度与简谐脉动来流的湍流度接近。上下边界采用对称边界条件,出口采用压强出口边界条件。
为了减小湍流的主要特征在计算域内的衰减,需要适当加密模型断面到入口处的网格。参考公式(15),并综合考虑计算效率的因素,模型到入口处网格的尺寸取Δx=B/(50×1)。对流项的离散采用三阶MUSCL格式,Δt取1。
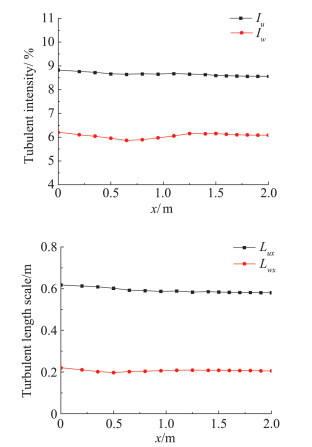
图 5为湍流度和积分尺度沿x轴的变化。可以看出,湍流度和积分尺度仅呈现轻微的衰减。
|
图 5 湍流度和积分尺度变化(y=0) Fig.5 Turbulent intensity and turbulent length scale along the x-axis (y=0) |
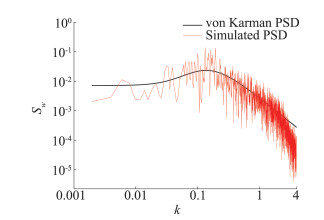
图 6为无障碍流场中(x,y)=(8B,0)处竖向脉动风速功率谱密度与目标值的比较。可见,除了较低频和高频以外,模拟值与目标值吻合良好。
|
图 6 (x,y)=(8B,0)处竖向脉动速度功率谱密度 Fig.6 Power spectrum of the vertical gust at (x, y)=(8B, 0) in the absence of body sections |
数值模拟竖向阶跃流会遇到以下几个问题:
(1) 由于控制流动的微分方程需要在空间和时间上进行离散,因此严格的竖向阶跃流在CFD数值模拟时是不可能实现的。
(2) 由于竖向阶跃流在空间和时间上的急剧变化,因此在求解流动方程时会导致非物理的数值振荡。
(3) 由于分子黏性、湍动能黏度、数值耗散等影响会抹平来流的阶跃特性。此外,由于流动在时间和空间上的演化,来流的阶跃特性也会受到影响。
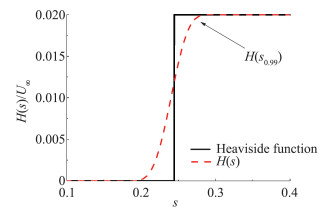
严格的阶跃变化是不可能实现的,因此采用一个光滑变化的“阶跃函数”H(s)来作为近似,如图 7所示。阶跃函数H(s)的幅值为Hmax,假设当H(s0.99)=0.99Hmax时阶跃函数达到稳定,其中s0.99为H(s)从零变化到0.99Hmax所用的时间。为了保证H(s)的阶跃特性又考虑到数值稳定性,我们取s0.99 < 0.1。与Küssner函数的演化特性相比,这是一个相当小的值。s0.99与网格尺寸、时间步、空间和时间离散格式等有关。
|
图 7 阶跃函数和H(s) Fig.7 Heaviside function and H(s) |
在竖向阶跃流的数值计算中,入口采用速度进口边界且使竖向速度做阶跃变化,出口采用压强出口边界条件,上、下边界的流动条件一致所以采用周期性边界条件。
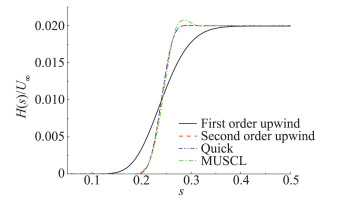
首先选取较小的网格△x=B/125,在均匀的结构化网格下采用较小的时间步0.0005s,二阶隐式时间离散格式,考察对流项离散格式对竖向阶跃流阶跃特性的影响,扩散项依然采用二阶中心差分格式。从图 8可以看出,一阶迎风格式由于假扩散严重,来流的阶跃特性遭到严重的破坏。二阶迎风格式、Quick格式的结果差别不大,都可以保证s0.99 < 0.1。而三阶的MUSCL格式虽然也可以保证s0.99 < 0.1,但是由于MUSCL格式没有采用通量限定,因此出现了明显的越界现象。考虑到Quick格式的数值色散要小于二阶迎风格式,所以本文对流项的离散采用Quick格式。
|
图 8 对流项离散格式对阶跃特性的影响 Fig.8 Tests of the interpolation schemes for the convection terms |
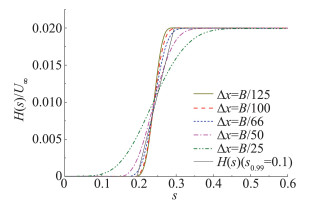
网格尺寸对竖向阶跃流的阶跃特性具有显著的影响。从图 9可以看出,随着网格间距△x的减小,阶跃来流的斜率也随之变大。当△x=B/100时,s0.99 < 0.1,可以近似保证来流的阶跃特性。
|
图 9 网格大小对阶跃特性的影响 Fig.9 Effect of the grid spacing on the characteristics of the vertical indicial wind |
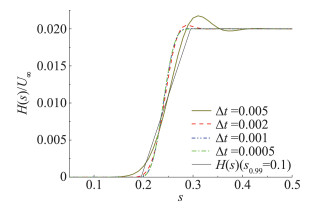
图 10所示为时间步对竖向阶跃来流阶跃特性的影响。可以看出,当时间步较大时,由于计算域内速度的突变,会产生较大的越界现象。当无量纲时间△t=0.001时,可以近似保证来流的阶跃特性。
|
图 10 时间步对阶跃特性的影响 Fig.10 Effect of the time step on the characteristics of the vertical indicial wind |
确定了不同来流条件的数值计算参数后,对接近于理想流线型的平板断面和箱梁断面的非定常气动力进行CFD模拟。数值模型的尺寸如图 11所示。

|
图 11 计算模型断面尺寸(单位:mm) Fig.11 Sections of the computational models (unit: mm) |
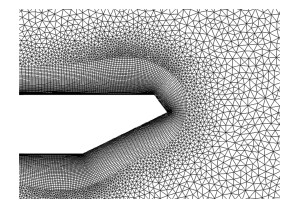
来流的水平速度U=8 m/s,对应的雷诺数Re=UB/ν ≈ 1.6×105。对于简谐脉动来流,竖向速度幅值取0.2262 m,对应2%的湍流度。对于竖向阶跃流,取Hmax/U=2%。所有断面的网格划分采用混合网格的形式。简谐脉动来流下箱梁断面的网格数为10.2万~156万,湍流的网格数为75万,竖向阶跃流的网格数为64万。图 12所示为简谐脉动来流下箱梁断面壁面附近的网格。
|
图 12 箱梁断面壁面附近的网格 Fig.12 Computational grid close to the box girder model |
计算域如图 1所示,图中给出了简谐脉动来流下的边界条件。模型的前缘距入口的距离为8B,模型的后缘距出口的距离为25B。上下侧边界之间的距离应该取得充分大,以避免边界对内部的流场产生影响,试算表明16B的距离可以满足计算需求。
需要注意的是,根据2.3节分析的竖向阶跃来流的网格要求,为了保证来流的阶跃特性,会导致模型前缘的计算域中网格过密,给计算造成一定的负担。此外,阶跃来流传播到断面前缘也需要一定的时间。为此,对流场使用非均匀的初始化。步骤如下:
(1) 在均匀来流的情况下(U=U∞,w=0),进行定常计算。
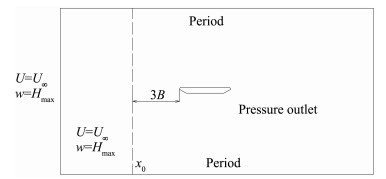
(2) 在x方向选择一个坐标点x0,待流场稳定后,将x<x0计算域的竖向速度w用Hmax进行初始化(如图 13所示),然后再进行非定常计算。
|
图 13 竖向阶跃流计算示意图 Fig.13 Diagram of the set up of the vertical indicial wind |
理想平板断面的气动导纳存在理论解,即Sears函数。穿越半无限空间的竖向脉动风的理想平板,其升力随时间的变化满足Küssner函数,因此平板断面首先被用来验证本文数值方法的准确性。
在简谐脉动来流下,由于平板的气动力呈简谐变化,因此数值计算模拟了5 s的气动力时程。湍流引起的气动力具有随机性,需要很长的采样时间,本文数值模拟了42 s的气动力时程。Küssner函数在无量纲时间s≈30时趋于定常,本文数值模拟了25 s的气动力时程,对应于无量纲时间s=50。本文的计算在曙光W580I工作站上进行(16物理核,32G内存,2T硬盘),完成上述计算需要的CPU核时和内存如表 1所示。可以看到,湍流法计算花费的时间最长,内存占用也是最多的。简谐脉动方法虽然一次计算时间最短,但是需要对所有感兴趣的频率点进行扫频,所以总的计算花费反而是最大的。相比其它两种方法,Küssner方法的计算效率最高。
| 表 1 三种气动导纳识别方法的计算效率比较 Table 1 Computing costs of the three numerical methods |
|
|
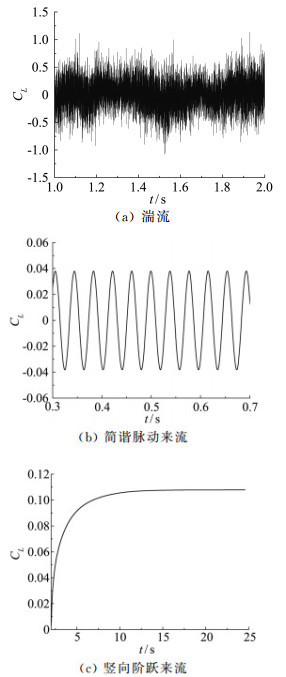
图 14所示为平板断面在三种来流下升力系数随时间的变化图。从图中可以看出平板断面由于没有涡脱,因此升力系数时程仅包含来流脉动的频率。而在宽频来流下,升力系数时程呈现出随机特性。在竖向阶跃来流下,升力系数先急剧增长,再经历了一段缓慢增长后,最终趋于稳定达到定常状态。
|
图 14 平板断面的升力系数时程 Fig.14 Time histories of lift coefficients for the thin plate section |
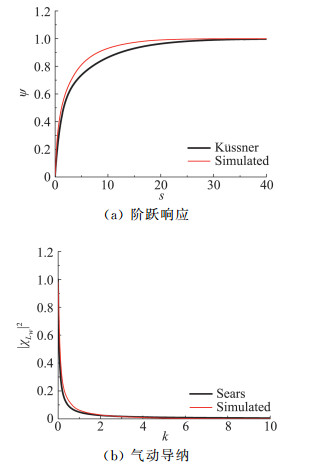
图 15为阶跃响应函数及由其得到的升力气动导纳函数。从图中可以看出识别得到的阶跃响应在初始时刻和最终时刻吻合较好,在中间时刻较Sears函数要大。这一差距可能是由流体的粘流引起,而Sear函数是在无粘性的有势流场中得到。
|
图 15 平板断面的阶跃响应函数及气动导纳函数 Fig.15 Indicial lift response function and aerodynamic admittance function for plate section |
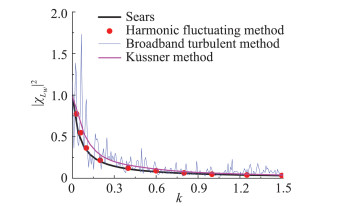
图 16给出了三种来流下识别得到的升力气动导纳函数。可以看到利用湍流法和简谐脉动法识别的气动导纳吻合良好,而且与Sears函数较为一致。Küssner法识别的气动导纳整体上也与Sears函数较为吻合,但在低频有一定的差距。这一差距的原因,主要是由于不满足流动的有势条件。此外,可能还由于Küssner法涉及到阶跃响应函数的识别、求导与傅立叶变换等多个步骤,见公式(14),在这个过程中存在着误差的积累与传递。
|
图 16 三种不同方法平板断面气动导纳函数的比较 Fig.16 The comparison of the aerodynamic admittance between three different methods for plate section |
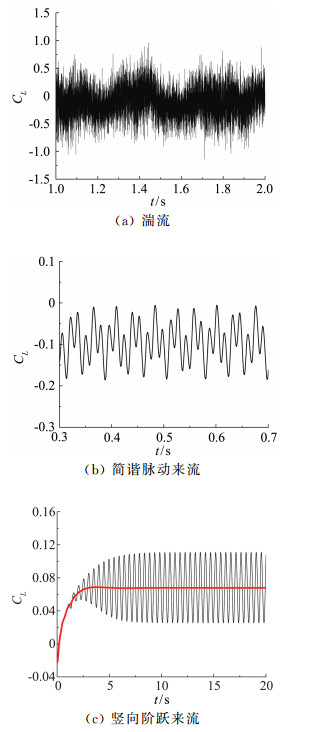
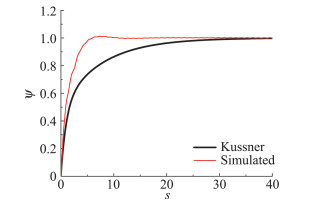
箱梁断面在桥梁工程中应用十分普遍。本文选取的箱梁断面宽高比B/D=10.2。图 17分别为箱梁断面在三种来流下的升力系数时程。在宽频来流下,同平板断面一样,升力系数时程呈现出随机特性。在简谐脉动来流下,由于断面尾部的涡脱效应,升力系数时程除了包含来流的脉动频率以外,还包含有涡脱频率,对应的Strouhal数为0.2。竖向阶跃来流下,升力系数时程与平板断面的情况有本质的区别,呈现出很大的周期性振荡,这也是由断面尾部的涡脱造成的。从阶跃响应函数和气动导纳的物理意义来看,它们并不包含涡脱的影响,这部分气动力由涡激力模型考虑。因此为了得到阶跃响应函数,首先使用FFT光滑滤波对升力系数进行处理,滤波光滑后的升力系数如图 17(c)所示。图 18为根据滤波光滑后的升力系数得到的阶跃响应函数。可以看到箱梁断面的阶跃响应与Küssner函数相差较大,呈现出一个峰值。这可能是因为当阶跃来流到达断面前缘时,在断面的前缘处引起瞬时的较大的边界层分离,随着边界层的再附及向下游传播,并最终与后缘脱落的漩涡合并,造成断面表面压强的变化引起的[23]。对于钝体断面,这种现象是Küssner方法所固有的。显然Küssner方法并不适用于这种形式的断面。
|
图 17 箱梁断面的升力系数时程 Fig.17 Time histories of lift coefficients for the box girder section |
|
图 18 箱梁断面的阶跃响应 Fig.18 Indicial lift response function for box girder section |
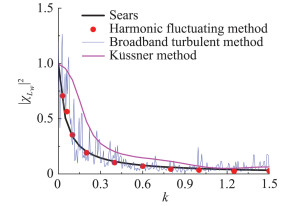
图 19所示为不同来流下箱梁断面的升力气动导纳函数。从图中可以看出,正弦来流和湍流下识别的气动导纳函数在低频范围内吻合良好,并且与Sears函数较为接近。在高频范围,正弦来流下识别的气动导纳函数略小于Sears函数,湍流下识别的气动导纳函数却略大于Sears函数。Zhang等人在文献[24]中讨论了气动导纳的风场依赖性,指出对于具有显著分离流的钝体断面,非定常气动力的叠加原理不再成立,气动导纳应表现出对来流特性的依赖性。本文的计算表明,扁平箱梁断面的气动导纳与来流风场特性仅仅是弱相关的。竖向阶跃来流下识别的气动导纳整体上与其它两种来流的结果相差较大,从前面的分析可见这种方法仅能应用于严格的流线型断面,即与风场特性完全无关的断面。
|
图 19 三种不同方法箱梁断面气动导纳函数的比较 Fig.19 The comparison of the aerodynamic admittance between three different methods for box girder section |
本文借助于CFD方法,研究了适用于简谐脉动来流、湍流和竖向阶跃来流三种风场的计算方法。在此基础上计算了平板和扁平箱梁断面受到的气动力,识别了阶跃响应和气动导纳函数,得出以下结论:
(1) 要准确模拟三种来流风场需要采取不同的数值计算策略。需要按标准保证足够的网格精度,而且对流项离散格式应采用高阶离散格式,如三阶的MUSCL格式。湍流的最小网格尺寸应根据最高截止频率按照简谐脉动来流的条件取值。竖向阶跃来流由于在计算域内的局部位置会发生急剧变化,因此对流项的离散需要采用有界的格式,以防止越界现象产生。另外较大的时间步也会引起越界现象。
(2) 三种方法识别得到的平板断面气动导纳与Sears函数吻合,说明了本文三种方法识别气动导纳的可行性。
(3) 简谐来流和湍流下识别的箱梁断面气动导纳差别不大,体现出了扁平箱梁断面气动导纳对来流风场的弱相关性。在竖向阶跃来流下识别的气动导纳函数与其它两种来流下识别的气动导纳函数有较大的差距,体现了Küssner方法应用于钝体断面的局限性。
(4) 三种方法相比较而言,湍流的计算效率最高,可以一次性识别出所有频率范围的气动导纳函数,但识别结果平滑性差随机跳跃性大;简谐来流方法进行多次扫频计算因而计算消耗大,但该法具有求解稳定、结果平滑可靠的优点;Küssner方法具有计算时间短的优势,而且可以识别出阶跃响应函数直接用于时域分析,但该法存在误差积累与传递的问题,且仅能适用于气动导纳与风场严格无关的断面。
| [1] |
DAVENPORT A G. Buffeting of a suspension bridge by storm winds[J]. Journal of the Structural Divion, 1962, 88(ST3): 233-268. |
| [2] |
LAROSE G L. Gust loading on streamlined bridge decks[J]. Journal of Fluids and Structures, 1998, 12(5): 511-536. DOI:10.1006/jfls.1998.0161 |
| [3] |
LAROSE G L. Experimental determination of the aerodynamic admittance of a bridge deck segment[J]. Journal of Fluids and Structures, 1999, 13(7): 1029-1040. |
| [4] |
WAGNER H. Vber die entstehung des dynamicschen auftriebes von tragflügeln[J]. Journal of Applied Mathematics and Mechanics, 1925, 5: 17-35. |
| [5] |
KVSSNER H G. Zusammenfassender bericht über den instationären auftriep von flugeln[J]. Luftfahrtforschung, 1936, 13(12): 410-424. |
| [6] |
GARRICK I. On some reciprocal relations in the theory of nonstationary flows[R]. NACA Report 629, 1938: 347-350.
|
| [7] |
CARACOGLIA L, JONES N P. A methodology for the experimental extraction of indicial functions for streamlined and bluff deck sections[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91: 609-636. DOI:10.1016/S0167-6105(02)00473-7 |
| [8] |
MIRANDA S D, PATRUNO L, RICCI M, et al. Numerical study of a twin box bridge deck with increasing gap ratio by using RANS and LES approaches[J]. Engineering Structures, 2015, 99: 546-558. DOI:10.1016/j.engstruct.2015.05.017 |
| [9] |
ANINA S, RUDIGER H, STANKO B. Numerical simulations and experimental validations of force coefficients and flutter derivatives of a bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 144: 172-182. DOI:10.1016/j.jweia.2015.04.017 |
| [10] |
DANIELS S J, CASTRO I P, XIE Z T. Numerical analysis of freestream turbulence effects on the vortex-induced vibrations of a rectangular cylinder[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 153: 13-25. DOI:10.1016/j.jweia.2016.03.007 |
| [11] |
WU T, KAREEM A. An overview of vortex-induced vibration(VIV) of bridge decks[J]. Frontiers of Structural and Civil Engineering, 96(10-11): 335-347. |
| [12] |
BRUSIANI F, MIRANDA S D, PATRUNO L, et al. On the evaluation of bridge deck flutter derivatives using RANS turbulence models[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 119: 39-47. DOI:10.1016/j.jweia.2013.05.002 |
| [13] |
HEJLESEN M M, RASMUSSEN J T, LARSEN A, et al. On estimating the aerodynamic admittance of bridge sections by a mesh-free vortex method[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 146: 117-127. DOI:10.1016/j.jweia.2015.08.003 |
| [14] |
唐煜, 郑史雄, 张龙奇, 等. 桥梁断面气动导纳的数值识别方法研究[J]. 空气动力学学报, 2015, 33(5): 706-713. TANG Y, ZHENG S X, ZHANG L Q, et al. Numerical method for identifying the aerodynamic admittance of bridge deck[J]. Acta Aerodynamic Sinica, 2015, 33(5): 706-713. (in Chinese) |
| [15] |
BRUNO L, TUBINO F. Aerodynamic admittance functions of bridge decksections by CWE[C]//Proceedings 8th National Conference on Wind Enginneering, Reggio Calabria, 2005.
|
| [16] |
张伟峰, 张志田, 张显雄. 桥梁断面气动导纳风场依赖特性的数值研究[J]. 空气动力学学报, 2018, 36(04): 677-686. ZHANG W F, ZHANG Z T, ZHANG X X. Numerical investigation on thewind-field-dependence property of bridge section aerodynamic admittances[J]. Acta Aerodynamica Sinica, 2018, 36(4): 677-686. DOI:10.7638/kqdlxxb-2016.0067 (in Chinese) |
| [17] |
张伟峰, 张志田, 张显雄, 等. 节段模型气动导纳的数值模拟与试验[J]. 中国公路学报, 2018, 31(6): 207-216. ZHANG W F, Zhang Z T, ZHANG X X, et al. Experimental and numerical investigation on aerodynamic admittances of section models[J]. China J Highw Transp, 2018, 31(6): 207-216. DOI:10.3969/j.issn.1001-7372.2018.06.007 (in Chinese) |
| [18] |
TUBINO F. Relationships among aerodynamic admittance functions, flutter derivatives and static coefficients for long-span bridges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93: 929-950. DOI:10.1016/j.jweia.2005.09.002 |
| [19] |
LIEPMANN H W. On the application of statistical concepts to the buffeting problem[J]. Journal of the Aeronautical Sciences, 1952, 19(12): 793-800. DOI:10.2514/8.2491 |
| [20] |
MA T T, ZHAO L, CAO S Y, et al. Investigations of aerodynamic effects on streamlined box girder using two-dimensional actively-controlled oncoming flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 122: 118-129. DOI:10.1016/j.jweia.2013.07.011 |
| [21] |
JONES R T.The unsteady lift on a wing of finite aspect ratio[R]. NASA Report 681, 1940.
|
| [22] |
DAVIDSON L. Hybrid LES-RANS: Inlet boundary conditions[C]. 3rd National Conference on Computational Mechanics, 2005: 7-22.
|
| [23] |
TURBELIN G, GIBERT R J. CFD calculations of indicial lift responses for bluff bodies[J]. Wind and Structures, 2002, 4(5): 245-256. |
| [24] |
ZHANG Z T, GE Y J, ZHANG W F. Superposability of unsteady aerodynamic loads on bridge deck sections[J]. Journal of Central South University, 2013, 20(11): 3202-3215. DOI:10.1007/s11771-013-1845-8 |
 2019, Vol. 37
2019, Vol. 37


