当流体中同时存在温度梯度和浓度梯度时,就会引发温度扩散和浓度扩散,并且两者相互作用,进而发生自然对流现象。这种由两者综合而引起的自然对流被称为双扩散对流[1]。双扩散对流现象是一种常见的自然现象,在海洋学、大气物理学、化学动力学等领域中也会涉及到这种流动,例如海洋环流、化学反应和大气扩散等方面[2-5]。
其中室内火灾的排烟是一个典型的双扩散对流问题。当室内发生火灾,室内温度急剧上升,并且伴随大量排烟,室内空气在温度差和浓度差的相互作用下运动。国内外学者对火灾物理现象的研究大都采用如CFAST[6-7]和FDS[8-9]等火灾模拟软件,以及大涡模拟方法(LES)和雷诺时均法(RANS)[10-11]。
对双扩散问题国内外众多学者进行了大量的研究。Al-Amiri等[12]基于Galerkin加权余量法对顶盖驱动的正方形腔体内的双扩散混合对流过程进行了研究,得出了在理查德森数Ri较低时,顶盖驱动作用会使方腔内传质和传热速率增加的结论。在此基础之上,Zhuo等[13]利用格子Boltzmann方法模拟分析了顶盖驱动深腔内的流动分岔,研究了长宽比对第一分岔问题的影响,得出了与时间相关的涡流随雷诺数Re呈现周期性和非周期性变化。雍玉梅等[14]利用格子Boltzmann方法,在前人基础上模拟了溶解的氧气分子在整个正方形方腔内的扩散过程,同时为控制气体传质过程的给热条件提供依据。Xu等[15-17]则采用有限元方法研究了内置发热圆开口方腔内,不同的特性参数和发热圆位置对含有发热圆开口方腔内双扩散自然对流的影响。
上述研究大都基于傅里叶导热定律和菲克扩散效应进行分析;然而当流体中温度和浓度梯度较大时,Soret和Dufour效应则不能忽略。Soret效应是指温度场的不均匀导致的传质现象,Dufour效应是指浓度场的不均匀导致的传热现象。Soret效应为正值时,表示温度梯度会驱使传质从高温到低温运动,负值时表示温度梯度会驱使传质从低温到高温运动。Dufour效应与之类似,不再赘述。
国内外学者对Soret和Dufour效应也做了相应研究。Nithyadevi和Yang[18]在考虑Soret和Dufour效应的情况下,采用有限体积法分析了水在部分加热方腔内的双扩散自然对流,并研究了不同加热位置、瑞利数、浮升力比等对流场和传热传质的影响。而Cheng[19]采用边界层近似解法,在考虑Soret和Dufour效应的条件下,研究了在充满多孔介质的倾斜波浪状表面的自由对流边界层,发现了随着Soret数的增大无量纲总传热率降低,而随着Dufour数的增大无量纲总传热率增加的规律。Wang等[20]则采用了SIMPLE算法,通过构造一个包含Soret和Dufour效应的水平方腔,研究了双扩散对流在非均匀网格中的振荡特性,得出了随着浮升力比和瑞利数的增加,双扩散对流会经过稳态对流,周期振荡,拟周期性震荡,混沌流动最后再恢复到周期振荡的发展过程。近些年来,更多的科研人员开始在磁流体力学(Magnetohydrodynamics,MHD)对流的研究中考虑Soret和Dufour效应[21-23]。
本文主要从室内火灾以及污染物扩散现象出发,抽象出内置高浓度发热圆方腔内双扩散自然对流现象问题,利用格子Boltzmann方法对其进行研究。格子Boltzmann作为一种数值模拟方法,具有天生的并行特性以及边界条件处理简单、程序易于实施、演化过程清晰等特点[24]。本文考虑Soret和Dufour效应对方腔内部传热传质现象的影响,得到了不同参数条件下方腔内部的流线、等温线和等浓度线分布特性,以及发热圆表面的平均努赛尔数Nuav和平均舍伍德数Shav的变化规律。
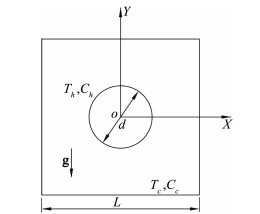
1 问题描述和计算模型 1.1 物理问题本文以室内火灾物理现象抽象如下模型:将室内简化为一个方腔,室内火灾点简化为方腔内发热圆。其简化物理模型如图 1所示。方腔模型四周壁面均为低温低浓度,方腔内部发热圆为高温高浓度,模型方腔的长宽均为L,方腔中心有一直径为d(d=0.4L)的发热圆,发热圆表面的温度为Th,浓度为Ch,四周壁面温度为Tc,浓度为Cc,重力加速度为g,其中Th>Tc,Ch>Cc。
|
图 1 物理模型 Fig.1 Physical model |
假设流体为不可压且不考虑黏性热耗散,采用Boussinesq假设[25],浮升力项中的密度由下式给出:
| $ \rho = {\rho _0}\left[ {1 - {\beta _T}\left( {T - {T_0}} \right) - {\beta _C}\left( {C - {C_0}} \right)} \right] $ | (1) |
其中:ρ0、T0和C0分别为参考密度、温度和浓度;βT为温度引起的体积膨胀系数,K-1;βC为浓度引起的体积膨胀系数,m3·kg-1。
基于以上假设,描述二维考虑Soret和Dufour效应的方腔内双扩散自然对流的宏观控制方程为:
| $ \nabla \cdot \mathit{\boldsymbol{u}} = 0 $ | (2) |
| $ \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \nabla \cdot \left( {\mathit{\boldsymbol{uu}}} \right) = - \frac{1}{{{\rho _0}}}\nabla \rho + \nu {\nabla ^2}\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{F}} $ | (3) |
| $ \frac{{\partial T}}{{\partial t}} + \nabla \cdot \left( {\mathit{\boldsymbol{u}}T} \right) = \alpha \left( {{\nabla ^2}T} \right) + {\kappa _{TC}}\left( {{\nabla ^2}C} \right) $ | (4) |
| $ \frac{{\partial C}}{{\partial t}} + \nabla \cdot \left( {\mathit{\boldsymbol{u}}C} \right) = D\left( {{\nabla ^2}C} \right) + {\kappa _{CT}}\left( {{\nabla ^2}T} \right) $ | (5) |
其中:u和p分别为二维速度矢量和压力;T和C分别为温度和浓度;ν、α和D分别是运动黏性系数、热扩散系数和质扩散系数;κTC和κCT分别代表Soret系数和Dufour系数;F为浮力项,即:
| $ \mathit{\boldsymbol{F}} = - \mathit{\boldsymbol{g}}\left[ {1 - {\beta _T}\left( {T - {T_0}} \right) - {\beta _C}\left( {C - {C_0}} \right)} \right] $ | (6) |
定义参考速度uR=α/L,引入下列无量纲变量:
| $ \begin{array}{l} \tau = \frac{{{u_R}t}}{L},X = \frac{x}{L},Y = \frac{y}{L},U = \frac{u}{{{u_R}}},V = \frac{v}{{{u_R}}}\\ P = \frac{p}{{\rho u_R^2}},\theta = \frac{{T - {T_c}}}{{{T_h} - {T_c}}},S = \frac{{C - {C_c}}}{{{C_h} - {C_c}}} \end{array} $ | (7) |
其中:t、p、T和C分别为时间、压力、温度和浓度,u、v分别为直角坐标系下水平方向和竖直方向的速度分量。
在上述条件下,图 1所示的方腔内双扩散自然对流问题在直角坐标系下的无量纲宏观数学描述方程如下:
| $ \frac{{\partial U}}{{\partial X}} + \frac{{\partial V}}{{\partial Y}} = 0 $ | (8) |
| $ \frac{{\partial U}}{{\partial \tau }} + U\frac{{\partial U}}{{\partial X}} + V\frac{{\partial U}}{{\partial Y}} = - \frac{{\partial P}}{{\partial X}} + \mathit{Pr}\left( {\frac{{{\partial ^2}U}}{{\partial {X^2}}} + \frac{{{\partial ^2}U}}{{\partial {Y^2}}}} \right) $ | (9) |
| $ \begin{array}{l} \frac{{\partial V}}{{\partial \tau }} + U\frac{{\partial V}}{{\partial X}} + V\frac{{\partial V}}{{\partial Y}} = - \frac{{\partial P}}{{\partial Y}} + \mathit{Pr}\left( {\frac{{{\partial ^2}V}}{{\partial {X^2}}} + \frac{{{\partial ^2}V}}{{\partial {Y^2}}}} \right) + \\ \;\;\;\;\;Ra \cdot \mathit{Pr}\left( {\theta - Br \cdot S} \right) \end{array} $ | (10) |
| $ \begin{array}{l} \frac{{\partial \theta }}{{\partial \tau }} + U\frac{{\partial \theta }}{{\partial X}} + V\frac{{\partial \theta }}{{\partial y}} = \left( {\frac{{{\partial ^2}\theta }}{{\partial {X^2}}} + \frac{{{\partial ^2}\theta }}{{\partial {Y^2}}}} \right) + \\ \;\;\;\;Df\left( {\frac{{{\partial ^2}S}}{{\partial {X^2}}} + \frac{{{\partial ^2}S}}{{\partial {Y^2}}}} \right) \end{array} $ | (11) |
| $ \begin{array}{l} \frac{{\partial S}}{{\partial \tau }} + U\frac{{\partial S}}{{\partial X}} + V\frac{{\partial S}}{{\partial y}} = \frac{1}{{Le}}\left[ {\left( {\frac{{{\partial ^2}S}}{{\partial {X^2}}} + \frac{{{\partial ^2}S}}{{\partial {Y^2}}}} \right) + } \right.\\ \left. {\;\;\;\;Sr\left( {\frac{{{\partial ^2}\theta }}{{\partial {X^2}}} + \frac{{{\partial ^2}\theta }}{{\partial {Y^2}}}} \right)} \right] \end{array} $ | (12) |
描述用到的6个无量纲准则数是普朗特数Pr、瑞利数Ra、浮升力比Br、路易斯数Le、Soret数Sr和Dufour数Df,其定义分别如下:
| $ \begin{array}{l} \mathit{Pr} = \frac{\nu }{\alpha },Le = \frac{\alpha }{D},\\ Ra = \frac{{\mathit{\boldsymbol{g}}{\beta _T}\left( {{T_h} - {T_c}} \right){L^3}}}{{\alpha \upsilon }},Br = \frac{{{\beta _C}\left( {{C_h} - {C_c}} \right)}}{{{\beta _T}\left( {{T_h} - {T_c}} \right)}},\\ Sr = \frac{{{\kappa _{CT}}\left( {{T_h} - {T_c}} \right)}}{{D\left( {{C_h} - {C_c}} \right)}},{D_f} = \frac{{{\kappa _{TC}}\left( {{C_h} - {C_c}} \right)}}{{\alpha \left( {{T_h} - {T_c}} \right)}}。\end{array} $ | (13) |
其中:ν、α、D和g分别表示运动粘度、热扩散系数、质扩散系数和重力加速度;在模拟分析中,瑞利数Ra设为105,普朗特数Pr设为0.71,路易斯数Le设为2.0。
边界条件设定如下:
发热圆表面的无量纲速度均为0,无量纲温度和浓度均为1, 即:U=V=0, θ=1.0, S=1.0。
四周壁面的无量纲速度、温度和浓度均为0, 即:U=V=0, θ=0, S=0。
2 Lattice Boltzmann模型本文基于Guo等[26]提出的不可压缩CLBGK模型进行分析,该模型的基本思想是用三个独立的LBGK方程分别模拟速度场、温度场和浓度场,然后通过Boussinesq假设近似将其耦合起来。
速度场模拟采用D2Q9模型,其演化方程为:
| $ \begin{array}{l} {f_i}\left( {\mathit{\boldsymbol{r}} + {\mathit{\boldsymbol{e}}_i}\Delta t,t + \Delta t} \right) - {f_i}\left( {\mathit{\boldsymbol{r}},t} \right) = \\ \;\;\;\; - \frac{1}{{{\tau _f}}}\left[ {{f_i}\left( {\mathit{\boldsymbol{r}},t} \right) - f_i^{{\rm{eq}}}\left( {\mathit{\boldsymbol{r}},t} \right)} \right] + \Delta t{\mathit{\boldsymbol{F}}_i} \end{array} $ | (14) |
其中ei为离散速度,采用Qian等[27]提出的离散速度模型,表示为:
| $ {\mathit{\boldsymbol{e}}_i} = \left\{ \begin{array}{l} \left( {0,0} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\;\;i = 0\\ c\left( {\cos \left[ {\left( {i - 1} \right){\rm{ \mathsf{ π} }}/2,\sin \left[ {\left( {i - 1} \right){\rm{ \mathsf{ π} }}/2} \right]} \right.} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\;\;i = 1 \sim 4\\ \sqrt 2 c\left( {\cos \left[ {\left( {2i - 9} \right){\rm{ \mathsf{ π} }}/4,\sin \left[ {\left( {2i - 9} \right){\rm{ \mathsf{ π} }}/4} \right]} \right.} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\;\;i = 5 \sim 8 \end{array} \right. $ | (15) |
其中:c=Δx/Δt为格子速度,Δx和Δt分别为网格步长和时间步长。声速
| $ f_i^{{\rm{eq}}} = \left\{ \begin{array}{l} {\rho _0} - \frac{{5p}}{{3{c^2}}} + {\rho _0}{s_i}\left( \mathit{\boldsymbol{u}} \right)\;\;\;\;\;\;\;\;\;,\;\;\;\;i = 0\\ \frac{p}{{3{c^2}}} + {\rho _0}{s_i}\left( \mathit{\boldsymbol{u}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\;\;\;i = 1 \sim 4\\ \frac{p}{{12{c^2}}} + {\rho _0}{s_i}\left( \mathit{\boldsymbol{u}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;,\;\;\;\;i = 5 \sim 8 \end{array} \right. $ | (16) |
| $ {s_i}\left( \mathit{\boldsymbol{u}} \right) = {\omega _i}\left[ {3\frac{{\left( {{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}} \right)}}{c} + 4.5\frac{{{{\left( {{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{u}}} \right)}^2}}}{{{c^2}}} - 1.5\frac{{{{\left| \mathit{\boldsymbol{u}} \right|}^2}}}{{{c^2}}}} \right] $ | (17) |
其中,ωi代表权重系数,取值如下所示:
| $ {\omega _i} = \left\{ \begin{array}{l} 4/9\;\;\;\;\;\;\;\;\;\;,\;\;\;i = 0\\ 1/9\;\;\;\;\;\;\;\;\;\;\;,\;\;\;i = 1,2,3,4\\ 1/36\;\;\;\;\;\;\;\;\;,\;\;\;i = 5,6,7,8 \end{array} \right. $ | (18) |
演化方程中外力项Fi表示为:
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_i} = - \frac{1}{{2c}}\left( {{\delta _{i2}} + {\delta _{i4}}} \right)\Delta t{\mathit{\boldsymbol{e}}_i} \cdot \mathit{\boldsymbol{g}}\left[ {{\beta _T}\left( {T - {T_0}} \right)} \right.\\ \;\;\;\;\;\;\left. { + {\beta _c}\left( {C - {C_0}} \right)} \right] \end{array} $ | (19) |
相应的流体宏观速度和压力的计算式为:
| $ \mathit{\boldsymbol{u}} = \sum\limits_{i = 1}^8 {{\mathit{\boldsymbol{e}}_i}{f_i}} ,p = \frac{3}{5}{c^2}\left[ {\sum\limits_{i = 1}^8 {{f_i}} + {s_0}\left( \mathit{\boldsymbol{u}} \right)} \right] $ | (20) |
温度场和浓度场模拟采用D2Q5模型,其演化方程分别为:
| $ \begin{array}{*{20}{c}} {{T_i}\left( {\mathit{\boldsymbol{r}} + {\mathit{\boldsymbol{e}}_i}\Delta t,t + \Delta t} \right) - {T_i}\left( {\mathit{\boldsymbol{r}},t} \right) = }\\ { - \frac{1}{{{\tau _T}}}\left[ {{T_i}\left( {\mathit{\boldsymbol{r}},t} \right) - T_i^{{\rm{eq}}}\left( {\mathit{\boldsymbol{r}},t} \right)} \right]} \end{array} $ | (21) |
| $ \begin{array}{*{20}{c}} {{C_i}\left( {\mathit{\boldsymbol{r}} + {\mathit{\boldsymbol{e}}_i}\Delta t,t + \Delta t} \right) - {C_i}\left( {\mathit{\boldsymbol{r}},t} \right) = }\\ { - \frac{1}{{{\tau _C}}}\left[ {{C_i}\left( {\mathit{\boldsymbol{r}},t} \right) - C_i^{{\rm{eq}}}\left( {\mathit{\boldsymbol{r}},t} \right)} \right]} \end{array} $ | (22) |
其中,τT和τC分别为温度分布函数和浓度分布函数的无量纲松弛时间,Tieq和Cieq分别为相应的平衡态分布函数[29],在考虑Soret和Dufour效应影响的情况下,表示为:
| $ T_i^{{\rm{eq}}} = \left\{ \begin{array}{l} T{m_0} - Df \cdot C\left( {1 - {m_0}} \right)\;\;\;\;,\;\;\;\;i = 0\\ \frac{T}{4}\left[ {1 - {m_0} + 2\frac{{\left( {{\mathit{\boldsymbol{e}}_i}u} \right)}}{{{c^2}}}} \right] + \frac{{Df \cdot C\left( {1 - {m_0}} \right)}}{4},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1 \sim 4 \end{array} \right. $ | (23) |
| $ C_i^{{\rm{eq}}} = \left\{ \begin{array}{l} C \cdot {l_0} - SrT\left( {1 - {l_0}} \right)\;\;\;\;,\;\;\;\;i = 0\\ \frac{C}{4}\left[ {1 - {m_0} + 2\frac{{\left( {{\mathit{\boldsymbol{e}}_i}u} \right)}}{{{c^2}}}} \right] + \frac{{SrT\left( {1 - {l_0}} \right)}}{4},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1 \sim 4 \end{array} \right. $ | (24) |
相应的宏观温度和浓度的计算式表示为:
| $ \theta = \sum\limits_{i = 1}^4 {{T_i}} ,\;\;\;\;S = \sum\limits_{i = 1}^4 {{C_i}} $ | (25) |
热扩散系数α和质扩散系数D表示为:
| $ \begin{array}{l} \alpha = \frac{1}{2}{c^2}\left( {{\tau _T} - \frac{1}{2}} \right)\Delta t\left( {1 - {m_0}} \right)\\ D = \frac{1}{2}{c^2}\left( {{\tau _C} - \frac{1}{2}} \right)\Delta t\left( {1 - {l_0}} \right) \end{array} $ | (26) |
发热圆表面的平均努赛尔数Nuav和平均舍伍德数Shav由下式确定:
下式中n表示发热圆表面法线方向上的单位矢量,φ表示圆角弧度值。
| $ N{u_{{\rm{av}}}} = - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {{{\left( {\frac{{\partial \theta }}{{\partial \mathit{\boldsymbol{n}}}}} \right)}_{{\rm{cylinder}}}}{\rm{d}}\varphi } $ | (27) |
| $ S{h_{{\rm{av}}}} = - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {{{\left( {\frac{{\partial S}}{{\partial \mathit{\boldsymbol{n}}}}} \right)}_{{\rm{cylinder}}}}{\rm{d}}\varphi } $ | (28) |
本模型发热圆曲面边界处理采用Bouzidi等[30]提出的空间插值的边界处理方法,方腔壁面的边界处理格式采用Guo等[31]提出的非平衡态外推格式;网格数采用200×200,速度、温度及浓度最大绝对残差均小于10-7。
3 程序验证为了对程序的准确性进行验证,本文采用该方法对竖直腔内双扩散自然对流进行了模拟,并将本文计算结果与文献[32]中所得结果进行对比。表 1给出了本文与对比文献[32]中方腔热壁面的Nuav和Shav的计算结果和误差,两者基本吻合。
| 表 1 不同Br下的Nuav和Shav的比较(Ra=1×105,Pr=1.0,Le=2.0,Sr=0.1,Df=0.1) Table 1 Comparisons of Nuav and Shav at different Br (Ra=1×105, Pr=1.0, Le=2.0, Sr=0.1, Df=0.1) |
|
|
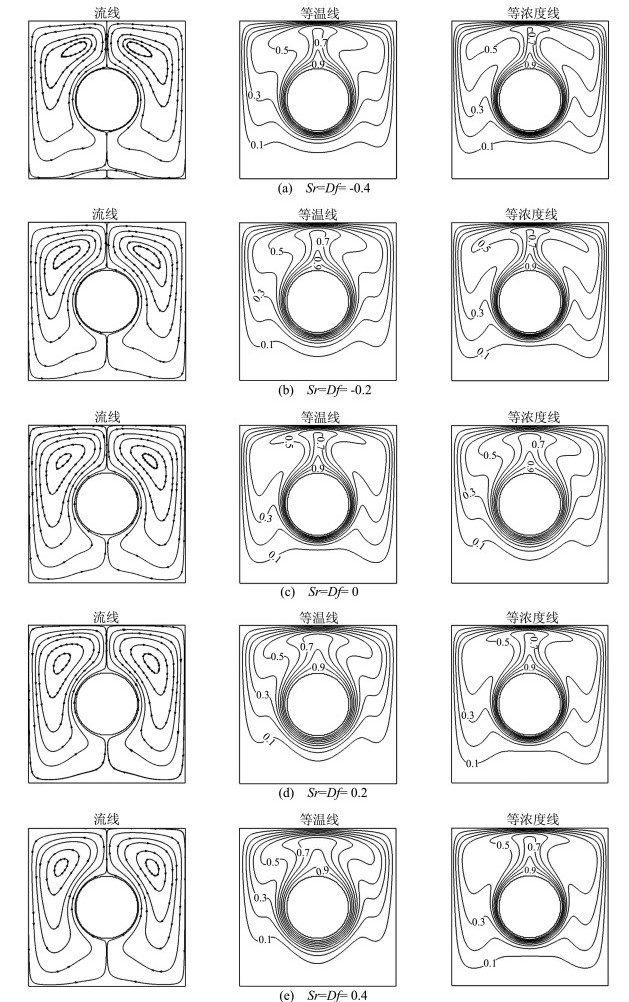
图 2为Br=5.0时,方腔内流场、温度场和浓度场在不同Sr数和Df数下的分布图。从图中可以看出,方腔内的流线、等温线和等浓度线均关于y轴对称,这是因为流体所处的边界条件以及所受的外力均关于y轴对称,且在瑞利数Ra=1×105的条件下,内部流场的流动没有振荡等非线性现象的产生。从流线图的分布可知,在方腔顶部左右两侧各形成一个涡结构。当Sr数和Df数继续同时减小时,左右两个涡开始向方腔顶部扩散,并且在方腔底部左右两侧又各自产生了一个二次涡结构,涡的强度和范围不太明显。从等温线可以看出,Sr=Df=-0.4时,发热圆上方出现了热羽流,并且随着Sr数和Df数的增大,发热圆上方的热羽流变得越来越弱,方腔底部两侧的等温线逐渐向发热圆靠近;发热圆上方附近的等温线的温度梯度较下方小。发热圆下方的等温线则变得稀疏,温度梯度变小,整体传热能力下降。观察等浓度线的变化可以发现,随着Sr数和Df数逐渐增大,发热圆上方的质羽流越来越弱,而且发热圆下方的质边界层越来越厚,传质能力逐渐变弱,两侧的质羽流向下方靠拢。由方程(11)和(12)可知,当Sr数和Df数减小时,方程(11)和(12)右侧数值的减小,方程左侧的数值亦会减小,即无量纲温度和浓度随时间和在x,y方向的偏导数减小,所以其传质能力和传热能力会均有所减弱。
|
图 2 不同Sr和Df数下的流线、等温线和等浓度线分布(Ra=1×105, Pr=0.71, Le=2.0, Br=5.0) Fig.2 Distributions of streamlines, isotherms and isoconcentrations at different Sr and Df(Ra=1×105, Pr=0.71, Le=2.0, Br=5.0) |
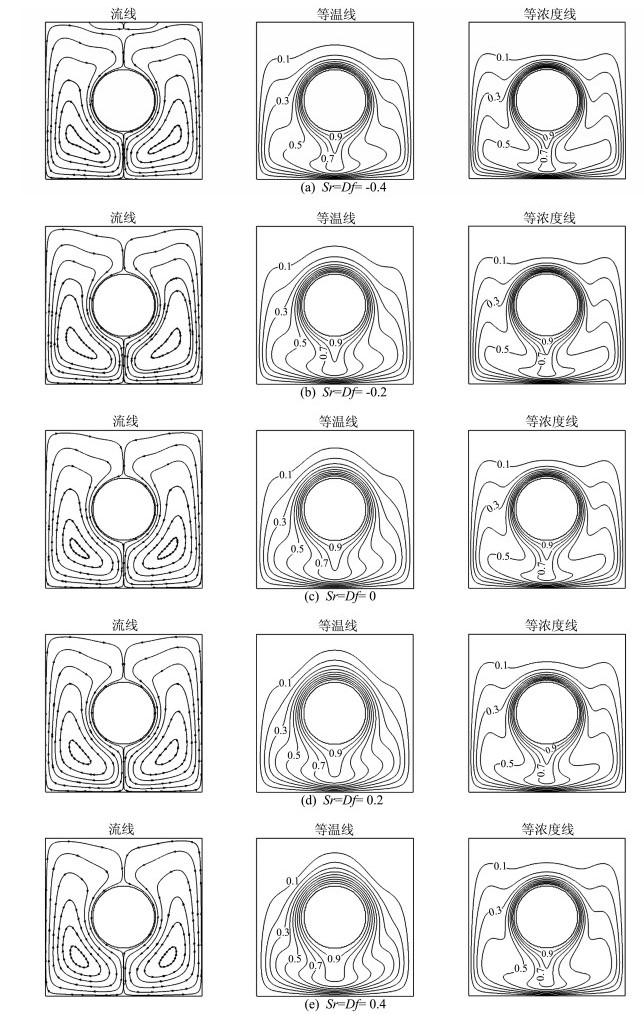
图 3为Br=-5.0时,方腔内流场、温度场和浓度场在不同Sr数和Df数下的分布图。从图 3中可以观察可知,当浮升力比Br=-5.0时,流线、等温度线和等浓度线的分布图与Br=5.0时的分布图基本呈反对称分布,因为Br并非单纯的浮力,而是质浮升力和热浮升力的比值,当Br=-5.0时,表明质浮升力和热浮升力方向相反,且质浮升力占主导地位,故两者基本呈反对称分布。从流线分布图可知,在流场中左右两侧对称各出现了一个涡结构且旋涡中心靠近方腔的底部;随着Sr数和Df数的同时减小,涡结构逐渐向发热圆顶部扩散;当Sr数和Df数小于-0.2时,除形成对称涡结构外,还会在发热圆的上方出现二次涡,且运动方向与主旋涡的运动方向相反。观察等温线和等浓度线分布图可以看出,随着Sr数和Df数的同时增大,发热圆下方的热羽流形态逐渐变弱,两侧的等温线慢慢向方腔底部偏移,传热强度变小;发热圆顶部的质羽流变化微弱,但底部的质羽流变得愈不明显,传质能力变小,但相对于传热能力的减弱程度较小。
|
图 3 不同Sr和Df数下的流线、等温线和等浓度线分布(Ra=1×105, Pr=0.71, Le=2.0, Br=-5.0) Fig.3 Distributions of streamlines, isotherms and isoconcentrations at different Sr and Df(Ra=1×105, Pr=0.71, Le=2.0, Br=-5.0) |
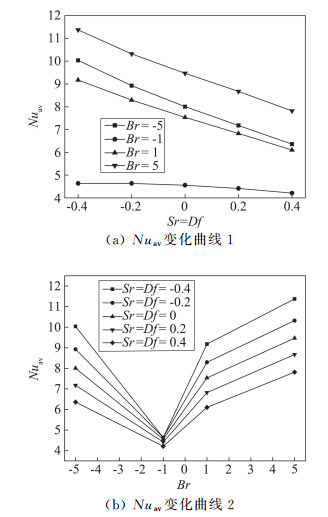
图 4是在不同浮升力比Br、Soret数Sr和Dufour数Df下,发热圆表面Nuav的曲线变化规律。从图 4(a)可以看出,当浮升力比Br不变时,发热圆表面Nuav随着Sr数和Df数的同时增加而几乎呈线性减小,说明传热能力随着Sr数和Df的同时增加而减弱。这是由于Sr数增强,温度场的不均匀对传质的影响增强,传热能力增强;但Df数增加,浓度场的不均匀对传热的影响也在增强,传热能力减弱,且Dufour效应的作用效果较大,即对传热能力的减弱能力更大,因此Nuav总体趋势减小,传热能力减弱。但观察可以发现,当Br=-1时, 发热圆表面的Nuav随着Sr数和Df数的增加下降幅度很小,几乎呈稳定趋势,这是因为当Br=-1时,质浮升力和热浮升力的大小相同且方向相反,故而相互抵消,此时主要靠自然对流进行换热,因此随着Sr数和Df数的同时增大,其传热能力变化不大。同样,从图 4(b)中可以观察到此趋势。进而观察图 4(b)可知,当Sr数和Df数一定时,随着浮升力比Br的增加,发热圆表面Nuav值先减小后增大,说明传热能力先减小后增大。这是因为当Br=-5时,质浮升力和热浮升力方向相反,但质浮升力占主导,会抵消一部分热浮升力作用,随着Br的逐渐增大,质浮升力和热浮升力的抵消效果逐渐增大,且在Br=-1处为低值点且Nuav值相差不大,这是质浮升力和热浮升力完全相互抵消所致,这时,传热能力最弱;当Br逐渐增加为正值时,质浮升力和热浮升力的方向相同,并且相互共同作用,Nuav值又开始逐渐增加,传热能力逐渐增强。
|
图 4 发热圆表面的Nuav的变化曲线 Fig.4 Curve of Nuav around the cylinder |
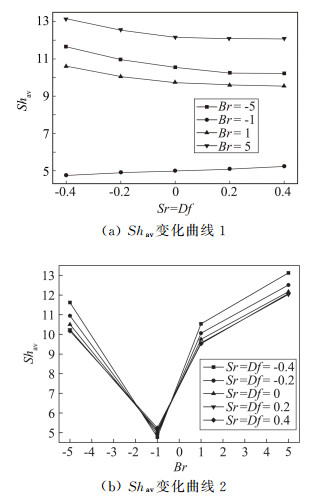
图 5是在不同浮升力比Br、Soret数Sr和Dufour数Df下,发热圆表面Shav的曲线变化规律。观察图 5(a)可知,当浮升力比Br不变时,Shav随着Sr数和Df数的同时增加而缓慢减小,因为Sr数的增加,温度场的不均匀对传质的影响增强,传质能力减弱;但Df数增加,浓度场的不均匀对传热的影响也在增强,传质能力增强,且Soret效应的作用效果较大,又因为条件中Le>1,传质强度本身较大,故其传质能力减小程度较小。但当Br=-1时,Shav随着Sr数和Df数的增加反而有所增加;这是因为当质浮升力和热浮升力相互抵消后,Le>1表示其传质强度较大,所以Shav会有所增加。从图 5(b)可以看出,当Sr数和Df数一定时,随着浮升力比Br的增加,发热圆表面Shav值先减小后增大,说明传质能力先减弱后增强,其同样是因为Br的不同导致质浮升力和热浮升力方向不同;且同样在Br=-1时,Shav值最小,传质能力最弱。
|
图 5 发热圆表面的Shav的变化曲线 Fig.5 Curve of Shav around the cylinder |
本文采用格子Boltzmann方法,在给定条件Ra=1×105,Pr=0.71,Le=2.0,并且考虑Soret和Dufour效应的情况下,对方腔内双扩散自然对流现象进行了研究;为了确保方法的准确性,与已有文献进行了对比验证。在不同浮升力比Br(-5≤Br≤5)、Soret数Sr(-0.4≤Sr≤0.4)和Dufour数Df(-0.4≤Df≤0.4)条件下,本文的数值模拟得出如下结论:
(1) 在相同的浮升力比Br下,随着Soret数Sr和Dufour数Df数值同时增大时,方腔内传热能力逐渐减弱;在相同Soret数Sr和Dufour数Df下,随着Br数的增大,传热能力先减小后增大。
(2) 在相同的浮升力比Br下,随着Soret数Sr和Dufour数Df数值同时增大时,方腔内传热能力逐渐减弱,但当Br=-1时,传热能力有所增加;在相同Soret数Sr和Dufour数Df下,随着Br数的增大,传质能力先减小后增大。
本文采用格子Boltzmann方法对内置高浓度发热圆的方腔内双扩散自然对流现象的研究可为室内污染物扩散过程中的热质耦合作用机理研究提供相应的理论分析支撑。
| [1] |
OSTRACH S. Natural convection with combined driving forces[J]. Physicochemical Hydrodynamics, 1980, 1: 233-247. |
| [2] |
MICHAUD G. Stratification of elements in a quiet atmosphere:diffusion processes[J]. Highlights of Astronomy, 2016, 4(2): S138-S139. |
| [3] |
ZHOU S Q, LU Y Z. Characterization of double diffusive convection steps and heat budget in the deep Arctic Ocean[J]. Journal of Geophysical Research Oceans, 2013, 118(12): 6672-6686. DOI:10.1002/2013JC009141 |
| [4] |
SHIBLEY N C, TIMMERMANS M L, CARPENTER J R, et al. Spatial variability of the Arctic Ocean's double-diffusive staircase[J]. Journal of Geophysical Research Oceans, 2017, 122(2): 980-994. DOI:10.1002/2016JC012419 |
| [5] |
JAGADHA S, HYMAVATHI D, KISHAN N. Soret and Dufour effects on the boundary layer radiative MHD Nanofluid flow over a vertical plate with chemical reaction[J]. Journal of Nanofluids, 2017, 6(1): 97-104. DOI:10.1166/jon.2017.1295 |
| [6] |
王致嫣. 基于CFAST模拟研究通风开口比例对室内火灾的影响[J]. 六盘水师范学院学报, 2016, 28(4): 23-25. WANG Z Y. The study of influences of ventilation opening fraction on compartment fires based on CFAST simulation[J]. Journal of Liupanshui Teachers College, 2016, 28(4): 23-25. (in Chinese) |
| [7] |
KIM H J, LILLEY D G. Heat release rates of burning items in fires[J]. Journal of Propulsion and Power, 2002, 18(4): 866-870. DOI:10.2514/2.6011 |
| [8] |
赵永昌, 朱国庆, 高云骥. 城市地下综合管廊火灾烟气温度场研究[J]. 消防科学与技术, 2017, 36(01): 37-40. ZHAO Y C, ZHU G Q, GAO Y J. Research on temperature filed of fire smoke in urban underground utility tunnel[J]. Fire Science and Technology, 2017, 36(01): 37-40. DOI:10.3969/j.issn.1009-0029.2017.01.012 (in Chinese) |
| [9] |
卓铸, 申凤阳. 基于FDS的钠火三维数值模拟研究[J]. 原子能科学技术, 2016, 50(11): 1979-1985. ZHUO Z, SHEN F Y. Research on three-dimensional numerical simulation of sodium fire based on FDS[J]. Atomic Energy Science & Technology, 2016, 50(11): 1979-1985. (in Chinese) |
| [10] |
张亦昕, 李炎锋, 张仁, 等. 不同地铁车站吊顶形式对火灾烟气扩散的影响[J]. 中国安全生产科学技术, 2016, 12(1): 117-121. ZHANG Y X, LI Y F, ZHANG R, et al. Influence of different forms of suspended ceiling on smoke diffusion of fire in a subway station[J]. Journal of Safety Science and Technology, 2016, 12(1): 117-121. (in Chinese) |
| [11] |
LIU P, GAO Y, LI S S. Comparison of LES and RANS models in compartment fires simulation[J]. Applied Mechanics & Materials, 2013, 301: 119-123. |
| [12] |
AL-AMIRI A M, KHANAFER K M, POP I. Numerical simulation of combined thermal and mass transport in a square lid-driven cavity[J]. International Journal of Thermal Sciences, 2007, 46(7): 662-671. DOI:10.1016/j.ijthermalsci.2006.10.003 |
| [13] |
ZHUO C, ZHONG C, CAO J. Filter-matrix lattice Boltzmann model for incompressible thermal flows[J]. Physical Review E, 2012, 85(85): 046703. |
| [14] |
雍玉梅, 杨超, 尹小龙, 等. 不可压热流体中气体传质扩散过程的LBM数值模拟[J]. 化工学报, 2012, 63(1): 25-35. YONG Y M, YANG C, YIN X L, et al. Numerical simulation of gas diffusion in an incompressible thermal fluid with lattice Boltzmann method[J]. CIESC Journal, 2012, 63(1): 25-35. DOI:10.3969/j.issn.0438-1157.2012.01.004 (in Chinese) |
| [15] |
徐洪涛, 肖瑞雪, 严祯荣, 等. 方腔内双扩散混合对流数值模拟[J]. 化工学报, 2014, 65(s1): 111-118. XU H T, XIAO R X, YAN Z R, et al. Numerical investigations of double diffusive mixed convection in enclosure[J]. CIESC Journal, 2014, 65(s1): 111-118. (in Chinese) |
| [16] |
XU H T, WANG Z Y, KARIMI F, et al. Numerical simulation of double diffusive mixed convection in an open enclosure with different cylinder locations[J]. International Communications in Heat & Mass Transfer, 2014, 52(2): 33-45. |
| [17] |
XU H, XIAO R, KARIMI F, et al. Numerical study of double diffusive mixed convection around a heated cylinder in an enclosure[J]. Journal of University of Shanghai for Science & Technology, 2014, 78(3): 169-181. |
| [18] |
NITHYADEVI N, YANG R J. Double diffusive natural convection in a partially heated enclosure with Soret and Dufour effects[J]. International Journal of Heat & Fluid Flow, 2009, 30(5): 902-910. |
| [19] |
CHENG C Y. Soret and Dufour effects on free convection boundary layers over an inclined wavy surface in a porous medium[J]. International Communications in Heat & Mass Transfer, 2011, 38(8): 1050-1055. |
| [20] |
WANG J, YANG M, HE Y L, et al. Oscillatory double-diffusive convection in a horizontal cavity with Soret and Dufour effects[J]. International Journal of Thermal Sciences, 2016, 106(7): 57-69. |
| [21] |
VEDAVATHI N, RAMAKRISHNA K, REDDY K J. Radiation and mass transfer effects on unsteady MHD convective flow past an infinite vertical plate with Dufour and Soret effects[J]. Ain Shams Engineering Journal, 2015, 6(1): 363-371. DOI:10.1016/j.asej.2014.09.009 |
| [22] |
PAL D, MANDAL G, VAJRAVALU K. Soret and Dufour effects on MHD convective-radiative heat and mass transfer of nanofluids over a vertical non-linear stretching/shrinking sheet[J]. Applied Mathematics & Computation, 2016, s 287-288(C): 184-200. |
| [23] |
ARUNA S, LAKSHMI K J. Soret and Dufour effects on MHD free convective flow past a semi-infinite vertical permeable moving porous plate with heat and mass transfer[J]. Journal of Nanofluids, 2017, 6(4): 657-667. DOI:10.1166/jon.2017.1364 |
| [24] |
何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用[M]. 科学出版社, 2009. HE Y L, WANG Y, LI Q. Lattice Boltzmann method:theory and applications[M]. Science Press, 2009. (in Chinese) |
| [25] |
陶文铨. 数值传热学[M]. 西安交通大学出版社, 2001. TAO W Q. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001. (in Chinese) |
| [26] |
GUO Z, SHI B, ZHENG C. A coupled lattice BGK model for the Boussinesq equations[J]. International Journal for Numerical Methods in Fluids, 2002, 39(4): 325-342. DOI:10.1002/(ISSN)1097-0363 |
| [27] |
QIAN Y H, D'HUMIÈRES D, LALLEMAND P. Lattice BGK models for Navier-Stokes equation[J]. Europhysics Letters (EPL), 1992, 17(6): 479-484. DOI:10.1209/0295-5075/17/6/001 |
| [28] |
GUO Z, SHI B, WANG N. Lattice BGK model for incompressible Navier-Stokes equation[J]. Journal of Computational Physics, 2000, 165(1): 288-306. DOI:10.1006/jcph.2000.6616 |
| [29] |
YU X, GUO Z, SHI B. Numerical study of cross diffusion effects on double diffusive convection with lattice Boltzmann method[C]. International Conference on Computational Science. Springer-Verlag, 2007: 810-817.
|
| [30] |
BOUZUDI M, FIRDAOUSS M, LALLEMAND P. Momentum transfer of a Boltzmann-lattice fluid with boundaries[J]. Physics of Fluids, 2001, 13(11): 3452-3459. DOI:10.1063/1.1399290 |
| [31] |
GUO Z L, ZHENG C G, SHI B C, et al. Non-equilibrium extrapolation method for velocity and pressure boundary conditions in the lattice Boltzmann method[J]. Chinese Physics, 2002, 11(4): 366-374. DOI:10.1088/1009-1963/11/4/310 |
| [32] |
REN Q, CHAN C L. Numerical study of double-diffusive convection in a vertical cavity with Soret and Dufour effects by lattice Boltzmann method on GPU[J]. International Journal of Heat & Mass Transfer, 2016, 93: 538-553. |
 2019, Vol. 37
2019, Vol. 37


