2. 中国空气动力研究与发展中心, 绵阳 621000
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
模型飞行试验[1]是利用飞行器缩尺或简化模型在真实大气环境中飞行,进行气动力/热、飞行力学等科学问题研究的一种试验手段,是空气动力学研究三大手段之一。它具有模型飞行不受外界约束,试验高度和速度范围大,能综合研究气动力、气动热、结构、动力、飞控等问题的特点,所得结果更真实可信。模型飞行试验的独特优势和重要价值历来都很受西方各航空航天发达国家的重视[2-3],特别是近年来在高超声速领域陆续开展了HIFiRE[4-7]、HyShot[8]、HyBoLT[9]、HyCAUSE[10]、EXPERT[11-12]、SHEFEX[13]、Pre-X[14]等飞行试验项目,为边界层转捩、激波边界层干扰等高超声速流动机理深入研究和地面气动力热预测方法修正提供了宝贵的真实飞行数据。
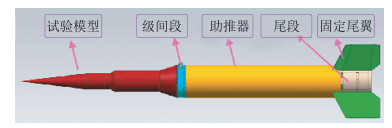
MF-1是中国空气动力研究与发展中心开展的单级火箭助推不分离无控高超声速空气动力学飞行试验研究项目,主要目的是通过在试验模型特定部位安装的温度、压力等传感器,对飞行试验全过程参数变化历程实现测量,为边界层转捩、激波边界层干扰机理研究提供真实飞行数据。MF-1试验飞行器全长6.23 m,最大直径0.6 m,由试验模型、级间段、助推器和尾段等组成(图 1)。
|
图 1 MF-1试验飞行器外形图 Fig.1 Sketch of MF-1 flight vehicle |
本文研究建立了MF-1飞行试验基准弹道设计及拉偏仿真方法模型,开展了MF-1飞行弹道设计和蒙特卡罗拉偏仿真,并对设计仿真结果和滚转共振等问题进行了分析。
1 弹道设计及仿真模型地球模型采用WGS84旋转椭球模型,利用六自由度弹道积分,通过调整发射倾角和发射方位角满足试验窗口和落点位置要求。
1.1 质心运动模型| $ \begin{array}{l} {{\dot x}_d} = {V_{xd}}\\ {{\dot y}_d} = {V_{yd}}\\ {{\dot z}_d} = {V_{zd}}\\ {{\dot V}_{xd}} = \left( {{N_x}{g_0} + \frac{{{F_x}}}{m}} \right)\cos \varphi \cos \psi + \left( {{N_y}{g_0} + \frac{{{F_y}}}{m}} \right) \cdot \\ \;\;\;\left( { - \sin \varphi \cos \gamma + \cos \varphi \sin \psi \sin \gamma } \right) + \left( {{N_z}{g_0} + \frac{{{F_z}}}{m}} \right) \cdot \\ \;\;\;\left( {\sin \varphi \sin \gamma + \cos\varphi \sin\psi \cos\gamma } \right) + {g_x} + {a_{xe}} + {a_{xc}}\\ {{\dot V}_{yd}} = \left( {{N_x}{g_0} + \frac{{{F_x}}}{m}} \right)\sin \varphi \cos \psi + \left( {{N_y}{g_0} + \frac{{{F_y}}}{m}} \right) \cdot \\ \;\;\;\left( {\cos \varphi \cos \gamma + \sin \varphi \sin \psi \sin \gamma } \right) + \left( {{N_z}{g_0} + \frac{{{F_z}}}{m}} \right) \cdot \\ \;\;\;\left( { - \cos \varphi \sin \gamma + \sin \varphi \sin\psi \cos\gamma } \right) + {g_y} + {a_{ye}} + {a_{yc}}\\ {{\dot V}_{zd}} = \left( { - {N_x}{g_0} - \frac{{{F_x}}}{m}} \right)\sin \psi + \left( {{N_y}{g_0} + \frac{{{F_z}}}{m}} \right) \cdot \\ \;\;\;\cos \psi \sin \gamma + \left( {{N_z}{g_0} + \frac{{{F_z}}}{m}} \right)\cos \psi \cos \gamma + {g_z} + {a_{ze}} + {a_{zc}} \end{array} $ | (1) |
式中:xd、yd、zd为飞行器在地球固连系中的位置坐标;Vxd、Vyd、Vzd为地球固连系速度分量;Nx、Ny、Nz为体轴系气动过载分量;Fx、Fy、Fz为发动机推力在体轴系中的分量;φ、ψ、γ为俯仰、偏航、滚转姿态角;gx、gy、gz为重力加速度分量;axe、aye、aze为向心牵连加速度分量;axc、ayc、azc为柯氏加速度分量;g0为常数9.81。
重力加速度、向心牵连加速度和柯氏加速度是位置坐标的函数,需利用地球物理关系进行推导和计算,具体公式和推导过程参见文献[15]。
1.2 绕质心转动模型质心转动的方程是建立在体轴系中的:
| $ {{\mathit{\boldsymbol{\dot \omega }}}_1} = {\mathit{\boldsymbol{J}}^{ - 1}} \cdot {\mathit{\boldsymbol{M}}_1} - {\mathit{\boldsymbol{J}}^{ - 1}} \cdot {{\mathit{\boldsymbol{\tilde \omega }}}_1} \cdot \mathit{\boldsymbol{J}} \cdot {\mathit{\boldsymbol{\omega }}_1} $ | (2) |
其中,ω1=(ωx1 ωy1 ωz1)T
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{I_x}}&{ - {I_{xy}}}&{ - {I_{zx}}}\\ { - {I_{xy}}}&{{I_y}}&{ - {I_{yz}}}\\ { - {I_{zx}}}&{ - {I_{yz}}}&{{I_z}} \end{array}} \right] $ |
| $ {{\mathit{\boldsymbol{\tilde \omega }}}_1} = \left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _{z1}}}&{{\omega _{y1}}}\\ {{\omega _{z1}}}&0&{ - {\omega _{x1}}}\\ { - {\omega _{y1}}}&{{\omega _{x1}}}&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_1} = {\left( {\begin{array}{*{20}{c}} {{M_{x1a}} + {M_{x1T}}}&{{M_{y1a}} + {M_{y1T}}}&{{M_{z1a}} + {M_{z1T}}} \end{array}} \right)^{\rm{T}}} $ |
Mx1a、My1a、Mz1a为绕质心的气动力矩分量,Mx1T、My1T、Mz1T为发动机推力偏斜及偏心产生的绕质心的力矩分量。
姿态角运动方程为:
| $ \begin{array}{l} \dot \varphi = \left( {{\omega _y}\sin \gamma + {\omega _z}\cos \gamma } \right)/\cos \psi \\ \dot \psi = {\omega _y}\cos \gamma - {\omega _z}\sin \gamma \\ \dot \gamma = {\omega _x} + \tan \psi \left( {{\omega _y}\sin \gamma + {\omega _z}\cos \gamma } \right) \end{array} $ | (3) |
式中ωx、ωy、ωz为体轴系角速率分量。
1.3 助推发动机推力模型发动机推力是基于发动机生产厂家提供的内弹道数据进行高度修正得到:
| $ F = {F_0} + {S_{T{\rm{ref}}}}\left( {{p_0} - p} \right) $ |
式中:F0为从内弹道数据差值得到的推力,STref为发动机喷管出口面积,p0为内弹道数据对应的地面大气压,p为飞行器当前高度对应的大气压。
发动机推力在飞行器体轴系中的分量为:
| $ \begin{array}{l} {F_x} = F\cos {\theta _T}\\ {F_y} = F\sin {\theta _T}\cos {\phi _T}\\ {F_z} = F\sin {\theta _T}\sin {\phi _T} \end{array} $ | (4) |
式中:θT为推力线相对于飞行器纵轴的偏斜角度,ϕT为推力偏斜周向角,即推力偏斜方向。
发动机推力产生的绕飞行器质心的力矩为:
| $ \begin{array}{*{20}{c}} {{M_{x1T}} = {F_z}{y_T} - {F_y}{z_T}}\\ {{M_{y1T}} = {F_x}{z_T} - {F_z}{x_T}}\\ {{M_{z1T}} = {F_x}{y_T} - {F_y}{x_T}} \end{array} $ | (5) |
式中xT、yT、zT为发动机推力作用点在飞行器体轴系中的坐标。
1.4 大气模型和风修正模型弹道设计采用的大气密度模型为靶场月平均大气密度统计模型,每个月的模型均以与一系列不同高度对应的大气密度当月平均值给出。弹道设计时,可以根据拟实施发射的月份选择对应的大气密度模型。
弹道设计采用的风场模型为靶场月平均风场统计模型,每个月的月平均模型均以与一系列不同高度对应的风速、风向当月平均值给出。弹道设计时,可以根据拟实施发射的月份选择对应的风场模型。
飞行器相对于大气的速度矢量为:
| $ \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{V}}_d} - {\mathit{\boldsymbol{V}}_w} $ | (6) |
其中:Vd为地面固连坐标系中的飞行器速度矢量,Vw为地面固连坐标系中的风速矢量。
在弹道设计和仿真中,飞行动压、迎角、侧滑角等均是基于风修正后的数据得到。
1.5 空气动力模型弹道设计和仿真中的空气动力学模型是由MF-1气动力团队提供的,是对于地面风洞试验和数值计算结果综合分析并经质心换算等工作后得到的,包括无底阻六分量数据、底阻修正数据、不同高度摩阻修正数据、动导数数据等。
1.6 发射架模型MF-1采用品字型三点同时离轨下挂式倾斜发射,滑轨有效长度6.5 m。在离架前采用固定弹道倾角、弹道偏角和飞行器姿态角的单自由度弹道积分模型,离架后采用1.1节中的正常六自由度弹道积分模型。
2 基准飞行弹道设计结果MF-1基准弹道设计,必须与助推发动机能力、发射场和落区选择等相结合来开展,其基本要求是能够满足对10~40 km高度试验窗口的覆盖。而且,由于试验飞行器无控,为了避免弹道太高、无气动阻尼的真空段太长导致的再入大气层迎角不确定度太大甚至尾部朝前的情况发生,弹道顶点高度在60~90 km之间为宜。在发射点和落区选定后,基准弹道设计的任务,就是通过设计发射架俯仰角和发射方位角,使得试验飞行器落于所选落点附近。
本文基准弹道设计算例采用的大气密度模型和风场模型来自于靶场12月份的月平均统计数据;固体火箭发动机内弹道数据采用生产厂家提供的-10 ℃发动机内弹道数据,发动机推力作用线沿发动机纵轴,无横移无偏斜。
弹道设计采用的试验飞行器满载和空载质心位置及质量惯量见表 1,其中的结构坐标系定义为:锥理论顶点为原点,X轴向后,Y轴向上,Z轴与X、Y构成右手系;体轴系定义为:质心为原点,X轴向前,Y轴向上,Z轴与X、Y构成右手系。
| 表 1 MF-1质心位置和质量惯量 Table 1 MF-1 gravity center, mass and moment of inertia |
|
|
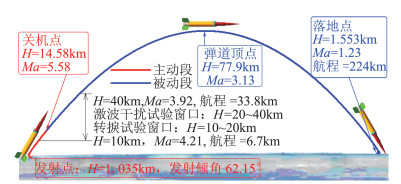
基于以上条件,对MF-1试验飞行器进行基准弹道设计得到的发射架仰角为62.148°、发射方位角为267.410°。图 2给出了MF-1基准弹道设计结果的飞行剖面示意图,表 2给出了基准弹道特征点参数,图 3给出了基准弹道参数曲线。
|
图 2 MF-1飞行剖面示意图 Fig.2 Sketch of the MF-1 flight profile |
| 表 2 MF-1基准弹道特征点参数 Table 2 Parameters of MF-1 standard trajectory feature points |
|
|
|
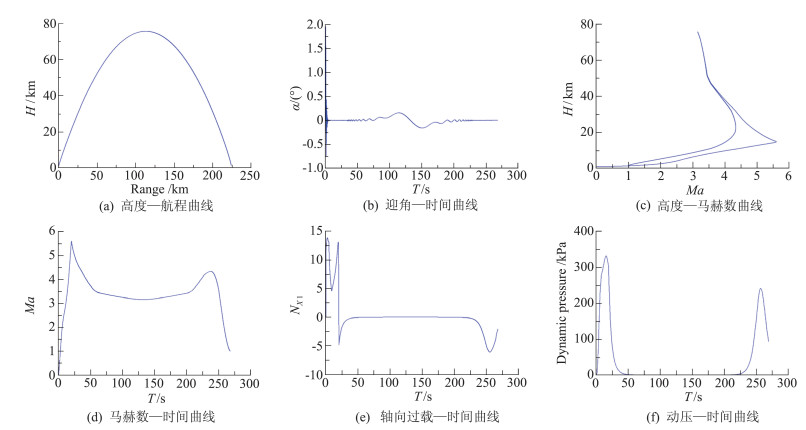
图 3 MF-1基准弹道参数曲线 Fig.3 Curves of MF-1 standard trajectory parameters |
从设计结果可见,发射离架后由于弹道下沉导致的最大飞行迎角不超过2°,此后飞行迎角迅速收敛到0°附近。随着高度迅速升高大气密度越来越稀薄,迎角振幅逐渐发散,最大振幅不超过0.2°,进入下降段后迎角振幅又向0°收敛。整个飞行过程中最大动压约330 kPa,最大轴向过载14左右。经MF-1气动力/热研究团队评估,该弹道满足MF-1气动研究试验窗口需求,气动热环境也属于可承受范围。
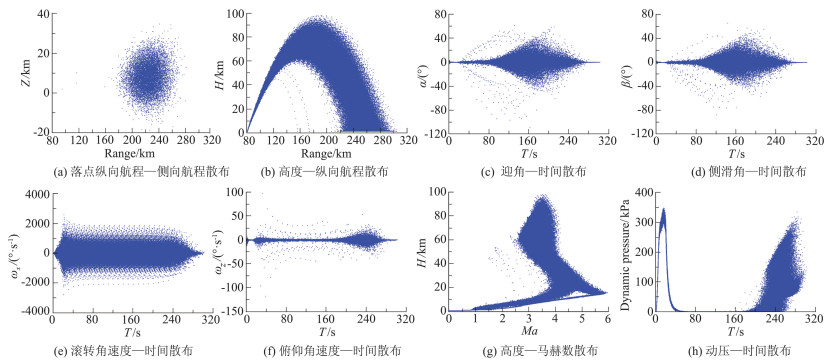
3 蒙特卡罗拉偏仿真结果MF-1蒙特卡罗拉偏仿真所采用的偏差因素及其分布,是由包括总体、气动、动力、发射架等专业在内的来自总体单位、型号部门、院校等单位的专家们经过多次会议讨论确定的,动力、发射架等拉偏依据主要来自产品给出的精度数据,所有的小不对称气动参数主要来自于尾翼安装偏差影响的气动力计算结果,其它拉偏参数也借鉴了多种类似飞行器型号经验。表 3给出了基于设计计算预估数据的MF-1六自由度弹道拉偏仿真偏差因素及取值,其中的小不对称参数按每片尾翼都存在7.5′安装角偏差估算得到,比如,估算滚转小不对称气动力时,假设四片尾翼安装角的方向均可产生同一个方向的滚转力矩;估算俯仰小不对称气动力时,假设四片尾翼安装角的方向均可产生同一个方向的俯仰力矩和法向力;偏航方向依此类推。图 4给出了10000条弹道的蒙特卡罗拉偏结果弹道参数散布图,其中的弹道参数历程散布是按照每条弹道起始时刻在0~10 s间随机均匀分布、每10 s一个弹道点的方式进行输出和作图的。从结果可见,在各种随机拉偏因素的影响下,弹道参数和落点参数均有较大散布。主要参数散布情况统计结果为:落点纵向航程均值223.75 km,均方差15.93 km;落点侧向航程均值8.14 km,均方差6.93 km;弹道顶点高度均值75.84 km,均方差6.09 km;弹道最大滚转角速率均值9.34°/s,均方差473.9°/s。
|
图 4 基于预估数据的MF-1蒙特卡罗飞行仿真结果 Fig.4 Monte Carlo flight simulation results for MF-1 based on predicted data |
| 表 3 MF-1六自由度蒙特卡罗飞行仿真偏差因素分布 Table 3 Random parameters distributions of MF-1 for 6-DOF Monte Carlo flight simulation |
|
|
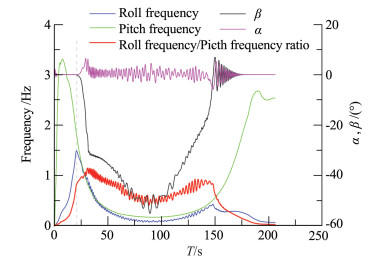
另外,从图 4的高度-航程散布可见,有几条弹道的高度明显低于其它弹道,航程也要近得多,经分析,这主要是由于在飞行过程中发生了滚转共振[16]连锁,气动阻力显著增加而导致的。飞行器在飞行过程中发生滚转共振连锁的原因,是由于在某些条件下其滚转频率与气动俯仰偏航频率在较长时间段内一直比较接近,从而引发共振,使得飞行器的飞行总迎角显著增大,横法向过载显著增加,甚至可能造成飞行器解体。以图 4中弹道高度最低的弹道(蒙特卡罗仿真的第9264条弹道)为例,图 5给出了该条弹道的滚转频率、俯仰频率、滚转与俯仰频率之比,以及迎角侧滑角的时间历程。从图可见,在关机点附近,俯仰频率与滚转频率趋于接近,二者之比迅速达到1附近,随着高度的增加和动压的减小,这两个频率的变化趋势也非常接近,导致二者之比的量级在较长时间内维持在1附近。这也使得侧滑角在关机点前后迅速增大到-30°~-40°,并维持了很长时间,属于典型的较长时间的滚转共振连锁。后来,随着MF-1试验飞行器重新进入稠密大气内飞行,俯仰频率迅速增加,与此同时滚转频率逐渐减小,滚转共振的条件不复存在,侧滑角也就迅速恢复到0°附近并振荡收敛。由此可见,关机点附近滚转频率与气动俯仰偏航频率是否接近1,可以近似作为MF-1可能滚转共振出现的判据。近似以滚转频率/俯仰频率的比值在0.7~1.5之间作为可能发生滚转共振的条件,从上述的拉偏仿真结果得到的可能发生滚转共振的概率为6.3%。
|
图 5 第9264条弹道滚转共振分析曲线 Fig.5 Curves of simulated No. 9264 trajectory for MF-1 roll resonance analysis |
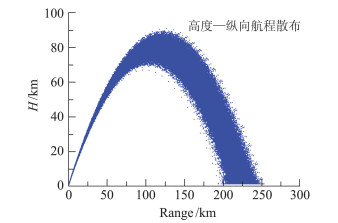
在MF-1完成制造总装出厂前,由于有了更为可信的气动力风洞试验数据以及合练产品的安装精度以及质量特性实测数据,使得用于飞行分析的数据可信度有了明显提高。特别是尾翼安装后的实测结果表明,安装精度远远高于之前的估计,四片尾翼安装角代数和仅为5′量级,这也必将导致拉偏后试飞器的滚转角速率散布显降低。在此基础上,进行的10000条拉偏弹道仿真结果表明,没有一条弹道满足上面的可能发生滚转共振的条件,说明基于总装后实测数据条件下,MF-1试飞器在上升段发生滚转共振的概率接近0,试飞器不会发生滚转共振而导致解体风险。图 6给出了基于总装后实测数据的10000条蒙特卡罗拉偏弹道的高度-时间分布。
|
图 6 基于出厂测量数据的MF-1蒙特卡罗飞行仿真结果 Fig.6 Monte Carlo flight simulation results for MF-1 based on final factory test data |
研究建立了MF-1试验飞行器弹道设计与拉偏仿真数学模型,并开展了飞行试验弹道设计与拉偏仿真分析。结果表明:
(1) 本文建立的弹道设计和仿真模型,可用于倾斜发射无控飞行器的弹道设计和偏差条件下的弹道及落点散布特性研究;
(2) 对于MF-1这类无控飞行器,在偏差条件下可能在飞行过程中发生滚转共振,导致飞行风险增加;
(3) MF-1严格控制了尾翼加工安装精度后,飞行过程中不会发生滚转共振。
| [1] |
张守言, 惠宇昕, 等. 模型自由飞试验[M]. 北京: 国防工业出版社, 2002. ZHANG S Y, HUI Y X, et al. Modeling free flight[M]. Beijing: National Defense Industry Press, 2002. (in Chinese) |
| [2] |
战培国. 美国空气动力学飞行试验平台综述[J]. 飞行力学, 2015, 33(5): 385-389. ZHAN P G. An overview of American aerodynamic flight testbeds[J]. Flight Dynamics, 2015, 33(5): 385-389. (in Chinese) |
| [3] |
叶蕾. 美国高超声速计划发展规律探索[J]. 飞航导弹, 2008(12): 20-24. YE L. A review of American aerodynamic flight test platform[J]. Aerodynamic Missile Journal, 2008(12): 20-24. (in Chinese) |
| [4] |
WADHAMS T P, MACELANV M G. Per-flight ground testing of the full-scale HIFiRE-1 at fully duplicated flight conditons[C]. 37th AIAA Fluid Dynamics Conference and Exhibit.
|
| [5] |
ODAM J, PAULL A, ALESI H. HIFiRE0 flight test data[R]. AAIA 2009-7293, 2009.
|
| [6] |
SMART M K, SUARWEERA M V. HIFiRE7-development of a 3-D scramjet for flight testing[R]. AAIA 2009-7259, 2009.
|
| [7] |
GURBER M, JACKSON K, EKULND D. Instrumentation and performance analysis plans for the HIFiRE flight 2 experiment[R]. AIAA 2009-5032, 2009.
|
| [8] |
NEUENHAHN T, OLIVIER H, PAULL A. Development of the HyShot stability demonstrator[R]. AIAA 2006-2960, 2006.
|
| [9] |
CHEN F J (FRANK), BERRY S A. HyBoLT flight experiment[R]. NASA/TM-2010-216725.
|
| [10] |
WALKER S, RODGERS F, PAULL A, et al. HyCAUSE flight test program[R]. AIAA 2008-2580, 2008.
|
| [11] |
MUYLAERT J, CIPOLLIN F, WALPOT L, et al. Flight experiments for hypersonic vehicle development expert[R]. RTO-EN-AVT-130.
|
| [12] |
BARRIO A M, SUDARS M, GAVIRA J, et al. EXPERT-The ESA experimental re-entry test-bed. trajectory and mission design[R]. AIAA 2011-6342, 2011.
|
| [13] |
文苏丽, 时兆峰. SHEFEX-全新的高超声速技术试验平台[J]. 飞航导弹, 2010(9): 24-28. WEN S L, SHI Z F. SHEFEX-, an new hypersonic technology test platform[J]. Aerodynamic Missile Journal, 2010(9): 24-28. (in Chinese) |
| [14] |
BAIOCCOP. Pre-X experimental re-entry lifting body-design of flight test experiments for critical aerothermal phenomena[R]. ADA476581.
|
| [15] |
和争春.飞船返回舱气动参数辨识及其有关问题研究[D].西安: 西北工业大学, 2004. HE Z C. Research on aerodynamic parameters identification and related problems for spaceship re-entry capsule[D]. Xi'an: Northwestern polytechnical University, 2004. |
| [16] |
蔡金狮, 董能力. 再入弹头滚转共振概率估算[J]. 宇航学报, 1995, 16(1): 1-7. CAI J S, DONG N L. Roll resonance probability estimation of reentry warhead[J]. Journal of Astronautics, 1995, 16(1): 1-7. (in Chinese) |
 2019, Vol. 37
2019, Vol. 37

