在流体力学领域,经常会遇到大量微小粒子在流体中运动的问题。这类问题中,往往还伴随着粒子数量和粒子尺寸分布的改变。比较典型的例子:水的同质凝结问题。对于这类问题,需要求解粒子的总量平衡方程(Population Balance Equation,PBE)。如果用拉格朗日法求解,需要追踪大量的粒子轨迹,计算量庞大,很难运用到实际问题当中。
矩方法,又可以称作内部坐标矩方法,通过求解内部坐标的各阶矩的输运方程,反应粒子数量及尺寸分布的变化。这里的内部坐标,可以是粒子的半径、表面积、体积等等。以球型粒子,内部坐标取粒子半径为例:零阶矩表示粒子数量,一阶矩表示粒子的半径和,二阶矩、三阶矩分别和粒子的表面积和、体积和为同一量纲(之间相差一个常数)。根据内部坐标的各阶矩,并对粒子分布函数进行适当假设,可以反推出粒子数量和粒子尺寸分布的信息。相比于运用拉格朗日描述的求解方法,矩方法大大简化了计算量,使得工程应用成为可能。
1 矩方法 1.1 传统矩方法矩方法最早是Hulburt[1]于1964年从经典统计力学角度引入的,并且应用此方法,讨论了水滴的凝结增长问题。下面对传统矩方法做一个简单介绍。首先,定义水蒸气凝结生成的液滴在相空间的数密度f(ξ, t),即分布函数。其中t为时间,ξ为可以描述诸如液滴尺寸、空间分布等状态特性的相空间坐标:
| $ \xi = \left[ {{\xi _1},{\xi _2},{\xi _3}, \cdots } \right] $ | (1) |
相空间坐标速度可以写成:
| $ \frac{{{\rm{d}}{\xi _i}}}{{{\rm{d}}t}} = {v_i}\left( {\xi ,t} \right);\;\;\;i = 1,2,3, \cdots $ | (2) |
进而得到了关于分布函数f(ξ, t)的控制方程:
| $ \frac{{\partial f}}{{\partial t}} + \sum\limits_i {\frac{{\partial \left\{ {{v_i}\left( {\xi ,t} \right)f} \right\}}}{{\partial {\xi _i}}} = h\left( {\xi ,t} \right)} $ | (3) |
其中h(ξ, t)为相空间中液滴数密度的增量。对于实际的三维空间中的相变问题,方程(3)退化成:
| $ \frac{{\partial f}}{{\partial t}} + \sum\limits_i^3 {\frac{{\partial \left\{ {{v_i}f} \right\}}}{{\partial {x_i}}}} + \sum\limits_j {\frac{{\partial \left\{ {{G_j}\left( {c,T,r} \right)f} \right\}}}{{\partial {r_j}}}} = B\left( {c,T,r} \right) $ | (4) |
其中:xi为笛卡尔坐标; vi为笛卡尔坐标中液滴的速度; ri为内部坐标; Gj(c, T, r)为液滴的增长率; B(c, T, r)为成核率; c、T是水蒸气浓度和温度,描述了影响凝结成核与增长的环境因素。假设液滴为球型,内部坐标取液滴半径,引入内部坐标的k阶矩:
| $ {\mu _k}\left( {x,t} \right) = \left\langle {{r^n}} \right\rangle = \int {{r^k}f\left( {x,r,t} \right){\rm{d}}r} ;\;\;\;k = 0,1,2, \cdots $ | (5) |
联立方程(4)和(5),得到了内部坐标矩的输运方程:
| $ \begin{array}{l} \frac{{\partial {\mu _k}}}{{\partial t}} + \sum\limits_i^3 {\frac{{\partial \left\{ {{v_i}{\mu _k}} \right\}}}{{\partial {x_i}}}} - k\left\langle {{r^{k - 1}}G\left( {c,T,r} \right)} \right\rangle = \\ \int {{r^k}B\left( {c,T,r} \right){\rm{d}}r} ;\;\;\;k = 0,1,2, \cdots \end{array} $ | (6) |
观察方程(6),一般来说,成核率由成核理论给出,在经典成核理论中[2-5],成核率与液滴的尺寸分布无关,因此等式右边并不涉及具体的积分运算。等式左边第三项为液滴增长项,由方程(6)可知,液滴增长率必须满足与半径成线性关系,否则k阶矩方程中还将包含非k阶矩,使得方程组无法封闭求解。然而,液滴的增长率并非严格满足液滴半径的线性关系,甚至相差很多,这一限制也成为传统矩方法的重要缺陷。在实际应用中,Hill[6]提出了与半径无关的平均增长率的概念,并且把它应用到细长管中凝结的研究中。其后的学者基本沿用这一处理方法,此方法虽然在数学上并不严格,但是得到的数值结果与实验吻合较好[7-8]。
另一方面,可以通过给出粒子分布函数f(ξ, t)的具体形式来封闭方程,并且f(ξ, t)中的未知量要关于内部变量独立。目前比较常用的分布函数为对数正态分布,假设粒子是球型,内部坐标取粒子半径,其形式如下:
| $ f\left( {r,t} \right) = \frac{1}{r} - \frac{{N\left( t \right)}}{{\sqrt {2{\rm{ \mathsf{ π} }}} \ln \sigma \left( t \right)}}\exp \left[ { - \frac{{{{\ln }^2}\left( {r/{r_g}} \right)}}{{2{{\ln }^2}\sigma \left( t \right)}}} \right] $ | (7) |
其中:rg是几何平均半径,σ(t)几何标准差,N(t)是粒子总数。f(r, t)中存在3个未知量,因此至少需要3个矩变量来建立矩方程。f(r, t)中的未知量和矩变量的关系如下:
| $ \left\{ \begin{array}{l} {r_g} = \sqrt {\mu _1^4/\mu _0^3{\mu _2}} \\ {\ln ^2}\sigma \left( t \right) = \ln \left( {{\mu _2}{\mu _0}/\mu _1^2} \right)\\ N\left( t \right) = {\mu _0} \end{array} \right. $ | (8) |
需要指出的是,f(ξ, t)的形式并不唯一,其他满足条件的分布也是可行的。
1.2 求积矩方法和直接求积矩方法前文提到,传统矩方法要求液滴增长率只能是液滴半径的线性关系,因此对许多应用都带来限制。为了解决这一问题,McGraw[9]发展出了求积矩方法(Quadrature Method of Moments, QMOM)。这一方法的核心思想是通过高斯求积法处理各阶矩,使积分形式转变成求和形式。根据这一思想,各阶矩和与矩相关的增长公式变形为如下形式:
| $ \left\{ \begin{array}{l} {\mu _k} = \int {{r^k}f\left( r \right){\rm{d}}r} = \sum\limits_{i = 1}^n {r_i^k{w_i}} \\ k\int {{r^{k - 1}}\phi \left( r \right)f\left( r \right){\rm{d}}r} \cong k\sum\limits_{i = 1}^n {r_i^{k - 1}\phi \left( {{r_i}} \right){w_i}} \end{array} \right. $ | (9) |
其中:ri是高斯点,wi是权重。高斯点取得越多,计算精度越高,同时计算量也越大。综合考虑计算量与计算精度,实际应用中一般取3个高斯点。具体计算时,首先根据P-B算法(product-difference algorithm)[10]构建一个三对角矩阵,求解该矩阵的特征值和特征向量,进一步求解得到高斯点与该点对应的权重。对于此方法的效率和稳定性,学者也进行了验证[11]。
虽然求积矩方法最初的目的是为了解决液滴增长率的限制问题,但它的意义却不止于此。首先,应用该方法避免了对分布函数f(ξ, t)的任何假设,f(ξ, t)的形式不需要显式知道。其次,高斯求积思想的引入,间接体现出矩与内部坐标之间的关系,为矩方法的进一步发展开阔了思路。在实际应用中,求积矩方法不仅可以用来研究液滴的增长问题,也被用来研究凝结,液滴聚合、破碎等问题[12-13]。
求积矩方法也存在着一定的局限性。求积矩方法追踪的仍然是各阶矩,这一点与传统矩方法并无本质区别。因此,求积矩方法不能处理相间、内部坐标间有相互作用的问题。另一方面,由于需要计算矩,求积矩方法在推广到多组分问题时,计算变得十分复杂。因而,在求积矩方法的基础上,Fox等[14]发展了直接求积矩方法(Direct Quadrature Method of Moments, DQMOM),分布函数f(ξ; x, t)通过Dirac函数表示出来:
| $ \left\{ \begin{array}{l} f\left( {\xi ;x,t} \right) = \sum\limits_{i = 1}^N {{w_i}\left( {x,t} \right)\delta \left[ {\xi - {{\left\langle \xi \right\rangle }_i}\left( {x,t} \right)} \right]} \\ \delta \left[ {\xi - {{\left\langle \xi \right\rangle }_i}\left( {x,t} \right)} \right] = \prod\limits_{j = 1}^{{N_S}} {\delta \left( {\xi - {{\left\langle {{\xi _j}} \right\rangle }_i}} \right)} \end{array} \right. $ | (10) |
其中:N表示求积点数,NS表示组分数。将f(ξ; x, t)代入PBE中,得到直接求积矩方法的控制方程。由于直接求积矩方法追踪的是高斯点和对应的权重,各高斯点拥有单独的相速度。因此,此方法可以体现各组分、各相以及各高斯点所代表的相坐标之间的差别。
直接求积矩方法的应用,可以参考Fox等的文章[15-16]。
1.3 近期矩方法的发展 1.3.1 有限区域试探函数矩方法有限区域试探函数矩方法(Finite size domain Complete set of trial functions Method Of Moments, FCMOM)[17-18],通过一系列正交的基函数来近似粒子分布函数f(ξ, t):
| $ f\left( {\xi ,t} \right) = \sum\limits_{n = 0}^\infty {{C_n}\left( t \right){\mathit{\Phi }_n}\left( \xi \right)} $ | (11) |
其中,Φn(ξ)是正交基函数,Cn(t)是膨胀因子。考虑到实际问题中,粒子的尺寸是有限的,可以将分布函数转换到有限区域[ξmin, ξmax]求解。并且可以通过无量纲化,进一步将求解域化简到标准无量纲区域[-1, 1]上。此时,原问题变成动边界问题。[-1, 1]上无量纲分布函数表示为:
| $ {\bar{f}}'\left( \bar{\xi },t \right)\underline{\backsim }\sum\limits_{n=0}^{M-1}{{{c}_{n}}\left( t \right){{\phi }_{n}}\left( {\bar{\xi }} \right)} $ | (12) |
| $ {\phi _n}\left( {\bar \xi } \right) = \sqrt {\frac{{2n + 1}}{2}} {P_n}\left( {\bar \xi } \right) $ | (13) |
进而可以得到系数的cn(t)表达式:
| $ \begin{array}{*{20}{c}} {{c_n} = \int\limits_{ - 1}^1 {\bar f'{\phi _n}{\rm{d}}\bar \xi } = \sqrt {\frac{{2n + 1}}{2}} \cdot \frac{1}{{{2^n}}}\sum\limits_{i = 0}^n {{{\left( { - 1} \right)}^{n - i}}} \cdot }\\ {\frac{{\left( {2i} \right)!}}{{\left( {2i - n} \right)!}}\left\{ {\frac{1}{{\left( {n - i} \right)! \cdot i!}}} \right\}{\mu _{2i - n}}} \end{array} $ | (14) |
方程(14)中,忽略阶数为负值的矩。
与其他方法相比,有限区域试探函数矩方法可以得到分布函数f(ξ, t)的近似表达式。
1.3.2 调节因子矩方法在求积矩方法中,由于矩的数值跨度太大,会造成求解矩阵的困难。另一方面,在直接求积矩方法中,往往由于源项过大,会造成负的权值点。针对这一问题,有学者[19]提出调节因子矩方法(Adjustable MOM)。
| $ {\mu _k} = \int {{\xi ^{k/P}}f\left( {\xi ,t} \right){\rm{d}}\xi } $ | (15) |
方程(15)中,P为调节因子,通过改变P的大小,可以对矩的数值范围进行调节。
1.3.3 扩展矩方法Falola等[20]发展了一套扩展矩方法(EMOM),将矩用一系列加权求和表示:
| $ {\mu _k} = \sum\limits_{i = 1}^n {{n_i}\xi _i^k} \cdot \Delta {\xi _i} $ | (16) |
其中ni为ξi处的粒子数密度。更高阶的表示,可以写成:
| $ {\mu _k} = \sum\limits_{i = 1}^n {{n_i}\xi _i^k} \cdot \Delta {\xi _i} $ | (17) |
这种方法可以看成是直接求积矩方法的特例,但是计算上更便捷。
1.3.4 扩展直接求积矩方法扩展直接求积矩方法(EQMOM)的思想与FCMOM方法较为相近,可以得到粒子分布函数的具体表达形式。对比公式(13),粒子分布函数改写为[21]:
| $ f\left( \xi \right) = \sum\limits_{\alpha = 1}^N {{w_\alpha }{\delta _\sigma }\left( {\xi ;{\xi _\alpha }} \right)} $ | (18) |
其中δσ(ξ; ξα)不再表示δ函数而是一个分布,如Gamma分布:
| $ {\delta _\sigma }\left( {\xi ;{\xi _\alpha }} \right) = \frac{{{\xi ^{{\lambda _\alpha } - 1}}{e^{ - \xi /\sigma }}}}{{\mathit{\Gamma }\left( {{\lambda _\alpha }} \right){\sigma ^{{\lambda _\alpha }}}}} $ | (19) |
δσ(ξ; ξα)也可以用对数正态分布表示[22]。
1.3.5 处理非圆粒子一般的矩方法中,大多假设粒子为圆形。Alexiadis等[23]引入了粒子形状因子,研究了处理非圆粒子的矩方法。并且将此方法应用于粒子聚合问题的研究,取得了较好的结果。
2 经典矩方法在水凝结研究中的应用如前所述,在液滴增长率与半径成非线性关系时,矩输运方程(6)在数学上不封闭。经典矩方法主要指根据Hill[6]提出的液滴平均增长率概念,解决封闭求解问题发展而来的矩方法。通过此方法得到的矩方程具有结构简单,计算量小的优点。此外,经典矩方法还可以方便的与常用的商业软件如FLUENT等结合,处理复杂流动中的水蒸气相变问题[24]。国内外学者应用矩方法研究了水蒸气凝结在燃烧加热高超声速风洞[25-26]、机翼气动特性[27-30]、汽轮机能量转换[31-32]、大气中气溶胶颗粒形成与传输[33-36]等众多领域开展了大量的研究工作。下面将对经典矩方法做一简要介绍,并且应用经典矩方法,对Prandtl-Meyer膨胀流动中的凝结问题进行了研究。
2.1 经典矩方法流动中随着状态参数的变化,当饱和度大于1时,水蒸气处于过饱和状态,将可能发生气液相变即凝结。水的凝结过程可以由液滴的形成(成核)和增长两个子过程来描述。假设液滴为球形,增长率可用其半径变化率dr/dt表示。Hill[6]提出,若忽略液滴的Kelvin效应,在Knudsen数较大(Kn>2),也即半径r较小时,其变化对dr/dt的影响较小。在这种情况下,可引入不随半径变化的平均增长率
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho {Q_k}} \right) + \nabla \cdot \left( {\mathit{\boldsymbol{v}}\rho {Q_k}} \right) = k\bar {\dot r}\rho {Q_{k - 1}} + {r^{ * k}}{J_n},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0,1,2, \cdots \end{array} $ | (20) |
其中:
| $ \rho {Q_n} = {\mu _n} = \int_{{r_b}}^\infty {{r^n}f{\rm{d}}r} $ | (21) |
若所考虑的多相体系中,凝结液滴很小,气液两相的差异可以忽略,将多相流动介质作为混合物处理,ρ为混合物密度,方程(6)中液滴运动速度也替换为流动速度。与μn定义于单位体积略有不同,矩Qn定义为单位混合物质量的相关量,如零阶矩Q0为单位质量混合物中的液滴数密度,而Q3为单位质量混合物中液滴所占的体积,与热力学参数直接相关。
一般来说,所求液滴尺寸分布的矩的阶数越高,矩方程个数越多,反映液滴尺寸分布的信息也越多。但考虑到具体计算的效率,一般只取低阶矩进行计算。经典矩方法采取四个低阶矩方程作为相变控制方程:
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho {Q_0}} \right) + \nabla \cdot \left( {\rho {Q_0}\mathit{\boldsymbol{v}}} \right) = {J_n}\\ \frac{\partial }{{\partial t}}\left( {\rho {Q_1}} \right) + \nabla \cdot \left( {\rho {Q_1}\mathit{\boldsymbol{v}}} \right) = \overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \rho {Q_0} + {J_n}{r^ * }\\ \frac{\partial }{{\partial t}}\left( {\rho {Q_2}} \right) + \nabla \cdot \left( {\rho {Q_2}\mathit{\boldsymbol{v}}} \right) = \overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \rho {Q_1} + {J_n}{r^{ * 2}}\\ \frac{\partial }{{\partial t}}\left( {\rho {Q_3}} \right) + \nabla \cdot \left( {\rho {Q_3}\mathit{\boldsymbol{v}}} \right) = 3\overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \rho {Q_2} + {J_n}{r^{ * 3}} \end{array} $ | (22) |
在建立矩方程时,没有考虑液相与气相间的速度滑移,将液滴与气体当作一个整体进行考虑。因此完整的控制方程包括了混合相的控制方程(不考虑黏性时为欧拉方程,考虑黏性时为纳维-斯托克斯方程)和矩方程。将相变控制方程与二维气体动力学Euler方程结合,就可以得到整个含有相变过程的高速流动控制方程组:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}} = \mathit{\boldsymbol{S}} $ | (23) |
其中:U为变量,F和G为通量,S为源项。分别有:
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = \left( \begin{array}{l} \rho \\ \rho u\\ \rho v\\ \rho E\\ \rho {Q_3}\\ \rho {Q_2}\\ \rho {Q_1}\\ \rho {Q_0} \end{array} \right);\;\;\;\;\mathit{\boldsymbol{F}} = \left( \begin{array}{l} \rho u\\ \rho {u^2} + p\\ \rho uv\\ \left( {\rho E + p} \right)u\\ \rho {Q_3}u\\ \rho {Q_2}u\\ \rho {Q_1}u\\ \rho {Q_0}u \end{array} \right);\\ \mathit{\boldsymbol{G}} = \left( \begin{array}{l} \rho v\\ \rho uv\\ \rho {v^2} + p\\ \left( {\rho E + p} \right)v\\ \rho {Q_3}v\\ \rho {Q_2}v\\ \rho {Q_1}v\\ \rho {Q_0}v \end{array} \right);\\ \mathit{\boldsymbol{S}} = \left( \begin{array}{l} 0\\ 0\\ 0\\ 0\\ {J_n}{r^{ * 3}} + 3\rho {Q_2}\overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \\ {J_n}{r^{ * 2}} + 2\rho {Q_1}\overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \\ {J_n}{r^ * } + \rho {Q_0}\overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \\ {J_n} \end{array} \right) \end{array} $ | (24) |
其中E表示单位质量混合物的总能量。由分布函数的定义,可知单位体积混合物中包含的液滴总体积:
| $ {V_l} = \int_{{r^ * }}^\infty {\frac{{4{\rm{ \mathsf{ π} }}}}{3}{r^3}f\left( r \right){\rm{d}}r} = \frac{{4{\rm{ \mathsf{ π} }}}}{3}\rho {Q_3} $ | (25) |
由此可以计算液态水的质量分数:
| $ g = \frac{{{\rho _l}{V_l}}}{\rho } = \frac{{4{\rm{ \mathsf{ π} }}}}{3}{\rho _l}{Q_3} $ | (26) |
ρl为液态水的密度。控制方程中的三阶矩方程也可改写:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\rho g} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho gu} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho gv} \right)}}{{\partial y}} = }\\ {\frac{{4{\rm{ \mathsf{ π} }}}}{3}{\rho _l}\left[ {{J_n}{r^{ * 3}} + 3\rho {Q_2}\overline {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}t}}} \right)} } \right]} \end{array} $ | (27) |
上式实际上是液态水质量的对流方程。上述方程组不封闭,还需要添加气体状态方程(由于液相质量占比很小,因此忽略液相体积对压强的影响)和压力、温度修正方程。气体状态方程在很多文献中都有涉及,此处不做赘述。
通过求解矩的演化过程,得到各阶矩随时间的变化情况,再对液滴分布函数作适当假设,就可以推导出液滴尺寸分布的信息。
2.3 伴随同质凝结的Prandtl-Meyer膨胀流动超声速气流经过一个转角,气体膨胀,马赫数上升,压力、密度、温度降低,形成一列中心稀疏波。在二维情况下,Prandtl和Meyer首次给出了流动的解析解,被收入大多数空气动力学教材中,因此这一列稀疏波又被称为Prandtl-Meyer(以下简称PM)膨胀波。当气体中包含水蒸气时,沿流线气体膨胀,压强降低,水蒸气分压也随之降低;同时,温度降低,水蒸气饱和蒸气压降低。由于水蒸气饱和蒸气压与温度呈幂指数关系,从而导致水蒸气饱和蒸气压更快的降低,使得水蒸气饱和度S(水蒸气分压与饱和蒸气压之比)沿流线逐步升高。当饱和度S大于1时,就可能发生凝结。
伴随凝结的PM流动,在科学实验和工业生产中也是常见的现象。例如,在超声速飞机机翼背风面,超声速气流膨胀,速度加快,温度降低。如果来流中水蒸气含量较高,水蒸气有可能发生凝结。凝结放出潜热,使局部压力提高,形成各种波系结构(后文称凝结波或凝结激波),改变了机翼上的压力分布,对机翼的受力产生影响。而在工业生产中,蒸汽轮机中的凝结问题也可以简化成伴随凝结的PM流动问题。一方面,凝结放热,影响流场结构,进而影响蒸汽轮机的效率。另一方面,在这种有限的区域内,由于凝结的自我抑制性,凝结波可能会产生自激振荡,给叶片施加一个周期性的载荷,影响叶片的使用寿命,同时产生噪声。
对于伴随凝结的PM流动问题,已有不少学者开展了相关研究。Smith[37]对典型的二维超声速流动绕过尖角膨胀形成的PM波中的凝结问题进行了实验研究,发现凝结区域向来流方向弯曲。这表明之前Steffen[38]研究此类问题时提出的假设“从拐点发出的射线上放热量相同”并不恰当。Kurshakov等[39]同样进行了实验研究,发现了膨胀扇中凝结导致的激波。凝结激波并不与拐点相连,而是在距拐点一定距离的区域形成。Frank[40]则首次观测到了凝结激波的非定常振荡现象,并对伴随凝结的定常和非定常流动进行了比较。Delale等采用渐近方法分析了PM流动中的凝结现象,并分为没有凝结激波的亚临界情况[41]和存在凝结激波的超临界情况[42]。结果表明:亚临界时凝结区域向来流方向弯曲,这与Smith的实验结果吻合;超临界时给出了凝结激波的起始位置,并不与拐点相接,也符合Kurshakov的实验观测结果。在具体的应用方面,White等[43]对蒸汽轮机叶片处的凝结问题进行了实验研究并进行了数值模拟。实验结果与数值结果吻合得较好。Kim等[44]通过实验和数值研究,提出了一种控制凝结的多孔结构,可减弱膨胀扇中凝结激波强度,且能完全抑制凝结激波的振荡。
PM流动膨胀会导致凝结现象发生,凝结释放热量将改变流场结构,流场变化进一步影响凝结的进行,两者耦合在一起,使得流动更为复杂。在一定参数范围内还可能产生振荡现象,呈现出强烈的非定常效应。这使得对伴随凝结的PM流动的分析变得相当困难。有界区域内的绕角PM流动与喷管中单纯的膨胀流动都可以看成是气流经过一列简单波进行膨胀,流动特征存在相似之处。对细长喷管中的凝结问题以及凝结波的振荡模式都有相应的研究[6-7, 45],而对于伴随凝结的绕角膨胀的PM流动,构型不同导致空间演化更为复杂,正如前人所说[46-48],仍需要进一步研究,深入认识其规律。数值模拟是研究凝结与流动耦合作用的一种有效手段,本节采用经典矩方法对PM流动中水蒸气同质凝结对流动的影响以及凝结放热引起的凝结激波进行了研究。
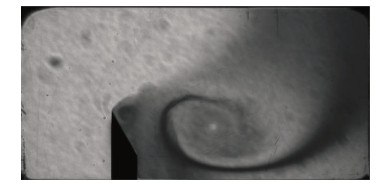
流动模型依据超声速G2喷管进行设计,如图 1所示。喷管喉道上游的收缩段与原始的超声速G2喷管收缩段相同。而在喉道下游的扩张段,上壁面是一个与喷管轴线平行的水平面,下壁面是与喷管轴线向外偏转30°角的斜面,拐点在喉道下游0.072 cm的位置,整个扩张段延伸到喉道下游6.5 cm处。超声速来流由二维喷管产生,在喷管喉道下游绕角膨胀,形成PM流动。气流经过短暂的膨胀,在拐点处略微超过声速,当地马赫数约为1.035。通过逐渐提高来流中水蒸气的饱和度,研究不同条件下凝结波的产生和运动形态。流动介质为氮气和水蒸气的混合气体,仅考虑水蒸气的同质凝结。计算采用自适应网格,根据前人应用经典矩方法研究凝结问题的经验[8],自适应加密后网格最小尺度达到0.1 mm量级,即可很好捕捉到各种凝结流场的结构。
|
图 1 伴随凝结的PM流动计算示意图 Fig.1 Sketch of Prandtl-Meyer flow with condensation |
初始时刻,在喉道下游设置一个间断面,间断面左侧上游设置高压,右侧下游设置低压。计算开始后,间断面处产生向上游运动的膨胀波和向下游运动的激波,并逐渐在喷管和膨胀扇中匹配出稳定的流场。如果直接启动凝结计算,凝结放热产生额外的凝结波,干扰了流动的匹配过程,使得流场很难稳定下来。因此,对于每个算例,首先模拟了未发生凝结情况下的流场,当流动达到稳定时再开启凝结计算。由于来流条件是一定的,通过不同方式建立起来的流场,最终都会趋向同一个结果。
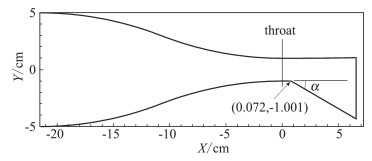
首先,对来流饱和度较小的情况进行了模拟。喷管入口处的温度Tini=330 K,压强pini=1 atm,水蒸气饱和度Sini=0.45。此来流条件下,喷管中水蒸气饱和度仍然小于1,经过拐点膨胀后,才会发生凝结。作为比较,同时计算了相同来流条件下,不启动凝结的情况。结果如图 2所示,图中箭头指向流动方向。可见当流动中伴随有水蒸气凝结时,温度场不再相对于拐点呈射线状分布,而是由于凝结潜热的释放,在膨胀扇中出现一个高温区域;在距离拐点较远处,由于凝结激波的影响,温度场还会发生一定程度的扭曲。凝结对压力场的影响相对较小,压力等值线仍大致呈射线状分布,说明PM流动的膨胀作用相较于水蒸气凝结的减质添热效应对压力场的影响更大。同时还可以看出壁面对压力场的影响:压力等值线趋向垂直于上壁面,当启动凝结计算后,这种趋势更加明显。
|
图 2 启动凝结(实线)与不启动凝结(虚线)时温度、压力分布对比 Fig.2 The distribution of temperature and pressure in PM flow with (solid line) and without (dashed line) condensation |
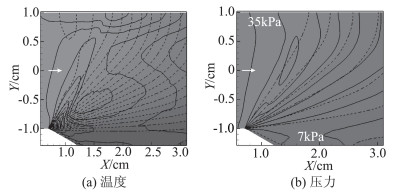
从有凝结时数值纹影图(图 3(a))中可以清晰地看到由水蒸气凝结放热产生的激波,激波从膨胀扇中发出,向来流方向弯曲,同时又距离拐点一定距离。这些特征都与前人的理论分析和实验结果吻合。流动膨胀过程会带来密度变小,越靠近拐点,膨胀越剧烈,因此纹影图中拐点附近显示为高密度梯度区域;激波同样会导致密度变化,波后密度升高,这与膨胀过程正相反。凝结放热随着距拐点距离缩小而逐渐集中,最终形成激波且强度逐渐加强;进一步靠近拐点,流动膨胀作用增强并逐步超过凝结激波作用,激波逐渐减弱并消失,拐点附近主要体现为膨胀带来的密度快速降低。这也是Kurshakov等观测到凝结激波不从拐点发出的物理原因。
|
图 3 定常凝结激波的数值纹影图 Fig.3 The numerical schlieren of PM flow with condensation |
从图 3(a)中还可以看到,在拐点下游附近、靠近斜面的区域也存在一道激波。这是由于拐点附近膨胀过快,凝结还来不及充分发展,气流已流过膨胀扇。然而在膨胀扇之后,水蒸气饱和度依然很高,水蒸气会继续凝结放热,形成了该激波。实际上,拐点在数学上是一个奇点,该点附近膨胀率和冷却率都趋向于无穷大。目前水蒸气同质凝结过程中使用的稳态成核理论和基于准静态的液滴增长理论在此流动条件下都存在问题。基于此,设计了另一个转角模型,用半径r=2mm的圆角替换了原拐角尖点,数值纹影如图 3(b)所示。可以看到在距离拐点较远的地方,流动形态和凝结激波位置并无显著差别;但在转角附近,凝结激波在距离壁面很近的地方还可以清晰的看到。这说明圆拐角确实弱化了此处的极端冷却率和膨胀率。同时,由于冷却率的降低,转角下游壁面处的激波形态也发生了改变。与尖点拐角相比,差别仅出现在拐角附近区域,说明拐角构型对凝结的影响具有局部性,在大尺度情形下可以忽略其影响。另外,真实流动在壁面附近存在边界层,边界层中流体速度变慢,膨胀率和冷却率必然不会很大,边界层对伴随凝结的PM流动的影响还需要进一步讨论。
当来流水蒸气含量较高时,会出现凝结激波振荡现象。气流绕过拐角偏转膨胀后发生凝结,释放大量潜热,促使膨胀扇中出现凝结激波;波后温度升高,凝结减弱,并促使凝结激波向上游运动。而逐渐减弱的凝结过程释放热量降低,导致激波强度逐渐减弱,最终在喉道附近消失。此时,流场恢复到了无凝结状态,重复之前凝结、激波相互影响的过程,呈现出凝结激波的振荡现象。如果提高来流中水蒸气含量,也即提高入口处的水蒸气饱和度Sini,凝结激波的振荡频率也会相应提高。为了统计激波振荡频率规律,保持入口来流压力不变pini=1 atm,计算了两种来流温度Tini=310 K、330 K下,振荡频率随来流水蒸气饱和度的变化关系,如图 4所示。来流温度相同时,凝结激波的振荡频率与水蒸气饱和度基本成线性关系。来流温度越高,相同饱和度下水蒸气含量越高,凝结量越大,凝结激波越强,振荡频率越高、随水蒸气饱和度上升得越快。
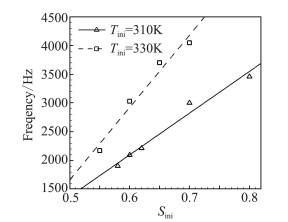
|
图 4 凝结激波的振荡频率随来流温度和来流水蒸气饱和度的变化关系 Fig.4 Oscillation frequency of condensation wave in dependency on the temperature and saturate ratio of incoming flow |
作为另一种主要的凝结现象,异质凝结也在生产和生活中占有重要地位。水蒸气异质凝结与同质凝结的主要区别在于形成凝结核的过程不同,同质成核是指水蒸气分子在一定条件下自发团聚成凝结核,而异质成核是指水蒸气在其他物质表面的凝结成核。生活中常见的雨、雾等自然现象,以及运用异质凝结清除颗粒等,都是水蒸气异质凝结的典型例子。目前关于异质凝结的研究主要集中在凝结的机理上,有关凝结与流动相互作用的研究还比较少。如前所述,矩方法将流动与凝结过程作为一个完整体系建立控制方程,正适合研究凝结与流动的相互作用。本节将经典矩方法进行拓展,应用到异质凝结领域,进而对激波管中的异质凝结问题进行参数研究。
3.1.1 异质凝结矩方法的建立与同质凝结一样,异质凝结也包含成核与增长两个子过程。异质成核中,研究较多的是水蒸气在杂质粒子上的成核过程。当杂质粒子完全被液态水包裹,则进入增长过程,杂质粒子的影响减弱以致于可以忽略。换言之,异质成核生成的液滴与同质成核生成的液滴在增长过程上没有差别。因此,异质凝结矩方法的建立主要是将异质成核过程整合到矩方程中。
关于异质成核过程的研究,有很长的历史。最早Volmer[49]通过动理论给出了不可溶物质平板表面上的异质成核率公式,Fletcher[50]将其推广到不可溶球形粒子表面,Kotake等[51]引入了表面张力的影响。Girshick等[5]提出的应用在同质成核理论中的自洽平衡态液滴数密度分布也被应用于异质成核理论。最近,范煜等[52]综合了上述理论并添加了线张力的影响,改进了异质成核公式。当前也有不少学者在分子尺度研究异质成核过程的特征与机理[53-56]。杂质粒子上异质成核过程十分复杂,大致包含3个阶段:首先,受固体粒子的影响,水蒸气分子优先在颗粒表面凝结生成大量离散的液簇;这些液簇逐渐增长、碰并,数量减少、体积变大,形成附着于颗粒表面的球冠状液滴;最终所有液滴合并为完整的液膜,完全覆盖颗粒表面,异质成核结束。此时的杂质粒子被称为活化粒子,活化粒子可以被看作液滴,随后的增长过程也与液滴的增长相同。
然而在宏观流动计算方法中完整模拟成核过程是非常困难的,本文采用“瞬间活化”假设对整个异质成核过程进行近似[57]。由同质成核理论可知,只有当液滴半径大于临界半径r*时液滴才会凝结增长。既然异质、同质凝结在增长阶段没有差别,这一结论也适用于异质成核生成的液滴。如果忽略液膜厚度,小于临界半径的粒子即使表面上被覆盖一层液膜,此液膜也会因为蒸发强于凝结而趋向消失。因此假设只有半径大于临界半径的颗粒才能活化,且忽略具体成核过程,直接形成液膜并增长(图 5)。此处的临界半径指的是根据当前的热力学状态,由同质凝结理论计算得到的临界半径。对于半径在百纳米以下的粒子,根据范煜等[52]提出的成核公式可知,粒子活化的时间很短,表面覆盖的液膜很薄,“瞬间活化”假设是合适的。
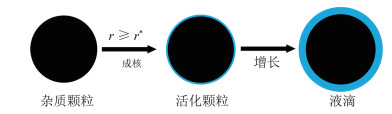
|
图 5 “瞬间活化”过程示意图 Fig.5 Schematic of instantaneous-wetting model |
杂质粒子一般不是均匀的颗粒,假设粒子为圆球形,半径分布满足函数g(r)。随着流动状态的改变,部分粒子被活化并发生凝结,活化粒子半径分布h(r, r*)不仅与粒子半径有关,也与临界半径r*有关。由“瞬间活化”假设可得
| $ h\left( {r,{r^ * }} \right) = \left\{ \begin{array}{l} g\left( r \right)\;\;\;\;\;{\rm{while}}\;\;\;\;r \ge {r^ * }\\ 0\;\;\;\;\;\;\;\;\;\;{\rm{while}}\;\;\;\;r < {r^ * } \end{array} \right. $ | (28) |
流场发展过程中,临界半径随时间变化r*=r*(t),活化粒子分布也随时间变化,则成核率Jhe=əh/ət,从而矩输运方程(6)可写为
| $ \begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho {Q_k}} \right) + \nabla \cdot \left( {\mathit{\boldsymbol{v}}\rho {Q_k}} \right) = k\bar {\dot r}\rho {Q_{k - 1}} + \phi _i^{{\rm{he}}},\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 0,1,2, \cdots \end{array} $ | (29) |
其中Qk仍然是关于液滴尺寸分布的k阶矩。异质凝结中液滴尺寸分布与同质凝结有无差别,以及杂质颗粒尺寸分布与液滴分布的关系,还是需要探讨的问题。上式与同质凝结矩方程(20)类似,主要差别仅在于成核过程项:
| $ \phi _k^{{\rm{he}}} = \int_r^\infty {{r^k}{J^{{\rm{he}}}}{\rm{d}}r} = \int_{{r^ * }}^\infty {{r^k}\left( {\partial h/\partial t} \right){\rm{d}}r} $ | (30) |
该项主要由杂质粒子尺寸分布及临界半径决定。能够将杂质粒子尺寸分布的影响也包含到计算模型中,也是异质矩方法的特点之一。
异质凝结矩方法的控制方程也由欧拉方程和矩方程(29)中前四阶构成,与同质凝结矩方法的控制方程(23)、(24)形式相同,仅需将源项S替换为:
| $ \begin{array}{l} {\mathit{\boldsymbol{S}}^{{\rm{he}}}} = \left[ {0,0,0,0,\varphi _{\rm{3}}^{{\rm{he}}} + 3\rho {Q_2}\overline {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}t}}} \right)} ,\varphi _{\rm{2}}^{{\rm{he}}} + 2\rho {Q_1}\overline {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}t}}} \right)} ,} \right.\\ \;\;\;\;{\left. {\varphi _1^{{\rm{he}}} + \rho {Q_0}\overline {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}t}}} \right)} ,\;\;\;\;\varphi _0^{{\rm{he}}}} \right]^{\rm{T}}} \end{array} $ | (31) |
由于异质凝结的三阶矩也包含了杂质颗粒的体积,三阶矩方程不能替换为液滴质量对流方程。由于活化颗粒的尺寸分布函数已知,可以很容易的计算出已凝结杂质颗粒的总体积
| $ {V_{p,3}} = \frac{{4{\rm{ \mathsf{ π} }}}}{3}\int_{{r^ * }}^\infty {{r^3}g\left( r \right){\rm{d}}r} $ | (32) |
因此,凝结液态水质量分数
| $ {g^{{\rm{he}}}} = \frac{{4{\rm{ \mathsf{ π} }}}}{3}\left( {{\rho _l}{Q_3} - \frac{{{\rho _l}}}{\rho }{V_{p,3}}} \right) $ | (33) |
与同质凝结矩方法类似,异质凝结矩方法也将液相与气相当作均匀混合物处理,不考虑相间作用。因此,凝结放出的潜热的影响,需要通过压力修正与温度修正来体现。其修正过程与同质凝结矩方法类似,此处不再赘述。
3.1.2 激波管中的异质凝结我们用拓展的矩方法对激波管中的异质凝结问题进行了研究。如图 6所示,激波管总长L=1 m,其中充满氮气和水蒸气的混合气体,气体中均匀分散有不可溶的惰性颗粒,充当异质凝结的凝结核。激波管中间D处设有一道隔膜,将整个激波管分为高压区(high-pressure section,HPS)和低压区(low-pressure section,LPS),压强分别为1 atm和0.5 atm;温度相同,均为295 K,水蒸气饱和度分别为0.9和0.45。计算域边界均采用固壁条件。在P1处设有探针,记录各参量随时间的变化情况。
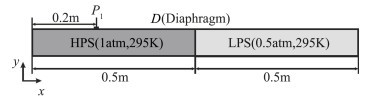
|
图 6 封闭激波管算例示意图 Fig.6 Sketch ofheterogeneous condensation in a closed shock tube |
为了对比分析凝结对流动的影响,分别计算了考虑与不考虑异质凝结两种情况,不考虑凝结仅关闭凝结源项计算即可。图 7给出了两种情况下激波管轴线上的密度在x-t平面内的等值线图。
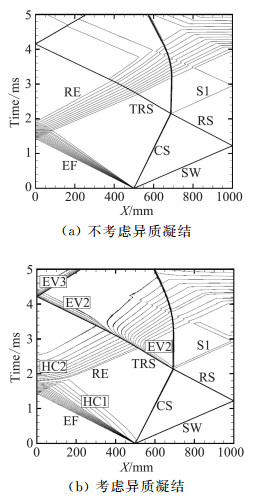
|
图 7 激波管轴线上的密度在x-t平面内的云图 Fig.7 Density contours for the closed shock tube problem in a space-time diagram without condensation (a) and with heterogeneous condensation (b) SW:激波,CS:接触间断,EF:膨胀波,RS:反射激波,TRS:透射反射激波,S1:接触间断上反射的弱激波,RE:反射膨胀波,HC1、HC2:异质凝结区域,EV1、EV2、EV3:蒸发区域。 |
在零时刻,激波管中间的隔膜被打开,高压段和低压段联通,产生了一道右行的激波(SW)和接触间断(CS)。激波过后,低压段密度升高。同时,一道膨胀波开始向左侧的高压段传播,并导致高压段密度降低。之后,膨胀波在高压段左侧壁面处反射,形成反射膨胀波(RE),进一步降低了高压段密度。另一方面,右行激波也在低压段的右侧壁面反射,形成反射激波(RS),进一步压缩了低压段的混合气体。反射激波与接触间断相交,产生一道左行的透射反射激波(TRS)和一道右行弱激波(S1)。透射反射激波又会和反射膨胀波相交,并在高压段左侧壁面再次反射。由此可见,激波管问题包含了多种非线性波系间的相互作用。从图 7(a)中可以看出,各种波系以及不同波系间的相互作用都被很好的模拟出来,这也从另一方面说明了此程序在模拟可压缩流动中,有很高的可靠性。当可压缩流动中还伴随有异质凝结时,凝结与不同波系之间又会产生相互影响。从图 7(b)中可以明显看出,激波管中的波系结构变得更加复杂。这主要由凝结时潜热的放出和液滴蒸发时从周围气体吸热量所导致的。
对比有无异质凝结的密度x-t图可以看出,激波管破膜后,膨胀波经过高压段,使高压段中混合气体温度降低,水蒸气饱和度升高,异质凝结发生(HC1)。当膨胀波在高压段左侧壁面反射后,高压段温度继续降低,异质凝结再次发生,在图 7(b)中用HC2标记出来。凝结放出潜热,被气体吸收,导致局部压力升高,产生压力波,并影响了膨胀波EF和反射膨胀波RE,使其形状产生畸变。而右行激波经过反射和透射,透射反射激波(TRS)进入凝结区域,激波后温度升高,水蒸气饱和度降低,液滴开始蒸发(EV1)。而后,透射反射激波穿过反射膨胀波的膨胀扇,抑制了膨胀扇中的凝结,导致膨胀扇发生扭曲,并使反射膨胀波后的液滴开始蒸发,形成第二个蒸发区EV2。最后透射反射激波经过高压段左侧壁面的再次反射,使高压段温度进一步提高,形成了第三个蒸发区EV3。蒸发过程中,液滴吸收气体的热量,在每个蒸发区都会形成一系列膨胀波,这一点与同质相变的结果相似[7, 58]。而与同质相变的不同之处在于,同质凝结往往发生在水蒸气饱和度较高的条件下(理论上水蒸气饱和度超过1就会发生同质凝结,但显著的同质凝结往往发生在水蒸气饱和度3以上的环境中)。这就导致同质凝结的强度较大,放热较为集中,形成显著的凝结波甚至是凝结激波,反观异质凝结就较为平缓。但对于同样的初始条件,不同凝结过程的放热总量是相同的,异质凝结对波系的影响也不容忽视。
3.2 相间滑移矩方法经典矩方法已被证明在处理凝结问题时高效、实用。然而,如前所述,不论处理的问题是同质凝结还是异质凝结,都有一个共同的基本假设,即忽略液相与气相之间的相互作用,将凝结生成的液滴和气体当作均匀混合物处理。一般来说,在液滴较小、流动较为平稳的情况下,液滴与气体热力学状态、流动状态均较为一致,即相间作用不显著,该假设是成立的。当流动变化剧烈(如激波、旋涡等)、液滴较大(如燃烧加热风洞中的同质凝结液滴尺寸可增长到微米级)时,气相与液相之间除了水蒸气凝结、液滴蒸发带来的相变潜热释放、吸收之外,还存在着由相间速度差异所带来的动量、能量交换以及由温度差异所带来的热量传导。在某些条件下,两相间存在着强烈的相互作用,或相间作用不强但持续时间长,相间差异被积累放大。如水蒸气在旋涡中的凝结问题[58],图 8给出了伴随水蒸气同质凝结的旋涡流动的消光结果。从图中可以看出,旋涡中心出现一个“白点”,是因为液滴跟随气流持续旋转,在离心力的作用下离开旋涡中心,并在边缘处聚集。这一现象通过经典凝结矩方法无法重现,并且由于旋涡中心温度最低,凝结最剧烈,经典矩方法模拟给出此处的液态水量是最多的,得到完全相反的结论。由此可见,在此条件下,气液两相间相互作用时不可忽略的。
为了考虑相间相互作用,一些学者将气液两相区分开,通过拉格朗日法追踪液相颗粒运动,气相仍用欧拉方法进行描述[59]。这种方法直观、可靠,但凝结生成的液滴数量极大,拉格朗日法计算量巨大,即使依靠经验对液滴进行分组,仍然需要追踪大量的液滴簇路径,大计算量是该方法最主要的瓶颈。也有学者针对矩方法进行改进,Marchisio等[14]在求积矩方法的基础上,提出了直接求积矩方法。由于每个积分点都有独立的相速度,因此通过添加必要的代数关系,就可以得到相间的相互作用。Brown等[60]在研究气溶胶问题时,多分散胶体系统用矩方程进行描述,其平均速度包括了惯性速度、扩散速度和胶体热泳速度的修正,考虑了相间的质量和热量交换,并发展出一套计算程序。但是,没有考虑相间的动量交换,不能描述液相对气相的影响。
本节在经典矩方法的基础上,将气液两相分开处理,建立了一套考虑两相间质量、动量和能量交换的凝结矩方法。此方法与一般的双流体模型方法[61-62]类似,气液两相都采用欧拉方法进行描述,相间具有速度滑移。液相平均速度与液滴尺寸分布无关。由于各阶矩描述的是液滴尺寸分布的信息,很自然的矩方程的对流速度采用液相的平均速度。与直接求积矩方法相比,此方法具有经典矩方法物理意义明确的特点,并且更容易通过计算流体力学方法实现。而与一般的双流体模型法相比,此方法并非简单的对液相参数进行统计平均,可以提供更多液相的信息。
3.2.1 相间滑移矩方法的建立与经典矩方法不同,由于考虑了相间的速度滑移,控制方程包含了三个部分:气相控制方程、液相控制方程以及矩方程。对于无粘问题,气相控制方程为欧拉方程;液相为弥散于气相中的液滴,忽略其对压力的影响,仅考虑液相的对流输运过程。凝结过程则由矩方程描述,需要注意的是经典矩方法中液滴与气相具有相同的速度,考虑速度滑移效应时,矩方程中对流速度应是液相速度。水蒸气凝结带来的质量交换和潜热释放、相间速度滑移引起的动量和能量交换都通过源项实现。因此,二维无粘情况下相间滑移矩方法控制方程的各项如下:
| $ \begin{array}{l} \mathit{\boldsymbol{U}} = \left( \begin{array}{l} {\rho _{\rm{g}}}\\ {\rho _{\rm{g}}}{u_{\rm{g}}}\\ {\rho _{\rm{g}}}{v_{\rm{g}}}\\ {\rho _{\rm{g}}}{E_{\rm{g}}}\\ {\rho _{\rm{d}}}\\ {\rho _{\rm{d}}}{u_{\rm{d}}}\\ {\rho _{\rm{d}}}{v_{\rm{d}}}\\ {\rho _{\rm{d}}}{E_{\rm{d}}}\\ {\rho _{\rm{g}}}\alpha \\ {\mu _2}\\ {\mu _1}\\ {\mu _0} \end{array} \right),\;\;\mathit{\boldsymbol{F}} = \left( \begin{array}{l} {\rho _{\rm{g}}}{u_{\rm{g}}}\\ {\rho _{\rm{g}}}u_{\rm{g}}^2 + {p_{\rm{g}}}\\ {\rho _{\rm{g}}}{u_{\rm{g}}}{v_{\rm{g}}}\\ \left( {{\rho _{\rm{g}}}{E_{\rm{g}}} + {p_{\rm{g}}}} \right){u_{\rm{g}}}\\ {\rho _{\rm{d}}}{u_{\rm{d}}}\\ {\rho _{\rm{d}}}u_{\rm{d}}^2\\ {\rho _{\rm{d}}}{u_{\rm{d}}}{v_{\rm{d}}}\\ {\rho _{\rm{d}}}{E_{\rm{d}}}{u_{\rm{d}}}\\ {\rho _{\rm{g}}}{u_{\rm{g}}}\alpha \\ {\mu _2}{\mu _{\rm{d}}}\\ {\mu _1}{\mu _{\rm{d}}}\\ {\mu _0}{\mu _{\rm{d}}} \end{array} \right),\\ \mathit{\boldsymbol{G}} = \left( \begin{array}{l} {\rho _{\rm{g}}}{v_{\rm{g}}}\\ {\rho _{\rm{g}}}{u_{\rm{g}}}{v_{\rm{g}}}\\ {\rho _{\rm{g}}}v_{\rm{g}}^2 + {p_{\rm{g}}}\\ \left( {{\rho _{\rm{g}}}{E_{\rm{g}}} + {p_{\rm{g}}}} \right)v\\ {\rho _{\rm{d}}}{v_{\rm{d}}}\\ {\rho _{\rm{d}}}{u_{\rm{d}}}{v_{\rm{d}}}\\ {\rho _{\rm{d}}}v_{\rm{d}}^2\\ {\rho _{\rm{d}}}{E_{\rm{d}}}{u_{\rm{d}}}\\ {\rho _{\rm{g}}}{v_{\rm{g}}}\alpha \\ {\mu _2}{v_{\rm{d}}}\\ {\mu _1}{v_{\rm{d}}}\\ {\mu _0}{v_{\rm{d}}} \end{array} \right),\;\;\;\;\;\;\;\mathit{\boldsymbol{S}} = \left( \begin{array}{l} {S_1}\\ {S_2}\\ {S_3}\\ {S_4}\\ {S_5}\\ {S_6}\\ {S_7}\\ {S_8}\\ {S_9}\\ {S_{10}}\\ {S_{11}}\\ {S_{12}} \end{array} \right) \end{array} $ | (34) |
其中下标“g”和“d”分别代表气相(gas)和液相(droplet)。α是气相中水蒸气的质量分数,三阶矩方程替换为水蒸气质量守恒方程。其它符号与前文一致。
源项Si表示由于相变带来的各类相间交换,是相间滑移矩方法的核心。S1、S5、S9分别是水蒸气相变导致的气相、液相及水蒸气质量变化源项。水蒸气在成核过程生成临界半径r*液滴,消耗水蒸气带来等量的液相质量增长率:
| $ {S_{m1}} = \frac{{4{\rm{ \mathsf{ π} }}}}{3}{r^{ * 3}}{\rho _l}J $ | (35) |
而液滴增长过程同样带来液相质量增长率:
| $ {S_{m2}} = 4{\rm{ \mathsf{ π} }}{\mu _2}{\rho _l}\overline {\left( {\frac{{{\rm{d}}r}}{{{\rm{d}}t}}} \right)} $ | (36) |
因此相变带来的总质量变化率Sm=Sm1+Sm2,从而
| $ {S_1} = {S_9} = - {S_5} = - {S_m} $ | (37) |
动量源项S2、S3、S6、S7包含伴随相变质量转换的动量交换和相间速度差异产生黏性力带来的动量交换,故:
| $ \begin{array}{l} {S_2} = - {S_6} = - {f_x} - {S_{m1}}{u_{\rm{g}}} - {S_{m2}}{u_{\rm{d}}}\\ {S_3} = - {S_7} = - {f_y} - {S_{m1}}{v_{\rm{g}}} - {S_{m2}}{v_{\rm{d}}} \end{array} $ | (38) |
对于刚成核的液滴,认为其速度为当地气相的速度。而液滴增长带来的液相增加质量,认为其速度为当地的液相平均速度。因此,成核带来的动量变化根据当地气相速度计算,液滴增长带来的动量变化根据当地的液相平均速度计算。f=(fx, fy)表示相间速度滑移带来的黏性作用力,其表达式如下:
| $ \mathit{\boldsymbol{f}} = {\rho _{\rm{d}}}\frac{{{\mathit{\boldsymbol{u}}_g} - {\mathit{\boldsymbol{u}}_{\rm{d}}}}}{{{\tau _v}}}\frac{{{C_D}\mathit{R}{\mathit{e}_{\rm{d}}}}}{{24}} $ | (39) |
其中:平均相对雷诺数Red=ρg|ug-ud|r/μ,μ为气相黏性系数,液滴平均半径r=μ1/μ0。液滴的平均动响应时间τv=2ρdr2/9μ。平均阻力系数CD使用Crowe[63]给出的经验公式。
能量源项S4、S8包含相间速度滑移带来的能量交换、相间温度差带来的热传导和凝结带来的潜热释放:
| $ \begin{array}{l} {S_4} = - {f_x}{u_{\rm{d}}} - {f_y}{v_{\rm{d}}} - q - {S_{m1}}{E_{c1}} - {S_{m2}}{E_{c2}}\\ {S_8} = {f_x}{u_{\rm{d}}} + {f_y}{v_{\rm{d}}} + q + {S_{m1}}{{E'}_{c1}} + {S_{m2}}{{E'}_{c2}} \end{array} $ | (40) |
其中,气液两相间热交换率[64]:
| $ q = {\rho _{\rm{d}}}{c_l}\frac{{{T_g} - {T_{\rm{d}}}}}{{{\tau _T}}}\frac{{Nu}}{2} $ | (41) |
cl是液态水的比热,Nu是努塞尔数,传热响应时间τT=cpρdr2/3kg,cp和kg分别是气相定压比热和热传导系数。与质量源项和动量源项不同,气相的能量源项和液相的能量源项不再是相反数的关系,这是因为凝结放出了潜热,能量不再守恒。凝结产生的能量变化关系如下:
| $ \begin{array}{l} {E_{c1}} = \left( {u_g^2 + v_g^2} \right)/2 + {c_{pv}}{T_{w1}} - L\left( {{T_{w1}}} \right),\\ {E_{c2}} = \left( {u_{\rm{d}}^2 + v_{\rm{d}}^2} \right)/2 + {c_{pv}}{T_{w2}} - L\left( {{T_{w2}}} \right),\\ {{E'}_{c1}} = \left( {u_g^2 + v_g^2} \right)/2 + {c_l}{T_{w1}},\\ {{E'}_{c2}} = \left( {u_{\rm{d}}^2 + v_{\rm{d}}^2} \right)/2 + {c_l}{T_{w2}}. \end{array} $ | (42) |
其中,Tw1、Tw2分别是成核过程和增长过程液滴表面的湿球温度[65]。成核时,凝结核较小,认为整个核的温度都是Tw1;增长过程中的液滴内部平均温度为液相温度Td,而表面湿球温度Tw2是新增长液膜的温度。一般来说,Tw1、Tw2和Td都不相同。凝结释放的潜热L是温度的函数[8],这里假设潜热全部被气相吸收,因此潜热项只出现在气相能量方程的源项中。另外,由于成核和增长过程中生成的液态水具有不同的速度,携带的动能也不同,分别用液相平均速度和气相速度计算。
与经典矩方法相比,通过上述源项使得相间滑移矩方法对同质成核和液滴增长的模拟更接近真实物理过程。
矩方程的源项S10、S11、S12与经典矩方法并无差别,为了完整重写如下:
| $ \begin{array}{l} {S_{10}} = J{r^{ * 2}} + 2{\mu _1}\overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \\ {S_{11}} = J{r^ * } + {\mu _0}\overline {\left( {{\rm{d}}r/{\rm{d}}t} \right)} \\ {S_{12}} = J \end{array} $ | (43) |
同样的,上述方程组还需要用气体状态方程进行封闭。如果忽略液相对气相压力的影响,则气体状态方程与之前并无不同。由于各相拥有单独的能量方程,并且水蒸气的相变潜热已经在能量方程的源项中体现出来,因此与经典矩方法不同,这里不再需要进行压力和温度的修正。
3.2.2 伴随凝结的旋涡运动为了考察相间滑移的影响,采用前述相间滑移矩方法计算了伴随凝结的旋涡运动。
首先讨论较为基础的兰金(Rankine)复合涡中的凝结问题。兰金涡由速度线性增长的涡核和二维位势涡组合而成,速度分布如下:
| $ v = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \mathit{\Omega r,}\\ \mathit{\Omega }{R^2}/r, \end{array}&\begin{array}{l} r \le R\\ r > R \end{array} \end{array}} \right. $ | (44) |
其中,R为涡核半径,Ω为旋转角速度。这一速度分布与气象学中的热带气旋类似,常被作为研究热带气旋的初步理论模型。需要指出的是,兰金涡一般被作为不可压旋涡来研究的,但对于可压缩流动,仍然可以借用其速度分布。其压强分布,可以通过可压缩流动的伯努利方程求解。
计算中流动介质为氮气和水蒸气的混合气体,通过调整二者质量比实现不同的初始饱和度。涡核半径R=2 cm,转动角速度Ω=14 870 s-1,这里角速度设置较大,以产生足够强的旋涡。选取半径100 cm的圆形计算域,如图 9所示,涡核位于计算域中心。由于计算域半径远大于涡核半径,边界条件的影响可以忽略。由于流动中没有强间断,最小网格尺度可略大,设为0.5 mm。远场压强p0=100 kPa、温度T0=298 K。
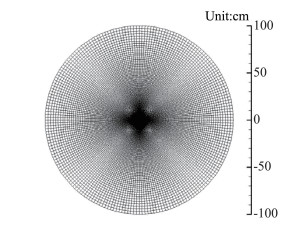
|
图 9 兰金涡算例网格示意图 Fig.9 Computation domain and mesh for Rankine vortex flow with condensation |
计算初始时全场赋值为未发生凝结的稳定兰金涡流场,水蒸气处于过饱和状态。而后启动计算,凝结随之发生。作为示例,图 10给出了远场水蒸气饱和度S0=1.2时旋涡中心的液相密度云图,颜色越深密度越大。旋涡外围由于饱和度不是太高,并没有同质凝结发生。随着向旋涡中心靠近,压力、温度均降低,凝结也逐步变得剧烈,液相密度增加。同时,凝结放出潜热,产生凝结波向外侧传播。早期凝结波较强,可能会抑制外侧凝结的产生,这从t=10 μs的液相密度分布可以清晰地看到。凝结生成的液滴,由于相间滑移并不严格跟随气体运动,而是在离心力的作用下沿径向向外迁移,导致旋涡中心液相密度降低。在t=410 μs之后,液相密度分布图显示,旋涡中心出现“白点”,并且随时间增大。

|
图 10 兰金涡中心区域液相密度演化, S0=1.2 Fig.10 Variation of liquid phase density distribution in Rankine vortex, S0=1.2 |
另外,还发现一个有趣的现象,随着时间发展,液相密度分布逐渐出现分层结构,形成一系列同心环。在涡核内部,气流旋转速度随半径近似线性变快,液滴在向外迁移的过程中被气流带动加速,受到更大的离心力,进一步促进向外迁移,这也是中心出现“白点”的原因;而在涡核外部,气流速度随着半径降低,液滴则被气流带动减速,离心力减小,向外迁移扩散速度变慢。涡核内产生的液滴将在涡核边缘聚集,形成内部第一道暗纹。在距离旋涡中心较远的区域,水蒸气饱和度虽然高于1,但不足以支持显著的同质凝结成核过程,当内部液滴迁移到此区域时,没有消耗的水蒸气会促使液滴继续凝结增长。这使得旋涡外侧的液滴尺寸要比内侧大的多,而大液滴跟随性更差,相间滑移作用更强,径向迁移更快。同时,凝结释放潜热使得温度升高、饱和度降低,抑制液滴增长,降低径向迁移。在相间滑移与凝结自我抑制的共同作用下,液滴在局部位置聚集,液相密度分布呈现环状结构。
随后,应用相间滑移矩方法对启动涡中的凝结问题进行了数值研究。参照路德维希(Ludwieg)管中斜劈诱导旋涡中的凝结实验[8]设置计算条件,如图 11所示。计算采用氮气和水蒸气的混合气体。计算域长110 cm,高10 cm。斜劈尺寸如图所示,左边界位于x=17 cm处。隔膜位于x=90 cm处,左侧为高压区,压力100 kPa,水蒸气饱和度S=0.88;右侧为低压区,压强为22 kPa,水蒸气组分含量与高压区相同。初始温度296 K。计算网格自适应加密,最大加密4层,加密后最小网格尺寸约为0.1 mm。
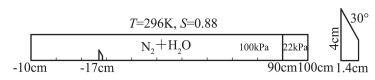
|
图 11 斜劈诱导启动涡算例示意图 Fig.11 Sketch of vortex shedding in Ludwieg tube with water vapor condensation |
计算启动后破膜,间断面处产生向高压段运动的膨胀波。当膨胀波到达斜劈后,在尖角处诱导产生旋涡。随着时间推进,旋涡不断增强,旋涡中心的温度不断降低,饱和度升高,随后发生凝结。图 12给出了不同时刻,旋涡中的气相温度和液相密度分布云图。从图中可以看出,当旋涡中的温度下降到250 K左右时(t=2.6 ms),水蒸气开始发生同质凝结。此时,旋涡外的温度要高于旋涡内的温度。随着时间的推进,旋涡缓慢向右运动,强度逐渐上升,涡心凝结加剧(t=2.8 ms),旋涡内的液相密度开始升高。伴随着凝结潜热的放出,涡心温度迅速升高,但还是略低于外部温度。此时温度最低处位于剪切层内。在t=3.0 ms时刻,旋涡中心过饱和的水蒸气已经凝结完全,涡心的温度随着旋涡强度的增加开始缓慢下降。凝结主要发生在旋涡边缘,可以观察到,在障碍物尖角右侧温度最高。在t=3.2 ms时刻,膨胀波中的凝结波与旋涡接触,两者作用的结果使得旋涡右侧出现凝结,此处温度升高。而旋涡中的温度继续缓慢降低。从液相密度图上还可以发现,剪切层上出现微弱的不稳定现象。在t=3.4 ms时刻,凝结波与旋涡作用,加剧了剪切层上的扰动。涡心的温度由于凝结波的影响开始回升。在t=3.6 ms时刻,凝结波基本扫过旋涡,涡心温度进一步上升。剪切层上的界面不稳定性发展出小的涡结构,并且伴随着大涡的运动被卷入旋涡内部。对比不同时刻的液相密度分布可以发现,旋涡中水蒸气凝结完全后,涡心的液相密度就开始逐渐降低。液滴随着气流持续旋转,在离心力的作用下向旋涡外侧运动。这说明相间滑移的影响在伴随凝结的旋涡运动中不可忽略。

|
图 12 启动涡中气相温度场(左)及液相密度场(右)的演化过程 Fig.12 Distribution of gas phase temperature (left) and liquid phase density (right) during the vortex shedding process |
图 13给出了凝结产生前期(t=2.8 ms)和后期(t=3.75 ms)启动涡中液相流线结果。可以看出,液相流线从旋涡中心发出,盘旋向外。这再次表明液滴在离心力的作用下,逐渐离开旋涡中心。前期凝结量不大,液滴仅在旋涡范围内运动。液相流线终止于斜劈壁面上。随着流动发展,液滴被甩出旋涡,液相流线向下游延伸。同时还可以发现,斜劈尖端的脱涡会对流线产生扰动。观察流线的疏密程度可以发现,靠近旋涡中心,流线较密,而在旋涡边缘,流线间距较大。这说明液滴在离开旋涡的过程中,向外速度逐渐加快,与前述兰金涡中液滴的迁移特征也是一致的。
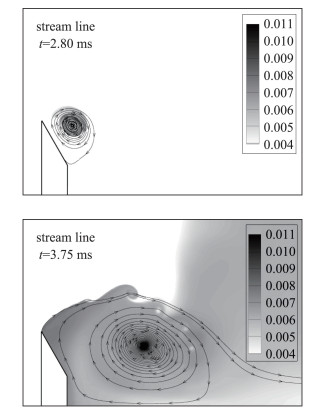
|
图 13 启动涡中凝结产生前期(t=2.8 ms)和后期(t=3.75 ms)液相流线示意图 Fig.13 Streamlines of the liquid phase in the starting vortex at different time |
图 14给出了t=3.75 ms时刻,实验和不同计算方法得到的液相密度分布结果。经典矩方法的计算模拟结果显示,旋涡中心的液相密度最高。这是因为旋涡中心凝结最为剧烈,液滴生成后完全跟随气流运动,无法离开旋涡中心,与实验结果是不符的。而相间滑移矩方法模拟能准确重现消光实验中观测到的旋涡中心的“白点”,同时与纹影实验结果一致,可以捕捉从斜劈尖端分离的涡结构。

|
图 14 不同方法得到的启动涡中凝结液相密度分布对比(t=3.75 ms) Fig.14 Distribution of liquid phase density in starting vortex by different methods(t=3.75 ms) |
也应该注意到,与实验结果相比,相间滑移矩方法仍还存在一些不足。实验观测表明液态水会向旋涡外围聚集,形成类似“旋臂”结构,两种数值方法都没有模拟出这一结构。另一方面,实验结果显示,不仅在涡心,旋涡中整体的液相密度都较低,而数值结果中旋涡中的液相密度偏高。分析原因,可能是由于没有考虑液滴碰并效应造成的。如果考虑液滴碰并,理论上液滴数密度将减少,平均半径将增大,液滴相对气流的跟随性变弱,相间差距更加明显。液滴将更快的离开旋涡,并且更容易在旋涡边缘聚集。
4 总结与展望本文首先介绍了矩方法的发展过程,包括传统矩方法、求积矩方法和直接求积矩方法。传统矩方法需要对分布函数的具体形式作出假设。求积矩方法克服了传统矩方法液滴增长率必须是半径线性关系的限制(这一限制实在内部坐标取液滴半径条件下做出的),并且不需要知道分布函数的具体形式。而直接求积矩方法中,虽然分布函数显式给出,但是不需要对其具体形式作出额外假设。传统矩方法,计算过程较为简单,各项物理含义清楚明了。求积矩方法需要进行矩阵计算,计算过程较为复杂,但仍然追踪各阶矩。直接求积矩方法,直接追踪高斯点和对应权值,可以反映相间、高斯点对应的内部坐标间的相互作用,这是前两者所不具备的。
随后,介绍了矩方法的扩展,包括推广到异质凝结以及考虑相间相互作用。通过引入“瞬间活化”假设,简化异质成核模型,仅需修改矩方程的源项,即可得到伴随异质凝结的流动问题的控制方程。应用该方法对激波管中异质凝结问题进行了参数研究,加深了对异质凝结和流动相互作用的认识。为了描述气、液相之间的相互作用,将气液两相分开处理,建立了一套考虑两相间质量、动量和能量交换的凝结矩方法。应用此方法研究了伴随同质凝结的旋涡运动问题,结果表明相间滑移矩方法能正确的捕捉到实验观测发现的“白点”现象,即凝结生成的液滴在离心力作用下离开旋涡中心,使得该区域液相密度极低。
近期,矩方法的发展主要在于具体问题的应用;弥补之前方法的不足;反推出分布函数的具体形式;处理非圆粒子等。今后,矩方法的发展还将主要集中在处理具体问题上,如:粒子的破碎、聚合,各相间的相互作用等方面。
| [1] |
HULBURT H M, KATZ S. Some problems in particle technology:A statistical mechanical formulation[J]. Chemical Engineering Science, 1964, 19(8): 555-574. DOI:10.1016/0009-2509(64)85047-8 |
| [2] |
VOLMER M, WEBER A. Keimbildung in übersättigten Gebilden[J]. Zeitschrift für Physikalische Chemie, 1926, 119U(1): 277-301. DOI:10.1515/zpch-1926-11927 |
| [3] |
FARKAS L. Keimbildungsgeschwindigkeit in übersättigten Dämpfen[J]. Zeitschrift für Physikalische Chemie, 1927, 125U(1): 236-242. DOI:10.1515/zpch-1927-12513 |
| [4] |
BECKER R, DÖRING W. Kinetische Behandlung der Keimbildung in übersättigten Dämpfen[J]. Annalen der Physik, 1935, 416(8): 719-752. DOI:10.1002/andp.19354160806 |
| [5] |
GIRSHICK S L, CHIU C P. Kinetic nucleation theory:A new expression for the rate of homogeneous nucleation from an ideal supersaturated vapor[J]. The Journal of Chemical Physics, 1990, 93(2): 1273-1277. DOI:10.1063/1.459191 |
| [6] |
HILL P G. Condensation of water vapour during supersonic expansion in nozzles[J]. Journal of Fluid Mechanics, 1966, 25(3): 593-620. DOI:10.1017/S0022112066000284 |
| [7] |
ADAM S, SCHNERR G H. Instabilities and bifurcation of non-equilibrium two-phase flows[J]. Journal of Fluid Mechanics, 1997, 348: 1-28. DOI:10.1017/S0022112097006745 |
| [8] |
LUO X. Unsteady flows with phase transition[R]. Eindhoven, The Netherlands: Eindhoven University of Technology, 2004.
|
| [9] |
McGRAW R. Description of aerosol dynamics by the quadrature method of moments[J]. Aerosol Science and Technology, 1997, 27(2): 255-265. DOI:10.1080/02786829708965471 |
| [10] |
GORDON R G. Error bounds in equilibrium statistical mechanics[J]. Journal of Mathematical Physics, 1968, 9(5): 655-663. DOI:10.1063/1.1664624 |
| [11] |
JOHN V, THEIN F. On the efficiency and robustness of the core routine of the quadrature method of moments (QMOM)[J]. Chemical Engineering Science, 2012, 75: 327-333. DOI:10.1016/j.ces.2012.03.024 |
| [12] |
BARRETT J C, WEBB N A. A comparison of some approximate methods for solving the aerosol general dynamic equation[J]. Journal of Aerosol Science, 1998, 29(1): 31-39. DOI:10.1016/S0021-8502(97)00455-2 |
| [13] |
MARCHISIO D L, VIGIL R D, FOX R O. Quadrature method of moments for aggregation-breakage processes[J]. Journal of Colloid and Interface Science, 2003, 258(2): 322-334. DOI:10.1016/S0021-9797(02)00054-1 |
| [14] |
MARCHISIO D L, FOX R O. Solution of population balance equations using the direct quadrature method of moments[J]. Journal of Aerosol Science, 2005, 36(1): 43-73. DOI:10.1016/j.jaerosci.2004.07.009 |
| [15] |
FOX R O, LAURENT F, MASSOT M. Numerical simulation of spray coalescence in an Eulerian framework:Direct quadrature method of moments and multi-fluid method[J]. Journal of Computational Physics, 2008, 227(6): 3058-3088. DOI:10.1016/j.jcp.2007.10.028 |
| [16] |
VIKAS V, WANG Z J, FOX R O. Realizable high-order finite-volume schemes for quadrature-based moment methods applied to diffusion population balance equations[J]. Journal of Computational Physics, 2013, 249: 162-179. DOI:10.1016/j.jcp.2013.05.002 |
| [17] |
STRUMENDO M, ARASTOOPOUR H. Solution of PBE by MOM in finite size domains[J]. Chemical Engineering Science, 2008, 63(10): 2624-2640. DOI:10.1016/j.ces.2008.02.010 |
| [18] |
ABBASI E, ARASTOOPOUR H. Numerical analysis and implementation of finite domain complete trial functions method of moments (FCMOM) in CFD codes[J]. Chemical Engineering Science, 2013, 102: 432-441. DOI:10.1016/j.ces.2013.08.034 |
| [19] |
SU J, et al. Solution of population balance equation using quadrature method of moments with an adjustable factor[J]. Chemical Engineering Science, 2007, 62(21): 5897-5911. DOI:10.1016/j.ces.2007.06.016 |
| [20] |
FALOLA A, BORISSOVA A, WANG X Z. Extended method of moment for general population balance models including size dependent growth rate, aggregation and breakage kernels[J]. Computers & Chemical Engineering, 2013, 56: 1-11. DOI:10.1016/j.compchemeng.2013.04.017 |
| [21] |
YUAN C, LAURENT F, FOX R O. An extended quadrature method of moments for population balance equations[J]. Journal of Aerosol Science, 2012, 51: 1-23. DOI:10.1016/j.jaerosci.2012.04.003 |
| [22] |
MADADI-KANDJANI E, PASSALACQUA A. An extended quadrature-based moment method with log-normal kernel density functions[J]. Chemical Engineering Science, 2015, 131: 323-339. DOI:10.1016/j.ces.2015.04.005 |
| [23] |
ALEXIADIS A, VANNI M, GARDIN P. Extension of the method of moments for population balances involving fractional moments and application to a typical agglomeration problem[J]. Journal of Colloid and Interface Science, 2004, 276(1): 106-112. DOI:10.1016/j.jcis.2004.03.052 |
| [24] |
岳言, 苏中地. 硫酸合水纳米颗粒在湍射流中演化过程的B-TEMOM模拟[J]. 中国计量大学学报, 2016, 27(4): 382-388. YUE Y, SU Z D. B-TEMOM sim ulation of the evolution in sul furic and water nanoparticles turbulent flows[J]. Journal of China University of Metrology, 2016, 27(4): 382-388. DOI:10.3969/j.issn.2096-2835.2016.04.005 (in Chinese) |
| [25] |
程万, 罗喜胜, 杨基明. 高超声速喷管中水蒸气凝结的数值研究[J]. 中国科学G辑:物理学力学天文学, 2009, 39(1672-1780): 1330. CHENG W, LUO XI S, YANG J M. Numerical analysis of water phase transition effects in hypersonic nozzles[J]. Science in China Series G-Physics, Mechanics & Astronomy, 2009, 39(9): 1330-1337. DOI:10.1360/2009-39-9-1330 (in Chinese) |
| [26] |
程万, 罗喜胜, 杨基明. 燃烧加热风洞中水蒸气相变的数值研究[J]. 空气动力学学报, 2010, 28(3): 272-278. CHENG W, LUO X S, YANG J M. Numerical analysis of water phase transition effects in combustion-heated wind tunnels[J]. Acta Aerodynamica Sinica, 2010, 28(3): 272-278. DOI:10.3969/j.issn.0258-1825.2010.03.006 (in Chinese) |
| [27] |
孙秀玲, 马晓永, 李亮, 等. RAE2822翼型湿空气非平衡凝结流动的研究[J]. 空气动力学学报, 2013, 31(5): 592-597. SUN X L, MA X Y, LI L, et al. Numerical prediction of the effects of condensation of moist air on the aerodynamic characteristics of the RAE 2822 airfoil[J]. Acta Aerodynamica Sinica, 2013, 31(5): 592-597. (in Chinese) |
| [28] |
刘燕, 岳巍澎. 海上湿气对翼型气动特性的影响初探[J]. 空气动力学学报, 2016, 34(4): 541-547. LIU Y, YUE W P. Study of the influence of moist air on airfoil aerodynamic characteristics[J]. Acta Aerodynamica Sinica, 2016, 34(4): 541-547. DOI:10.7638/kqdlxxb-2015.0205 (in Chinese) |
| [29] |
孙秀玲, 李亮, 李国君. 湿空气凝结对ONERA M6机翼气动特性影响的数值研究[J]. 空气动力学学报, 2010, 28(2): 143-148. SUN X L, LI L, LI G J. Numerical study of the effects of condensation of moist air on the aerodynamic characteristics of the ONERA M6 wing[J]. Acta Aerodynamica Sinica, 2010, 28(2): 143-148. DOI:10.3969/j.issn.0258-1825.2010.02.004 (in Chinese) |
| [30] |
孙秀玲, 李亮, 马晓永, 等. 普朗特-迈耶流中湿空气非平衡凝结影响的研究[J]. 空气动力学学报, 2013, 31(4): 425-429. SUN X L, LI L, MA X Y, et al. Influences of the non-equilibrium condensation of moist air on Prandtl-Meyer flows[J]. Acta Aerodynamica Sinica, 2013, 31(4): 425-429. (in Chinese) |
| [31] |
WROBLEWSKI W, DYKAS S. Two-fluid model with droplet size distribution for condensing steam flows[J]. Energy, 2016, 106: 112-120. DOI:10.1016/j.energy.2016.03.052 |
| [32] |
HUGHES F R, STARZMANN J, WHITE A J, et al. A comparison of modeling techniques for polydispersed droplet spectra in steam turbines[J]. Journal of Engineering for Gas Turbines and Power-Transactions of the Asme, 2016, 138(4): 9. DOI:10.1115/1.4031389 |
| [33] |
LEE J, HA K S, HWANG J. Application of moment method for predicting condensational growth of nuclear aerosols in a severe accident[J]. Nuclear Technology, 2017, 200(3): 241-249. DOI:10.1080/00295450.2017.1372984 |
| [34] |
GRABOWSKI W W, MORRISON H. Modeling condensation in deep convection[J]. Journal of the Atmospheric Sciences, 2017, 74(7): 2247-2267. DOI:10.1175/jas-d-16-0255.1 |
| [35] |
FREDERIX E M A, et al. Extension of the compressible PISO algorithm to single-species aerosol formation and transport[J]. International Journal of Multiphase Flow, 2015, 74: 184-194. DOI:10.1016/j.ijmultiphaseflow.2015.04.015 |
| [36] |
ALSHAARAWI A, BISETTI F. The effect of mixing rates on the formation and growth of condensation aerosols in a model stagnation flow[J]. Journal of Aerosol Science, 2015, 81: 34-46. DOI:10.1016/j.jaerosci.2014.11.004 |
| [37] |
SMITH L T. Experimental investigation of the expansion of moist air around a sharp corner[J]. AIAA Journal, 1971, 9(10): 2035-2037. DOI:10.2514/3.6458 |
| [38] |
STEFFEN H H. Theorie und Experiment zur Untersuchung der ebenen, zentrierten Expansionsstr omung mit W rmezufuhr. 1966.
|
| [39] |
KURSHAKOV A V, SALTANOV G A, TKALENKO R A. Theoretical and experimental investigation of condensation in a centered rarefaction wave[J]. Journal of Applied Mechanics and Technical Physics, 1971, 12(5): 732-735. DOI:10.1007/bf00851128 |
| [40] |
FRANK W. Condensation phenomena in supersonic nozzles[J]. Acta Mechanica, 1985, 54(3): 135-156. DOI:10.1007/bf01184842 |
| [41] |
DELALE C F, CRIGHTON D G. Prandtl-Meyer flows with homogeneous condensation. Part 1. Subcritical flows[J]. Journal of Fluid Mechanics, 1998, 359: 23-47. DOI:10.1017/S0022112097008379 |
| [42] |
DELALE C F, CRIGHTON D G. Prandtl-Meyer flows with homogeneous condensation. Part 2. Supercritical flows[J]. Journal of Fluid Mechanics, 2001, 430: 231-265. DOI:10.1017/S0022112000003189 |
| [43] |
WHITE A J, YOUNG J B, WALTERS P T. Experimental validation of condensing flow theory for a stationary cascade of steam turbine blades[J]. Philosophical Transactions of the Royal Society of London. Series A:Mathematical, Physical and Engineering Sciences, 1996, 354(1704): 59-88. DOI:10.1098/rsta.1996.0003 |
| [44] |
KIM H D, MATSUO S, SETOGUCHI T. Passive control applied to Prandtl-Meyer expansion flow with homogeneous condensation[J]. Aerospace Science and Technology, 2004, 8(5): 369-376. DOI:10.1016/j.ast.2004.02.002 |
| [45] |
OSWATITSCH K. Condensation phenomena in supersonic nozzles[M]//SCHNEIDER W, PLATZER M. Contributions to the Development of Gasdynamics: Selected Papers. Translated on the Occasion of K. Oswatitsch's 70th Birthday, 1980, Vieweg+Teubner Verlag: Wiesbaden. p. 397-418.
|
| [46] |
DELALE C F, SCHNERR G H, ZIEREP J. Asymptotic solution of transonic nozzle flows with homogeneous condensation.Ⅰ. Subcritical flows[J]. Physics of Fluids A:Fluid Dynamics, 1993, 5(11): 2969-2981. DOI:10.1063/1.858704 |
| [47] |
DELALE C F, SCHNERR G H, ZIEREP J. Asymptotic solution of transonic nozzle flows with homogeneous condensation. Ⅱ. Supercritical flows[J]. Physics of Fluids A:Fluid Dynamics, 1993, 5(11): 2982-2995. DOI:10.1063/1.858705 |
| [48] |
KIM I W, et al. The effect of non-equilibrium condensation on the drag coefficient in a transonic airfoil flow[J]. Journal of Thermal Science, 2012, 21(6): 518-524. DOI:10.1007/s11630-012-0576-8 |
| [49] |
VOLMER M. VBER Keimbildung und keimwirkung als spezialfälle der heterogenen katalyse[J]. Zeitschrift für Elektrochemie und angewandte physikalische Chemie, 1929, 35(9): 555-561. |
| [50] |
FLETCHER N H. Size effect in Heterogeneous nucleation[J]. The Journal of Chemical Physics, 1958, 29(3): 572-576. DOI:10.1063/1.1744540 |
| [51] |
KOTAKE S, GLASS I I. Flows with nucleation and condensation[J]. Progress in Aerospace Sciences, 1979, 19: 129-196. DOI:10.1016/0376-0421(79)90003-4 |
| [52] |
FAN Y, et al. A modified expression for the steady-state heterogeneous nucleation rate[J]. Journal of Aerosol Science, 2015, 87: 17-27. DOI:10.1016/j.jaerosci.2015.05.001 |
| [53] |
XU W, et al. Effect of surface free energies on the heterogeneous nucleation of water droplet:A molecular dynamics simulation approach[J]. Journal of Chemical Physics, 2015, 142(5): 12. DOI:10.1063/1.4906877 |
| [54] |
SUH D, YASUOKA K. Aspect ratio effect of nanorods on heterogeneous nucleation rates by molecular dynamics[J]. Journal of Thermal Science and Technology, 2016, 11(3): JTST0044-JTST0044. DOI:10.1299/jtst.2016jtst0044 |
| [55] |
OU X W, et al. Heterogeneous condensation of water on the mica (001) surface:A molecular dynamics simulation work[J]. Journal of Physical Chemistry C, 2017, 121(12): 6813-6819. DOI:10.1021/acs.jpcc.7b00855 |
| [56] |
WANG Z, QIN F, LUO X. Numerical investigation of effects of curvature and wettability of particles on heterogeneous condensation[J]. The Journal of Chemical Physics, 2018, 149(13): 134306. DOI:10.1063/1.5040878 |
| [57] |
SMOLDERS H J, NIESSEN E M J, VAN DONGEN M E H. The random choice method applied to non-linear wave propagation in gas-vapour-droplets mixtures[J]. Computers & Fluids, 1992, 21(1): 63-75. DOI:10.1016/0045-7930(92)90033-R |
| [58] |
LUO X, et al. Effects of homogeneous condensation in compressible flows:Ludwieg-tube experiments and simulations[J]. Journal of Fluid Mechanics, 2007, 572: 339-366. DOI:10.1017/S0022112006003727 |
| [59] |
YANG Y, SHEN S. Numerical simulation on non-equilibrium spontaneous condensation in supersonic steam flow[J]. International Communications in Heat and Mass Transfer, 2009, 36(9): 902-907. DOI:10.1016/j.icheatmasstransfer.2009.06.001 |
| [60] |
BROWN D P, et al. A method of moments based CFD model for polydisperse aerosol flows with strong interphase mass and heat transfer[J]. Computers & Fluids, 2006, 35(7): 762-780. DOI:10.1016/j.compfluid.2006.01.012 |
| [61] |
DYKAS S, WRÍBLEWSKI W. Single-and two-fluid models for steam condensing flow modeling[J]. International Journal of Multiphase Flow, 2011, 37(9): 1245-1253. DOI:10.1016/j.ijmultiphaseflow.2011.05.008 |
| [62] |
DYKAS S, WRÍBLEWSKI W. Two-fluid model for prediction of wet steam transonic flow[J]. International Journal of Heat and Mass Transfer, 2013, 60: 88-94. DOI:10.1016/j.ijheatmasstransfer.2012.12.024 |
| [63] |
CROWE C T. Drag coefficient of particles in a rocket nozzle[J]. AIAA Journal, 1967, 5(5): 1021-1022. DOI:10.2514/3.4119 |
| [64] |
CHAPMAN S, COWLING T G. The mathematical theory of non-uniform gases[M]. Cambridge: Cambridge University Press, 1991: 447.
|
| [65] |
LUO X, et al. On phase transition in compressible flows:modelling and validation[J]. Journal of Fluid Mechanics, 2006, 548: 403-430. DOI:10.1017/S0022112005007809 |
 2019, Vol. 37
2019, Vol. 37