2. 中国空气动力研究与发展中心 计算空气动力研究所, 四川 绵阳 621000
2. Computational Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
大规模分布式并行计算快速发展,使计算流体力学(Computational Fluid Dynamics, CFD)具备了解决复杂外形工程问题的能力。大规模CFD并行计算成为飞行器气动性能计算[1]、多体分离安全性评估[2]和飞行器外形优化[3-5]的有效手段。
CFD并行计算属于数据通信密集型,采用的数值格式和软件并行设计对并行效率影响很大[6]。Knight首先系统性地阐述了并行计算机系统架构和CFD并行程序设计模式[7]。国内陆林生和董超群等[8]研究了并行程序概念设计方法,陈刚和王磊等[9]提出了面向大规模并行的软件实现方法。近年来,CFD并行计算广泛应用于航空航天等领域[10-12],但并行规模都在万核以下。
对于分布式并行系统,消息传递接口(Message Passing Interface, MPI)是最成熟和有效的并行程序实现规范,广泛应用于计算力学领域。OpenMPI和MPICH是两种广泛使用的MPI编程程序包,都成功用于CFD并行程序编码[13-14]。
在使用并行解算器模拟流动前,通常需要采用合适的方法对生成的网格进行多核并行分区。分区算法极大地影响着并行计算时的负载平衡和并行效率。对于非结构网格,采用多级不规则图算法的Metis程序库[15],是目前应用最广、最快速和高质量的并行分区工具。由于没有拓扑结构的限制,分区后的非结构网格通常比结构网格有更高的负载平衡性能。
非结构网格的有限体积方法通常采用积分形式的雷诺平均Navier-Stokes方程和湍流模型方程[16]。二阶MUSCL (Monotonic Upwind Scheme for Conservation Laws)类数值格式具有类似紧致性质,即某个网格单元通量的计算只需要临近共面单元的流场信息,因而广泛应用于CFD计算软件且发展较为成熟。并行计算时,仅需要通过MPI交换并行交界面两侧单元的流场数据,有利于并行计算的实现和减少并行传递的数据量。
本文通过基于非结构混合网格和有限体积方法,采用紧致型二阶数值格式,发展了适用于复杂工程问题的万核级并行实现方法,测试和评估了并行效率。
1 数值方法雷诺平均Navier-Stokes方程(RANS)守恒形式的积分方程为:
| $ \frac{\partial }{{\partial \tau }}\iiint\limits_V {WdV} + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\nolimits_\mathit{\Omega } {\left( {{\mathit{\boldsymbol{H}}_c} \cdot \mathit{\boldsymbol{n}} - {\mathit{\boldsymbol{H}}_v} \cdot \mathit{\boldsymbol{n}}} \right){\text{d}}S} = 0 $ | (1) |
式中,
对流通量可以表示为:
| $ {\mathit{\boldsymbol{H}}_c} = \left[ {\begin{array}{*{20}{c}} {\rho V}\\ {\rho uV + {n_x}p}\\ {\rho vV + {n_y}p}\\ {\rho wV + {n_z}p}\\ {\rho HV} \end{array}} \right] $ | (2) |
式中,p是静压,ρ是密度,V是逆变速度:
| $ V = {n_x}u + {n_y}v + {n_z}w $ | (3) |
H为焓值,定义为:
| $ H = e + \frac{{{u^2} + {v^2} + {w^2}}}{2} + \frac{p}{\rho } $ | (4) |
式中,e为流动内能。
黏性通量相对比较复杂,本文略去,具体内容可以参考文献[17]。
在网格单元内积分,得到离散形式的控制方程:
| $ \frac{{\partial \left( {V\mathit{\boldsymbol{W}}} \right)}}{{\partial \tau }} + \sum\limits_{k = 1}^N {\left( {{\mathit{\boldsymbol{H}}_{ck}} \cdot {\mathit{\boldsymbol{n}}_k} - {\mathit{\boldsymbol{H}}_{vk}} \cdot {\mathit{\boldsymbol{n}}_k}} \right){S_k}} = 0 $ | (5) |
式中,V是网格单元体积,N是与该网格单元共面网格单元总数。
控制方程的离散采用格心格式的有限体积法,时间项采用LU-SGS迭代[18],湍流模型为一方程的SA模型[19]。对流项采用Roe格式[20],黏性项采用中心格式[21]。
格心格式的有限体积方法,流场未知变量存储在网格单元的形心上,如图 1所示的三角形形心点J1、J2和J3。然而,对流通量和黏性通量计算却需要网格单元对应的网格面心上的流场值,如K1、K2和K3。只有采用一阶格式时,面上的流场值等于形心值。当采用紧致型的二阶格式时,网格面心上左右两侧的流场值由同侧的网格单元体心值构造。计算黏性通量时,面心流场值采用中心格式,以K1面为例,表示为:

|
图 1 通量计算模板示意图 Fig.1 Stencil for flux calculation |
| $ {Q_{K1}} = \frac{1}{2}\left( {{\mathit{\boldsymbol{W}}_I} + {\mathit{\boldsymbol{W}}_{J1}}} \right) $ | (6) |
K2和K3面心流场值可以类似得到。黏性通量可以表示为:
| $ {\mathit{\boldsymbol{H}}_{v,K1}} = f\left( {{\mathit{\boldsymbol{Q}}_{K1}}} \right) $ | (7) |
黏性通量计算的具体表达式参考文献[21]。
采用Roe格式时,对流通量可以表示为
| $ {\mathit{\boldsymbol{H}}_{c,K1}} = f\left( {{\mathit{\boldsymbol{Q}}_{K1,L}} + {\mathit{\boldsymbol{Q}}_{K1,R}}} \right) $ | (8) |
式中,QK1, L和QK1, R分别为面K1左右两侧的流场值,通过各自同侧的体心值构造
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Q}}_{K1,L}} = f\left( {{\mathit{\boldsymbol{W}}_1}} \right)\\ {\mathit{\boldsymbol{Q}}_{K1,R}} = f\left( {{\mathit{\boldsymbol{W}}_{J1}}} \right) \end{array} \right. $ | (9) |
采用Roe格式计算对流通量的具体表达式参考文献[20]。
需要指出的是,如果采用更高阶的数值格式,面心流场值的构造将会用到更多临近网格单元上的体心值。对于本文所述的二阶格式,只需要紧邻的网格单元体心值,因而并行计算时,只有并行交界面两侧的网格单元需要进行流场数据的交换。
式(5)中的第二项通常称为残差项,记为:
| $ \mathit{\boldsymbol{R}} = \sum\limits_{k = 1}^N {\left( {{\mathit{\boldsymbol{H}}_{ck}} \cdot {\mathit{\boldsymbol{n}}_k} - {\mathit{\boldsymbol{H}}_{vk}} \cdot {\mathit{\boldsymbol{n}}_k}} \right){S_k}} $ | (10) |
则式(5)表示为:
| $ {V_I}\frac{{\Delta {\mathit{\boldsymbol{W}}_I}}}{{\Delta {\tau _I}}} = - {\mathit{\boldsymbol{R}}_I} $ | (11) |
为了增加计算的数值稳定性和提高收敛速度,时间项通常采用隐式格式[17],即
| $ \frac{{{V_I}}}{{\Delta {\tau _I}}}\Delta \mathit{\boldsymbol{W}}_I^n = - \frac{1}{2}\mathit{\boldsymbol{R}}_I^{n + 1} - \frac{1}{2}\mathit{\boldsymbol{R}}_I^n $ | (12) |
式中:
| $ \Delta W_I^n = W_I^{n + 1} - W_I^n $ | (13) |
通过对残差项的线化,可以得到
| $ \left[ {\frac{{{V_I}}}{{\Delta {\tau _I}}} + \frac{1}{2}{{\left( {\frac{{\partial \mathit{\boldsymbol{R}}}}{{\partial \mathit{\boldsymbol{W}}}}} \right)}_I}} \right]\Delta \mathit{\boldsymbol{W}}_I^n = - \mathit{\boldsymbol{R}}_I^n $ | (14) |
上式求解采用LU-SGS迭代方法,具体内容可参考文献[18]。定常流场由边界条件决定,迭代过程中,边界信息由边界单元逐渐向流场内部传递,直到收敛。通常情况下,可能需要迭代上千步甚至更多流场才能收敛,当网格量较大时,计算量巨大,单核计算需要很长的时间。对于工程复杂外形,并行计算是减少计算时间的有效方法。
2 并行实现算法采用LU-SGS迭代方法,当前步流场计算依赖于前一步的流场,当流场为非定常时依赖更多。但对于某一迭代步,采用紧致二阶格式,网格单元的流场值只与相邻一层网格有关。因此对于分布式并行计算系统,采用对空间进行分区更适合CFD并行计算,并采用MPI进行多个分区间流场数据的交换。并行实现算法主要包括网格分区算法和流场数据交换算法。
2.1 网格分区技术非结构网格分区方法采用基于图论算法的Metis程序库,该程序库使用多级二分法或多级多支分区算法,如图 2所示。
分区算法以网格数据构成的图作为输入,由网格面和网格单元组成。包含n个节点V和m个边E的图G定义为:
| $ \left\{ \begin{array}{l} G = \left( {V,E} \right)\\ V = \left[ {{V_1},{V_2}, \cdots ,{V_{\rm{n}}}} \right]\\ E = \left[ {{E_1},{E_2}, \cdots ,{E_m}} \right] \end{array} \right. $ | (15) |
需要指出的是,对于格心格式的有限体积法,图定义中的节点和边分别指网格中的网格单元和网格面。输入的图信息通常采用压缩存储格式(Compressed Storage Format,CSR),该格式广泛应用于稀疏图的存储。网格连接关系表示成图的信息可以用两个整数数组来指定:xadj和adjncy,数组长度分别为n+1和2m。xadj[i+1]-xadj[i]的值表示与第i个网格单元共面的网格单元个数,数组adjncy中第xadj[i]到第xadj[i+1]位置存储了相应的共面网格单元的编号。以图 1网格数据为例,数组xadj和adjncy存储数据如图 3所示。

|
图 3 非结构网格连接关系CSR表示 Fig.3 Graph data in CSR format of unstructured grid |
图 4给出了M6机翼网格并行分区表面网格的示意图,共3个并行分区,其中相同颜色的网格单元属于相同的计算进程。

|
图 4 M6机翼网格分区图 Fig.4 Partitioned grid of M6 wing with Metis |
本文并行算法基于分布式大规模并行计算机系统,采用所有CPU都参与迭代计算的对等并行模式,MPI数据传递采用非阻塞通信,尽量加大计算和通信的重叠,只在必要的地方进行数据同步以保证计算的正确性。
采用对等并行模式,首先需要对网格进行前处理,按指定的并行规模采用Metis划分网格。为了减少每个计算进程内存消耗以提高程序的运行效率,每个分区网格只保存必需的局部网格数据和并行分区边界上网格单元及顶点的对应关系。网格分区完成后,每个计算进程读入相应分区的网格,独立地逐一计算各自分区中每个网格单元的通量。
格心格式的有限体积法,并行边界间数据传递需要的对应关系包括网格单元与网格单元和网格顶点与网格顶点间的对应关系,其中网格单元间对应关系主要用于流场变量的迭代,网格顶点间的对应关系用于二阶格式中梯度的计算。并行网格对应关系建立耗时长,然而对于定常问题只需要计算一次,程序设计时宜采用存储该对应关系,以空间换时间,提高并行效率。
对于串行计算,封闭的边界条件决定了当前流场的特征,边界信息由边界网格单元向内部网格单元传播。并行计算时,对于单个计算进程,只有部分边界网格存在相应的分区网格中,边界条件不再封闭。将并行交界面上的网格面视为特殊类型的边界面时,则边界面满足封闭性质。同时,与真实边界面类似地采用虚拟边界单元,真实边界面对应的虚拟单元用于施加边界条件,并行边界面对应的虚拟单元则用来存储并行交换的数据。在计算网格单元的通量时,并行边界面与真实边界面采用相同的计算方法,程序设计亦能与串行程序保持一致。并行边界与虚拟单元设计如图 5所示,则对应任意并行计算进程,计算及存储模式和串行时保持一致。

|
图 5 并行边界及虚拟单元 Fig.5 Ghost elements for data exchange between different processors |
MPI并行接口中并行数据必须以连续内存的方式提供,程序设计必须考虑减少并行计算时额外数据拷贝的开销以提高并行效率。格心格式有限体积法任何分区内的某个单元只对应唯一其它分区内的唯一单元,可以采用先物理网格单元后虚拟网格单元的网格排序策略,使对应的每一个并行分区需要接收的数据在内存中集中连续存放,如图 6所示,消除了网格单元并行数据的拷贝过程。
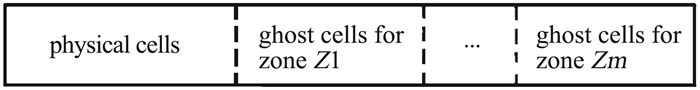
|
图 6 并行物理网格单元及虚拟网格单元排序存储示意图 Fig.6 Memory pattern for physical elements and ghost elements of grid data |
采用两个算例分别对本文非结构流动解算器的并行正确性和并行效率进行测试。算例一使用网格量相对较少的旋成体外形,迭代计算直到流场收敛,比较分析串行计算和并行计算结果的一致性;算例二使用运输机构型,其网格量大,用于测试大规模并行计算的效率,其最大的并行规模达18816核。
并行加速比S和效率E定义为:
| $ \left\{ \begin{array}{l} S = \frac{{{T_0}}}{{{T_n}}}\\ E = \frac{S}{{n/{n_0}}} \times 100\% \end{array} \right. $ | (16) |
式中:n为测试并行核数,T为每步计算平均时间;n0为并行测试基数核数,T0为基数核数对应的每步计算平均时间。
并行计算使用中国空气动力研究与发展中心计算空气动力研究所分布式并行计算机系统。该系统包含300个计算节点,每个节点64核,CPU主频约为2.8 GHz。
3.1 并行正确性及收敛性测试正确性测试模型为旋成体外形绕流模拟,旨在分析并行和串行计算结果的一致性。来流条件为:速度V= 1200 m/s,高度H=24 km,侧滑角β= 0°,迎角α=2.0°。由于流动对称,宜采用半模计算,网格如图 7所示,网格单元总数约为200万,单元类型包括四面体、棱柱和金字塔。计算核数分别为:1、32、64、128、256、512、1024、2048、4096和8192。

|
图 7 旋成体外形计算网格 Fig.7 Computing grid of revolving body |
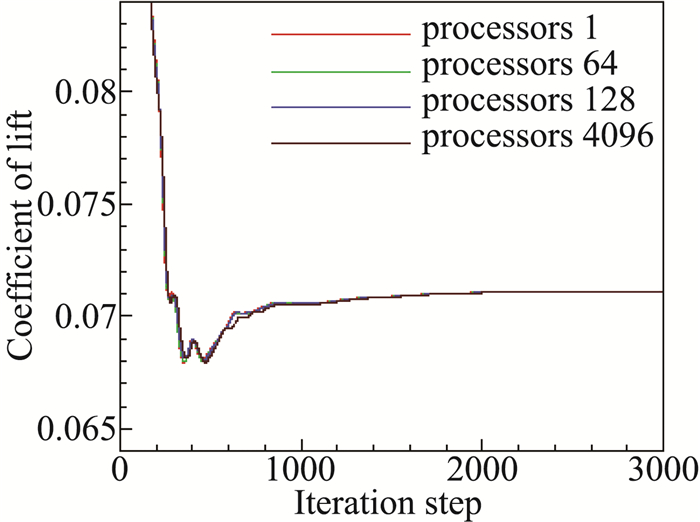
图 8~图 10分别给出了升力、阻力和俯仰力矩系数的收敛历程。由于并行计算和串行计算迭代过程中,网格单元通量计算的顺序并不完全相同,因此收敛过程有小量的差别,但收敛趋势一致且收敛后的值在误差范围内相同。不同核数对应收敛后的数值列于表 1,可以看出,并行计算收敛数值和串行计算偏差小于10-5。
|
图 8 升力系数收敛曲线 Fig.8 Convergence history of lift |

|
图 9 阻力系数收敛曲线 Fig.9 Convergence history of drag |

|
图 10 俯仰力矩系数收敛曲线 Fig.10 Convergence history of pitch moment |
| 表 1 并行计算与串行计算收敛数值的比较 Table 1 Result comparison between parallel and serial computation |
|
|
图 11和图 12分别给出了加速比和并行效率随计算核数增加的变化,可以看出,512核是加速比快速偏离理论值的临界核数,大于该值后效率快速降低,主要原因为网格单元很少,并行通信占用较多的时间。

|
图 11 加速比随计算核数变化 Fig.11 Speed up versus processors |

|
图 12 并行效率随计算核数变化 Fig.12 Efficiency versus processors |
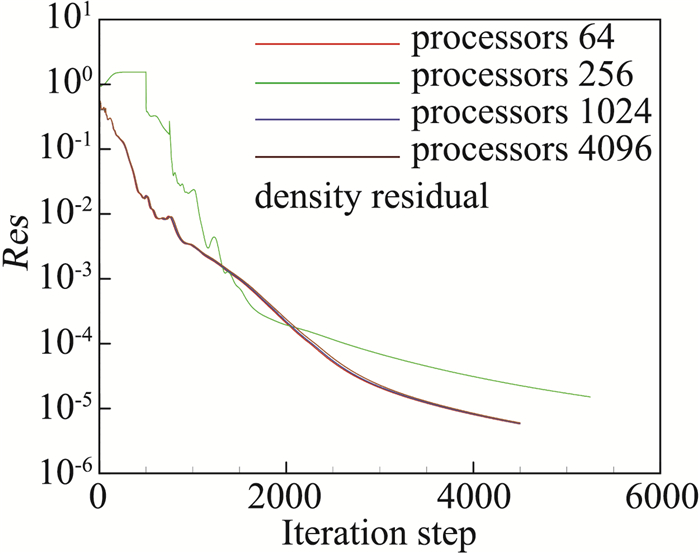
图 13和图 14分别给出了并行核数为64、256、1024和4096四种情况下密度和残差的收敛曲线,随着并行核数的增加,除256核外其它并行规模下残差收敛速度基本一致。
|
图 13 密度残差收敛曲线 Fig.13 Convergence history of density residual |

|
图 14 能量残差收敛曲线 Fig.14 Convergence history of energy residual |
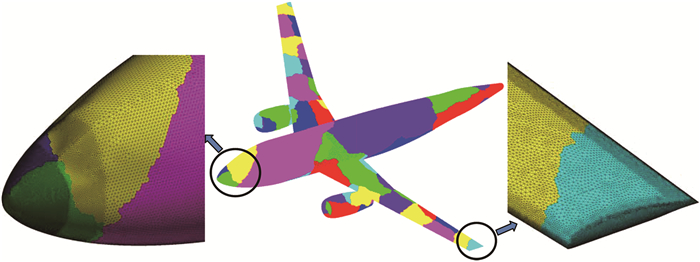
用于并行效率测试的模型为运输机绕流模拟,网格单元总数约为1.2亿。64个并行分区后的表面网格如图 15所示,由飞机头部和翼梢局部放大图可以看出,计算网格很密,其有利于准确模拟飞行阻力。来流条件为:飞行速度V=300 m/s,飞行高度H=11 km,侧滑角β= 0°,迎角α= 2.0°。
|
图 15 运输机构型并行分区后的表面网格 Fig.15 Partitioned surface grid for transport aircraft |
为了增加可靠性,效率测试每步计算时间是取迭代200步的平均时间。由于网格量大,单核计算时间太长,因此并行加速比S和效率E测试都是以64核为基准。
并行加速比随并行核数增加变化曲线如图 16所示,可以看出,该解算器并行性能很好,加速比为线性甚至超线性。出现超线性的原因主要有:a)非结构网格没有拓扑限制,采用Metis并行分区后容易达到很高的负载平衡性能;b)在分布式并行系统中,每个计算进程拥有其单独的缓存。随着并行规模增加,缓存总量增加,因此每个核拥有的缓存增加,提高了缓存命中率;c)当并行规模增加后,每个核网格量减小,需要的内存等资源减少,有利于提高并行系统的性能。

|
图 16 加速比随计算核数变化 Fig.16 Speed up versus processors |
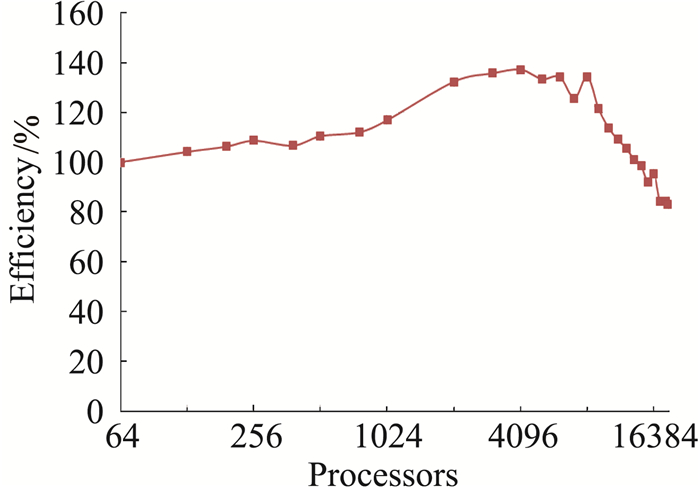
并行效率随并行规模增加变化曲线如图 17所示,可以看出,由于加速比性能优越,在并行核数小于14336时,并行效率都在100%以上,直到18816核,并行效率都保持在80%以上。
|
图 17 并行效率随计算核数变化 Fig.17 Efficiency versus processors |
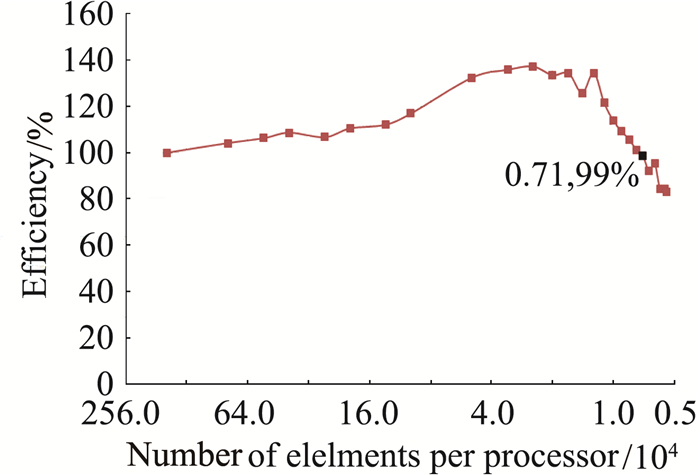
图 18给出了并行效率与每核网格单元数的关系,当网格单元数太少,并行数据交换耗费的时间相比迭代计算时间不再是小量时,并行效率随网格单元数减少快速下降。不同的数值格式和并行实现下降的拐点不同,本文在每核网格单元数大于1万时,都能保持很高的并行效率。
|
图 18 并行效率随每核网格单元数变化 Fig.18 Efficiency versus numbers of grid elements |
本文发展了基于分布式并行系统的大规模流动模拟方法,包括离散控制方程的紧致型数值格式、
基于Metis的网格分区技术和并行边界处理及虚拟单元技术等。数值结果表明,软件并行计算与串行计算结果一致,并行效率高。
与串行计算相比,并行计算流动收敛过程有小量的差别,但收敛数值在合理的误差范围内一致。在一定的并行核数范围内,表现出超线性的加速比特性。由于加速比性能好,所有的测试算例都具有很高的并行效率。另外,要保证有较高的并行效率,每核网格单元数不能太少。
总之,本文方法能有效地计算复杂飞行器构型的气动性能,并可充分利用大规模并行计算减少流动模拟时间和提高计算效率。
| [1] |
何开锋, 钱炜祺, 陈坚强, 等. 基于流体力学和电磁学方程数值求解的飞行器气动隐身一体化设计[J]. 空气动力学学报, 2009, 27(2): 180-185. HE K F, QIAN W Q, CHEN J Q, et al. Integrated aircraft design of aerodynamic and stealthy performance with numerically solving fluid dynamics and electro-magnetics equations[J]. Acta Aerodynamica Sinica, 2009, 27(2): 180-185. DOI:10.3969/j.issn.0258-1825.2009.02.007 (in Chinese) |
| [2] |
LI B, TANG J, ZHOU N C. Numerical simulation of missile launching with rudder deflection[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30(2): 107-115. |
| [3] |
Lyu Z, Martinsy J A. RANS-based aerodynamic shape optimization of a blended-wing-body aircraft[R]. AIAA-2013-2586.
|
| [4] |
唐静, 邓有奇, 马明生, 等. 飞翼气动优化中参数化和网格变形技术[J]. 航空学报, 2015, 36(5): 1480-1490. TANG J, DENG Y Q, MA M S, et al. Parametrization and grid deformation techniques for flying-wing aerodynamic optimization[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1480-1490. (in Chinese) |
| [5] |
RONZHEIMERA, HEPPERLE M, BREZILLON J. Aerodynamic optimal engine integration for a business jet configuration[R]. AIAA-2012-1841.
|
| [6] |
Roose D, Driessche R V. 并行计算机和计算流体力学并行算法[J]. 力学进展, 1998, 28(1): 111-125. ROOSE D, DRIESSCHE R V. Parallel computers and parallel algorithms for CFD[J]. Advances in Mechanics, 1998, 28(1): 111-125. DOI:10.3321/j.issn:1000-0992.1998.01.010 (in Chinese) |
| [7] |
KNIGH D. Parallel computing in computational fluid dynamics[C]//AGARD Confernce Proceedings/Progress and Challenges in CFD Methods and Algorithms, 1996.
|
| [8] |
陆林生, 董超群, 王玲秋, 等. 并行程序概念设计方法研究[J]. 计算机学报, 2003, 26(9): 1086-1093. LU L S, DONG C Q, WANG L Q, et al. Researh on parallel program conceptual designing method[J]. Chinese Journal of Computers, 2003, 26(9): 1086-1093. DOI:10.3321/j.issn:0254-4164.2003.09.008 (in Chinese) |
| [9] |
陈刚, 王磊, 陆忠华, 等. 万核级并行飞机气动模拟软件CCFD研制[J]. 华中科技大学学报(自然科学版), 2011, 39(增刊1): 99-101. CHEN G, WANG L, LU Z H, et al. Development of ten-thousand-core parallel software CCFD for aircraft aerodynamics simulation[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 2011, 39(Sup. 1): 99-101. (in Chinese) |
| [10] |
WIART C, HILLEWAERK K. Development and validation of a massively parallel high-order solver for DNS and LES of industrial Flows[C]//IDIHOM: Industrialization of High-Order Methods-A Top-Down Approach, 2015, 251-292.
|
| [11] |
潘沙, 李桦, 夏智勋. 高性能并行计算在航空航天CFD数值模拟中的应用[J]. 计算机工程与科学, 2012, 34(8): 191-198. PAN S, LI H, XIA Z X. High-performance parallel computiation application for aerospace CFD numerical simulation[J]. Computer Engineering & Science, 2012, 34(8): 191-198. DOI:10.3969/j.issn.1007-130X.2012.08.030 (in Chinese) |
| [12] |
HUANG X C, XIAO A. Iteration and parallel computation on computational fluid dynamics[C]//International Conference on Intelligent Computation Technology & Automation, 2014: 318-321.
|
| [13] |
SHEKE S, KALYAN W. Parallel multigrid solver for Navier-Stokes equation using Open MPI[J]. International Journal of Computer Science Trends and Technology, 2015, 3(5): 131-134. |
| [14] |
BERGER M J, AFTOSMIS M J, MARSHALL D D. Performance of a new CFD flow solver using a hybrid programming paradigm[J]. Journal of Parallel & Distributed Computing, 2005, 65(4): 414-423. |
| [15] |
KARYPIS G, KUMAR V. A fast and high quality multilevel scheme for partitioning irregular graphs[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392. |
| [16] |
PULLIAM T H. Early development of implicit methods for computational fluid dynamics at NASA Ames[J]. Computers & Fluids, 2009, 38(2): 491-495. |
| [17] |
BLAZEK J. Computational fluid dynamics:principles and applications[M]. Elsevier: Elsevier press, 2015.
|
| [18] |
KIM J S, KWON O J. Improvement on block LU-SGS scheme for unstructured mesh navier-stokes computations[R]. AIAA-2002-1061.
|
| [19] |
SPALART S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA-92-0439, 1992.
|
| [20] |
ROEP L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [21] |
HASELBACHER A, BLAZEK J. Accurate and efficient discretisation of the Navier-Stokes equations on mixed grids[J]. AIAA Journal, 2000, 38(11): 2094-2102. DOI:10.2514/2.871 |
 2019, Vol. 37
2019, Vol. 37



