2. 中国空气动力研究与发展中心 低速空气动力研究所, 四川 绵阳 621000
2. Low Speed Aerodynamics Research Institute of China Aerodynamics Research and Development Center, Mianyang Sichuan 621000, China
飞机结冰严重威胁飞机的飞行安全[1-2]。为此,美国联邦航空管理局(FAA)在适航条例FAR 25部附录C中明确定义了飞机与其防除冰系统设计所必须考虑的结冰条件范围。然而,直到1994年10月31日在印第安纳州罗斯劳恩附近发生的ATR-72飞机坠毁事故,让人们对结冰条件范围有了重新认识。事故调查表明[3],冻雨在机翼除冰套之后副翼之前的上翼面形成了冰脊,冰脊导致了飞机的非指令滚转,而导致此次事故的冻雨超出了FAR 25部附录C定义的结冰条件, 出现了直径超过100 μm的过冷大水滴(Supercooled Large Droplet,SLD)。
研究人员发现,相比于FAR25附录C规定的常规水滴,SLD结冰条件的特点是存在一定数量较大直径的水滴且分布广,结冰环境温度较高[4],在运动、撞击过程中会发生变形、破碎和飞溅等显著的动力学行为[5-7],这些都可能导致更严重的结冰现象。因此,FAA于2014年11月在适航条例中新增了附录O“SLD结冰条件”及相关适航符合性要求。而在传统结冰数值模拟中,有两个最基本的假设[8-9]:一是水滴的刚性球假设,即水滴在运动过程中始终保持球形,不发生变形和破碎行为;二是水滴在碰撞固壁后不发生飞溅行为,即水滴撞击量与结冰量守恒。显然,在SLD条件下,这些假设不再成立,因此,需要发展SLD的动力学模型,以使得SLD结冰计算更加符合真实的结冰物理过程。
在SLD的动力学特性中,撞击飞溅特性主要指水滴铺展过程的最大铺展因子α(最大铺展圆的直径与初始水滴直径之比)、飞溅临界判则数K以及飞溅后子液滴模型(直径、速度、质量比等),这些量对结冰计算中的水滴收集率影响最大[10]。Scheller &Bousfield (1995)、Pasandideh-Fard(1996)、Clanet(2004)、Roisman (2009)、Eggers(2010)、Sen(2016)等[11-16]主要开展了水滴撞击固体表面的最大铺展因子α与撞击参数We、Re数等的函数关系研究,Tang[17](2017)研究了粗糙度Ra对最大铺展因子α的影响。Stow and Hadfield(1981)、Mundo(1995)、Cossali(1997)、Range and Feuillebois(1998)等[18-21]主要研究了We、Re、Oh以及粗糙度对飞溅临界判则数的影响规律。在飞溅子液滴模型研究方面,Lee and Ryou[22]、Stanton and Rutland[23]、Trujillo[23]等发展了基于不同统计方法的模型,其中美国LEWICE软件在3.0版本中加入了SLD飞溅模型,其子液滴模型就是在Trujillo模型的基础上改进而来的。然而,现有这些模型仍需发展,美国NASA在最近的结冰发展展望中仍然提到了需要发展SLD数值模型。就现有模型来看,在计算飞溅子液滴直径、速度等信息时,均未包含粗糙度Ra这一影响因素,而表面粗糙度对水滴撞击飞溅有重要影响已是公认的事实。因此,本文是在总结现有模型局限性的基础上,通过实验研究粗糙度对飞溅子液滴动力学的影响规律,希望为进一步完善、改进现有SLD飞溅模型提供支撑。
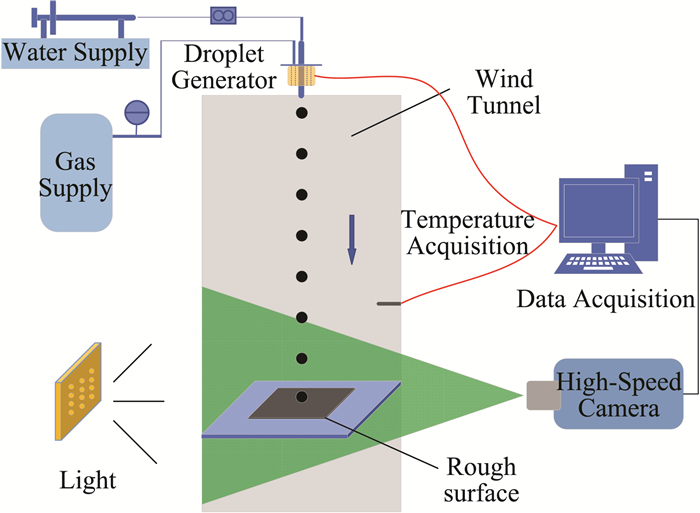
1 实验设计 1.1 实验系统图 1是实验系统总体布局图。实验系统主要由三部分组成:风道、水滴发生系统和高速摄像系统。风道温度可连续调节,最低达-15 ℃。
|
图 1 实验系统总体布局图 Fig.1 Schematic of experimental apparatus |
风道由稳定段、收缩段、实验段以及扩散段组成。收缩段采用二元维多辛斯基曲线设计,收缩比为4,长0.2 m,其入口截面尺寸为0.3 m×0.3 m,出口截面尺寸为0.3 m×0.075 m;水滴的撞击过程发生在风道实验段,实验段长为0.24 m,其截面尺寸为0.3 m× 0.075 m,实验前对风道的湍流段进行了评估,风速为36.5 m/s时,湍流度 <8.5%。
实验系统中最关键的是水滴发生装置,由水气两路组成,由于表面张力的作用,喷嘴会聚集较大水滴才能在重力作用下滴落,因此,采用均匀吹气的方式,通过微流量注射泵精确控制水滴的体积,产生所需直径的水滴。同时在风道和喷嘴口布置温度传感器,实时测量水滴和风道内气流的温度,当水滴温度满足过冷要求后,再进行吹气,释放水滴,这也是采用吹气控制水滴发生的原因之一。
实验采用MotionXtra的HG-100K高速摄像机拍摄,设置拍摄像素为1024×1024 pixels,帧数为1500 fps,该相机可以精确地确定水滴的撞击速度和子液滴的飞溅情况。
1.2 实验方法(1) 基本理论
水滴撞击动力学发展至今[26],主要由以下无量纲数控制着水滴撞击过程:
| $ 雷诺数\;\;\mathit{Re} = \frac{{\rho D{V_0}}}{\mu } $ | (1) |
| $ 韦伯数\;\;\mathit{We} = \frac{{\rho DV_0^2}}{\sigma } $ | (2) |
| $ 奥内佐格数\;\;Oh = \frac{\mu }{{{{\left( {\rho \sigma D} \right)}^{1/2}}}} = \frac{{W{e^{1/2}}}}{{\mathit{Re}}} $ | (3) |
| $ {\rm{Mundo}}\;飞溅判则数\;\;\;K = Oh \cdot \mathit{R}{\mathit{e}^{1.25}} $ | (4) |
其中,ρ、μ和σ分别代表水滴的密度、黏性和表面张力,D和V0分别代表水滴直径和撞击速度。
当然,考虑重力等加速度效应影响时,还有无量纲数Bo数、Fr数,但是因为水滴撞击表面有着剧烈的相互作用,重力效应可以忽略不计,因此可以不考虑这两个无量纲数。本文着重考虑粗糙度对水滴撞击过程的影响,遂引入无量纲数St:
| $ St\;数\;\;\;\;St = Ra/D $ | (5) |
其中Ra表征表面粗糙度,单位为μm。
(2) 实验流程
为捕获水滴撞击过程,首先需要利用水滴发生器产生所需直径的单颗水滴,为保证水滴充分过冷,待水滴在喷嘴悬挂一定时间,温度由喷嘴处温度传感器获知。当水滴温度与气流温度基本一致时,通过吹气释放水滴,沿风道中心线运动,待其运动接近撞击表面时,触发高速摄像机记录整个撞击过程。为研究粗糙度对水滴撞击飞溅特性的影响,撞击表面贴上不同目数的粗糙度纸。
水滴直径、水滴速度这两个参数的测量都需要在实验前放置一个标尺进行标定,精度共同取决于相机分辨率、图像处理程序的精度。
(3) 实验条件
实验粗糙度范围是Ra=65~210 μm,温度范围是-1.5 ℃~23 ℃,水滴直径和速度根据实际测量结果确定,具体条次如表 1所示,其中表第二列为实验用砂纸的目数,指在1平方英寸的面积上筛网的孔数,目数越低,筛孔越少,表面就越粗糙。
| 表 1 实验条件 Table 1 The experimental conditions |
|
|
(1) 子液滴直径和速度
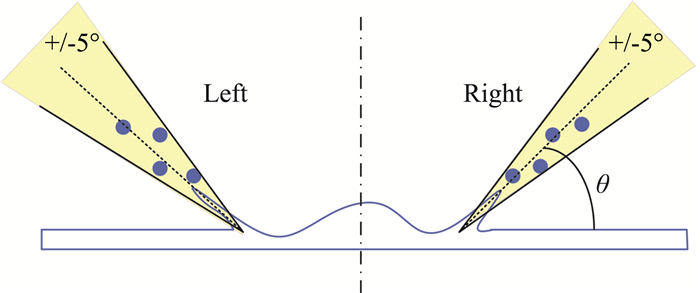
飞溅会形成多个子液滴,本文主要统计在撞击自由边缘飞溅方向正负5°范围内的清晰可见的子液滴,如图 2黄色区域所示,分别测量左右该范围内子液滴的直径和速度,再将左右两个区域的值进行平均。
|
图 2 水滴飞溅示意图 Fig.2 Sketch of droplet splashing |
水滴直径和速度测量精度和误差依赖于相机分辨率、图像处理程序以及拍摄频率。在本实验中,相机物距和焦距一定,在1024×1024分辨率,1500 fps拍摄速度的情况下,高速相片每一像素代表 0.025 mm,两张照片时间间隔约为1/1500 s,根据实际数据处理情况,水滴直径的测量误差为±0.125 mm,速度的测量误差为±0.1875 m/s。
(2) 子液滴飞溅角度
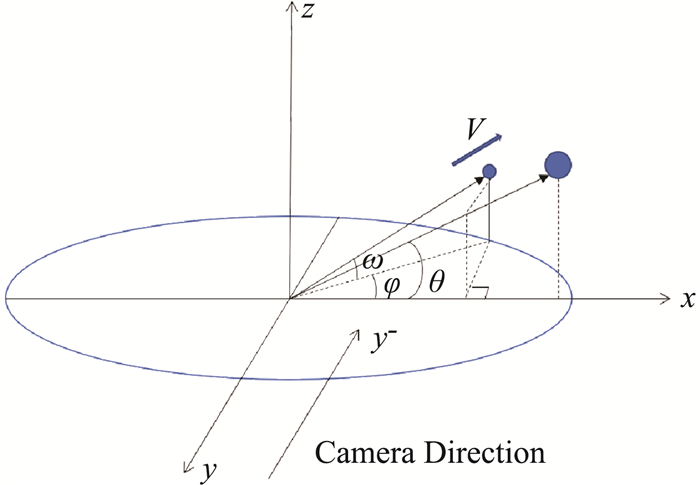
水滴飞溅角度示意图如图 3所示,其中θ为测量角度,ω为实际飞溅角度,φ为液滴与原点连线在xy平面的投影与x轴的夹角,由于相机是从正侧面(y-方向)进行拍照,因此所有不在xz平面水滴的测量角度θ都与实际飞溅角度ω存在一定偏差。
|
图 3 水滴飞溅角度示意图 Fig.3 Splashing angle of secondary droplet |
根据如图 3所示的几何关系,不在xz平面子液滴的真实飞溅角度ω与从图像中直接测量得到的角度θ之间的关系是:
| $ \tan \omega = \tan \theta \cdot \cos \varphi $ | (6) |
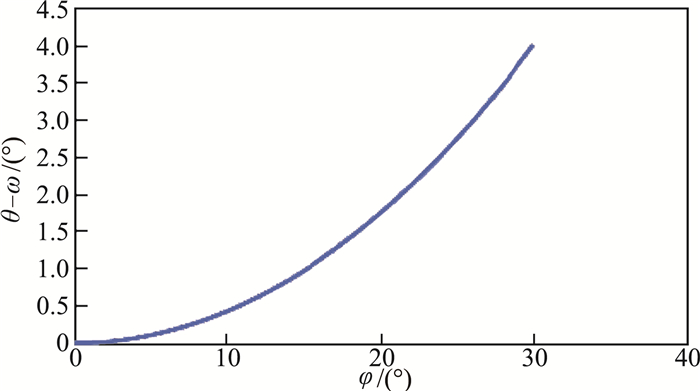
如图 4所示,由于高速相片中水滴的主要集中范围是θ < 40°,φ < 30°,因此真实飞溅角度ω与测量值θ具体偏差Δ=| θ-ω | < 4°。
|
图 4 飞溅角度误差分析 Fig.4 Error analysis of splashing angle |
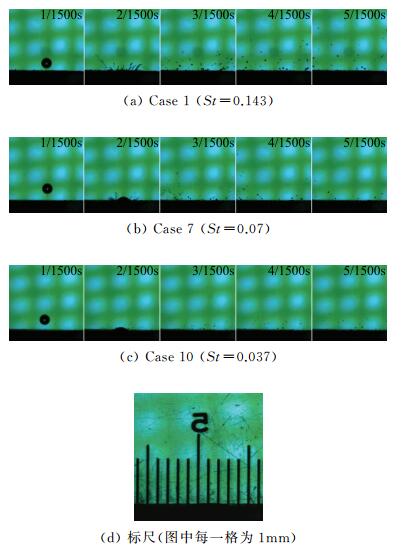
图 5展示的是温度23℃,粗糙度分别为St=0.143,St=0.07,St=0.037(Case 1、7、10)的三种典型实验系列高速相片,图片右上角为时间尺度,图 5(d)为空间尺度。本文主要利用图像和拟合曲线处理软件,对Case 1~22的所有高速相片中的子液滴进行统计分析,结果和分析如下。
|
图 5 实验照片 Fig.5 Photographs of experiments |
实验首先进行了五次重复性实验,实验工况为表 1中Case 2至6,具体实验条件如表 2所示。
| 表 2 重复性实验条件与结果 Table 2 Conditions of repetitive test |
|
|
为便于规律分析,将子液滴的直径d、速度Vs、角度ω分别无量纲化为:
| $ \beta = d/D $ | (7) |
| $ \gamma = {V_s}/{V_0} $ | (8) |
| $ \delta = \omega /{\omega _0} $ | (9) |
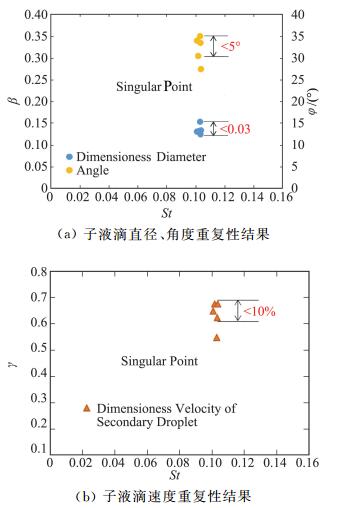
五次实验子液滴的直径、角度、速度信息统计结果如图 6所示,需要说明的是,每次实验子液滴直径、角度、速度值是指从图像中获取的左右两个飞溅方向(x+和x-)的平均值。从图 6中可以看出,飞溅角度小于5°,子液滴无量纲直径小于0.03,无量纲速度小于10%,重复性结果一致性较好。
|
图 6 重复性实验结果 Fig.6 Results of repetitive test |
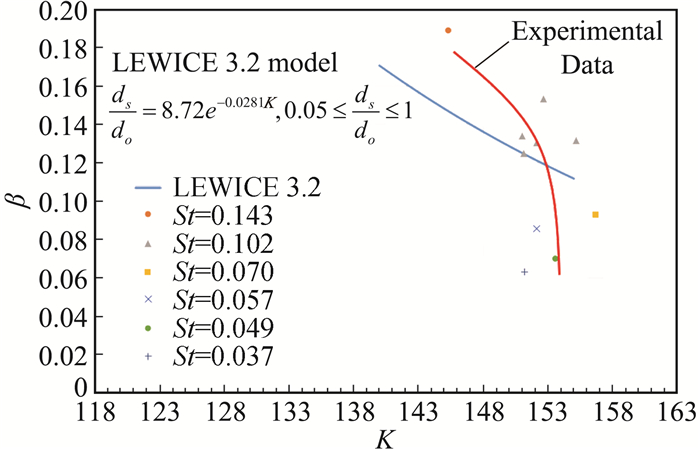
图 7给出的是Case1~10在常温23℃条件下,不同粗糙度、不同撞击参数时子液滴无量纲直径的变化规律。图中蓝色曲线是美国知名结冰计算软件LEWICE 3.2版本给出的子液滴直径数学模型,由该模型可以看出,在不考虑粗糙度影响时,子液滴直径随着撞击参数K的增大较缓慢减小,而一旦引入粗糙度St的影响,子液滴无量纲直径β会在K变化较小的情况下,迅速减小,这也至少说明表面粗糙度对子液滴直径大小的影响在140 < K < 160区间已起到主要作用。
|
图 7 子液滴无量纲直径随K值变化图 Fig.7 Variation of the dimensionless diameter of sub-droplets with K value |
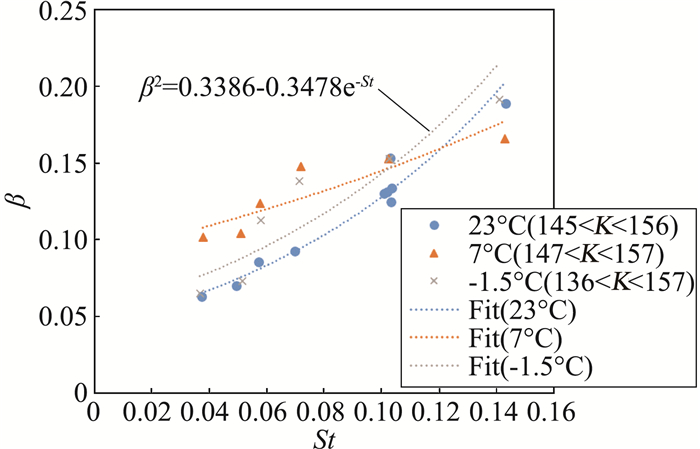
图 8是不同温度条件下,水滴无量纲直径随撞击参数K的变化规律。从图中可以看出,水滴温度的影响较小,无明显规律, 故以-1.5℃的拟合曲线代表St对β的影响模型:
| $ {\beta ^2} = 0.3386 - 0.3478{{\rm{e}}^{ - St}} $ | (10) |
|
图 8 不同水滴温度下子液滴无量纲直径随St值变化图 Fig.8 Variation of the dimensionless diameter of sub-droplets with St value at different temperatures |
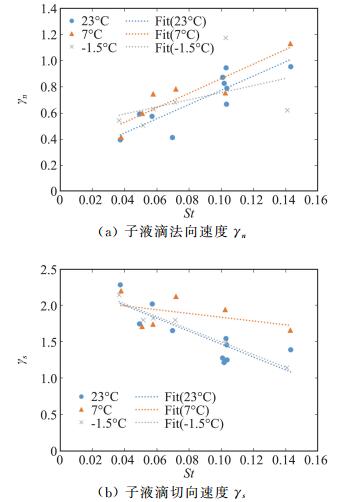
图 9(a)、(b)分别是飞溅子液滴法向(z+)和切向(x+和x-)速度随St值的变化规律。从图中可以看出,呈现了相反了的变化规律,随着St值的增大,γn增加,而γs减小,这是因为实验初始水滴垂直撞击粗糙表面,入射角为90°,越粗糙的表面,两个或几个粗糙颗粒之间的波谷越深,越容易阻碍水滴在撞击铺展或者飞溅时向切向方向运动,而在力的相互作用下,会把更多的能量提供给了与入射方向相反的方向。
|
图 9 不同水滴温度下子液滴无量纲速度随St值变化图 Fig.9 Variation of the dimensionless velocity of sub-droplets with St value at different temperatures |
在撞击参数140 < K < 160,拟合得到式(11)和式(12)的子液滴飞溅速度模型:
| $ 法向:\gamma _n^2 = - 1.1105 - 4.3224/\ln St $ | (11) |
| $ 切向:{\gamma _s} = 8.1967 + 9.3549S{t^{1/2}}\ln St $ | (12) |
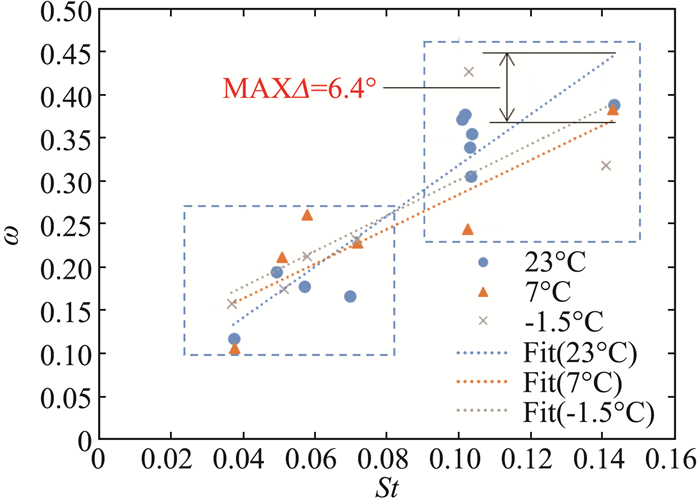
图 10是不同温度条件下,子液滴无量纲角度随撞击参数K的变化规律。由于水滴几乎均垂直撞击,因此,无量纲角度计算式(9)中ω0取为90°。从图 10中可以看出,子液滴无量纲角度δ与粗糙度St呈现正相关,并且随着St的增大,温度对δ的影响开始显现,但也不是特别明显,在实验范围中,最大差值仅为6.4°,也只比统计偏差高出2°,因此,温度影响相比粗糙度影响量仍然是小量。
|
图 10 不同子液滴温度下子液滴无量纲角度随St值变化图 Fig.10 Variation of the dimensionless angle of sub-droplets with St value at different temperatures |
在不考虑温度影响的情况下,在撞击参数140 < K < 160范围,拟合得到子液滴飞溅角度模型:
| $ \omega = 0.7642 + 0.1936\ln St $ | (13) |
本文利用水滴撞击实验系统,开展了水滴撞击不同粗糙度表面的动力学实验,研究了表面粗糙度对水滴撞击飞溅特性的影响规律,通过数据分析得出以下结论:
1) 在撞击参数140 < K < 160范围,粗糙度对撞击产生的子液滴的直径起主要影响作用,表面越粗糙,子液滴平均直径越大。
2) 粗糙度对子液滴法向和切向速度的影响规律不同,随着St值的增大,γn增加,而γs减小。
3) 子液滴无量纲角度δ与粗糙度St呈现正相关,并且当St>0.1时,温度对δ的影响开始显现,但相比粗糙度仍然是小量。
| [1] |
BARNHART B P, et al. Simulation model development for icing effects flight training[J]. Journal of Aerospace, 2002, 111(1): 84-99. |
| [2] |
FARHAD SABRI, OCTAVIAN TRIFU, et al. In-flight ice accretion simulation in SLD conditions[C]//25th AIAA Applied Aerodynamics Conference, 25-28 June 2007, Miami.
|
| [3] |
National Transportation Safety Board. Aircraft accident report, in-flight icing encounter and loss of control simmons airlines[R]. d. b. a. American Eagle Flight 4184 Avions de Transport Regional(ATR) Model 72-212, N401AM Roselawn, Indiana October 31, 1994.
|
| [4] |
林贵平, 卜雪琴, 申晓斌, 等. 飞机结冰与防冰技术[M]. 北京: 北京航空航天大学出版社, 2016.
|
| [5] |
ANIL D SHAH, MICHAEL W PATNOE, ERVINL BERG. Droplet size distribution and ice shapes[C]//36th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, Nevada: AIAA, 1998.
|
| [6] |
LUXFORD G, HAMMOND D, IVEY P. Modelling, imaging andmeasurement of distortion, drag and break-up of aircraft-icing droplets[R]. AIAA 2005-0071.
|
| [7] |
TAN S C. Effects of large droplet dynamics on airfoil impingement of distortion, drag and breakup of aircraft icing droplets[C]//43rd AIAA Aerospace Science Meeting and Exhibit, Reno, Nevada: AIAA, 2005.
|
| [8] |
HONSEK R, HABASHI W G. FENSAP-ICE: Eulerian modeling of droplet impingement in the SLD regime of aircraft icing[R]. AIAA 2006-465, 2006.
|
| [9] |
JUNG S K, KIM J H, MYONG R S. Numerical model for Eulerian droplet impingement in supercooled large droplet conditions[R]. AIAA 2013-0244, 2013.
|
| [10] |
WILLIAM B WRIGHT, MARK G POTAPCZUK. Semi-empirical modeling of SLD physics[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2004-412, January 2004.
|
| [11] |
SCHELLER B L, BOUSFIELD D W. Newtonian drop impact with a solid surface[J]. AIChE J, 1985, 41: 1357-67. |
| [12] |
PASANDIDEH-FARD M, QIAO Y M, CHANDRA S, et al. Capillary effects during droplet impact on a solid surface[J]. Phys Fluids, 1996, 8: 650-59. DOI:10.1063/1.868850 |
| [13] |
CLANET C, BEGUIN C, RICHARD D, et al. Maximal deformation of an impacting drop[J]. J Fluid Mech, 2004, 517: 199-208. DOI:10.1017/S0022112004000904 |
| [14] |
ROISMAN I V. Inertia dominated drop collisions. Ⅱ. An analytical solution of the Navier-Stokes equations for a spreading viscous film[J]. Phys Fluids, 2009, 21: 052104. DOI:10.1063/1.3129283 |
| [15] |
EGGERS J, FONTELOS M, JOSSERAND C, et al. Drop dynamics after impact on a solid wall:theory and simulations[J]. Phys Fluids, 2010, 22: 062101. DOI:10.1063/1.3432498 |
| [16] |
SEN S, VAIKUNTANATHAN V, SIVAKUMAR D. Experimental investigation of biofuel drop impact on stainless steel surface[J]. Exp Therm Fluid Sci, 2014, 54: 38-46. DOI:10.1016/j.expthermflusci.2014.01.014 |
| [17] |
TANG CHENGLONG, QIN MENGXIAO, et al. Dynamics of droplet impact on solid surface with different roughness[J]. International Journal of Multiphase Flow, 2017, 96: 56-69. DOI:10.1016/j.ijmultiphaseflow.2017.07.002 |
| [18] |
STOW C D, HADFIELD M G. An experimental investigation of fluid-flow resulting from the impact of a water drop with an unyielding dry surface[J]. P Roy Soc Lond A Mat, 1981, 373: 419-441. DOI:10.1098/rspa.1981.0002 |
| [19] |
MUNDO C, SOMMERFELD M, TROPEA C. Droplet-wall collisions-experimental studies of the deformation and breakup process[J]. Int J Multiphase Flow, 1995, 21. |
| [20] |
COSSALI G E, COGHE A, MARENGO M. The impact of a single drop on a wetted solid surface[J]. Exp Fluids, 1997, 22: 463-472. DOI:10.1007/s003480050073 |
| [21] |
RANGE K, FEUILLEBOIS F. Influence of surface roughness on liquid drop impact[J]. J Colloid Interf Sci, 1998, 203: 16-30. DOI:10.1006/jcis.1998.5518 |
| [22] |
LEE S H, RYOU H S. Development of a new model and heat transfer analysis of impinging diesel sprays on a wall[J]. Atomization and Sprays, 2001, 11: 85-105. DOI:10.1615/AtomizSpr.v11.i1 |
| [23] |
STANTON D W, RUTLAND C J. Multi-dimensional modeling of heat and mass transfer of fuel films resulting from impinging sprays[J]. Soc Auto Eng, 1998, 960628. |
| [24] |
TRUJILLO M F, MATTHEWS W S, LEE C F, et al. Modeling and experiment of impingement and atomization of a liquid spray on a wall[J]. Int J Engine Research, 2000, 1(1): 87-104. DOI:10.1243/1468087001545281 |
| [25] |
WILLIAM B WRIGHT. Validation results for LEWICE 3.0[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada: AIAA, 2005.
|
| [26] |
YARIN A L. Drop impact dynamics:splashing, spreading, receding, bouncing[J]. Annu Rev Fluid Mech, 2006, 38: 159-192. DOI:10.1146/annurev.fluid.38.050304.092144 |
 2019, Vol. 37
2019, Vol. 37

