2. 第一飞机设计研究院, 陕西 西安 710089
2. The First Aircraft Institute of AVIC, Xi'an Shaanxi 710089, China
空中加油作为飞机发展的一项关键技术,对提高飞机的作战性能和作战半径有着无法取代的作用。作为当前国内和国际上的主流空中加油方式,即软管锥套式空中加油系统(简称软式加油),其优点是可同时给几架战机加油,能够实现“伙伴式加油”;其缺点是软管-锥套系统对大气乱流非常敏感,加油对接时对飞行员要求非常高,并且加油速度较慢,增加了飞行员的失误率。虽然软式加油从1949年问世以来经过逐步改进,性能不断提高,但据相关文献统计,空中加油飞行的事故率仍高达2.5%,远高于事故高发的起飞着陆阶段。大气紊流、加油机尾流、受油机头波均会影响加油对接的安全性,尤其是加油机的复杂尾流场是影响加油软管锥套气动稳定性的最主要因素,当软管锥套安装位置不理想或某些条件下,锥套常常会产生无规则的位置飘摆,使对接加油过程充满不确定性[1]。
在加油软管锥套气动稳定性研究中,国外主要采用数值计算和试验手段。数值计算方面主要包括加油机尾流模型的建立和模拟以及软管锥套系统的动力学模型的建立与模拟。1996年Proctor首先用数值计算的方法模拟了飞机的尾涡特性;1999年James W.Kamman等采用有限元多体动力学理论将线缆离散化,变成一个个由刚性杆通过无摩擦球铰连接的集中质量点,其受到的力等效到集中质量点处,形成集中参数模型[2-3];2007年William B. Ribbens将加油软管简化为一个个由弹簧连接的集中质量点,相邻的三个节点与中间的两端软管构成梁系统,由简支梁公式求出弹性恢复力[4]。在试验方面多是采用飞行试验直接验证加油过程中软管与锥套的稳定性,而风洞试验多集中在研究加油机尾流场上[1]。例如2002年和2004年Edward G. Dickes等人分别进行了KC-135加油机和ICE-101受油机、三角翼无人机的风洞试验,直接测量尾流特性,而关于软管与锥套的气动稳定性风洞试验鲜有报道,目前可查的资料仅是2012年巴西航空工业公司对KC-390加油机在DNW风洞进行了一期气动稳定性试验的视频影像。
国内在加油软管锥套气动稳定性研究方面开展得较晚,2010年以前研究软式空中加油的学者很少[5]。在数值计算方面从2007年起,陈博、胡孟权、王伟、张仕明等人陆续进行了加油机尾流场模型和加油软管动力学模型研究,模拟了机翼尾涡对加油软管锥套稳定性的影响[6-8];在飞行试验方面国内主要利用轰油-6加油机与歼-8加油对接,2006年实现了轰油-6加油机与歼-10加油对接,在飞行试验中主要依靠受油机飞行员对准加油锥套完成锁定,锥套的受扰无规则飘摆经常使飞行员屡试屡败[1];而加油软管与锥套的气动稳定性风洞试验在国内尚属空白。
由于加油机尾流场极其复杂既包括机翼尾涡也包括平尾垂尾的影响,想要通过数学模型完全准确模拟是不可能的,且软管锥套的稳定性对流场变化极其敏感,因此,数值模拟的准确性难以保证;而直接进行飞行试验成本高风险大,试验成功率往往对飞行员的经验有极大依赖。因此作为低成本低风险的试验方式,发展一种试验结果可靠的加油软管锥套气动稳定性风洞试验技术是非常有必要的。2017年中国空气动力研究与发展中心低速所在国内首次形成了加油软管锥套气动稳定性风洞试验能力,模拟了某型加油机加油软管锥套收放过程中的气动稳定性,以及不同加油吊舱、起落架鼓包、加油平台位置等对软管和锥套稳定性的影响,试验结果对于该加油机选型优化、加油系统位置布置等提供了依据,并对提高空中加油飞行试验的安全性有重要意义。
1 相似准则相似准则是风洞试验的基础,除了最基本的几何相似以外,风洞试验数据要正确应用到实际中必须满足一定的相似准则[9]。加油软管锥套气动稳定性试验涉及到流体(空气)与固体(包括加油机、软管、锥套)的相互耦合作用,本文将分别从流体流动和软管锥套运动两方面讨论该试验需要满足的相似条件。
1.1 流动相似准则流动相似准则可由维纳-斯托克斯方程推出[9-10],对于一般情况(非定常、可压缩、黏性、完全气体流动),模型流场和真实流场相似必须满足以下相似准则相等:
| $ Ma = v/a\left( {马赫数相似准则,Ma} \right) $ | (1) |
| $ \mathit{Re} = \rho vl/\mu \left( {雷诺数相似准则,\mathit{Re}} \right) $ | (2) |
| $ Fr = v/\sqrt {\mathit{lg}} \left( {弗劳德数相似准则,Fr} \right) $ | (3) |
| $ Sr = l/vt\left( {斯特劳哈尔数相似准则,Sr} \right) $ | (4) |
加油软管锥套气动稳定性低速风洞试验是为了获得锥套的运动轨迹,其不仅与软管锥套所受重力、气动力相关,还与软管的弹性变形相关,是复杂的流固耦合过程,很难用物理方程准确描述,因此本文通过量纲分析法来导出结构动力相似准则。
任一时刻锥套质心的位置(x, y, z)和姿态角θ与下列物理量相关:加油机的迎角α、侧滑角β、速度v、机翼平均气动弦长bA、空气密度ρ、黏性系数μ、软管质量mr、软管软管抗弯刚度EI、软管直径dr、锥套质量mz、锥套直径dz、锥套转动惯量J、重力加速度g、时间t、软管收放速度vl。根据加油软管的材料和结构特性[1],忽略软管绕中轴线的扭转运动以及轴向拉压变形。因此可以得到如下关系式:
| $ \begin{array}{l} \left( {x,y,z,\theta } \right) = f\left( {\alpha ,\beta ,v,{b_A},\rho ,\mu ,g,t,{m_r},} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {EI,{d_r},{v_l},{m_z},{d_z},J} \right) \end{array} $ | (5) |
选择ρ、v、bA为基本物理量,根据Π定理可写出Πμ为:
| $ \begin{array}{l} {\mathit{\Pi }_\mu } = \frac{\mu }{{{\rho ^{{\lambda _1}}}{v^{{\lambda _2}}}b_A^{{\lambda _3}}}} \Rightarrow \dim \mu = \dim \left( {{\rho ^{{\lambda _1}}}{v^{{\lambda _2}}}b_A^{{\lambda _3}}} \right) \Rightarrow \\ \;\;\;\;\;\;\;\;{\lambda _1} = 1,{\lambda _2} = 1,{\lambda _3} = 1,则\\ {\mathit{\Pi }_\mu } = \frac{\mu }{{\rho v{b_A}}}\left( {{\mathit{\Pi }_\mu }\;即为雷诺数相似准则,\mathit{Re}} \right) \end{array} $ | (6) |
同理可得到:
| $ \begin{array}{l} {\mathit{\Pi }_g} = \frac{g}{{{v^2}/{b_A}}} = \frac{{g{b_A}}}{{{v^2}}}\\ \;\;\;\;\;\;\;\;\left( {{\mathit{\Pi }_g}\;即为弗劳德数相似准则,\mathit{Fr}} \right) \end{array} $ | (7) |
| $ \begin{array}{l} {\mathit{\Pi }_t} = \frac{t}{{{b_A}/v}} = \frac{{vt}}{{{b_A}}}\\ \;\;\;\;\;\;\;\;\left( {{\mathit{\Pi }_t}\;即为斯特劳哈尔数相似准则,\mathit{Sr}} \right) \end{array} $ | (8) |
| $ {\mathit{\Pi }_{mr}} = \frac{{{m_r}}}{{\rho b_A^3}},{\mathit{\Pi }_{mz}} = \frac{{{m_z}}}{{\rho b_A^3}}\left( {质量相似准则} \right) $ | (9) |
| $ {\mathit{\Pi }_{EI}} = \frac{{EI}}{{\rho {v^2}b_A^4}}\;\;\;\;\left( {软管刚度相似准则} \right) $ | (10) |
| $ {\mathit{\Pi }_J} = \frac{J}{{\rho b_A^5}}\left( {锥套转动惯量相似准则} \right) $ | (11) |
| $ \begin{array}{l} {\mathit{\Pi }_{{d_r}}} = \frac{{{d_r}}}{{{b_A}}},{\mathit{\Pi }_{{d_z}}} = \frac{{{d_z}}}{{{b_A}}},{\mathit{\Pi }_{{v_l}}} = \frac{{{v_l}}}{v}\\ \;\;\;\;\left( {几何相似准则和收放速度相似准则} \right) \end{array} $ | (12) |
由于α、β、θ本身是无量纲量,且Πx=x/bA、Πy=y/bA、Πz=z/bA,因此式(5)可以写为无量纲关系式:
| $ \begin{array}{l} \left( {\frac{x}{{{b_A}}},\frac{y}{{{b_A}}},\frac{z}{{{b_A}}},\theta } \right) = f\left( {\alpha ,\beta ,\mathit{Re},Fr,Sr,\frac{{{m_r}}}{{\rho b_A^3}},\frac{{EI}}{{\rho {v^2}b_A^4}},} \right.\\ \;\;\;\;\;\left. {\frac{{{d_r}}}{{{b_A}}},\frac{{{v_l}}}{v},\frac{{{m_z}}}{{\rho b_A^3}},\frac{{{d_z}}}{{{b_A}}},\frac{J}{{\rho b_A^5}}} \right) \end{array} $ | (13) |
根据相似定理,要想使得风洞试验获得的锥套轨迹与真实飞行中相似,式(13)中右边所有无量纲量必须相等,由此可得风洞试验时模型及试验条件的相关参数。
1.3 关于相似准则的几点讨论与其他风洞试验技术一样,加油软管锥套气动稳定性风洞试验不能同时满足上述所有相似准则,只能分析主要矛盾做到部分模拟。
Ma是气体压缩性对流动影响的一种度量,当流速较低(Ma < 0.4)时,气体的压缩性可忽略不计。空中加油时飞行速度不高,通常在200~600 km/h,进行低速风洞试验时,侧重研究飞行速度范围Ma < 0.4,因此本文试验未模拟Ma相似准则。
Re是体现流体的黏性对流动影响的相似准则,凡是与流体黏性相关的试验都要求模型试验雷诺数等于真实飞行雷诺数。然而,对于一般风洞来说,鉴于风洞尺寸和试验风速受限,这一点很难满足。但是大量研究表明,当Re超过某一临界数值后进入自准区,某些气动特性不再随Re的变化而变化[9, 10]。而本文试验Re在106量级,处于自准区内(前期利用该加油机模型进行了测力试验,结果表明Re >106后模型气动力系数基本不随风速变化),认为绕模型加油机流动与绕实物流动相似,因此本文未完全模拟Re相似准则。
Fr相似准则是惯性力与重力之比,表征重力作用对流动的影响;Sr相似准则是非定常惯性力与惯性力之比,表征流体的非定常性。由于本文试验的锥套轨迹与重力及软管的释放时间密切相关,因此必须模拟这两个相似准则。
由式(7)可知风洞试验风速v与真实飞行速度v′满足
综上,加油软管锥套气动稳定性低速风洞试验需满足几何、弗劳德数、斯特劳哈尔数、质量、软管刚度(模型软管可作柔性体考虑)、锥套转动惯量以及收放速度相似准则。
2 试验设备与方法2017年中国空气动力研究与发展中心低速所基于加油机型号研制需求,发展了空中加油机加油软管锥套气动稳定性风洞试验技术,并在FL-12风洞首次将其应用于某型加油机加油吊舱、中心线平台等关键部件的选型优化,该次试验也是国内首例加油软管锥套气动稳定性风洞试验。
2.1 试验模型试验模型比例尺为1/20,其中加油机、加油吊舱、中心线平台模型均为全金属模型;根据第1.3节中的分析可知模型加油软管的刚度非常小,因此采用柔性橡胶管来模拟(左、右机翼下加油软管直径为3.5 mm,机身下加油软管直径为4.5 mm,如图 1所示);锥套为硬质塑料模型(锥套直径约为41mm,如图 2所示)。对于该类型试验模型设计的难点在于加油软管与锥套,根据式(3)和式(4)可知,软管和锥套模型的质量、锥套的转动惯量均与空气密度比相关,而试验过程中要模拟飞行高度分别为500 m、4000 m、8000 m和11000 m时的空中加油过程,且加油软管还需模拟有、无燃油状态,因此本次试验设计了多套加油软管和锥套,在加油软管中插入不同直径的钢丝绳作为配重满足变质量需求,在锥套内布置不同质量的配重块满足变质量和变惯量需求。

|
图 1 加油软管模型图 Fig.1 Refueling hose model |

|
图 2 锥套模型图 Fig.2 Drogue model |
由于加油软管和锥套的气动稳定性对于加油机的尾流场极为敏感,试验所采用的支撑方式必须尽可能减小对软管和锥套附近流场的影响,因此试验采用大迎角支撑装置将模型背撑正装于风洞试验段中心,如图 3所示。

|
图 3 模型安装图 Fig.3 Model installation |
对于软式空中加油,重点研究的是软管收放过程中以及固定管长时的气动稳定特性,重点关注的特征参数是锥套的垂向下沉量和振动幅值。
模拟软管自动收放时,在机身内部安装舵机和绕线盘,在风洞外通过遥控设备控制无限偏舵机驱动绕线盘旋转,实现中心线平台处加油软管和锥套的放出和回收,如图 4所示。由于机翼内部空间的限制,无法安装舵机,因此无法模拟机翼下软管锥套的收放。需要注意的是,软管锥套能够顺利放出的基本条件是锥套产生的阻力必须大于收放系统的摩擦力,而试验时锥套的阻力较小,这就要求收放装置与软管的摩擦尽可能小,可从表面光滑度、软管排布方式、润滑剂使用等方面做工作。对于固定软管长度时的气动稳定性试验,利用双目立体视觉测量系统获得标记点的三维空间坐标信息,从而得到锥套的下沉量和振动幅值。由于双目系统视场范围有限,无法获取收放过程中以及锥套大幅摆动时的振动信息,因此在风洞两侧安装高清摄像机以实时记录整个试验过程中软管和锥套的运动状态。

|
图 4 收放装置 Fig.4 Retraction-extension device |
需要说明的是,本文所涉及的自动收放试验仅定性地研究了软管锥套收放过程中的稳定特性,未精细模拟收放速度对软管锥套气动稳定特性的影响,但是下一步工作将会对此展开研究,模型软管的收放速度可根据公式(12)确定,并利用伺服电机精确控制。
2.3 双目测量系统准确测量软管锥套的位移振动信息是气动稳定性试验的关键,测量方式必须满足以下要求:标记点无附加质量,不会影响软管锥套的运动轨迹;标记点足够清晰,能准确地从背景中分辨出来;采样频率足够高,至少要在锥套振动频率的5倍以上,以确保采集信息的完整性和准确性。基于此采用了非接触式的双目立体视觉测量系统来测量标记点的位移参数,采样频率20帧/s,采样时长10 s。
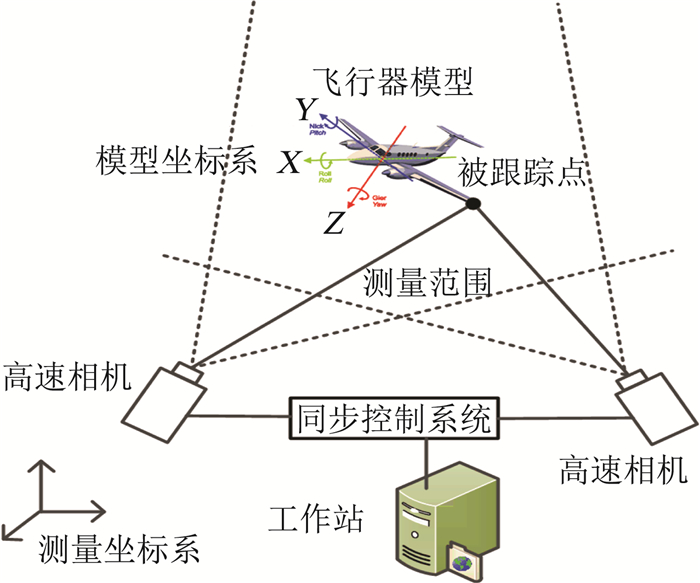
双目测量系统硬件主要由双高速数字CCD摄像头、图像采集卡、计算机、同步触发及其它辅助设备组成,其工作原理如图 5所示。试验前首先标定摄像头,获得摄像头的光学参数及其方位参数;试验中通过两个CCD相机同步采集模型的运动图像(如图 6所示),图像数据传送至计算机后,利用软件自动识别和定位模型上的反光标记点,然后计算标记点三维空间坐标,获得锥套的位移振动参数[11]。由于本次试验重点关注的是锥套位移变化,因此仅在软管末端与锥套连接处粘贴标记点;若要获得整个软管的运动轨迹,可在软管上分布布置多个标记点。由于双目系统视场范围有限(大约0.5 m×0.5 m),试验时一次只能测量一个锥套的位移振动信息。
|
图 5 双目测量系统工作原理图 Fig.5 Binocular system |

|
图 6 双目测量采集图像 Fig.6 Picture collected by binocular system |
试验采用反光标记点以便于在图像处理时能够更准确更容易识别(如图 6所示),该标记点反光原理同普通交通用反光漆,利用立方体颗粒折射原理,光线偏折180°,并利用手电筒进行补光提高标记点的分辨率。
3 试验结果 3.1 典型试验结果将本文形成的加油软管锥套气动稳定性风洞试验技术应用于某型加油机空中加油过程模拟,获得了一些典型的试验结果:收放过程中软管锥套的气动稳定性与风速相关;在一定的风速、迎角侧滑角边界下,软管锥套会发生甩鞭现象;当软管回收到较短长度时软管锥套易出现打圈现象;风速越大锥套的下沉量越小。这些典型的试验结果与相关数值计算和飞行试验结果一致[1, 5],从而在一定程度上验证了本文所形成的试验技术的正确性,确保了利用该试验技术获得关键加油部件(加油吊舱、中心线平台)不同构型下的软管锥套气动稳定特性并用于选型优化的合理性。
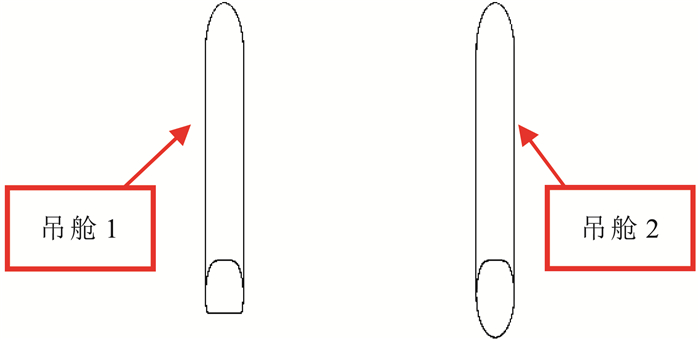
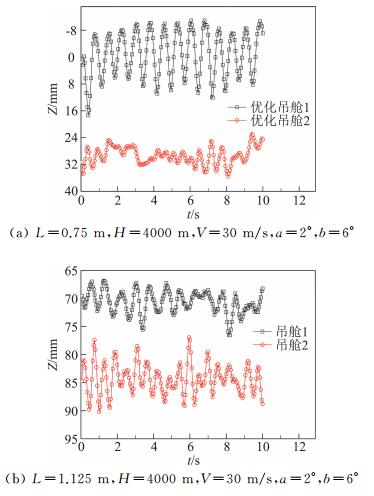
3.2 关键加油部件不同构型下的气动稳定特性加油吊舱后体会产生涡[12],对锥套的稳定性产生影响,优化加油吊舱构型尽可能减小涡的强度以提高锥套稳定性十分必要。图 7给出了两种加油吊舱构型图,图 8给出了左机翼下加油软管放出长度分别为0.75 m、1.125 m时,不同吊舱构型下锥套标记点的垂向位移图,以吊舱出口中心为原点,垂直向下为正。表 1给出了相应的平均垂向下沉量和最大振动幅值。根据软式空中加油特点,锥套的垂向下沉量越大,受油机与加油机的垂向距离越大,加油过程越安全;锥套的振动幅值越小,锥套位置越稳定,加油过程效率越高,通常认为锥套的最大振动幅值超过1个锥套直径(41 mm)即判定为不稳定状态。因此由上述图表结果可知,软管长度0.75 m时,吊舱构型2下的锥套垂向下沉量和振动幅值都优于构型1;软管长度1.125 m时,吊舱构型2下的锥套垂向下沉量优于构型1,虽然锥套振动幅值略大,但稳定性依然良好。综上可得,吊舱构型2的性能参数更佳。从理论上分析是因为吊舱1后端上缘较宽,产生的升力较大,会产生较强的脱体涡,影响锥套的稳定性,且距离吊舱越近影响越大,后续可以通过进一步的尾流场测量试验进行验证。
|
图 7 两种加油吊舱构型示意图 Fig.7 Two different pod configurations |
|
图 8 吊舱构型对左机翼下加油软管垂向位移的影响 Fig.8 Influence of different pod configurations on vertical displacement of left-wing refueling hose |
| 表 1 不同加油吊舱构型下的平均垂向位移量及最大振动幅值 Table 1 Average vertical displacement and maximal swing amplitude for different pod configurations |
|
|
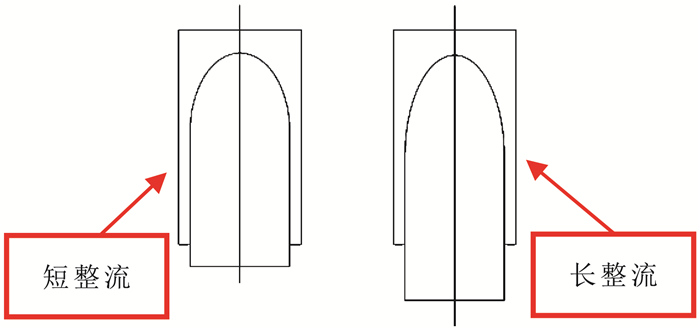
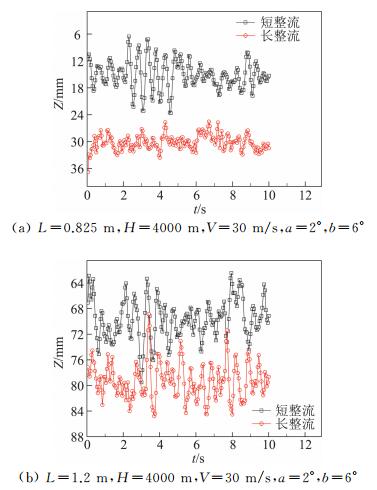
图 9给出了两种中心线平台构型图,图 10给出了机身下软管放出长度分别为0.825 m、1.2 m时,不同平台构型下锥套标记点的垂向位移图,以平台出口中心为原点,垂直向下为正。表 2给出了相应的平均垂向下沉量和最大振动幅值。结果表明,长整流构型下锥套的垂向下沉量更大,振动幅值也较小,长整流的整流效果更佳。
|
图 9 两种中心线平台构型示意图 Fig.9 Two different central platform configurations |
|
图 10 中心线平台构型对机身下加油软管垂向位移的影响 Fig.10 Influence of different central platform configurations on vertical displacement of refueling hose under fuselage |
| 表 2 不同中心线平台构型下的平均垂向位移量及最大振动幅值 Table 2 Average vertical displacement and maximal swing amplitude for differentcentral platform configurations |
|
|
综上分析可知,利用本文所形成的加油软管锥套气动稳定性风洞试验技术,能够很好地模拟软管锥套收放过程中的甩鞭、打圈等状态以及固定管长时的气动稳定特性,并能获得锥套的下沉量、振动幅值、振动频率等信息,为加油吊舱、中心线平台的选型优化提供有效的试验数据支持。
4 结论本文根据N-S方程和量纲分析法建立并分析了空中加油机加油软管锥套气动稳定性风洞试验需满足的相似准则,给出了模型安装、利用自动舵机实现软管锥套自动收放、采用双目系统测量锥套位移信息等方面的具体方法,形成了完整的加油软管锥套气动稳定性风洞试验技术,并将其应用于某型加油机加油吊舱、中心线平台等关键加油部件的选型优化。试验结果表明,该技术能有效模拟处于加油机尾流场下的软管锥套收放过程和固定管长时的气动稳定性,能测量锥套的位移振动信息,为加油机部件选型优化、提高空中加油飞行安全性及加油效率等提供重要的试验数据依据。
此次试验是国内首次进行加油软管锥套气动稳定性研究的风洞试验,还存在着不足之处,如软管收放速度未能精确模拟、双目系统视场较小、标记点捕获需要用手电筒补光、只模拟了加油机尾流场对软管锥套的影响而未考虑受油机头波流场的影响等。随着试验技术的发展,下一步我们可使用伺服电机无级变精确控制收放速度,建立多目立体视觉测量系统同时测量多个锥套的位移信息、形成加/受油双机试验技术等等,使得试验效率更高,试验结果更准确。
| [1] |
王海涛, 董新民, 等. 空中加油动力学与控制[M]. 北京: 国防工业出版社, 2016.
|
| [2] |
KAMMAN J W, HUSTON R L. Multibody dynamics modeling of variable length cable systems[J]. Multibody System Dynamics, 2001, 5(3): 211-221. DOI:10.1023/A:1011489801339 |
| [3] |
KAMMAN J W, HUSTON R L. Modeling of variable length towed and tethered cable systems[J]. Journal of Guidance, Control and Dynamics, 1999, 22(4): 602-608. DOI:10.2514/2.4423 |
| [4] |
RIBBENS W B, SAGGIO F, WIERENGA R, et al. Dynamic modeling of an aerial refueling hose & drogue system[J]. AIAA J, 2007, 25(6): 25-28. |
| [5] |
张仕明.软式空中加油管收放过程动力学分析与优化[D].南京: 南京航空航天大学, 2014. ZHANG S M. Analysis and optimization of an aerial refueling hose & drogue system in deployment and retrieval process[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.(in Chinese) |
| [6] |
陈博. 加油机尾流场建模与仿真分析[J]. 飞行力学, 2007, 25(4): 73-04. CHEN B. Modeling and simulation of the tanker's wake field[J]. Flight Dynamics, 2007, 25(4): 73-04. DOI:10.3969/j.issn.1002-0853.2007.04.020 (in Chinese) |
| [7] |
胡孟权, 聂鑫, 王立明. "插头-锥管"式空中加油软管平衡拖拽位置计算[J]. 空军工程大学学报, 2009, 10(5): 22-26. HU M Q, NIE X, WANG L M. Determination of hose static catenary shape in "probe-drogue" in-flight refueling system[J]. Journal of Air Force Engineering University(Natural Science Edition), 2009, 10(5): 22-26. DOI:10.3969/j.issn.1009-3516.2009.05.005 (in Chinese) |
| [8] |
王伟, 刘喜藏, 王鹏, 等. 空中加油软管-锥套动态建模与仿真[J]. 电子设计工程, 2012, 20(17): 135-137. WANG W, LIU X C, WANG P, et al. Dynamic modeling and simulation of aerial refueling hose-drogue[J]. Electronic Design Engineering, 2012, 20(17): 135-137. DOI:10.3969/j.issn.1674-6236.2012.17.049 (in Chinese) |
| [9] |
王铁成. 空气动力学实验技术[M]. 北京: 航空工业出版社, 1995.
|
| [10] |
王勋年, 等. 低速风洞试验[M]. 北京: 国防工业出版社, 2002.
|
| [11] |
倪章松, 等. FL-12风洞勤务指南[M]. 四川绵阳: 中国空气动力研究与发展中心, 2012.
|
| [12] |
吕美茜, 程存虎. 先进布局飞机空中加油流场特性分析[J]. 空气动力学学报, 2008, 26(2): 231-233. LV M Q, CHENG C H. An analysis of flow field characteristics for an advanced configuration aircraft during aerial refueling[J]. Atca Aerodynamica Sinica, 2008, 26(2): 231-233. DOI:10.3969/j.issn.0258-1825.2008.02.018 (in Chinese) |
 2019, Vol. 37
2019, Vol. 37

