间断Galerkin有限元方法(Discontinuous Galerkin finite element method,DG)[1]是一种适合于非结构网格的高精度格式。Reed & Hill[2]在1973年将其用于求解中子输运方程问题。DG方法具有计算精度高,计算模板紧致,并行能力强,自适应方便等优点,适用于非结构网格,适合处理复杂外形及复杂边界。作为一种内自由度方法,DG方法通过提高单元内变量多项式的阶数实现高阶精度,其内存需求高、计算量大,随着空间精度的提高,其内存需求量和计算量非线性增加,因此发展高阶精度DG方法的高效隐式时间迭代方法有重要的学术研究和工程应用价值。
隐式迭代方法需要计算大型的非线性系统,如何高效求解是其重要研究内容。目前多种隐式迭代方法已成功应用于间断Galerkin有限元方法等高阶精度方法,如Lower Upper-Symmetric Gauss-Seidel (LU-SGS)[3-6],GMRES(Generalized Minimal Residual)[7-9],Implicit Integration Factor(IIF)[10]等。非线性系统的计算方法和近似处理方法直接影响高阶DG的计算稳定性以及计算效率。
Landmann[11]、杨小权[12-13]、程剑[14]等在二维非结构网格上通过精确求解右端项残值对变量自由度的雅可比矩阵来提高计算的CFL,从而提高DG方法在黏性计算的计算效率。
DG方法是一种内自由度方法,具有计算模板紧致的特点,这两大特性带来了如下优点:
(1) 单元高斯积分点的变量值来自单元内变量分布多项式,通过多项式求导能够获取变量值对变量自由度的偏导数,这使得精确计算无黏通量对变量自由度的雅可比矩阵较为容易。
(2) 单元边界面上变量梯度只与当前单元及其面相邻单元有关,无需重构,故能较为简单地精确给出变量梯度对边界面左右变量自由度的偏导数。
基于以上优点,本文在三维非结构网格基础上,发展了求解右端项残值雅可比矩阵(简称残值雅可比)的精确计算方法,同时建立了简化计算、部分精确计算方法,实现雅可比矩阵元素的简化和精确计算,并在此基础上结合PETSC(Portable, Extensible Toolkit for Scientific Computation)库[15]建立了GMRES隐式迭代方法。采用NACA0012翼型首先研究了每步重启步数及残差收敛参数对基于残值雅可比矩阵精确计算的GMRES计算效率影响;然后采用NACA0012翼型、ONERA-M6机翼比较了基于残值雅可比矩阵精确计算的GMRES相比基于矩阵近似计算的GMRES以及LU-SGS/TVD-RK的计算效率;最后采用方腔流动以及平板层流边界层验证了本文方法在黏性流数值模拟中的计算效率。
1 数值方法 1.1 控制方程在直角坐标系下,三维非定常可压缩Euler/Navier-Stokes方程组的守恒形式为:
| $ \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \nabla \cdot \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{U}} \right) = ivis\left( {\nabla \cdot {\mathit{\boldsymbol{F}}_v}\left( {\mathit{\boldsymbol{U}},\nabla \mathit{\boldsymbol{U}}} \right)} \right) $ | (1) |
当ivis=0时为Euler方程,ivis=1时为N-S方程。式中U为守恒变量,
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}} = \left[ \begin{array}{l} \rho \\ \rho u\\ \rho v\\ \rho w\\ \rho E \end{array} \right],{F^x} = \left[ \begin{array}{l} \rho u\\ \rho {u^2} + p\\ \rho uv\\ \rho uw\\ \left( {\rho E + p} \right)u \end{array} \right]}\\ {{F^y} = \left[ \begin{array}{l} \rho v\\ \rho vu\\ \rho {v^2} + p\\ \rho vw\\ \left( {\rho E + p} \right)v \end{array} \right],{F^z} = \left[ \begin{array}{l} \rho w\\ \rho wu\\ \rho wv\\ \rho {w^2} + p\\ \left( {\rho E + p} \right)w \end{array} \right]} \end{array} $ | (2) |
| $ F_v^x = \left[ \begin{array}{l} 0\\ {\tau _{xx}}\\ {\tau _{xy}}\\ {\tau _{xz}}\\ {\mathit{\Theta }_x} \end{array} \right],F_v^y = \left[ \begin{array}{l} 0\\ {\tau _{yz}}\\ {\tau _{yy}}\\ {\tau _{yz}}\\ {\mathit{\Theta }_y} \end{array} \right],F_v^z = \left[ \begin{array}{l} 0\\ {\tau _{zx}}\\ {\tau _{zy}}\\ {\tau _{zz}}\\ {\mathit{\Theta }_z} \end{array} \right] $ | (3) |
式中,ρ、p分别为密度和压力;x、y、z分别为笛卡尔坐标系下的坐标分量;u、v、w分别为笛卡尔坐标系下的速度分量;E为总能;τxx、τyy、τzz、Θx、Θy、Θz具体形式见参考文献[16]。
1.2 DG空间离散空间离散前首先将整个求解区域划分为互不重叠的非结构单元,对于三维问题,包括三棱柱、四面体、六面体和金字塔单元。
令ivis=1,将方程(1)两端乘以测试函数
| $ \begin{array}{l} \int\limits_\mathit{\Omega } {\frac{{\partial U}}{{\partial t}}{\phi _i}{\rm{d}}\mathit{\Omega }} + \int\limits_\mathit{\Omega } {\nabla \cdot \mathit{\boldsymbol{F}}{\phi _i}{\rm{d}}\mathit{\Omega }} = \int\limits_\mathit{\Omega } {\nabla \cdot {\mathit{\boldsymbol{F}}_v}{\phi _i}{\rm{d}}\mathit{\Omega }} \\ \begin{array}{*{20}{c}} {\int\limits_\mathit{\Omega } {\frac{{\partial U}}{{\partial t}}{\phi _i}{\rm{d}}\mathit{\Omega }} + \int\limits_{\partial \mathit{\Omega }} {\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{n}}{\phi _i}{\rm{d}}\mathit{\Gamma }} - \int\limits_\mathit{\Omega } {\mathit{\boldsymbol{F}} \cdot \nabla {\phi _i}{\rm{d}}\mathit{\Omega }} = }\\ {\int\limits_{\partial \mathit{\Omega }} {{\mathit{\boldsymbol{F}}_v} \cdot \mathit{\boldsymbol{n}}{\phi _i}{\rm{d}}\mathit{\Gamma }} - \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{F}}_v} \cdot \nabla {\phi _i}{\rm{d}}\mathit{\Omega }} } \end{array} \end{array} $ | (4) |
其中,n为单元边界面的外法向,
| $ {U_e} = \sum\limits_{j = 1}^N {u_j^e\left( t \right){\phi _j}\left( {x,y,z} \right)} $ | (5) |
其中,uje(t)(简写为uj)为单元的自由度,
| $ \begin{array}{l} RHS = RH{S_v} + RH{S_f}\\ RH{S_v} = RH{S_{i\_v}} + RH{S_{v\_v}}\\ RH{S_{i\_v}} = \int\limits_\mathit{\Omega } {\mathit{\boldsymbol{F}} \cdot \nabla {\phi _i}{\rm{d}}\mathit{\Omega }} \\ RH{S_{v\_v}} = - \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{F}}_v} \cdot \nabla {\phi _i}{\rm{d}}\mathit{\Omega }} \\ RH{S_f} = RH{S_{i\_f}} + RH{S_{v\_f}}\\ RH{S_{i\_f}} = - \int\limits_{\partial \mathit{\Omega }} {\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{n}}{\phi _i}{\rm{d}}\mathit{\Gamma }} \\ RH{S_{v\_f}} = \int\limits_{\partial \mathit{\Omega }} {{\mathit{\boldsymbol{F}}_v} \cdot \mathit{\boldsymbol{n}}{\phi _i}{\rm{d}}\mathit{\Gamma }} \end{array} $ | (6) |
最后化简得:
| $ \mathit{\boldsymbol{M}}\frac{{{\rm{d}}{u_j}}}{{{\rm{d}}t}} = RHS $ | (7) |
其中:
| $ \begin{array}{l} RH{S_{i\_v}} = \sum\limits_{l = 1}^{vp} {\omega \left( l \right)\left( {\mathit{\boldsymbol{F}} \cdot \nabla {\phi _i}} \right)\left| {{J_l}} \right|} \\ RH{S_{v\_v}} = - \sum\limits_{l = 1}^{vp} {\omega \left( l \right)\left( {{\mathit{\boldsymbol{F}}_v} \cdot \nabla {\phi _i}} \right)\left| {{J_l}} \right|} \\ RH{S_{i\_f}} = - \sum\limits_{f = 1}^{nface} {\sum\limits_{k = 1}^{fp} {{\omega _f}\left( k \right){\mathit{\boldsymbol{H}}_c}{\phi _i}\left| {{J_{fk}}} \right|} } \\ RH{S_{v\_f}} = \sum\limits_{f = 1}^{nface} {\sum\limits_{k = 1}^{fp} {{\omega _f}\left( k \right){\mathit{\boldsymbol{H}}_v}{\phi _i}\left| {{J_{fk}}} \right|} } \end{array} $ | (8) |
M为质量矩阵,其元素为mij,RHSv、RHSf分别为体积分项残值和面积分项残值,RHSi_v、RHSv_v分别为体积分项残值中的无黏残值和黏性残值,RHSi_f、RHSv_f分别为面积分项残值中的无黏残值和黏性残值,这四项采用高斯数值积分计算,如公式(8)。ω(l)、ωf(k)分别为高斯面积分和体积分加权系数,
隐式迭代方法具有较高的效率,尤其是在高精度计算时,目前隐式方法主要有直接求解法、近似因子分解法和迭代法三种。直接求解法在求解网格规模较大问题时相当困难,后两种方法在近四十年间得到了大量的研究,并在CFD中广泛应用。
对方程(7)采用一阶欧拉后差得到:
| $ \begin{array}{l} \frac{M}{{\Delta t}}\Delta u_j^{n + 1} = RH{S^{n + 1}} \approx RH{S^n} + \frac{{\partial \left( {RH{S^n}} \right)}}{{\partial u_j^n}}\Delta u_j^{n + 1}\\ \frac{M}{{\Delta t}}\Delta u_j^{n + 1} - \frac{{\partial \left( {RH{S^n}} \right)}}{{\partial u_j^n}}\Delta u_j^{n + 1} = RH{S^n}\\ \mathit{\boldsymbol{A}}\Delta u_j^{n + 1} = RH{S^n} \end{array} $ | (9) |
方程(9)的第三项为一大型线性系统Ax=B,以三维DG(P3)为例,矩阵A的维数为n_cell×(5×20),其中n_cell为单元总数,5为方程组个数,20为P3次多项式的自由度,直接存储该矩阵并且求逆,其存储量和计算量太大,一般采用迭代法求解该线性系统。
将残值的面积分项和体积分项带入方程(9)中第二式的左端RHS得:
| $ \frac{M}{{\Delta t}}\Delta u_j^{n + 1} - \frac{{\partial \left( {RHS_v^n + RHS_f^n} \right)}}{{\partial u_j^n}}\Delta u_j^{n + 1} = RH{S^n} $ | (10) |
将残值项带入方程(10),对其采用链式法则得:
| $ \begin{array}{l} \left[ {\frac{M}{{\Delta t}} - \frac{{\partial \left( {RH{S_{i\_f}} + RH{S_{i\_v}} + RH{S_{v\_f}} + RH{S_{v\_v}}} \right)}}{{\partial u_j^n}}} \right]\Delta u_j^{n + 1}\\ \;\;\;\; = RH{S^n}\\ \frac{{\partial \left( {RH{S_{i\_f}}} \right)}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{i\_f}}} \right)}}{{\partial {U^n}}}\frac{{\partial {U^n}}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{i\_f}}} \right)}}{{\partial {U^n}}}{\phi _j}\\ \frac{{\partial \left( {RH{S_{i\_v}}} \right)}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{i\_v}}} \right)}}{{\partial {U^n}}}\frac{{\partial {U^n}}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{i\_v}}} \right)}}{{\partial {U^n}}}{\phi _j}\\ \frac{{\partial \left( {RH{S_{v\_f}}} \right)}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{v\_f}}} \right)}}{{\partial {U^n}}}\frac{{\partial {U^n}}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{v\_f}}} \right)}}{{\partial {U^n}}}{\phi _j}\\ \frac{{\partial \left( {RH{S_{v\_v}}} \right)}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{v\_v}}} \right)}}{{\partial {U^n}}}\frac{{\partial {U^n}}}{{\partial u_j^n}} = \frac{{\partial \left( {RH{S_{v\_v}}} \right)}}{{\partial {U^n}}}{\phi _j} \end{array} $ | (11) |
求解
在迭代求解Ax=B过程中如果精确给出矩阵A中的矩阵元素,方程两端的匹配性和相容性更好,这将提高求解过程的CFL数,增强求解过程稳定性,提高计算效率。
1.3.1 右端项残差雅可比矩阵精确求解方法在精确求解右端项残差雅可比矩阵时,需确保残值雅可比的无黏通量和黏性通量完全与右端项残值中的通量一致,因此本文针对Roe[17]格式以及BR2[18]黏性计算格式建立对应的雅可比矩阵精确求解方法。
文献[19]给出了Roe格式的具体表达形式,由方程(8)的第三式及方程(11)的第二式,通过链式法则求导,
| $ \frac{{\partial \left( {RH{S_{i\_f}}} \right)}}{{\partial u_j^n}} = - \sum\limits_{s = 1}^{nface} {\sum\limits_{k = 1}^{fp} {{\omega _s}\left( k \right)\frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{Roe}}}}}}{{\partial U}}{\phi _i}\left| {{J_{sk}}} \right|{\phi _j}} } $ | (12) |
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{Roe}}}}\left( {{U_L},{U_R},\mathit{\boldsymbol{n}}} \right)}}{{\partial R}} = \\ \;\;\;\frac{{\partial \left\{ {\frac{1}{2}\left[ {{\mathit{\boldsymbol{F}}_c}\left( {{U_L}} \right) + {\mathit{\boldsymbol{F}}_c}\left( {{U_R}} \right) - \left| {{\mathit{\boldsymbol{A}}_{{\rm{Roe}}}}} \right|\left( {{U_R} - {U_L}} \right)} \right]} \right\}}}{{\partial U}} \end{array} $ | (13) |
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{Roe}}}}\left( {{U_L},{U_R},\mathit{\boldsymbol{n}}} \right)}}{{\partial {U_L}}} = \\ \;\;\;\frac{1}{2}\left\{ {{\mathit{\boldsymbol{A}}_c}\left( {{U_L}} \right) - \frac{{\partial \left[ {\left| {{\mathit{\boldsymbol{A}}_{{\rm{Roe}}}}} \right|\left( {{U_R} - {U_L}} \right)} \right]}}{{\partial {U_R}}}} \right\} \end{array} $ | (14) |
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{H}}_{{\rm{Roe}}}}\left( {{U_L},{U_R},\mathit{\boldsymbol{n}}} \right)}}{{\partial {U_R}}} = \\ \;\;\;\frac{1}{2}\left\{ {{\mathit{\boldsymbol{A}}_c}\left( {{U_R}} \right) - \frac{{\partial \left[ {\left| {{\mathit{\boldsymbol{A}}_{{\rm{Roe}}}}} \right|\left( {{U_R} - {U_L}} \right)} \right]}}{{\partial {U_R}}}} \right\} \end{array} $ | (15) |
| $ \begin{array}{l} \left| {{\mathit{\boldsymbol{A}}_{{\rm{Roe}}}}} \right|\left( {{U_R} - {U_L}} \right) = \left[ {\begin{array}{*{20}{c}} {{a_4}}\\ {\tilde u{a_4} + {n_x}{a_5} + {a_6}}\\ {\tilde v{a_4} + {n_y}{a_5} + {a_7}}\\ {\tilde w{a_4} + {n_z}{a_5} + {a_8}}\\ {f'} \end{array}} \right]\\ f' = \tilde H{a_4} + \tilde V{a_5} + \tilde u{a_6} + \tilde v{a_7} + \tilde w{a_8} - {a_1}\frac{{{{\tilde c}^2}}}{{\gamma - 1}} \end{array} $ | (16) |
公式(16)中各符号及具体表达式可参看文献。
由上式可知,
(1) 首先计算出Roe格式中边界面左右的原始变量
(2) 然后再计算出Roe平均量
(3) 其次再计算出
(4) 最后给出
黏性通量的雅可比矩阵由于包含了
| $ \begin{array}{l} {\mathit{\boldsymbol{H}}_v}\left( {{U_L},{U_R},\nabla {U_L},\nabla {U_R},\mathit{\boldsymbol{n}}} \right) = \\ \;\;\;\;\frac{1}{2}\left( {{\mathit{\boldsymbol{F}}_v}\left( {{U_L},\nabla {U_L} + {\eta _e}{r_{Lf}}} \right) + } \right.\\ \;\;\;\;\left. {{\mathit{\boldsymbol{F}}_v}\left( {{U_R},\nabla {U_R} + {\eta _e}{r_{Rf}}} \right)} \right) \cdot \mathit{\boldsymbol{n}} \end{array} $ | (17) |
对于当前单元L,进一步写为:
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{F}}_v}\left( {{U_L},\nabla {U_L} + {\eta _e}{r_{Lf}},\mathit{\boldsymbol{n}}} \right)}}{{\partial u_j^L}} = \\ \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial {U_L}}}\frac{{\partial {U_L}}}{{\partial u_j^L}} + \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial \left( {\nabla {U_L}} \right)}}\frac{{\partial \left( {\nabla {U_L}} \right)}}{{\partial u_j^L}} + \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial {r_{{L_f}}}}}\frac{{\partial {r_{{L_f}}}}}{{\partial u_j^L}}\\ \frac{{\partial {\mathit{\boldsymbol{F}}_v}\left( {{U_R},\nabla {U_R} + {\eta _e}{r_{Rf}},\mathit{\boldsymbol{n}}} \right)}}{{\partial u_j^L}} = \frac{{\partial {\mathit{\boldsymbol{F}}_v}}}{{\partial {r_{{R_f}}}}}\frac{{\partial {r_{{R_f}}}}}{{\partial u_j^L}} \end{array} $ | (18) |
公式(18)看到,计算
(1) 由局部提升算子rLf公式求出所有守恒变量的局部提升算子对各自对应的守恒变量自由度的
| $ \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{r}}_{{L_f}}}}}{{\partial u_j^L}} = {M^{ - 1}}\sum\limits_{k = 1}^{fp} { - \frac{1}{2}{\mathit{\boldsymbol{n}}_f}\phi _{{j_k}}^L\phi _{{i_k}}^L{\omega _k}\left| {{J_k}} \right|} \\ \frac{{\partial {\mathit{\boldsymbol{r}}_{{R_f}}}}}{{\partial u_j^L}} = {M^{ - 1}}\sum\limits_{k = 1}^{fp} {\frac{1}{2}{\mathit{\boldsymbol{n}}_f}\phi _{{j_k}}^L\phi _{{i_k}}^R{\omega _k}\left| {{J_k}} \right|} \end{array} $ | (19) |
(2) 计算守恒变量及其方向导数对其守恒变量自由度的偏导数。
| $ \begin{array}{l} \frac{{\partial {U_L}}}{{\partial u_j^L}} = \phi _j^L,\frac{{\partial {U_R}}}{{\partial u_j^L}} = 0\\ \frac{{\partial U_\zeta ^L}}{{\partial u_j^L}} = \frac{{\partial \phi _j^L}}{{\partial \zeta }},\;\;\;\;\;\frac{{\partial U_\zeta ^R}}{{\partial u_j^L}} = 0,\;\;\;\;\zeta = x,y,z \end{array} $ | (20) |
(3) 计算
| $ \begin{array}{l} \frac{{\partial {u_L}}}{{\partial {U_L}}} = \left[ {\frac{{\partial {{\left( {\rho u} \right)}_L}}}{{\partial {U_L}}} - {u_L}\frac{{\partial {\rho _L}}}{{\partial {U_L}}}} \right]/{\rho _L}\\ \frac{{\partial {v_L}}}{{\partial {U_L}}} = \left[ {\frac{{\partial {{\left( {\rho v} \right)}_L}}}{{\partial {U_L}}} - {v_L}\frac{{\partial {\rho _L}}}{{\partial {U_L}}}} \right]/{\rho _L}\\ \frac{{\partial {w_L}}}{{\partial {U_L}}} = \left[ {\frac{{\partial {{\left( {\rho w} \right)}_L}}}{{\partial {U_L}}} - {w_L}\frac{{\partial {\rho _L}}}{{\partial {U_L}}}} \right]/{\rho _L}\\ \frac{{\partial {T_L}}}{{\partial {U_L}}} = \frac{{\gamma - 1}}{R}\left[ {\frac{{\partial {{\left( {\rho E} \right)}_L}}}{{\partial {U_L}}}\frac{1}{{{\rho _L}}} - f''} \right.\\ \;\;\;\;\;\;\;\left. { + \left( {\frac{{u_L^2 + v_L^2 + w_L^2}}{{\rho _L^2}} - \frac{{{{\left( {\rho E} \right)}_L}}}{{\rho _L^2}}} \right)\frac{{\partial {\rho _L}}}{{\partial {U_L}}}} \right]\\ f'' = \frac{{{u_L}}}{{{\rho _L}}}\frac{{\partial {{\left( {\rho u} \right)}_L}}}{{\partial {U_L}}} + \frac{{{v_L}}}{{{v_L}}}\frac{{\partial {{\left( {\rho v} \right)}_L}}}{{\partial {U_L}}} + \frac{{{w_L}}}{{{\rho _L}}}\frac{{\partial {{\left( {\rho w} \right)}_L}}}{{\partial {U_L}}} \end{array} $ | (21) |
(4) 结合(19)、(20)、(21),计算
| $ \begin{array}{*{20}{c}} {\frac{{\partial u_\zeta ^L}}{{\partial u_j^L}} = \left[ {\frac{{\partial \left( {\rho u} \right)_\zeta ^L}}{{\partial u_j^L}} - \frac{{\partial {u_L}}}{{\partial u_j^L}}\rho _\zeta ^L - \frac{{\partial \rho _\zeta ^L}}{{\partial u_j^L}}{u_L}} \right]/{\rho _L} - u_\zeta ^L\frac{{\partial {\rho _L}}}{{\partial u_j^L}}/{\rho _L}}\\ {\frac{{\partial v_\zeta ^L}}{{\partial u_j^L}} = \left[ {\frac{{\partial \left( {\rho v} \right)_\zeta ^L}}{{\partial u_j^L}} - \frac{{\partial {v_L}}}{{\partial u_j^L}}\rho _\zeta ^L - \frac{{\partial \rho _\zeta ^L}}{{\partial u_j^L}}{v_L}} \right]/{\rho _L} - v_\zeta ^L\frac{{\partial {\rho _L}}}{{\partial u_j^L}}/{\rho _L}}\\ {\frac{{\partial w_\zeta ^L}}{{\partial u_j^L}} = \left[ {\frac{{\partial \left( {\rho w} \right)_\zeta ^L}}{{\partial u_j^L}} - \frac{{\partial {w_L}}}{{\partial u_j^L}}\rho _\zeta ^L - \frac{{\partial \rho _\zeta ^L}}{{\partial u_j^L}}{w_L}} \right]/{\rho _L} - w_\zeta ^L\frac{{\partial {\rho _L}}}{{\partial u_j^L}}/{\rho _L}} \end{array} $ | (22) |
| $ \begin{array}{l} \frac{{\partial T_\zeta ^L}}{{\partial u_j^L}} = \frac{1}{{{\rho _L}}}\frac{{r - 1}}{R}\left\{ {\frac{{\partial \left( {\rho E} \right)_\zeta ^L}}{{\partial u_j^L}} - {f_1} - {f_2}} \right.\\ \;\;\left. { - \left( {\frac{{\left( {\rho E} \right)_\zeta ^L}}{{{\rho _L}}} - \left( {{u_L}u_\zeta ^L + {v_L}v_\zeta ^L + {w_L}w_\zeta ^L} \right)} \right)\frac{{\partial {\rho _L}}}{{\partial u_j^L}}} \right\}\\ {f_1} = \frac{{\partial {{\left( {\rho E} \right)}^L}}}{{\partial u_j^L}}\frac{{\rho _\zeta ^L}}{{{\rho _L}}} + \frac{{{{\left( {\rho E} \right)}_L}}}{{{\rho _L}}}\frac{{\partial \rho _\zeta ^L}}{{\partial u_j^L}} - 2\frac{{{{\left( {\rho E} \right)}_L}}}{{\rho _L^2}}\rho _\zeta ^L\frac{{\partial {\rho _L}}}{{\partial u_j^L}}\\ {f_2} = \frac{{\partial {{\left( {\rho u} \right)}_L}}}{{\partial u_j^L}}u_\zeta ^L + {\left( {\rho u} \right)_L}\frac{{\partial u_\zeta ^L}}{{\partial u_j^L}} + \frac{{\partial {{\left( {\rho v} \right)}_L}}}{{\partial u_j^L}}v_\zeta ^L\\ \;\;\;\; + {\left( {\rho v} \right)_L}\frac{{\partial v_\zeta ^L}}{{\partial u_j^L}} + \frac{{\partial {{\left( {\rho w} \right)}_L}}}{{\partial u_j^L}}w_\zeta ^L + {\left( {\rho w} \right)_L}\frac{{\partial w_\zeta ^L}}{{\partial u_j^L}} \end{array} $ | (23) |
(5) 结合(23)计算出层流黏性系数μL对守恒变量自由度的偏导数。
| $ \frac{{\partial {\mu _L}}}{{\partial u_j^L}} = {\mu _\infty }\frac{{{T_\infty } + {S_1}}}{{T_\infty ^{1.5}}}\left( {\frac{{1.5{T_L}^{0.5}}}{{{T_L} + {S_1}}} - \frac{{{T_L}^{1.5}}}{{{{\left( {{T_L} + {S_1}} \right)}^2}}}} \right)\frac{{\partial {T_L}}}{{\partial u_j^L}} $ | (24) |
(6) 结合(23)计算应力张量对守恒变量自由度的偏导数
(7) 按照黏性通量表达式给出
(8) 最后按照公式(18)求出黏性通量的雅可比矩阵。
同理求出当前单元相邻一侧单元的黏性通量的面积分项的雅可比矩阵。对于边界单元的边界面,将其按内部边界来获得无黏通量雅可比矩阵,并由边界黏性通量获得黏性雅可比矩阵。
采用类似方式计算黏性通量体积分项的雅可比矩阵。
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {{\mathit{\boldsymbol{F}}_v} \cdot \nabla {\phi _i}} \right)}}{{\partial u_j^L}} = \frac{{\partial \left( {{\mathit{\boldsymbol{F}}_v}} \right)}}{{\partial {U_L}}}\frac{{\partial {U_L}}}{{\partial u_j^L}} + \frac{{\partial \left( {{\mathit{\boldsymbol{F}}_v}} \right)}}{{\partial \nabla {U_L}}}\frac{{\partial \nabla {U_L}}}{{\partial u_j^L}}}\\ { + \frac{{\partial \left( {{\mathit{\boldsymbol{F}}_v}} \right)}}{{\partial {R_L}}}\frac{{\partial {R_L}}}{{\partial u_j^L}}} \end{array} $ | (25) |
由方程总体提升算子的计算公式求出
为提高计算效率,方程(11)左端项中的RHSi_f采用简单的LF数值通量格式。
| $ \begin{array}{l} RH{S_{i\_f}} = - \sum\limits_{s = 1}^{nface} {\sum\limits_{k = 1}^{fp} {{\omega _s}\left( k \right){\mathit{\boldsymbol{H}}_{LLF}}{\phi _i}\left| {{J_{sk}}} \right|} } \\ \frac{{\partial \left( {RH{S_{i\_f}}} \right)}}{{\partial u_j^n}} = - \sum\limits_{s = 1}^{nface} {\sum\limits_{k = 1}^{fp} {{\omega _s}\left( k \right)\frac{{\partial {\mathit{\boldsymbol{H}}_{LLF}}}}{{\partial U}}{\phi _i}\left| {{J_{sk}}} \right|{\phi _j}} } \end{array} $ | (26) |
在有限体积方法中,残差中黏性通量的雅可比矩阵采用黏性谱半径简化代替,本文同样采用类似的方法来处理。
| $ \frac{{\partial \left( {RH{S_{v\_f}} + RH{S_{v\_v}}} \right)}}{{\partial u_j^n}} \approx {\mathit{\Lambda }_v}{\phi _i}{\phi _j} $ | (27) |
| $ {\mathit{\Lambda }_v} = \frac{1}{\mathit{\Omega }}\sum\limits_{s = 1}^{nface} {\left[ {\max {{\left( {\frac{4}{{3\rho }},\frac{\gamma }{\rho }} \right)}_s}{{\left( {\frac{{{\mu _L}}}{{\mathit{P}{\mathit{r}_L}}} + \frac{{{\mu _T}}}{{\mathit{P}{\mathit{r}_T}}}} \right)}_s}{S_s}} \right]} $ | (28) |
其中Ω为当前单元的体积,Ss为当前单元边界面S的面积,nface为当前单元体总的面数, γ为比热比,Pr为普朗特数。
将基函数梯度类比于面的法向量,得到与对流通量雅可比矩阵
| $ \frac{{\partial \left( {RH{S_{i\_v}}} \right)}}{{\partial u_j^n}} = \sum\limits_{l = 1}^{vp} {\omega \left( l \right)\frac{{\partial \left( {\mathit{\boldsymbol{F}}\left( {{U_l}} \right) \cdot \nabla {\phi _i}} \right)}}{{\partial {U^n}}}\left| {{J_l}} \right|{\phi _j}} $ | (29) |
GMRES算法是以Galerkin原理为基础的Krylov子空间投影法,通过Arnoldi过程构造Krylov子空间的正交基,同时求解一个最小二乘法问题在Krykov子空间上选择最优解,使得每一步子迭代时的残值模最小。理想状态下GMRES具有平方收敛速度,计算效率高。该方法在基于结构网格和非结构网格的有限体积和有限差分方法中得到大量应用。线性系统的收敛速度与左端项系数矩阵的条件数有关,其矩阵条件数越小,收敛速度越快,一般采用预处理方法来改善系数矩阵条件数。本文采用PETSc科学计算可移植扩展工具包调用GMRES以及预处理技术。
| $ \begin{array}{l} {\rm{For}}\;l = 1,m\;{\rm{Do}}\;\;\;\;\;\;\;\;\;m\;次重启迭代\\ {v_0} = R - \bar AD{U_0}\;\;\;\;\;\;\;\;初始残差\\ {r_0} = {P^{ - 1}}{v_0}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;预处理\\ b = {\left\| {{r_0}} \right\|_2}\\ {v_1} = {r_0}/b\\ {\rm{For}}\;j = 1,k\;{\rm{Do}}\;\;\;\;\;\;\;\;\;\;\;\;内迭代\\ {y_{j + 1}} = \bar A{v_j}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;矩阵向量乘\\ {w_{j + 1}} = {P^{ - 1}}{y_{j + 1}}\;\;\;\;\;\;\;\;\;\;\;\;\;预处理\\ {\rm{For}}\;i = 1,j\;{\rm{Do}}\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Gram - Schmidt}}\\ {h_{i,j}} = {w_{j + 1}} \times {v_i}\\ {w_{j + 1}} = {w_{j + 1}} - {h_{i,j}}{v_i}\\ {\rm{End}}\;{\rm{Do}}\\ {h_{j + 1,j}} = {w_{j + 1}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Hessen}}\;{\rm{berg}}\;矩阵元素\\ {v_{j + 1}} = {w_{j + 1}}/{h_{j + 1,j}}\;\;\;\;\;\;\;\;\;{\rm{Krylov}}\;向量\\ {\rm{End}}\;{\rm{Do}}\\ z = {\min _{\hat z}}{\left\| {b{e_1} - H\hat z} \right\|_2}\;\;\;\;\;最小二乘问题\\ DU = D{U_0} + \sum\nolimits_{i = 1}^m {{z_i}{v_i}} \;\;更新逼近解\\ D{U_0} = DU\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;重启\\ {\rm{End}}\;{\rm{Do}} \end{array} $ | (30) |
对于大型问题,为减小内存开销,一般采用带预处理的重启型GMRES算法。本文采用的预处理方法为ILU0(incomplete LU factorizations with zero fill-in),预处理矩阵为左端项系数矩阵,算法的具体过程如上所示。
2 数值算例分析为验证本文发展的基于残值雅可比矩阵精确求解方法的GMRES的计算效率,本节采用二维、三维算例,通过比较残差雅可比精确求解方法、残值雅可比近似求解方法以及LU-SGS的收敛速度来验证残值无黏项雅可比矩阵精确求解方法和黏性项雅可比矩阵精确求解方法的计算效率。验证算例包括:NACA0012亚声速无黏绕流、ONERA-M6机翼亚声速无黏绕流、方腔流动以及平板层流流动。整个测试在中国空气动力研究与发展中心的计算集群上开展,计算节点为Intel(R) Xeon(R) E5-2660 V3,主频2.60 GHz。为方便描述,以GMRES-Ex、GMRES-Ap、GMRES-Ap1表示迭代方法为GMRES且残值雅可比分别为完全精确求解、完全近似求解以及雅可比中无黏项精确求解和黏性项近似求解;LU-SGS表示迭代方法为LU-SGS且残值雅可比都近似处理;RK表示显式时间迭代。
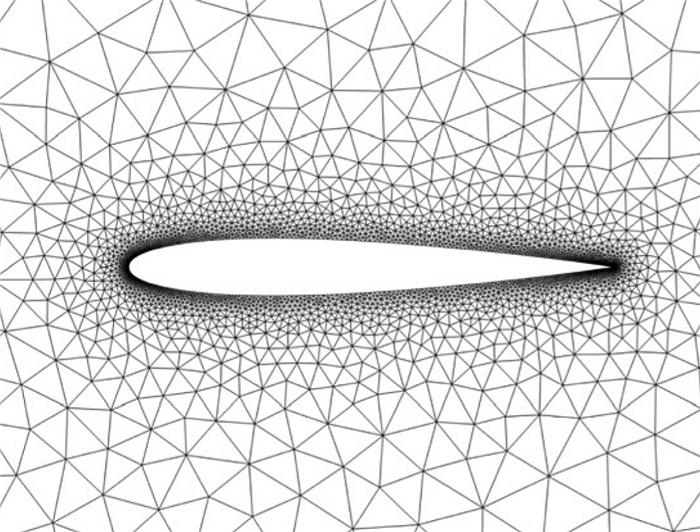
2.1 NACA0012亚声速无黏绕流本小节以NACA0012翼型为例,首先考察本文的GMRES方法的重启次数及每步收敛判定系数对计算效率的影响,在此基础上针对本算例选择最佳的重启次数和每步收敛判定系数;然后对比分析不同隐式迭代方法、残值雅可比不同计算方法及显式时间迭代的计算效率。计算网格如图 1,物面共有398个单元,对称面共7020个三角形单元,通过展向拉伸对称面单元得到三棱柱单元。计算的来流马赫数Ma=0.4,来流迎角0°,计算采用12核。分析GMRES参数影响时DG方法的计算精度为二阶。
|
图 1 NACA0012物面附近计算网格 Fig.1 Mesh near NACA0012 surface |
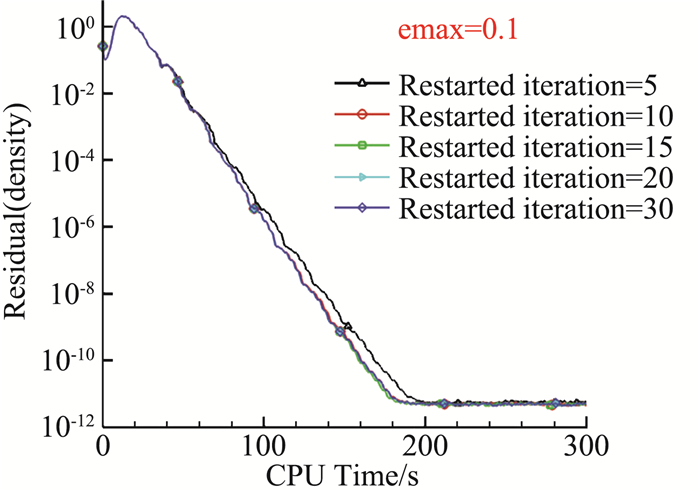
图 2给出了GMRES每步不同重启次数(Restarted iteration)对密度残值收敛速度影响,此时每步收敛判定系数emax=0.1。从残值随CPU计算时间收敛曲线看到,Restarted iteration=5的收敛速度最慢,当Restarted iteration≥10后不同Restarted iteration对收敛速度基本没影响。
|
图 2 GMRES不同重启次数的残值收敛曲线 Fig.2 Residual convergence history for different restarted iterations of GMRES |
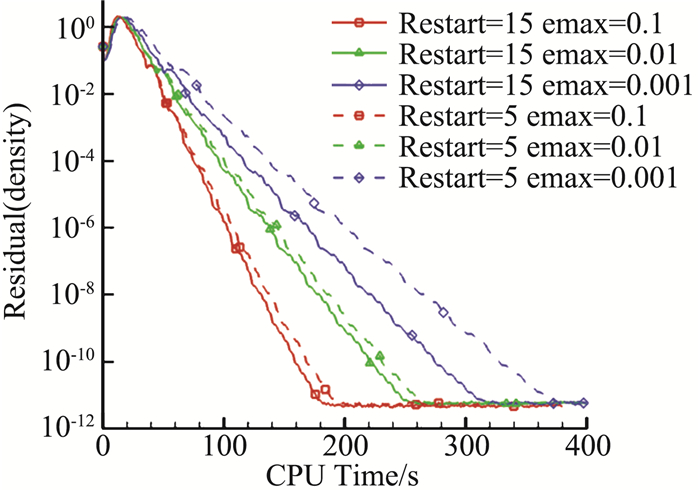
图 3给出了Restarted iteration=5、15时GMRES每步收敛判定系数对密度残差收敛速度影响。可以看到,不同判定系数对收敛速度有较大影响,随着系数增大,收敛速度明显增大,emax=0.1收敛的总时间约为emax=0.001的1/2。同时看到在相同emax时,Restarted iteration=15的收敛速度都快于Restarted iteration=5。故在后面的GMRES隐式迭代中,取Restarted iteration=15,emax=0.1。
|
图 3 GMRES不同收敛判定系数的残值收敛曲线 Fig.3 Residual convergence history for different convergence coefficients of GMRES |
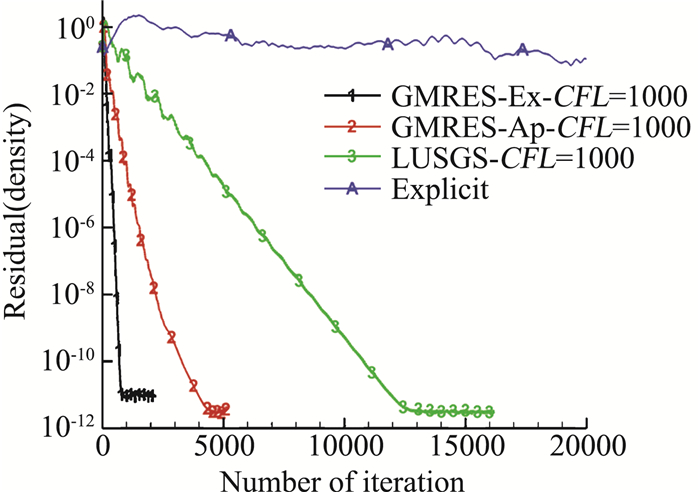
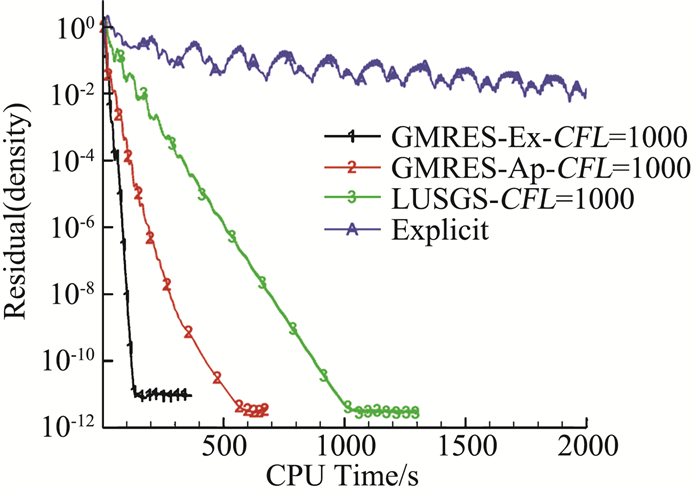
图 4给出了DG(P1)在CFL=1000时不同迭代方法的收敛曲线,CFL在1000步以内从1逐渐增大到1000。GMRES_Ex、GMRES_Ap和LU-SGS三种方法的残值收敛所需的迭代步数远小于显式迭代,GMRES_Ex隐式迭代所需的迭代步数最小。相同CFL下GMRES_Ex残值收敛的迭代步数约只有GMRES_Ap的1/5,GMRES_Ap残值收敛的迭代步数只有LU-SGS的1/3。三种隐式时间迭代的单步计算时间GMRES_Ex > GMRES_Ap > LU-SGS,从残值随计算时间曲线图 5看,GMRES_Ex隐式迭代所需的计算时间最小。GMRES_Ex残值收敛的计算时间约为GMRES_Ap的1/4,GMRES_Ap残值收敛的计算时间只有LU-SGS的1/2。相比LU-SGS,基于残值雅可比精确求解方法的GMRES计算效率提高了约8倍。
|
图 4 CFL=1000,不同迭代方法残值收敛曲线(残差与迭代步) Fig.4 Residual convergence history for different iteration methods (Res. vs. step) |
|
图 5 CFL=1000,不同时间迭代方法残值收敛曲线(残差与时间) Fig.5 Residual convergence history for different iteration methods (Res. vs. time) |
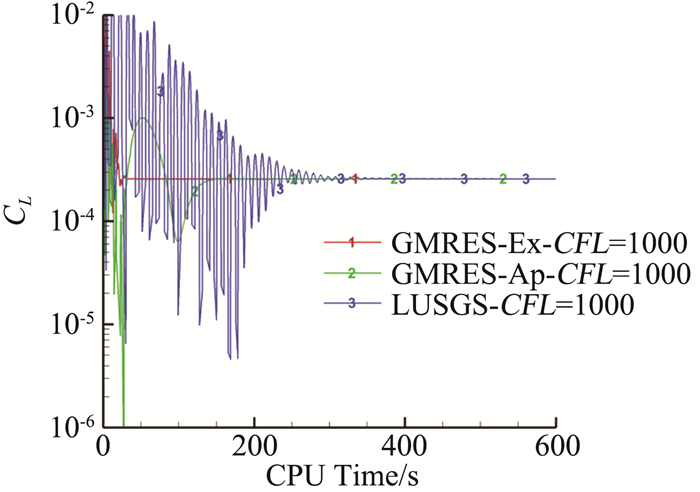
图 6给出了不同隐式时间迭代方法得到的升力系数随计算时间变化曲线。由图看到,三种隐式方法得到的升力系数相同,GMRES计算得到的升力系数经过前期短时间的震荡后几乎单调收敛,其气动力收敛速度远高于LU-SGS。
|
图 6 二阶精度下不同方法的升力系数收敛曲线 Fig.6 Lift coefficient convergence history for different iteration methods for DG(P1) |
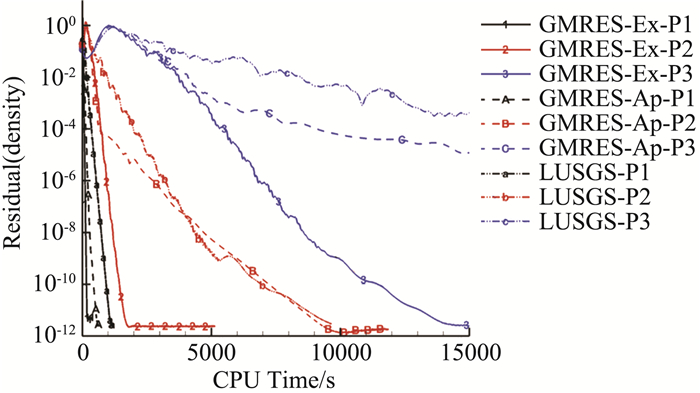
图 7给出了不同精度下,不同隐式离散方法的密度残值的收敛曲线。计算的最大CFL数取100,CFL在1000步内从1逐渐增大到100。从图看到,随着计算精度的提高,收敛所需的时间急剧增大,不同计算精度下,GMRES_Ex的计算效率都最高。
|
图 7 不同计算精度下,不同迭代方法残值收敛曲线 Fig.7 Residual convergence history for different iteration method for different orders of accuracy (Res. vs. time) |
表 1给出了不同计算精度下,不同隐式时间离散方法的计算时间,其中耗时比以GMRES_Ex计算时间为基准。首先分析相同雅可比矩阵计算方法下不同计算精度的收敛时间,从表看到随着DG计算精度的提高,收敛所需计算时间非线性增加,以GMRES_Ex为例,DG(P2)和DG(P3)的计算时间分别约为DG(P1)的8.9倍和74.3倍。其次分析相同计算精度下,不同隐式时间迭代方法的计算时间,对于DG(P1)、DG(P2)、DG(P3),GMRES_Ap的计算时间分别约为GMRES_Ex的3.0倍、5.4倍、6.3倍,LU-SGS的计算时间分别约为GMRES_Ex的5.8倍、5.6倍、7.0倍。从以上分析看到,相比残值雅可比近似求解方法,本文发展的残值雅可比精确求解技术能够显著提高GMRES的计算效率,这对计算量巨大的DG方法来说具有重要意义。
| 表 1 不同精度以及不同隐式迭代方法下NACA0012的计算时间 Table 1 Computation time of different iteration methods with different orders of accuracy for NACA0012 airfoil |
|
|
为进一步验证本文发展的基于残值雅可比矩阵精确求解方法的GMRES方法在三维外形的计算效率,本节开展了ONERA-M6机翼[20]的亚声速无黏绕流流场的数值模拟。计算条件为Ma=0.4, α=0°。网格如图 8,网格共约14.8万个四面体单元,为较好模拟机翼前后缘,机翼前后缘及空间分别采用各向异性和各向同性四面体网格,采用64核并行计算。

|
图 8 ONERA-M6机翼计算网格 Fig.8 Tetrahedral mesh for ONERA-M6 |
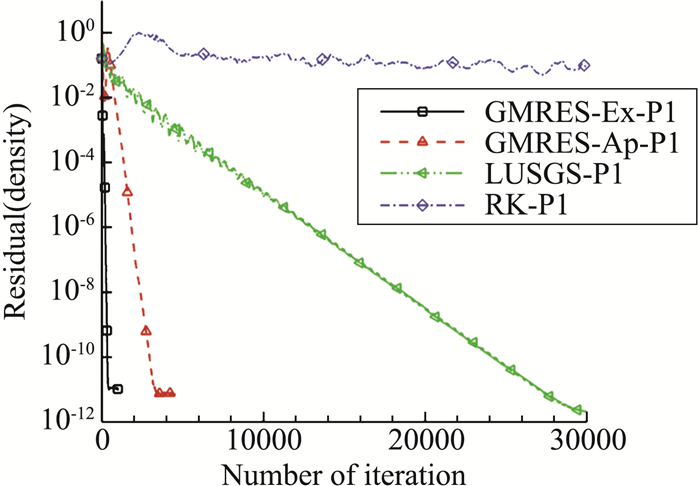
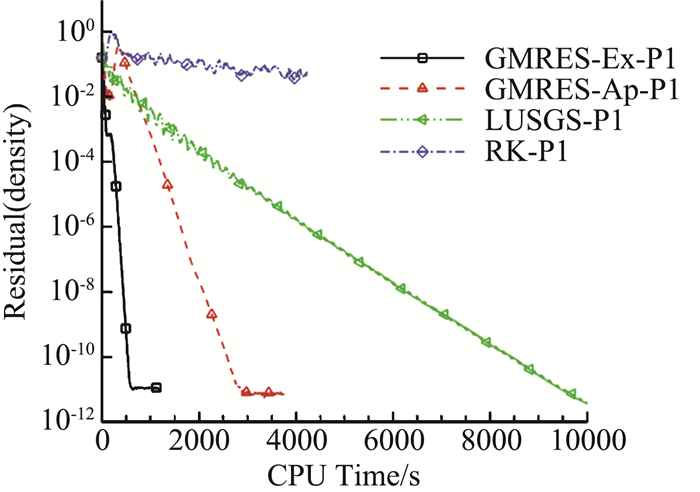
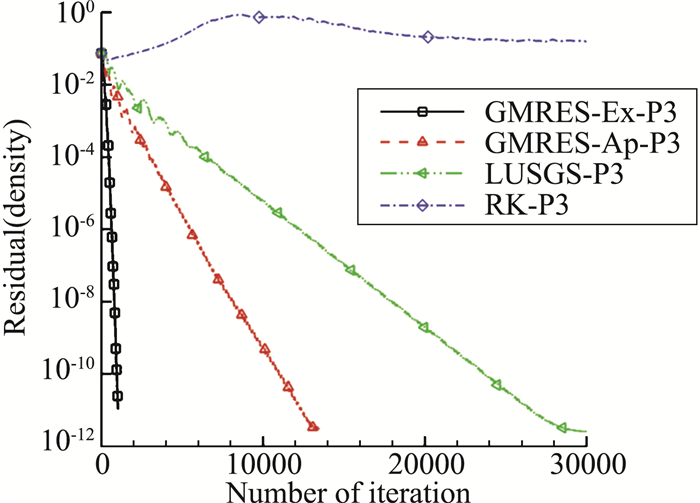
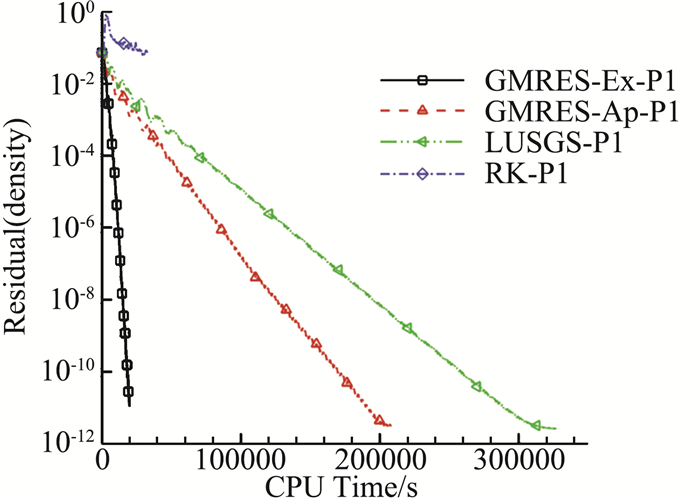
图 9~图 12分别给出了DG(P1)、DG(P3)下密度残值的收敛曲线,同时给出了RKDG显式收敛曲线。不同计算精度下GMRES_Ex隐式计算的CFL=1000,GMRES_Ap和LU-SGS的CFL数采用能够稳定计算的最大值,P1阶时CFL=100,P3阶时CFL=20,RK的CFL=0.3。以残差下降到10-12量级为标准,对于DG(P1)、DG(P3),GMRES_Ap所需要的计算时间约为GMRES_Ex的5倍和10倍,LU-SGS所需要的计算时间约为GMRES_Ex的16倍和14倍。
|
图 9 M6机翼DG(P1)的密度残值收敛曲线(残差与迭代步) Fig.9 Residual convergence history of DG(P1) for M6 wing(Res. vs. step) |
|
图 10 M6机翼DG(P1)的密度残值收敛曲线(残差与时间) Fig.10 Residual convergence history of DG(P1) for M6 wing(Res. vs. time) |
|
图 11 M6机翼DG(P3)的密度残值收敛曲线(残差与迭代步) Fig.11 Residual convergence history of DG(P3) for M6 wing (Res. vs. step) |
|
图 12 M6机翼DG(P3)的密度残值收敛曲线(残差与时间) Fig.12 Residual convergence history of DG(P3) for M6 wing(Res. vs. time) |
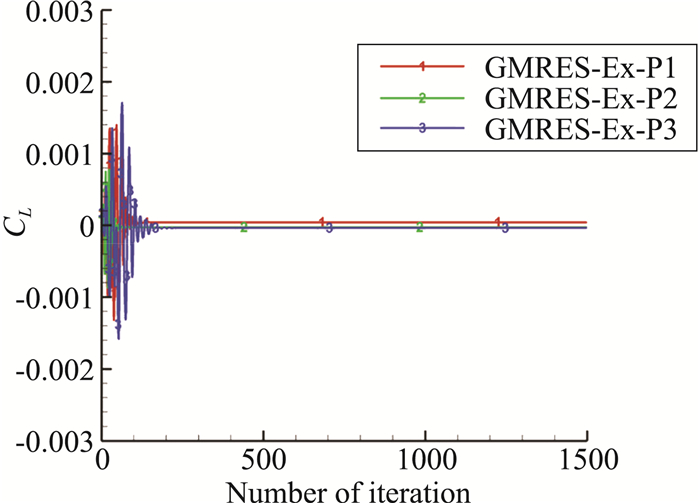
图 13给出了不同精度DG方法采用GMRES_Ex获得的升力系数随迭代步数变化曲线。从图看到,不同精度下的升力系数都能500~1000迭代步内收敛,显示了本文的基于残值雅可比精确求解的GMRES方法在计算效率方面的优势。
|
图 13 DG不同精度的M6机翼升力系数收敛曲线 Fig.13 Lift coefficient convergence history of DG with different orders of accuracy for ONERA-M6 |
表 2给出了不同计算精度下,不同隐式方法模拟ONERA-M6机翼无黏绕流的时间,其中耗时比以GMRES_Ex计算时间为基准。从表可知基于残值雅可比精确求解的GMRES计算效率远高于雅可比矩阵近似求解的GMRES和LU-SGS,在DG(P3)时,GMRES_Ex的计算效率相比另外两种方法提高了一个数量级以上。
| 表 2 不同精度以及不同隐式时间离散方法下M6机翼的计算时间 Table 2 Computation time of iteration methods with different orders of accuracy for ONERA-M6 |
|
|
方腔流动是一个经典层流标准算例。它描述的是一类顶盖驱动流动,顶盖以给定速度u=1 m/s驱动方腔内流动,不同雷诺数下方腔内有不同的流态。本节采用该算例验证建立的残值雅可比精确求解方法,分析精确计算残值中无黏项和黏性项的雅可比矩阵对计算效率影响。
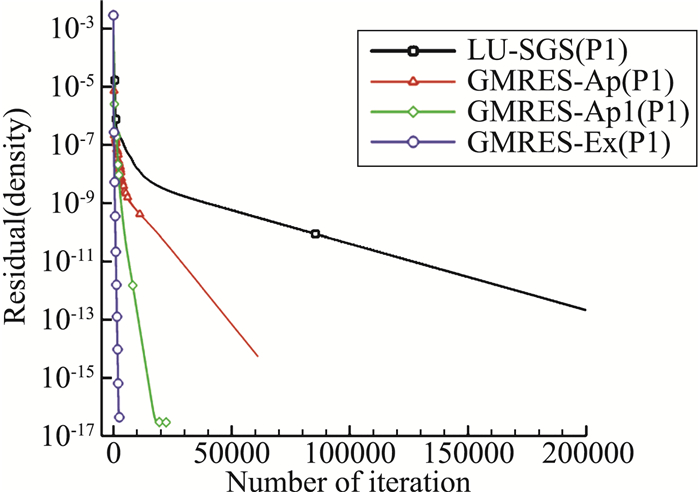
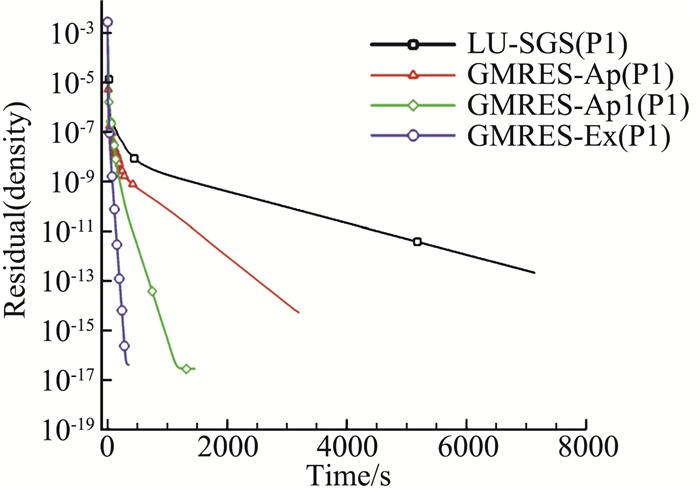
图 14、图 15给出了不同隐式迭代方法及残值雅可比不同求解方法下DG(P1)的密度残值收敛曲线,GMRES-Ex的CFL数在200步内从1增加到1000。LU-SGS、GMRES-Ap、GMRES-Ap1的CFL数均采用能够稳定计算的最大值,CFL数在1000步内从1增加到100。数值模拟发现,对于LU-SGS、GMRES-Ap、GMRES-Ap1这三种方法,当CFL数大于100后CFL数对收敛速度影响很小,因此采用CFL数=100来比较计算效率是合适的。由于LU-SGS及GMRES-Ap收敛需要较长时间,本文并未给出其完全收敛的收敛曲线。从图看到GMRES-Ex及GMRES-Ap1的密度残值很快下降到10-17次方量级,GMRES-Ex的收敛时间最短,GMRES-Ap1的收敛时间次之,LU-SGS的收敛时间最长。
|
图 14 方腔DG(P1)的密度残值收敛曲线(残差与迭代步) Fig.14 Residual convergence history of DG(P1) for square cavity(Res. vs. step) |
|
图 15 方腔DG(P1)的密度残值收敛曲线(残差与时间) Fig.15 Residual convergence history of DG(P1) for square cavity(Res. vs. time) |
表 3统计了二阶计算精度下,不同隐式迭代方法及残值雅可比不同求解方法的模拟时间。以GMRES-Ex模拟时间为基准,当密度残值都下降到2.12×10-13时,GMRES-Ap1、GMRES-Ap、LU-SGS的计算时间分别是GMRES-Ex的3.4倍、12.3倍、37.4倍。从表可知GMRES-Ex的计算效率远高于LU-SGS,体现了本文发展的残值雅可比精确求解方法的计算优势,同时看到即使只对残值中无黏项的雅可比矩阵精确求解同样能够提高计算效率,精确求解黏性项雅可比矩阵能够带来计算效率提升。
| 表 3 DG(P1)不同隐式时间离散方法的方腔计算时间 Table 3 Computation time of DG(P1) with different iteration methods for square cavity |
|
|
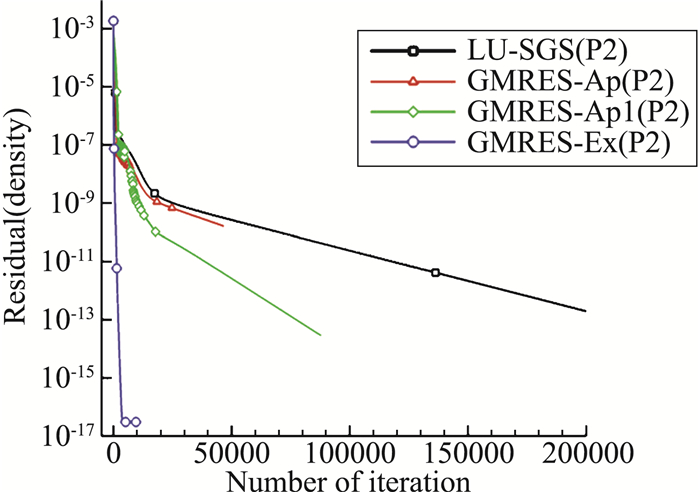
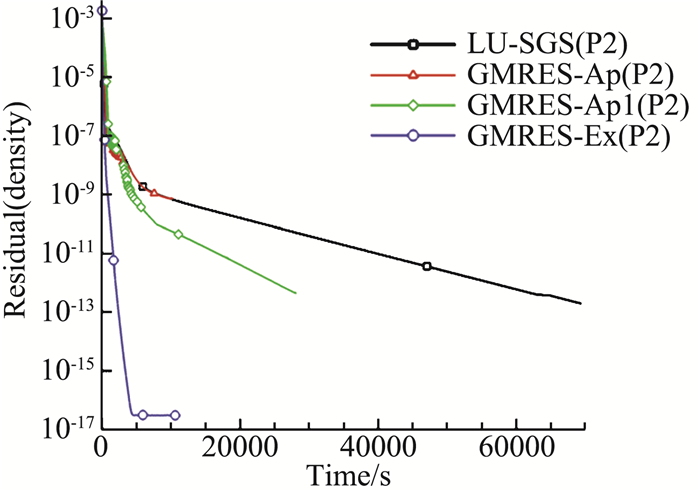
图 16、图 17给出了不同隐式迭代方法及残值雅可比不同求解方法下DG(P2)的密度残值收敛曲线,GMRES-Ex的CFL数在200步内从1增加到1000,GMRES-Ap、GMRES-Ap1、LU-SGS的CFL数在5000步内从1增加到100。由于GMRES-Ex残值雅可比精确求解,保证迭代求解过程中能取较大的CFL数,且基本不受计算精度影响,而基于雅可比近似求解的GMRES-Ap、GMRES-Ap1的CFL数受计算精度影响较大。
|
图 16 方腔DG(P2)的密度残值收敛曲线(残差与迭代步) Fig.16 Residual convergence history of DG(P2) for square cavity(Res. vs. step) |
|
图 17 方腔DG(P2)的密度残值收敛曲线(残差与时间) Fig.17 Residual convergence history of DG(P2) for square cavity(Res. vs. time) |
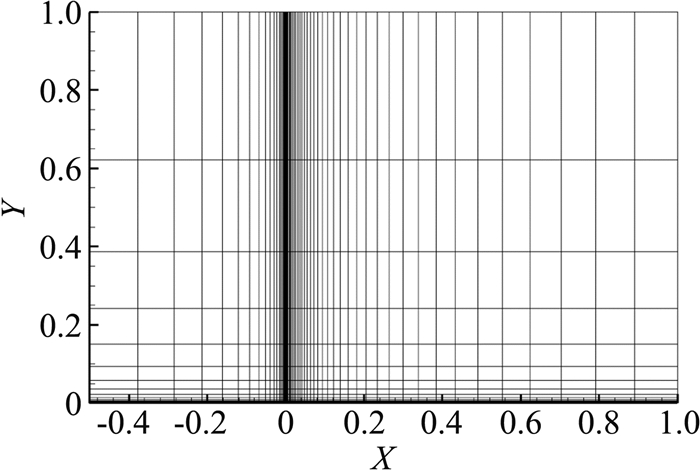
最后本文将残值雅可比精确求解方法用于二维平板层流边界层的数值模拟。平板为厚度为0的绝热壁,来流马赫数为0.2,来流雷诺数为105,来流温度为288.15 K。计算区域为x=(-0.5,1),y=(0,1),平板前缘点位于(0,0),后缘点位于(1,0)。网格点为61×17,平板前方分布20个单元,平板表面分布40个单元,y方向共布置16个单元,展向一个网格单元。平板前后缘X方向的尺寸为0.001,0.11。第一层网格高度为0.0005。计算包括两套网格,分别为六面体网格以及由六面体剖分而得的四面体网格。图 18、图 19展示了计算网格。
|
图 18 平板层流边界层计算网格(六面体) Fig.18 Hexahedron mesh for laminar flow over flat plate |
|
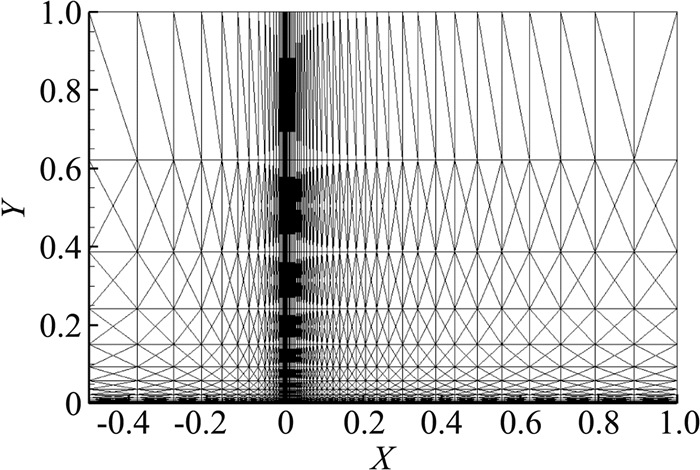
图 19 平板层流边界层计算网格(四面体) Fig.19 Tetrahedral mesh for flat laminar flow over flat plate |
表 4给出了两种网格在不同计算精度下得到的总摩阻系数,同时给出了Blasius解。从表可知,随着计算精度增大,总的摩阻系数增大。对于六面体和四面体网格,随着计算精度增加,摩阻系数逐步向Blasius解靠近。
| 表 4 不同网格和精度下平板的摩擦阻力系数 Table 4 Skin drag coefficient of flat with different grids and orders of accuracy of DG |
|
|
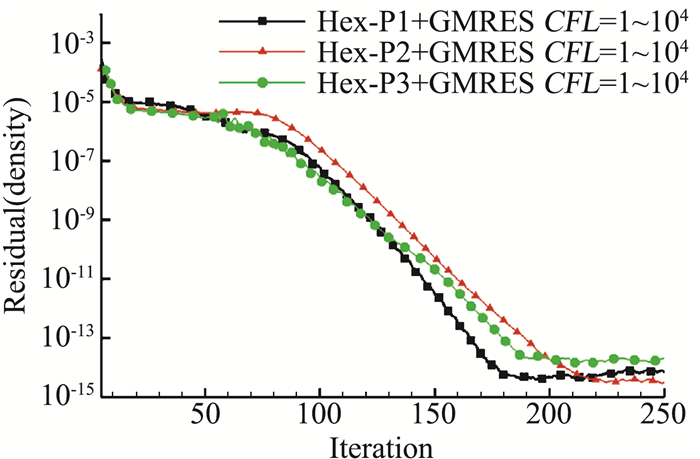
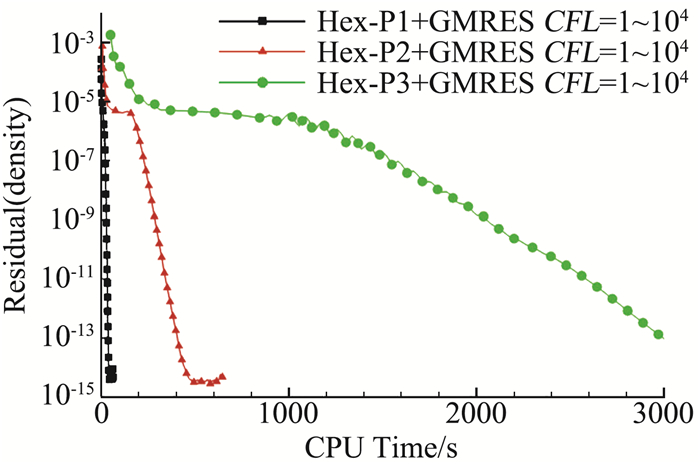
图 20、图 21给出了采用不同精度DG方法的密度残值收敛历程,计算网格为六面体网格。不同计算精度都采用GMRES迭代,精确求解方程残值雅可比,CFL数从1增加到104。从图看到本文的数值方法在200步以内将残值降到10-15量级,进一步验证了本文的残差雅可比精确求解方法的准确性以及隐式迭代方法的计算效率。
|
图 20 平板边界层六面体网格收敛历程(残差与迭代步) Fig.20 Residual convergence history of DG with different orders of accuracy for flat plate(Res. vs. time) |
|
图 21 平板边界层六面体网格收敛历程(残差与时间) Fig.21 Residual convergence history of DG with different orders of accuracy for flat plate(Res. vs. time) |
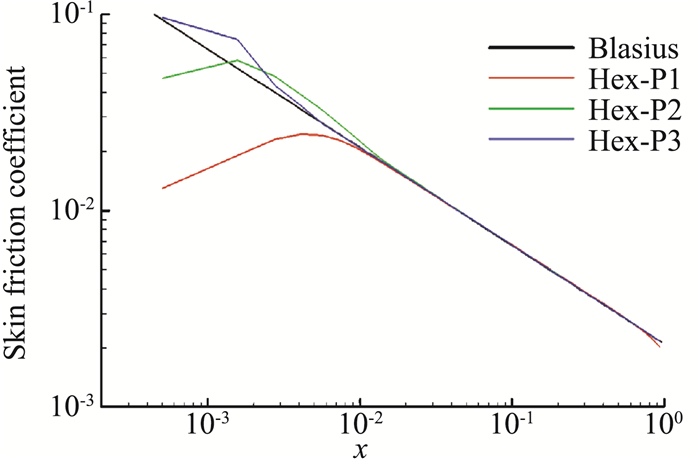
图 22给出了不同精度DG方法得到的平板的摩阻分布,同时也给出了Blasius摩阻分布,X、Y坐标都为对数坐标。总的来看,除去平板前缘,不同精度的摩阻分布与Blasius解分布基本重合,计算精度越高,重合度越高。高精度的优势主要体现在平板前缘附近的摩阻系数。从图看到,DG(P1)在x < 10-2范围内与Blasius解有较大差别,且x越小,差别越大,DG(P2)、DG(P3)在x < 10-3范围内才与Blasius解出现明显区别。
|
图 22 六面体网格下不同计算精度的平板摩阻系数分布 Fig.22 Comparison of the skin friction calculated from DG with different orders of accuracy for flat plate on hexahedral mesh |
本文在三维非结构网格上建立了高阶精度DG方法,针对高阶精度DG方法计算量大这一难题,发展了一种基于右端项残值雅可比矩阵精确计算的高效GMRES隐式迭代方法。采用NACA0012、ONERA-M6、方腔流动、平板层流边界层算例,通过对比基于残值雅可比矩阵不同计算方法的GMRES、LU-SGS隐式时间迭代以及显式TVD-RK的计算效率,体现了不同残值雅可比矩阵计算方法对计算效率的影响以及GMRES和LU-SGS的计算效率。从对比结果看到:右端项残值雅可比矩阵精确求解方法更好保证方程组左右两端的匹配性和相容性,基于矩阵精确求解方法的GMRES能够显著提高不同精度下DG方法数值模拟的CFL数,大幅提高计算效率。
致谢: 感谢上海大学杨小权对本文雅可比矩阵精确求解部分提供的帮助!
| [1] |
COCKBURN B, SHU C W. The Runge-Kutta discontinuous Galerkin method for conservation laws V:multidimensional systems[J]. Journal of Computational Physics, 1998, 141: 99-224. |
| [2] |
REED W H, HILL T R. Triangular mesh methods for the neutron transport equation[R]. Los Alamos Scientific Laboratory Report, LAUR-73-479, 1973.
|
| [3] |
马明生, 龚小权, 邓有奇, 等. 一种适用于非结构网格的间断Galerkin有限元LU-SGS隐式方法[J]. 西北工业大学学报, 2016, 34(4): 754-760. MAM S, GONG X Q, DENG Y Q, et al. An implicit LU-SGS scheme for the discontinuous Galerkin method on unstructured grids[J]. Journal of Northwestern Polytechnical University, 2016, 34(4): 754-760. (in Chinese) |
| [4] |
郭永恒, 杨永, 张强. 一种高效的隐式间断Galerkin方法研究[J]. 空气动力学学报, 2012, 30(2): 230-233. GUO Y H, YANG Y, ZHANG Q. A high efficient implicit discontinuous Galerkin method[J]. Acta Aerodynamica Sinica, 2012, 30(2): 230-233. (in Chinese) |
| [5] |
TAKANORI H, KEISUKE S, WANG Z J. Animplicit LU-SGS scheme for the spectral volume method on unstructured tetrahedral grids[J]. Communications in Computational Physics, 2009, 6(5): 978-996. DOI:10.4208/cicp |
| [6] |
刘伟, 张来平, 赫新, 等. 基于Newton/Gauss-Seidel迭代的DGM隐式方法[J]. 力学学报, 2012, 44(4): 792-796. LIU W, ZHANG L P, HE X, et al. An implicit algorithm for discontinuous Galerkin method based on Newton/Gauss-seidel iterations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(4): 792-796. DOI:10.6052/0459-1879-11-352 (in Chinese) |
| [7] |
PERSSON P O, PERAIRE J. Newton-GMRES preconditioning for discontinuous Galerkin discretizations of the Navier-Stokes equations[J]. SIAM Journal on Scientific Computing, 2008, 30(6): 2709-2733. DOI:10.1137/070692108 |
| [8] |
CRIVELLINI A, BASSI F. An implicit matrix-free discontinuous Galerkin solver for viscous and turbulent aerodynamic simulations[J]. Computers & Fluids, 2011, 50: 81-93. |
| [9] |
LASLO T D, DAVID L D. Discontinuous Galerkin solutions of the Navier-Stokes equations using linear multigrid preconditioning[R]. AIAA 2007-3942.
|
| [10] |
CHEN S Q, ZHANG T T. Krylov implicit integration factor methods for spatial discretization on high dimensional unstructured meshes:application to discontinuous Galerkin methods[J]. Journal of Computational Physics, 2011, 230: 4336-4352. DOI:10.1016/j.jcp.2011.01.010 |
| [11] |
LANDMANN B. A parallel discontinuous Galerkin code for the Navier-Stokes and Reynolds-averaged Navier-Stokes equations[D]. Stuttgart, university of Stuttgart, 2008.
|
| [12] |
党亚斌, 刘凯礼, 孙一峰, 等. 用隐式高精度间断伽辽金方法模拟可压层流和湍流[J]. 空气动力学学报, 2018, 36(3): 535-541. DANG Y B, LIU K L, SUN Y F, et al. Implicit high order discontinuous Galerkin method for compressible laminar and turbulent flow simulation[J]. Acta Aerodynamica Sinica, 2018, 36(3): 535-541. DOI:10.7638/kqdlxxb-2017.0183 (in Chinese) |
| [13] |
YANG X Q, CHENG J, WANG C J, et al. A fast, implicit discontinuous Galerkin method based on analytical Jacobians for the compressible Navier-Stokes equations[R]. AIAA 2016-1326.
|
| [14] |
CHENG J, LIU X D, YANG X Q, et al. A direct discontinuous Galerkin method for the compressible Navier-Stokes equations on arbitrary grids[R]. AIAA 2016-3334.
|
| [15] |
BALAY S, ABHYANKAR S, ADAMS M, et al. PETSc users manual[OL]. http://www.mcs.anl.gov/petsc/documentation/index.html.
|
| [16] |
BLAZEK J. Computational fluid dynamics: principles and applications[M]. London Elsevier Science, 2001.
|
| [17] |
ROE P L. Approximate riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43: 357-372. DOI:10.1016/0021-9991(81)90128-5 |
| [18] |
BASSI F, REBAY S, MARIOTTI G, et al. A high-order accurate discontinuous finite element method for inviscid and viscous turbomachinery flows[C]//In Proceedings of the 2nd European Conference on Turbomachinery Fluid Dynamics and Thermodynamics, March 5-71997, 99-108.
|
| [19] |
KRIST S L, BIEDRON R T, RUMSEY C L. CFL3D User's Manual (Version 5.0)[EB]. NASA/TM-1998-208444.
|
| [20] |
SCHMITT V, CHARPIN F. Pressure distributions on the ONERA-M6 wing at transonic Mach numbers[R]. Experimental Data Base for Computer Program Assessment, AGARD AR138, 1979.
|
 2019, Vol. 37
2019, Vol. 37


