2. 同济大学 桥梁工程系, 上海 200092;
3. 桥梁结构抗风技术交通运输行业重点实验室(同济大学), 上海 200092
2. Department of Bridge Engineering, Tongji University, Shanghai 200092, China;
3. Key Laboratory of Transport Industry of Wind Resistance Technology for Bridges Structures(Tongji University), Ministry of Transport, Shanghai 200092, China
与平均每年发生千余次龙卷风的美国相比,我国发生龙卷风的频次仅约100次/年。然而,由于我国龙卷风发生区人口密集,且龙卷风预警系统及抗灾设施基础较薄弱,因此,从人员伤亡数量、房屋损毁程度等指标看,龙卷风对我国的影响并不亚于美国[1]。仅2016年6月23日发生在江苏盐城阜宁的一起EF4级龙卷风事件,就造成至少99人死亡、846人受伤,超过3000余栋房屋和数百座高压输电线受损[2]。1961年至2010年的50年间气象资料统计显示,我国龙卷风多发区,特别是EF2级以上强龙卷集中在江苏省,其次为同处沿海的上海、广东、海南等省市[3]。与普通建筑结构相比,大跨度桥梁等线状水平结构遭遇龙卷风袭击的可能性大大增加[4]。而我国多座重要跨江跨海大跨度桥梁工程主要集中在上述龙卷风多发的省份。因此,有必要对位于龙卷风多发省份的重要大跨度桥梁结构考虑龙卷风灾害风险。
近年来,对于龙卷风特性及其引起的结构风荷载和风致响应的现场实测、实验模拟、数值仿真等逐渐增多,但主要还是关注普通建筑结构,如低矮建筑[5-8]、高层建筑[9],以及重要性级别高的工业建筑,如核电站冷却塔[10-12]等,针对桥梁结构的研究还很少。极少数关于桥梁在龙卷风作用下的结构响应数值分析因缺乏龙卷风下的风荷载参数,仍采用常规风洞实验的风荷载参数进行计算分析[13-15]。因此,基于龙卷风模拟装置,开展桥梁断面在龙卷风作用下的风荷载参数物理识别,是对桥梁抗龙卷风设计和灾害评估具有重要支撑作用的基础性工作。
另一方面,由于龙卷风物理模拟的实现方式不同、风荷载实验参数和流程的要求不同,因此,不同物理模拟实验结果难以用统一的标准进行评价,导致结构龙卷风荷载研究目前仍停留在定性的层面。为保证结构龙卷风荷载实验结果的准确性,阐明风荷载识别中的关键相似参数及其对荷载识别结果的影响成为首要前提。涡流比作为表征龙卷风旋转强度的参数,是决定旋涡形状和风速/气压降特性的重要相似参数,在目前龙卷风模拟中均会重点考虑[16-17]。在龙卷风模拟器中,由安装在装置上部的吸气扇提供上升气流,由安装在周围的导流板提供切向循环气流。此外,实际龙卷风的高宽比为入流高度与上升气流半径之比,其对结构风荷载影响的研究还很少。表 1总结了实际龙卷风和中小型龙卷风模拟器所模拟的龙卷风部分相似参数[18]。可以看出,除雷诺数相似无法满足,目前的龙卷风模拟装置具有足够的模拟涡流比和高宽比的能力。
| 表 1 实际和模拟龙卷风的相似参数对比[18] Table 1 Comparison of similarity parameters of real tornadoes and simulated tornadic vortices[18] |
|
|
本文尝试通过刚体模型测压实验方法,利用龙卷风模拟器,对大跨度桥梁主梁断面在模拟龙卷风作用下的表面风压分布和三分力系数等风荷载参数进行识别。由于桥梁断面一般距离地面(或水面)垂直距离较大,因此本文除考虑涡流比这一重要相似参数外,还将着重研究高宽比这一相似参数对结果的影响,从而揭示龙卷风对桥梁断面风荷载的作用规律,为类似远地面线状水平结构的龙卷风荷载物理模拟提供参考。
1 实验概况 1.1 龙卷风模拟器实验在同济大学风洞试验室移动式龙卷风模拟器(图 1)中进行。该装置由三个同轴圆筒构成,风机和导流板位于装置顶部,气流经风机吸收,通过导流板和外围圆筒,在升降平台与蜂窝网间形成龙卷风涡旋。通过改变图 1所示的模拟器控制参数,如:风机转速、导流板角度θv、收束层高度H0、模拟器水平移动速率VH等。通过将利用该模拟器模拟得到的龙卷风涡旋平均切向风速和气压降分布规律与实测数据进行对比,证明该模拟器可用于对真实龙卷风风场形态的模拟再现[19]。
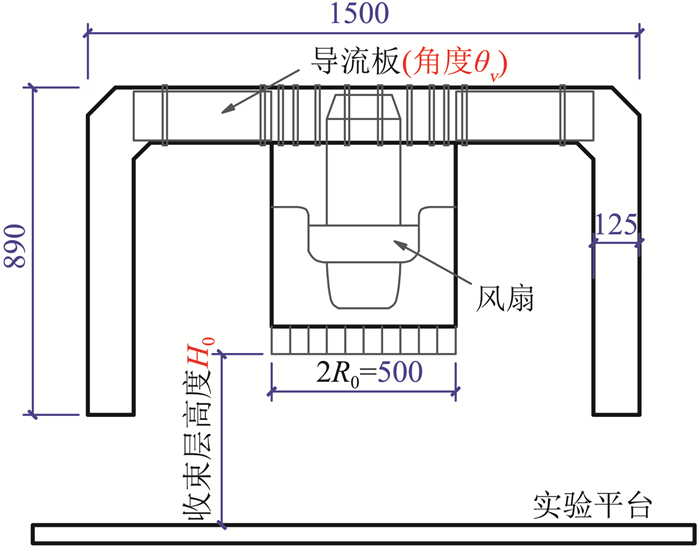
|
图 1 龙卷风模拟器(单位:mm) Fig.1 The tornado simulator (Unit: mm) |
实验模型以主跨1500 m斜拉桥试设计方案的扁平流线型钢箱主梁断面为设计原型,桥面宽(含风嘴)41 m、高为5 m,桥下净空50 m。模型的几何缩尺比为1:250,即模型的梁宽164 mm,梁高20 mm。模型总长1.8 m,与龙卷风模拟器试验平台的长度一致,模型底面距离测试平台高度200 mm。模型在靠近平台中心区域的648 mm范围内布设测压孔,共计28排,各排间距24 mm,如图 2(a)所示。在每一排测点里,沿主梁断面周向设置测压点16个,如图 2(b)所示。模型测压点总数为448个。
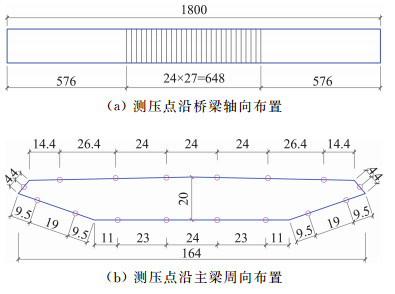
|
图 2 实验模型(单位:mm) Fig.2 Pressure-tapped model(Unit: mm) |
(1) 相似参数
实验中主要考虑龙卷风气流高宽比(H0/R0)和涡流比(Sr)这两个相似参数对桥梁龙卷风荷载的影响。其中,因上升气流半径固定为R0=0.25m,通过调节升降平台高度实现不同高宽比的模拟;而不同涡流比则通过改变图 1所示龙卷风模拟装置顶部导流板角度θv实现,其计算公式为:
| $ Sr = \frac{{{R_0}}}{{2{H_0}}}\tan {\theta _v} $ | (1) |
上式中各参数取值及两个相似参数结果如表 2所示。
| 表 2 相似参数取值 Table 2 Similarity parameters in the experiments |
|
|
在表 2中,在不同收束层高度情况下,分别进行了不同涡流比条件下的测试,因此可以讨论某一高宽比下,涡流比对实验结果的影响。此外,通过改变收束层高度和导流板角度,还可以实现高宽比不同、但涡流比相同(近)的龙卷风气流模拟,如:在高宽比为1.8和2.6的情况下,通过将导流板角度分别调至30°和40°,使涡流比均为0.16,因此可以讨论相同涡流比条件下,高宽比对实验结果的影响。
实验的雷诺数按下式计算:
| $ { Re} = \frac{Q}{{{H_0}v}} $ | (2) |
式中,Q为上升气流流量,H0为收束层高度,ν为空气运动黏度。本文设置的风扇转速为1500转/分钟,对应测得不同涡流比条件下的上升气流流量为1.40~1.52 m3/s,可知本文实验的雷诺数为1.45×105~1.58×105。
(2) 其他参数
龙卷风荷载实验中另一重要参数为模拟器中心与测压模型中心的距离r,如图 3所示。实验中,模型固定在测试平台正中,龙卷风模拟器的可移动风扇部分自平台左侧向右侧平移,范围r从-0.3 m至0.3 m,平移间隔为24 mm,共平移27个位置。考虑测压模型的宽度为164 mm,则相对移动距离为r/b=-1.83~1.83。
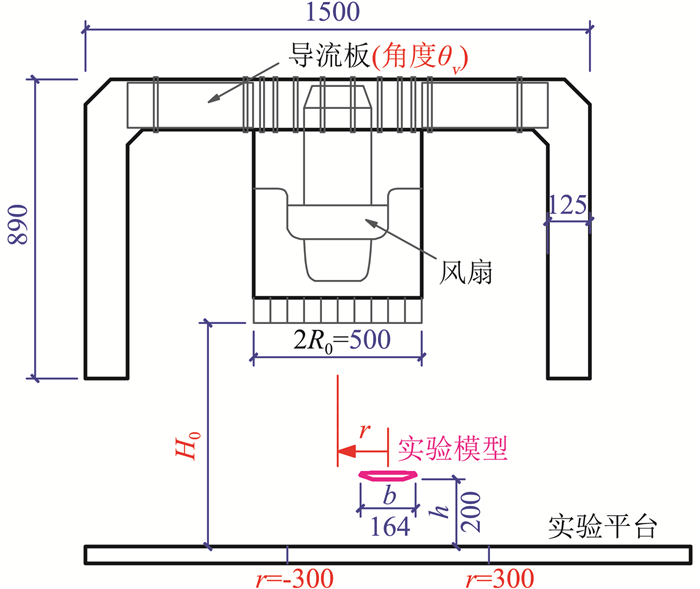
|
图 3 实验参数(单位:mm) Fig.3 Experimental parameters (Unit: mm) |
图 4为主梁模型所在高度处(h=0.2 m)切向风速水平分布(风场测试时,无主梁模型)。图中比较了相同高宽比条件下不同涡流比的影响,也考虑了相同涡流比条件下不同高宽比的影响。四种工况下,模拟器得到的龙卷风涡旋的平均切向风速均符合真实龙卷风的“M”形分布,即在涡核半径内,最大切向风速随与涡核中心距离的增加而增大,在涡核半径外,其随着距离的增加而减小。无论哪一种高宽比条件下,涡流比对平均切向风速分布和最大值的影响都很明显,且涡核直径(即涡核中心两侧最大平均切向风速的间距)随涡流比的增大而增大。但对于同一涡流比,两种高宽比条件下的结果差异不大。
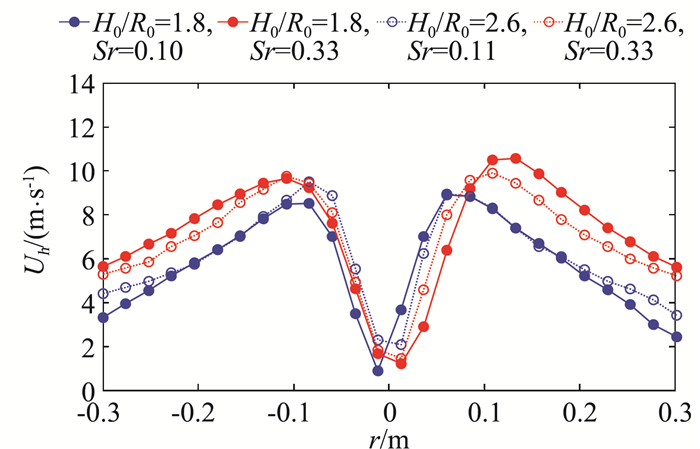
|
图 4 模型高度处平均切向风速分布 Fig.4 Mean tangential wind speed distributions at the model height |
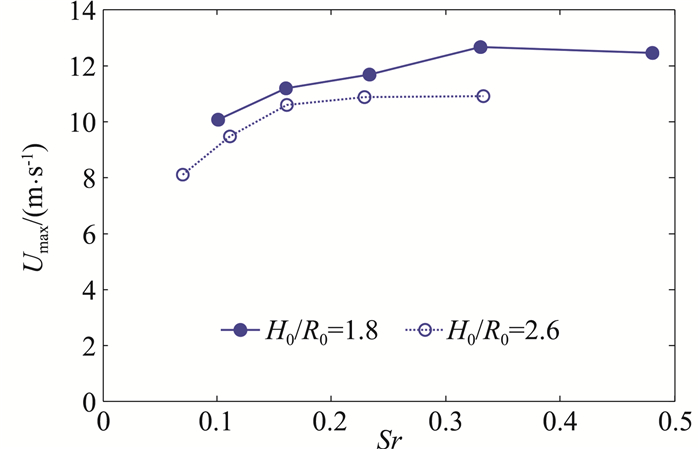
图 5总结了两种高宽比条件下,模拟龙卷风涡旋的整个风场中最大平均切向风速随涡流比的变化规律。当涡流比较小时,最大平均切向风速随涡流比增大而显著增大;当涡流比较大时,最大平均切向风速则不随涡流比变化而变化。而对比同一涡流比下、两种高宽比对应的最大平均切向风速,小高宽比的风速值较大,但两者相差在10%以内。
|
图 5 相似参数对最大平均切向风速的影响 Fig.5 Variation of unfavorable mean tangential wind speeds due to similarity parameters |
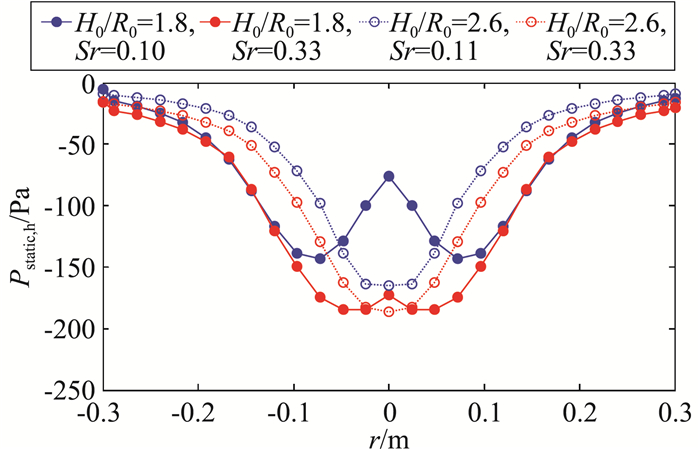
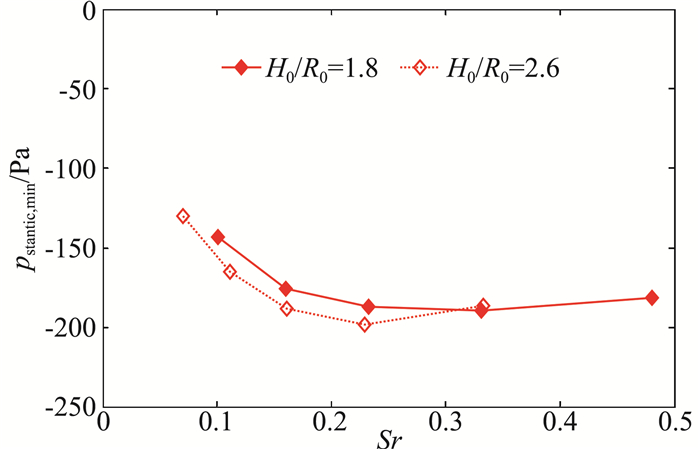
龙卷风造成的涡核中心附近的气压降是龙卷风涡旋的又一典型特征,也是造成结构风致破坏的主要原因之一。图 6对比了四种工况下主梁模型所在高度处(h=0.2 m)气压降均值的水平分布。在两种高宽比下,气压降(绝对值)随着涡流比的增大而增大。而与切向风速类似,高宽比对气压降均值的分布和最大值的影响都较小。针对图 7所示的整个风场中最小平均气压降,当涡流比较小时,最小平均气压降绝对值随涡流比增大而显著增大,也随高宽比增大而增大。两个高宽比下的最小平均气压降相差10%以内。
|
图 6 模型高度处平均气压降分布 Fig.6 Mean pressure drop distributions at the model height |
|
图 7 相似参数对最大平均气压降的影响 Fig.7 Variation of unfavorable mean pressure drops due to similarity parameters |
从主梁模型对应高度处的风场参数如切向平均风速、平均气压降结果来看,影响模拟龙卷风特性的最关键相似参数是涡流比,而高宽比对上述两项指标的影响很小。若针对整个风场中切向平均风速和平均气压降的最不利值,实验中的高宽比对最不利平均气压降和最不利切向平均风速的影响均在10%以内。
3 表面风压分布 3.1 风压系数定义对于实验模型表面第k个测压孔测得的压强pk,将图 5所示风场中最大风速Umax作为参考风速,则各测点k处的无量纲的风压系数Cpk为:
| $ {C_{pk}} = \frac{{{p_k} - {p_0}}}{{\frac{1}{2}\rho U_{\max }^2}} $ | (3) |
式中,p0为不受龙卷风风场影响的静压,约等于0。
3.2 涡核半径处从风场特性可知,切向平均风速和气压降均值的最不利位置分别位于涡核半径和涡核中心处,因此针对主梁表面风压分布和三分力系数等风荷载参数的讨论主要针对这两个最不利位置处的结果。
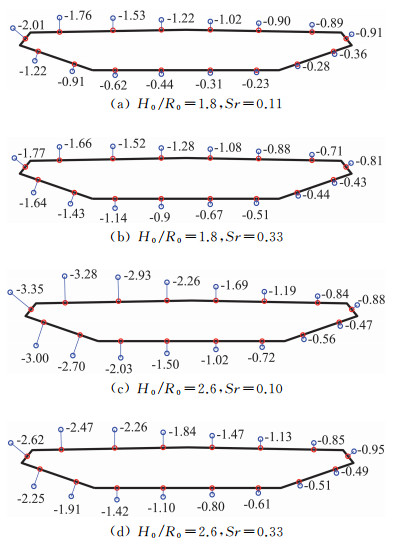
由于龙卷风风场具有明显的三维空间特性,因此,沿实验模型轴向不同断面的表面平均风压分布也不相同,本节以靠近模型中心的最中间一排断面为例进行讨论,其表面风压系数相对于其他断面的值更不利。图 8为两种高宽比和两种涡流比条件下,主梁位于涡核半径处的中间断面表面平均风压分布。与常规风洞桥梁主梁表面风压周向分布有明显区别的是,龙卷风作用下主梁表面平均风压系数均为负值。由于此时涡核中心靠近主梁模型的左侧,主梁表面左侧风压系数绝对值明显大于右侧。从图 8(a)和8(b),以及8(c)和8(d)的对比看,主梁表面平均风压系数的最不利值随涡流比的增大而减小。然而,与涡流比对平均风压系数造成的差别相比,高宽比对其产生的影响更大:涡流比0.1时,最不利平均风压系数分别为:-2.01(H0/R0=1.8)和-3.35(H0/R0=2.6),相差67%;涡流比0.33时,分别为-1.77(H0/R0=1.8)和-2.62(H0/R0=2.6),相差48%。这一差别远大于高宽比对无模型的风场切向风速和气压降带来的影响,说明实验模型与不同高宽比下龙卷风涡旋间的相互作用程度不同,使得高宽比成为桥梁龙卷风荷载模拟的关键相似参数。
|
图 8 涡核半径处主梁表面平均风压系数 Fig.8 Mean pressure coefficients of the deck at the radius of the tornadic vortices |
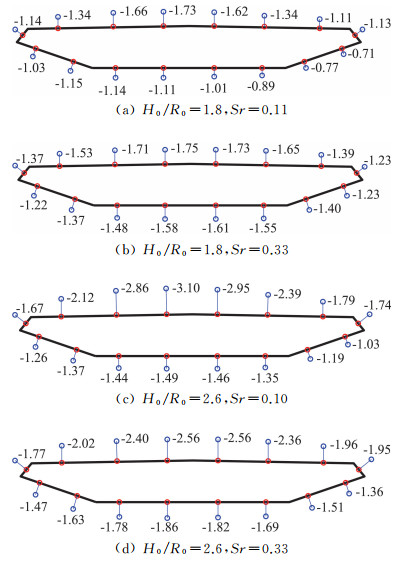
与图 8类似,图 9为两种高宽比和两种涡流比条件下,主梁位于涡核中心处的中间断面表面平均风压分布。由于此时模拟器位于模型正上方,所有工况下主梁表面风压都呈对称分布,且受涡核中心气压降影响,所有平均风压系数均为负值。当高宽比为1.8时,涡流比对主梁上表面影响不大,但会增大下表面平均风压系数,造成整体升力减小;当高宽比为2.6时,随着涡流比的增加,主梁上表面平均风压系数减小、下表面平均风压系数增大,造成整体升力减小。与涡核半径处结果类似,高宽比对平均风压系数最不利值的影响显著:对涡流比0.1的情况相差79%,对涡流比0.33相差46%。
|
图 9 涡核中心处主梁表面平均风压系数 Fig.9 Mean pressure coefficients of the deck at the center of the tornadic vortices |
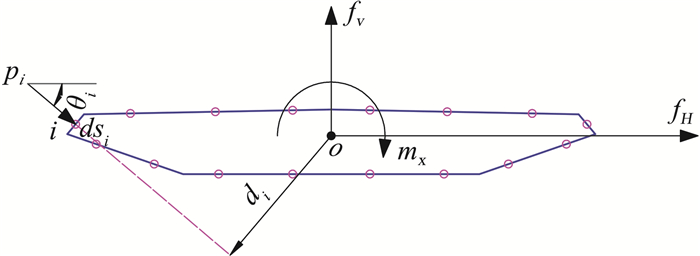
由模型每个设有测压点的断面内所有测点表面压力积分可以确定断面三分力系数:不包括摩擦阻力在内的阻力系数、升力系数和升力矩系数)。如图 10所示,在断面中心O建立坐标系,并取断面的体轴作为z、y轴,设第i个测压孔所在斜面的法线与z轴的夹角为θi,断面中心O与第i个测压孔所在斜面的法线间的垂直距离为di,第i个测压孔附件dsi微元上的压强为pi,则作用在dsi微元上展向单位长度的阻力dfHi,升力dfVi,和升力矩dmxi为:
|
图 10 三分力系数定义 Fig.10 Definition of aerodynamic coefficients |
| $ \left\{ \begin{array}{l} {\rm{d}}{f_{Hi}} = {p_i}{\rm{d}}{s_i}\cos {\theta _i}\\ {\rm{d}}{f_{Vi}} = - {p_i}{\rm{d}}{s_i}\sin {\theta _i}\\ {\rm{d}}{m_{xi}} = - {p_i}{\rm{d}}{s_i}{d_i} \end{array} \right. $ | (4) |
对断面内所有的n个测压孔(n=16)的微元阻力dfHi、微元升力dfVi和微元升力矩dmxi求和,即可到这一断面在展向单位长度上的阻力fH、升力fV和升力矩mx。将风场中的最大风速作为参考风速,则每个断面的三分力系数表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_{fH}} = \frac{{{f_H}}}{{\frac{1}{2}\rho {U_{{{\max }^2}}}D}} = \frac{{\sum\limits_{i = 1}^n {{\rm{d}}{f_{Hi}}} }}{{\frac{1}{2}\rho {U_{{{\max }^2}}}D}}}\\ {{C_{fV}} = \frac{{{f_V}}}{{\frac{1}{2}\rho {U_{{{\max }^2}}}B}} = \frac{{\sum\limits_{i = 1}^n {{\rm{d}}{f_{Vi}}} }}{{\frac{1}{2}\rho {U_{{{\max }^2}}}B}}}\\ {{C_{mx}} = \frac{{{m_x}}}{{\frac{1}{2}\rho {U_{{{\max }^2}}}BD}} = \frac{{\sum\limits_{i = 1}^n {{\rm{d}}{m_{xi}}} }}{{\frac{1}{2}\rho {U_{{{\max }^2}}}BD}}} \end{array}} \right. $ | (5) |
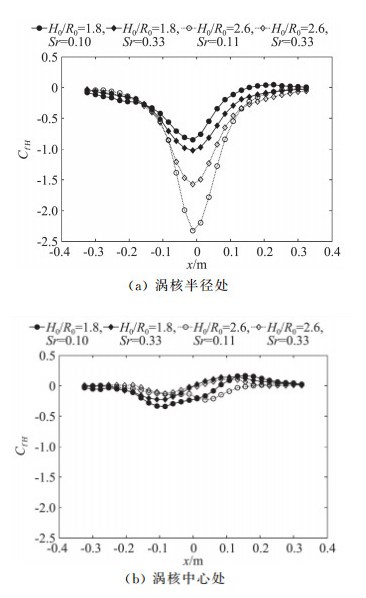
图 11为两种高宽比和两种涡流比条件下,主梁位于涡核半径(图 11(a))和涡核中心处(图 11(b))时各测压断面的平均阻力系数结果,图中横坐标方向为桥梁轴向(x方向)。由于龙卷风涡旋作用偏于主梁一侧,造成主梁在涡核半径处的阻力系数远大于位于涡核中心处的结果。其中,图 11(a)中,大高宽比时的两种涡流比下的平均阻力系数最不利值(发生在模型中间断面,x值接近于0)为小高宽比结果的1.5~2.5倍。这也再次表明高宽比是影响桥梁龙卷风荷载模拟结果的关键相似参数。需要指出,模型两侧测压断面的阻力系数结果接近0,说明此处几乎不受龙卷风涡旋产生的风荷载作用,因此,实验模型测点布置的范围是合理的。
|
图 11 相似参数对主梁断面平均阻力系数的影响 Fig.11 Variation of drag coefficients of the deck due to similarity parameters |
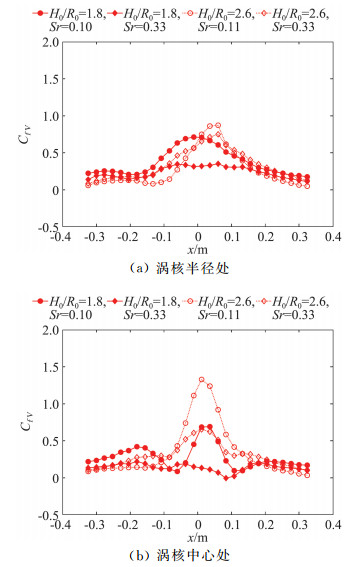
图 12对比了两种高宽比和两种涡流比条件下,主梁位于涡核半径(图 12(a))和涡核中心处(图 12(b))时各测压断面的平均升力系数结果。可以看出,除了高宽比为2.6、涡流比为0.11的情况,主梁在涡核半径处和涡核中心处的平均升力系数区别不大。与平均阻力系数结果类似,各工况下平均升力系数最不利值发生在中间断面附近。涡流比越大,主梁上下表面压力差越小,导致平均升力系数也越小。当主梁位于涡核半径处时,高宽比对平均升力系数的影响不明显;当主梁位于涡核中心处时,平均升力系数随着高宽比的增大而增大。
|
图 12 相似参数对主梁断面升力系数的影响 Fig.12 Variation of lift force coefficients of the deck due to similarity parameters |
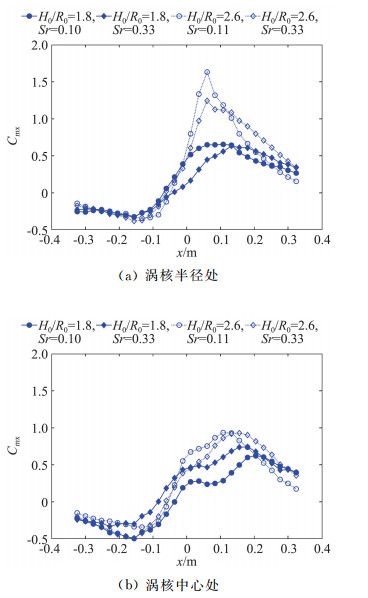
图 13为两种高宽比和两种涡流比条件下,主梁位于涡核半径(图 13(a))和涡核中心处(图 13(b))时各测压断面的平均升力矩系数结果。与阻力系数和升力系数在中间断面取最不利值不同,平均升力矩系数的正、负最不利值出现在距离模型中间断面0.1 m附近。涡流比和高宽比对于平均升力矩系数的影响主要集中在x=0~0.2 m,而对其他部分的断面结果的改变很小。相比于涡流比,高宽比对主梁在涡核半径处的平均升力矩系数影响更为显著,两种高宽比下的最不利值相差近1倍。
|
图 13 相似参数对主梁断面升力矩系数的影响 Fig.13 Variation of pitching moment coefficients of the deck due to similarity parameters |
与基于常规边界层风洞获取结构风荷载的实验手段相比,目前基于龙卷风模拟装置识别结构风荷载的过程还存在诸如气流模拟的实现方式不同、实验关键参数的选取不同、实验流程未统一等影响结构龙卷风荷载物理模拟结果准确性的诸多问题。本文以大跨度桥梁流线型箱梁断面的风荷载特性为实验对象,基于龙卷风模拟装置和刚体模型测压实验方法,探究了涡流比、高宽比等龙卷风涡旋的相似参数对风荷载识别结果的影响,在此基础上讨论了桥梁主梁这一远地面线状水平结构在模拟龙卷风作用下的风荷载特性及其关键相似参数。
1) 相同高宽比条件下,主梁表面平均风压系数和断面三分力系数的最不利值随涡流比的增大而减小。相同涡流比条件下,主梁表面平均风压系数和断面三分力系数的最不利值随高宽比的增大而增大。与高宽比对龙卷风风场特性的影响相比,其对主梁表面风压分布和断面三分力系数的影响要显著的多。高宽比和涡流比是影响桥梁主梁龙卷风荷载的关键相似参数。
2) 模拟龙卷风作用下主梁表面风压分布和断面三分力系数等风荷载特性与常规边界层风洞实验的结果明显不同,其中,主梁表面平均风压系数受龙卷风气压降影响而全部为负值,断面三分力系数沿桥梁轴向变化明显,桥梁风荷载的片条假定不再适用。
3) 除相似参数外,桥梁主梁的风荷载特性还受龙卷风气流中心距离实验模型的相对位置的影响。两者间的相对距离也是实验需要考虑的关键参数。
| [1] |
XUE M, ZHAO K, WANG M, et al. Recent significant tornadoes in China[J]. Adv. Atmos. Sci., 2016, 33(11): 1209-1017. DOI:10.1007/s00376-016-6005-2 |
| [2] |
YANG Q, GAO R, BAI F, et al. Damage to buildings and structures due to recent devastating wind hazards in East Asia[J]. Natural Hazards, 2018, 92(3): 1321-1353. DOI:10.1007/s11069-018-3253-8 |
| [3] |
范雯杰, 俞小鼎. 中国龙卷的时空分布特征[J]. 气象, 2015, 41(7): 793-805. FAN W J, YU X D. Characteristics of spatial-temporal distribution of tornadoes in China[J]. Meteorological Monthly, 2015, 41(7): 793-805. (in Chinese) |
| [4] |
TAMURA Y. Wind-induced damage to buildings and disaster risk reduction[C]//Proc. of 7th Asia-Pacific Conference on Wind Engineering. Taipei, 2009.
|
| [5] |
SENGUPTA A, HAAN F L, SARKAR P P, et al. Transient loads on buildings in microburst and tornado winds[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2008, 96(10): 2173-2187. |
| [6] |
SABAREESH G R, MATSUI M, TAMURA Y. Characteristics of internal pressures and net local roof wind forces on a building exposed to a tornado-like vortex[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 112: 52-57. DOI:10.1016/j.jweia.2012.11.005 |
| [7] |
CASE J, SARKAR P P, SRITHARAN S. Effect of low-rise building geometry on tornado-induced loads[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 133: 124-134. |
| [8] |
WANG J, CAO S, PA NG, W, et al. Experimental study on tornado-induced wind pressures on a cubic building with openings[J]. Journal of Structural Engineering, 2018, 144(2): 04017206. DOI:10.1061/(ASCE)ST.1943-541X.0001952 |
| [9] |
YANG Z, SARKAR P, HU H. An experimental study of a high-rise building model in tornado-like winds[J]. Journal of Fluids & Structures, 2011, 27(4): 471-486. |
| [10] |
CAO S, WANG J, CAO J, et al. Experimental study of wind pressures acting on a cooling tower exposed to stationary tornado-like vortices[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 145: 75-86. DOI:10.1016/j.jweia.2015.06.004 |
| [11] |
WANG J, CAO S, PANG W, et al. Wind-load characteristics of a cooling tower exposed to a translating tornado-like vortex[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2016, 158: 26-36. DOI:10.1016/j.jweia.2016.09.008 |
| [12] |
LIU Z, ZHANG C, ISHIHARA T. Numerical study of the wind loads on a cooling tower by a stationary tornado-like vortex through LES[J]. Journal of Fluids & Structures, 2018, 81: 656-672. |
| [13] |
陈艾荣, 刘志文, 周志勇. 大跨径斜拉桥在龙卷风作用下的响应分析[J]. 同济大学学报(自然科学版), 2005, 33(5): 569-574. CHEN A, LIU Z, ZHOU Z. Tornado effects on large span cable-stayed bridges[J]. Journal of Tongji University (Natural Science), 2005, 33(5): 569-574. DOI:10.3321/j.issn:0253-374X.2005.05.001 (in Chinese) |
| [14] |
CAO B, SARKAR P P. Numerical simulation of dynamic response of a long-span bridge to assess its vulnerability to non-synoptic wind[J]. Engineering Structures, 2015, 84: 67-75. DOI:10.1016/j.engstruct.2014.11.009 |
| [15] |
HAO J, WU T. Tornado-induced effects on aerostatic and aeroelastic behaviors of long-span bridge[C]//Proc. of the 2016 World Congress on Advances in Civil Environmental & Materials Research. Jeju, 2016.
|
| [16] |
HAAN JR F L, SARKAR P P, GALLUS W A. Design, construction and performance of a large tornado simulator for wind engineering applications[J]. Engineering Structures, 2008, 30(4): 1146-1159. DOI:10.1016/j.engstruct.2007.07.010 |
| [17] |
REFAN M, HANGAN H, WURMAN J. Reproducing tornadoes in laboratory using proper scaling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 135: 136-148. DOI:10.1016/j.jweia.2014.10.008 |
| [18] |
CHURCH C R, SNOW J T, BAKER G L, et al. Characteristics of tornado-like vortices as function of swirl ratio:A laboratory investigation[J]. Journal of the Atmospheric Sciences, 1979, 36: 1755-1776. DOI:10.1175/1520-0469(1979)036<1755:COTLVA>2.0.CO;2 |
| [19] |
王锦, 周强, 曹曙阳, 等. 龙卷风风场的试验模拟[J]. 同济大学学报(自然科学版), 2014, 42(11): 1654-1659. WANG J, ZHOU Q, CAO S, et al. Physical study on tornado-like flow based on Tornado Vortex Simulator[J]. Journal of Tongji University (Natural Science), 2014, 42(11): 1654-1659. DOI:10.11908/j.issn.0253-374x.2014.11.004 (in Chinese) |
 2019, Vol. 37
2019, Vol. 37

