为进一步降低太空运输成本和提高运输可靠性,众多国家已开始重点发展可重复使用飞行器。美国、俄罗斯、日本及欧洲多国自20世纪80年代以来已开展了大量研究工作[1, 2],围绕单级入轨(SSTO, Single Stage to Orbit)和两级入轨(TSTO, Two Stage to Orbit)模式分别提出了多种概念方案[3-5]。
两级入轨方案可让已完成工作任务的部件在合适的时刻从系统中分离并返回地面,从而显著减少推进剂消耗量并降低发射成本[6]。在现有技术水平条件下,相比于单级入轨空天飞机,更适合天地往返运输任务。但由于两级入轨方案需考虑空气动力学、防热、结构、推进、轨迹、控制、工程费用等众多因素,且不能直接应用传统火箭或航空飞行器的规模评估方法[7-8],因此在概念设计阶段获得一个相对闭合的方案是非常困难的挑战。
目前,国内外尚未见适合于两级入轨系统的完整概念设计方法公开发表,更没有一个现实的两级入轨飞行器供参考。针对TSTO方案的研究工作主要集中于全系统的规模评估及气动布局选择等方面。在飞行器规模评估研究方面,已开展的研究工作主要分为两类。一类是通过飞行器总体参数的统计数据,利用回归分析方法获得飞行器尺寸和质量间的关系[9-10]。该类研究着重于质量评估,并未考虑飞行器是否具备实际的入轨能力。另一类则是通过能量守恒关系,在一定载荷需求下根据假定的结构质量系数分析推进剂消耗率,从而分析飞行器质量规模[11-12]。该类方法则无法获知飞行器尺寸信息,即无法判断飞行器的有效容积是否可装载需求的推进剂。也有部分工作将两类研究相结合,从地面起飞状态出发,通过浸润面积等尺度参数实现二者的关联[13],验证飞行器规模的可行性[14]。
本文针对水平起降两级入轨可重复使用飞行器系统,使用总体参数回归分析方法获得结构的质量和容积规模,在考虑发动机不同模态性能和飞行器推阻特性的情况下,提出了一种基于运载能力的适用于两级入轨可重复使用飞行器规模评估的逆向分析方法。以此为基础,设计了一种两级入轨方案,并以2 T有效载荷、LEO近地轨道为任务需求,对飞行器尺寸和质量进行了评估,分析了飞行器结构质量与尺寸间的关系,以及推进剂参数、发动机性能和飞行剖面对飞行器规模的影响。本方法为开展两级入轨可重复使用飞行器初步设计提供了理论依据,也有助于对可重复使用运载器总体设计方案开展进一步优化。
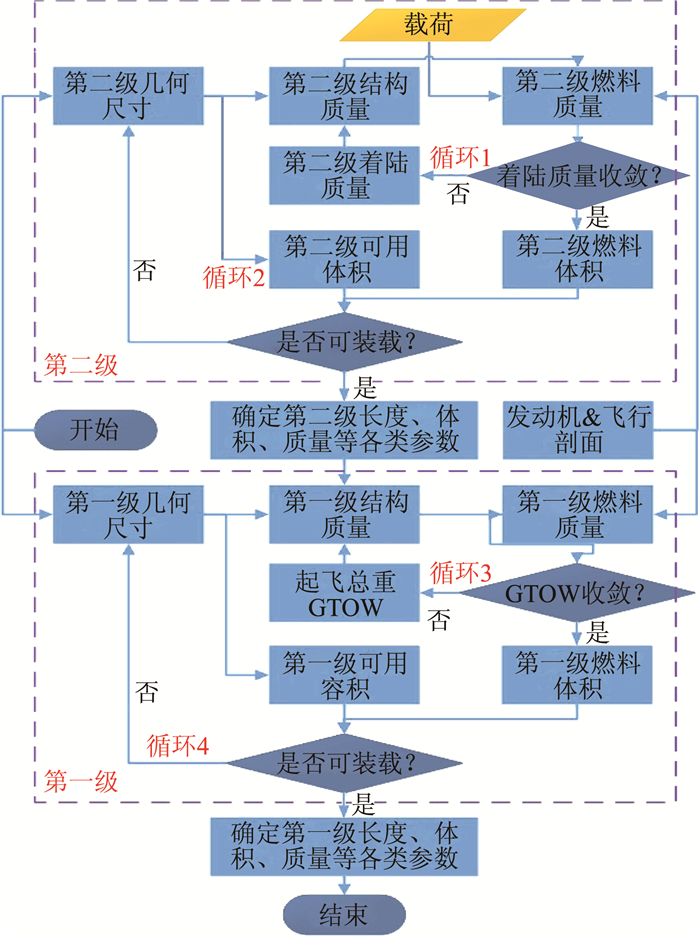
1 系统规模评估方法首先确定飞行任务的载荷质量和载荷体积。根据入轨需求和飞行剖面,从第二级的规模预测出发,建立各级飞行器外形、燃料、动力、结构质量等总体参数间的关联,最终获得具有实际参考意义的两级入轨全系统规模的评估方法。具体步骤包括:
(1) 从基于尺寸的结构质量评估方法出发,获得飞行器第二级结构质量,在计入有效载荷质量的基础上,分析第二级所需推进剂质量。
(2) 根据结构尺寸获知的结构有效容积,判断该容积是否足够装载第二级推进剂和有效载荷,并进行循环迭代,使飞行器有效容积等于推进剂体积和有效载荷体积之和。由此,获得第二级飞行器尺寸和质量规模。
(3) 与步骤(1)类似,采用基于尺寸的结构质量计算方法,获得飞行器第一级的结构质量。在将第二级总质量作为第一级载荷的基础上,分析第一级所需推进剂质量。
(4) 与步骤(2)类似,根据结构尺寸获知的结构有效容积,判断该容积是否足够装载第一级推进剂,并进行循环迭代,使飞行器有效容积等于推进剂体积。由此,获得第一级飞行器尺寸和质量规模。
通常情况下,第一级结构质量计算包括起飞总重(GTOW)参数,第二级结构质量计算包括着陆质量参数。因此,在步骤(1)和步骤(3)的质量计算中也需进行迭代分析,以获得准确的质量数据。
具体流程如图 1所示。
|
图 1 飞行器规模评估方法总体流程 Figure 1 Flow chart of aircraft weight and size estimation method |
下面具体介绍规模评估过程中第一级、第二级质量评估和不同模态的推进剂质量评估方法。
1.1 结构质量计算方法结构质量评估是飞行器概念设计阶段一个非常重要但相对薄弱的环节[8]。目前,飞行器设计部门通常会基于自身已开发飞行器的总体参数数据,利用成熟的回归分析方法推导自己的重量评估公式。本文针对TSTO两级飞行器的结构特点,结合工程实践,形成了如下结构质量评估的关联方法。
1.1.1 第一级结构质量本文主要针对水平起降TSTO可重复使用飞行器开展研究。其第一级需背负大质量第二级飞行器,同时需达到相当的飞行高度和飞行速度。基于此,参照文献[8]和文献[15]选取了包括机身、机翼、垂尾和着陆机构等在内的主要结构质量计算公式:
| $ 机身:{W_{{\rm{body}}}} = 0.383612W_{{\rm{TO}}}^{0.35}N_z^{0.25}{L^{0.5}}{D^{0.849}}{W^{0.685}} $ | (1) |
| $ \begin{array}{l} 机翼:{W_{{\rm{wing}}}} = 0.007145{\left( {{W_{{\rm{TO}}}}{N_z}} \right)^{0.5}}{\rm{S}}_w^{0.622}{A^{0.785}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {t/c} \right)_{{\rm{root}}}^{ - 0.4}{\left( {1 + \lambda } \right)^{0.05}}{\left( {\cos \mathit{\Lambda }} \right)^{ - 1}}{\rm{S}}_{{\rm{scw}}}^{0.04} \end{array} $ | (2) |
| $ \begin{array}{l} 垂尾:{W_{{\rm{tail}}}} = 0.452{\left( {{W_{{\rm{TO}}}}{N_z}} \right)^{0.5}}S_{{\rm{vert}}}^{0.718}M{a^{0.34}}b_{{\rm{vert}}}^{ - 1} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {1 + {S_{{\rm{rud}}}}/{S_{{\rm{vert}}}}} \right)^{0.348}}A{R_{{\rm{vert}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {1 + {R_{{\rm{vert}}}}} \right)^{0.25}}{\left( {\cos {\mathit{\Lambda }_{{\rm{vert}}}}} \right)^{ - 0.323}} \end{array} $ | (3) |
| $ 着陆:{M_{\lg }} = 62.21{\left( {{W_{{\rm{TO}}}} \times {{10}^{ - 3}}} \right)^{0.84}} $ | (4) |
| $ 着陆:{M_{\lg }} = 62.21{\left( {{W_{{\rm{TO}}}} \times {{10}^{ - 3}}} \right)^{0.84}} $ | (5) |
目前,世界上已发展了多型可重复使用航天运载器,也基于总体参数的统计数据形成了运载器各部分结构质量的评估方法。参照文献[16]和文献[17]选取了机身、机翼、垂尾和热防护系统(TPS)等在内的主要结构质量计算公式:
| $ 机身:{M_{{\rm{fuse}}}} = 2.167A_{{\rm{body}}}^{1.075} $ | (6) |
| $ \begin{array}{l} 机翼:\\ {M_{{\rm{wing}}}} = {N_z}{M_{{\rm{land}}}}{\left[ {\frac{1}{{1 + \eta \left( {\frac{{{S_{{\rm{body}}}}}}{{{S_{\exp }}}}} \right)}}} \right]^{0.386}}{\left( {\frac{{{S_{{\rm{exp}}}}}}{{{t_{{\rm{root}}}}}}} \right)^{0.572}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\left[ {{K_{{\rm{wing}}}}b_{{\rm{str}}}^{0.572} + {K_{{\rm{ct}}}}b_{{\rm{body}}}^{0.572}} \right] \end{array} $ | (7) |
| $ 垂尾:{M_{{\rm{tail}}}} = 26.06{\left[ {{S_{{\rm{vert}}}}\left( {\frac{t}{c}} \right)_{{\rm{vert}}}^{0.244}b_{{\rm{vert}}}^{0.0364}} \right]^{0.8674}} $ | (8) |
| $ \begin{array}{l} {\rm{TPS:}}{M_{{\rm{tps}}}} = 1.366{A_{{\rm{body}}}} + 2.845\left( {2{S_{\exp }}} \right) + \\ \;\;\;\;\;\;\;1.572\left( {2{S_{{\rm{vert}}}}} \right) + 3.468\left( {2{S_{{\rm{bf}}}}} \right) + 0.508{A_{{\rm{body}}}} \end{array} $ | (9) |
以上第一级和第二级质量计算公式中,A为展弦比,Abody为机身表面积,ARvert为尾翼展弦比,bstr为半弦长位置机翼展长,bbody为机身最大宽度,bvert为尾翼展长,D为机身高度,L为机身长度,Ma为马赫数,Mland为着陆质量,Nz为极限过载,Sbody为机身投影面积,Sexp为机翼外露面积,Srud为方向舵面积,Sscw为操纵面总面积,Svert为垂尾面积,Sw为梯形机翼面积,Sbf为体襟翼面积,troot为翼根厚度,(t/c)root为翼型相对厚度,W为机身宽度,WTO为起飞质量,λ为机翼尖梢比,Λ为25%MAC机翼后掠角,Λvert为25%MAC垂尾后掠角,Rvert为尾翼锥度比。
以航天飞机为例,可利用上述第二级结构质量计算公式计算得出的各部件质量,如表 1所示。可以看出,各部分结构质量计算值与实际重量吻合良好,相比真实飞行器[18],误差均在8%以内。因此,在TSTO可重复使用运载器的初步设计过程中,该方法可作为结构质量的评估方法。
| 表 1 航天飞机各部件计算质量与相对误差 Table 1 Estimated weight and relative errors for space shuttle components |
|
|
不管使用何种动力形式,飞行器的加速过程均可由牛顿第二定律建立起飞行状态与推进剂消耗之间的关系。用发动机比冲表示推力,可建立飞行器加速运动一般方程:
| $ m\frac{{{\rm{d}}V}}{{{\rm{d}}t}} + mg\sin \gamma = - g{I_{{\rm{sp}}}}\left( {1 - \frac{D}{T}} \right)\frac{{{\rm{d}}m}}{{{\rm{d}}t}} $ | (10) |
式中,m为飞行器质量;V为飞行器速度;T为发动机推力;D为飞行器阻力;g为重力加速度;γ为飞行器爬升角。
记飞行开始时的速度和高度分别为V1和H1,结束时的速度和高度分别为V2和H2。对火箭推进模态,由于飞行器推阻比极大,且火箭发动机在飞行过程中Isp近似恒定,由式(10)积分可得
| $ \mu = \exp \left( {\frac{{\Delta V + \Delta {V_g}}}{{g{I_{{\rm{sp}}}}}}} \right) $ | (11) |
式中,μ为飞行状态前后质量比;ΔV=V2-V1为飞行器速度增量;ΔVg=2g(H2-H1)/(V1+V2)为重力损失量或势能增加量。在不考虑重力损失量ΔVg的情况下,式(11)将变为常见的Tsiolkovsky火箭公式。
对涡喷、亚燃冲压和超燃冲压等吸气式推进模态,飞行器推阻比较小,阻力损失不可忽略,且比冲Isp也不再为常数,采用火箭推进模态的推进剂质量计算方法将不再适宜。本文在式(10)的基础上引入发动机功率TV的概念:
| $ TV = - \eta q\frac{{{\rm{d}}m}}{{{\rm{d}}t}} $ | (12) |
其中,η为发动机热效率;q为燃料热值。将式(12)代入式(10),并写为式(11)的形式有:
| $ \mu = \exp \left( {\frac{{\Delta V + \Delta {V_g}}}{{g{I_{{\rm{eff}}}}}}} \right) $ | (13) |
式中,
| $ {I_{{\rm{eff}}}} = \frac{{2\eta q}}{{g\left( {{V_1} + {V_2}} \right)}}\left( {1 - \frac{D}{T}} \right) $ | (14) |
此时,Ieff可理解为吸气推进模态下燃料的等效比冲。上述推进剂质量计算方法在不同的飞行剖面情况下均可使用,仅需代入不同阶段的速度和高度参数即可。
2 TSTO方案初步设计未来的TSTO可重复使用飞行器的第一级可采用吸气式组合动力,包括TBCC和RBCC,或可重复使用火箭(RR, Reusable Rocket)等,而第二级则由于需要完成入轨飞行,只能采用RR。考虑到燃料经济性和燃料体积因素,两级发动机均适于采用碳氢燃料[19]。基于此,本文对TSTO方案进行了初步设计。
借鉴航天飞机、X-37和X-34等天地往返飞行器的气动布局[20],再考虑到各级飞行器的燃料在飞行器内部的装填,本文借鉴提出了一种两级运载器的气动布局方案。二级采用带边条的小展弦比后掠机翼及单垂尾方案,形成了本文TSTO系统的第二级。第一级同样采用与二级相同长细比的机身结构以获得高容积利用率,机翼部分则根据极大起飞重量及爬升加速等气动性能需求,增大了翼展和翼面面积,并采用翼梢小翼增升并确保横航向安定。作为初步的原理概念设计,先考虑将一级发动机放在机身腹部,并未开展详细设计研究。图 2给出了本文设计的两级入轨飞行器方案。

|
图 2 两级入轨飞行器方案示意图 Figure 2 Schematic diagram of two-stage-to-orbit vehicles |
依据两级不同的推进系统特点和有效比冲概念的推进剂使用效率[14],初步选定高度30 km、马赫数6为级间分离点。而对于最大飞行马赫数6的飞行器,采用TBCC推进系统具有相对较好的经济性。在飞行轨迹低速段,利用涡轮发动机提供动力比利用火箭助推产生的比冲大一个量级[21]。参考TBCC三种工作模态的工作马赫数范围和基本性能特点,参照文献[12]和文献[22]超燃发动机全高度等效比冲等参数,并结合一定的先进系数,初步制定了如表 2所示不同发动机模态的具体工况和性能参数。燃料方面,主要考虑采用液体推进剂。为便于后续的对比分析,这里也同时给出了固体推进剂的相关参数,如表 3所示。
| 表 2 不同发动机模态的具体工况和性能参数 Table 2 Working condition and performance parameters of different engine modes |
|
|
| 表 3 推进剂参数 Table 3 Propeller parameters |
|
|
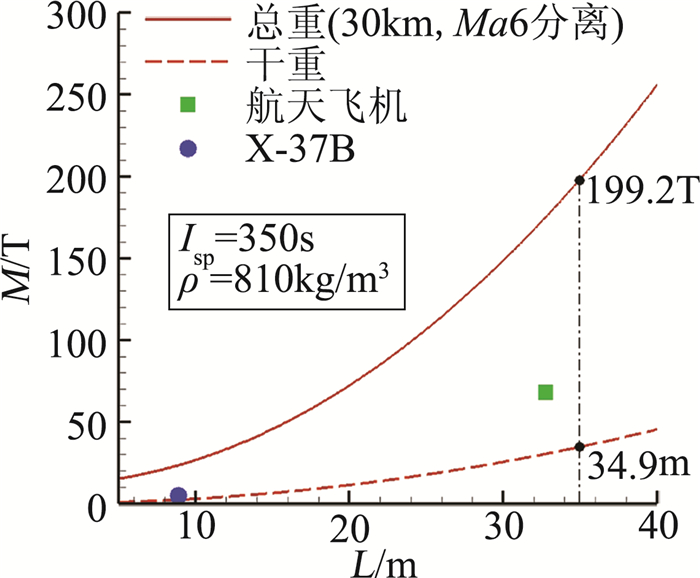
基于设计的高度30 km、马赫数6级间分离和高度100 km、速度7450 m/s入轨条件,首先分析了第二级入轨飞行器结构质量与飞行器外形尺寸间的关系。图 3为飞行器的第二级质量随机身长度变化曲线。从图中可以看出,飞行器质量随机身长度增加呈快速上升趋势。对比航天飞机和X-37B的质量数据,本文设计的类X-34二级布局方案在相同长度上质量略小,这与其机身结构更为细长,翼展和翼面面积更小直接相关,这也表明需要在飞行器质量与飞行器装填空间、飞行器气动特性间进行综合评估。
|
图 3 第二级质量随机身长度变化曲线 Figure 3 Weight curve over body length of stage two |
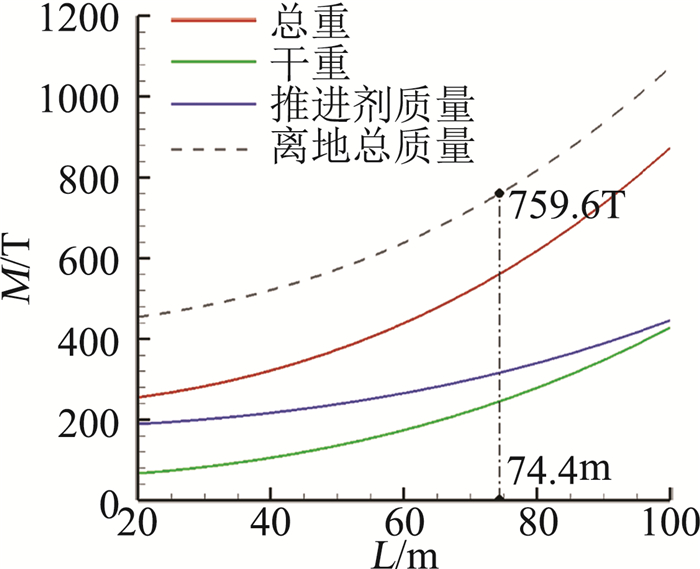
根据本文提出的规模评估流程,第二级在该分离状态下最终确定的参数包括:机身长度35.1 m、总重199.2 T、干重34.9 T、推进剂重量162.4 T。以此为基础,本文继续开展了第一级的规模评估工作。如图 4为飞行器的第一级质量随机身长度变化曲线。从图中可以看出,随机身长度的增加,飞行器结构质量的增长速度相较于推进剂质量的增长更为迅速。根据本评估流程,第一级最终参数为:机身长度74.4 m、起飞总重759.6 T。
|
图 4 第一级质量随机身长度变化曲线 Figure 4 Weight curve over body length of stage one |
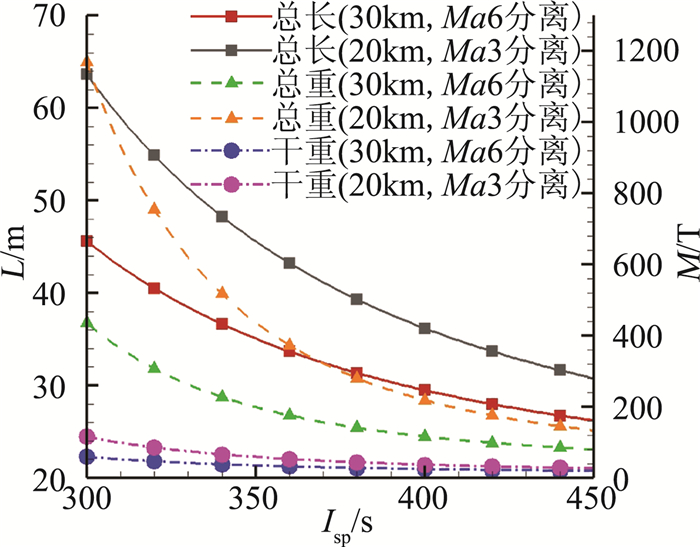
发动机比冲,即单位重量推进剂产生的冲量,是描述推进系统效率的一个重要参数。对于第二级所采用的火箭发动机,直接分析了比冲变化对飞行器第二级规模的影响。图 5和图 6分别为飞行器第二级分别使用液体燃料和固体燃料情况下结构规模随发动机比冲变化的曲线图。从图中可以看出,不管使用液体燃料还是固体燃料,结构质量均随发动机比冲的增大而快速降低。
|
图 5 第二级液体燃料不同比冲参数对结构规模的影响 Figure 5 Influence of different liquid fuel Isp on structure weight and size of stage two |
|
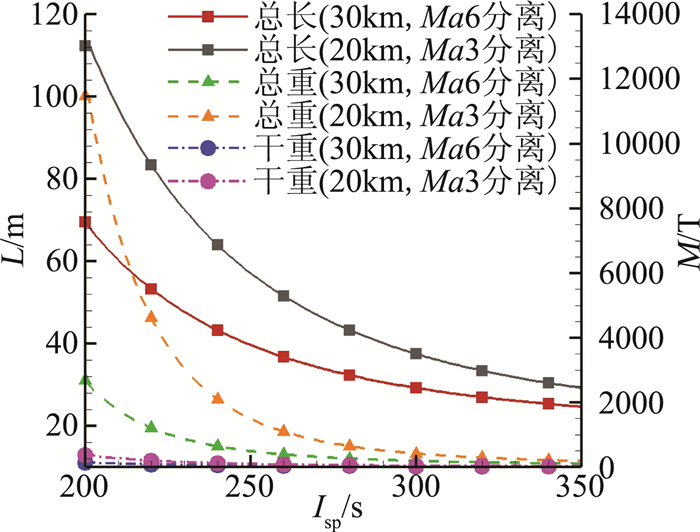
图 6 第二级固体燃料不同比冲参数对结构规模的影响 Figure 6 Influence of different solid fuel Isp on structure weight and size of stage two |
对液体燃料发动机来说,发动机比冲从350 s提高10%至385 s,可使结构长度从35.1 m缩短12.0%至30.9 m,结构干重从34.9 T减小22.6%至27.0 T。而对固体燃料发动机来说,发动机比冲从280 s提高10%至308 s,则可使结构长度从32.3 s缩短12.4%至28.3 s,结构干重从29.6 T减小23.6%至22.6 T。应该说,结构规模缩小的速度比发动机比冲提高的速度更快。因此,提升发动机比冲是控制两级入轨飞行器第二级规模的有效手段。
与此同时,计算比较了两种燃料下第二级结构规模,如表 4所示。采用固体燃料可以获得较小的结构尺寸,但结构重量明显较采用液体燃料高。综合比较两者的具体数值,我们认为在长度参数相差不大的情况下,采用液体推进剂更利于控制第二级总重,对两级入轨飞行器的第一级负担更小,这也是选择液体燃料推进剂的一个重要原因。
| 表 4 不同燃料情况下的飞行器规模 Table 4 Structural weight and size under different fuel |
|
|
对于第一级采用的TBCC发动机来说,本文通过发动机热效率和燃料热值参数引入了发动机功率的概念来描述发动机效率。由此分析了发动机热效率变化对飞行器第一级和整体规模的影响。表 5为TBCC发动机的不同工作模态热效率均在基准值基础上提高或降低5%情况下的飞行器规模分析结果。当发动机热效率提高5%时,机身长度、起飞总重、干重和推进剂质量分别从74.4 m、759.6 T、244.7 T和315.6 T减小到了67.9 m、639.5 T、200.1 T和240.2 T,相对变化为-8.7%、-15.8%、-18.2%和-23.9%。而当发动机热效率降低5%时,机身长度、起飞总重、干重和推进剂质量分别增大至84.1 m、980.8 T、325.6 T和456.0 T,相对变化为+13.0%、+29.1%、+33.1%和+44.5%。应该说,发动机热效率对飞行器结构规模的影响同样显著。
| 表 5 发动机热效率对飞行器规模的影响 Table 5 Influence of engine thermal efficiency on structure weight and size |
|
|
同样的,提高飞行器推阻比也有利于飞行器第一级和整体规模的控制。表 6为发动机不同推阻比对结构规模的影响结果。从表中可以看出,不管通过增大推力或是减小气动阻力的手段,只要能提高飞行器的推阻比参数,均能大幅度缩小第一级的结构规模。实际上,当前TSTO最大的制约因素就是发动机的推进能力与飞行器的阻力及重量间的匹配程度较低。在发动机推进能力有限的情况下,降低飞行器的助力具有十分重要的意义。
| 表 6 发动机推阻比变化对飞行器规模的影响 Table 6 Influence of engine thrust on structure weight and size |
|
|
不同的飞行剖面,即发动机不同模态工作范围的改变也会对结构规模产生影响。表 7为对比计算的三种不同飞行剖面。A方案为原始设计方案,B方案和C方案在此基础上对部分参数进行了调整。其中,B方案增大了涡喷发动机的工作范围,从起飞一直工作到马赫数3.0。C方案则减小了涡喷发动机的工作范围至马赫数2.0即转换为冲压模态。
| 表 7 第一级不同发动机模态的工作范围 Table 7 Working range of different engine modes on stage one |
|
|
表 8为不同方案下的结构规模计算结果。从该结果来看,调整第一级的飞行剖面,对飞行器规模会产生一定影响。但考虑到不同的发动机需要工作在适合的范围内,所以在有限的调整幅度下,它对结构规模的影响也是有限的。因此,在概念设计阶段选取一个固定飞行剖面的方式是适宜的。在概念设计完成后可对飞行剖面及模态转换条件做进一步的优化设计。
| 表 8 不同方案的飞行器规模计算结果 Table 8 Results of weight and size for different schemes |
|
|
本文以飞行任务载荷目标为出发点,在综合考虑飞行器入轨能力、起飞总重、燃料装载能力和总体尺寸的情况下,提出了一种适用于水平起降两级入轨可重复使用飞行器的规模评估分析方法。该方法突破了以往针对两级入轨飞行器的质量评估方法仅将质量和入轨能力联系起来的方式,综合考虑了飞行器内部载荷和燃料的装载能力,可有效降低现有方法的迭代分析工作量,提升方法的实用性。
基于此方法,本文还针对一种两级入轨可重复使用飞行器概念方案,对其尺寸和质量进行了评估。获得了如下几点符合一般概念的定量化结论:(1)发动机效率对飞行器整体规模影响显著,其对质量的影响量远大于发动机效率的改变量;(2)液体燃料在起飞总重方面有优势,在尺寸基本一致的情况下质量轻30%;(3)飞行剖面对飞行器规模影响幅度有限,但根据不同方案间10%~20%的变化量来看,精细化设计仍不容忽视。
本文所建规模评估方法和方案分析结果为进一步开展两级入轨可重复使用飞行器设计奠定了基础。
| [1] |
Han P X, Mu R J, Cui N G, et al. A survey on development of reusable booster vehicle in USA[J]. Missiles and Space Vehicles, 2010(5): 56-61. (in Chinese) 韩鹏鑫, 穆荣军, 崔乃刚, 等. 美国可重复使用助推器发展综述[J]. 导弹与航天运载技术, 2010(5): 56-61. DOI:10.3969/j.issn.1004-7182.2010.05.015 |
| [2] |
Han P X, Cui N G, Mu R J, et al. Survey on development of RBV in Japan and europe[J]. Missiles and Space Vehicles, 2010(4): 31-36. (in Chinese) 韩鹏鑫, 崔乃刚, 穆荣军, 等. 日本与欧洲可重复使用助推飞行器发展综述[J]. 导弹与航天运载技术, 2010(4): 31-36. DOI:10.3969/j.issn.1004-7182.2010.04.007 |
| [3] |
Buffo M. Technical comparison of seven nations' spaceplane programs[C]//AIAA Space Programs and Technologies Conference. Huntsville, 1990.
|
| [4] |
Parkinson R, Webb E. An-225/Hotol[C]//AIAA/DGLR 5th International Aerospace Planes and Hypersonics Technologies Conference. Munich, Germany, 1993.
|
| [5] |
Olds J, Ledsinger L, Bradford J, et al.Stargazer A TSTO Bantam X vehicle concept utilizing rocket based combined cycle propulsion[C]//9th International Space Planes and Hypersonic Systems and Technologies Conference. Norfolk, VA, 1999.
|
| [6] |
Yu M L. A study of the two-stage-to-orbit re-usable launch vehicle scheme[J]. Journal of the Academy of Equipment Command & Technology, 2006, 17(1): 1-5. (in Chinese) 余梦伦. 两级入轨重复使用运载器的方案探讨[J]. 装备指挥技术学院学报, 2006, 17(1): 1-5. DOI:10.3783/j.issn.1673-0127.2006.01.001 |
| [7] |
Sutton G P, Biblarz O. Rocket propulsion elements[M]. 7th ed. New York: John Wiley & Sons, 2001.
|
| [8] |
Nicolai L M, Carichner G E. Fundamentals of aircraft and airship design volume Ⅰ-aircraft design[M]. Reston: American Institute of Aeronautics and Astronautics, 2010.
|
| [9] |
Rohrschneider R R, Olds J R. A comparison of modern and historic mass estimating relationships on a two stage to orbit launch vehicle[C]//AIAA Space 2001-Conference and Exposition. Albuquerque, NMs, 2001.
|
| [10] |
Chen J N, Wang H P, Zhang Y. Research on estimating structural weight for reusable launch vehicle[J]. Aeronautical Computing Technique, 2011, 41(3): 50-54. (in Chinese) 陈江宁, 王和平, 张毅. 可重复使用运载器结构重量估算方法研究[J]. 航空计算技术, 2011, 41(3): 50-54. DOI:10.3969/j.issn.1671-654X.2011.03.013 |
| [11] |
Huang G Q, Nan Y, Lu Y P. The ascent trajectory optimization of Two-Stage-to-Orbit (TSTO) space plane[J]. Journal of Astronautics, 2010, 31(3): 641-647. (in Chinese) 黄国强, 南英, 陆宇平. 二级入轨空天飞机上升轨迹优化[J]. 宇航学报, 2010, 31(3): 641-647. DOI:10.3873/j.issn.1000-1328.2010.03.003 |
| [12] |
Jiang Y Z, Jiang C W, Gao Z X, et al. Mass estimation method and its application for horizontal takeoff horizontal landing two stage to orbit system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 4(40): 473-478. (in Chinese) 姜亚中, 蒋崇文, 高振勋, 等. 水平起降两级入轨系统的质量估算方法及应用[J]. 北京航空航天大学学报, 2014, 4(40): 473-478. |
| [13] |
Chaput A J. Preliminary sizing methodology for hypersonic vehicles[J]. Journal of Aircraft, 1992, 29(2): 172-179. DOI:10.2514/3.46141 |
| [14] |
Joseph M, Hank M E F, Dean R Eklund. TSTO reusable launch vehicles using airbreathing propulsion[C]//42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Sacramento, California, 2006.
|
| [15] |
Wang H P. The overall design of modern aircraft (Chinese-English version)[M]. Xi'an: Northwestern Polytechnical University Press, 1995. (in Chinese) 王和平. 现代飞机总体设计(中英对照)[M]. 西安: 西北工业大学出版社, 1995. |
| [16] |
MacConochie I O, Klich P J. Techniques for the de-termination of mass properties of earth-to-orbit transportation systems[R]. NASA TN-78661. 1978.
|
| [17] |
Raymer, Daniel P. Aircraft design:a conceptual approach[M]. Washington D. C.: American Institute of Aeronautics and Astronautics, 1999.
|
| [18] |
MacConochie I O, Klich P J. Techniques for the determination of mass properties of earth-to-orbit transportation systems[R]. NASA TM-78661, 1978.
|
| [19] |
M. A. Brock M E F. Two-stage-to-orbit reusable launch vehicle propulsion performance study[C]//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Fort Lauderdale, Florida, 2004.
|
| [20] |
Feng Y, Liu S S, Lu F S, et al. Study on a new RLV lifting body concept and its aerodynamic configuration optimization design[J]. Acta Aerodynamica Sinica, 2017, 35(4): 563-571. (in Chinese) 冯毅, 刘深深, 卢风顺, 等. 一种可重复使用天地往返升力体飞行器概念及其气动布局优化设计研究[J]. 空气动力学学报, 2017, 35(4): 563-571. DOI:10.7638/kqdlxxb-2017.0067 |
| [21] |
Barber T A, Maicke B A, Majdalani J. Current state of high speed propulsion-gaps, obstacles and techno-logical challenges in hypersonic applications[C]//45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Denver, Colorado, 2009.
|
| [22] |
Caldwell R A, Franke M E. Weight analysis of TSTO reusable launch vehicles[C]//Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Tucson, Arizona, 2005.
|
 2018, Vol. 36
2018, Vol. 36

