美国在《2030年CFD远景规划》[1]中认为,自适应网格技术和误差估计是复杂流动和复杂几何外形数值模拟的重大瓶颈技术。网格是计算流体力学(CFD)解决复杂外形工程应用的关键,是该学科的重要内容。在网格理论研究方面,除了传统的生成算法外,近些年几何守恒律(Geometric Conservation Law, GCL)问题也受到关注。它直接影响计算结果精度,是解决“误差估计”的基础。
1 几何守恒律的研究现状几何守恒律的概念最早是Thomas和Lombard于1978年在AIAA会议上提出[2],随后在AIAA期刊正式发表[3]。但对几何守恒律问题的研究,最早可见于1961年Trulio和Trigger的工作报告中对一维坐标下“体积守恒(Conservation of Volume)”问题的讨论[4]。
对于笛卡尔坐标系(t, x, y, z)的三维守恒型Euler方程:
| $ \frac{{\partial U}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} + \frac{{\partial H}}{{\partial z}} = 0 $ | (1) |
应用于复杂外形时,需要进行坐标变换,在计算空间中(τ, ξ, η, ζ)形式如下:
| $ \frac{{\partial \hat U}}{{\partial \tau }} + \frac{{\partial \hat F}}{{\partial \xi }} + \frac{{\partial \hat G}}{{\partial \eta }} + \frac{{\partial \hat H}}{{\partial \zeta }} = 0 $ | (2) |
其中:
| $ \hat U = U/J $ |
| $ \hat F = \left( {{\xi _t}U + {\xi _x}F + {\xi _y}G + {\xi _z}H} \right)/J $ |
| $ \hat G = \left( {{\eta _t}U + {\eta _x}F + {\eta _y}G + {\eta _z}H} \right)/J $ |
| $ \hat H = \left( {{\zeta _t}U + {\zeta _x}F + {\zeta _y}G + {\zeta _z}H} \right)/J $ |
对于流动参数为常数的均匀流场,以上方程变成:
| $ \begin{array}{l} {I_t} = \frac{\partial }{{\partial \tau }}\left( {\frac{1}{J}} \right) + \frac{\partial }{{\partial \xi }}\left( {\frac{{{\xi _t}}}{J}} \right) + \frac{\partial }{{\partial \eta }}\left( {\frac{{{\eta _t}}}{J}} \right) + \frac{\partial }{{\partial \zeta }}\left( {\frac{{{\zeta _t}}}{J}} \right)\\ \;\;\; = \frac{\partial }{{\partial \tau }}\left( {\frac{1}{J}} \right) + \frac{{\partial {{\hat \xi }_t}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_t}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_t}}}{{\partial \zeta }} = 0 \end{array} $ | (3) |
这是Thomas针对有限差分法给出的微分形式的GCL方程,但未对此进行深入讨论,因为他们主要关注有限体积法在网格变形时涉及到的GCL问题。对于有限体积法,基于ALE(Arbitrary Lagrange-Euler)描述下的三维Euler方程:
| $ \frac{\partial }{{\partial t}}\iiint\limits_\mathit{\Omega } {Q{\text{d}}\sigma } + \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_{\partial \mathit{\Omega }} {{F_c}\left( {Q,{\mathit{\boldsymbol{x}}_c}} \right) \cdot \mathit{\boldsymbol{n}}{\text{d}}s} = 0 $ | (4) |
其中,Ω为控制体,
| $ \frac{\partial }{{\partial t}}\iiint\limits_\mathit{\Omega } {{\text{d}}\sigma } = \iint\limits_{\partial \mathit{\Omega }} {{\mathit{\boldsymbol{x}}_c} \cdot \mathit{\boldsymbol{n}}{\text{d}}s} $ | (5) |
根据式(5),对于静止网格xc=0,有限体积法不存在GCL问题,即使是运动网格,如果没有变形,式(5)也自动满足。国内采用结构网格与物体刚性固连运动开展动导数研究的文献[5-8]和相关学术专著[9]采纳了以上结论。但是,从本文推导来看,这种结论仅对梯度重构界面通量的有限体积法成立,对于采用有限差分法重构界面通量的高精度格式不一定正确。本文后面的例子表明,所有包含有四边形的网格均存在几何参数计算不相容引入误差的风险。
下面考察有限差分法产生GCL问题的数学本质。推导物理空间(t, x, y, z)的守恒控制方程变换到计算空间(τ, ξ, η, ζ)得到如下原始形式:
| $ \begin{array}{l} \frac{{\partial \hat U}}{{\partial \tau }} + \frac{{\partial \hat F}}{{\partial \xi }} + \frac{{\partial \hat G}}{{\partial \eta }} + \frac{{\partial \hat H}}{{\partial \zeta }}\\ = U\left[ {\frac{\partial }{{\partial \tau }}\left( {\frac{1}{J}} \right) + \frac{\partial }{{\partial \xi }}\left( {\frac{{{\xi _t}}}{J}} \right) + \frac{\partial }{{\partial \eta }}\left( {\frac{{{\eta _t}}}{J}} \right) + \frac{\partial }{{\partial \zeta }}\left( {\frac{{{\zeta _t}}}{J}} \right)} \right] + \\ \;\;\;F\left[ {\frac{\partial }{{\partial \xi }}\left( {\frac{{{\xi _x}}}{J}} \right) + \frac{\partial }{{\partial \eta }}\left( {\frac{{{\eta _x}}}{J}} \right) + \frac{\partial }{{\partial \zeta }}\left( {\frac{{{\zeta _x}}}{J}} \right)} \right] + \\ \;\;\;G\left[ {\frac{\partial }{{\partial \xi }}\left( {\frac{{{\xi _y}}}{J}} \right) + \frac{\partial }{{\partial \eta }}\left( {\frac{{{\eta _y}}}{J}} \right) + \frac{\partial }{{\partial \zeta }}\left( {\frac{{{\zeta _y}}}{J}} \right)} \right] + \\ \;\;\;H\left[ {\frac{\partial }{{\partial \xi }}\left( {\frac{{{\xi _z}}}{J}} \right) + \frac{\partial }{{\partial \eta }}\left( {\frac{{{\eta _z}}}{J}} \right) + \frac{\partial }{{\partial \zeta }}\left( {\frac{{{\zeta _z}}}{J}} \right)} \right]\\ = U{I_t} + F{I_x} + G{I_y} + H{I_z} = 0 \end{array} $ | (6) |
只是在时间和空间导数连续条件下,使用了式(3)及以下恒等式:
| $ \begin{array}{l} {I_x} = \left[ {\frac{{\partial {{\hat \xi }_x}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_x}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_x}}}{{\partial \zeta }}} \right] = 0\\ {I_y} = \left[ {\frac{{\partial {{\hat \xi }_y}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_y}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_y}}}{{\partial \zeta }}} \right] = 0\\ {I_z} = \left[ {\frac{{\partial {{\hat \xi }_z}}}{{\partial \xi }} + \frac{{\partial {{\hat \eta }_z}}}{{\partial \eta }} + \frac{{\partial {{\hat \zeta }_z}}}{{\partial \zeta }}} \right] = 0 \end{array} $ | (7) |
从理论上讲,带有源项的方程(6)才是原始方程(1)的等价形式,但坐标变换系数大多采用网格位置的差分来近似求解,此时恒等式(3)和式(7)可能不成立,在这种情况下方程(2)与方程(1)不等价,把它作为曲线坐标系下的等价形式进行CFD计算,得到的数值解必然存在误差。研究GCL算法的目的是消除由于几何参数计算引起的误差。
在GCL研究领域,把涉及网格变形和时间导数的式(3)称为体积守恒律,把仅有空间导数的式(7)称为面积守恒律[10]。动网格和静网格均须考虑面积守恒律,这点已受到广泛关注,亦是目前GCL研究的主要内容。下面对相关研究文献进行综述。
有限差分法GCL研究可以追溯到CFD应用于复杂外形流场模拟的初期。1977年Steger[11]采用二阶中心格式来计算坐标变换系数,发现即使对均匀来流也存在质量不守恒的现象,后来Hindman[12-13]等人进一步给出了这种误差导致非物理解、引起数值振荡的算例。此后,1978年Steger和Pulliam[14]采用一种加权平均算法计算坐标变换系数,解决了二阶中心格式离散流动方程时遇到的GCL问题。随着高精度格式进入实用阶段,人们发现Steger的算法难以推广,GCL问题重新引起重视。
2002年Visbal和Gaitonde[15]采用与流动方程相同的高阶离散格式计算坐标变换系数,成功解决了高阶紧致格式(CS)的GCL问题。2010年Nonomura等人把Visbal[16]的算法推广到WCNS格式,但是在应用于WENO格式时遇到难题,最后通过修改WENO格式来迎合GCL[17-18]。2011年,为解决紧致类格式的GCL问题,邓小刚分析了构建GCL算法的充分条件,提出坐标变换系数的守恒算法(Conservative Metric Method: CMM)[19],并证明Steger等人的算法是CMM的二阶精度特例,Visbal等人的算法是CMM的高阶精度应用例证,并于2013年从计算几何学角度提出坐标变换系数计算结果唯一的对称守恒算法(Symmetrical Conservative Metric Method, SCMM) [20]。下面对这一算法简单介绍。
引入差分算子符号,一级算子离散流动方程
| $ {{\hat \xi }_x} = {y_\eta }{z_\zeta } - {y_\zeta }{z_\eta } = \delta _\zeta ^2\left[ {\left( {\delta _\eta ^3y} \right)z} \right] - \delta _\eta ^2\left[ {\left( {\delta _\zeta ^3y} \right)z} \right] $ | (8) |
理论上导数乘积满足交换律:yηzζ=zζyη,差商离散以后交换律不再成立。为解决这个离散过程产生出来的问题,Steger等人和Thomas等人引入算子δ3构造对称算法,例如导数yηzζ的差商采用
| $ 0.5\left\{ {\delta _\zeta ^2\left[ {z\left( {{\delta ^3}y} \right)} \right] + \delta _\eta ^2\left[ {y\left( {\delta _\zeta ^3z} \right)} \right]} \right\} $ | (9) |
在δ1取高精度格式,计算时涉及多个网格点位置,式(9)的数值解不同,这种算法不再适用。邓小刚等人把坐标变换系数和六面体几何参数关联起来建立SCMM算法,将坐标变换系数如
| $ \delta _\xi ^1 = \delta _\xi ^2 = \delta _\xi ^3 $ | (10) |
在此基础上构建具有唯一性的SCMM算法。例如
| $ \begin{array}{*{20}{c}} {{{\hat \xi }_x} = 0.5\left\{ {\delta _\zeta ^2\left[ {z\left( {\delta _\eta ^3y} \right)} \right] + \delta _\eta ^2\left[ {y\left( {\delta _\zeta ^3z} \right)} \right] - } \right.}\\ {\left. {\delta _\eta ^2\left[ {z\left( {\delta _\zeta ^3y} \right)} \right] - \delta _\zeta ^2\left[ {y\left( {\delta _\eta ^3z} \right)} \right]} \right\}} \end{array} $ | (11) |
同时还有对J-1的计算要求,这里不再详述。由于紧致格式可写成若干中心格式的组合,因此,按照上面离散坐标变换系数的高阶格式可以表示为几个矢量面积的线性组合,很容易将SCMM推广到高阶精度紧致格式。但是对于其它不满足以上算子条件的高精度格式,很难应用。
关于有限差分下的体积守恒律问题,Abe[21-22]等人借鉴Zhang[28]等人在有限体积框架下对GCL问题所做的工作,通过改变与网格运动相关的坐标变换系数的计算方式,使体积守恒律得到满足。
综上所述,有限差分法的GCL研究现状是,邓小刚等人成功地解决了面积守恒律问题[18-19],Abe等人成功解决了体积守恒律问题,但以上工作都是针对紧致格式等中心格式的,对其它格式缺乏普适性。
2 构造普适性GCL算法的难点前面分析了GCL问题的数学本质,下面通过具体实例讨论在离散过程中几何参数的误差是如何产生的。以二维问题为例,采用中心差分格式计算图 1中(i, j)点坐标变换产生的导数,其中Jocobi行列式为:
| $ \begin{array}{l} J_{i,j}^{ - 1} = {x_\xi }{y_\eta } - {x_\eta }{y_\xi } = \left| {\begin{array}{*{20}{c}} {{x_\xi }}&{{x_\eta }}\\ {{y_\xi }}&{{y_\eta }} \end{array}} \right|\\ \;\;\;\;\; \approx \left| {\begin{array}{*{20}{c}} {\frac{{{x_{i + 1,j}} - {x_{i - 1,j}}}}{{2\Delta \xi }}}&{\frac{{{x_{i,j + 1}} - {x_{i,j - 1}}}}{{2\Delta \eta }}}\\ {\frac{{{y_{i + 1,j}} - {y_{i - 1,j}}}}{{2\Delta \xi }}}&{\frac{{{y_{i,j + 1}} - {y_{i,j - 1}}}}{{2\Delta \eta }}} \end{array}} \right| \end{array} $ | (12) |
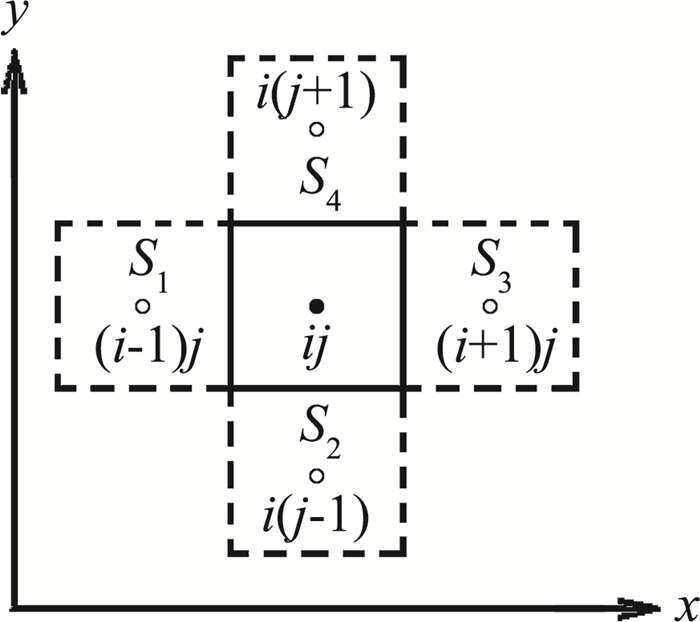
|
图 1 计算空间网格编码 Figure 1 Grid points |
其余系数ξx、ξy、ηx和ηy也可以采用类似的差分格式得到。在计算空间内Δξ=Δη=1,内层差分采用二阶中心差分,外层考虑最简单的一阶迎风格式,对守恒律方程(6)进行数值离散得到:
| $ \left\{ \begin{array}{l} {I_x} = \frac{1}{2}\left[ {\left( {{y_{i + 1,j + 1}} - {y_{i,j + 1}} - {y_{i + 1,j - 1}} + {y_{i,j - 1}}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {\left( {{y_{i + 1,j + 1}} - {y_{i + 1,j}} - {y_{i - 1,j + 1}} + {y_{i - 1,j}}} \right)} \right]\\ {I_y} = \frac{1}{2}\left[ { - \left( {{x_{i + 1,j + 1}} - {x_{i,j + 1}} - {x_{i + 1,j - 1}} + {x_{i,j - 1}}} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {{x_{i + 1,j + 1}} - {x_{i + 1,j}} - {x_{i - 1,j + 1}} + {x_{i - 1,j}}} \right)} \right] \end{array} \right. $ | (13) |
在任意曲线条件下难以保证Ix=0和Iy=0,如果这些参数随空间变化产生的误差不同,即使是均匀流场也无法维持均匀和稳定。
建立SCMM算法时采用三维空间网格,没有讨论不存在δξ3的二维情况。但是沿着SCMM算法思路来定性分析二维问题,对于包含有四边形的网格,如图 2所示,面积的计算有很多选择,先取中点然后按照上面Ji, j-1的形式计算是1种,按照相邻边取矢量至少有4种,在四点不共面的情况下每种算法得到的值不完全相等。按照SCMM算法提出的唯一性要求可以得出如下结论:只要网格包含四边形网格面,均需要关注GCL问题,处理不好会导致几何参数不相容引起的误差。尽管有限差分法和有限体积法两类GCL的方程不同,通过上面算例和分析可以看出,静止结构网格的有限体积法也存在GCL问题。
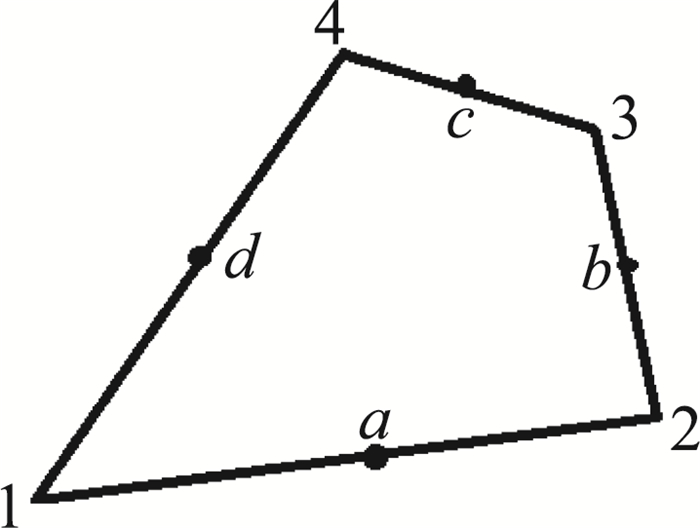
|
图 2 四边形网格的面积计算 Figure 2 Surface of quadrilateral |
对于紧致类格式,按照SCMM算法计算静止网格的面积和体积可以满足GCL,但是,对于建立在迎风格式基础上的带有限制器的高精度格式,建立与流动方程算子δξ1匹配的几何参数算子δξ2非常困难。例如,对于以上式(12),原则上也可以采用一阶迎风格式计算几何参数,但是通量
| $ \hat F_{i + \frac{1}{2},j}^ + = \hat F_{ij}^ + + \frac{1}{2}\min \bmod \left( {\Delta \hat F_{i - \frac{1}{2},j}^ + ,\Delta \hat F_{i + \frac{1}{2},j}^ + } \right) $ | (14) |
由于
对于不变形网格,在二维情况下三角形网格、三维情况下四面体网格,采用单元梯度来构造二阶或者更高精度的,计算过程中不涉及相邻网格的几何参数,有限体积法的几何参数计算表达式唯一且相容,不存在GCL问题。但是对于结构网格基础上的有限体积法,通过式(13)可以看出,如果沿用有限差分法,采用扩展模板的方法来构造高精度格式,同样存在不满足GCL的风险,因此,前述文献关于“不变形结构网格不存在GCL问题”的结论值得进一步讨论。
近两年国内学者在WENO格式的GCL研究方面取得进展[29-30],给出的均匀流场算例结果误差曲线不能保持直线,计算初期变化明显,后期增长变缓。从研究思路看,和SCMM类似,采用调整坐标变换系数的算法来满足GCL,同样面临把系数的解析值代入不一定满足的问题。
3 基于等价方程的GCL补偿算法为了便于理解本文针对有限差分法建立基于修正方程的GCL补偿算法,下面简单介绍非结构变形网格的GCL算法分类和建立GCL算法的思路。
刘君等人对非结构变形网格的GCL进行了研究[23],提出如下观点:GCL方程(5)是流体力学在均匀流场条件下的退化方程,不是理论上必须满足的新约束条件,而不满足GCL产生非物理解的机理是计算过程中体积增量与面积运动形成的体积不等。采用图 3所示网格单元来说明。
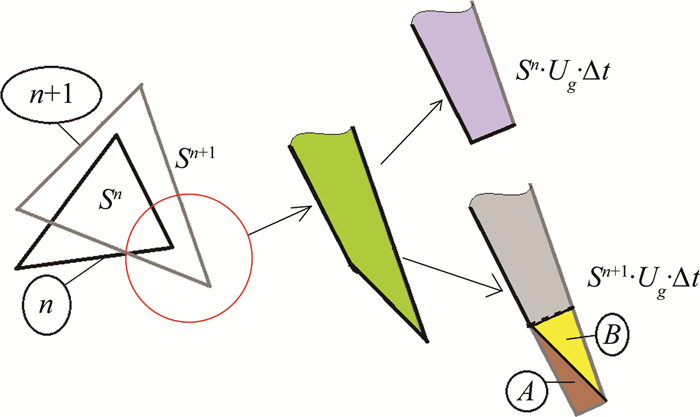
|
图 3 非结构网格几何守恒律机理 Figure 3 GCL for unstructured grids |
假设垂直纸面方向为单位厚度,这样继续采用体积和面积描述几何参数。从tn推进到tn+1时刻,微元体积从Vn变化为Vn+1,其中第i个面Sin以速度ugi运动的同时变形为Sin+1。如果采用显式算法离散方程(5)的右端项,由于Sin运动形成的体积为
| $ \begin{array}{l} {V^{n + 1}} - {V^n} = \Delta V \ne \sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{u}}_{gi}} \cdot {\mathit{\boldsymbol{n}}_i}S_i^n\Delta t} \\ 或\;\Delta V \ne \sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{u}}_{gi}} \cdot {\mathit{\boldsymbol{n}}_i}S_i^{n + 1}\Delta t} \end{array} $ |
通过以上简单模型认识到计算过程中体积增量与面积运动形成体积不等是产生非物理解的机理,以此来考察国内外文献构造的多种GCL算法,本质都是修改右端项使得面积运动形成的体积等于体积增量ΔV。
2015年,Chang等人[24]对现有的有限体积的几何守恒律算法进行了分类,按照误差消除方式的不同,分为带源项的“体积约束方法(Volume Constrained Method,VCM)”和不带源项的“面积约束方法(Face Constrained Method,FCM)”。2016年,根据选择的修正参数的不同,刘君[25]把以上算法进一步细分为四类:
(1) 1978年Thomas等人[1]提出的修正面积的GCL算法,引入平均面积:
| $ S_i^{n + \frac{1}{2}} = 0.5\left( {S_i^n + S_i^{n + 1}} \right) $ | (15) |
这类算法对网格运动速度没有限制,但仅适用于两个时间层的格式。
(2) 1995年Farhat等人[26]构造时间二阶精度隐格式(BDF2)时遇到tn-1和tn+1时刻之间多套网格的GCL问题,提出修正速度的GCL算法。为了满足几何相容,计算过程中每个时间层根据面积计算速度,推导过程复杂,涉及20个参数,增加了计算量。后来2006年Mavriplis等人[27]研究了Farhat算法,发现存在参数不唯一的问题,针对BDF2格式,有些情况下并非全都严格满足几何相容条件,他们提出如下网格运动速度算法:
| $ \mathit{\boldsymbol{u}}_{gi}^ * \cdot \mathit{\boldsymbol{n}} = \frac{{3\Delta V_i^n \cdot \Delta V_i^{n - 1}}}{{2\Delta t \cdot S_i^{n + 1}}},\;\;\;\;\;\;\;\mathit{\boldsymbol{u}}_{gi}^ * \ne {\mathit{\boldsymbol{u}}_{gi}} $ | (16) |
(3) 2004年Zhang等人[28]采用时间两层隐式格式(Crank-Nicolson格式)构造隐式格式,提出同时修正面积和网格速度的算法:
| $ {\mathit{\boldsymbol{u}}_{gi}} \cdot {\mathit{\boldsymbol{n}}_i} = \frac{{\Delta {V_i}}}{{\Delta tS_i^{n + 1}}} $ | (17) |
(4) 2009年刘君[23]基于以上机理认识,提出修正体积的第四类GCL算法。例如对BDF2格式,采用如下体积代替tn+1时刻方程左端项的几何体积Vn+1:
| $ V' = \frac{1}{3}\left( {4{V^{n + 1}} - {V^{n - 1}} + 2\Delta t\sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{u}}_{gi}} \cdot {\mathit{\boldsymbol{n}}_i}S_i^{n + 1}} } \right) $ | (18) |
也可以选择修正其它时间层的体积。
通过以上分类比较,可以看出前三类GCL算法(FCM方法)的思路是修改离散方程右端项中的几何参数来满足方程左端项的体积增量,刘君提出的第四类GCL算法(VCM方法)直接根据方程两侧的几何参数不相容量来消除误差。按照以上思路来分析有限差分法:
(1) 首先,微分形式的GCL方程同样是流体力学控制方程的退化方程,不是理论上必须满足的新约束条件,离散过程后几何参数不相容是GCL的机理;
(2) SCMM算法思路是通过构造坐标变换系数的离散格式满足相容关系式:Ix=Iy=Iz=0,以此来消除曲线坐标系下方程(6)的右端项,类似于有限体积法前三类GCL算法;
(3) 沿着刘君提出的第四类基于有限体积的GCL算法思路,直接通过几何参数不相容量
本文的补偿算法对时间和空间没有区别,尽管目前还没有看到有限差分法变形网格的GCL算法,但是下面讨论中包含
守恒控制方程从物理空间(t, x, y)坐标系变换到计算空间(τ, ξ, η)坐标系的完整形式是:
| $ \frac{{\partial \hat U}}{{\partial \tau }} + \frac{{\partial \hat F}}{{\partial \xi }} + \frac{{\partial \hat G}}{{\partial \eta }} = U{I_t} + F{I_x} + G{I_y} $ | (19) |
前面已经论证过,几何参数的计算格式导致
| $ \frac{{\partial \hat U}}{{\partial \tau }} + \frac{{\partial \hat F}}{{\partial \xi }} + \frac{{\partial \hat G}}{{\partial \eta }} = 0 $ | (20) |
如果不能保证以上GCL恒等式成立,离散以后和原始方程(1)不等价,称为离散近似方程。
引入符号
| $ \begin{array}{l} \hat F = \left[ {F,G} \right] \cdot {\left[ {{{\hat \xi }_x},{{\hat \xi }_y}} \right]^{\rm{T}}} = \mathit{\Phi } \cdot {\mathit{\Gamma }^{\rm{T}}}\\ \hat G = \left[ {F,G} \right] \cdot {\left[ {{{\hat \eta }_x},{{\hat \eta }_y}} \right]^{\rm{T}}} = \mathit{\Phi } \cdot {\mathit{\Pi }^{\rm{T}}} \end{array} $ | (21) |
由于坐标变换系数和流动参数之间不相关,因此,在连续空间求导数,得到如下关系式:
| $ \begin{array}{l} \frac{{\partial \hat F}}{{\partial \xi }} = \mathit{\Phi } \cdot {\left( {\frac{{\partial \mathit{\Gamma }}}{{\partial \xi }}} \right)^{\rm{T}}} + \frac{{\partial \mathit{\Phi }}}{{\partial \xi }} \cdot {\mathit{\Gamma }^{\rm{T}}}\\ \frac{{\partial \hat G}}{{\partial \eta }} = \mathit{\Phi } \cdot {\left( {\frac{{\partial \mathit{\Pi }}}{{\partial \eta }}} \right)^{\rm{T}}} + \frac{{\partial \mathit{\Phi }}}{{\partial \eta }} \cdot {\mathit{\Pi }^{\rm{T}}} \end{array} $ | (22) |
实际上从式(1)到式(2)推导过程中也用到式(22):
| $ \mathit{\Phi } \cdot {\left( {\frac{{\partial \mathit{\Gamma }}}{{\partial \xi }}} \right)^{\rm{T}}} + \mathit{\Phi } \cdot {\left( {\frac{{\partial \mathit{\Pi }}}{{\partial \mu }}} \right)^{\rm{T}}} = F{I_x} + G{I_y} $ |
如果采用相同的算子离散,忽略高阶小量后,式(22)依然成立:
| $ \begin{array}{l} {\delta ^1}\hat F = \mathit{\Phi } \cdot {\left( {{\delta ^1}\mathit{\Gamma }} \right)^{\rm{T}}} + \left( {{\delta ^1}\mathit{\Phi }} \right) \cdot {\mathit{\Gamma }^{\rm{T}}}\\ {\delta ^1}\hat G = \mathit{\Phi } \cdot {\left( {{\delta ^1}\mathit{\Pi }} \right)^{\rm{T}}} + \left( {{\delta ^1}\mathit{\Phi }} \right) \cdot {\mathit{\Pi }^{\rm{T}}} \end{array} $ | (23) |
引入符号
下面按照这个左右两侧格式相同的原则来推导一阶迎风格式的通量分裂:
| $ \begin{array}{l} \hat U_{ij}^{n + 1} = \hat U_{ij}^n - \Delta \tau \left[ {\left( {{{\hat F}^ + }_{ij} - {{\hat F}^ + }_{i - 1,j}} \right) + \left( {\hat F_{i + 1,j}^ - - \hat F_{ij}^ - } \right) + } \right.\\ \left. {\left( {{{\hat G}^ + }_{ij} - {{\hat G}^ + }_{i,j - 1}} \right) + \left( {\hat G_{i,j + 1}^ - - \hat G_{ij}^ - } \right)} \right] + \\ \Delta \tau F_{ij}^ + \left[ {\left( {{{\hat \xi }_x}\left| {_{ij}} \right. - {{\hat \xi }_x}\left| {_{i - 1,j}} \right.} \right) + \left( {{{\hat \eta }_x}\left| {_{ij}} \right. - {{\hat \eta }_x}\left| {_{i,j - 1}} \right.} \right)} \right] + \\ \Delta \tau F_{ij}^ - \left[ {\left( {{{\hat \xi }_x}\left| {_{i + 1,j}} \right. - {{\hat \xi }_x}\left| {_{ij}} \right.} \right) + \left( {{{\hat \eta }_x}\left| {_{i,j + 1}} \right. - {{\hat \eta }_x}\left| {_{ij}} \right.} \right)} \right] + \\ \Delta \tau {G^ + }_{ij}\left[ {\left( {{{\hat \xi }_y}\left| {_{ij}} \right. - {{\hat \xi }_y}\left| {_{i - 1,j}} \right.} \right) + \left( {{{\hat \eta }_y}\left| {_{ij}} \right. - {{\hat \eta }_y}\left| {_{i,j - 1}} \right.} \right)} \right] + \\ \Delta \tau G_{ij}^ - \left[ {\left( {{{\hat \xi }_y}\left| {_{i + 1,j}} \right. - {{\hat \xi }_y}\left| {_{ij}} \right.} \right) + \left( {{{\hat \eta }_y}\left| {_{i,j + 1}} \right. - {{\hat \eta }_y}\left| {_{ij}} \right.} \right)} \right] \end{array} $ | (24) |
按照式(23)展开计算方程(24)中的分裂格式,以其中一项为例:
| $ \begin{array}{*{20}{c}} {\hat F_{i - 1,j}^ + = \hat F_{ij}^ + - {{\hat \xi }_x}\left| {_{ij}} \right.\left( {F_{ij}^ + - F_{i - 1,j}^ + } \right) - {{\hat \xi }_y}\left| {_{ij}} \right.\left( {G_{ij}^ + - G_{i - 1,j}^ + } \right) - }\\ {F_{ij}^ + \left( {{{\hat \xi }_x}\left| {_{ij}} \right. - {{\hat \xi }_x}\left| {_{i - 1,j}} \right.} \right) - G_{ij}^ + \left( {{{\hat \xi }_y}\left| {_{ij}} \right. - {{\hat \xi }_y}\left| {_{i - 1,j}} \right.} \right)} \end{array} $ |
整理后写为:
| $ \begin{array}{l} \left( {\hat F_{ij}^ + - \hat F_{i - 1,j}^ + } \right)\\ - F_{ij}^ + \left( {{{\hat \xi }_x}\left| {_{ij}} \right. - {{\hat \xi }_x}\left| {_{i - 1,j}} \right.} \right) - G_{ij}^ + \left( {{{\hat \xi }_y}\left| {_{ij}} \right. - {{\hat \xi }_y}\left| {_{i - 1,j}} \right.} \right)\\ \;\; = {{\hat \xi }_x}\left| {_{ij}} \right.\left( {F_{ij}^ + - F_{i - 1,j}^ + } \right) + {{\hat \xi }_y}\left| {_{ij}} \right.\left( {G_{ij}^ + - G_{i - 1,j}^ + } \right)\\ \;\; = \hat F_{ij}^ + - \left( {{{\hat \xi }_x}\left| {_{ij}} \right.F_{i - 1,j}^ + + {{\hat \xi }_y}\left| {_{ij}} \right.G_{i - 1,j}^ + } \right)\\ \;\; = \hat F_{ij}^ + - \tilde F_{i - 1,j}^ + \end{array} $ | (25) |
这样一来,补偿源项以后的修正方程的一阶迎风格式可以变成如下简洁形式:
| $ \begin{array}{l} \hat U_{ij}^{n + 1} = \hat U_{ij}^n - \Delta \tau \left[ {\left( {\hat F_{ij}^ + - \tilde F_{i - 1,j}^ + } \right) + \left( {\tilde F_{i + 1,j}^ - - \hat F_{ij}^ - } \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\hat G_{ij}^ + - \tilde G_{i,j - 1}^ + } \right) + \left( {\tilde G_{i,j + 1}^ - - \hat G_{ij}^ - } \right)} \right] \end{array} $ | (26) |
上式与原始方程的一阶迎风格式比较,只是把所有离散点的坐标变换系数换成(i, j)点的参数。从前面对基于梯度重构的有限体积法在静止网格上没有GCL误差的机理分析,本文提出的基于修正方程的GCL补偿算法,尽管初始离散中包含有相邻点的坐标变换系数,但是最终形式和计算过程中不受相邻点的坐标变换系数影响,二者的思路是一致的。
进一步按照以上思路同样可以处理有限差分法的体积几何守恒律。对于
| $ \begin{array}{l} \hat U_{ij}^{n + 1} = \hat U_{ij}^n + \Delta \tau U\frac{\partial }{{\partial \tau }}\left( {\frac{1}{J}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\Delta \tau \left[ {\left( {\hat F_{ij}^ + - \tilde F_{i - 1,j}^ + } \right) + \left( {\tilde F_{i + 1,j}^ - - \hat F_{ij}^ - } \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\;\;\;\left( {\hat G_{ij}^ + - \tilde G_{i,j - 1}^ + } \right) + \left( {\tilde G_{i,j + 1}^ - - \hat G_{ij}^ - } \right)} \right] \end{array} $ | (27) |
由于对一阶显式时间推进
| $ \left\{ \begin{array}{l} \hat U_{ij}^{n + 1} = \left( {\frac{U}{J}} \right)_{ij}^{n + 1},\hat U_{ij}^n = \left( {\frac{U}{J}} \right)_{ij}^n\\ \Delta \tau U_{ij}^n\frac{\partial }{{\partial \tau }}{\left( {\frac{1}{J}} \right)_{ij}} = U_{ij}^n\left[ {\left( {\frac{1}{J}} \right)_{ij}^{n + 1} - \left( {\frac{1}{J}} \right)_{ij}^n} \right] \end{array} \right. $ | (28) |
式(27)可进一步简化为:
| $ \begin{array}{l} U_{ij}^{n + 1} = U_{ij}^n - \Delta \tau \left[ {\left( {\hat F_{ij}^ + - \tilde F_{i - 1,j}^ + } \right) + \left( {\tilde F_{i + 1,j}^ - - \hat F_{ij}^ - } \right) + } \right.\\ \;\;\;\;\;\;\;\left. {\left( {\hat G_{ij}^ + - \tilde G_{i,j - 1}^ + } \right) + \left( {\tilde G_{i,j + 1}^ - - \hat G_{ij}^ - } \right)} \right] \end{array} $ | (29) |
以上是针对一阶格式进行推导的,随后,我们针对空间二阶迎风格式及Runge-Kutta等高阶时间精度格式也进行了推导,公式同样成立。但尚未对隐式时间格式进行推导证明。
4 验证算例目前大家对GCL问题的研究大多基于高精度格式,实际上最早的GCL是为了消除均匀流场在曲线坐标系下计算时出现的因网格计算引起的误差问题。因此,对GCL问题,有效的验证算例应该是均匀流场问题。对于均匀流场问题,流场参数导数为0,因此高精度格式和一阶格式的表现是一样的,如果一阶格式出现GCL误差,高精度格式只能减小误差,不能消除,如果一阶格式没有出现GCL误差,则证明网格是均匀网格,高精度格式也应该没有误差。综上,本文选择采用一阶格式计算均匀流场问题作为验证算例。
为消除边界条件的影响,计算区域取为0≤x≤5, 0≤y≤5,共501×501个网格点,其中有效显示区域为2≤x≤3, 2≤y≤3,为非均匀网格,如图 4所示,剩余区域均为均匀网格。图 4中网格中心的圆半径为0.1 2,网格以网格坐标标号为变量生成。
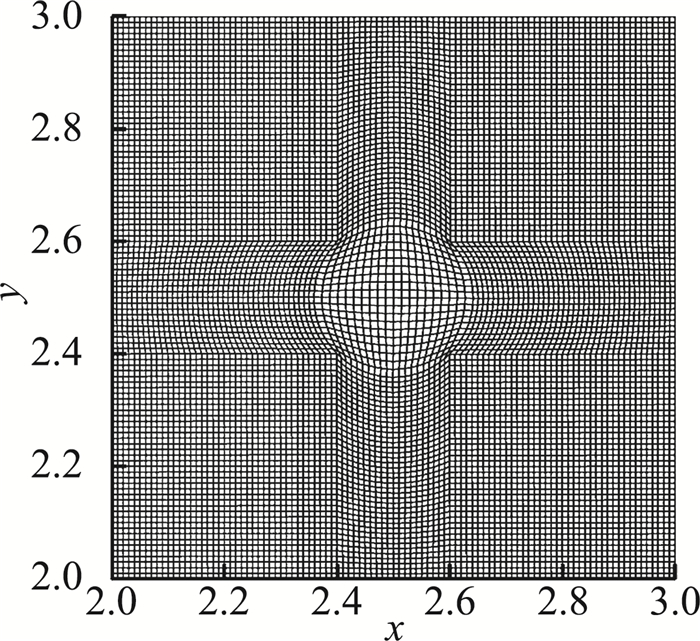
|
图 4 网格示意图 Figure 4 Grids for uniform flow |
计算初始条件设为(ρ, u, v, p)=(1, u, 0, 1),其中u=c·Ma。在计算中,声速
上下边界条件为固壁,左右边界条件是基于Riemann问题求解的进、出口边界。
控制方程分别采用离散近似方程式(20)与离散等价方程式(19),并分别记为方法一与方法二。两种计算方法皆分别采用包含FDS及FVS在内的AUSM、HLLC、Roe、VanLeer四种格式计算,这四种格式都是CFD常用的基础格式。
对四种格式AUSM、HLLC、Roe、VanLeer,以ξ方向为例,对流通量导数及半点重构式(30)进行求解:
| $ \begin{array}{l} \left\{ \begin{array}{l} {\left( {\frac{{\partial \hat F}}{{\partial \xi }}} \right)_i} = \frac{{{{\hat F}_{i + \frac{1}{2}}} - {{\hat F}_{i - \frac{1}{2}}}}}{{\Delta \xi }},\;\;\;\;方法一\\ {\left( {\frac{{\partial \hat F}}{{\partial \xi }}} \right)_i} = \frac{{{{\tilde F}_{i + \frac{1}{2}}} - {{\tilde F}_{i - \frac{1}{2}}}}}{{\Delta \xi }},\;\;\;\;方法二 \end{array} \right.\\ U_{i + \frac{1}{2}}^L = {U_i},\;\;\;\;U_{i + \frac{1}{2}}^R = {U_{i + 1}} \end{array} $ | (30) |
其中,
对不同马赫数Ma,计算非均匀网格图 4上的均匀流场问题,方法一计算结果密度误差云图如图 5至图 8所示,而方法二计算误差全为0,故在此不再显示。
|
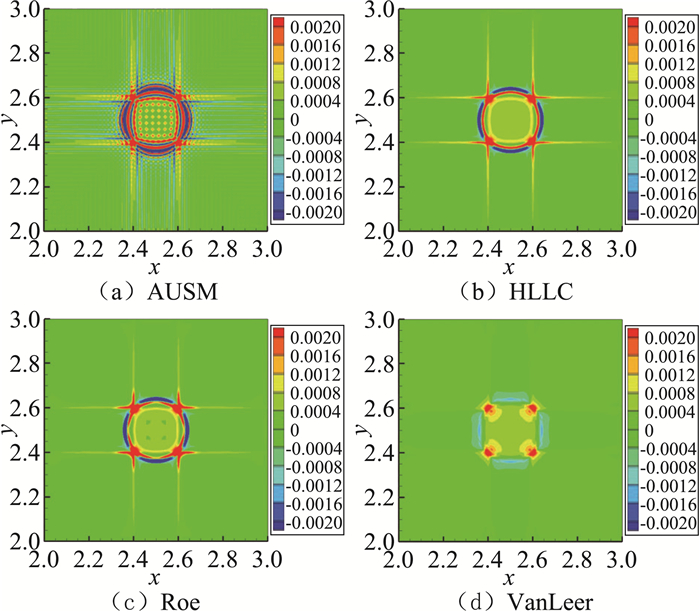
图 5 Ma=0.0时方法一计算密度误差云图 Figure 5 Error distributions of density(Ma=0.0) |
|
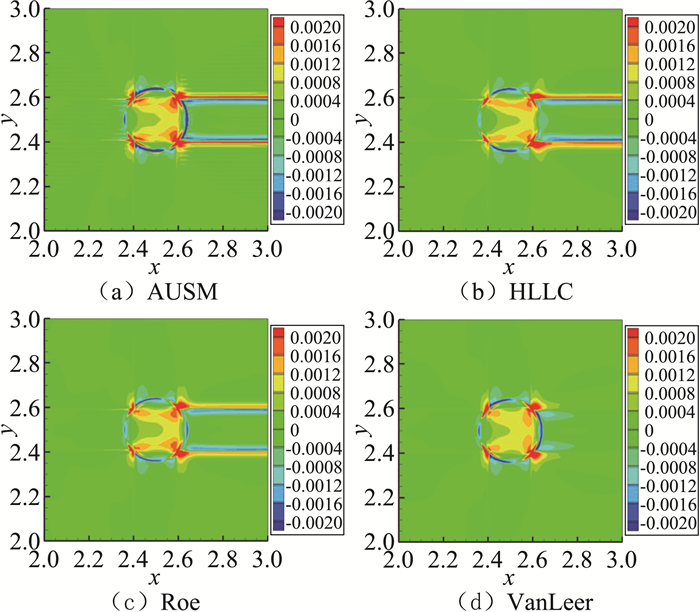
图 6 Ma=0.9时方法一计算密度误差云图 Figure 6 Error distributions of density(Ma=0.9) |
|
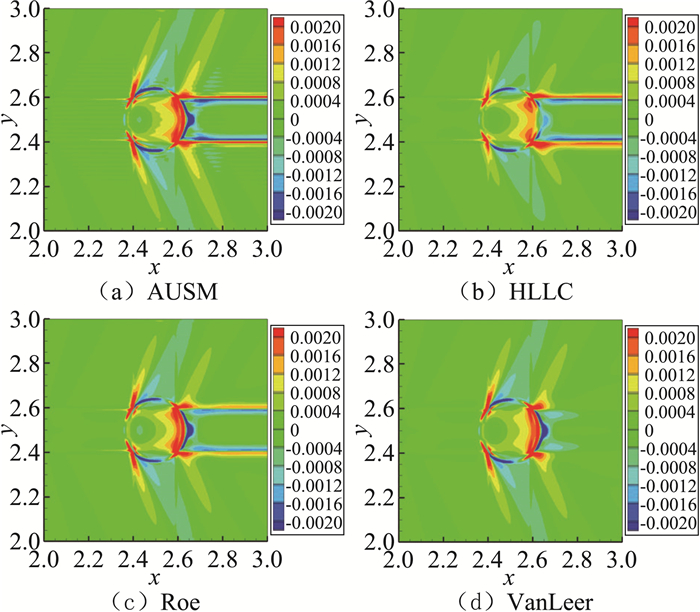
图 7 Ma=1.1时方法一计算密度误差云图 Figure 7 Error distributions of density(Ma=1.1) |
|
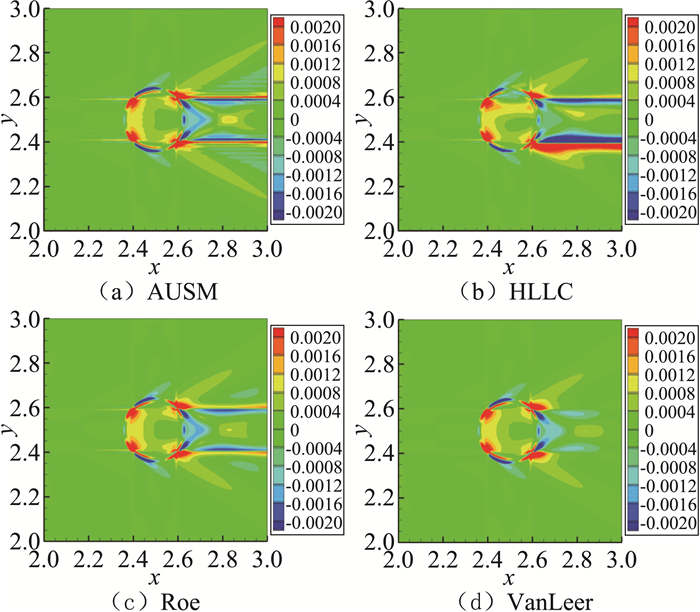
图 8 Ma=2.0时方法一计算密度误差云图 Figure 8 Error distributions of density(Ma=2.0) |
由图 5至图 8可以看出,在马赫数为0时,虽然四种格式计算的误差各不相同,但都集中在网格中心圆周围,因此处网格尺度变化最大,且正交特性最差。随着马赫数的增加误差向下游传播,直到马赫数Ma>1,误差沿着马赫锥方向向下游传播。
四种格式中,HLLC格式与Roe格式密度误差云图分布最为相似,这是因为这两种格式都是基于近似Riemann解的思路提出的。但在进入超声速后,两者的区别越来越明显,这是因为对Riemann问题,Roe格式认为间断的左右状态之间形成的是激波,通过构造一个中间状态来模拟计算;HLLC格式则认为间断的左右状态之间存在接触间断,通过构造两个中间状态来进行计算,更能够精确地模拟接触间断。
对运动网格,设计网格运动情况如图 9所示,网格以图 4为基准,如图 9所示进行每一时间步为5°的左右旋转周期运动,正向最大旋转角度为顺时针旋转30°,如图 9(a)所示,反向最大旋转角度为逆时针旋转30°,如图 9(b)所示。

|
图 9 运动网格示意图 Figure 9 Moving and deforming grids for uniform flow |
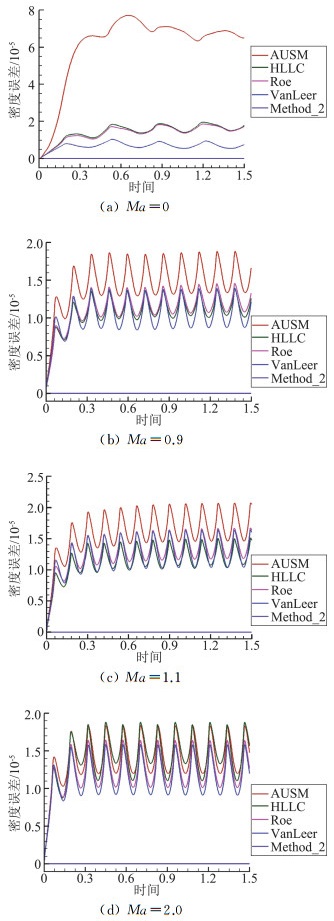
同样针对不同马赫数、四种格式下方法一及方法二计算结果密度误差绝对值的变化曲线如图 10所示。由于方法二计算密度误差在四种格式下全为0,所以将四条曲线合为一条,以Method_2表示。
|
图 10 动网格下密度误差曲线 Figure 10 Density errors varies with time |
图 10所示的误差曲线,每一时间点的误差值是图 4及图 9所示区域所有点的误差绝对值的平均值。由图 10可以看出,方法一在四种格式下计算动网格上的均匀流,均存在误差,其中仍然是HLLC格式与Roe格式的计算结果最为接近。然后随着马赫数的逐渐增大,四种格式对误差的计算结果也逐渐靠近。但对于方法二,不论采用何种格式,误差总为0,因此可以用Method_2一条曲线表示。
5 结论通过理论推导和数值研究,得到如下结论:
(1) 由于离散条件下坐标变换恒等式不再成立,导致目前CFD领域广泛使用的曲线贴体坐标系下基本方程与直角坐标系下原始方程可能不等价。等价方程应该带有源项,由此提出离散等价方程概念。通过分析源项的产生机理,提出离散等价方程左右两侧格式需要满足的准则。
(2) 在准则指导下,根据坐标变换系数和流动参数之间呈线性关系的特点,提出新的耦合算法,并且采用算子理论进行证明。这种从经典CFD角度看属于冻结系数降低精度的算法,对于离散等价方程是保持格式精度并满足几何守恒律的。
(3) 一阶迎风格式数值算例表明,新的几何守恒律算法对坐标变换系数没有要求,可以直接使用准确的解析解,适合于FDS和FVS通量分裂格式。原则上算子理论推导出来的结论与具体格式无关,但用于高精度格式的效果还需要验证。
| [1] |
Slotnick J, Khodadoust A, Alonso J, et al. CFD vision 2030 study: a path to revolutionary computational aerosciences[R]. NASA CR-2014-218178.
|
| [2] |
Thomas P D, Lombard C K. The geometric conservation law-a link between finite-difference and finite-volume methods of flow computation on moving grids[R]. AIAA 1978-1208. doi: 10.2514/6.1978-1208
|
| [3] |
Thomas P D, Lombard C K. Geometric conservation law and its application to flow computations on moving grids[J]. American Instkute of Aeronautics and Astronautics Joumal, 1979, 17(10): 1030-1037. DOI:10.2514/3.61273 |
| [4] |
Trulio J G, Trigger K R. Numerical solution of the one-dimensional Lagrangian hydrodynamic equations[R]. Lawrence Radiation Laboratory, UCRL-6267, 12679461, 1961.
|
| [5] |
Yang Y J, Cui E J, Zhou W J. Numerical research on rock characteristic about a slender delta-wing[J]. Acta Aerodynamica Sinica, 2007, 25(1): 34-44. (in Chinese) 杨云军, 崔尔杰, 周伟江. 细长三角翼摇滚运动数值研究[J]. 空气动力学学报, 2007, 25(1): 34-44. DOI:10.3969/j.issn.0258-1825.2007.01.007 |
| [6] |
Yang Y J, Cui E J, Zhou W J. Numerical research on roll and sideslip coupling motions about a slender delta-wing[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(1): 14-19. (in Chinese) 杨云军, 崔尔杰, 周伟江. 细长三角翼滚转/侧滑耦合运动数值研究[J]. 航空学报, 2007, 28(1): 14-19. DOI:10.3321/j.issn:1000-6893.2007.01.002 |
| [7] |
Han B, Xu M, Li G N, et al. Comparative research on the dynamic rolling characteristic od double delta wing and wing-body configuration[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 417-426. (in Chinese) 韩冰, 徐敏, 李广宁, 等. 双三角翼及其翼身组合的滚转运动特性比较研究[J]. 航空学报, 2014, 35(2): 417-426. DOI:10.7527/S1000-6893.2013.0246 |
| [8] |
Liu W. Nonlinear dynamics analysis for mechanism of slendar wing rock and study of numerical simulation method[D]. Changsha: National University of Defense Technology, 2004. (in Chinese) 刘伟.细长机翼摇滚机理的非线性动力学分析及数值模拟方法的研究[D].长沙: 国防科技大学, 2004. http://cdmd.cnki.com.cn/Article/CDMD-90002-2005144377.htm |
| [9] |
Yan C. Computational fluid mechanics method and its application[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2006. (in Chinese) 阎超. 计算流体力学方法及应用[M]. 北京: 北京航空航天大学出版社, 2006. |
| [10] |
Zhang H, Reggio M, Trepanier J Y, et al. Discrete form of the GCl for moving meshes and its implementation in CFD schemes[J]. Computers and Fluids, 1993, 22(1): 9-23. DOI:10.1016/0045-7930(93)90003-R |
| [11] |
Steger J L. Implicit finite difference simulation of flow about arbitrary geometrics with application to airfoils[R]. AIAA 1977-665.
|
| [12] |
Richard G H. Geometrically induced errors and their relationship to the form of the governing equations and the treatment of generalized mappings[R]. AIAA 1981-1008.
|
| [13] |
Richard G H. Generalized coordinate forms of governing fluid equations and associated geometrically induced errors[J]. American Institute of Aeronautics and Astronautics Journal, 1982, 20(10): 1359-1367. DOI:10.2514/3.51196 |
| [14] |
Steger J L. Implicit finite difference simulation of flow about arbitrary two-dimensional geometrics with application to airfoils[J]. American Instkute of Aeronautics and Astronautics Joumal, 1978, 16(7): 679-686. DOI:10.2514/3.7377 |
| [15] |
Visbal M R, Gaitonde D V. ON the use of higher-order finite-difference schemes on curvilinear and deforming meshes[J]. Journal of Computational Physics, 2002, 181: 155-185. DOI:10.1006/jcph.2002.7117 |
| [16] |
Nonomura T, Iizuka N, Fujii K. Free-stream and vortex preservation properties of high-order WENO and WCNS on curvilinear grids[J]. Computers and Fluids, 2010, 39: 197-214. DOI:10.1016/j.compfluid.2009.08.005 |
| [17] |
Nonomura T, Terakado D, Abe Y, et al. A new technique for finite difference WENO with geometric conservation law[R]. AIAA 2013-2569. doi: 10.2514/6.2013-2569
|
| [18] |
Nonomura T, Terakado D, Abe Y, et al. A new technique for freestream preservation of finite-difference WENO on curvilinear grid[J]. Computers & Fluids, 2015, 107: 242-255. DOI:10.1016/j.compfluid.2014.09.025 |
| [19] |
Deng X G, Mao M L, Tu G H, et al. Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2011, 230: 1100-1115. DOI:10.1016/j.jcp.2010.10.028 |
| [20] |
Deng X G, Min Y B, Mao M L, et al. Further studies on geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2013, 239: 90-111. DOI:10.1016/j.jcp.2012.12.002 |
| [21] |
Abe Y, Iizuka N, Nonomura T, et al. Conservative metric evaluation for high-order finite difference schemes with the GCL identities on moving and deforming grids[J]. Journal of Computational Physics, 2013, 232: 14-21. DOI:10.1016/j.jcp.2012.08.031 |
| [22] |
Abe Y, Iizuka N, Nonomura T, et al. Geometric interpretations and spatial symmetry property of metrics in the conservative form for high-order finite-difference schemes on moving and deforming grids[J]. Journal of Computational Physics, 2014, 260: 163-203. DOI:10.1016/j.jcp.2013.12.019 |
| [23] |
Liu J, Bai X Z, Zhang H X, et al. Discussion about GCL for deforming grids[J]. Aeronautical Computing Technique, 2009, 36(4): 1-5. (in Chinese) 刘君, 白晓征, 张涵信, 等. 关于变形网格"几何守恒律"概念的讨论[J]. 航空计算技术, 2009, 36(4): 1-5. DOI:10.3969/j.issn.1671-654X.2009.04.001 |
| [24] |
Chang X H, Ma R, Zhang L P, et al. Further study on the geometric conservation law for finite volume method on dynamic unstructured mesh[J]. Computers & Fluids, 2015, 120(5): 98-110. |
| [25] |
Liu J, Liu Y, Chen Z D. Unstructured deforming mesh and discrete geometric conservation law[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(8): 2395-2407. (in Chinese) 刘君, 刘瑜, 陈泽栋. 非结构变形网格和离散几何守恒律[J]. 航空学报, 2016, 37(8): 2395-2407. DOI:10.7527/S1000-6893.2016.0141 |
| [26] |
Lesoinne M, Farhat C. Geometric conservation laws for aeroelastic computations using unstructured dynamic meshes. AIAA 95-1709, 1995. doi: 10.2514/6.1995-1709
|
| [27] |
Mavriplis D J, Yang Z. Construction of the discrete geometric conservation law for high-order timeaccurate simulations on dynamic meshes[J]. Journal of Computational Physics, 2006, 213(2): 557-573. DOI:10.1016/j.jcp.2005.08.018 |
| [28] |
Zhang L P, Wang Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers & Fluids, 2004, 33(7): 891-916. DOI:10.1016/j.compfluid.2003.10.004 |
| [29] |
朱志斌, 杨武兵, 禹旻. 满足几何守恒律的WENO格式及其应用[J]. 计算力学学报, 2017, 34(6): 779-784. |
| [30] |
Zhu Y J, Sun Z S, Ren Y X, et al. A numerical strategy for freestream preservation of the high order weighted essentially non-oscillatory schemes on stationary curvilinear grids[J]. Journal of Scientific Computing, 2017, 72(3): 1021-1048. |
 2018, Vol. 36
2018, Vol. 36

