2. 西安交通大学 航天航空学院, 陕西 西安 710049
2. School of Aerospace Engineering, Xi'an Jiaotong University, Xi'an 710049, China
低速、大展弦比飞机结构减重是飞机设计中面临的重要问题。此类飞机往往柔性大,气动力和结构相互作用下气动弹性变形明显。气动弹性变形使得气动载荷重新分布,气动载荷大小及分布规律与刚性飞机相比变化明显[1-2]。大展弦比机翼气动载荷作用下几何非线性效应明显[3],结构刚度受载荷状态影响且结构变形又影响气动力的分布,气动/结构一体化优化成为重要的研究方向[4]。
目前飞机设计主要根据经验来布置机翼的梁和肋的位置,结构的形状和尺寸受制于传统制造技术。如果取消制造技术的约束,将设计重点转移到根据载荷形式确定结构,去除不需要的材料,将有效提高结构效率,达到减重的最终目标。结构优化设计中, 拓扑优化方法被认为是一种根据给定的设计空间确定结构材料分布的有效的数学方法。在过去的一段时间内,基于拓扑优化的方法并没有得到有效的应用,其中很重要的一个原因是优化后的结构无法采用传统制造工艺完成或者加工成本过高[5]。最近,随着增材制造技术的发展,采用3D打印工艺已经可以实现复杂三维结构的快速加工制造,基于拓扑优化方法实现机翼结构优化并完成制造已成为可能。通过增材制造技术加工制造结构不受传统制造工艺的限制,此外,增材制造技术可以显著减少传统设计中用于保持结构完整性的连接结构,有效达到减重的效果[6]。以气动弹性特性为目标,采用拓扑优化方法实现结构减重的研究工作也在逐渐开展,并形成新的研究领域[7]。
本文以大展弦比机翼翼段为研究对象,以巡航飞行气动载荷为边界条件,以结构减重指标为优化约束,以整体柔度最小为优化目标,采用拓扑优化方法完成翼段的结构优化设计,并采用3D打印工艺完成了设计样件的加工制造,探索了一种新的气动/结构一体化分析、优化和制造方法。
1 气动载荷计算本文以低速、大展弦比机翼翼段为研究对象。机翼弦长为40 mm,展长为480 mm,翼型为NACA0015。
1.1 计算方法和模型采用基于松耦合策略的CFD/CSD耦合计算方法求解大展弦比机翼静气动弹性变形下的气动载荷[8-9]。分别求解流体动力学方程和结构静力学方程,耦合面的压力和位移通过插值方法进行交换。流场求解控制方程基于Arbitrary Lagrangian Eulerian(ALE)描述的守恒型三维可压积分形式N-S方程;结构求解采用商业有限元求解器,并考虑结构大变形下的几何非线性效应,流体内部网格更新采用基于RBF的TFI方法[10-12]。
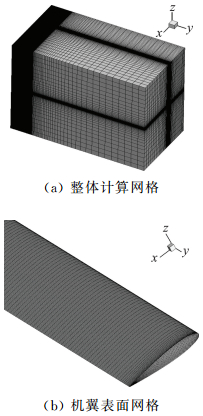
流体网格采用ICEM建模,上下前后的远场距离为15倍弦长,整个流体网格数约为300万。由于计算模型为大展弦比柔性机翼,在气动载荷作用下结构变形较大,所以在机翼表面加密了网格。
静气动弹性结构解算采用有限元方法,网格采用Hypermesh建立,有限元节点总数为154706。对某种3D打印尼龙材料进行了材料拉伸试验,试验测得弹性模量为2500 MPa,泊松比为0.41。采用该参数作为机翼静气动弹性计算的结构模量。
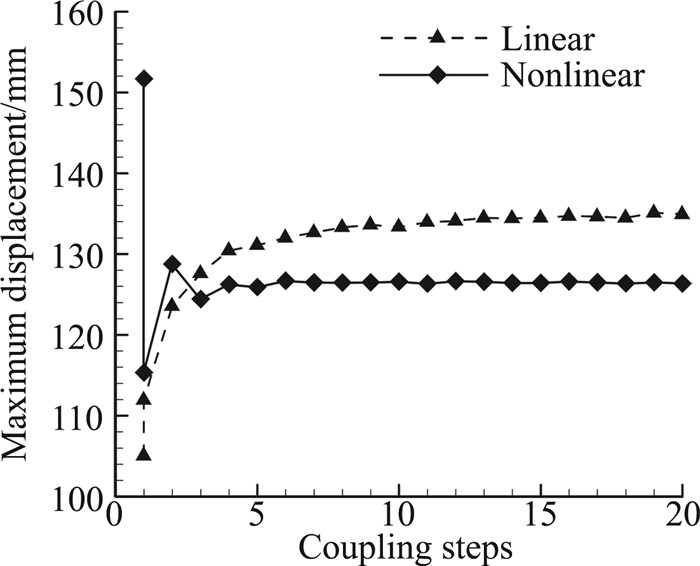
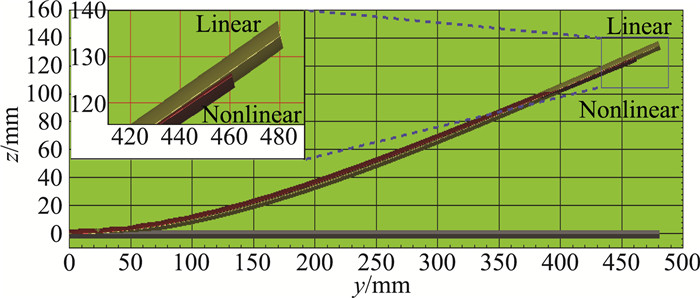
1.2 气动载荷计算结果巡航飞行来流速度为30 m/s,迎角为4°,高度为0 km。图 2表示迭代过程中结构最大变形变化,经过20步迭代,结构变形达到收敛,静气动弹性计算结束,以收敛状态下气动载荷作为结构分析所用量。线性计算结构收敛最大变形为134.6 mm。非线性计算静平衡状态最大变形为126.4 mm,最大变形量约为展长的26.32%。线性与非线性计算结果相差16.7%,结果表明结构几何非线性对结果影响很大,对于柔性机翼的气动弹性特性研究需考虑几何非线性效应[12-13]。
|
图 1 流体计算网格 Figure 1 Mesh for CFD |
|
图 2 结构静气动弹性变形迭代收敛情况 Figure 2 Iteration of static aeroelastic simulation |
|
图 3 静平衡状态下机翼的总体变形和局部放大 Figure 3 Comparison between linear and nonlinear structure |
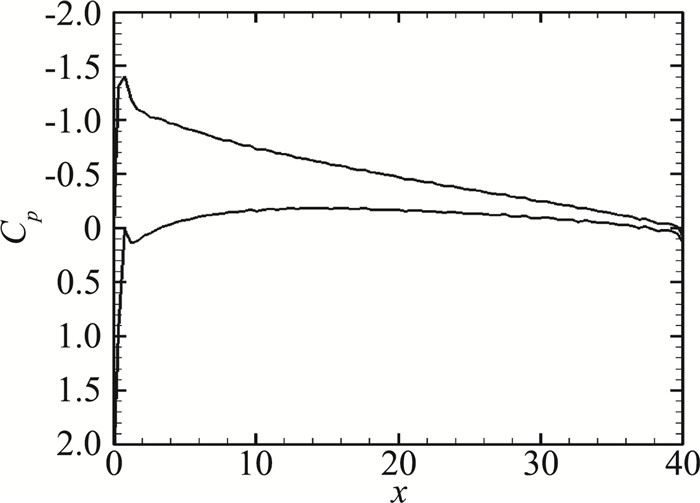
气动载荷为后续拓扑优化设计提供边界条件。本研究对象由于翼展大、蒙皮厚度薄,受工业级3D打印机成型尺寸和精度的限制,作为机理性研究,本文选取其中某翼段为研究对象。气动载荷由全翼载荷提取,截面气动载荷压力分布如图 4所示。
|
图 4 截面压力系数Cp分布曲线 Figure 4 Cp distribution of wing section |
拓扑优化设计是指在给定结构外形、给定结构各元件的材料和相关载荷,以及给定整个结构的强度、刚度、工艺等约束条件下,对结构进行整体和元件优化设计。优化设计一般由设计变量、目标函数和约束条件三要素组成:设计变量是发生改变从而提高性能的一组参数;目标函数是关于设计变量的函数,用来评价设计的优劣;在设计时应遵守几何、刚度、强度、稳定性等约束条件。设计变量、目标函数与约束条件一起构成了优化设计的数学模型。拓扑优化选取结构元件的有无作为设计变量,为0-1型逻辑设计变量。形状优化是选取结构内部形状或节点位置作为设计变量。尺寸优化是选取结构元件的几何尺寸作为设计变量[14]。
优化数学模型可表述为:
| $ \begin{array}{l} {\rm{Minimize:}}\;\mathit{f}\left( X \right) = f\left( {{x_1}, {x_2}, \ldots, {x_n}} \right)\\ {\rm{Subject}}\;{\rm{to:}}\;\mathit{g}\left( X \right) \le 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1, \ldots, m\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;h\left( X \right) \le 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;k = 1, \ldots, {m_h}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;X_i^L \le {X_i} \le X_i^U, \;\;\;\;\;\;\;\;\;i = 1, \ldots, n \end{array} $ | (1) |
其中,X=(x1, x2, …, xn)是设计变量,f(X)是设计目标,g(X)和h(X)是需要进行约束的设计响应。
目前工程上较高效、稳健的优化方法是基于数学规划方法,通过求解灵敏度构造近似显式模型,采用小步长迭代找到最优解。设计灵敏度是设计响应对优化变量的偏导数,对于有限元方法
| $ \left[K \right]\left\{ U \right\} = \left\{ P \right\} $ | (2) |
两边对设计变量X求偏导得到:
| $ \frac{{\partial \left[K \right]}}{{\partial X}}\left\{ U \right\} + \left[K \right]\frac{{\partial \left[U \right]}}{{\partial X}} = \frac{{\partial \left[P \right]}}{{\partial X}} $ | (3) |
则对位移向量U的偏导数为:
| $ \frac{{\partial \left[K \right]}}{{\partial X}} = {\left[K \right]^{ - 1}}\left( {\frac{{\partial \left[P \right]}}{{\partial X}} - \frac{{\partial \left[K \right]}}{{\partial X}}\left\{ U \right\}} \right) $ | (4) |
通常设计响应是位移向量U的函数
| $ g = {Q^{\rm{T}}}\left\{ U \right\} $ | (5) |
因此,设计响应对设计变量的偏导数为:
| $ \frac{{\partial g}}{{\partial X}} = \frac{{\partial {Q^{\rm{T}}}}}{{\partial X}}\left\{ U \right\} + {Q^{\rm{T}}}\frac{{\partial \left\{ U \right\}}}{{\partial X}} $ | (6) |
本文采用商用软件Hypermesh的Optistruct模块进行拓扑优化分析。Optistruct拓扑优化采用密度法(SIMP方法),即将有限元模型设计空间中每个单元的“单元密度”作为设计变量,该单元密度与结构的材料参数有关(如单元密度与材料弹性模量E之间具有某种函数关系),单元密度在0~1之间连续取值,优化求解后单元密度接近1表示该单元位置处的材料很重要,需要保留。单元密度为0表示该单元处的材料不重要,可以去除。从而达到材料的高效率利用,实现轻量化设计。
目前机翼结构材料多选用刚度很大的复合材料,本身具有很好的刚度特性,但是实际生产中,往往超重严重,重量是制约气动弹性效应明显的轻质飞机的主要指标。因此,在本文分析中,把减重指标作为约束,把刚度作为优化目标,然后通过施加载荷,评估结构变形是否满足目标。
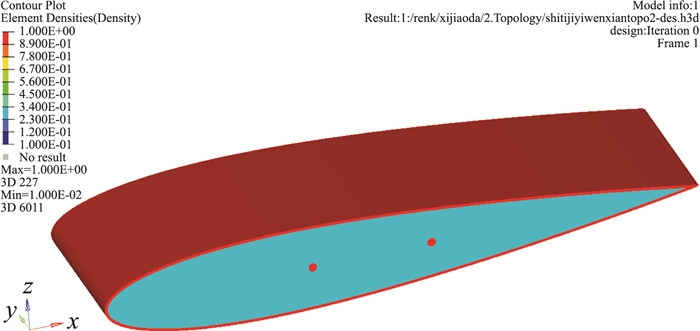
2.2 拓扑优化计算对翼段模型施加气动载荷,翼段展弦比为0.3。相对实体机翼,以减重60%为优化约束,以整体柔度最小(刚度最大)为优化目标。优化过程中,初始设计空间如图 5所示,设置蒙皮和前后梁为非优化区(图中红色区域),前后梁设置为不变形。可设计空间为图中蓝色区域。
|
图 5 翼段初始设置空间 Figure 5 Initial design space for topology optimization |
蒙皮厚度设置为1 mm,前后梁直径均为3 mm,优化结果如图 6所示。结构优化后结果显示,在上下蒙皮之间保留树状支撑结构,其余不承载区域结构被优化掉,大大降低了结构重量,相对初始实心结构减重63%左右。整体优化结果与文献[15-16]结果类似,只是由于气动载荷不同,形式略有差别。

|
图 6 拓扑优化结果 Figure 6 Result of topology optimization |
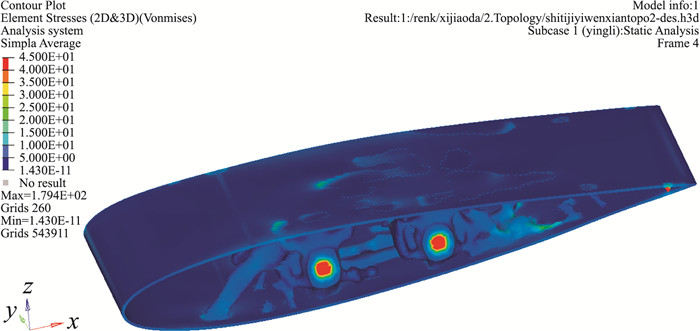
通过有限元计算验证优化结构是否满足气动载荷作用下的强度要求。使用Von Mises应力作为强度判断准则。结构在气动载荷作用下的应力云图如图 7所示。
|
图 7 优化结果强度校核 Figure 7 Strength check of topology optimization structure |
结果显示,在前后梁根部,结构应力较大。其余部位应力被有效分散,最大应力小于45 MPa,在尼龙材料的许用应力范围内,满足强度要求。
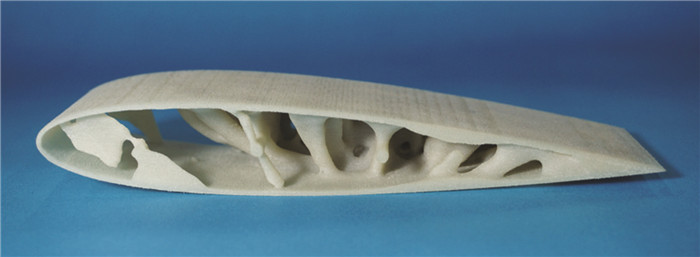
4 优化结构3D打印通过结构优化软件中的光顺命令,导出结构拓扑优化三维模型,并采用选择性激光烧结工艺,使用纤维增强尼龙材料打印了优化结构,如图 8所示。打印结构在尺寸和表面粗糙度方面均达到了设计要求,表明采用拓扑优化方法得到的复杂空间三维结构具备使用3D打印制造技术实现的可行性。
|
图 8 翼段结构3D打印模型示意图 Figure 8 3D print of topology optimization structure |
本文采用CFD/CSD耦合数值计算方法, 针对某大展弦比飞机巡航状态开展了机翼静气动弹性计算。研究了结构几何非线性对气动力的影响,并采用翼段气动载荷作为结构拓扑优化分析的边界条件,完成了拓扑优化,3D打印制造了优化结构。结果显示:
(1) 几何非线性对大展弦比机翼气动载荷影响明显;
(2) 基于拓扑优化方法,可以在保证结构刚度的条件下,有效实现减重;
(3) 3D打印技术可以实现复杂三维拓扑结构的打印,在尺寸和表面粗糙度等方面可以满足设计要求。
本文探索了一种基于3D打印技术实现大展弦比机翼结构减重的技术路径。不受目前传统设计思路和制造技术约束的结构优化方法,在结构减重方面具有重要的潜在应用价值。
| [1] |
Chen G B, Zou C Q, Yang C. Aeroelastic design foundation[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2004. (in Chinese) 陈桂彬, 邹丛青, 杨超. 气动弹性设计基础[M]. 北京: 北京航空航天大学出版社, 2004. |
| [2] |
Li F, Bai P. Low Reynolds number aerodynamics of aircraft[M]. Beijing: China Aerospace Press, 2016. (in Chinese) 李锋, 白鹏. 飞行器低雷诺数空气动力学[M]. 北京: 中国宇航出版社, 2016. |
| [3] |
Xie C C, Wu Z G, Yang C. Aeroelastic analysis of flexible large aspect ratio wing[J]. Journal of Beijing University of Aeronautics and Astronautics, 2003, 29(12): 1097-1090. (in Chinese) 谢长川, 吴志刚, 杨超. 大展弦比柔性机翼的气动弹性分析[J]. 北京航空航天大学学报, 2003, 29(12): 1097-1090. DOI:10.3969/j.issn.1001-5965.2003.12.009 |
| [4] |
Nie X Y, Liu Z Y, Yang G W. Aircraft structure stiffness and aerodynamics optimization design based on kriging surrogate model[J]. Physics of Gases, 2017, 2(2): 8-16. (in Chinese) 聂雪媛, 刘中玉, 杨国伟. 基于Kriging代理模型的飞行器结构刚度气动优化设计[J]. 气体物理, 2017, 2(2): 8-16. |
| [5] |
Krog L, Tucker A, Rollema G, et al. Topology optimization of aircraft wing box ribs[C]//Proceedings of the Altair Technology Conference. Airbus UK Ltd, Advance Numerical Simulations Department, 2004.
|
| [6] |
Yang R, Liu Y, Qian W, et al. Topology optimization for structural design of fuselage flutter model[J]. Journal of Mechanical Engineering, 2011, 47(11): 59-63. (in Chinese) 杨睿, 刘玚, 钱卫, 等. 面向机身颤振模型结构设计的拓扑优化方法[J]. 机械工程学报, 2011, 47(11): 59-63. |
| [7] |
Mian H H, Wang G, Ye Z Y. Numerical investigation of structural geometric nonlinearity effect in high-aspect-ratio wing using CFD/CSD coupled approach[J]. Journal of Fluids and Structures, 2014, 49: 186-201. DOI:10.1016/j.jfluidstructs.2014.04.011 |
| [8] |
Guo L, Lyu J N, Ji C, et al. Identification of flutter boundary for a hypersonic vehicle wing as X-15 by experiment and numerical simulation[R]. AIAA 2017-2237.
|
| [9] |
Zhang X, Chen P J, Zuo Y T. A novel multidisciplinary design optimization of aircraft based on CFD/CSD coupling[J]. Physics of Gases, 2016, 1(2): 47-54. (in Chinese) 张效, 陈平剑, 左英桃. CFD/CSD耦合飞行器多学科优化设计新方法[J]. 气体物理, 2016, 1(2): 47-54. |
| [10] |
Tsai H F, Wong A, Cai J, et al. Unsteady flow calculations with a parallel multiblock moving mesh algorithm[J]. AIAA Journal, 2001, 39(6): 1021-1029. DOI:10.2514/2.1442 |
| [11] |
Zeng Z, Wang G, Ye Z Y. Enhanced RBF mesh deformation method and multi-body trajectory simulation[J]. Acta Aerodynamica Sinica, 2015, 33(2): 170-177. (in Chinese) 曾铮, 王刚, 叶正寅. RBF整体网格变形与多体轨迹仿真[J]. 空气动力学学报, 2015, 33(2): 170-177. DOI:10.7638/kqdlxxb-2014.0143 |
| [12] |
Nie X Y, Huang C D, Yang G W. Numerical analysis for aeroelastic with structural geometrical nonlinearity using a CFD/CSD-coupled method[J]. Journal of Vibration and Shock, 2016, 35(8): 48-53. (in Chinese) 聂雪媛, 黄程德, 杨国伟. 基于CFD/CSD耦合的结构几何非线性静气动弹性数值方法研究[J]. 振动与冲击, 2016, 35(8): 48-53. |
| [13] |
Fu Z C, Chen Z J, Liu Z Q. Geometric nonlinear aeroelastic behavior of high aspect ratio wings[J]. Engineering Mechanics, 2017, 34(4): 231-240. (in Chinese) 付志超, 陈占军, 刘子强. 大展弦比机翼气动弹性的几何非线性效应[J]. 工程力学, 2017, 34(4): 231-240. |
| [14] |
Wang W, Yang W, Chang N. Integrate shape/size optimization into a high aspect-ratio flying wing design[J]. Structure & Environment Engineering, 2007, 34(5): 49-54. (in Chinese) 王伟, 杨伟, 常楠. 大展弦比飞翼结构形状、尺寸综合优化设计[J]. 强度与环境, 2007, 34(5): 49-54. DOI:10.3969/j.issn.1006-3919.2007.05.008 |
| [15] |
Walker D, Liu D, Jennings A. Topology optimization of an aircraft wing[R]. AIAA 2015-0976.
|
| [16] |
Walker D, Liu D, Jennings A. Wing design utilizing topology optimization and additive manufacturing[R]. AIAA 2016-1246.
|
 2018, Vol. 36
2018, Vol. 36

