螺旋颤振是倾转旋翼机固定翼模式下的重要气动弹性稳定性问题,其本质是一种自激振动。大速度前飞时,旋翼轴向来流速度大,桨叶的挥舞、摆振运动会在桨盘平面内产生较大的交变载荷,并通过倾转机构传向机翼,从而引发机翼受迫振动。随着速度增加,当机翼自身的气动与结构阻尼无法耗散振动能量时,发生失稳现象。颤振失稳可导致机体结构迅速破坏,严重影响飞行安全。
美国Bell公司从20世纪50年代开始实施倾转旋翼工程样机的研制,相关高校与科研机构围绕倾转旋翼机气动弹性稳定性问题开展了一系列研究工作。Wayne Johnson在大量工程假设的前提下,提出了倾转旋翼/机翼耦合系统的九自由度模型[1],该模型得到了持续改进,后被广泛应用于倾转旋翼机螺旋颤振稳定性研究。Nixon建立了半展长倾转旋翼机模型的动力学模型[2],该模型考虑了复合材料的弹性耦合特性,随后研究了机翼刚度、旋翼挥舞-变距耦合系数、桨叶频率等重要结构参数对气动弹性稳定性的影响规律,此外Nixon还采用气动弹性剪裁方法研究了机翼蒙皮铺设与大梁形状对颤振边界的影响[8]。Jinho Paik研究了提升倾转旋翼机螺旋颤振稳定性的主、被动方法[3],被动方法通过对旋翼、机翼动力学参数优化设计来达到增稳的目的。在试验方面,Bell公司参照V-22研制了缩比1:5的WRATS试验模型,相关学者利用该模型进行了各类动力学试验研究[7, 13],有效支撑了倾转旋翼机动力学理论研究。国内,南京航空航天大学的董凌华、岳海龙在倾转旋翼机气动弹性响应以及稳定性等方面开展了理论研究与原理性试验[11-12],对提高螺旋颤振稳定性的方法进行了有益探索。
以上研究中,螺旋颤振稳定性求解大多在旋翼拉力配平下进行,很少考虑风车状态这种稳定性最差的飞行状态,无法体现稳定性边界;在螺旋颤振稳定性参数影响研究方面,以桨毂、机翼以及倾转机构的参数为主,这些参数变动牵扯面广,不易实现。本研究从倾转旋翼/短舱/机翼耦合结构动力学理论推导入手,建立了适用于稳定性分析的气动弹性耦合动力学方程及求解方法。针对风车状态的配平结果,开展了螺旋颤振稳定性分析,将计算值同国外文献结果进行了对比,吻合良好。随后研究了后掠、下反以及尖削三种旋翼桨尖设计对机翼颤振模态的影响规律,在此基础上,对比了不同桨尖形状设计所能产生的稳定性改善效果,对倾转旋翼机动力学设计有一定的指导意义。
1 倾转旋翼/短舱/机翼耦合模型 1.1 稳定性方程采用Hamilton能量原理建立倾转旋翼-短舱-机翼耦合动力学方程:
| $ \delta \mathit{\Pi = }\int_{{t_1}}^{{t_2}} {\left( {\delta U - \delta T - \delta W} \right){\rm{d}}t} = 0 $ | (1) |
式中δU、δT分别为弹性势能与动能的变分,δW代表气动力虚功。对于旋翼/短舱/机翼耦合系统,可表示为:
| $ \begin{array}{l} \delta \mathit{\Pi = }\left( {\sum\limits_{m = 1}^{{N_b}} {\delta {U_b}} } \right) + \delta {U_h} + \delta {U_w}\\ \delta \mathit{T = }\left( {\sum\limits_{m = 1}^{{N_b}} {\delta {T_b}} } \right) + \delta {T_h} + \delta {T_w}\\ \delta \mathit{W = }\left( {\sum\limits_{m = 1}^{{N_b}} {\delta {W_b}} } \right) + \delta {W_w} \end{array} $ | (2) |
式(2)中下标b、h、n、w分别代表桨叶、桨毂、发动机短舱以及机翼的贡献;短舱视为刚体,不考虑其弹性变形与气动力。
桨叶与机翼建模均采用线性梁单元,其自由度向量为q ={u、v、w、
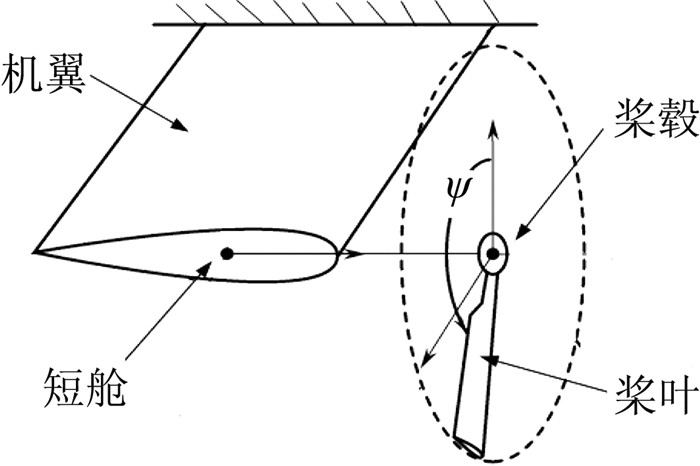
|
图 1 倾转旋翼/短舱/机翼耦合结构 Figure 1 Tiltrotor/nacelle/wing coupling system |
对δT、δU、δW进行线化处理,利用翼尖节点自由度与桨毂中心自由度的耦合关系,可得到形如下式的气动弹性稳定性方程:
| $ \left[ {{M_Q}} \right]\left\{ \begin{array}{l} {\mathop q\limits^{ * * } _r}\\ {\mathop q\limits^{ * * } _w} \end{array} \right\} + \left[ {{C_Q}} \right]\left\{ \begin{array}{l} {\mathop q\limits^ * _r}\\ {\mathop q\limits^ * _w} \end{array} \right\} + \left[ {{K_Q}} \right]\left\{ \begin{array}{l} {q_r}\\ {q_w} \end{array} \right\} = 0 $ | (3) |
式中qr、qw分别代表旋翼、机翼的自由度。
1.1.1 结构动力学模型桨叶与机翼弹性势能均可通过下式计算:
| $ \delta U = \int_0^L {\iint_A {\left( {{\sigma _{xx}}\delta {\varepsilon _{xx}} + {\sigma _{x\eta }}\delta {\varepsilon _{x\eta }} + {\sigma _{x\zeta }}\delta {\varepsilon _{x\zeta }}} \right){\text{d}}\eta {\text{d}}\zeta {\text{d}}x}} $ |
式中,σ、ε代表桨叶或机翼剖面应力与应变,η、ζ为剖面内任意点在剖面坐标系中的坐标,L代表旋翼半径或机翼半展长,应变ε可通过变形协调关系得到,应变σ根据胡克定律计算。
桨毂弹性势能主要考虑铰链弹簧的贡献。对于万向铰桨毂:
| $ \delta {U_h} = {K_{\beta G}}\left( {{\beta _{Gc}}\delta {\beta _{Gc}} + {\beta _{Gs}}\delta {\beta _{Gs}}} \right) $ | (4) |
式中,βGc、βGs为万向铰横向与纵向周期挥舞角,KβG为万向铰弹簧刚度。
桨叶弹性轴上任意点在惯性坐标系中的位置矢量可写为:
| $ \begin{array}{l} \mathit{\boldsymbol{R}} = \left( {\left\{ {{x_h},{y_h},{z_h}} \right\} + \left\{ {0,0,h} \right\}\left[ {{T_{wi}}} \right] + } \right.\\ \;\;\;\left. {\left\{ {x + u,v,w} \right\}\left[ {{T_{ci}}} \right] + \left\{ {0,\eta ,\zeta } \right\}\left[ {{T_{di}}} \right]} \right)\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_i}}\\ {{\mathit{\boldsymbol{J}}_i}}\\ {{\mathit{\boldsymbol{K}}_i}} \end{array}} \right\} \end{array} $ |
上式中xh、yh、zh为桨毂中心线位移,h为翼尖节点与桨毂中心的间距,Twi、Tci、Tdi分别代表翼尖坐标系、桨根坐标系、剖面变形坐标系与惯性坐标系Ii-Ji-Ki之间的转换矩阵。
绝对速度可表示位移矢量R相对于时间求导,V=dR/dt=VxIi+VyJi+VzKi,桨叶动能变分为:
| $ \delta {T_b} = \int_0^R {\iint_A {\rho \mathit{\boldsymbol{V}} \cdot \delta \mathit{\boldsymbol{V}}{\text{d}}\eta {\text{d}}\zeta {\text{d}}x}} $ |
动能推导需考虑桨尖后掠角Λ1与下反角Λ2对梁单元弹性轴造成的弯折,小角度假设不再适用,应采用分段建模的方法引入几何非线性效应。平直段与弯折段之间的坐标转换矩阵为:
| $ {\mathit{\boldsymbol{T}}_\mathit{\Lambda }} = \left[ {\begin{array}{*{20}{c}} {\cos {\mathit{\Lambda }_1}\cos {\mathit{\Lambda }_2}}&{\sin {\mathit{\Lambda }_1}\cos {\mathit{\Lambda }_2}}&{\sin {\mathit{\Lambda }_2}}\\ { - \sin {\mathit{\Lambda }_1}}&{\cos {\mathit{\Lambda }_1}}&0\\ { - \cos {\mathit{\Lambda }_1}\sin {\mathit{\Lambda }_2}}&{ - \sin {\mathit{\Lambda }_1}\sin {\mathit{\Lambda }_2}}&{\cos {\mathit{\Lambda }_2}} \end{array}} \right] $ |
机翼动能Tw采用类似的推导方法,只需进行相应的坐标转换。桨毂与短舱视为刚体,其动能可表示为质点惯性力的体积分形式。
1.1.2 气动模型桨叶气动力虚功等于广义气动力LvA、LwA、M
| $ \delta {W_b} = \int_0^R {\left( {L_v^A\delta v + L_w^A\delta w + M_\varphi ^A{\delta _\varphi }} \right){\rm{d}}x} $ |
广义气动力由环量项与非环量项组成:
| $ \begin{array}{l} L_v^A = {\left( {L_v^A} \right)_C}\\ L_w^A = {\left( {L_w^A} \right)_C} + {\left( {L_w^A} \right)_{NC}}\\ M_\varphi ^A = {\left( {M_\varphi ^A} \right)_C} + {\left( {M_\varphi ^A} \right)_{NC}} \end{array} $ | (5) |
环量气动力在剖面坐标系中的无量纲表达式为:
| $ \begin{array}{l} {\left( {\bar L_w^A} \right)_C} \approx \frac{{\gamma u_T^2}}{{6a}}\left( {{C_L} - {C_D}\frac{{{u_P}}}{{{u_T}}}} \right)\\ {\left( {\bar L_v^A} \right)_C} \approx \frac{{\gamma u_T^2}}{{6a}}\left( { - {C_L}\frac{{{u_P}}}{{{u_T}}} - {C_D}} \right)\\ {\left( {\bar M_\varphi ^A} \right)_C} \approx \frac{{\gamma u_T^2}}{{6a}}\frac{c}{R}{C_m} - {e_d}{\left( {\bar L_w^A} \right)_C} \end{array} $ | (6) |
式(6)中uP、uT为桨叶剖面相对于气流的法向与切向速度, CL、CD、Cm翼型升力、阻力以及力矩系数;c为剖面弦长,ed为剖面气动中心相对于弹性中心的间距,γ、a为洛克数与升力线斜率。还需将式(6)转换到桨根坐标系下。
剖面相对气流速度Vs由桨叶自身运动与来流两部分组成:
| $ {\mathit{\boldsymbol{V}}_s} = \mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_a} $ |
V已在动能推导中得到,来流速度Va可表示为:
| $ {\mathit{\boldsymbol{V}}_a} = \left( {\left\{ {\mu ,0,0} \right\} + \left\{ {0,0, - {\lambda _i}} \right\}\left[ {{T_{hi}}} \right]} \right)\left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_i}}\\ {{\mathit{\boldsymbol{J}}_i}}\\ {{\mathit{\boldsymbol{K}}_i}} \end{array}} \right\} $ |
其中μ为前进比,λi为诱导入流比。
非环量气动力由翼型挥舞与的变矩振荡引起
| $ \begin{array}{l} {\left( {L_w^A} \right)_{NC}} = \frac{{\gamma \pi }}{{12a}}\frac{c}{R}\left[ { - \frac{{\ddot w}}{R} + \frac{{\ddot \theta }}{R}\left( {\frac{c}{4} + {e_d}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {x + \mu \sin \psi \cos {\alpha _p}} \right)\dot \theta } \right] \end{array} $ |
| $ \begin{array}{l} {\left( {M_\varphi ^A} \right)_{NC}} = \frac{{\gamma \pi }}{{12a}}\frac{c}{R}\left[ { - \frac{c}{{4R}} + \frac{{{e_d}}}{R}\left( {\frac{{\ddot w}}{R} - \ddot \theta } \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{e_d}}}{R}\left( {x + \mu \sin \psi \cos {\alpha _p}} \right)\dot \theta - \frac{{{c^2}\ddot \theta }}{{32{R^2}}}} \right] \end{array} $ |
式中θ为桨距,αp为旋翼轴倾角,ψ为方位角。
机翼气动力虚功计算采用与桨叶类似的方法。令桨叶剖面相对气流速度表达式中的转速Ω与预锥角βp为0,即得到机翼剖面的相对气流速度。
1.2 倾转旋翼风车状态配平模型风车状态是指在倾转旋翼机固定翼前飞状态下发动机空中停车时,旋翼在气流的作用下像风车一样自转,此时驾驶员应迅速操纵旋翼维持转速,使发动机具备风车启动的条件,风车启动是飞行安全的重要保障。研究表明相比较其他飞行状态,风车状态下的颤振稳定性最差,因此研究该状态下的气动弹性稳定性,对确定倾转旋翼机颤振稳定性边界有重要意义。
倾转旋翼风车状态配平的过程为:1)通过调整总距θ75使旋翼功率P为0;2)功过调整周期变矩θc、θs使旋翼俯仰Mpitch、滚转力矩Mroll为0,因此配平方程可表示为:
| $ \left\{ \begin{array}{l} {F_1} = P\left( {{\theta _{75}},{\theta _c},{\theta _s}} \right) = 0\\ {F_2} = {M_{{\rm{roll}}}}\left( {{\theta _{75}},{\theta _c},{\theta _s}} \right) = 0\\ {F_3} = {M_{{\rm{pitch}}}}\left( {{\theta _{75}},{\theta _c},{\theta _s}} \right) = 0 \end{array} \right. $ | (7) |
采用Newton迭代格式:
| $ {\left\{ \begin{array}{l} {\theta _{75}}\\ {\theta _c}\\ {\theta _s} \end{array} \right\}_{i + 1}} = {\left\{ \begin{array}{l} {\theta _{75}}\\ {\theta _c}\\ {\theta _s} \end{array} \right\}_i} - {\left[ \mathit{\boldsymbol{J}} \right]^{ - 1}}{\left\{ \begin{array}{l} {F_1}\\ {F_2}\\ {F_3} \end{array} \right\}_i} $ | (8) |
J为Jocabian矩阵,可通过差分法计算。
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {\partial {F_1}/\partial {\theta _{75}}}&{\partial {F_1}/\partial {\theta _c}}&{\partial {F_1}/\partial {\theta _s}}\\ {\partial {F_2}/\partial {\theta _{75}}}&{\partial {F_2}/\partial {\theta _c}}&{\partial {F_2}/\partial {\theta _s}}\\ {\partial {F_3}/\partial {\theta _{75}}}&{\partial {F_3}/\partial {\theta _c}}&{\partial {F_3}/\partial {\theta _s}} \end{array}} \right] $ |
收敛条件:
| $ \sqrt {F_1^2 + F_2^2 + F_3^2} \le {\rm{error}} $ |
error为收敛误差。
1.3 特征值求解方法稳定性方程(3)是典型的线性周期系统方程,其刚度、阻尼矩阵的周期为转速Ω,可采用Floquet理论进行特征值求解。首先进行降阶处理,令:
| $ Y = \left\{ {\begin{array}{*{20}{c}} Q\\ {\mathop Q\limits^ * } \end{array}} \right\},\;\;\;\;\;\mathop Y\limits^ * = \left\{ {\begin{array}{*{20}{c}} {\mathop Q\limits^ * }\\ {\mathop Q\limits^{ * * } } \end{array}} \right\} $ |
将二阶方程转换为一阶形式:
| $ \begin{array}{l} \mathop Y\limits^ * = AY\\ A = \left[ {\begin{array}{*{20}{c}} {\left[ 0 \right]}&{\left[ I \right]}\\ { - {{\left[ {{M_Q}} \right]}^{ - 1}}\left[ {{K_Q}} \right]}&{ - {{\left[ {{M_Q}} \right]}^{ - 1}}\left[ {{C_Q}} \right]} \end{array}} \right] \end{array} $ | (9) |
根据Floquet理论,周期方程(9)在任意方位角ψ处的解可表示为初始方位角ψ0处的线性组合:
| $ Y\left( \psi \right) = \left[ {\mathit{\Phi }\left( {\psi ,{\psi _0}} \right)} \right]Y\left( {{\psi _0}} \right) $ | (10) |
将式(10)代入式(9)中,得到:
| $ \left[ {\mathop {\mathit{\Phi }}\limits^ * } \right] = \left[ A \right]\left[ \mathit{\Phi } \right] $ | (11) |
Φ为状态转换矩阵,满足初始条件:
| $ \left[ {\mathit{\Phi }\left( {{\psi _0},{\psi _0}} \right)} \right] = \left[ I \right] $ | (12) |
式(11)、式(12)可组成带初值条件的一阶微分方程,可令ψ0=0,采用形如式(13)的4阶龙格-库塔法求解任意方位角对应的转换矩阵Φ(ψ, 0)。
| $ \left\{ \begin{array}{l} \left[ {{\mathit{\Phi }_{n + 1}}} \right] = \left[ {{\mathit{\Phi }_n}} \right] + \frac{h}{6}\left( {{K_1} + 2{K_2} + 2{K_3} + {K_4}} \right)\\ {K_1} = \left[ {{A_n}} \right]\left[ {{\mathit{\Phi }_n}} \right]\\ {K_2} = \left[ {A\left( {{\psi _n} + \frac{h}{2}} \right)} \right]\left( {\left[ {{\mathit{\Phi }_n}} \right] + \frac{h}{2}{K_1}} \right)\\ {K_3} = \left[ {A\left( {{\psi _n} + \frac{h}{2}} \right)} \right]\left( {\left[ {{\mathit{\Phi }_n}} \right] + \frac{h}{2}{K_2}} \right)\\ {K_4} = \left[ {A\left( {{\psi _n} + h} \right)} \right]\left( {\left[ {{\mathit{\Phi }_n}} \right] + h{K_3}} \right) \end{array} \right. $ | (13) |
其中h为方位角步长。周期系统的特征值矩阵为:
| $ \left[ \mathit{\Lambda } \right] = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\ln \left[ \mathit{\Theta } \right] $ | (14) |
Λ为对角阵,Θ为矩阵Φ(2π, 0)的特征值矩阵。
2 算例与分析以XV-15倾转旋翼机为例,对其风车状态下的螺旋颤振特性进行分析。计算所用的基本动力学参数,见表 1。
| 表 1 XV-15基本动力学参数 Table 1 Dynamics parameters of XV-15 |
|
|
计算不同前进比下,机翼的法向弯曲、弦向弯曲以及扭转模态频率及阻尼的变化,并同文献[6]中给出的结果进行对比。文献[6]是NASA STI项目办发布的科技报告,XV-15机翼的模态特性采用业界公认的旋翼飞行器综合分析软件CAMRAD Ⅱ计算得到,建模参数来自XV-15的制造商Bell公司,具有较高的可信度和参考价值。
图 2、图 3分别为机翼模态频率、阻尼比随倾转旋翼机前飞速度的变化曲线,其中Beam、Chord、Torsion分别代表一阶法向弯曲、弦向弯曲以及扭转模态。由图 2可见,随着前飞速度增加,弦向弯曲与扭转模态频率略有降低,法向模态频率变化不大。图 3显示出机翼法向、弦向弯曲模态阻尼随前飞速度增加而显著降低;当前进比达到0.9时弦向模态阻尼小于0,进入不稳定区域,此时机翼将发生颤振失稳现象;当前进比超过1.0时,法向弯曲模态进入不稳定区域;机翼扭转模态阻尼随速度变化不大。
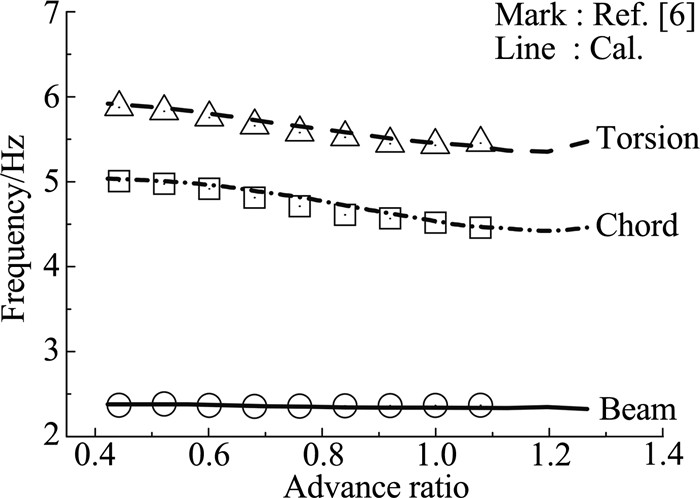
|
图 2 机翼模态频率随前进比变化 Figure 2 Wing modal frequency versus airspeed |
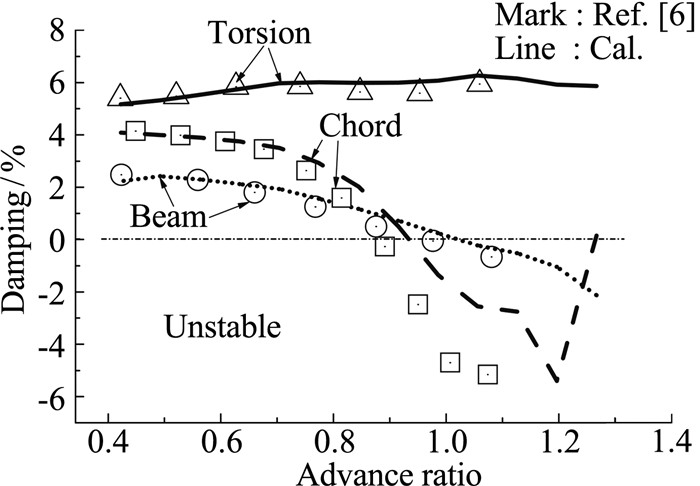
|
图 3 机翼模态阻尼随前进比变化 Figure 3 Wing modal damping versus airspeed |
为验证理论方法的有效性,图 2、图 3将本文计算的机翼模态特性与文献[6]中给出的结果进行了对比。频率结果在整个速度区间均吻合良好;法向弯曲与扭转模态阻尼也呈现出较高的吻合度;弦向模态阻尼在大前进比下同文献值偏差较明显,但两者变化规律趋于一致。
2.2 桨尖外形参数对机翼模态阻尼影响分析先进几何外形能有效改善桨尖失速特性,提升旋翼气动性能。常用的桨尖形状设计有后掠、尖削以及下反。
除了影响气动特性之外,复杂桨尖形状还能引起桨叶挥舞-摆振-扭转弹性耦合效应,对旋翼/短舱/机翼耦合系统的动力学特性也有显著影响。为研究桨尖形状变化对倾转旋翼机螺旋颤振稳定性的影响,令桨尖变化起始位置为0.8R,前进比为0.98,计算机翼模态特性随桨尖后掠角、尖削比以及下反角的变化,图 5~图 7分别给出了相应的结果曲线。
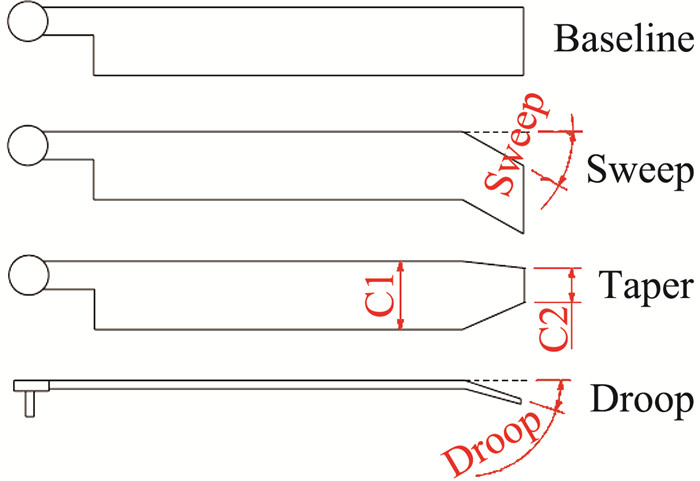
|
图 4 先进桨尖构型 Figure 4 Advanced tip configurations |
|
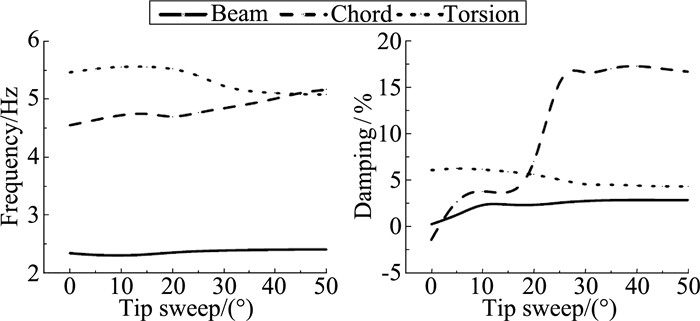
图 5 机翼模态特性随桨尖后掠角变化 Figure 5 Wing modal characteristics versus sweep angle |
|
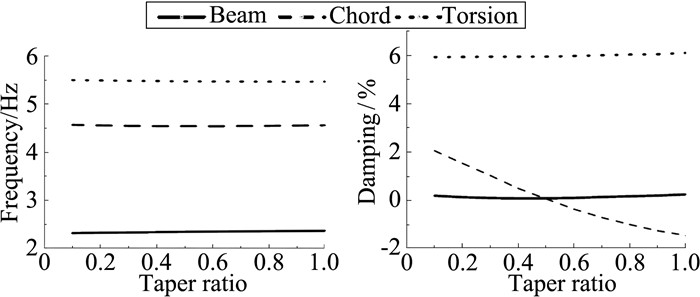
图 6 机翼模态特性随桨叶尖削比变化(C2/C1) Figure 6 Wing modal characteristics versus taper ratio |
|
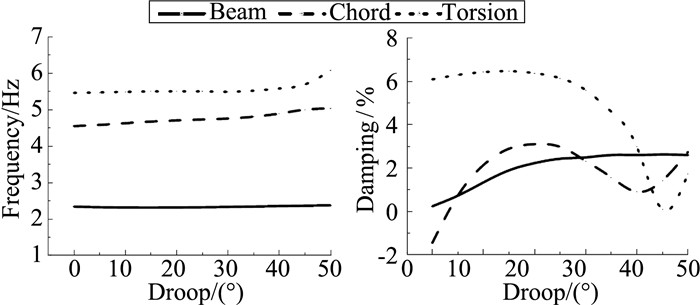
图 7 机翼模态特性随桨尖下反角变化 Figure 7 Wing modal characteristics versus droop angle |
图 5可见,弦向模态阻尼随桨尖后掠变化明显,尤其在0°~30°范围内,阻尼迅速上升,超过30°后趋于平稳。法向与扭转模态阻尼随后掠角变化幅度相对较小,法向阻尼在0°~10°后掠范围内逐步增加,随后趋于稳定,扭转阻尼在0°~30°后掠角变化范围内呈下降趋势;图 6给出了桨叶尖削对机翼模态特性的影响规律,横坐标为尖削比,数值越小尖削幅度越大(1.0代表未尖削),随着尖削幅度增大,机翼弦向阻尼得到明显增强,在尖削比0.5附近摆脱不稳定状态,法向与扭转模态变化不大。图 7为机翼模态特性随桨尖下反变化曲线,随着下反角增大,法向阻尼先上升后趋向平稳;弦向与扭转阻尼在下反角0°~30°范围内存在极大值,其中弦向弯曲阻尼极大值点约为20°下反附近,扭转阻尼极大值位于15°附近。
2.3 面向螺旋颤振增稳的桨尖设计为进一步验证桨尖形状对螺旋颤振的增稳效果,分别对表 2中五种桨尖构型,计算机翼模态阻尼随前飞速度的变化。
| 表 2 五种桨尖构型 Table 2 Parameters of five configurations |
|
|
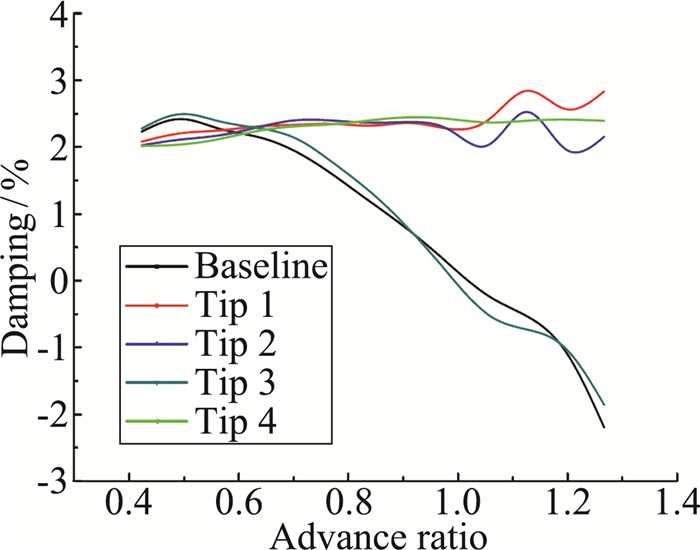
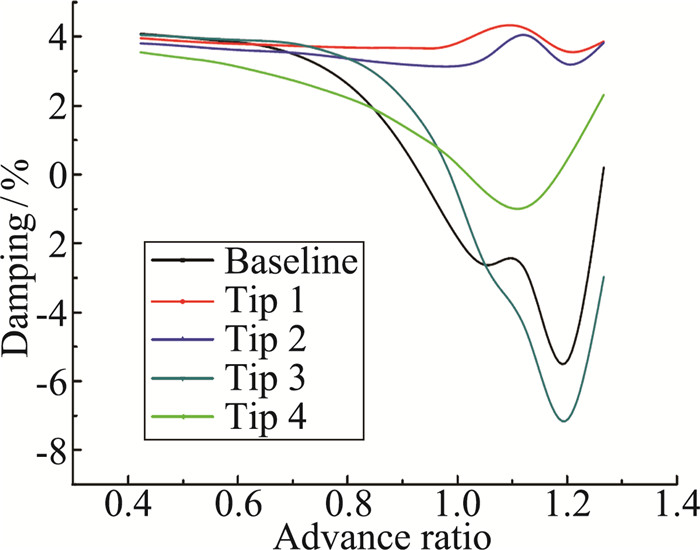
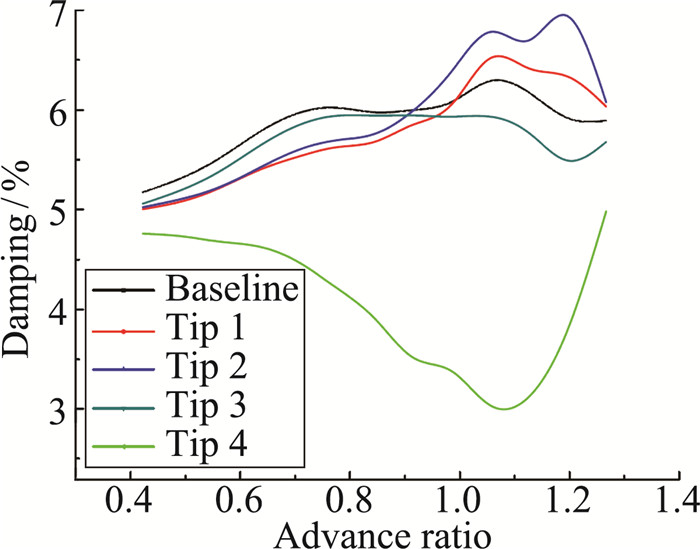
图 8为五种桨尖构型对应的法向模态阻尼随前飞速度变化曲线。当前进比小于0.6时,后掠、下反桨尖设计在一定程度上降低了模态阻尼,随着前飞速度增加,基准构型对应的阻尼逐步降低进入负值区间,Tip1、Tip2、Tip4构型对应的阻尼未出现下降趋势,在整个速度区间均维持在正值。桨叶尖削对机翼法向模态阻尼的影响微乎其微。图 9为机翼弦向模态阻尼随前进比变化曲线。可见当前进比小于0.7时,Tip1、Tip2构型阻尼略低于基准构型;前进比超过0.7后,基准构型对应的阻尼迅速下降,而Tip1、Tip2构型对应的阻尼值变化平稳。当前进比大于0.8时,采用“后掠+下反+尖削”的Tip4构型阻尼值降幅较大,但仍远大于基准构型。当前进比大于1.05时,Tip3构型阻尼超过基准构型。图 10为机翼扭转模态阻尼随前飞速度比变化曲线。可见在较大的一个速度范围内,后掠、下反以及尖削设计会导致模态阻尼下降,直到前进比大于0.9后,Tip1、Tip2构型阻尼值才会超过有基准构型,而Tip3、Tip4构型则会削弱扭转阻尼。由于扭转模态的稳定性裕度较大,因此五种构型在整个速度区间都不存在扭转模态失稳的问题。
|
图 8 机翼法向弯曲模态阻尼对比 Figure 8 Comparison of beam modal damping |
|
图 9 机翼弦向弯曲模态阻尼对比 Figure 9 Comparison of chord modal damping |
|
图 10 机翼扭转模态阻尼对比 Figure 10 Comparison of torsion modal damping |
本文在倾转旋翼/短舱/机翼耦合系统动力学模型的基础上重点研究了后掠、下反、尖削这三种常见的旋翼桨尖设计对机翼模态特性的作用效果,得到了不同桨尖设计在整个速度区间对倾转旋翼机螺旋颤振稳定性的影响规律。得出以下结论:
(1) 当倾转旋翼机达到一定的前飞速度时,机翼的法向与弦向弯曲模态较容易发生颤振失稳,这是由于机翼法向刚度低,而弦向气动阻尼不足;
(2) 桨尖后掠、下反、尖削设计对倾转旋翼机螺旋颤均有一定程度的增稳作用,在大前飞速度下作用尤为明显。而“后掠+下反+尖削”的组合式桨尖设计,对颤振稳定性的作用效果并不等于三种单独设计之和,需要采用优化的方式获得最佳组合。
| [1] |
Johnson W. Dynamics of tilting proprotor aircraft in cruise flight[R]. NASA TN-D-7677. California: Ames Research Center and U. S. Army Air Mobility R&D Laboratory, 1974.
|
| [2] |
Nixon M W. Aeroelastic response and stability of tiltrotors with elastically coupled composite rotor blade[D]. Maryland: University of Maryland, 1993.
|
| [3] |
Jinho Paik. The aeroelastic stability improvements of soft-inplane tiltrotors by active and passive approaches[D]. Pennsylvania: The Pennsylvania State University, 2009.
|
| [4] |
Howard A K T. The aeromechnical stability of soft-inplane tiltrotors[D]. Pennsylvania: The Pennsylvania State University, 2001.
|
| [5] |
Acree C W. Effects of swept tips on V-22 whirl flutter and loads[R]. NASA TM 2005-213458. California: Ames Research Center, 2005.
|
| [6] |
Acree C W, Peyran R J. Rotor design options for improving XV-15 whirl-flutter stability margins[R]. NASA TP-2004-212262. California: Ames Research Center, 2004.
|
| [7] |
Nixon M W, Langston C W, Singleton J D. Aeroelastic stability of a four-bladed semi-articulated soft-inplane tiltrotor model[C]//American Helicopter Society 59th Annual Forum, 2003.
|
| [8] |
Nixon M W, Piatak D J. Aerolastic tailoring for stability augmentation and performance enhancements of titrotor aircraft[C]//International Forum on Aeroelasticity and Structural Dynamics, 1999.
|
| [9] |
Ghiringhelli G L, Masarati P. Multi-body analysis of the 1/5 scale wind tunnel model of the V-22 tiltrotor[C]//American Helicopter Society 55th Annual Forum. Montreal, Canada, 1999.
|
| [10] |
Srinivas V, Chopra I. Formulation of a comprehensive aeroelastic analysis for tiltrotor aircraft[C]//37th Structures, Structural Dynamics, and Materials Conference. Salt Lake City, Utah, 1996.
|
| [11] |
董凌华.倾转旋翼/机翼气动弹性耦合动力学研究[D].南京航空航天大学, 2011.
|
| [12] |
岳海龙.倾转旋翼机倾转时旋翼/短舱/机翼耦合结构气动弹性响应研究[D].南京航空航天大学, 2011.
|
| [13] |
Nixon M W, Langston C W, Singleton J D. Experimental investigations of generalized predictive control for tiltrotor stability augmentation[C]//International Forum of Aeroelasticity and Sturctural Dynamics. Madirid, Spain, 2001.
|
| [14] |
Paik J, Gandhi F. Design optimization for soft-inplane tiltrotor whirl flutter stability improvement[C]//American Helicopter Society 63th Annual Forum. Virginia Beach, 2007.
|
| [15] |
Johnson W. An assessment of the capability to calculate tilting prop-rotor aircraft performance, loads, and stability[R]. NASA TP-2291, 1984.
|
| [16] |
Zhao Q J, Jiang S, Li P, et al. Aerodynamic optimization analyses of tiltrotor/propeller based on CFD method[J]. Acta Aerodynamica Sinica, 2017, 35(4): 544-553. (in Chinese) 招启军, 蒋霜, 李鹏, 等. 基于CFD方法的倾转旋翼/螺旋桨气动优化设计[J]. 空气动力学学报, 2017, 35(4): 544-553. DOI:10.7638/kqdlxxb-2017.0061 |
| [17] |
Li C H, Xu G H. Modeling and analytical investigation on rotor/wing aerodynamic interaction for tiltrotor aircraft[J]. Acta Aerodynamica Sinica, 2008, 26(2): 156-162. (in Chinese) 李春华, 徐国华. 倾转旋翼机旋翼对机翼气动干扰的建模及分析[J]. 空气动力学学报, 2008, 26(2): 156-162. DOI:10.3969/j.issn.0258-1825.2008.02.004 |
 2018, Vol. 36
2018, Vol. 36

