2. 中国航天科技集团公司第七研究院 第七设计部, 四川 成都 610100
2. The Seventh Design Department, Aerospace Science and Technology Corporation, the Seventh Research Institude, Chengdu 610100, China
动稳定性导数是影响弹箭飞行稳定性和可控性的重要气动参数,因此在弹箭气动外形设计过程中,准确预测动稳定性导数非常重要。动稳定性导数可通过工程算法、实验方法(风洞实验、飞行试验)以及计算流体力学(CFD)方法获得。工程算法只适用于简单的外形,且精度较低。而实验方法所需的时间较长,实验费用比较昂贵,且由干扰因素引起的误差也是不能避免的。CFD方法作为一种经济且相对准确的的方法,而被广泛应用于求解飞行器的动稳定性导数。文献[1-2]通过采用准定常方法对弹箭稳态锥进运动进行模拟,得到了不同外形弹箭的俯仰组合动导数。文献[3-4]采用基于ALE动态变形网格的非定常方法对带翼导弹标准模型(BFM)的俯仰和滚转阻尼导数进行了预测,仿真结果与实验结果吻合良好。文献[5-6]使用频域方法预测了带翼导弹在不同条件下的俯仰动导数,结果表明当缩减频率在一定范围内取值时,该方法具有和双时间步方法相当的精度,但当减缩频率降低到一定值后,结果不再理想。文献[7-9]分别采用滑移网格方法和刚性动网格方法对飞机和带翼导弹的强迫俯仰振动过程进行模拟,得到了模型在不同迎角下的俯仰组合动导数,该方法可避免网格变形对计算结果的影响。文献[10]建立了适用于高速细长体导弹的滚转动导数风洞实验装置,并得到了一致性良好的实验结果。文献[11]结合CFD仿真方法和Kriging代理模型得到了不同设计参数下乘波体的动导数,并将结果用于乘波体的荷兰滚模态分析。
以上研究对弹箭动导数求解具有一定借鉴价值,但这些研究只考虑了弹箭的单自由度角运动状态,而忽略了弹箭耦合运动带来的影响。文献[12-14]的研究结果表明飞行器耦合运动产生的非定常迟滞特性与单自由度运动产生的迟滞特性不一致,旋转运动对纵向俯仰组合动导数有显著影响,使得组合动导数变得极不稳定,同时当转速较大时,旋转运动还将显著增大横向组合动导数的非线性。而关于耦合运动对弹箭动导数的影响的研究还未见报道。弹箭在实际飞行过程中,通常同时存在俯仰、滚转运动以及弹轴绕速度方向的锥进运动,因此研究弹箭在耦合运动状态下的动导数变化规律,对研究弹箭的非定常气动特性和飞行稳定性更具有实用价值。
本文在已有的风洞实验数据基础上,提出了一种基于欧拉转动定理和滑移网格技术的复杂角运动模拟方法,并将得到的角速度结果指定给球形滑移网格区,从而模拟弹箭复杂角运动过程。通过对得到的气动力系数迟滞环进行参数辨识,得到了弹箭在耦合运动状态下的俯仰组合动导数和升力系数动导数,并分析了滚转频率和锥进频率对结果的影响规律。
1 动导数计算方法基于小幅强迫振动法[7-8],采用非定常CFD方法模拟滚转运动、锥进运动与强迫俯仰运动耦合的角运动过程,并采用积分法对所得弹箭气动系数迟滞环进行辨识,求解相应的弹箭动稳定性导数,以分析耦合运动对其动导数的影响规律。
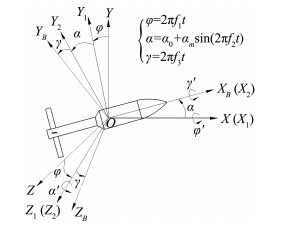
1.1 耦合运动描述图 1即为本文模拟的弹箭三自由度耦合角运动过程示意图。图中坐标系OXYZ、OXBYBZB分别为基准坐标系和弹体固连坐标系。弹体固连坐标系可由基准坐标系经过三次旋转得到,即首先绕OX轴逆时针转过φ(进动角),再绕所得OZ1轴逆时针转α(迎角),最后绕所得OXB轴逆时针转γ(滚转角)。在如图所示坐标系下,弹箭一边绕弹轴做匀速滚转运动,一边在迎角平面内做强迫俯仰运动,同时迎角平面绕OX轴匀速偏转。该角运动过程可描述为
| $ \left\{ \begin{array}{l} \varphi = 2\pi {f_1}t\\ \alpha = {\alpha _0} + {\alpha _m}\sin \left( {2\pi {f_2}t} \right)\\ \gamma = 2\pi {f_3}t \end{array} \right. $ | (1) |
|
图 1 耦合运动示意图 Figure 1 The coupled motion of roll-cone-pitch |
其中,f1为弹箭绕OX轴的进动频率,f2为弹箭做强迫俯仰运动的俯仰频率,f3为滚转频率, 三个角运动频率单位均为Hz。α为弹箭在迎角平面内的瞬时迎角,α0为初始迎角,αm为迎角振动幅值,γ为滚转角,φ为进动角。当f1、f2和f3取值不同时,弹箭对应做不同形式的运动:(1)当f2≠0、f1=f3=0时,弹箭做单纯的强迫俯仰运动;(2)当f1≠0、f2=f3=0时,弹箭做单纯的锥进运动;(3)当f3≠0、f1=f3=0时,弹箭做单纯的滚转运动;(4)当f2≠0、f1=0、f3≠0不为0时,弹箭做俯仰滚转耦合角运动;(5)当f2≠0、f1≠0、f3=0,弹箭做俯仰锥进耦合运动;(6)当f2≠0、f1≠0、f3≠0时,弹箭即做三自由度(俯仰、滚转、锥进)耦合角运动。
由弹体坐标系的定义可得,基准坐标系到弹体固连坐标系的坐标转换矩阵为:
| $ {N_{AB}}\left( {\alpha ,\varphi ,\gamma } \right) = \\ \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&{\cos \varphi \sin \alpha }&{\sin \alpha \sin \varphi }\\ { - \cos \gamma \sin \alpha }&{\cos \alpha \cos \gamma \cos \varphi - \sin \gamma \sin \varphi }&{\cos \varphi \sin \gamma + \cos \alpha \cos \gamma \sin \varphi }\\ {\sin \alpha \sin \gamma }&{ - \cos \gamma \sin \varphi - \cos \alpha \cos \varphi \sin \gamma }&{\cos \gamma \cos \varphi - \cos \alpha \sin \gamma \sin \varphi } \end{array}} \right] $ | (2) |
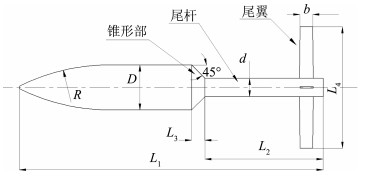
本文的计算对象为如图 2所示的一种带有四片尾翼的弹箭。为提高飞行稳定性,该弹采用了长尾杆结构,使整个弹的压心向弹体尾部移动,以提高弹体的稳定储备量。弹箭基本几何参数如下:弹径为D,全弹长为L1=6.8D,弹头部曲面半径R=4.57D, 尾杆长度为L2=2.6D,尾杆直径为d=0.48D,尾杆与圆柱部之间通过一个45°的锥形部连接,锥形部长度L3=0.3D; 尾翼倾角为0°,翼展为L4=2.8D,翼片宽度为b=0.28D。
|
图 2 几何模型 Figure 2 Geometry model |
滑移网格方法是模拟非定常流动过程的常用方法。该方法将流场划分为外部静止区和内部滑移区。计算模型的运动与内部滑移区网格的运动是同步的,因此通过指定内部滑移区网格的运动规律,即可实现对计算模型运动规律的模拟。两区域在交界面处通过插值计算进行数据传递。滑移网格方法在计算过程中,不需要进行网格重构,计算精度不会受网格变形的影响,具有计算量小易于实现的优点。因此,本文采用滑移网格方法对弹箭耦合角运动过程进行模拟。
流场求解采用三维非定常雷诺平均N-S方程,其积分形式如下:
| $ \frac{\partial }{{\partial t}}\iiint\limits_V {\mathit{\boldsymbol{W}}{\text{d}}V} + \iint\limits_{\partial V} {\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{n}}}{\text{d}}s = \frac{1}{{\mathit{Re}}}\iint\limits_{\partial V} {{\mathit{\boldsymbol{F}}_v} \cdot \mathit{\boldsymbol{n}}}{\text{d}}s $ |
式中V为任意控制体;W是守恒变量;F为无黏通量;Fv为黏性通量;∂V为控制体的边界;n为控制体边界单位外法向矢量;Re为雷诺数。
采用有限体积法对方程进行空间离散,其中无黏通量采用Roe进行计算,界面变量采用二阶MUSCL格式进行重构;黏性通量采用二阶中心差分进行计算。湍流模型采用标准k-ε两方程模型。远场来流采用压力远场条件,弹体边界采用无滑移边界条件,壁面区域采用标准壁面函数,并取弹体直径D为参考长度,取弹箭横截面积为参考面积。
求解迭代采用双时间步推进。每个时间步内,迭代次数取为25次,以保证在每一个时间步内计算达到收敛。每个时间步内模型的角速度的计算方法将在1.2.3节做进一步介绍。前期的计算结果表明,当计算时间达到3个俯仰运动周期时,俯仰力矩系数和升力系数计算结果均达到稳定振荡状态,因此后续计算中将第3个俯仰周期的计算结果作为最终的结果。
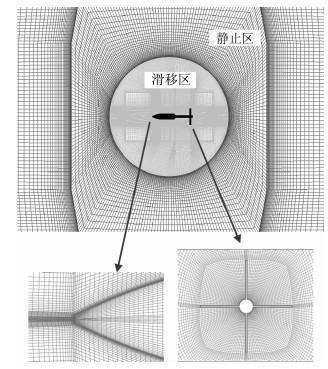
1.2.3 网格划分构建合理的网格滑移面是滑移网格技术使用的关键。为满足模拟弹箭复杂角运动的需要,将内部滑移区取为球形,外部静止区取为圆柱形,两区域的交界处的网格滑移面即为球面。将计算模型放置在球心位置,并使计算模型的质心与球心重合。这种网格划分方式的目的在于,当球形网格区域绕球心以任意姿态转动时,都能保证滑移区网格和静止区网格均不发生干涉。同时由于模型的质心与球心重合,因此内部滑移区网格绕球心的角运动可以直接等同于计算模型绕质心的角运动。
采用结构网格对流场进行划分。远场区域的径向和轴向高度值分别取为30D和70D,以防止外边界处反射对结果的影响。O形网格技术被用于加密弹体周围的附面层网格。在黏性边界层内布置了25层网格,第一层网格的厚度被取为10 μm,并且网格延伸率被控制在1.1以下,以保证壁面y+值小于0.5。为进行网格无关系验证,按本文提出的网格划分方案,通过对滑移区网格进行局部加密得到了网格数量为200万、340万、480万的三套网格。利用三套网格对来流马赫数Ma=0.6,初始迎角为3°,f1=f2=f3=80和f1=80、f2=f3=0两种非定常运动状态进行了仿真求解,结果表明,当网格数量大于340万时,所得弹箭各项气动力系数的迟滞环随网格数增加无显著变化,即达到网格无关性要求,因此本文采用网格数为340万的网格(见图 3)划分方案进行计算。
|
图 3 流场网格 Figure 3 Grid meshing of flow field |
采用滑移网格技术模拟既定的绕心运动,需要指定每个时间步上的角速度矢量ω,若已知时间步长恒定为Δt,则弹箭在第n个时间步的角位移为
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{\eta }}_i} = {\mathit{\boldsymbol{\omega }}_i} \cdot \Delta t\\ \mathit{\boldsymbol{\eta }} = \sum\limits_{i = 1}^n {\Delta {\mathit{\boldsymbol{\eta }}_i}} \end{array} \right. $ | (3) |
式(3)中:η为弹箭第n个时间步的姿态角矢量,ωi、Δηi分别为第i个时间步内的角速度矢量和角位移矢量。
目前,滑移网格技术在应用中角速度矢量ω通常采用求导法计算,通过对既定的运动方程求导并向基准坐标系投影从而得到ω的表达式。由坐标转换关系可得弹箭角速度矢量ω表达式:
| $ \mathit{\boldsymbol{\omega }} = \mathit{\boldsymbol{\dot \varphi }} + \mathit{\boldsymbol{\dot \alpha }} + \mathit{\boldsymbol{\dot \gamma }} $ | (4) |
式中:
通过对式(1)求导并结合坐标转换矩阵,将结果投影到基准坐标系(OXYZ)可得ωd的表达式为:
| $ \left\{ \begin{array}{l} {\omega _{dx}} = 2\pi {f_3}{\alpha _m}\cos \left( \alpha \right) + 2\pi {f_1}\\ {\omega _{dy}} = 2\pi {f_3}\cos \left( \varphi \right)\sin \left( \alpha \right) - \\ \;\;\;\;\;\;\;\;\;2\pi {f_2}{\alpha _m}\cos \left( {2\pi {f_2}t} \right)\sin \left( \varphi \right)\\ {\omega _{dz}} = 2\pi {f_3}\sin \left( \varphi \right)\sin \left( \alpha \right) + \\ \;\;\;\;\;\;\;\;\;2\pi {f_2}{\alpha _m}\cos \left( {2\pi {f_2}t} \right)\cos \left( \varphi \right) \end{array} \right. $ | (5) |
上述角速度计算方法相对简单,但实际仿真过程中发现,利用求导法求得的角速度进行模拟并不能得到理想的结果。因为由求导法计算的角速度矢量仅是每个时间步起始点的值,而时间步长Δt为有限值,因此在每个时间步内必然存在积分误差,且时间步长越大误差越大,且随着计算周期的增加,弹箭角运动的累积误差也随之增加,最终弹箭运动规律严重偏离式(1)给出的角运动规律。
为此本文提出了基于欧拉转动定理的角运动计算方法,其实质是通过对每个时间步内的角速度进行修正,从而消除每个时间步内的角位移误差。推导过程如下:设第i个时间步开始时刻为t1,由式(1)可得姿态角为α1、γ1、φ1,将姿态角带入式(2)可得转换矩阵为NAB1(α1,γ1,φ1),并记对应的弹体固连坐标系为LB1;设第i+1个时间步开始时刻(即第i个时间步结束时刻)为t2=t1+Δt,同样的,由式(1)可得姿态角为α2、γ2、φ2,将姿态角带入式(2)可得对应转换矩阵为NAB2(α2,γ2,φ2),并记录对应的弹体固连坐标系为LB2;由此可得从LB1到LB2的坐标系转换矩阵表达式为:
| $ {N_{12}} = {N_{AB2}} \cdot N_{AB1}^{ - 1} = \left[ {\begin{array}{*{20}{c}} {{n_{11}}}&{{n_{12}}}&{{n_{13}}}\\ {{n_{21}}}&{{n_{22}}}&{{n_{23}}}\\ {{n_{31}}}&{{n_{32}}}&{{n_{33}}} \end{array}} \right] $ | (6) |
式中,nij为转换矩阵各分量,为节约篇幅这里不具体给出。
另一方面,由欧拉转动定理可知,弹箭第i+1时间步对应的弹体固连坐标系,一定可由第i时间步对应的弹体固连系经过一次旋转得到,即必存在单位矢量u(ux, uy, uz),以及使LB1绕单位矢量u经过一次旋转与LB2重合的角度θ。此时对应的转换矩阵为著名的罗德里格斯转换矩阵:
| $ R = \\ \left[ {\begin{array}{*{20}{c}} {\cos \theta + u_x^2\left( {1 - \cos \theta } \right)}&{{u_x}{u_y}\left( {1 - \cos \theta } \right) - {u_z}\sin \theta }&{{u_x}{u_z}\left( {1 - \cos \theta } \right) + {u_y}\sin \theta }\\ {{u_y}{u_x}\left( {1 - \cos \theta } \right) + {u_z}\sin \theta }&{\cos \theta + u_y^2\left( {1 - \cos \theta } \right)}&{{u_y}{u_z}\left( {1 - \cos \theta } \right) - {u_x}\sin \theta }\\ {{u_x}{u_z}\left( {1 - \cos \theta } \right) - {u_y}\sin \theta }&{{u_z}{u_y}\left( {1 - \cos \theta } \right) + {u_x}\sin \theta }&{\cos \theta + u_z^2\left( {1 - \cos \theta } \right)} \end{array}} \right] $ | (7) |
根据N12=R可联立解得:
| $ \left\{ \begin{array}{l} \theta = {\rm{arccos}}\left( {\left( {\sum\limits_{i = 1}^3 {{n_{ii}} - 1} } \right)/2} \right)\\ {u_x} = \left( {{n_{32}} - {n_{23}}} \right)/\left( {2\sin \theta } \right)\\ {u_y} = \left( {{n_{13}} - {n_{31}}} \right)/\left( {2\sin \theta } \right)\\ {y_z} = \left( {{n_{21}} - {n_{12}}} \right)/\left( {2\sin \theta } \right) \end{array} \right. $ | (8) |
当时间步较小时,近似取第i时间步的角速度矢量为ω=u·(θ/Δt),并向基准坐标系(OXYZ)投影即可得到由欧拉方法计算的近似角速度矢量:
| $ {\mathit{\boldsymbol{\omega }}_e} = \frac{{{\rm{arccos}}\left( {\left( {\sum\limits_{i = 1}^3 {{n_{ii}} - 1} } \right)/2} \right)}}{{2\Delta t\sin \theta }} \cdot N_{AB1}^{ - 1} \cdot \left[ {\begin{array}{*{20}{c}} {{n_{32}} - {n_{23}}}\\ {{n_{13}} - {n_{31}}}\\ {{n_{21}} - {n_{12}}} \end{array}} \right] $ | (9) |
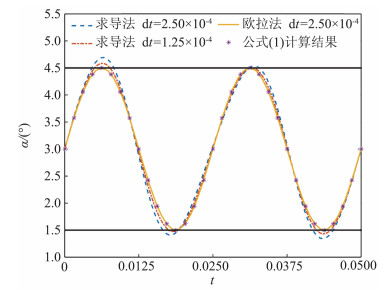
在利用滑移网格求解过程中,角速度矢量分别采用求导法(式5)和欧拉转动法(式9)在每个时间步为内部滑移网格区指定角速度。对式(1)给出的耦合角运动进行模拟求解,其中取f1=30、f2=40、f3=20,并提取了弹箭在仿真过程中的实际角运动规律结果如图 4所示。由图可知,利用求导法得到弹箭俯仰角与式(1)给出的正弦曲线存在较大偏差,且相对误差呈周期振荡;而由欧拉转动法得到的弹箭俯仰角变化规律,与正弦曲线完全重合。结果表明,利用该方法可实现对弹箭复杂角运动的精确模拟,从而提高计算精度。值得注意的是,本文所提出的角运动模拟方法,不仅适用于俯仰滚转耦合运动,还适用于更为复杂的已知运动方程的绕心运动。
|
图 4 求导法和欧拉转动法对角运动的模拟精度对比 Figure 4 Comparation of simulation accuracy on angle motion between derivative method and Euler rotation method |
为求解计算弹箭在耦合角运动状态下的俯仰组合动导数和升力系数动导数,需要对CFD仿真得到的气动系数迟滞环进行参数辨识。采用积分法对气动系数迟滞环进行辨识求解,具体推导过程如下:
由式(1)可得弹箭在迎角平面内的迎角运动方程:
| $ \left\{ \begin{array}{l} \alpha = {\alpha _0} + {\alpha _m}\sin \left( {{\omega _a}t} \right)\\ \dot \alpha = \omega {\alpha _m}\cos \left( {{\omega _a}t} \right) = q\\ \ddot \alpha = - {\omega ^2}{\theta _0}\sin \left( {{\omega _a}t} \right) = \dot q \end{array} \right. $ | (10) |
式中,ωa=2πf2为俯仰角速度圆频率;q为瞬时俯仰角速度。
弹箭做小幅强迫俯仰振动时,其非定常气动力和力矩的泰勒展开式为:
| $ \begin{array}{l} {M_z} = {M_{z0}} + M_z^\alpha \cdot \Delta \alpha + M_z^{\dot \alpha } \cdot \Delta \dot \alpha + M_z^q \cdot q\\ \;\;\;\;\;\;\; + M_z^{\dot q} \cdot \dot q + o\left( {\Delta \alpha ,q} \right) \end{array} $ | (11) |
式中,Mz0为初始迎角处的静态俯仰力矩系数,Mzα为静态俯仰力矩系数,
将式(10)带入式(11),利用三角函数系的正交性,在一个周期上进行积分,并进行无量纲化处理(详细推导过程可参见文献[15, 16]), 可得俯仰组合动导数的计算公式为:
| $ {C_1} = \frac{1}{{\pi {\alpha _m}}}\int_{ - {T_0}/2}^{{T_0}/2} {{M_z}\cos \left( {\bar \omega t} \right){\rm{d}}t} $ | (12) |
式中,ω=ωL/2V∞为减缩频率,V∞为来流速度,L为参考长度,T0为振荡周期。
类似的通过对弹箭升力系数迟滞环进行积分可得升力系数组合动导数C2计算公式为
| $ {C_2} = \frac{1}{{\pi {\alpha _m}}}\int_{ - {T_0}/2}^{{T_0}/2} {{C_L}\cos \left( {\bar \omega t} \right){\rm{d}}t} $ | (13) |
需要指出的是,仿真直接得到的通常是在基准坐标下的空气动力和力矩系数的结果.本文讨论的俯仰力矩系数和升力系数均是相对于迎角平面,其中俯仰力矩的方向垂直于迎角平面(弹轴OXB和OX组成的平面),升力方向位于迎角平面内并垂直于OX轴,因此需要将俯仰力矩系数和升力系数向迎角平面投影,即:
| $ {M_z} = {{M'}_z}\sin \varphi + {{M'}_y}\cos \varphi $ | (14) |
| $ {C_L} = {{C'}_L}\sin \varphi - {{C'}_z}\cos \varphi $ | (15) |
式中:M′z、M′y分别为基准坐标系下的气动力矩系数,Mz为迎角平面内的气动力矩系数。C′L、C′z分别为基准坐标系下的升力系数和侧向力系数,CL为迎角平面内的气动力矩系数。
将式(14)、式(15)分别带入式(12)、式(13)可得弹箭在迎角平面内的俯仰组合动导数和升力系数动导数计算公式分别为:
| $ \left\{ \begin{array}{l} {C_1} = \frac{1}{{\pi {\alpha _m}}}\int_{ - {T_0}/2}^{{T_0}/2} {\left( {{{M'}_z}\sin \varphi + {{M'}_y}\cos \varphi } \right)\cos \left( {\bar \omega t} \right){\rm{d}}t} \\ {C_2} = \frac{1}{{\pi {\alpha _m}}}\int_{ - {T_0}/2}^{{T_0}/2} {\left( {{{C'}_L}\sin \varphi - {{C'}_z}\cos \varphi } \right)\cos \left( {\bar \omega t} \right){\rm{d}}t} \end{array} \right. $ | (16) |
采用带翼导弹标准模型BFM[9]动导数实验数据检验本文所采用的CFD仿真方法以及动导数辨识方法的准确性。基于本文1.2节所述数值仿真方法以及1.3节所述动导数辨识方法,对BFM标模在马赫数为1.58、1.76、1.89、2.16、2.48,起始迎角为1.5°、振幅为1.5°条件下的强迫俯仰振动进行了求解计算(仿真过程中取f1=f3=0,f2≠0,即可模拟弹箭的强迫俯仰振动)。参考长度取BFM标模的圆柱部直径D0,参考面积取圆柱部横截面积,质心位置到弹头部距离为5D0。将俯仰组合动导数的计算结果与文献[17, 18]的实验结果进行对比,结果如图 5所示。由图 5可知,俯仰组合动导数计算结果与实验结果变化规律一致,两者绝对值均随马赫数增加而减小,其中仿真值略小于实验值,相对误差在Ma=1.89时最大为6.4%。结果表明,所采用数值仿真方法和动导数辨识方法对带尾翼弹箭的动导数求解具有较高精度。
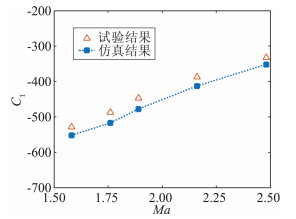
|
图 5 BFM标模俯仰组合动导数随马赫数变化曲线 Figure 5 Curve of pitching and rolling damping derivative of BFM model with Mach number |
由于缺少计算模型的动导数实验数据,无法直接对该模型的动导数计算精度进行分析。作为补充,采用已有的滚转风洞实验数据对非定常数值方法的计算精度进行检验。实验模型几何结构与图 2一致,但尾翼倾角为13°(图 2中的模型尾翼倾角为0°)。风洞实验在南京理工大学HG-4号风洞进行,实验安装图如图 6所示。弹体通过隔转轴承安装在天平轴上,使弹体可绕天平轴进行自由滚转。实验过程中,实验模型在斜置尾翼产生的导旋力矩下做滚转运动,并最终达到稳定转速。实验测量了Ma=0.6时模型在不同迎角下的稳定转速和所受空气动力,表 1给出了Ma=0.6时模型在不同迎角下所达到的稳定转速。

|
图 6 风洞实验安装图 Figure 6 Wind tunnel test setup |
| 表 1 Ma=0.6时,平衡转速实验结果 Table 1 Test results of balance speed for Ma=0.6 |
|
|
采用1.2节所述的非定常滑移网格方法模拟弹箭的滚转运动过程,在仿真过程中,取f1=f2=0,f3按表 1给出的结果取值,以保证仿真条件与实验条件的一致。升力系数仿真结果和实验结果进行对比,结果如图 7所示。由图可知,数值仿真结果与实验结果吻合较好,最大相对误差小于10%,表明本文采用的数值仿真方法能对计算模型的气动参数进行准确预测。
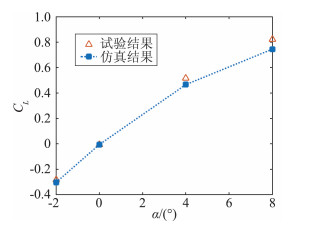
|
图 7 Ma=0.6时,升力系数随迎角变化曲线 Figure 7 Curve of lift coefficient with the angle of attack (Ma=0.6) |
采用本文1.2节所述角运动模拟方法,对弹箭滚转、锥进运动与强迫俯仰运动相耦合的角运动过程进行模拟。计算条件如下:取计算马赫数Ma为0.65,起始迎角α0取为3°,迎角振荡幅值αm取为1.5°,质心位置到弹顶距离取为0.4D。仿真过程中,弹箭俯仰振荡频率f2取为定值20 Hz,锥进频率f1和滚转频率f3取值范围为0到100 Hz,并制定了如表 2所示的4组仿真方案,记为F1、F2、F3、F4,其中F1方案用于分析弹箭在俯仰滚转耦合运动状态下滚转频率对动导数辨识结果的影响,F3方案用于分析弹箭在锥进俯仰耦合状态下锥进频率对动导数辨识结果的影响,F2和F4方案用于分析弹箭同时存在锥进、滚转以及俯仰运动的三自由度耦合运动状态下锥进频率和滚转频率对动导数辨识结果的影响。
| 表 2 仿真方案 Table 2 Simulation scheme |
|
|
从四组仿真方案中选取了三种具有代表性的情况的结果,用于分析滚转运动和锥进运动对弹箭气动力迟滞环以及绕流特性的影响,分别记为P1、P2、P3、P4:①P1是仅存在强迫俯仰振荡的情况(f1=0 Hz,f3=0 Hz,f2=20 Hz);②P2是滚转运动与强迫俯仰振荡耦合的情况(f1=0 Hz,f3=80 Hz,f2=20 Hz);③P3是锥进运动与强迫俯仰振荡耦合的情况(f1=80 Hz,f3=0 Hz,f2=20 Hz)。④补充了同时存在俯仰滚转和锥进运动(f1=80 Hz,f3=80 Hz,f2=20 Hz)的情况进行对比分析,并记为P4。
图 8给出了四种条件下弹箭俯仰力矩系数滞回曲线仿真结果。由图可知,P2、P3、P4的结果的绝对值整体小于P1的结果,其中P4尤为显著,说明在弹箭做强迫俯仰振动过程中,滚转运动或锥进运动的存在,均会导致弹箭俯仰力矩系数绝对值减小,当同时存在滚转运动和锥进运动时,变化尤为显著。P2、P3、P4的结果与P1的结果相比,当存在滚转运动或锥进运动时,俯仰力矩系数滞回曲线不再光滑,而是出现了明显的振荡和偏移。其中由滚转运动(P2)引起的迟滞环振荡相比于由锥进运动(P3)引起的振荡更为显著。这是因为在弹箭在强迫俯仰运动过程中,滚转运动或锥进运动的存在均会引起弹身及尾翼周围的流场不再对称,产生周期性的干扰力和力矩,使迟滞环发生振荡。滚转运动还会引起尾翼相对于迎角平面的方位角不断改变,这将进一步增强俯仰力矩系数的振荡。而本文所定义的锥进运动,并不会引起尾翼相对于迎角平面的方位角发生改变,因此锥进运动引起的迟滞环振荡相对较弱。从图中还可以看出,P3的结果的绝对值小于P2,表明在滚转频率和锥进频率取值相同的情况下,由锥进运动引起的俯仰力矩系数的减小更为显著。此外,P4的迟滞环的振荡和偏移都非常显著,说明锥进运动和滚转运动对结果的影响存在叠加效果。图 9为四种条件下弹箭升力系数滞回曲线仿真结果。将图 9和图 8对比可知,升力系数滞回曲线的变化规律和俯仰力矩系数滞回曲线的变化规律是相似的,只是在数值上有一定差异。滚转运动或锥进运动的存在均会导致弹箭升力数迟滞出现明显的振荡和偏移,且当滚转和锥进运动同时存在时,这种变化尤为显著。以上分析表明,弹箭在耦合角运动状态下的气动力和力矩系数迟滞环,与单纯的强迫俯仰振动得到的迟滞环相比存在显著差异,这必然对弹箭动导数的稳定性辨识结果产生影响。
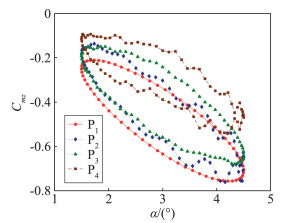
|
图 8 俯仰力矩系数滞回曲线 Figure 8 Hysteresis curve of pitching moment coefficient |
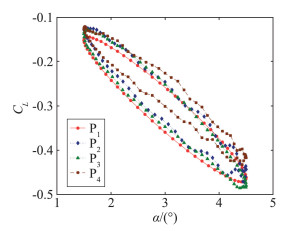
|
图 9 升力系数滞回曲线 Figure 9 Hysteresis curve of lift coefficient |
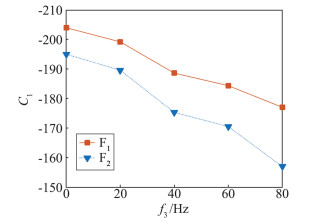
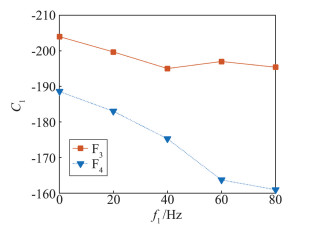
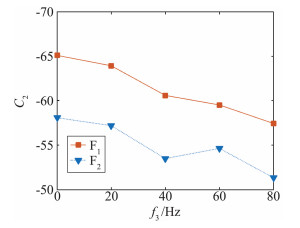
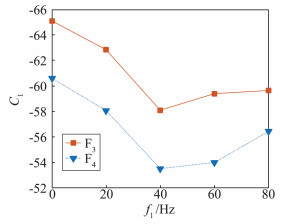
为定量分析弹箭滚转运动对其俯仰动导数辨识结果的影响程度,采用1.3节所述方法对俯仰力矩系数和升力系数迟滞曲线进行参数辨识,得到结果如图 10~图 13所示。
|
图 10 俯仰组合动导数随滚转频率的变化曲线 Figure 10 Pitch damping derivative changing with the roll frequency |
|
图 11 俯仰组合动导数随锥进频率的变化曲线 Figure 11 Pitch damping derivative changing with the coning frequency |
|
图 12 升力系数动导数随滚转频率的变化曲线 Figure 12 Lift coefficient derivative changing with the roll frequency |
|
图 13 俯仰组合动导数随锥进频率的变化曲线 Figure 13 Lift coefficient derivative changing with the coning frequency |
图 10和图 11分别是根据表 1给出的仿真方案得到的俯仰组合动导数随滚转频率和锥进频率的变化曲线。由图可知,俯仰组合动导数随滚转频率和锥进频率增加均具有减小趋势,且滚转频率引起的减小幅值更为显著。F2和F4的结果均分别小于F1和F3的结果,表明由滚转运动引起的结果的减小与由锥进运动引起的结果的减小,存在叠加效果。但从图中可以看出,F2与F1之间的差值以及F4与F3之间的差值分别随滚转频率增加而有所增大,其中图 11尤为明显,表明当同时存在滚转运动和锥进运动时,由滚转运动引起的结果的减小与由锥进运动引起的结果的减小,并非简单的线性叠加关系,即滚转运动和锥进运动对弹箭俯仰动导数的影响存在耦合效应。
图 12和图 13分别是根据表 1给出的仿真方案得到的升力系数动导数随滚转频率和锥进频率的变化曲线。由图可知,F2和F4的结果均分别小于F1和F3的结果,表明滚转运动和锥进运动对升力系数的影响同样存在的叠加效果。图 12的结果显示,弹箭升力系数动导数随滚转频率增加而明显的减小趋势。其中仅存在滚转运动时(F1),升力系数动导数随滚转频率增加而单调减小,且变化规律是接近线性的。当同时存在锥进运动时(F2),升力系数变化规律出现振荡,这是因为滚转运动和锥进运动与强迫俯仰运动的共同作用使弹箭绕流特性更加复杂,尤其在尾锥以及尾翼等部位的压力分布出现了非线性变化,从而引起了弹箭整体所受空气动力的改变。由图 13可知,升力系数动导数随锥进频率增加不再单调减小,而是按先减小后增大的规律变化,变化规律具有明显非线性特性,且当锥进频率F1=40 Hz时,升力系数动导数达到最小值。图 12和图 13结果的差异,体现了滚转运动与锥进运动对动导数辨识结果的影响存在明显的差异。
表 3给出了滚转力矩系数和升力系数的部分计算结果,表中的相对变化率是相对于仅存在强迫俯仰运动(f1=0 Hz,f2=0 Hz)的情况而言。从表中可以看出,除f1=80 Hz,f2=0 Hz(即锥进运动与强迫俯仰运动耦合)的情况外,俯仰组合动导数和升力系数动导数均达到10%以上,其中当滚转频率f3=80 Hz、锥进频率f1=40 Hz时,俯仰组合动导数减小了23.1%,升力系数动导数减小了21.2%,结果表明,弹箭在三自由度耦合角运动(滚转运动和锥进运动与强迫俯仰运动相耦合)状态下,动稳定性导数的辨识结果与单纯的强迫俯仰振动的结果相比具有显著差异,因此在进行弹箭动导数计算和稳定性分析时需被充分考虑。
| 表 3 不同条件下的动导数计算结果对比 Table 3 Comparation of dynamic derivative under different conditions |
|
|
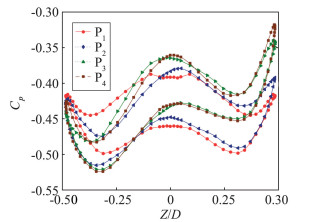
为进一步分析滚转运动和锥进运动对弹箭所受空气动力的影响,提取了四种情况(P1~P4)下,弹箭尾锥位置和水平尾翼位置的压力分布情况,结果如图 14和图 15所示。图 14是弹箭在瞬时迎角为3°尾锥部的周向压力分布情况。由图 14可知,当弹箭只作单纯的强迫俯仰振动时(无滚转无锥进,对应曲线P1),弹箭尾锥部左右两侧压力对称,且迎风面压力明显大于背风面。当弹箭存在滚转运动时(P2)或锥进运动时(P3),尾锥部压力分布不再对称,主要表现为弹箭右侧压力大于左侧压力,且迎风面和背风面压力差亦发生改变。原因为弹箭尾锥部锥度较大,弹箭绕流在尾锥部形成明显的涡。当弹箭无滚转无锥进时,尾锥部的涡较对称,此时尾锥部的压力分布是对称的;当弹箭存在滚转或锥进运动时,由于空气黏性的作用,弹箭附面层位移厚度和涡结构将发生非对称畸变,即产生马格努斯效应,使尾锥部周向压力分布发生改变。此外,对比P2和P3的结果可知,锥进运动产生的非对称性更为显著。当弹箭同时存在滚转和锥进运动时(P4),尾锥部压力分布非对称性进一步增加,表明滚转运动和锥进运动对弹箭绕流特性的影响存在耦合效应,且这种耦合效应是非线性的。
|
图 14 尾锥部的压力分布 Figure 14 Pressure distribution of the tail cone |
|
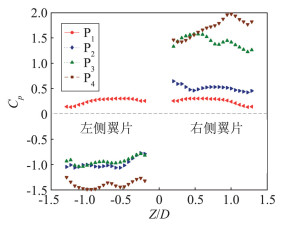
图 15 水平尾翼压力分布 Figure 15 Pressure distribution of the horizontal tail |
图 15给出了弹箭在瞬时迎角为3°时,水平尾翼的压力分布情况(考虑到升力系数和俯仰力矩系数主要受水平尾翼的压力分布的影响,因此只提取了水平尾翼的压力分布)。由图可知,当无滚转且无锥进时(P1),由于迎角存在,左右尾翼的下侧翼面压力均大于上侧压力,且压力分布是左右对称的。当存在滚转运动(P2)或锥进运动(P3)时,尾翼翼面微元的瞬时迎角发生改变,并与初始迎角叠加,使尾翼压力分布不再对称,表现为右侧翼面压力值增大,左侧压力系数由正值变为负值。对比曲线P2和曲线P3可知,左侧翼在滚转频率f3=80 Hz和锥进频率f1=80 Hz两种情况下压力系数是接近相等的,而右侧翼在两种情况下的压力系数显著不同。表明由滚转运动和锥进运动引起的水平尾翼压力分布变化是不同的。当同时存在滚转和锥进时(P4),左右两翼片的压力系数绝对值均大于仅存在滚转或锥进运动的情况。表明滚转运动和锥进运动对尾翼压力分布的影响存在耦合效应,且这种耦合效应是非线性的。尾翼压力分布的改变必然引起弹箭升力系数以及俯仰力矩系数发生改变。
以上分析表明,当存在一定迎角时,滚转运动和锥进运动,使弹箭表面(尤其在弹箭尾锥和尾翼处)的压力分布不再对称,即产生马格努斯效应,这必然引起弹箭所受空气动力发生改变。由于弹箭在耦合角运动状态下,弹箭迎角随强迫俯仰运动过程不断改变,由滚转运动和锥进运动引起的马格努斯效应也将随之改变,从而形成周期性的诱导力和力矩。此外,滚转运动还会引起尾翼相对于迎角平面的相位角不断改变,引起弹箭所受空气动力发生振荡。以上两方面的原因导致弹箭在耦合角运动状态下的气动力系数迟滞环与单纯的强迫俯仰过程相比发生了明显振荡和偏移,从而对弹箭动稳定性导数的辨识结果产生影响。
4 结论通过对弹箭在俯仰滚转耦合角运动状态下的气动特性进行数值仿真研究,得出以下结论:
1) 本文提出的基于欧拉转动定理和滑移网格技术的复杂角运动模拟方法,可在弹箭非定常流场求解过程中,有效消除弹箭姿态角计算的累积误差。此方法不仅适用于模拟弹箭俯仰滚转耦合角运动,而且对任意给定形式的角运动同样适用。将数值仿真结果与已有的实验数据进行对比验证了所采用的数值仿真方法以及动导数辨识方法具有较高的准确性;
2) 弹箭在三自由度耦合角运动(滚转运动和锥进运动与强迫俯仰运动相耦合)状态下,气动力系数迟滞环发生明显的振荡和偏移,且动稳定性导数的辨识结果与单纯的强迫俯仰振动的结果相比具有显著差异,其中,当滚转频率f3=80、锥进频率f1=40时,俯仰组合动导数减小了23.1%,升力系数动导数减小了21.2%,因此在进行弹箭动导数计算和稳定性分析时需被充分考虑。
| [1] |
Weinacht P. Navier-stokes predictions of pitch-damping for a family of flared projectiles[C]//9th Applied Aerodynamics Conference. 1991: 3339. https://arc.aiaa.org/doi/abs/10.2514/6.1991-3339
|
| [2] |
Despirito J. Navier-Stokes predictions of dynamic stability derivatives:evaluation of steady-state methods[J]. Journal of Spacecraft and Rockets, 2009, 46(6): 1142. DOI:10.2514/1.38666 |
| [3] |
Oktay E. CFD predictions of dynamic derivatives for missiles[C]//40th AIAA Aerospace Sciences Meeting and Exhibit, 2002, 276. https://arc.aiaa.org/doi/abs/10.2514/6.2002-276
|
| [4] |
Tao Y, Fan Z, Zhao Z, et al. Predictions of dynamic damping coefficients of basic finner based on CFD[J]. Journal of Aerospace Power, 2010(1): 018. |
| [5] |
Murman S M. Reduced-frequency approach for calculating dynamic derivatives[J]. AIAA Journal, 2007, 45(6): 1161. DOI:10.2514/1.15758 |
| [6] |
陈琦, 陈坚强, 谢昱飞, 等. 谐波平衡法在非定常流场中的应用[J]. 航空学报, 2014, 35(3): 736-743. Chen Qi, Chen Jianqiang, Xie Yufei, et al. Application of a harmonic balance method in rapid predictions of dynamic stability derivatives[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 35(3): 736-743. |
| [7] |
叶川, 马东立. 利用CFD技术计算飞行器动导数[J]. 北京航空航天大学学报, 2013, 39(02): 196-200, 219. Ye Chuan, Ma Dongli. Aircraft dynamic derivatives calculation using CFD techniques[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(02): 196-200, 219. |
| [8] |
米百刚, 詹浩, 朱军. 基于CFD数值仿真技术的飞行器动导数计算[J]. 空气动力学学报, 2014, 32(6): 834-839. Mi Baigang, Zhan Hao, Zhu Jun. Caculation of dynamic derivatives for aircraft based on CFD technique[J]. Acta Aerodynamica Sinica, 2014, 32(6): 834-839. DOI:10.7638/kqdlxxb-2012.0206 |
| [9] |
米百刚, 詹浩, 王斑. 基于刚性动网格技术的动导数数值模拟[J]. 航空动力学报, 2014, 29(11): 2659-2664. Mi Baigang, Zhan Hao, Wang Ban. Numerical simulation of dynamic derivatives based on rigid moving mesh technique[J]. Journal of Aviation Power, 2014, 29(11): 2659-2664. |
| [10] |
么虹, 才义, 徐志福. 细长体导弹高速动导数试验技术研究[J]. 空气动力学学报, 2017, 35(2): 214-219. Yao Hong, Cai Yi, Xu Zhifu. Investigation on testing technique of high-speed dynamic stability derivatives for slender missile[J]. Acta Aerodynamica Sinica, 2017, 35(2): 214-219. DOI:10.7638/kqdlxxb-2016.0147 |
| [11] |
刘文, 张陈安, 王发民. 乘波体荷兰滚模态特性研究[J]. 空气动力学学报, 2017, 35(3): 444-453. Liu Wen, Zhang Chen'an, Wang Famin. Study on characteristics of dutch roll mode for hypersonic waverider[J]. Acta Aerodynamica Sinica, 2017, 35(3): 444-453. DOI:10.7638/kqdlxxb-2017.0024 |
| [12] |
黄达, 吴根兴. 飞机偏航-滚转耦合运动非定常空气动力实验[J]. 南京航空航天大学学报, 2005, 37(4): 408-411. Huang Da, Wu Genxing. Experiment on fighter oscillating in large amplitude yaw-roll motion[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2005, 37(4): 408-411. DOI:10.3969/j.issn.1005-2615.2005.04.002 |
| [13] |
史志伟, 黄达, 吴根兴, 等. 耦合运动非定常气动模型对飞机飞行特性仿真的影响[J]. 航空学报, 2008, 29(6): 1424-1428. Shi Zhiwei, Huang Da, Wu Genxing, et al. Effects of coupled motion unsteady aerodynamic model on flight characteristics simulation of aircraft[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1424-1428. DOI:10.3321/j.issn:1000-6893.2008.06.003 |
| [14] |
吴金华, 孙海生, 沈志洪, 等. 旋转流场下的振荡动导数试验技术研究[J]. 实验流体力学, 2014, 28(4): 54-58. Wu Jinhua, Sun Haisheng, Shen Zhihong, et al. Investigation of test technique of oscillatory dynamic derivative in rotational flow field[J]. Journal of Experiments in Fluid Mechanics, 2014, 28(4): 54-58. |
| [15] |
Wang X. Computational fluid dynamics predictions of stability derivatives for airship[J]. Journal of Aircraft, 2012, 49(3): 933-940. DOI:10.2514/1.C031634 |
| [16] |
Ronch A D. Computation of dynamic derivatives using CFD[C]//28th AIAA Applied Aerodynamics Conference, Chicago, lllinois, 2010.
|
| [17] |
Lrving S. Dynamic and static stability measurements of the basic finner at supersonic speeds, Navord Report 4516[R]. U.S Naval Ordnance Laboratory White OAK. Maryland, 1960.
|
| [18] |
Moore F G. Dynamic derivatives for missile configurations to Mach number three[J]. Journal of Spacecraft and Rockets, 1978, 15(2): 65-69. DOI:10.2514/3.57289 |
 2018, Vol. 36
2018, Vol. 36


