前掠翼潜在的优异操纵性和过失速机动飞行时的优势是吸引战斗机设计师的关键因素[1]。20世纪后期,随着新型复合材料和机翼气动弹性剪裁技术[2]的发展,前掠翼跨声速气弹扭转发散问题基本得到解决,使前掠翼有可能像后掠翼一样在现代商用飞机和军用飞机上得到广泛的应用和发展。有些研究资料表明在任务一定的条件下,前掠翼飞机比后掠翼飞机的阻力降低10%~20%,重量轻5%~25%,成本也可大大降低[3]。尤其令人瞩目的是,美国航空航天局(NASA)成功开发X-29前掠翼技术验证机,之后一直在秘密研制一种“Switchblade”变前掠翼战斗轰炸机以及一种高空长航时前掠翼隐身无人机“暗星(Darkstar)”,另外,截止2014年,俄罗斯苏霍伊飞机设计局成功研发的SU-47“金雕”前掠翼战斗机仍在进行飞行试验工作。这些机型的研发和试验大大增加了国内外学者对前掠翼飞机应用的信心和热情[4-8]。
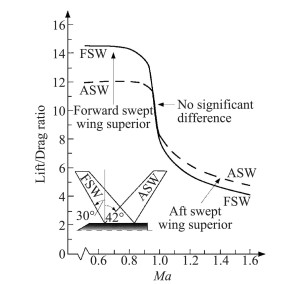
早期基于势流理论,得到前掠翼大量理论成果,但其研究工作中相同翼展和梢根比下前掠翼前缘掠角总小于后掠翼前缘掠角,同时前掠翼后缘掠角大于后掠翼,在这种情况下,得到低马赫数下前掠翼的优点[9-11]:(1)更小的诱导阻力;(2)更大的升力线斜率;(3)逐渐减弱的抬头趋势;(4)更小的结构展长:(5)与当量后掠翼相比更小的质量;(6)前掠翼根首先引起流动分离,能同时保证副翼效率和滚转阻尼,在流动分离的情况下拥有更好的侧滑稳定性和操纵效率;(7)跨声速时无明显优势,超声速下前掠翼甚至存在气动上的劣势(见图 1)。
|
图 1 不同马赫数下前掠翼与后掠翼 Figure 1 Forward- and aft-swept wings at different Mach Numbers |
但是,NASA在X-29的设计实验试飞结果[11-17]却与上述结论中(1)(2)相悖。对采用圆弧翼型的翼身组合体进行风洞实验[10, 15]中,通过正吹和反吹获得前掠32°与后掠60°机翼的低速纵向气动性能并进行对比。来流条件马赫数为0.3、雷诺数为1.4×106时得到前掠翼的升力线斜率小于后掠翼,前掠翼最大升力系数(CLmax=0.96,αCLmax=40°)小于后掠翼(CLmax=1.2,αCLmax=28°),但失速迎角大于后掠翼。但是两机翼掠角不同,并不是在同一基础上进行对比,不能全面反应两者性能的优劣[3]。
Poll[18]等针对无根梢比尖前缘双凸翼型机翼,采用不同掠角方向和边条进行了马赫数为0.1的低速风洞试验,实验结果显示前掠翼升力线性段为-5°~9°,后掠翼升力线性段为-5°~13°,两者在小迎角时升力线斜率基本相同,前掠翼在迎角35°取得最大升力系数为1.15,后掠翼在迎角40°取得最大升力系数为1.12,结论与NASA结论相差很大。
西北工业大学张彬乾与德国布伦瑞克工业大学Laschka对前掠翼及前掠翼鸭翼布局[19-21]进行了一系列的低速风洞实验,对前掠翼良好的升阻特性、力矩特性与失速特性进行了验证,并对前掠翼前后缘涡系对升阻力特性的影响进行分析,进而对利用边条和鸭翼对前掠翼构型的流动控制进行研究。
美国安柏瑞德航空大学Traub[22]等研究了箭形机翼的边条位置对机翼纵向气动性能的影响,对无梢根比的Λ=-65°、Λ=65°的前后掠翼,展弦比均为2,分别在前后缘根部加装翼展长度30%的边条翼,在风速25 m/s,Re=1.8×105下进行风洞实验。实验显示在迎角大于4°时前掠翼升力小于后掠翼。流线显示前掠翼翼根有较大范围的分离区,后掠翼翼尖的分离则相对较小。
刘文法[23]针对40°的前掠翼和后掠翼模型在Ma=0.4时进行CFD计算结果,发现在α < 16°时后掠翼升力系数大于前掠翼,α>16°前掠翼升力较大,同时前掠翼失速迎角为32°,后掠翼仅为12°,前掠翼的失速性能明显好于后掠翼。
面对文献中的不同结论,深入分析前掠翼气动特性,从物理机制上探讨前掠翼的流动机理,增加对前掠翼流动和气动特性的理解是非常迫切的工作。为避免机翼其他参数对流动的影响,本文设计采用了相同翼型剖面、相同展弦比、无根梢比的前掠45°(Λ=-45°)与后掠45°(Λ=45°)机翼,提出了展向动量测定法,结合数值模拟方法在Ma=0.2、Re=4.6×106条件下深入分析前掠翼与后掠翼的纵向气动性能,结合展向动量测定法定量分析了前掠翼与后掠翼的流动机理。
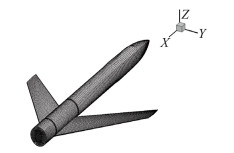
1 算例验证为验证数值模拟的准确性,本文采用慕尼黑工业大学Breitsamter等[1]在2001年慕尼黑工业大学流体力学实验室开展的针对前掠翼身组合体的低速风洞实验进行验证。风洞实验区直径1.5 m,长3 m,最大风速为55 m/s,湍流度为0.3%~0.4%。模型为机翼前掠40°的翼身组合体,机翼翼型为NACA64A010,如图 2所示。试验风速为40 m/s,基于参考弦长的Re=0.46×106。本文分别采用课题组自研的基于雷诺平均N-S方程流场求解器General Fluid & Structure Interaction (GFSI)与ANSYS FLUENT进行数值模拟,采用结构化网格,机体面网格数为37 820,体网格数为5 076 260,首层网格y+约等于1,采用SST湍流模型,计算与风洞实验结果对比见图 3。
|
图 2 前掠翼几何模型与面网格 Figure 2 Geometry model and surface mesh of forward-swept wing body |
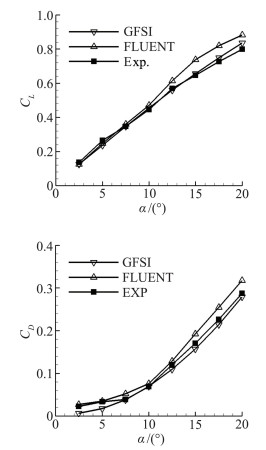
由图 3可以看出,GFSI,FLUENT计算结果与实验结果基本吻合,而FLUENT结果在大迎角时计算值偏大,GFSI对前掠翼的数值模拟计算误差更小,故选用GFSI作为数值模拟求解器。
|
图 3 翼身融合体升阻力随迎角变化 Figure 3 Wing body's lift and drag |
根据牛顿第二定律(式1),施加在物体表面的力等于物体动量的时间变化率。对于飞行器来说,飞行器无动力飞行过程中受到的力即源自包含飞行器控制体内的动量的时间变化率。包含飞行器控制体内动量的时间变化率分为两部分:1)经由控制体表面单位时间净流入(流出)的动量(动量通量);2)由非定常扰动引起单位时间控制体的动量增量。在定常流场计算中式(2)中∂/∂t≡0,则作用在物体上的力仅由动量通量项决定,则得到式(3)。
| $ \mathit{\boldsymbol{F = }}\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {m\mathit{\boldsymbol{V}}} \right) = \dot m\mathit{\boldsymbol{V}} $ | (1) |
| $ \mathit{\boldsymbol{F = }}\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S {\left( {\rho \mathit{\boldsymbol{V}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}} \right)\mathit{\boldsymbol{V}}} \mathit{\boldsymbol{ + }}\frac{\partial }{{\partial t}}\mathop{{\int\!\!\!\!\!\int\!\!\!\!\!\int}\mkern-31.2mu \bigodot}\limits_\nu {\rho \mathit{\boldsymbol{V}}{\rm{d}}\nu } $ | (2) |
| $ \dot m\mathit{\boldsymbol{V}} = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc}\limits_S {\left( {\rho \mathit{\boldsymbol{V}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}} \right)\mathit{\boldsymbol{V}}} $ | (3) |
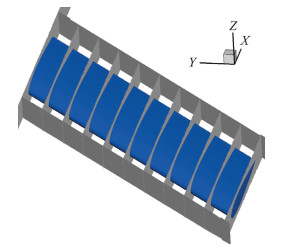
对前掠翼翼升力机理进行分析,将机翼沿展向分为10个控制体(图 4),并对每个控制体内的动量通量进行积分计算,深入分析前后掠翼升力物理机制上的异同。
|
图 4 机翼沿展向控制体示意图 Figure 4 Spanwise control body for momentum method |
对前掠翼气动性能的研究中,大多文献的研究中未能避免根梢比对性能的影响。在NASA的实验中甚至采用机翼模型正反吹来进行性能的对比分析,造成模型前掠翼为32°掠角,后掠翼为60°掠角,掠角的差异对性能的影响也未能避免。为避免其他机翼参数对机翼性能产生影响,本文设计了前掠45°(Λ=-45°)与后掠45°(Λ=45°)机翼进行计算与对比分析,前后掠机翼均采用NACA0012翼型,展长为4 m,展弦比均为4,根梢比均为1。
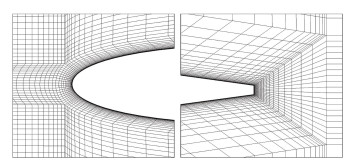
数值计算采用半翼展模型,空间流场为机翼参考弦长的100倍(前后上下左各100倍)。为排除网格对数值模拟结果的影响,采用结构化网格进行空间离散,前后掠翼面网格分布完全相同,附面层相同,体网格数目也完全相同。分别采用两套网格(带附面层和不带附面层)进行有黏和无黏流场计算,其中黏性网格机翼面网格数为12 176,首层网格y+约等于1,附面层为30层,体网格数为6 802 039;无黏网格机翼面网格数量为13 275,体网格数为3 841 201。机翼外形与网格见图 5、图 6、图 7。

|
图 5 前掠翼与后掠翼面网格 Figure 5 Forward- and aft-swept wings' surface grid |
|
图 6 有黏网格附面层网格局部放大图 Figure 6 Boundary layer mesh of viscous computation |
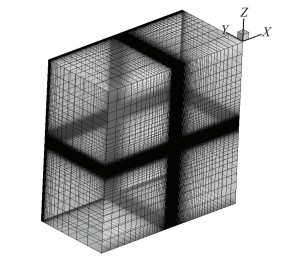
|
图 7 计算流域及远场网格 Figure 7 Flow field and far field grid |
采用GFSI作为流场求解器,计算状态为Ma=0.2,Re=4.6×106。采用绝热壁面边界,迎风格式为Roe格式,其中有黏计算采用SST湍流模型。
4 前掠翼升阻力特性分析数值模拟计算得到前后掠翼升阻力特性曲线,如图 8、图 9、图 10。
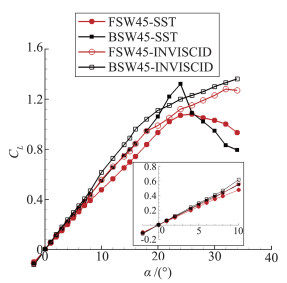
|
图 8 前后掠翼升力特性曲线 Figure 8 Forward- and aft-swept wings' lift curves |
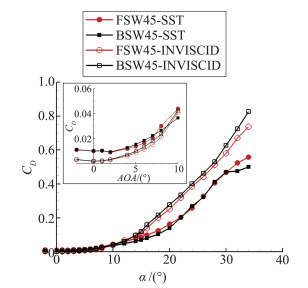
|
图 9 前后掠翼阻力特性曲线 Figure 9 Forward- and aft-swept wings' drag curves |
|
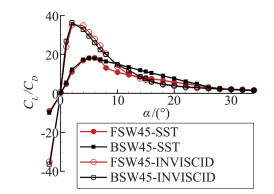
图 10 前后掠翼升阻比特性曲线 Figure 10 Forward- and aft-swept wings' lift/drag ratio |
由图 8中小迎角下前掠翼与后掠翼升力均随迎角增加而线性增长,无黏和有黏条件下相同迎角时前掠翼的升力系数均小于后掠翼,且升力线斜率小于后掠翼,升力表现稍劣。无黏计算无法准确计算大迎角分离流动,其升力变化不符合物理规律,无法体现流动的非线性。有黏计算中前掠翼最大升力系数CLmax=1.08小于后掠翼CLmax=1.32,失速迎角αstalling=26°大于后掠翼αstalling=24°,失速后后掠翼升力迅速减小,而前掠翼升力减小则十分缓慢,前掠翼大迎角失速特性较好。
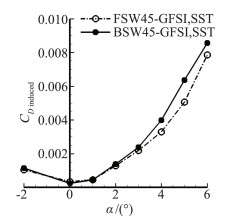
对于图 9,小迎角下前掠翼阻力在各迎角均小于后掠翼,且两者之间阻力差随迎角增加不断扩大。但7°~8°迎角前掠翼阻力突增,主要是由于前掠翼翼根附面层堆积,使得翼根更早发生分离,前掠翼阻力大于后掠翼。而在后掠翼失速后,后掠翼阻力逐渐与前掠翼持平。取无限翼展机翼计算其阻力CD_in,则三维有限翼展机翼翼尖下洗引起的诱导阻力为CD_induced=CD-CD_in,计算结果如图 11。有黏计算中前掠翼小迎角下诱导阻力均小于后掠翼,从而验证了前掠翼诱导阻力小的结论。
|
图 11 前后掠翼小迎角诱导阻力 Figure 11 Forward- and aft-swept wings' induced drag |
图 10给出前掠翼与后掠翼升阻比曲线。无黏条件下后掠翼升阻比在3°迎角之前好于前掠翼,3°迎角之后前掠翼升阻比大于后掠翼,由于前掠翼升力在整个迎角范围内均小于后掠翼,其升阻比在3°迎角之后优于后掠翼的主要原因在于前掠翼相比后掠翼更小的诱导阻力。而有黏条件下前掠翼小迎角气动效率也小于后掠翼,仅在最大升阻比位置处(α=6°, (CL/CD)max=18.2)优于后掠翼(α=6°, (CL/CD)max=17.9),之后由于前掠翼翼根分离阻力上升,其气动效率迅速下降,直到失速迎角附近前掠翼与后掠翼气动效率相当。另外说明黏性作用对前掠翼升阻力特性影响比较大,具体地说黏性作用使得前掠翼在无黏小迎角条件下的升阻比优势丧失。主要的原因有两点:(1)前掠翼有黏条件下升力较无黏条件下平均下降8.94%(1°≤α≤6°),后掠翼相同条件下平均下降7%;(2)前掠翼有黏条件下阻力较无黏条件增加3.5%,后掠翼相同条件下平均增加3.14%。黏性作用导致前掠翼在有黏条件下气动效率劣于后掠翼。这说明文献中采用势流理论对前掠翼气动性能进行预测是不合理的,得到的结论与真实情况往往不同。
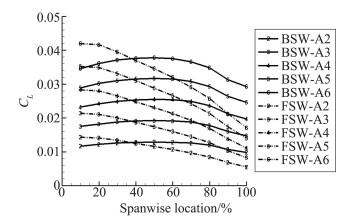
5 前掠翼流动机理分析提取有黏计算结果小迎角(0°~6°)时机翼升力沿翼展方向分布如图 12。图中相同迎角下前掠翼升力向翼根汇聚,升力翼根处大于后掠翼,翼梢处小于后掠翼。前掠翼升力展向分布更接近椭圆分布。根据普朗特升力线理论,有限翼展机翼升力分布为椭圆分布时其诱导阻力最小,则升力展向分布特征决定了前掠诱导阻力小,这也从图 11中得到验证。
|
图 12 前后掠机翼升力沿展向分布 Figure 12 Forward- and aft-swept wings' spanwise lift distribution |
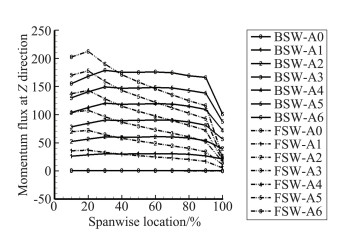
利用展向动量测定法对前掠翼与后掠翼的升力形成机理进行分析。从机翼绕流流场的选取固定六面体控制体区域,将控制体沿展向分为10个局部控制体(见图 4),由于X方向的动量通量项对升力贡献有限,为方便计算,仅取Z方向的动量通量项(式4)对升力的形成机制进行分析。由式4计算机翼不同展向位置控制体内(式中密度ρ,分速度u、v、w均为无量纲量),得到不同展向位置Z向动量通量分布如图 13所示。
| $ {{\left( \dot{m}\mathit{\boldsymbol{V}} \right)}_{Z}}=\iint\limits_{{{S}_{Z}}}{\rho uw\text{d}x\text{d}y}+\iint\limits_{{{S}_{Z}}}{\rho vw\text{d}x\text{d}y}+\iint\limits_{{{S}_{Z}}}{\rho ww\text{d}x\text{d}y} $ | (4) |
|
图 13 Z向动量通量沿展向分布 Figure 13 Z direction spanwise momentum flux distribution |
图 13中Z向动量通量沿展向分布前掠翼
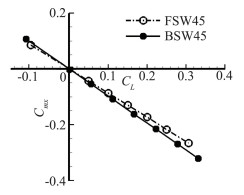
前掠翼靠近翼根处翼面升力大,靠近翼梢处翼面升力小的升力分布形式对结构也带来显而易见的优势,即翼根弯矩比后掠翼更小,计算两机翼翼根弯矩Cmx随升力变化如图 14,前掠翼与后掠翼翼根弯矩与升力基本成线性变化关系,相同升力下前掠翼的翼根弯矩仅为后掠翼的89.4%,这将对前掠翼布局的结构设计带来极大的裕度,对提高布局整体刚度和结构减重带来极大的优势。
|
图 14 前后掠翼翼根弯矩随升力变化 Figure 14 Forward- and aft-swept wings' bending torque |
利用课题组研发的流场求解器GFSI进行前掠翼标模计算,计算结果与实验结果吻合良好。设计了相同翼展、相同弦长、根稍比均为1的前掠45°机翼和后掠45°机翼,对其低速气动性能进行了有黏和无黏计算,对其升阻力特性进行对比分析,分析计算了其诱导阻力。提出展向动量测定法对前掠翼升力形成机理进行深入分析,进一步探讨了前掠翼升力分布特征对机翼翼根弯矩特性的影响。综上得到结论如下:
(1) 前掠翼升力的展向输运形成了典型的翼根升力大,翼尖升力小的接近椭圆分布特点,其诱导阻力更小。而后掠翼升力展向输运相对较为微弱。
(2) 有黏条件前掠翼下升力较大,阻力增加也更多,黏性作用对前掠翼气动效率影响更大,说明以往文献中仅采用势流理论对前掠翼升力特性预测是不合理的,同时“前掠翼升力大,升力线斜率大”的结论也是不准确的。对前掠翼的流体计算应着眼于有黏条件的计算。
(3) 小迎角时前掠翼气动效率低于后掠翼,仅在最大升阻比的迎角下前掠翼气动效率优于后掠翼,在中等迎角前掠翼气动效率较低,但前掠翼失速迎角大,失速后升力缓慢减小,大迎角失速特性优异。
(4) 在相同升力下前掠翼翼根升力大,翼尖升力小的升力分布特性使得前掠翼翼根弯矩小于后掠翼翼根弯矩,对机翼结构设计减重提供了优势。
| [1] |
Breitsamter C, Laschka B. Vortical flowfield structure at forward swept-wings configurations[J]. Journal of Aircraft, 2001, 38(2): 193-207. DOI:10.2514/2.2758 |
| [2] |
Krone N J. Divergence elimination with advanced composite. AIAA-75-1009[R]. Reston: AIAA, 1975. DOI: 10.2514/6.1975-1009
|
| [3] |
方宝瑞. 飞机气动布局设计[M]. 北京: 航空工业出版社, 1997: 947-948. Fang Baorui. Aircraft aerodynamic configuration design[M]. Beijing: China Aviation Press, 1997: 947-948. |
| [4] |
Gupta S C. Aerodynamic characteristics of forward sweep[C]//Flight Simulation Technologies Conference and Exhibit, Guidance, Navigation, and Control and Co-located Conferences, 1990-3401, 1990. DOI: 10.2514/6.1990-3041
|
| [5] |
Spacht G. The forward swept wing: a unique design challenge[C]//AIAA Aircraft Systems Meeting, Anaheim, California, 1980-1885, 1980. DOI: 10.2514/6.1980-1885
|
| [6] |
Xue Rongrong, Ye Zhengyin, Wang Gang. Aerodynamic characteristic comparison of the Forward-and back-swept wings[C]//30th Congress of the International Council of the Aeronautical Science. ICAS Proceedings, Daejeon, Korea, Sep 23-30, 2016.
|
| [7] |
Krone N J. Forward swept wing flight demonstrator[C]//AIAA Aircraft Systems and technology Meeting. Anaheim, California, 1980, 1980-1882. DOI: 10.2514/6.1980-1882
|
| [8] |
Nangia R K, Palmer M E. Flying wings (blended wing bodies) with aft-and forward-sweep, relating design camber and twist to longitudinal control[C]//AIAA Atmospheric Flight Mechanics Conference & Exhibit. Monterey, California. 2002, 2002-4616. DOI: 10.2514/6.2002-4616
|
| [9] |
Truckernbrodt E. How to Improve the performance of transport aircraft by variation of wing aspect-ratio and twist[C]//12th Congress of the International Council of the Aeronautical Science. ICAS Proceedings, 1980: 1-17.
|
| [10] |
Lobert G. Spanwise lift distribution of forward-and aft-swept wings in comparison to the optimum distribution form[J]. Journal of Aircraft, 1981, 18(6): 496-498. DOI:10.2514/3.44717 |
| [11] |
Huffman J K, Fox C H. Subsonic longitudinal and lateral-directional static aerodynamic characteristics for closed-coupled wing-canard model in both swept back and swept forward configurations[R]. NASA TM-74092, 1978.
|
| [12] |
Murri D G, Nguyen L T, Grafton S B. Wind tunnel free-flight investigation of a model of a forward swept wing fighter configuration[R]. NASA TP-2230, 1984.
|
| [13] |
Mann M J, Mercer C E. Forward swept wing configuration designed for high maneuverability by use of a transonic computational method[R]. NASA TP-2628, 1986.
|
| [14] |
Mann M J, Huffman J K, Fox C H. Subsonic longitudinal and lateral-directional characteristics of a forward-swept-wing fighter configuration at angles of attack up to 47°[R]. NASA TP-2727, 1987.
|
| [15] |
Huffman J K, Fox C H. Subsonic longitudinal and lateral-directional static aerodynamic characteristics for a model with swept back and swept forward wings[R]. NASA TM-74093, 1978.
|
| [16] |
Moore M, Frei D. X-29 forward swept wing aerodynamic overview[C]//Applied Aerodynamic Conference, Fluid Dynamics and Co-located Conferences. Danver. MA. 1983, 1983-1834. DOI: 10.2514/6.1983-1834
|
| [17] |
Mann M J, Mercer C E. A forward swept wing fighter configuration designed by a transonic computational method[J]. Journal of Aircraft, 1986, 23(6): 506-512. DOI:10.2514/3.56774 |
| [18] |
Poll D I A, Qiu C H. Some effects of sweep direction and strakes for wings with sharp leading edges[R]. Cranfield Institute of Technology, 1984.[WX(4.5mm, 75.5mm]
|
| [19] |
张彬乾, Laschka B. 前掠翼气动特性研究[J]. 西北工业大学学报, 1989, 7(3): 321-328. Zhang Binqian, Laschka B. On forward swept-wing's aerodynamic characteristics[J]. Journal of Northwestern Polytechnical Univ, 1989, 7(3): 321-328. |
| [20] |
张彬乾, Laschka B. 前掠翼鸭式布局中鸭翼的气动特性[J]. 西北工业大学学报, 1990, 8(3): 327-334. Zhang Binqian, Laschka B. On aerodynamic characteristics of canard in canard-forward-swept wing configuration[J]. Journal of Northwestern Polytechnical Univ, 1990, 8(3): 327-334. |
| [21] |
张彬乾, Laschka B. 前掠翼根部流动分离的控制[J]. 航空学报, 1992, 13(5): 241-246. Zhang Binqian, Laschka B. Control of the flow separation at the root part of Forward-Swept Wing(FSW)[J]. Journal of Northwestern Polytechnical Univ, 1992, 13(5): 241-246. DOI:10.3321/j.issn:1000-6893.1992.05.001 |
| [22] |
Traub L W, Jesse L. Aerodynamic characteristics of forward and aft-swept arrow wings[J]. Journal of Aircraft, 2009, 46(4): 1454-1457. DOI:10.2514/1.43098 |
| [23] |
刘文法, 王旭, 米康. 前掠翼与后掠翼布局流动机理的数值研究[J]. 空军工程大学学报·自然科学版, 2008, 9(6): 11-15. Liu Wenfa, Wang Xu, Mi Kang. The numerical research on flow mechanism of forward-swept wing and backward swept wing configurations[J]. Journal of Air Force Engineering University (Natural Science Edition), 2008, 9(6): 11-15. |
 2018, Vol. 36
2018, Vol. 36


