间断Galerkin有限元方法(DG-FEM)最早是由Reed和Hill在1973年提出并应用于求解中子输运方程[1],且由Lesaint和Raviart在1974年首次对该方法进行了收敛阶分析,并应用于水平对流方程的数值计算中[2]。此后,Wellford和Oden在1975-1976年间,首先使用DG方法进行了波在弹性介质中的传播研究[3],Delfour和Trochu也在1978年将此方法运用到了最佳控制问题[4],但均局限求解线性方程。Chavent等最早将间断Galerkin有限元方法推广到非线性守恒律问题[5],并通过引入梯度限制器使得计算格式稳定[6],但在时间和空间方向上均只能实现低阶收敛。20世纪80年代末到90年代初,Cockburn和Shu通过引进稳定的Runge-Kutta方法[7]并配合改进的梯度限制器[8],克服了这一局限,保证了在光滑区域上获得正常的数值精度以及清晰的间断解[9],继而使用广义梯度限制器和具有高阶精度的RK方法使得数值结果重新获得了高阶精度[10]并将其推广到一维方程组[11]、高维标量守恒律[12]及高维方程组[13],即著名的RKDG方法。
间断Galerkin有限元方法具有良好的守恒性、收敛性等数学特性,并且结合了有限体积法与连续有限元法的诸多优点。首先,该方法只需要简单地增加单元自由度即可实现高阶精度,且每个单元都是相互独立的,对一般非规则网格具有更强的适应性,利于处理复杂的区域边界和具有复杂边界条件的问题;另外,该方法的质量矩阵是单元的而非整体的,对该矩阵求逆相对容易,继而可以方便的构造显示半离散格式;同时,数值通量具体形式的定义具备很强的灵活性,不同的定义方法可以反映具体问题的物理特性,从而保证波占优问题的稳定性。
尽管间断Galerkin有限元方法拥有众多的优点,但是该方法在每个单元需要求解的变量数都有所增加,而且随着精度的提高,变量数是非线性增长的,在复杂外形的大型数值模拟过程中,所需的计算量和存储量已无法满足实际工程问题的数值模拟需求。构造更加高效的隐式算法[14]、引入并行计算[15]等成为缓解上述问题的有效办法。Aktins和Shu则从另一个角度出发,针对使用间断Galerkin有限元方法求解过程中数值积分带来的计算量和存储量大的不利影响,提出了无数值积分的DG方法[16-17]以解决这个问题。
不同于Aktins和Shu以简单的单项式作为基函数的无数值积分DG方法,本文在单元基函数为Lagrange插值多项式的DG格式的基础上,又引入了基于Jacobi正交多项式的单元近似函数表达式,并通过应用该多项式的正交与求导等性质,无需数值积分的运算过程,方便、直接地构造出了一维和二维守恒律间断Galerkin有限元方法的显式半离散格式。基于该格式相关思想,将有利于构造更为高效的高阶间断Galerkin有限元计算方法。
1 数值方法 1.1 一维守恒律考虑一维守恒律
| $ \frac{{\partial u\left( {x,t} \right)}}{{\partial t}} + \frac{{\partial f\left( u \right)}}{{\partial x}} = 0,x \in \mathit{\Omega = }\left[ {L,R} \right] $ | (1) |
及相应的初始条件和边界条件,其中u为要求解的量,f(u)为线性或非线性通量函数。将求解区域Ω划分为K个互不重叠的单元Dk= [xlk, xrk],在每个单元上选取Np个节点xlk=x1k, x2k, …, xNpk=xrk并进行Lagrange插值,继而分别构造出N=Np-1次单元多项式近似解函数及单元多项式近似通量函数
| $ u_h^k\left( {x,t} \right) = \sum\limits_{j = 1}^{Np} {u_h^k\left( {x_j^k,t} \right)l_j^k\left( x \right)} ,x \in {D^k} $ | (2) |
| $ f_h^k\left( {u_h^k} \right) = \sum\limits_{j = 1}^{Np} {f_h^k\left( {x_j^k,t} \right)l_j^k\left( x \right)} ,x \in {D^k} $ | (3) |
其中,ljk(x)为N次Lagrange插值基函数,uhk(xjk, t)和fhk(xjk, t)分别表示xjk处的解和通量的值,且均是时间t的单值函数。
在每一个单元上应用Galerkin加权余量法的基本思想,使单元方程余量正交于该单元内的Np个单元权(基)函数,即
| $ \int_{{D^k}} {\left( {\frac{{\partial u_h^k}}{{\partial t}} + \frac{{\partial f_h^k}}{{\partial x}}} \right)l_i^k\left( x \right){\rm{d}}x} = 0,1 \le i \le Np $ | (4) |
对方程(4)进行分部积分,并引入数值通量[18]f*代替单元边界处的通量项,之后再做一次分部积分,即可构造出间断Galerkin有限元方法下一维守恒律的积分表达式
| $ \begin{array}{l} \int_{{D^k}} {\left( {\frac{{\partial u_h^k}}{{\partial t}} + \frac{{\partial f_h^k}}{{\partial x}}} \right)l_i^k\left( x \right){\rm{d}}x} \\ = \left[ {\left( {f_h^k - {f^ * }} \right)l_i^k\left( x \right)} \right]_{x_l^k}^{x_r^k},1 \le i \le Np \end{array} $ | (5) |
将单元多项式近似解函数(2)和单元多项式近似通量函数(3)带入方程(5)中,整理可得相应矩阵形式的积分表达式
| $ M_{ij}^k\frac{{\rm{d}}{u_j^k}}{{{\rm{d}}t}} + S_{ij}^kf_j^k = \left[ {\left( {f_h^k - {f^ * }} \right)l_i^k\left( x \right)} \right]_{x_l^k}^{x_r^k} $ | (6) |
其中,ujk=uhk(xjk, t), fjk=fhk(xjk, t),且
以积分表达式(6)为数值求解的出发点,一般需要通过数值积分的方法确定每一个单元上的质量矩阵和刚度矩阵,为了避免这一运算过程,首先引入参考变量r∈I= [-1, 1]及线性变换
| $ x\left( r \right) = x_l^k + \frac{{1 + r}}{2}{h^k},{h^k} = x_r^k - x_l^k $ | (7) |
继而单元多项式近似解函数(2)可以写为参考变量的形式
| $ u_h^k\left( {x\left( r \right),t} \right) = \sum\limits_{j = 1}^{Np} {u_h^k\left( {x_j^k,t} \right){l_j}\left( r \right)} ,r \in I $ | (8) |
在参考区间I上的Np个插值节点rj(j=1, 2, …, Np)选取为多项式
| $ \begin{array}{l} f\left( r \right) = \left( {1 - {r^2}} \right)\frac{{\rm{d}}}{{{\rm{d}}x}}{{\tilde J}_N}\left( r \right)\\ \;\;\;\;\;\;\;\; = \left( {1 - {r^2}} \right)\frac{{\rm{d}}}{{{\rm{d}}x}}\left[ {\tilde J_n^{\alpha ,\beta }\left( x \right)\left| {_{\alpha = 0,\beta = 0}} \right.} \right] \end{array} $ | (9) |
的Np个根[19],其中
| $ \left\{ \begin{array}{l} \tilde J_n^{\alpha ,\beta }\left( x \right) = \frac{{J_n^{\alpha ,\beta }\left( x \right)}}{{\sqrt {\gamma _n^{\alpha ,\beta }} }}\\ \gamma _n^{\alpha ,\beta } = \frac{{{2^{\alpha + \beta + 1}}\mathit{\Gamma }\left( {n + \alpha + 1} \right)\mathit{\Gamma }\left( {n + \beta + 1} \right)}}{{\left( {2n + \alpha + \beta + 1} \right)\mathit{\Gamma }\left( {n + 1} \right)\mathit{\Gamma }\left( {n + \alpha + \beta + 1} \right)}} \end{array} \right. $ | (10) |
| $ \frac{{\rm{d}}}{{{\rm{d}}x}}\tilde J_n^{\alpha ,\beta }\left( x \right) = \sqrt {n\left( {n + \alpha + \beta + 1} \right)} \tilde J_{n - 1}^{\alpha + 1,\beta + 1}\left( x \right) $ | (11) |
| $ \left\{ \begin{array}{l} \int_{ - 1}^1 {\tilde J_n^{\alpha ,\beta }\left( x \right)\tilde J_m^{\alpha ,\beta }\left( x \right){\omega _{\alpha ,\beta }}\left( x \right){\rm{d}}x} = {\delta _{nm}}\\ {\omega _{\alpha ,\beta }}\left( x \right) = {\left( {1 - x} \right)^\alpha }{\left( {1 + x} \right)^\beta } \end{array} \right. $ | (12) |
式中,Jnα, β(x)为标准Jacobi正交多项式,Γ(x)为经典Gamma函数,δnm为Kronecker函数。由式(9)所确定的插值节点被称作Legendre-Gauss-Lobatto(LGL)积分点,其值可以由Jacobi正交多项式及其相关性质获得[21]。
在选定了单元插值节点以后,引入单元多项式近似解函数的另一种表达形式
| $ u_h^k\left( {x\left( r \right),t} \right) = \sum\limits_{n = 1}^{Np} {\hat u_n^k\left( t \right){{\tilde J}_{n - 1}}\left( r \right),r \in I} $ | (13) |
由于(8)式和(13)式逼近的是同一函数的同阶多项式,因此一定存在恒等关系
| $ \sum\limits_{n = 1}^{Np} {\hat u_n^k\left( t \right){{\tilde J}_{n - 1}}\left( r \right)} = \sum\limits_{j = 1}^{Np} {u_n^k\left( {{r_j},t} \right){l_j}\left( r \right)} $ | (14) |
将LGL点ri(i=1, 2, …, Np)依次带入关系式(14)中并定义广义Vandermonde矩阵
| $ {V_{ij}} = {{\tilde J}_{j - 1}}\left( {{r_i}} \right) $ | (15) |
则有
| $ {\left( {{V^T}} \right)_{ij}}{l_j}\left( r \right) = {{\tilde J}_{j - 1}}\left( r \right),i = 1,2, \cdots ,Np $ | (16) |
基于以上关系表达式,可以将任意单元Dk上的质量矩阵变换至参考单元上的质量矩阵Mij
| $ \begin{array}{l} M_{ij}^k = \int_{Dk} {l_i^k\left( x \right)l_j^k\left( x \right){\rm{d}}x} \\ \;\;\;\;\;\; = {J^k}\int_{ - 1}^1 {{l_i}\left( r \right){l_j}\left( r \right){\rm{d}}r} \\ \;\;\;\;\;\; = {J^k}{M_{ij}} \end{array} $ | (17) |
Jk为线性坐标变换下的雅克比行列式。
将式(16)代入Mij的表达式中,并应用正交关系(12)式(取α=0, β=0),则有
| $ \begin{array}{l} {M_{ij}}\\ = \int_{ - 1}^1 {\sum\limits_{n = 1}^{Np} {\left( {{V^T}} \right)_{in}^{ - 1}{{\tilde J}_{n - 1}}\left( r \right)} \sum\limits_{m = 1}^{Np} {\left( {{V^T}} \right)_{jm}^{ - 1}{{\tilde J}_{m - 1}}\left( r \right){\rm{d}}r} } \\ = \sum\limits_{n = 1}^{Np} {\sum\limits_{m = 1}^{Np} {\left( {{V^T}} \right)_{in}^{ - 1}\left( {{V^T}} \right)_{jm}^{ - 1}\int_{ - 1}^1 {{{\tilde J}_{n - 1}}\left( r \right){{\tilde J}_{m - 1}}\left( r \right){\rm{d}}r} } } \\ = \sum\limits_{n = 1}^{Np} {\left( {{V^T}} \right)_{in}^{ - 1}\left( {{V^T}} \right)_{jn}^{ - 1}} \end{array} $ | (18) |
即参考单元质量矩阵的表达式为
| $ M = {\left( {V{V^T}} \right)^{ - 1}} $ | (19) |
对于单元刚度矩阵,由线性坐标变换可直接转化为参考区间上的刚度矩阵,即
| $ \begin{array}{l} S_{ij}^k = \int_{Dk} {l_i^k\left( x \right)\frac{{{\rm{d}}l_j^k\left( x \right)}}{{{\rm{d}}x}}{\rm{d}}x} \\ \;\;\;\;\; = \int_{ - 1}^1 {{l_i}\left( r \right)\frac{{{\rm{d}}{l_j}\left( r \right)}}{{{\rm{d}}r}}{\rm{d}}r} \\ \;\;\;\;\; = {S_{ij}} \end{array} $ | (20) |
将(16)式两端同时对r求导,并定义
| $ V{r_{ij}} = \frac{{{\rm{d}}{{\tilde J}_j}}}{{{\rm{d}}r}}\left| {_{{r_i}}} \right.,D{r_{ij}} = \frac{{{\rm{d}}{l_j}}}{{{\rm{d}}r}}\left| {_{{r_i}}} \right. $ | (21) |
则可得微分矩阵Dr的表达式为
| $ Dr = Vr{V^{ - 1}} $ | (22) |
将参考单元上的质量矩阵与微分矩阵相乘
| $ \begin{array}{l} {\left( {MDr} \right)_{ij}} = \sum\limits_{n = 1}^{Np} {{M_{in}}D{r_{nj}}} \\ \;\;\;\;\;\;\;\;\;\;\;\; = \sum\limits_{n = 1}^{Np} {\int_{ - 1}^1 {{l_i}\left( r \right){l_n}\left( r \right)\frac{{{\rm{d}}{l_j}}}{{{\rm{d}}r}}\left| {_{{r_n}}} \right.{\rm{d}}r} } \\ \;\;\;\;\;\;\;\;\;\;\;\; = \int_{ - 1}^1 {{l_i}\left( r \right)\sum\limits_{n = 1}^{Np} {\frac{{{\rm{d}}{l_j}}}{{{\rm{d}}r}}\left| {_{{r_n}}} \right.{l_n}\left( r \right){\rm{d}}r} } \\ \;\;\;\;\;\;\;\;\;\;\;\; = \int_{ - 1}^1 {{l_i}\left( r \right)\frac{{{\rm{d}}{l_j}\left( r \right)}}{{{\rm{d}}r}}{\rm{d}}r} = {S_{ij}} \end{array} $ | (23) |
即参考单元刚度矩阵的表达式为
| $ S = MDr $ | (24) |
至此,将式(17)、(20)代入积分表达式(6)中,方程两端对M求逆并应用矩阵关系式(24),整理即可得显式半离散格式
| $ \begin{array}{l} \frac{{{\rm{d}}u_j^k}}{{{\rm{d}}t}} = - \frac{2}{{{h^k}}}D{r_{ij}}f_j^k\\ \;\;\;\;\;\;\;\; + \frac{2}{{{h^k}}}M_{ij}^{ - 1}\left[ {\left( {f_h^k - {f^ * }} \right)l_i^k\left( x \right)} \right]_{x_l^k}^{x_r^k} \end{array} $ | (25) |
观察该显示半离散格式,M和Dr可通过(19)和(22)式获得,且矩阵V和Vr可由LGL点以及Jacobi正交多项式及其关系式(10)和(11)唯一确定,该过程简单有效,且无需引入数值积分的运算过程。
1.2 二维守恒律考虑二维守恒律
| $ \frac{{\partial u\left( {\mathit{\boldsymbol{x}},t} \right)}}{{\partial t}} + \nabla \cdot \mathit{\boldsymbol{f}}\left( u \right) = 0,\mathit{\boldsymbol{x}} \in \Omega \in {R^2} $ | (26) |
及相应的初始条件和边界条件,其中,x =(x, y), f =(f1, f2)。
使用K个直边三角形单元Dk对Ω进行相容的几何剖分,并在每个单元上定义N阶单元多项式近似解函数和单元多项式近似通量函数
| $ u_h^k\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{j = 1}^{Np} {u_h^k\left( {\mathit{\boldsymbol{x}}_j^k,t} \right)l_j^k\left( \mathit{\boldsymbol{x}} \right)} ,\;\;\;\;\mathit{\boldsymbol{x}} \in {D^k} $ | (27) |
| $ \mathit{\boldsymbol{f}}_h^k\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{j = 1}^{Np} {\mathit{\boldsymbol{f}}_h^k\left( {u_h^k\left( {\mathit{\boldsymbol{x}}_j^k,t} \right)} \right)l_j^k\left( \mathit{\boldsymbol{x}} \right),} \;\;\;\;\mathit{\boldsymbol{x}} \in {D^k} $ | (28) |
其中ljk(x)为节点xjk处的二维Lagrange插值基函数。同理,可以构造出二维守恒律DG方法的积分表达式
| $ \begin{array}{l} \int_{{D^k}} {\left( {\frac{{\partial u_h^k}}{{\partial t}} + \nabla \cdot \mathit{\boldsymbol{f}}_h^k} \right)l_i^k\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \\ = \oint_{\partial {D^k}} {\mathit{\boldsymbol{\hat n \times }}\left( {\mathit{\boldsymbol{f}}_\mathit{\boldsymbol{h}}^\mathit{\boldsymbol{k}}\mathit{\boldsymbol{ - }}{\mathit{\boldsymbol{f}}^\mathit{\boldsymbol{*}}}} \right)\mathit{\boldsymbol{l}}_\mathit{\boldsymbol{i}}^\mathit{\boldsymbol{k}}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} ,1 \le i \le Np \end{array} $ | (29) |
引入参考单元I ={ r =(r, s)|(r, s)≥-1, r+s≤0}及坐标变换
| $ \mathit{\boldsymbol{x}} = - \frac{{r + s}}{2}{\mathit{\boldsymbol{v}}^1} + \frac{{r + 1}}{2}{\mathit{\boldsymbol{v}}^2} + \frac{{s + 1}}{2}{\mathit{\boldsymbol{v}}^3} $ | (30) |
其中,v1、v2、v3表示单元Dk上三个顶点的物理坐标,则可得积分表达式的矩阵形式
| $ \begin{array}{l} {J^k}{M_{ij}}\frac{{{\rm{d}}u_j^k}}{{{\rm{d}}t}}\\ + {J^k}{\left( {{S_r}} \right)_{ij}}\left( {r_x^kf_{1j}^k + r_y^kf_{2j}^k} \right)\\ + {J^k}{\left( {{S_s}} \right)_{ij}}\left( {s_x^kf_{1j}^k + s_y^kf_{2j}^k} \right)\\ = \oint_{\partial {D^k}} {\left[ {{n_x}\left( {f_{h1}^k - f_1^ * } \right) + {n_y}\left( {f_{h2}^k - f_2^ * } \right)} \right]l_i^k\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \end{array} $ | (31) |
式中,Jk为坐标变换Jacobi行列式,M, Sr和Ss为参考单元上的质量矩阵及刚度矩阵,且分别定义为
| $ {M_{ij}} = \int_I {{l_i}\left( \mathit{\boldsymbol{r}} \right){l_j}\left( \mathit{\boldsymbol{r}} \right){\rm{d}}\mathit{\boldsymbol{r}}} $ | (32) |
| $ \begin{array}{l} {\left( {{S_r}} \right)_{ij}} = \int_I {{l_i}\left( \mathit{\boldsymbol{r}} \right)\frac{{\partial {l_j}\left( \mathit{\boldsymbol{r}} \right)}}{{\partial r}}{\rm{d}}\mathit{\boldsymbol{r}}} \\ {\left( {{S_s}} \right)_{ij}} = \int_I {{l_i}\left( \mathit{\boldsymbol{r}} \right)\frac{{\partial {l_j}\left( \mathit{\boldsymbol{r}} \right)}}{{\partial s}}{\rm{d}}\mathit{\boldsymbol{r}}} \end{array} $ | (33) |
对于参考单元上的Np个插值节点,可将LGL点做如下推广[22],首先,在顶点坐标分别为v1=(-1, -
| $ \left( {{\lambda ^1},{\lambda ^3}} \right) = \left( {\frac{i}{N},\frac{j}{N}} \right),{\lambda ^2} = 1 - {\lambda ^1} - {\lambda ^3} $ | (34) |
其中,0≤λ1, λ2, λ3≤1, (i, j)≥0, i+j≤N,继而可以得到这些节点的物理坐标xe(λ1, λ2, λ3)。
引入增量函数
| $ \begin{array}{l} \mathit{\boldsymbol{w}}\left( {{\lambda ^1},{\lambda ^2},{\lambda ^3}} \right) = {b^1}{\mathit{\boldsymbol{w}}^1} + {b^2}{\mathit{\boldsymbol{w}}^2} + {b^3}{\mathit{\boldsymbol{w}}^3}\\ \left\{ \begin{array}{l} {\mathit{\boldsymbol{w}}^1} = \tilde w\left( {{\lambda ^3} - {\lambda ^2}} \right)\left( {\begin{array}{*{20}{c}} 1\\ 0 \end{array}} \right),\;\;\;\;\;\;\;\;\;\;\;\;\;{b^1} = 4{\lambda ^3}{\lambda ^2}\\ {\mathit{\boldsymbol{w}}^2} = \tilde w\left( {{\lambda ^1} - {\lambda ^3}} \right)\frac{1}{2}\left( \begin{array}{l} - 1\\ \sqrt 3 \end{array} \right),\;\;\;\;\;{b^2} = 4{\lambda ^3}{\lambda ^1}\\ {\mathit{\boldsymbol{w}}^3} = \tilde w\left( {{\lambda ^2} - {\lambda ^1}} \right)\frac{1}{2}\left( \begin{array}{l} - 1\\ - \sqrt 3 \end{array} \right),\;\;\;\;\;{b^3} = 4{\lambda ^2}{\lambda ^1}\\ \tilde w\left( r \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \frac{{w\left( r \right)}}{{1 - {r^2}}},\\ 0, \end{array}&\begin{array}{l} r \ne \pm 1\\ r = \pm 1 \end{array} \end{array}} \right.\\ w\left( r \right) = \sum\limits_{i = 1}^{Np} {\left( {r_i^{{\rm{LGL}}} - r_i^e} \right)l_i^e\left( r \right)} \end{array} \right. \end{array} $ | (35) |
式中,riLGL和rie分别代表LGL节点和等距节点,lie(r)为定义在rie上的一维Lagrange插值多项式,则定义在该等边三角形上的插值节点的物理坐标为x = xe+ w,继而可以通过(30)式相应地获得参考单元I上的节点坐标。
在确定二维插值节点之后,同样需要引入另一种单元多项式近似函数表达形式
| $ u_h^k\left( {\mathit{\boldsymbol{r}},t} \right) = \sum\limits_{n = 1}^{Np} {\hat u_n^k\left( t \right){\varphi _n}\left( \mathit{\boldsymbol{r}} \right)} ,\mathit{\boldsymbol{r}} \in I $ | (36) |
且φn(r)的具体表达式为
| $ \begin{array}{l} {\varphi _n}\left( \mathit{\boldsymbol{r}} \right) = \sqrt 2 {{\tilde J}_i}\left( a \right)\tilde J_i^{\left( {2i + 1,0} \right)}\left( b \right){\left( {1 - b} \right)^i}\\ \left\{ \begin{array}{l} a = 2\frac{{1 + r}}{{1 - s}} - 1,b = s\\ n = i + \left( {N + 1} \right)j + 1 - \frac{j}{2}\left( {j - 1} \right)\\ \left( {i,j} \right) \ge 0,i + j \le N \end{array} \right. \end{array} $ | (37) |
仿照一维守恒律构造相关矩阵的思想,由式(37)及插值节点可以定义矩阵
| $ {V_{ij}} = {\varphi _j}\left( {{\mathit{\boldsymbol{r}}_i}} \right) $ | (38) |
| $ {\left( {{V_r}} \right)_{ij}} = \frac{{\partial {\varphi _j}}}{{\partial r}}\left| {_{{\mathit{\boldsymbol{r}}_i}}} \right.,{\left( {{V_s}} \right)_{ij}} = \frac{{\partial {\varphi _j}}}{{\partial s}}\left| {_{{\mathit{\boldsymbol{r}}_i}}} \right. $ | (39) |
继而可以得到二维格式的质量矩阵、微分矩阵和刚度矩阵的表达式
| $ M = {\left( {V{V^{\rm{T}}}} \right)^{ - 1}} $ | (40) |
| $ {D_r} = {V_r}{V^{ - 1}},{D_s} = {V_s}{V^{ - 1}} $ | (41) |
| $ {S_r} = M{D_r},{S_s} = M{D_s} $ | (42) |
与一维守恒律稍有不同,需要计算面积分项
| $ \int_{\partial {D^k}} {\hat n \cdot \left( {\mathit{\boldsymbol{f}}_h^k - {\mathit{\boldsymbol{f}}^ * }} \right)f_i^k\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} $ | (43) |
由于在直边三角形单元上,当单元近视解函数为N阶多项式时,每条边上将刚好分布有N+1个节点,以其中一条边为例可计算积分如下
| $ \begin{array}{l} \int_{{\rm{edge}}} {\hat n \cdot \left( {\mathit{\boldsymbol{f}}_h^k - {\mathit{\boldsymbol{f}}^ * }} \right)l_i^k\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \\ = \sum\limits_{j = 1}^{N + 1} {\hat n \cdot \left( {\mathit{\boldsymbol{f}}_j^k - {\mathit{\boldsymbol{f}}^ * }} \right)\int_{{\rm{edge}}} {l_i^k\left( \mathit{\boldsymbol{x}} \right)l_j^k\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} } \end{array} $ | (44) |
其中1≤i≤Np, 1≤j≤N+1,且
| $ M_{ij}^{k,e} = \int_{{\rm{edge}}} {l_i^k\left( \mathit{\boldsymbol{x}} \right)l_j^k\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} $ | (45) |
为定义在三角单元边上的质量矩阵,该矩阵的元素可以由边上的节点按照一维问题处理得到。综上,即可完整的构造出二维守恒律DG方法的显式半离散格式。
2 算例与分析 2.1 一维线性波动方程考虑具体的一维线性波动方程
| $ \frac{{\partial u}}{{\partial t}} + 2{\rm{ \mathit{ π} }}\frac{{\partial u}}{{\partial x}} = 0,x \in \left[ {0,2{\rm{ \mathit{ π} }}} \right] $ | (46) |
且受制于如下初始条件和边界条件
| $ \left\{ \begin{array}{l} u\left( {x,0} \right) = \sin \left( x \right)\\ u\left( {0,t} \right) = - \sin \left( {2{\rm{ \mathit{ π} }}t} \right) \end{array} \right. $ | (47) |
该方程的精确解为u(x, t)=sin(x-2πt),选取Lax-Friedrichs数值通量,并使用Runge-Kutta方法进行时间上的迭代求解。表 1给出了T=10时刻,N和K取不同值时L1范数定义下的整体误差及相应条件下的数值精度。
| 表 1 求解单波方程得到的L1误差及数值精度 Table 1 L1 error and numerical precision of wave equation |
|
|
分析表中的结果可知,首先,无论是增加单元个数K还是增加单元多项式近似函数阶数N,整体误差均是逐渐减小的,即该格式是明显收敛的;此外,当单元多项式近似函数阶数N保持不变时,随着单元个数K的增加,由整体误差所确定的数值精度均逐渐逼近于间断Galerkin有限元方法的理论精度N+1阶。
2.2 一维可压缩Euler方程组考虑经典激波管(SOD)问题,其控制方程为一维守恒型可压缩Euler方程组
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} = 0\\ \mathit{\boldsymbol{U}} = \left( \begin{array}{l} \rho \\ \rho u\\ E \end{array} \right),\;\;\;\;\mathit{\boldsymbol{F = }}\left( \begin{array}{l} \rho u\\ \rho {u^2} + p\\ u\left( {E + p} \right) \end{array} \right) \end{array} $ | (48) |
其中,u、ρ、p分别为流向速度,密度和压力,E是单位体积动能和内能的和,即E=ρ(e+u2/2),此外,由完全气体假设下的状态方程可得p=(γ-1)(E-ρu2/2)。
初始条件给定为
| $ \left\{ \begin{array}{l} \rho \left( {x,0} \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1.0,\\ 0.125, \end{array}&\begin{array}{l} x < 0.5\\ x \ge 0.5 \end{array} \end{array}} \right.\\ \rho u\left( {x,0} \right) = 0\\ E\left( {x,0} \right) = \frac{1}{{\gamma - 1}}\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 1,\\ 0.1, \end{array}&\begin{array}{l} x < 0.5\\ x \ge 0.5 \end{array} \end{array}} \right. \end{array} \right. $ | (49) |
对该问题应用与一维线性波动方程相同的构造方法进行求解,为消除非物理振荡,需要在RK方法的每一步使用经典MUSCL限制器[23]。
图 1和图 2分别给出了使用该方法在K=500, N=2和N=3时,T=0.2时刻求解激波管问题所获得的数值解与精确解的比较结果。由图可以看出,该方法可以有效的捕捉到激波的准确位置,在光滑区域获得精度较高的解,同时,在限制器的作用下,可以完全消除非物理振荡。
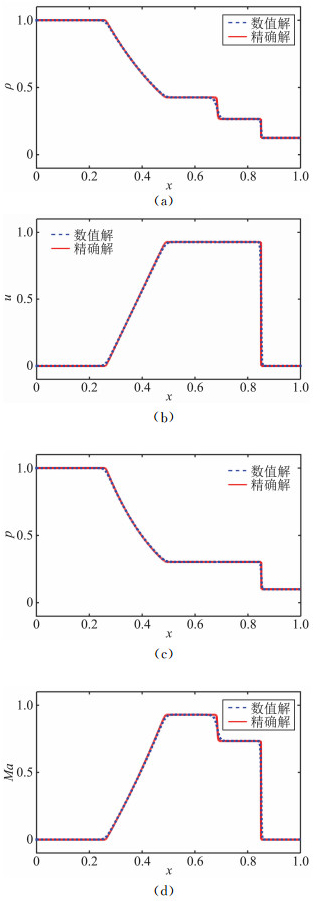
|
图 1 N=2, K=500时,求解激波管问题得到的数值解与精确解比较 Figure 1 Comparison of numerical solution and exact solution of shock-tube problems when N=2, K=500 |
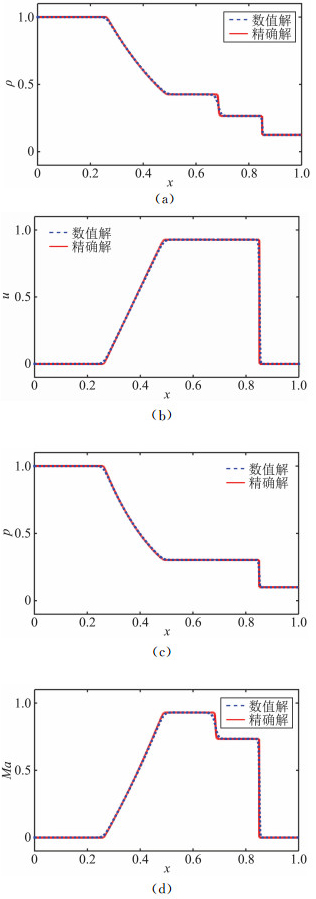
|
图 2 N=3, K=500时,求解激波管问题得到的数值解与精确解比较 Figure 2 Comparison of numerical solution and exact solution of shock-tube problems when N=3, K=500 |
此外,对比图 1和图 2所示结果可以发现,两种情况下所得的数值解差别不大,这是由于在限制器的作用下,不可避免的影响了该方法运用高阶基函数时的优势,针对这一问题,可以通过增加单元个数或者使用高阶基函数配合更先进的限制器使计算结果得到改进。
2.3 二维可压缩Euler方程组考虑控制方程为二维守恒型Euler方程组
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{U}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{F}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{G}}}}{{\partial y}} = 0\\ \mathit{\boldsymbol{U}} = \left( {\begin{array}{*{20}{c}} \rho \\ {\rho u}\\ {\rho v}\\ E \end{array}} \right),\mathit{\boldsymbol{F}} = \left( {\begin{array}{*{20}{c}} {\rho u}\\ {\rho {u^2} + p}\\ {\rho uv}\\ {u\left( {E + p} \right)} \end{array}} \right),\mathit{\boldsymbol{G}} = \left( {\begin{array}{*{20}{c}} {\rho u}\\ {\rho uv}\\ {\rho {v^2} + p}\\ {v\left( {E + p} \right)} \end{array}} \right) \end{array} $ | (50) |
其中,u, v, p, ρ分别为流向速度,法向速度,压力和密度,E是单位体积动能和内能的和,且有E=ρ[e+(u2+v2)/2],以及完全气体假设下的状态方程p=(γ-1)[E-ρ(u2+v2)/2]。对此方程可以根据二维守恒律的处理方法构造相应的显式半离散格式。
考虑具有精确解
| $ \left\{ \begin{array}{l} u = 1 - \beta {e^{\left( {1 - {r^2}} \right)}}\frac{y}{{2{\rm{ \mathit{ π} }}}}\\ v = \beta {e^{\left( {1 - {r^2}} \right)}}\frac{{x - 5 - t}}{{2{\rm{ \mathit{ π} }}}}\\ \rho = {\left[ {1 - \left( {\frac{{\gamma - 1}}{{16\gamma {{\rm{ \mathit{ π} }}^2}}}} \right){\beta ^2}{e^{2\left( {1 - {r^2}} \right)}}} \right]^{\frac{1}{{\gamma - 1}}}}\\ p = {\rho ^\gamma } \end{array} \right. $ | (51) |
的等熵涡问题,式中,
表 2显示了由初始网格逐步均匀加密后得到的L1范数定义下密度ρ的整体误差以及相应条件下的数值精度,h代表初始网格中各单元的大小。
| 表 2 密度ρ的L1误差及数值精度 Table 2 L1 error and numerical precision of density |
|
|
从表中的结果可以看出,同样地,二维模式下该格式仍是明显收敛的,虽然由于非结构网格导致数值精度存在一定的波动,但总体上仍趋向于间断Galerkin有限元方法的最优收敛阶N+1阶。
考虑同样由二维可压缩Euler方程组控制的前台阶问题,初始条件给定为马赫数为3的超声速均匀流场
| $ \left\{ \begin{array}{l} \rho = \gamma \\ \rho u = 3\gamma \\ \rho v = 0\\ E = \frac{1}{{\gamma - 1}} + \frac{9}{2}\gamma \end{array} \right. $ | (52) |
流入边界条件由初始值给定,墙边界条件取为如下反射边界条件
| $ \left\{ \begin{array}{l} {\rho ^ + } = {\rho ^ - }\\ \rho {u^ + } = \rho {u^ - } - 2{n_x}\left( {{n_x}\rho {u^ - } + {n_y}\rho {v^ - }} \right)\\ \rho {v^ + } = \rho {v^ - } - 2{n_y}\left( {{n_x}\rho {u^ - } + {n_y}\rho {v^ - }} \right)\\ {E^ + } = {E^ - } \end{array} \right. $ | (53) |
因假设流出边界处仍为超声速流场,所以不需要强加边界条件。求解过程中,在RK方法的每一时间步均使用了适用于二维可压缩Euler方程组的梯度的限制器[24]。
图 3和图 4分别显示了选取K=25330,N=2和N=3时,在T=4时刻整个求解区域上密度ρ,压力p以及马赫数Ma的等值线图。将该方法的计算结果与文献[25]中的结果进行比较,整体求解区域上均吻合的很好,数值解达到了理想的精度,且激波的位置被准确的捕捉到。同时,与一维情况相同,限制器的作用对选取高阶基函数时的计算结果造成了一定程度的影响,同样的,可以通过增加单元个数或使用更先进的限制器加以改进。
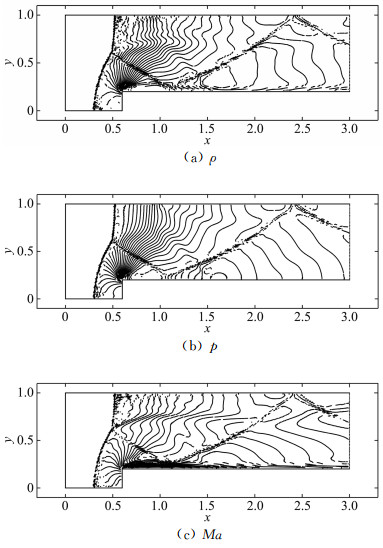
|
图 3 N=2, K=25330时,前台阶问题的密度、压力和马赫数等值线图 Figure 3 Density, pressure, and Mach number contours of front steps problem when N=2, K=25330 |

|
图 4 N=3, K=25330时,前台阶问题的密度、压力和马赫数等值线图 Figure 4 Density, pressure and Mach number contours of front steps problem when N=3, K=25330 |
本文以单元基函数为Lagrange插值多项式,单元插值节点为LGL点(二维情形下插值节点为LGL点的扩展)的DG格式作为求解出发点,同时引入了基于Jacobi正交多项式的单元近似函数表达式,通过建立两种不同基函数的联系,构造了一维和二维守恒律无数值积分的间断Galerkin有限元方法显式半离散格式。应用该方法对具有连续解或间断解的不同算例进行数值模拟,验证了其所得的计算结果可以很好的达到间断Galerkin有限元方法的理论高阶精度,且该方法配合适当的限制器,可以有效的处理含有间断的问题。由于不再需要通过数值积分来计算各单元的体积分与面积分,在保证了高阶精度的同时,理论上可以减少数值计算所需内存量及计算量。但是,在处理含间断问题时,为了完全抑制数值振荡,使用限制器是必须的,继而不可避免的会对激波造成污染,同时会一定程度地破坏解在光滑区域上的高阶精度,也即在一定程度上限制了该计算方法运用高阶基函数的优势。进一步的研究,可以应用该思想构造高阶以及三维问题的无数值积分DG求解格式,并具体地对比验证其在内存使用量及计算量方面的优势,继而考虑配合其他方法及更为先进的限制器构造更为高效的且可以达到高阶精度的间断Galerkin有限元方法计算格式。
| [1] |
Reed W H, Hill T R. Triangularmesh methodsfor the neutrontransportequation[R]. Los Alamos Report LA-UR-73-479, 1973.
(  0) 0) |
| [2] |
Lesaint P, Raviart P A. On a finite element method for solving the neutron transport equation[J]. Mathematical Aspects of Finite Elements in Partial Differential Equations, 1974(33): 89-123. (  0) 0) |
| [3] |
Wellford L C, Oden J T. A theory of discontinuous finite element galerkin approximations of shock waves in nonlinear elastic solids part 1:Variational theory[J]. Computer Methods in Applied Mechanics and Engineering, 1976, 8(1): 1-16. DOI:10.1016/0045-7825(76)90049-9 (  0) 0) |
| [4] |
Delfour M C, Trochu F. Discontinuous finite element methods for the approximation of optimal control problems governed by hereditary differential systems[M]//Springer Berlin Heidelberg, 1978: 256-271.
(  0) 0) |
| [5] |
Chavent G, Salzano G. A finite-element method for the 1-D water flooding problem with gravity[J]. Journal of Computational Physics, 1982, 45(3): 307-344. DOI:10.1016/0021-9991(82)90107-3 (  0) 0) |
| [6] |
Chavent G, Cockburn B. The local projection discontinuous-Galerkin finite element method for scalar conservation laws[J]. RAIRO-Modélisation Mathématique et Analyse Numérique, 1989, 23(4): 565-592. (  0) 0) |
| [7] |
Shu C W. Total-variation-diminishing time discretizations[J]. SIAM Journal on Scientific and Statistical Computing, 1988, 9(6): 1073-1084. DOI:10.1137/0909073 (  0) 0) |
| [8] |
Shu C W. TVB uniformly high-order schemes for conservation laws[J]. Mathematics of Computation, 1987, 49(179): 105-121. DOI:10.1090/S0025-5718-1987-0890256-5 (  0) 0) |
| [9] |
Cockburn B, Shu C W. The Runge-Kutta local projection discontinuous-Galerkin finite element method for scalar conservation laws[J]. RAIRO-Modélisation Mathématique et Analyse Numérique, 1991, 25(3): 337-361. (  0) 0) |
| [10] |
Cockburn B, Shu C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. Ⅱ. General framework[J]. Mathematics of Computation, 1989, 52(186): 411-435. (  0) 0) |
| [11] |
Cockburn B, Lin S Y, Shu C W. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws Ⅲ:one-dimensional systems[J]. Journal of Computational Physics, 1989, 84(1): 90-113. DOI:10.1016/0021-9991(89)90183-6 (  0) 0) |
| [12] |
Cockburn B, Hou S, Shu C W. The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. Ⅳ. The multidimensional case[J]. Mathematics of Computation, 1990, 54(190): 545-581. (  0) 0) |
| [13] |
Cockburn B, Shu C W. The Runge-Kutta discontinuous Galerkin method for conservation laws Ⅴ:multidimensional systems[J]. Journal of Computational Physics, 1998, 141(2): 199-224. DOI:10.1006/jcph.1998.5892 (  0) 0) |
| [14] |
Guo Y H, Yang Y, Zhang Q. A high efficient implicit discontinuous Galerkin method[J]. Acta Aerodynamica Sinica, 2012, 30(2): 250-253. (in Chinese) 郭永恒, 杨永, 张强. 一种高效的隐式间断Galerkin方法研究[J]. 空气动力学学报, 2012, 30(2): 250-253. DOI:10.3969/j.issn.0258-1825.2012.02.021 (  0) 0) |
| [15] |
Xia Y D, Wu Y Z, Lv H Q, et al. , Parallel computation of a high-order discontinuous Galerkin method on unstructured grids[J]. Acta Aerodynamica Sinica, 2011, 29(05): 537-541. (in Chinese) 夏轶栋, 伍贻兆, 吕宏强, 等. 高阶间断有限元法的并行计算研究[J]. 空气动力学学报, 2011, 29(05): 537-541. DOI:10.3969/j.issn.0258-1825.2011.05.001 (  0) 0) |
| [16] |
Atkins H L, Shu C W. Quadrature-free implementation of discontinuous Galerkin method for hyperbolic equations[J]. AIAA Journal, 1996, 36(5): 775-782. (  0) 0) |
| [17] |
Atkins H L. Continued development of the discontinuous Galerkin method for computational aeroacoustic applications[M]. American Institute of Aeronautics and Astronautics, 1997.
(  0) 0) |
| [18] |
Cockburn B, Shu C W. Runge-Kutta discontinuous Galerkin methods for convection-dominated problems[J]. Journal of Scientific Computing, 2001, 16(3): 173-261. DOI:10.1023/A:1012873910884 (  0) 0) |
| [19] |
Hesthaven J S, Gottlieb S, Gottlieb D. Spectral methods for time-dependent problems-[M]. Cambridge University Press, 2007.
(  0) 0) |
| [20] |
Zhao T G, Zhang J H. Some properties of Jacobi orthogonal polynomials[J]. Journal of Gansu Normal Colleges, 2009, 14(5): 1-3. (in Chinese) 赵廷刚, 张建宏. Jacobi正交多项式的一些性质[J]. 甘肃高师学报, 2009, 14(5): 1-3. (  0) 0) |
| [21] |
AN J. The solving method and algorithm implementation of the zeros of derivative of Jacobi polynomial[J]. Journal of Guizhou Normal University, 2014, 32(4): 42-45. (in Chinese) 安静. Jacobi多项式及其导数零点的求解方法及算法实现[J]. 贵州师范大学学报:自然科学版, 2014, 32(4): 42-45. (  0) 0) |
| [22] |
Gordon W J, Hall C A. Construction of curvilinear co-ordinate systems and applications to mesh generation[J]. International Journal for Numerical Methods in Engineering, 1973, 7(4): 461-477. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [23] |
LeVeque R J. Finite volume methods for hyperbolic problems[M]. Cambridge university press, 2002.
(  0) 0) |
| [24] |
Tu S, Aliabadi S. A slope limiting procedure in discontinuous Galerkin finite element method for gasdynamics applications[J]. International Journal of Numerical Analysis and Modeling, 2005, 2(2): 163-178. (  0) 0) |
| [25] |
Guo Y H, Yang Y, Liu Y O. An original designed limiter for discontinuous Galerkin method[J]. Acta Aerodynamica Sinica, 2014, 32(4): 462-467. (in Chinese) 郭永恒, 杨永, 刘逸鸥. 一种基于间断Galerkin格式的新型限制器设计[J]. 空气动力学学报, 2014, 32(4): 462-467. DOI:10.7638/kqdlxxb-2012.0157 (  0) 0) |
 2018, Vol. 36
2018, Vol. 36


