旋翼流场是复杂非定常、涡占主导地位的流场。为了进行流场细节(特别是桨尖涡)捕捉,相应CFD计算使用的网格数量较多,为了获得周期解,数值模拟需要进行多个旋翼旋转周期,而每个旋转周期上又要进行多个物理时间计算。一般情况下,由于桨叶/桨叶之间及桨叶/机身之间存在大幅相对运动,计算通常基于嵌套网格系统,这进一步提高了计算的复杂度。旋翼流场数值模拟通常占用较大的计算资源且十分耗时[1]。
并行计算技术是有效缩短计算时间消耗的重要途径。近年来,流场计算方面的并行技术已经发展得相对成熟,如文献[2-4]。考虑到基于嵌套网格的旋翼流场数值模拟在每个计算物理时间上都要进行网格装配,较好的方法将会有效缩减网格装配时间对流场计算时间的占比,从而进一步提高整体并行的计算效率。
关于网格装配,先前已经开展过不少工作,发展的方法可以分为两大类,一是显式方法,即首先进行网格的“洞切割”,围绕生成的洞边界,构建插值边界,进行插值边界的贡献单元搜索,建立插值单元和贡献单元的对应关系。二是隐式方法,即对所有网格单元,均进行贡献单元搜索工作,通过比较单元及其贡献单元之间的几何关系(体积、长宽比等)来自动确定数据交换的边界。显式方法由于需要搜索的贡献单元数目较少,因而具备较快的计算速度,但由于需要算法给定洞切割范围,也需要进行必须的几何交叉问题判断及付出相应的计算程序复杂度代价。比较经典的方法如洞映射方法[5]、目标X射线方法[6]和纯几何切割的方法等[7]。对于隐式方法[8],由于需要全局贡献单元搜索,时间消耗较为严重。可以看出,无论是基于显式还是隐式网格装配方法,贡献单元搜索都是不可缺少的步骤,目前发展的贡献单元搜索方法包括穷举法(Brute Force)、最近邻居法Nearest Neighbor(NN)[9],Neighbor to Neighbor(N2N)方法[10],Alternating Digital Tree(ADT)方法[11]、结构辅助网格方法Structured Auxiliary Mesh(SAM)[12]、近似反映射方法Approximate Inverse Map (AIM)[13]和精确反映射Exact Inverse Map(EIM)[14]等。其中ADT方法是一种较为经典的方法,鲁棒性较好,而使用结构辅助网格方法能够提供比ADT方法快一阶的计算速度[15],是一种高效的计算方法。N2N方法的问题是搜索路径可能遇到边界面,需要附加计算重启过程。精确反映射方法速度很快,但仍涉及很多复杂的几何交叉判断问题。国内研究者们的研究成果包括“透视图”方法[16]、“距离缩减”[17]和一些其他方法[18-20]等。
考虑到旋翼流场计算的多周期多物理时间步特性,网格装配对整体计算效率影响较大。为缩短网格装配时间,降低其对于整体流场计算时间的占比,本文进行算法方面的改进,目的是提高网格装配效率的同时尽量减少几何判断和计算代码的复杂程度,网格装配算法具有一般性,不受物体形状和网格拓扑的限制,并使得计算的内存消耗在可容忍的范围之内。具体工作如下:一是采用基于构造曲面外形的压缩存储的辅助结构网格进行并行洞切割,方法速度快且能够适应任意物面形状。二是基于可自适应的结构辅助网格Adaptive Structured Auxiliary Mesh(ASAM),完成贡献单元初始位置定位,并结合N2N搜索和局部穷举法,形成了无判断边界的并行贡献单元确定方法,称为Inverse Map No Boundary Adjudication(IM_NBA)。通过以上措施,实现了网格装配过程的最大限度并行化。
在流场计算方面,本文采用并行化的隐式双时间方法数值求解Navier-Stokes方程,无黏通量采用ROE格式和梯度重构方法计算,湍流项用Spalart-Allmaras模型模拟。
为了便于演示,文中首先给出了一个二维嵌套网格洞切割和贡献单元搜索的算例。然后基于以上方法,对不同的旋翼模型网格系统,在工作站上,通过计算测试给出了采用改进的网格装配方法时的装配过程并行加速效果及装配时间对计算时间的占比。
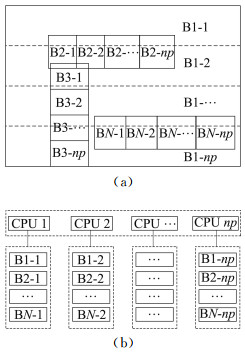
1 并行网格装配方法 1.1 网格分区对于网格数目和拓扑不变情况下,网格分区仅需在计算开始的时候进行一次,即把网格划分成多个区域,并把网格信息传递到对应处理器上。对于多块嵌套的旋翼网格系统,设背景网格块编号为B1,各个小网格块编号分别为B2,B3,…,BN,其中N为网格块总数,网格分区采用Metis工具[21]对每块网格分别进行。分区完成后的网格为BN_1,BN_2,…,BN_np,其中np为处理器个数。分布在第一个处理器上的子网格块为B1_1,B2_1,…,BN_1;第np个处理器上的子网格块为B1_np,B2_np,…,BN_np。网格分区的逻辑视图如图 1所示。
|
图 1 嵌套网格分区示意图 Figure 1 Schematic of embedded grid partition |
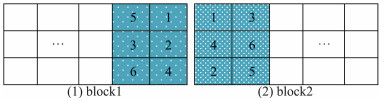
需要注意的是,进行网格划分后要自行生成网格分区之间的交叠边界,以实现处理器之间的数据交互。由于本文计算采用二阶格式故构建两层单元的数据交换边界。如图 2所示,其中有阴影部分为两块分区网格向外扩展的的重叠区域。
|
图 2 网格子块扩展边界示意图 Figure 2 Schematic of halo cells for grid sub-blocks |
并行洞切割过程包括“洞构造面”(Scons)构建,辅助结构网格生成、洞切割及插值边界确定等。
1.2.1.1 “洞构造面”构建由主处理器读入整体网格,对每块网格上的所有物面,向外推出几层,构建出一层网格面,用来作为洞边界生成的判据。该过程只需在计算开始的时候进行一次。把该构造面的几何信息广播给所有处理器。在所有处理器上均储存该构造面信息。由于构造面只是一层网格面,因而对计算内存的需求较小。
1.2.1.2 洞切割辅助结构网格生成和压缩存储以构造面为基准,生成“辅助结构网格立柱”,根据某种规则(如每块网格上的单元数)确定辅助结构网格的“分辨率”(Nresolution)。辅助结构网格的空间范围由Scons的最大最小坐标确定。设与坐标轴y轴平行的方向为“立柱方向”(Direction),该方向作为压缩存储方向,其余方向为“立柱平面方向”,对三维问题,空间三个方向(x,y,z)排除“立柱方向”后剩余(x,z)两个方向,申请数组大小Nresolution×Nresolution;对于二维问题,剩余一个方向(x),申请数组大小为Nresolution。每个辅助结构网格“立柱单元”(以平面方向为基底,以立柱方向为高)坐标范围由Scons和“分辨率”确定,根据每块构造曲面网格面在非“立柱方向”的最大最小坐标,即可确定该网格面所交叠的辅助结构网格立柱。
辅助结构网格采用压缩存储方式,即对于每个“立柱单元”,仅标记不连续的包含构造面的单元位置,并存储该单元下一单元是否落洞的信息,如此可以节约大量内存。下面以二维翼型图的方式进行说明。
图 3(a)为根据构造网格面标记的辅助结构网格中的单元(标记了M),图 3(b)给出了不使用压缩存储方式时,需要记录的结构网格单元位置(标记了M)。图 3(c)给出了y方向立柱压缩存储时需要记录的辅助结构网格单元位置,图 3(d)给出了x方向立柱压缩存储时需要记录的辅助结构网格单元位置(M(0)表示本辅助网格被记录,且在该立柱中该单元后面到下一个记录单元之间的网格为落洞,M(1)表示不落洞)。如此可以节约大量的存储空间。注意采用y方向立柱压缩存储的图(c)与(a)比较去除了连续重复位置(M(1,2),M(1,3),M(1,4),M(1,5),M(4,3),M(4,4),M(5,2)),X方向压缩存储的(d)与(a)比较中去除了连续重复位置(M(2,3),M(3,3),M(4,3),M(2,6))。进行压缩存储的存储量在二维情况下是O(Nresolution),三维情况下是O(Nresolution×Nresolution)。

|
图 3 洞切割辅助结构网格存储 Figure 3 Storage of structured auxiliary mesh for hole cutting |
结构网格单元后方的单元是否落洞的判断方法是从后面结构网格的格心引-Direction方向射线,按照与该立柱内构造面交点的个数奇数还是偶数来判定,仅需判断有限的几个网格面,计算量很小。
可以发现本文的压缩存储法对于构造面是“凹面”的情况仍然有效,具有一般性。
1.2.1.3 “洞切割”和插值边界元interpolate point(IP)确定在每个处理器上,对该处理器上的所有网格循环,通过调用辅助结构网格压缩存储数组及其检索数组,根据简单坐标比较,即可确定单元是否是洞单元,而后把所有与洞单元邻接的非洞单元标记成插值边界元,进行后续的贡献单元搜索工作。
1.2.2 并行贡献单元搜索确定了插值边界单元后,需要寻找这些单元的贡献单元。这里提出了一种可自适应的辅助结构网格方法Adaptive Structured Auxiliary Mesh(ASAM),用辅助结构网格方法给定贡献单元搜索的起始点,给定搜索开始点后,采用N2N方法进行贡献单元确定,对于搜索路径遇到边界面的问题,采用了单个结构辅助网格内的单元局部穷举法,避免了复杂几何交叉的判定(辅助结构网格自适应过程也可以有效排除边界面)。称之为不判断边界的反映射方法Inverse Map No Boundary Adjudication(IM_NBA)。具体步骤如下:
1) 网格块外边界范围信息广播。在各个处理器之间交换信息,使得每个处理器均知道其他处理器上所有网格块的最大最小坐标范围。
2) 插值边界单元交互。对任意处理器,对其上面所有要进行贡献单元搜索的单元IP,判断这些待寻找贡献单元的坐标是否在其他处理器上网格边界范围内,如果在,打包发送给对应的处理器。
3) 辅助结构网格定位。对任一处理器n,子网格块为B1_n,B2_n,……BN_n,对其每个子网格块,按照某一基准(如子网格块的单元数)建立一定分辨率的辅助结构网格(注意:该辅助结构网格的最大最小坐标由其他处理器发送过来的插值边界元IP的最大最小坐标动态确定,而不是该块网格在该处理器上的坐标范围确定,如此大大缩小了辅助结构网格的范围,排除了大量的不可能待搜索单元。)。通过对待搜索插值单元及网格块上的网格单元进行一次大循环,建立压缩存储数组,输入辅助结构网格单元号,即可取出与该辅助结构网格单元有空间交叠的候选贡献单元网格及落入该辅助结构网格空间范围内的待搜索单元。实际存储时,不存储所有的辅助结构网格,而是仅对用到的辅助结构网格单元(辅助结构网格内有待搜索插值点及候选贡献单元)进行存储,这样可以降低存储容量,压缩存储数组通过建立的索引数组来查询。
由以上操作可知,选择合适的辅助结构网格分辨率是较为重要的,太大的分辨率导致每个辅助结构网格内存储了太多可能的候选贡献单元,使得搜索路径增长,搜索时间效率下降。太小的分辨率将会带来索引数组的容量增加,也无疑增加了存储负担。
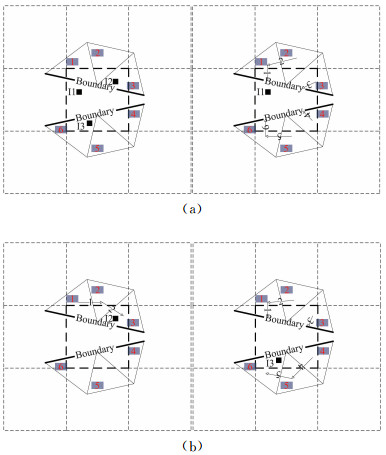
4) 无边界交叉判断的N2N贡献单元搜索和辅助结构网格细化。对任一辅助结构网格单元,取出其包含的待搜索单元及候选贡献单元,对每个待搜索的插值单元,以该辅助网格内的候选贡献单元范围为边界,使用N2N方法,进行贡献单元搜索。搜索时,把每一个途经的单元进行记录,当搜索路径遭遇边界面(外场面、网格分区面等),搜索路径指向边界面外时,需要在该辅助结构网格单元内的候选贡献单元中取出路径未经历过的单元,重新启动N2N搜索,此过程为局部的穷举法,如果N2N搜索指向一个已经途径过的候选单元时,再次重启N2N搜索,直至找到需要的贡献单元,或者遍历经过了该辅助结构网格中的所有贡献单元,仍然没有找到贡献单元时,认为待搜索点在该处理器的该网格块上没有贡献单元。通过以上步骤,完全避免了繁琐的边界判断问题。还需注意的是,对于待搜索点的位置位于两个或多个网格的交线、交点很近时,N2N搜索的路径将会在可能的贡献单元之间跳跃(仅对三维情况,四边形网格面四点不共面),这时启用模糊判断规则,即搜索路径出现重复时,即认为锁定了贡献单元。图 4给出了某个辅助结构网格单元内的待搜索贡献单元(I1,I2, I3)及其候选贡献单元,其中I1在边界外,I2、I3有贡献单元,并分别给出了三个点的搜索路径。
|
图 4 贡献单元搜索路径示意图 Figure 4 Schematic of donor searching path |
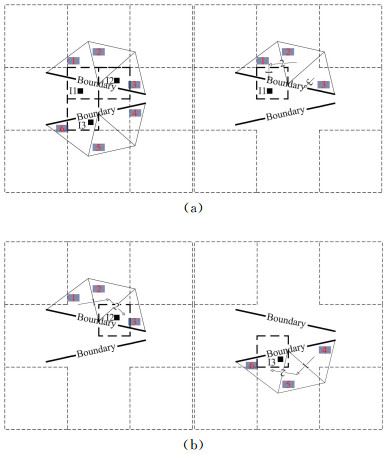
对于一个辅助结构网格内包含较多候选贡献单元的情况,搜索路径会比较长,时间效率下降,因而可以对辅助结构网格再次细分。对细分化后的结构网格单元,仍需做一次前处理,把属于各个细分化辅助结构网格单元中的待搜索点和候选贡献单元放入对应位置,取出细分化结构网格,即可取出其对应的待搜索点和候选贡献单元。进行辅助结构网格细分化后,贡献单元的搜索路径可能会大幅缩短,如图 5所示。注意,附加的前处理过程仍需要耗费计算时间,在实际计算时,仅对辅助结构网格内包含较多数量的待搜索点和贡献单元的情况进行网格细分,如此在储存容量和搜索速度之间进行了平衡。细化过程还会去除一些辅助结构网格(辅助结构网格体积缩小后,其内不再包含待搜索点或候选贡献单元)。
|
图 5 自适应辅助结构网格的贡献单元搜索路径 Figure 5 Donor searching path with ASAM |
在进行辅助网格自适应时,由于其是在各个单个辅助结构网格内进行搜索时进行,仅针对该辅助结构网格内的插值单元和候选贡献单元进行再划分归类,过程针对某一个辅助结构网格内单元进行动态内存申请和释放;另一方面,由于网格细分化,导致一些细分的辅助结构网格内不再拥有待搜索点,其交叠的候选贡献单元也可以不再存储。因而只要限定细分化的上限为一有限数值,则对整体存储容量不会产生较大影响,甚至能够有效缩减存储容量,如此可以采用分辨率较低的基础辅助结构网格,获得较快速的贡献单元搜索效果。
1.2.3 贡献单元信息回收和确定如果一个待搜索插值单元的贡献单元或贡献单元的邻元是边界元,则认为该贡献单元是不合理的(二阶格式构建),认为未找到贡献单元。此方法保证了网格分区边界的扩展边界元不能作为贡献单元。一个待搜索插值单元在多个处理器网格块上的贡献单元通过MPI数据传递回收,如果该待搜索点在所有处理器上均没有贡献单元,认为此点没有贡献单元。
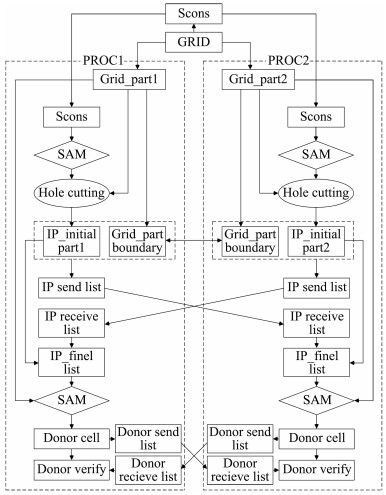
图 6为2个进程时的并行网格装配过程的计算流程图。
|
图 6 并行网格装配流程 Figure 6 Schematic of parallel grid assembly |
基于有限体积法的惯性系下三维Navier-Stokes方程可以写为
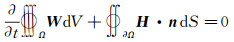
|
(1) |
| $ \mathit{\boldsymbol{W}}{\left[ {\begin{array}{*{20}{c}} \rho &{\rho \mathit{\boldsymbol{V}}}&{\rho E} \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{F}} - \mathit{\boldsymbol{W}}{V_t} $ |
| $ \begin{array}{l} \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\rho \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}}}&{\rho \mathit{\boldsymbol{V}}\left( {\mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}}} \right) \cdot \mathit{\boldsymbol{n}} + P\mathit{\boldsymbol{n}}} \end{array}} \right.\\ \;\;\;\;\;\;{\left. {\rho E\left( {\mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}}} \right) + \rho \mathit{\boldsymbol{V}} \cdot \mathit{\boldsymbol{n}}} \right]^{\rm{T}}} \end{array} $ |
其中,P、ρ、V 分别为压强、密度和速度;n 为单位外法矢;体积为Ω,边界为∂Ω;W、H 分别为守恒变量和对流矢量。
2.2 隐式双时间Hybrid-LUSGS方法推进对于旋翼非定常流场,采用隐式双时间方法来进行时间推进。引入二阶时间精度的双时间法[22]后,控制方程可以写为:
| $ \begin{array}{*{20}{c}} {\left( {\frac{1}{{\Delta \tau }} + \frac{3}{{2\Delta t}}} \right)V_i^{n + 1}\Delta \overrightarrow {W_i^m} + \frac{{\partial \overrightarrow {R_i^m} }}{{\partial \overrightarrow {{W_i}} }}\Delta \overrightarrow {W_i^m} + \frac{{\partial \overrightarrow {R_i^m} }}{{\partial \overrightarrow {{W_j}} }}\Delta \overrightarrow {W_j^m} = }\\ { - \left( {\overrightarrow {R_i^m} + \frac{{3V_i^{n + 1}\overrightarrow {W_i^m} - 4V_i^n\overrightarrow {W_i^n} + V_i^{n - 1}\overrightarrow {W_i^{n - 1}} }}{{2\Delta t}}} \right)} \end{array} $ | (2) |
式中:m为伪时间;n为物理时间;Δτ为伪时间增量;Δt为物理时间增量;对于控制方程AΔW=-R,其中A为nelt×nelt矩阵(nelt为网格单元的总数)。隐式无矩阵存储的LU-SGS方法[23]如下。
| $ A\Delta W = \left( {L + D + U} \right)\Delta W = - R $ | (3) |
向前扫略步:
| $ \left( {L + D} \right)\Delta {W^ * } = - R $ | (4) |
向后扫略步:
| $ \left( {D + U} \right)\Delta W = D\Delta {W^ * } $ | (5) |
在并行计算时,由于网格分区,每个线程上的网格不是整体网格,因而原始的LU-SGS方法不再适用,本文采用以下步骤(Hybrid LUSGS)[24]:
1) 雅克比迭代方式计算每个单元上的守恒量增量:
| $ \Delta W_i^ * = - {Q_i}/D $ | (6) |
2) 不同处理器之间交换扩展边界单元的ΔWi*;
3) 各个处理器上计算守恒变量的增量:
| $ \begin{array}{l} \Delta W_i^ * = \Delta W_i^ * + \frac{{ - \sum\nolimits_{j\left( {j < i} \right)} {\left\{ {\frac{1}{2}\left[ {\overrightarrow {{F_c}} \left( {{W_j} + \Delta W_j^ * ,{n_{ij}}} \right) - \overrightarrow {{F_c}} \left( {{W_j},{n_{ij}}} \right) - {V_t}\Delta W_j^ * - \left| {{\lambda _{i,j}}} \right|\Delta W_j^ * } \right]\left| {{S_{i,j}}} \right|} \right\}} }}{D}\\ \Delta {W_i} = \Delta W_i^ * - \frac{{\sum\nolimits_{j\left( {j > i} \right)} {\left\{ {\frac{1}{2}\left[ {\overrightarrow {{F_c}} \left( {{W_j} + \Delta {W_j},{n_{ij}}} \right) - \overrightarrow {{F_c}} \left( {{W_j},{n_{ij}}} \right) - {V_t}\Delta {W_j} - \left| {{\lambda _{i,j}}} \right|\Delta {W_j}} \right]\left| {{S_{i,j}}} \right|} \right\}} }}{D} \end{array} $ | (7) |
更新守恒变量(网格分区扩展边界元不更新);
4) 不同处理器之间交换插值边界的守恒变量。
2.3 通量计算使用动网格上的ROE格式[25]进行无粘通量计算,为保证计算空间精度,交接面的通量确定采用数值重构技术。用Venkatakrishnan限制器[26]避免插值过程中的过冲。
粘性通量计算采用中心格式,其中涡粘性系数的计算采用Spalart-Allmaras湍流模型[27],如下:
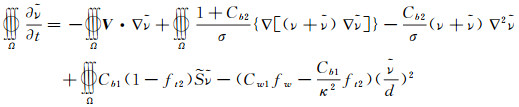
|
(8) |
湍流模型方程与主控方程采用松耦合的方式进行,时间离散方法与主控方程相同。需要注意的是由于桨叶等物体间存在相对运动,任意网格点的壁面距离需要在每个物理时间重新计算,该过程也可以完全并行进行(各个处理器上都存储壁面坐标即可)。
2.4 嵌套网格间数据交换插值单元物理量的值通过贡献单元的邻居上物理量的值插值得到。
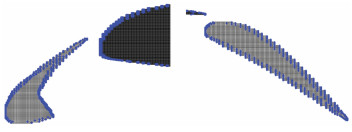
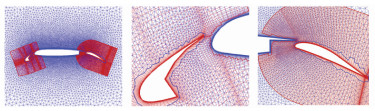
3 算例研究 3.1 二维多段翼型示例为了方便展示本文基于自适应辅助结构网格贡献单元搜索方法的效果,针对二维多段翼型网格进行了洞切割和贡献单元搜索测试。其中主翼网格作为背景网格,拓扑采用混合网格形式(四边形/三角形),襟翼和缝翼网格块均采用四边形网格。以物面为边界,向外扩展4层构建构造曲面,以构造曲面为依据生成洞切割辅助结构网格,图 7为用于洞切割的辅助结构网格,未加粗部分为理论存储(黑色),加粗部分(蓝色)为采用压缩存储时实际存贮的辅助网格。可见采用压缩存储技术可以大大缩减内存消耗,使得采用更加致密的辅助结构网格以获取更好的洞切割效果成为可能。图 8是洞切割后用于计算的三段翼型网格示意图。
|
图 7 洞切割辅助结构网格示意图 Figure 7 Schematic of hole cutting SAM |
|
图 8 洞切割后的三段翼型网格 Figure 8 Multi-wing grid after hole cutting |
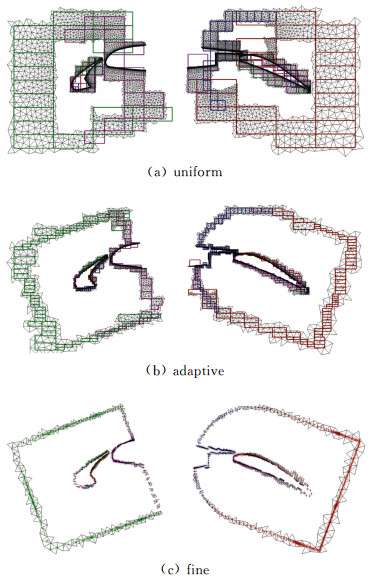
图 9给出了采用不同的辅助结构网格进行贡献单元初始位置定位的示意图(不同颜色的网格线代表其属于不同的处理器)。其中三种情况分别对应着均匀辅助结构网格(同一处理器,同一网格块使用尺度相同的结构网格辅助单元,划分的尺度人工给定)(图 9(a)),自适应辅助结构网格(图 9(b))和极致密辅助结构网格(图 9(c))。图中还给出了辅助结构网格中对应的候选贡献单元(黑色网格线)。可见,对于均匀的辅助结构网格,每个结构网格单元内包含了较多的候选贡献单元,使得每个结构辅助网格内的贡献单元搜索过程较长;图 9(b)是图 9(a)网格依据其中每个辅助结构网格单元中的待搜索点数和候选贡献单元数进行自适应的结果,在较小的代价下,缩小了贡献单元搜索的范围;图 9(c)采用了极致密的辅助结构网格(人工给定极小的划分尺度),几乎一次锁定了需要的贡献单元。需要注意的是,采用极致密的辅助结构网格,对于三维情况,内存开销将过于巨大,因而此处给出的仅是对于二维计算问题的演示性说明。
|
图 9 辅助结构网格用于贡献单元定位 Figure 9 SAM for donor cell localization |
“Caradonna & Tung旋翼”[28],桨叶2片,翼型NACA0012,展弦比6,无扭转尖削。计算状态为桨尖马赫数0.877,安装角8°。网格由背景和两块桨叶网格组成。为方便比较,使用两种不同的背景网格(BA1, BA2),网格数(百万)和拓扑见表 1。
| 表 1 计算网格 Table 1 Grids for calculation |
|
|
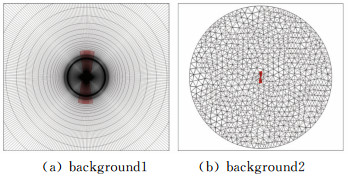
图 10为两种不同背景网格时的网格示意图。
|
图 10 “Caradonna & Tung旋翼”网格 Figure 10 Embedded grid for "Caradonna & Tung rotor" |
表 2为计算得到的不同背景网格、不同的线程数时,单次流场内迭代计算情况下,网格装配时间与计算时间的比率。其中“hc”表示洞切割,ds表示贡献单元搜索,mpga表示网格装配过程中用于处理器之间信息传递和比较确认的时间,1 iter表示一次流场内迭代。由表可以看出,在网格装配过程中,贡献单元搜索时间占网格装配时间的较大比重,洞切割时间与贡献单元搜索时间在同一量级,但比重相对较小。而对于本文这种显式构建插值边界情况,由于待搜索单元数目较少,处理器之间数据传递的用时很少,在目前测试的算例中几乎可以忽略。在该测试中,进行一次流场内迭代情况下,网格装配占整体时间的最大比例约为6%。对于采用双时间方法计算的旋翼流场,网格装配时间对全局计算时间的占比取决于内迭代次数的选取,可见对于本文算例,内迭代大于7次的情况下,网格装配的时间则下降到流场计算时间的1%以下。由图还可以看出,随着线程数的增加,用于贡献单元搜索的时间占比也在增加(网格装配部分加速比低于流场计算加速比)。
| 表 2 单次流场计算时各部分用时比率 Table 2 Time consumption comparison for difference processes in calculation with 1 flow field iteration |
|
|
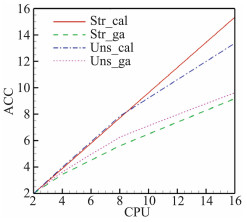
图 11为两套网格下的流场计算和网格装配时间的加速比(均假定2进程时的加速比为2),可以发现,随着线程数的增加,用于流场计算(图中标注“cal”)的加速比增长率较好,而用于网格装配(图中标注“ga”)部分的加速比效果相对较差。“Str”表示六面体背景网格,“Uns”表示四面体背景网格。究其原因是在进行多线程计算时,网格切分过程保证了各个线程上拥有近似相同的计算单元数,但对于每个处理器,其进行贡献单元搜索的单元数并不平均且随时间变化,图 12给出了8线程情况下各线程上面待进行贡献单元搜索单元的个数(背景网格1),贡献单元搜索完成时间决定于进行贡献单元搜索耗时最长的线程的执行时间。
|
图 11 计算和网格装配的加速比 Figure 11 Acceleration ratio of calculation and grid assembly |
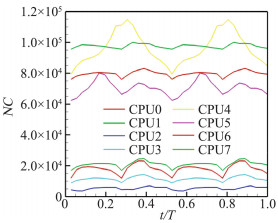
|
图 12 一旋翼旋转周期内各处理器上待搜索贡献单元数 Figure 12 Interpolation point numbers in different threads in 1 rotor revolution |
图 13为计算得到的各个桨叶剖面压强系数及与试验值的对比,在多数截面上,计算与试验的吻合度较好(r/R=0.68处有一定差异),且采用两套背景网格计算得到的结果实际差异很小,图 14为计算得到的特征截面涡量等值图。

|
图 13 桨叶各截面上的表面压强系数比较 Figure 13 Cp comparison for different rotor blade sections |
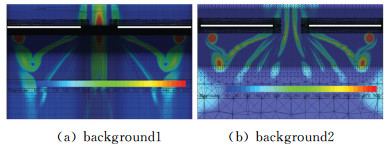
|
图 14 旋翼流场涡量 Figure 14 Vorticity magnitude of rotor flow fields |
为讨论自适应辅助结构网格定位贡献单元初始位置对网格装配过程的影响,这里采用4片桨叶的“HELISHAPE 7A”旋翼为计算模型,计算状态是桨尖悬停马赫数0.616,前进比0.167,挥舞变距规律见文献[29]。计算网格采用六面体网格,背景网格数约为816万,每片桨叶的小网格数约为228万。
为验证可自适应辅助网格的计算加速效果,采用了不同的辅助结构网格分辨率进行了计算效率的测试,计算分别采用4个和8个线程并行进行。采用4个线程时,每个线程上,背景网格单元约为204万,每块桨叶网格约为57万。辅助结构网格分辨率Nres按照以下公式确定:
| $ {N_{{\rm{res}}}} = {\rm{coefficient}} \times \sqrt[{{\rm{dimen}}}]{{{\rm{nelt}}}} $ | (9) |
其中:coefficient为系数,dimen是维度,nelt为计算单元数。计算采用辅助网格的分辨率(每个方向)近似值见表 3(背景网格为BA,桨叶网格为BL,T代表线程数),计算时,限定最大的自适应分辨率为3,则可以把计算内存波动影响减到很小。
| 表 3 辅助结构网格分辨率 Table 3 SAM resolution of grid blocks |
|
|
图 15为测试得到的不同分辨率时,采用与不采用自适应辅助结构网格方法情况下,从辅助结构网格生成到贡献单元搜索确定的时间长度比较,图中时间按照t0(采用网格分辨率系数0.1时的网格装配时间)正则化处理。可以看出,随着辅助结构网格分辨率增加,网格装配时间迅速缩短,过大的分辨率不会获得计算时间优势。在采用系数0.2时,采用自适应方法得到的网格装配时间已经接近网格装配速度的极值,这表明采用自适应辅助结构网格时,可以采用更小的网格分辨率,获得较高的网格装配速度。对三维情况,内存占用与分辨率三次方成比例,这表明采用自适应辅助结构网格方法可以带来较大的内存节约。同时也可以看出,在采用较粗的辅助网格时(如采用网格分辨率系数0.1的辅助网格),改进的方法可以提供近似十倍于与原方法的加速效果。这表明当前方法在低内存开销情况下,可以用来大幅度提高贡献单元搜索速度。
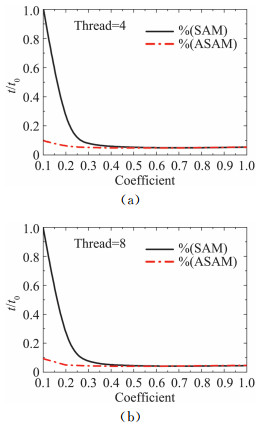
|
图 15 SAM和ASAM方法时的贡献单元搜索时间比较 Figure 15 Comparison of donor searching time with SAM and ASAM |
图 16为采用系数0.2时的特征截面上辅助结构和自适应辅助结构网格图。
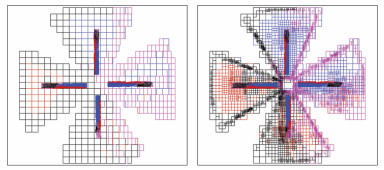
|
图 16 辅助结构与自适应辅助结构网格示意图 Figure 16 Schematic of SAM and ASAM |
图 17为计算得到的不同桨叶截面在方位角为90°时,计算的表面压强与试验值对比。计算与试验的吻合程度较好。

|
图 17 桨叶各截面压强(方位角90°) Figure 17 Sectional Cp of blade surface (azimuth=90°) |
对用于旋翼流场计算的并行网格装配方法进行了改进研究,并进行了计算测试,得到结论如下:
1) 压缩存储的并行辅助结构网格洞切割方法有效降低了计算内存消耗,内存消耗为辅助网格分辨率(维度-1)次方量级,使得采用更加致密的洞切割辅助结构网格成为可能,计算方法对凹形边界仍然有效,具有一般性。
2) 基于辅助结构网格、N2N及局部穷举法,构建了新的无边界交叉几何判断的贡献单元搜索方法,采用辅助结构网格自适应技术,有效缩减了贡献单元搜索的路径长度。在当前测试情况下,采用较粗的辅助网格时改进的方法(ASAM)可以提供近似十倍于原方法(SAM)的加速效果。这表明当前方法在低内存开销情况下,可以用来大幅度提高贡献单元搜索速度。
3) 实现了完全并行化的网格装配过程,并行网格装配方法理论上不受CPU数的限制,尽管网格装配部分的加速效果低于流场部分并行加速效果,但当前计算测试情况下,方法仍有效地缩减了网格装配时间,使得在多进程并行的情况下,网格装配时间占单次流场计算迭代时总时间长度的6%以下,在使用双时间方法且内迭代大于7次时,网格装配的时间则下降到流场计算时间的1%以下。对于需要多个物理时间迭代的旋翼非定常流场计算来说,方法具备较好的计算效果。
| [1] |
Strawn R C, Caradonna F X, Duque E P N. 30 years of rotorcraft computational fluid dynamics research and development[J]. Journal of the American Helicopter Society, 2006, 51(1): 5-21. DOI:10.4050/1.3092875 (  0) 0) |
| [2] |
Lawson S J, Woodgate M, Steijl R, et al. High performance computing for challenging problems in computational fluid dynamics[J]. Progress in Aerospace Sciences, 2012, 52: 19-29. DOI:10.1016/j.paerosci.2012.03.004 (  0) 0) |
| [3] |
Blades E L, Sreenivas K, Hyams D G. Arbitrary overlapping interfaces for unsteady unstructured parallel flow simulations[R]. AIAA 2003-276, 2003. https://www.researchgate.net/publication/268566487_Arbitrary_Overlapping_Interfaces_for_Unsteady_Unstructured_Parallel_Flow_Simulations
(  0) 0) |
| [4] |
Strang W Z, Tomaro R F, Grismer M J. The defining methods of cobalt 60: A parallel, implicit, unstructured Euler/Navier-Stokes flow solver[R]. AIAA 99-0786, 1999.
(  0) 0) |
| [5] |
Meakin R L. Domain connectivity among systems of overset grids[R]. NASA-CR-193390. https://www.researchgate.net/publication/24326076_Domain_connectivity_among_systems_of_overset_grids
(  0) 0) |
| [6] |
Meakin R L. Object X-rays for cutting holes in composite overset structured grids[R]. AIAA 2001-2537, 2001. https://www.researchgate.net/publication/246988380_Object_X-rays_for_cutting_holes_in_composite_overset_structured_grids
(  0) 0) |
| [7] |
Noack R W. A direct cut approach for overset hole cutting[C]//18th AIAA Computational Fluid Dynamics Conference, June 25-28, 2007, Miami, FL. https://www.researchgate.net/publication/268262141_A_Direct_Cut_Approach_for_Overset_Hole_Cutting
(  0) 0) |
| [8] |
Lee Y, Baeder J D. Implicit hole cutting-A new approach to overset grid connectivity[R]. AIAA 2003-4128, 2003. https://www.researchgate.net/publication/268483663_Implicit_Hole_Cutting_-_A_New_Approach_to_Overset_Grid_Connectivity
(  0) 0) |
| [9] |
Bercovier M, Pirroneau O, Sastri V. Finite elements and characteristics for some parabolic-hyperbolic problems[J]. Appl Math Model, 1983, 7: 89-96. DOI:10.1016/0307-904X(83)90118-X (  0) 0) |
| [10] |
Madrane A, Heinrich R, Gerhold T. Implementation of the chimera method in unstructured hybrid DLR finite volume tau-Code[C]//6th Overset Composite Grid and Solution Technology Symposium, October, 2002, Ft. Walton Beach, Florida, USA.
(  0) 0) |
| [11] |
Bonet J, Peraire J. An alternate digital tree (ADT) algorithm for 3D geometric searching and intersection problems[J]. ASME International Journal for Numerical Methods in Engineering, 1991, 31: 1-17. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [12] |
Pissanetzky S, Basombrio F G. Efficient calculation of numerical values of a polyhedral function[J]. Int J Numer Meth Eng, 1981, 17: 231-237. DOI:10.1002/(ISSN)1097-0207 (  0) 0) |
| [13] |
Sitaraman J, Floros M, Wissink A, et al. Parallel domain connectivity algorithm for unsteady flow computations using overlapping and adaptive grids[J]. Journal of Computational Physics, 2010, 229: 4703-4723. DOI:10.1016/j.jcp.2010.03.008 (  0) 0) |
| [14] |
Roget B, Sitaraman J. Robustness and accuracy of donor search algorithms on partitioned unstructured grids[C]//10th symposium on overset composite grids and solution technology, September 20-23, 2010, NASA AMES Research center moffett field, California USA.
(  0) 0) |
| [15] |
Khoshniat M, Stuhne G R, Steinman D A. Relative performance of geometric search algorithms for interpolating unstructured mesh data[C]//Medical Image Computing and Computer Assisted Invention-MICCAI, 6th international conference, November 15-18, 2003, Montreal, Canada. https://pdfs.semanticscholar.org/6f45/7b14d2867f3cdb5694c4fd73c46060fa9ea6.pdf
(  0) 0) |
| [16] |
Wang B, Zhao Q J, Xu G, et al. A new moving embedded grid method for numerical simulation of unsteady flow-field of the helicopter rotor in forward flight[J]. Acta Aerodynamica Sinica, 2012, 30(1): 14-21. (in Chinese) 王博, 招启军, 徐广, 等. 一种适合于旋翼前飞非定常流场计算的新型运动嵌套网格方法[J]. 空气动力学学报, 2012, 30(1): 14-21. DOI:10.3969/j.issn.0258-1825.2012.01.003 (  0) 0) |
| [17] |
Yang W Q, Song B F, Song W P. Distance decreasing method for confirming corresponding cells of overset grids and its application[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(2): 205-212. (in Chinese) 杨文青, 宋笔锋, 宋文萍. 高效确定重叠网格对应关系的距离缩减法及其应用[J]. 航空学报, 2009, 30(2): 205-212. DOI:10.3321/j.issn:1000-6893.2009.02.003 (  0) 0) |
| [18] |
Zhao Q J, Xu G H. Grid generation technique for helicopter rotor CFD including blade motions[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2004, 36(3): 288-293. (in Chinese) 招启军, 徐国华. 计入桨叶运动的旋翼CFD网格设计技术[J]. 南京航空航天大学学报, 2004, 36(3): 288-293. DOI:10.3969/j.issn.1005-2615.2004.03.004 (  0) 0) |
| [19] |
Zhang Y, Ye L, Yang S. Numerical study on flow fields and aerodynamics of tilt rotor aircraft in conversion mode based on embedded grid and actuator model[J]. Chinese Journal of Aeronautics, 2015, 28(1): 93-102. DOI:10.1016/j.cja.2014.12.028 (  0) 0) |
| [20] |
Li T H, Yan C. A new method of hole-point search in grid embedding technique[J]. Acta Aerodynamica Sinica, 2001, 19(2): 156-160. (in Chinese) 李亭鹤, 阎超. 一种新的分区重叠洞点搜索方法-感染免疫法[J]. 空气动力学学报, 2001, 19(2): 156-160. DOI:10.3969/j.issn.0258-1825.2001.02.004 (  0) 0) |
| [21] |
Karypis G, Kumar V. METIS unstructured graph partitioning and sparse matrix ordering system version 2. 0[M]. University of Minnesota, Department of Computer Science, Mineapolis, MN 55455, August 1995.
(  0) 0) |
| [22] |
Jameson A. Time-dependent calculations using multigrid with applications to unsteady flows past airfoils and wings[R]. AIAA 91-1596, 1991.
(  0) 0) |
| [23] |
Luo H, Baum J D. A fast, matrix-free implicit method for computing low mach number flows on unstructured grids[R]. AIAA 99-3315, 1999. https://www.tandfonline.com/doi/abs/10.1080/10618560008940720
(  0) 0) |
| [24] |
Stoll P, Gerlinger P, Bruggemann D. Domain decomposition for an implicit LU-SGS scheme using overlapping grids[R]. AIAA 97-1896, 1997.
(  0) 0) |
| [25] |
Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372. DOI:10.1016/0021-9991(81)90128-5 (  0) 0) |
| [26] |
Venkatakrishnan V. On the accuracy of limiters and convergence to steady state solutions[R]. AIAA 93-0880, 1993.
(  0) 0) |
| [27] |
Spalart P R, Allmaras S R. A one-equation turbulence model for aerodynamic flows[R]. AIAA-1992-439, 1992. https://www.researchgate.net/publication/236888804_A_One-Equation_Turbulence_Model_for_Aerodynamic_Flows
(  0) 0) |
| [28] |
Caradonna F X, Tung C. Experimental and analytical studies of a model helicopter rotor in hover[J]. Vertica, 1981, 5(1): 149-161. (  0) 0) |
| [29] |
Biava M, Bindolino G, Vigevano L. Single blade computations of helicopter rotors in forward flight[R]. AIAA 2003-52, 2003. https://www.researchgate.net/publication/259134770_Single_Blade_Computations_of_Helicopter_Rotors_in_Forward_Flight
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36

