摩阻是飞行器在高超声速飞行时所受总阻力的重要组成部分,相关的研究表明,摩阻最高可能占高超声速飞行器总阻力的50%[1]。准确地预测摩阻,在飞行器性能的评估、减阻以及CFD计算模型的确认等方面都有重要的作用[2-3]。虽然摩阻在高超声速飞行器的研制中非常重要,但要准确地进行测量却面临较大技术难题。在高超声速条件下,特别是高焓高马赫数状态,一般只能通过脉冲型风洞进行流场的模拟,有效试验时间只有几个到几十个毫秒,对测试传感器的频响提出了相对较高的要求。
为了进行飞行器摩阻特性研究工作,国际和国内开展了多项的理论预测和试验工作,发展了多种摩阻理论预测方法和测量手段[4-10]。在各种测量方法中,利用摩阻天平进行测量是获得飞行器模型表面摩阻的最直接的手段。国际上,从20世纪50、60年代开始,相继开展了摩阻传感器的研制工作,发展了应变式摩阻传感器[11-13]、压电式摩阻传感器[1, 14-17]、MEMS摩阻传感器[6]、光纤摩阻传感器[18]等多种摩阻测量手段。
澳大利亚昆士兰大学为了进行脉冲型风洞摩阻测量,研制了基于剪切型压电陶瓷敏感元件的摩阻传感器,该传感器利用剪切型压电陶瓷片的剪切压电效应实现摩阻的测量,频响可达到40 kHz[1]。美国CUBRC为了在LENS激波风洞上进行摩阻测量,也研制了基于压电陶瓷的摩阻传感器,通过三个压电陶瓷柱实现摩阻的测量,其中两个压电陶瓷柱用于摩阻的测量,中间的一个压电陶瓷柱用于风洞启动时加速度的补偿[14]。
本文基于压电陶瓷材料,研制了悬臂梁结构的摩阻天平。在天平结构设计中,采用有限元设计的方法,对其性能进行了预估,确定了天平的结构参数。本文研制的摩阻天平,虽然在频响方面有所牺牲,但大幅度提高了天平的灵敏度,降低了在激波风洞等脉冲风洞中进行摩阻测量的难度。
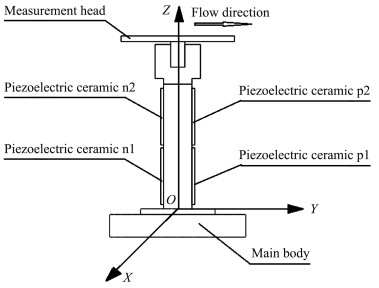
1 摩阻天平设计摩阻天平的结构如图 1所示,由三部分构成,摩阻天平主体、测量头以及压电陶瓷片。摩阻天平主体采用悬臂梁结构,采用刚度较大的材料制作,以降低在摩阻作用下的变形,并在量程范围内保持线性变形。测量头安装在摩阻天平本体的悬臂梁上,直接与试验气流接触,用于将气流的摩阻传递到悬臂梁上,采用铝合金等轻质材料制成,以降低测量头的质量,提高摩阻天平的频响,同时也可以通过更换不同材质的测量头来满足不同测量环境的要求。在力敏梁上粘贴四片压电陶瓷片进行摩阻的测量。压电片的定义如下:靠近力敏梁根部为1号,靠近测量头的为2号,沿Y轴正向为p,沿Y轴负向为n。压电陶瓷片选用正压型PZT-5压电陶瓷片,极化方向平行于Y轴。
|
图 1 摩阻天平结构示意图及坐标系定义 Figure 1 Sketch of skin friction balance and reference frame |
在摩阻测量试验中,由于高超声速气流的粘性带来的摩擦阻力作用在测量头上,引起测量头位置的变化,测量头位置变化将引起力敏梁的变形,粘贴在力敏梁上的压电陶瓷片感受力敏梁变形带来的应力,从而实现摩阻的测量。由于在摩阻测量的同时,测量头还处在试验气流的压力之下,在测量头的表面会感受到垂直于测量头的压力,而且这个压力分布还不均匀,从而引起力敏梁的变形,压电陶瓷片同样会感受到压力作用带来的应力,从而会对摩阻的测量结果带来影响。在摩阻天平的设计中,要尽量减小这个压力作用对摩阻输出的影响,提高摩阻测量结果的数据质量。
2 摩阻天平有限元分析有限元分析方法作为一种辅助设计手段,已经广泛应用在传感器的设计中。在本项研究中,使用ANSYS有限元分析的方法对摩阻天平的性能进行了预估,包括天平的频响分析和静力分析。
2.1 有限元模型在有限元分析中,压电陶瓷片采用正压型的PZT-5,摩阻天平本体材料选择30CrMnSiA,测量头的材料选择超硬铝合金705A,材料的性能参数如表 1所示。
| 表 1 材料参数表 Table 1 Material parameters |
|
|
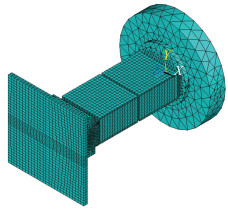
在有限元建模中,压电陶瓷片选用SOLID5单元,SOLID5单元具有三维磁场、热场、电场、压电场和结构场分析能力,并能在各场之间实现有限的耦合。因为压电片上会出现力场和压电场的耦合,所以建模中采用SOLID5压电耦合单元模拟4片压电片。摩阻天平本体和测量头采用SOLID45单元。SOLID45单元用于构造三维固体结构,单元通过8个节点来定义,每个节点有3个沿着x、y、z方向平移的自由度。单元具有塑性、蠕变、膨胀、应力强化、大变形和大应变能力。天平结构在外激励的作用下会产生应力、应变,故采用SOLID45三维实体单元模拟其他材料[19]。划分网格时尽可能采用求解精度更高的六面体结构划分单元,同时也可以降低有限元模型的求解规模。建立的摩阻天平的有限元模型如图 2所示。
|
图 2 摩阻天平的有限元模型 Figure 2 Finite element model |
模态分析为传感器的结构设计和性能评估提供了一个强有力的工具,其主要目的是获得摩阻天平的各阶振动频率和振型,以判断其是否能够满足激波风洞测量的需求。由于激波风洞的有效试验时间只有几个到十几个毫秒,摩阻天平的设计中,必须综合考虑天平的频响和灵敏度,以确定其是否能够满足激波风洞试验测量的需求。在激波风洞测量中,为保证测量的准确性,必须保证天平结构的低频模态频率f>2/t(t为有效试验时间),当风洞的有效试验时间为4 ms时,要求摩阻天平的最低频率要大于500 Hz。
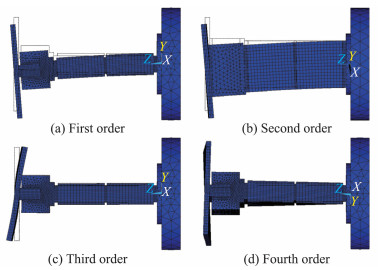
在有限元分析中,分别计算了力敏梁厚度为2、3、3.5、4、4.5、5 mm的摩阻天平的前4阶振动频率,结果如表 2所示。摩阻天平的前4阶振型由图 3给出。从图中可以看出,其中一阶振动模态为沿Y轴的弯曲振动,即沿力敏梁厚度方向的振动;二阶振动模态为沿X轴的弯曲振动,即沿力敏梁宽度方向的振动;三阶振动模态为测量头的振动,四阶振动模态为绕Z轴的扭曲振动。
| 表 2 不同力敏梁厚度的摩阻天平前四阶频率 Table 2 The first four orders response frequency of the skin friction balance with different thickness cantilever beam |
|
|
|
图 3 摩阻天平前4阶振型 Figure 3 The first four modal shapes of skin friction balance |
模态分析的结果表明,摩阻天平的一阶频响随着力敏梁厚度的增加而增加,为了获得较高的频响,需要适当提高天平力敏梁的厚度。与文献[1]中剪切型摩阻天平相比,悬臂梁型摩阻天平的频响相对偏低,只有几千赫兹,但可以满足激波风洞毫秒级试验时间的需求。
2.3 静力分析静力分析是用来计算结构在固定不变的载荷下的响应,一般不考虑惯性和阻尼的影响,适合求解惯性和阻尼对结构响应的影响不重要的问题。摩阻天平的灵敏度、线性度、抗干扰能力是其设计的关键,使用ANSYS软件进行静力分析的方法能够获得上述几个性能指标,从而很好地评估天平设计的合理性。
静力分析的目的是为了获得天平输出与施加载荷之间的关系。在静力分析中,共考虑了三种载荷,一种是摩阻,即作用在摩阻天平测量头上平行于气流方向的力;一种是气流压力,即垂直于测量头表面的压力载荷;最后一种是由于垂直于测量头表面的压力分布不均匀引起的力矩载荷。分别计算了在三种载荷作用下,天平的输出,以及综合加载时天平的输出,评估了不同载荷作用下摩阻天平的输出线性度以及抗干扰能力。
1) 摩阻载荷
在摩阻天平的量程范围内,针对力敏梁厚度为4 mm的摩阻天平,分别计算了0.049N、0.098N、0.196N、0.294N、0.392N、0.49N,六种摩阻载荷下摩阻天平各压电片的输出电势,以及经过组合后的摩阻输出电势,其中Vf=(Vp1+Vn1)-(Vp2+Vn2),结果如表 3所示。从表中可以看出,对称布置的压电陶瓷片的输出电势相同,符号相同。
| 表 3 摩阻作用下各压电片的输出电势 Table 3 The voltage output of piezoelectric ceramics with different skin friction |
|
|
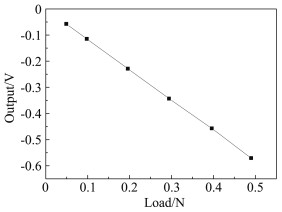
图 4给出了施加的载荷与摩阻天平的输出电势之间的关系,从图中可以看出摩阻天平的输出与施加的载荷之间具有较好的线性关系。
|
图 4 摩阻天平的输出与载荷之间的关系 Figure 4 Relationship between voltage output and skin friction load |
表 4给出了不同力敏梁厚度的摩阻天平的电压灵敏度,结果表明,随着力敏梁厚度的增加,摩阻天平的电压灵敏度非线性降低,从天平设计的角度来看,需要综合考虑灵敏度和频响的影响,从而确定力敏梁的厚度,根据有限元分析的结果,摩阻天平力敏梁的厚度选择3.5-5mm比较合适,一方面摩阻天平的频响能够满足要求,同时也能保持较高的灵敏度。
| 表 4 不同力敏梁厚度下摩阻天平对摩阻输出的灵敏度 Table 4 Sensitivity of the skin friction balance with different thickness cantilever beam |
|
|
2) 压力载荷
压力载荷通过在测量头的表面施加固定的压力载荷进行计算,施加的压力分别为4000 Pa、5000 Pa和6000 Pa,表 5给出了在不同压力作用下各压电片以及摩阻的输出情况,从各压电片的输出情况可以看出,在压力载荷作用下,配对粘贴的压电陶瓷片(例如p1和n1)的输出电势的大小几乎相等,符号相反,其和相互抵消,从而在压力的作用下,通过压电片的极性的组合可以抵消压力干扰的影响。
| 表 5 压力作用下各压电片的输出电势 Table 5 The voltage output of piezoelectric ceramics with different pressures |
|
|
3) 力矩载荷
分别对摩阻天平施加2.45×10-4、4.90×10-4、9.8×10-4、1.96×10-3 N·m的力矩载荷,得到的各个压电陶瓷片和摩阻的输出电势如表 6所示。从表中可以看出,在力矩的作用下,粘贴在力敏梁上的四片压电陶瓷片的输出电势大小几乎相等,符号相同,说明在力矩载荷的作用下,摩阻的输出也非常小,力矩对摩阻输出的影响可忽略不计。
| 表 6 力矩作用下各压电片的输出电势 Table 6 The voltage output of piezoelectric ceramics with different moments |
|
|
4) 综合加载
在摩阻天平上同时施加0.196N的摩阻(F)与分布不均匀的压力载荷(P),压力载荷沿摩阻测量的方向从4500Pa线性变化到5500Pa,在单独加载和综合加载的情况下,各个压电陶瓷片和摩阻的输出电势如表 7所示,从表中可以看出,由于非均匀压力对摩阻输出带来的干扰较小,相比较没有压力载荷作用下的摩阻输出,在非均匀压力作用下,摩阻天平的输出增大了约0.4%。
| 表 7 综合加载和分别加载时各压电片的输出电势 Table 7 The voltage output of piezoelectric ceramics with different loads |
|
|
静力分析的结果表明,采用压电陶瓷作为摩阻天平的敏感元件,利用压电材料的方向选择性可以很好地抑制由于气流压力作用对摩阻天平输出的干扰。摩阻天平在保证对摩阻敏感的同时,能够通过结构的设计来降低气流压力作用对天平输出的影响,其设计能够满足摩阻测量的需求。
3 摩阻天平性能根据有限元分析的结果,设计制作了力敏梁厚度为4mm的摩阻天平,并进行了校准。在摩阻天平的应用中,使用电荷放大器将天平产生的电荷转变成电压,因此,天平校准得到的灵敏度系数是电荷灵敏度系数,而有限元计算得到的是电压灵敏度系数。对于压电陶瓷来说,电荷灵敏度系数与电压灵敏度系数通过如下的公式进行计算。
| $ \frac{Q}{F} = \frac{U}{F} \cdot \frac{{{\varepsilon _0}{\varepsilon _z}S}}{D} $ | (1) |
其中,ε0是真空介电常数,εz为PZT压电陶瓷的Z向相对介电常数,Q为电荷,U为电压,F为力载荷,S为压电陶瓷片的面积,D为压电陶瓷片的厚度。
利用上述公式,将校准得到的摩阻天平的灵敏度转化为电压灵敏度,其灵敏度为0.957 V/N,与计算得到的1.16 V/N相比,大约为计算值的82.5%,这可能是由于在摩阻天平的粘贴过程中,使用环氧树脂胶进行粘贴,而在计算中,没有对粘贴胶层进行模拟。
在风洞试验中,测量了该摩阻天平的一阶频率,为2563 Hz,与计算值2746 Hz相比,比计算值低6.7%,这可能是由于在计算中,对摩阻天平的结构进行了一定程度的简化,造成了计算值与实际测量值的差异。
表 8给出了在风洞试验中,平板模型表面同一个测点,同一个流场状态三个车次的摩阻测量结果。从表中可以看出摩阻测量的重复性较好,说明研制的摩阻天平的性能比较稳定,能够满足激波风洞摩阻测量试验的需求。
| 表 8 风洞试验结果 Table 8 Shock tunnel test results |
|
|
本文基于压电敏感元件对摩阻天平进行了设计,使用有限元分析软件利用力电耦合模型对天平的性能进行了预估,依据有限元设计的结果制作了压电式摩阻天平,并在激波风洞上进行了平板模型表面摩阻测量试验。研究结果表明,在压电天平的设计中,利用压电材料的方向选择性,可以有效地抑制气流作用在模型表面的压力对摩阻测量结果的影响,降低分量间的干扰,降低风洞试验中摩阻测量的不确定度水平。
| [1] |
Silvester T B, Morgan R G. Skin-friction measurements and flow establishment within a long duct at superorbital speeds[J]. AIAA Journal, 2008, 46(2): 527-536. DOI:10.2514/1.32668 (  0) 0) |
| [2] |
Lv Z G, Li G J, Zhao R J, et al. Direct measurement of skin friction at hypersonic shock tunnel[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(6): 81-85. (in Chinese) 吕治国, 李国君, 赵荣娟, 等. 激波风洞高超声速摩阻直接测量技术研究[J]. 实验流体力学, 2013, 27(6): 81-85. DOI:10.3969/j.issn.1672-9897.2013.06.015 (  0) 0) |
| [3] |
Ma H Q, Gao H, Bi Z X. Direct measurement of skin friction for hypersonic flight vehicle[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 83-88. (in Chinese) 马洪强, 高贺, 毕志献. 高超声速飞行器相关的摩擦阻力直接测量技术[J]. 实验流体力学, 2011, 25(4): 83-88. DOI:10.3969/j.issn.1672-9897.2011.04.016 (  0) 0) |
| [4] |
Luo X C, Zhang K Y. Analysis of friction drag in scramjet isolator[J]. Acta Aerodynamica Sinica, 2009, 27(1): 124-128. (in Chinese) 骆晓臣, 张堃元. 隔离段内超声速流动摩擦阻力分析[J]. 空气动力学学报, 2009, 27(1): 124-128. DOI:10.3969/j.issn.0258-1825.2009.01.023 (  0) 0) |
| [5] |
Wei Y B, Zhang K Y, Luo X C. Analysis and investigation of internal drags trait in two-dimensional hypersonic inlets[J]. Acta Aerodynamica Sinica, 2010, 28(1): 104-108. (in Chinese) 卫永斌, 张堃元, 骆晓臣. 二元高超声速进气道内部阻力特性分析与研究[J]. 空气动力学学报, 2010, 28(1): 104-108. DOI:10.3969/j.issn.0258-1825.2010.01.017 (  0) 0) |
| [6] |
Naughton J W, Sheplak M. Modern developments in shear-stress measurement[J]. Progress in aerospace seciences, 2002, 8: 515-570. (  0) 0) |
| [7] |
Hazelton D M, Bowersox R D W, Skin friction correlations for high enthalpy flows[R]. AIAA 98-1963, 1998.
(  0) 0) |
| [8] |
Crafton J, Fonov S, Forlines A, et al. Skin friction measurements using elastic films[R]. AIAA 2010-42.
(  0) 0) |
| [9] |
Liu Tianshu, Montefort J, Woodiga S, et al. Global luminescent oil-film skin-fricton meter[J]. AIAA Journal, 2008, 46(2): 476-485. DOI:10.2514/1.32219 (  0) 0) |
| [10] |
Le Jialing, Ganimedov V L, Muchanaja M I, et al. The calculation of aerodynamic heating and viscous friction forces on the surface of hypersonicc flight vehicle[J]. Experiments and Measurements in Fluid Mechanics, 2002, 16(1): 8-20. (  0) 0) |
| [11] |
Schetz J A. Direct measurement of skin friction in complex flows[R]. AIAA 2010-44. https://www.researchgate.net/publication/268561564_Direct_Measurement_of_Skin_Friction_in_Complex_Flows_Using_Movable_Wall_Elements
(  0) 0) |
| [12] |
Rolling A J, Schetz J A. Direct skin friction measurements with shock-impingement compensation in complex turbulent flows[C]//25th AIAA Aerodynamic Measurement Technology and Ground Testing Conference, AIAA paper 2006-3838. https://www.researchgate.net/publication/268560790_Direct_Skin_Friction_Measurements_with_Shock-Impingement_Compensation_in_Complex_Turbulent_Flows
(  0) 0) |
| [13] |
Smith T B, Schetz J A, Bui T T. Development of direct-measuring skin-friction gauges for hypersonic flight tests[J]. AIAA Journal, 2003, 41(8): 1429-1437. DOI:10.2514/2.2125 (  0) 0) |
| [14] |
Holden M S. An experimental investigation of turbulent boundary layers at high mach number and reynolds numbers[R]. NASA report, CR-112147. https://www.researchgate.net/publication/24330497_AN_EXPERIMENTAL_INVESTIGATION_OF_TURBULENT_BOUNDARY_LAYERS_AT_HIGH_MACH_NUMBER_AND_REYNOLDS_NUMBERS
(  0) 0) |
| [15] |
Kelly G M, Simmons J M, Paull A. Skin-f/riction gauge for use in hypervelocity impulse facilities[J]. AIAA Journal, 1991, 30(3): 844-845. (  0) 0) |
| [16] |
Reddeppa P, Jagadeesh G. Measurement of direct skin friction in hypersonic shock tunnels[R]. AIAA 2005-1412. https://www.researchgate.net/publication/268567538_Measurement_of_Direct_Skin_Friction_in_Hypersonic_Shock_Tunnels
(  0) 0) |
| [17] |
Lv Z G, Li G J, Zhao R J, et al. The development of piezoelectric skin friction balance for shock tunnel[C]//The 8th International Symposium on Strain-Gauge Balances 2012.
(  0) 0) |
| [18] |
Vasudevan B, Measurement of skin friction at hypersonic speeds using fiber-optic sensors[C]//13th International Space Planes and Hypersonics Systems and Technology, AIAA 2005-3323.
(  0) 0) |
| [19] |
Lin L. Finite element analysis of piezoelectric ceramic materials based on AYSYS[J]. Science & Technology Information, 2009, 36: 39-40. (in Chinese) 林玲. 基于ANSYS的压电陶瓷材料有限元仿真分析[J]. 科技资讯, 2009, 36: 39-40. (  0) 0) |
 2018, Vol. 36
2018, Vol. 36


