倾转旋翼机是一种独特的飞行器,它可以像螺旋桨飞机一样快速有效地向前飞行,同时,也可以像普通直升机一样垂直起降、悬停。然而,在悬停状态下,旋翼下洗气流直接冲击到机翼上表面,使倾转旋翼机有效载重大大降低。这种垂直方向的阻力,又称为向下载荷,大约占了旋翼总拉力的10%[1]。
对于悬停状态下倾转旋翼机向下载荷减缓措施国外学者已开展了大量的研究,国内公开发表的相关文献则较少。目前最常见的策略是采用后缘襟翼。通过偏转后缘襟翼使翼型在来流方向投影面积变小,可以显著地减小垂直阻力。Maisel等[2]通过实验方法研究了不同长度后缘襟翼以及襟翼偏角对翼型向下载荷影响,研究结果表明当偏转角超过某个最优角度后,阻力系数又会上升,这是由于在襟翼上表面出现了流动分离现象;Felker等[3]采用了缩比为0.658的V-22倾转旋翼机旋翼与机翼模型,开展了悬停状态下旋翼不同拉力系数对机翼垂直阻力的影响;Wood等[4]通过在机翼上安装一种被称为“wind plow”的装置使有效载重提高了0.8%~2.4%;文献[5]提出在翼型上下表面分别安装平板来减小垂直方向阻力,并详细分析了平板安装位置和高度对气动特性影响。近年来,欧洲ERICA项目[6]发展了一种新型倾转机翼构型,通过偏转外侧段机翼可以使阻力大大降低,但机构实施起来复杂、难度大。另一种减阻策略是采用主动流动控制技术(AFC),例如定常吹吸气技术[7]、周期激励技术[8]等,文献[9]详细介绍了波音公司AFC在V-22倾转旋翼机上的应用。
由于在-90°来流迎角下,机翼下表面处于非定常分离区,对数值方法的精度和效率提出了更高要求。高精度的计算方法也能更好地为开展降载措施研究提供依据。倾转旋翼机通常采用直机翼,但倘若直接基于三维构型开展降载研究,不仅网格数多、占用计算资源大,而且计算时间难以忍受,因而现有CFD计算研究通常基于二维剖面开展。Stremel[10]通过求解二维不可压层流N-S方程比较了相同计算条件下不同翼型所受到的垂直阻力;文献[11]研究了雷诺数和湍流模型对翼型向下载荷的影响;El-Alti等[12]采用大涡模拟方法对NACA 64A223翼型流场特性进行了研究。
为了进一步提高倾转旋翼机悬停状态下的有效载重,本文采用CFD方法系统研究了被动控制技术在向下载荷减缓方面的应用,具体策略包括后缘襟翼、克鲁格襟翼、前缘下垂以及扰流板,并详细分析了各影响参数,研究成果能为工程型号设计提供参考。
1 CFD计算方法 1.1 非定常N-S方程求解直角坐标系下二维非定常N-S方程为[13]:
| $ \frac{{\partial \mathit{\boldsymbol{W}}}}{{\partial t}} + \frac{{\partial \mathit{\boldsymbol{f}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{g}}}}{{\partial y}} = \left( {\frac{{\partial \mathit{\boldsymbol{R}}}}{{\partial x}} + \frac{{\partial \mathit{\boldsymbol{S}}}}{{\partial y}}} \right) $ | (1) |
式中W为守恒量,f、g为对流通量,R、S为黏性通量。
采用有限体积空间离散法、双时间推进法求解非定常N-S方程。远场采用无反射边界条件。
1.2 DES方法雷诺平均N-S方程(RANS)不适于模拟存在大尺度涡的湍流流动,更准确的方法是大涡模拟(LES)。DES方法把RANS和LES结合起来模拟大分离流动,其主要思想是:在湍流附面层内采用RANS模拟附面层内的湍流流动,在其它区域采用Smagorinski大涡模拟。本文采用基于SA一方程湍流模型的DES方法来模拟翼型非定常大分离流动。SA模型求解与湍流黏性系数μT相关变量
| $ \begin{array}{l} \frac{{D\tilde v}}{{Dt}} = {C_{b1}}\tilde \Omega \tilde v - {C_{w1}}{f_w}{\left( {\frac{{\tilde v}}{d}} \right)^2} + \frac{1}{\sigma }\left\{ {\nabla \cdot \left[ {\left( {{v_L} + \tilde v} \right)\nabla \tilde v} \right] + } \right.\\ \;\left. {\left( {{C_{b2}}{{\left( {\nabla \tilde v} \right)}^2}} \right)} \right\} \end{array} $ | (2) |
其中
当湍流生成项与物面衰减项达到平衡时,即:
| $ {C_{b1}}\mathit{\tilde {\Omega}} \tilde v = {C_{w1}}{f_w}{\left( {\frac{{\tilde v}}{d}} \right)^2} $ | (3) |
此时湍流黏性与
| $ \tilde v \propto \tilde \Omega {d^2} $ | (4) |
而在Smagorinski大涡模拟方法中,其亚格子尺度湍流黏性随当地旋转率
| $ {\left( {\tilde v} \right)_{{\text{SGS}}}} \propto \mathit{\tilde {\Omega}} {\Delta ^2} $ | (5) |
| $ \Delta = \max \left( {\Delta x, \Delta y, \Delta z} \right) $ | (6) |
比较式(4)和(5)可知:如果把式(4)中的d置换为Δ,则SA模型就充当了Smagorinski大涡模拟。因此,基于SA模型的DES方法将d替换为[15]:
| $ \tilde d = \min \left( {d, {C_{{\text{DES}}}}\Delta } \right) $ | (7) |
| $ {C_{{\text{DES}}}} = 0.65 $ | (8) |
则当
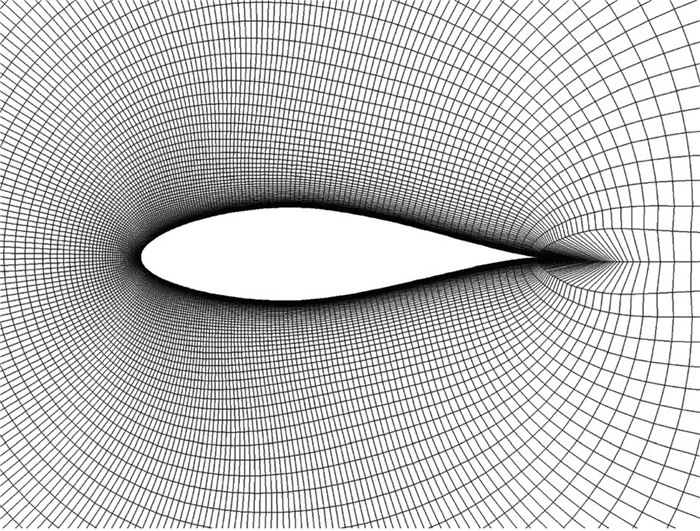
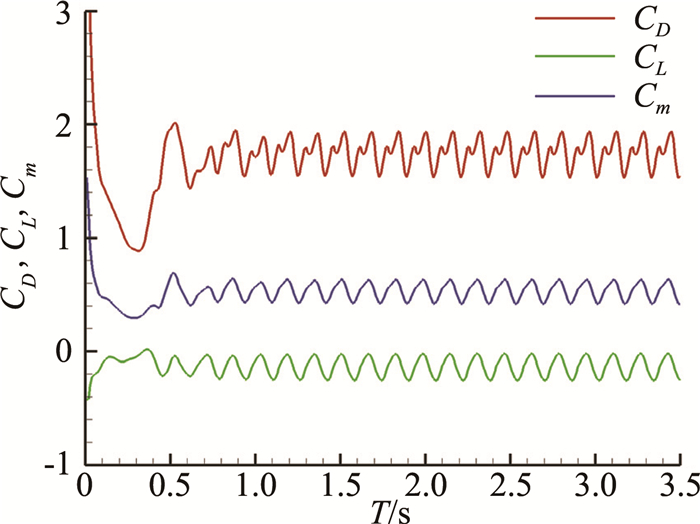
以具有丰富实验数据的NACA 64A223翼型[2]为研究对象验证本文计算方法的可靠性。选取的计算状态为Ma=0.138, α=-90°, Re=1.0×106。图 1给出了物面附近计算网格,采用O型网格,第一层网格高度为1.0×10-6,远场边界位于50倍弦长处。DES模型从RANS到LES的转换是由网格控制的,因而网格的规模和质量会影响湍流模型的转换进而严重影响计算结果[16]。本文在验证算例中生成了粗、中、细三套计算网格,网格数分别为159×121,239×177和319×235,并分别记作Mesh1、Mesh2和Mesh3;表 1给出了计算得到的一个周期内三种不同网格平均气动力系数和实验值[2]的对比,Mesh2计算结果和实验值吻合得最好。图 2给出了Mesh2翼型非定常升力系数、阻力系数和俯仰力矩系数随时间的变化曲线,大约在1s后气动系数呈现出周期变化。
|
图 1 NACA 64A223翼型物面附近网格 Figure 1 Mesh for NACA 64A223 airfoil |
| 表 1 不同网格平均气动力系数计算值和实验值对比 Table 1 Comparison of average aerodynamic coefficients |
|
|
|
图 2 非定常气动力系数随时间变化曲线 Figure 2 Time-dependent lift, drag and pitching moment |
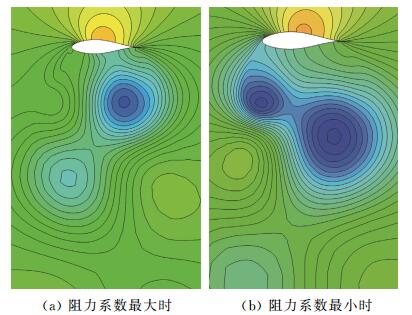
图 3给出了流场瞬时压力云图。当阻力系数最大时,如图 3(a),在翼型后缘下方1倍弦长处有一顺时针方向的涡;而当阻力系数最小时,如图 3(b),在翼型前缘下方1倍弦长处出现了一逆时针方向的涡,在后缘下方1.5倍弦长处有一顺时针方向的涡。正是由于涡的周期性脱落变化导致气动系数呈现出周期结果。
|
图 3 流场瞬时压力云图 Figure 3 Computed instantaneous pressure contours |
V-22倾转旋翼机机翼采用的翼型为A821201,相对厚度为23%[3]。本文采用CFD方法研究被动控制技术在A821201翼型向下载荷被动减缓中的应用,具体措施包括后缘襟翼、克鲁格襟翼、前缘下垂以及扰流板。计算马赫数Ma=0.2,来流迎角为-90°,雷诺数Re=4.66×106。
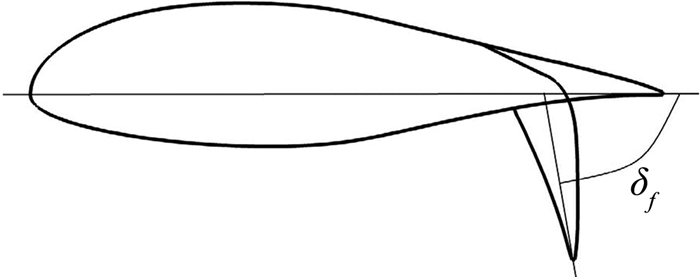
3.1 后缘襟翼A821201翼型后缘襟翼长度为30%c(c为翼型弦长),偏转角δf的定义如图 4所示。
|
图 4 后缘襟翼偏转角δf定义 Figure 4 Trailing edge flap deflection angle definition |
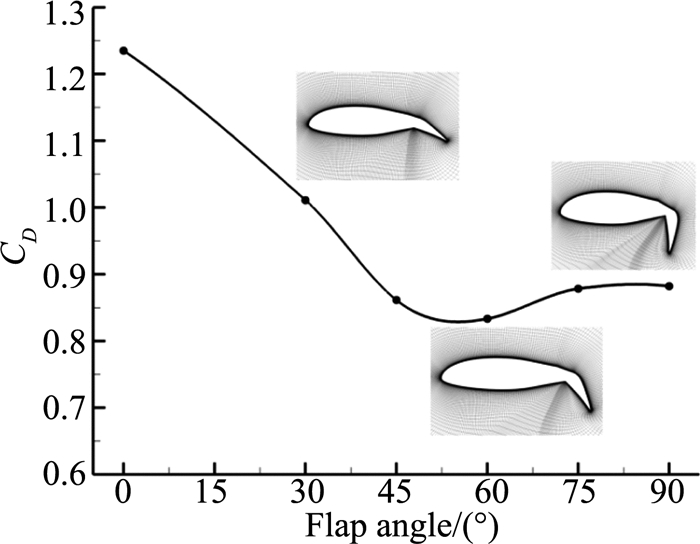
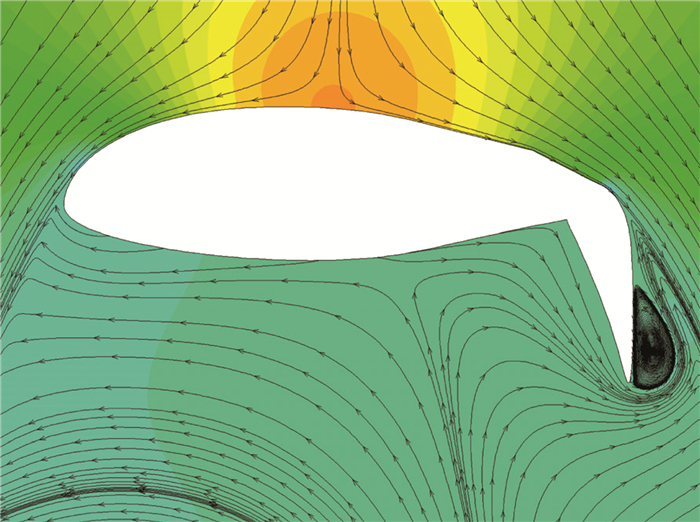
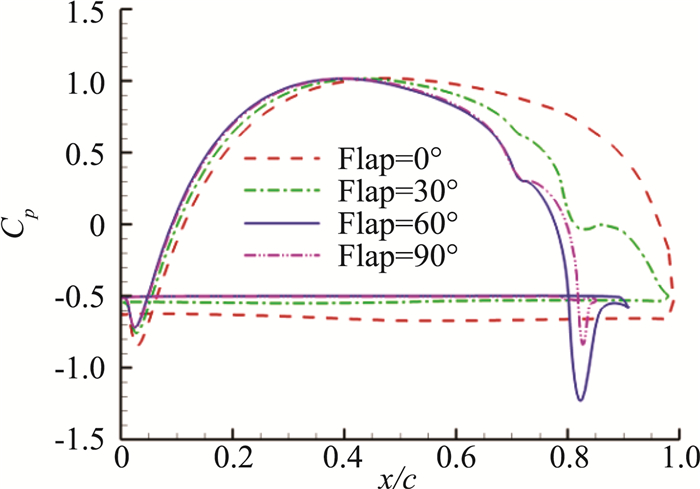
通过偏转后缘襟翼可以减小翼型在来流方向投影面积,并且增大后缘弯度,使气流在通过襟翼时发生加速。图 5给出了平均阻力系数随后缘襟翼偏转角δf的变化。阻力系数最小值在60°左右,与文献[17]得出的结论一致。δf=60°时阻力系数相对于原始翼型减小了32.5%。当δf>60°后,由于襟翼上表面已处于完全分离状态,如图 6所示,阻力系数会进一步增大, 并趋于收敛。图 7给出了不同后缘襟翼偏转角下平均压力系数分布。各构型下,翼型前缘都会产生较小的向上作用力。由于翼型下表面处于分离区,压力系数值相同。随着偏转角增加,下表面压力系数增大。后缘襟翼偏转改变了翼型后缘附近流场特性,当δf=60°时襟翼产生的向上作用力最大。
|
图 5 阻力系数随后缘襟翼偏转角δf变化 Figure 5 Effect of trailing edge flap on vertical drag |
|
图 6 瞬时压力云图和流线,δf=75° Figure 6 Instantaneous pressure contours and streamlines, δf=75° |
|
图 7 平均压力系数随后缘襟翼偏角δf变化 Figure 7 Effect of trailing edge flap on Cp distribution |
现有向下载荷减缓研究通常集中在后缘,而对前缘减阻措施研究开展较少。鉴于前缘减阻措施对后缘流场特性影响较小,下文研究中令后缘襟翼偏角60°保持不变。采用的克鲁格襟翼长度为25%c,其偏转角δk定义如图 8所示。

|
图 8 克鲁格襟翼偏转角δk定义 Figure 8 Kruger deflection angle definition |
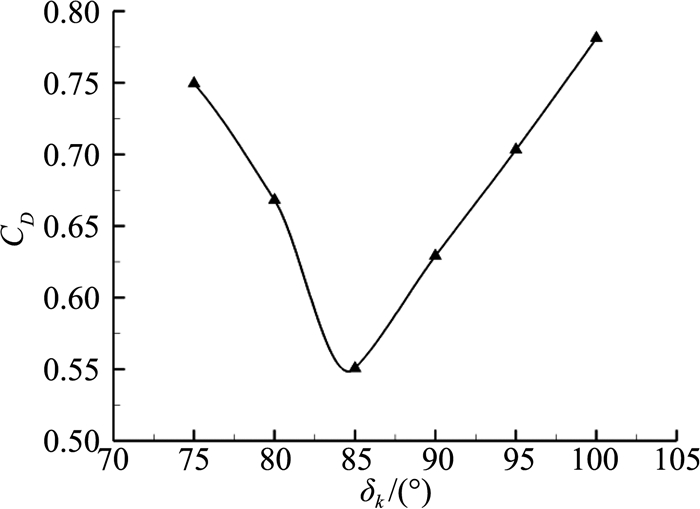
图 9给出了平均阻力系数随δk的变化曲线。随着δk增大,阻力系数先减小后增大。在δk=85°时达到最小值,其相对于δf=60°无克鲁格襟翼时阻力系数减小了33.9%。在δf=60°、δk=85°组合构型下,阻力系数相对于原始A821201翼型减小了55.4%。当δk>85°后,阻力系数呈直线上升趋势,这主要是由于组合构型在来流方向投影面积不断增大。
|
图 9 阻力系数随克鲁格襟翼偏转角δk变化 Figure 9 Effect of Kruger flap on vertical drag |
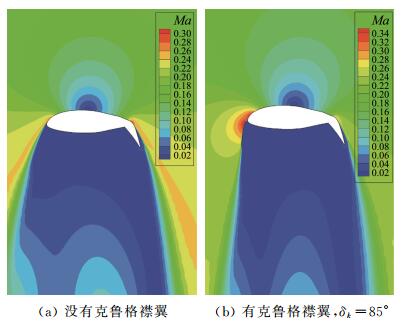
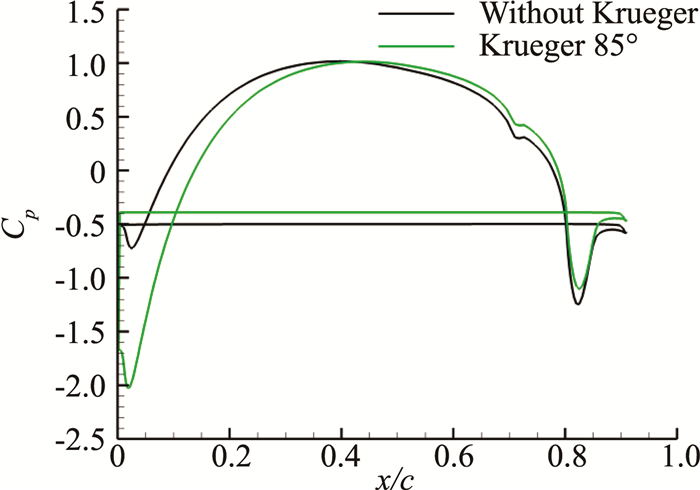
克鲁格襟翼增大了翼型前缘弯度,使气流通过前缘时发生加速。图 10给出了有/无克鲁格襟翼作用时流场马赫数云图。图 11给出了平均压力系数分布对比。克鲁格襟翼增大了翼型下表面压力系数,并且能使前缘产生更大的向上作用力,前缘压力系数最低点的位置保持不变。
|
图 10 流场瞬时马赫数云图 Figure 10 Computed instantaneous Mach contours |
|
图 11 有/无克鲁格襟翼平均压力系数分布 Figure 11 Cp distribution, with and without Kruger flap |
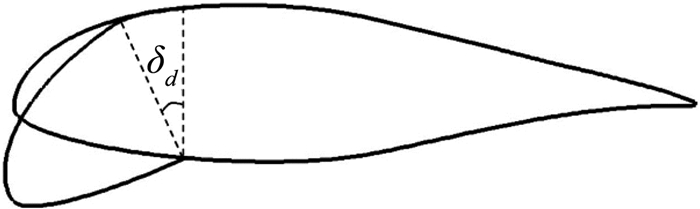
为了和克鲁格襟翼减阻能力进行比较,前缘下垂长度同样选取为25%c,偏转角δd的定义如图 12所示。
|
图 12 前缘下垂偏转角δd定义 Figure 12 Droop-nose deflection angle definition |
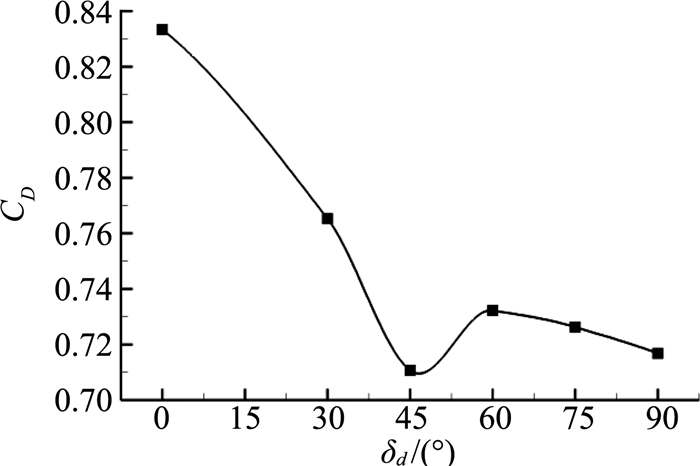
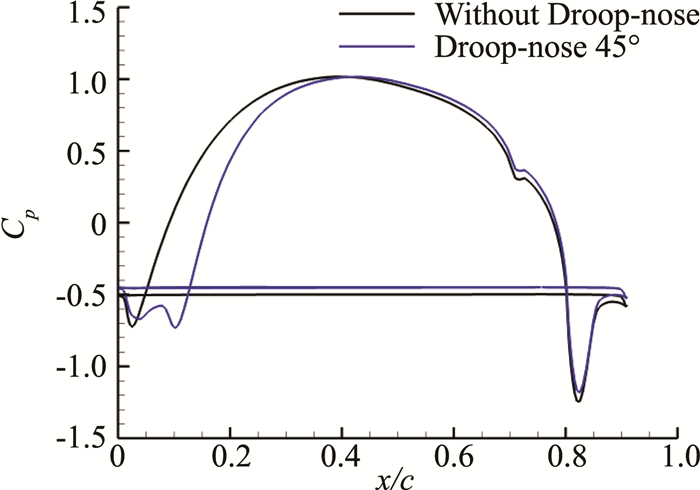
前缘下垂同样增大了翼型弯度,使气流通过前缘时发生加速。图 13给出了平均阻力系数随δd变化曲线。随着偏转角增大,阻力系数迅速下降,并在δd=45°达到最小值,相对于只偏转60°后缘襟翼的构型减小了14.7%;当δd>45°后,阻力系数则先上升后下降,但数值上差异较小,这主要是由于弯度太大使翼型前缘上表面出现了流动分离。图 14给出了有/无前缘下垂时翼型平均压力系数分布。相比来说,前缘下垂减阻效果不如克鲁格襟翼。
|
图 13 阻力系数随前缘下垂偏转角δd变化 Figure 13 Effect of Droop-nose deflection angle on vertical drag |
|
图 14 有无前缘下垂平均压力系数分布 Figure 14 Cp distribution, with and without Droop-nose |
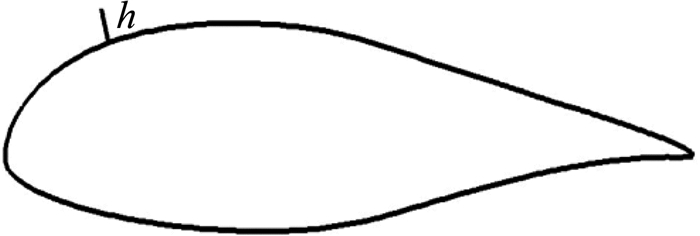
通过在翼型上表面安装扰流板,进一步开展减阻措施研究。安装位置位于15%弦长处,扰流板高度h的定义如图 15所示。本文研究不同高度扰流板对翼型阻力系数的影响。
|
图 15 扰流板高度h定义 Figure 15 Definition of spoiler height |
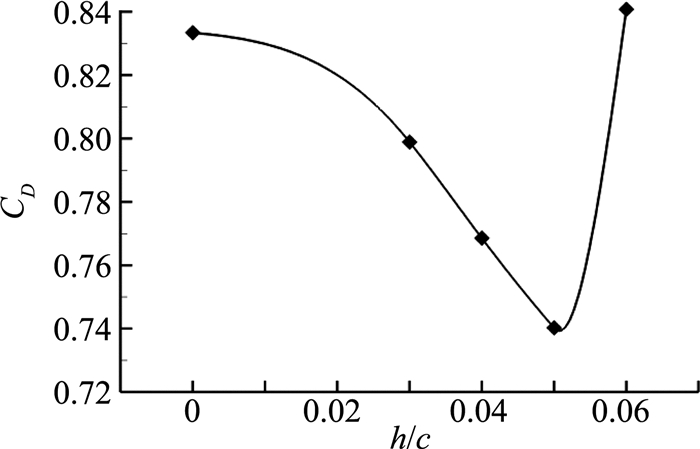
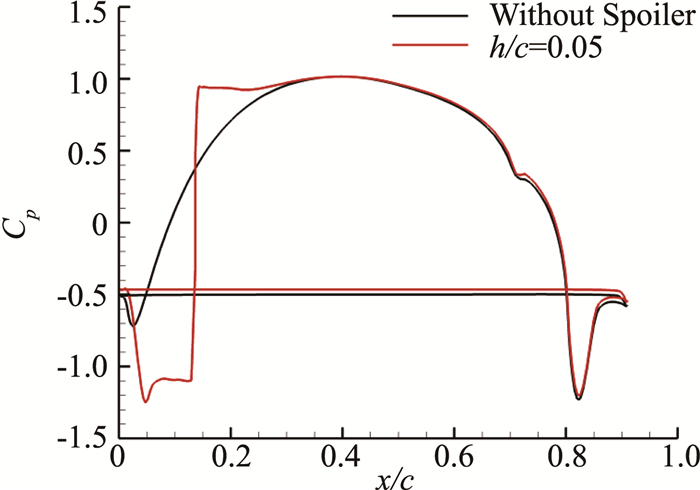
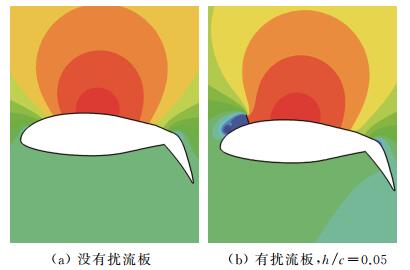
图 16给出了计算得到的平均阻力系数随扰流板高度的变化曲线。当h/c=0.05时,翼型阻力最小,相对于只偏转60°后缘襟翼,阻力系数减小了11.1%;当h/c>0.05,阻力系数突升,这是由于扰流板高度太高,超过临界高度使翼型前缘上表面完全分离。图 17给出了有无扰流板作用时翼型平均压力系数分布,气流在扰流板右侧发生滞止,压力系数达到驻点值1;气流在扰流板左侧出现分离区,并迅速加速,使得翼型前缘上表面压力系数降低,因而前缘会产生较大的向上作用力。图 18给出了有无扰流板作用时流场压力云图,从图 18(b)可以看出,在扰流板左侧存在一个低压区。
|
图 16 阻力系数随扰流板高度h/c变化 Figure 16 Effect of spoiler height on vertical drag |
|
图 17 有无扰流板平均压力系数分布 Figure 17 Cp distribution, with and without spoiler |
|
图 18 流场瞬时压力云图 Figure 18 Computed instantaneous pressure contours |
采用双时间步长、有限体积法求解非定常N-S方程,基于SA一方程湍流模型的DES方法,发展了一种翼型在-90°迎角下非定常大分离流数值模拟方法,计算结果和实验值吻合很好。
对悬停状态下倾转旋翼机向下载荷被动减缓措施进行了研究。通过研究得到以下结论:
(1) 通过偏转后缘襟翼可以减小向下载荷,在δf=60°时,阻力系数达到最小值,相对于原始翼型阻力系数减小了32.5%;
(2) 在δf=60°基础上,分别研究了克鲁格襟翼、前缘下垂和扰流板的减阻能力。当δk=85°时,阻力系数达到最小值;当δd=45°时,阻力系数达到最小值;当h/c=0.05时,阻力系数最小。减阻能力比较:克鲁格襟翼>前缘下垂>扰流板。
(3) 最优组合构型为δf=60°、δk=85°,其向下载荷相对于原始A821201翼型减小了55.4%。
| [1] |
Potsdam M A, Strawn R C. CFD simulations of tiltrotor configurations in hover[J]. Journal of American Helicopter Society, 2005, 50(1): 82-94. DOI:10.4050/1.3092845 (  0) 0) |
| [2] |
Maisel M, Laub G, McCroskey W J. Aerodynamic characteristics of two-dimensional wing configurations at angles of attack near 90°[R]. NASA TM-88373, 1986.
(  0) 0) |
| [3] |
Felker F, Shinoda P R, Hefferman R M, et al. Wing force and surface pressure data from a hover test of a 0. 658-scale V-22 rotor and wing[R]. NASA TM-102244, 1990.
(  0) 0) |
| [4] |
Wood T L, Pereya M A. Reduction of tiltrotor download[C]//AHS 49th Annual Forum, 1993.
(  0) 0) |
| [5] |
Stremel P M. Effect of fences on airfoil aerodynamics at 90 degree incidence[J]. AIAA Journal, 1996, 34(10): 1984-1989. DOI:10.2514/3.13343 (  0) 0) |
| [6] |
Garcia A J, Barakos G N. CFD simulations on the ERICA tiltrotor using HMB2[R]. AIAA 2016-0329.
(  0) 0) |
| [7] |
Angle I I. Experimental and computational investigation into the use of the Coanda effect on the Bell A821201 airfoil[J]. Applications of Circulation Control Technology, 2006, 214: 277-291. (  0) 0) |
| [8] |
McVeigh M A, Nagib H, Wood T, et al. Full-scale flight tests of active flow control to reduce tiltrotor aircraft download[J]. Journal of Aircraft, 2011, 48(3): 786-796. DOI:10.2514/1.46956 (  0) 0) |
| [9] |
Jacot D, Mabe J. Boeing active flow control system for the V-22[R]. AIAA 2000-2473.
(  0) 0) |
| [10] |
Stremel P M. Calculation of unsteady airfoil loads with and without flap deflection at-90 degree incidence[R]. AIAA-91-3336, 1991.
(  0) 0) |
| [11] |
Stremel P M. Effect of Reynolds number and turbulence on airfoil aerodynamics at-90 degree incidence[J]. AIAA Journal, 1994, 32(3): 449-454. (  0) 0) |
| [12] |
El-Alti M, Kjellgren P, Davidson L. On the download alleviation for the XV-15 wing by active flow control using large-eddy simulation[C]//ERCOFTAC Workshop: Direct and Large-Eddy Simulation 7, 2008.
(  0) 0) |
| [13] |
Guo T Q. Transonic unsteady aerodynamics and flutter computations for complex assemblies[D]. Nanjing University of Aeronautics and Astronautics, 2006. (in Chinese 郭同庆. 复杂组合体跨声速非定常气动力和颤振计算[D]. 南京航空航天大学, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10287-2007194020.htm (  0) 0) |
| [14] |
Guo T Q, Lu Z L, Tang D, et al. A CFD/CSD model for aeroelastic calculations of large-scale wing turbines[J]. Science China Technological Sciences, 2013, 56(1): 1-7. (  0) 0) |
| [15] |
Scott M. DES and RANSsimulations of delta wing vortical flows[R]. AIAA 2002-0587, 2002.
(  0) 0) |
| [16] |
Wang H B, Sun M B, Wu H Y, et al. Improved DES-like method for simulation of turbulent flows[J]. Journal of Aerospace Power, 2011, 26(10): 2167-2173. (in Chinese) 汪洪波, 孙明波, 吴海燕, 等. 一种改进的类DES湍流模拟方法[J]. 航空动力学报, 2011, 26(10): 2167-2173. (  0) 0) |
| [17] |
Grife R, Darabi A, Wygnanski I. Download reduction on a three dimensional V-22 model using active flow control[C]//1st AIAA Flow Control Conference, 2002.
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36


