失速是航空航天领域中一种普遍存在的流动现象,失速研究具有重要的学术和应用价值。传统认为静态失速是当迎角增大到某一定值时,在翼型上表面会出现大规模分离流动,从而导致升力突然下降和阻力突然增加及非定常压力脉动放大等负面效应,这对飞行器的整体气动特性和操纵性能产生严重影响[1]。随着航空航天新技术的不断发展,对现代飞行器的性能要求越来越高,如大迎角机动性,苏27过失速“眼镜蛇”机动时迎角超过了120°,用于改善飞机起降性能的增升襟翼也经常在大迎角条件下工作,特别是利用迎角40°左右存在的二次升力峰值和阻力是着陆时增升增阻的一种理想选择[2]。因此,只有深入理解大迎角复杂分离流动演化规律,才能更好地控制失速现象,使飞行器可用迎角逾越静态失速这一传统禁区。
深入理解大迎角复杂分离流动演化规律,首先需要获取较准确的流场。近年来,LES方法和DES方法被广泛地应用于分离流动的模拟中[3-7]。在获取较准确的流场信息后,通常采用非线性理论、模态分解等方法对流动结构进行分析。从非线性动力学角度讲,静态失速中存在滞后、突跳及分岔现象。Mittal等[8]通过数值模拟对翼型静态失速迎角附近的迟滞现象进行了研究,并发现迟滞现象的发生是由于流动具有对历史行为的记忆能力。张家忠等[9]对翼型失速的非线性动力学特性进行研究,发现静态失速是一种“鞍—结”分岔现象。另一方面,在获得流动结构的众多方法中,本征正交分解方法(Proper Orthogonal Decomposition,POD)被广泛使用。自Lumley[10]首先将POD方法引入湍流研究以来,Sirovich[11]引入了snapshot方法来研究波动流的动力学问题。康伟等[12]基于POD方法,采用非线性动力学理论对翼型绕流的多模态耦合机制进行分析,研究了模态耦合作用与流动稳定性的关系。
动力学模态分解(Dynamic Mode Decomposition,DMD)是近年来在整体稳定性Koopman分析的基础上发展起来的一种低维系统分解技术,可以同时得到流动在时间和空间上的主要特征,且可按照频率对模态进行排序,这与POD按照能量对模态进行排序的思路有所不同[13]。DMD方法由Schmid于2008年首次提出,并采用DMD方法分别对数值模拟和实验得到流场数据进行分析。Rowleyz等[14]采用DMD方法对横向射流中的非线性流动进行分析,通过与DNS、线化N-S方程、以及POD方法得到的频率进行对比,发现DMD得到频率与DNS的结果相同,而其他方法得到的频率均与DNS结果存在较大差距。Roy等[15]将DMD方法和POD方法应用于反应流的稳定性分析中,并将两种方法的结果进行了比较。Jovanović等[16]研究了基于DMD的稀疏动态模态分解。Seena[17]等将DMD方法应用于凹腔自激振荡流动中。Muld[18]等应用POD和DMD方法提取了高速火车流场结构。国内王晋军等[19]率先开展了对DMD方法的研究,其将DMD应用于NACA0015翼型加装Gurney襟翼后的尾流速度场的分析中。Mariappan[20]和Mohan[21]等应用DMD方法分析翼型的动态失速。然而,目前还没有见到基于DMD方法对大迎角静态失速分离流场进行分析的研究文献。
翼型大迎角分离涡的演化包含了涡量生成、积聚和耗散,其中的流动机理非常复杂。本文采用DMD方法对分离涡的演化过程进行稳定性分析。首先基于SST-DES方法对NACA0012进行数值模拟得到非定常流场数据。实际翼型大迎角分离流动会存在明显的三维效应,且通常基于DES方法进行计算时,对物面展向长度和网格数量有一定的要求,文献[22]中对此进行了较详细的分析。但受计算资源的限制,本文数值模拟中网格展向仅拉伸一层。事实上,对于一些经典的三维分离流动,例如圆柱、凹腔等流动,大部分学者及文献也均是从二维的角度进行计算和分析。
1 计算方法及验证算例三维非定常N-S方程在直角坐标系中的积分守恒形式为:
| $ \frac{\partial }{{\partial t}}\iiint\limits_\mathit{\Omega} {\mathit{\boldsymbol{Q}}{\text{d}}V} + \iint\limits_{\partial \mathit{\Omega} } {\mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{Q}} \right) \cdot \mathit{\boldsymbol{n}}{\text{d}}S} = \iint\limits_{\partial \mathit{\Omega} } {{\mathit{\boldsymbol{F}}^V}\left( \mathit{\boldsymbol{Q}} \right) \cdot \mathit{\boldsymbol{n}}{\text{d}}S} $ | (1) |
其中Ω为控制体,∂Ω为控制体单元边界,Q为守恒变量,Q=[ρ, ρu·ρv, ρw, ρE]T,F(Q)为无黏通量,FV(Q)为黏性通量。其中ρ、P、T、E分别为密度、压强、温度和单位质量流体的总能,u、v、w分别为x、y、z方向的速度分量。
采用基于剪切应力输运SST k-w两方程湍流模型的SST-DDES混合方法对流场进行模拟,采用有限体积方法进行空间离散,空间格式采用Roe,时间推进采用LU-SGS。
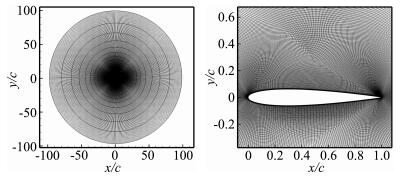
目前公开的翼型大迎角实验结果较少,本文采用文献[23]中NACA0012的实验数据。实验条件为Ma=0.15、Re=6×106。通常采用DES方法进行计算时,对物面展向长度和网格数量有一定的要求,文献[22]中对此进行了较详细的分析。但受计算资源的限制,数值模拟中网格展向仅拉伸1层。图 1为生成的结构网格,翼型弦长为1 m。为了避免使用拉伸比很大的“C”型网格,采用420×180的“O”型结构网格。其中翼型上表面300个点,下表面120个点,物面网格第一层高度为5×10-6 m,满足y+ < 1,附面层径向采用40层网格,增长率为1.25。为准确模拟分离,对上翼面附近区域的网格进行加密,网格层数为100层,增长率为1,之后采用40层过渡到远场,远场距离物面约为100倍弦长。非定常计算中的时间步长为5×10-4 s。
|
图 1 计算网格 Figure 1 Computation grid |
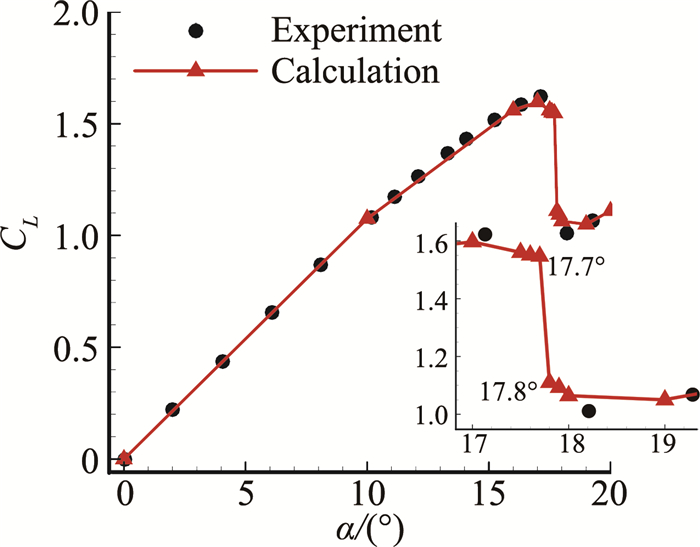
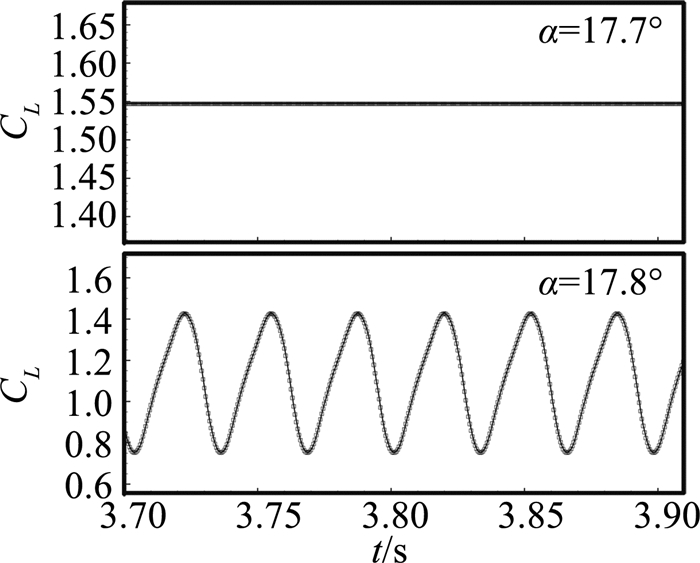
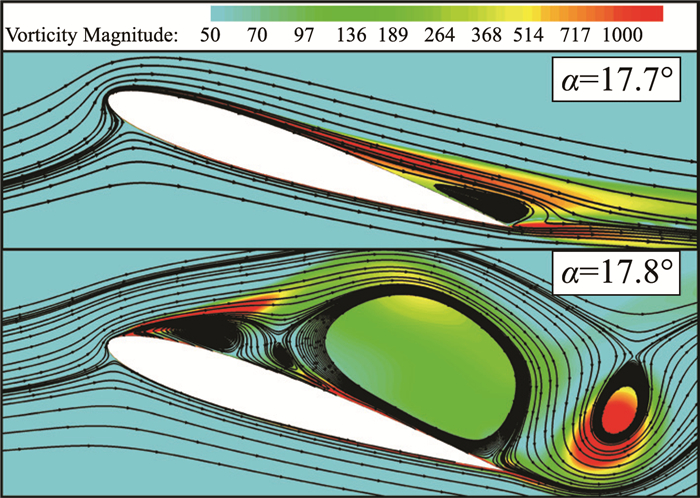
图 2为升力系数(时间平均下的升力系数)随迎角的变化曲线。实验数据中,迎角为17.13°时,升力系数达到最大,当迎角为18.21°时,升力系数突然大幅下降。本文计算结果中,当迎角为17°时,升力系数达到最大。为进一步细致了解17°至18°之间的流动,在迎角17.5°至18°之间,每隔0.1°进行一次非定常计算。当迎角由17.7°进一步增加到17.8°时,升力系数突然大幅下降,且开始呈现周期性变化。图 3为17.7°和17.8°的升力系数随时间的变化,图 4为流场流线和涡量云图。上述结果表明本文的计算结果与实验数据吻合较好,说明本文计算结果是可信的。
|
图 2 平均升力系数随迎角的变化 Figure 2 Lift coefficient varying with angle of attack |
|
图 3 升力系数随时间的变化 Figure 3 Lift coefficient varying with time |
|
图 4 流场流线和涡量云图 Figure 4 Streamline and contours of vorticity |
DMD方法只基于流动快照而不受模型限制,通过提取流动中的模态,准确地描述流动结构。对于线化流动而言,被提取的模态可以用来表征全局稳定模态。对于非线性流动而言,DMD的模态描述了在数据序列中起支配作用的流动结构。以下为其数学推导过程。
动态模态分解的数据来源是数值仿真或者物理实验,可以快照序列的形式呈现,序列由矩阵V1N表示,
| $ \mathit{\boldsymbol{V}}_1^N = \left\{ {{\mathit{\boldsymbol{v}}_1}, {\mathit{\boldsymbol{v}}_2}, {\mathit{\boldsymbol{v}}_3}, \cdots, {\mathit{\boldsymbol{v}}_N}} \right\} $ | (2) |
其中,vi代表第i个流场,vi∈CM。在上述定义中,下标1表示序列中的第一个元素,下标N表示进入序列中的最后一个元素,即矩阵V1N的第一列和最后一列。我们可以假设这个序列的时间间隔为常量Δt。
第一步,假设线性映射A是快照vi到vi+1的映射,即:
| $ {\mathit{\boldsymbol{v}}_{i + 1}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_i} $ | (3) |
且在全部区域和整个时间段内的采样都满足上述映射关系。对于缓慢变化的系统,乘法准则是上述假设的基础。
| $ \begin{gathered} \mathit{\boldsymbol{V}}_2^N = \left\{ {{\mathit{\boldsymbol{v}}_2}, {\mathit{\boldsymbol{v}}_3}, {\mathit{\boldsymbol{v}}_4}, \cdots {\mathit{\boldsymbol{v}}_N}} \right\} \hfill \\ \;\;\;\;\;\; = \left\{ {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_1}, \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_2}, \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_3}, \cdots, \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_{N-1}}} \right\} \hfill \\ \;\;\;\;\;\; = \mathit{\boldsymbol{AV}}_1^{N-1} \hfill \\ \end{gathered} $ | (4) |
系统矩阵A能够将时-空物理场沿时间维度平移Δt,因此A的特征值刻画了V1N的时间演化特性。然而,实际应用中A是一个含有数据量极大的矩阵,因此希望将A转化为一个小型矩阵。用小型矩阵的特征值来估算A的特征值,这样DMD方法才能应用于实际动力学问题。
对于秩为r的数据列V1N-1, A与其简化后的矩阵可以通过V1N-1的POD模态联系起来,
| $ \mathit{\boldsymbol{A}} \approx \mathit{\boldsymbol{UF}}{\mathit{\boldsymbol{U}}^*} $ | (5) |
其中F∈Cr×r, U*为POD模态U的复共轭转置矩阵,U可以由V1N-1的奇异值分解得到,即:
| $ \mathit{\boldsymbol{V}}_1^{N-1} = \mathit{\boldsymbol{U \boldsymbol{\varSigma} }}{\mathit{\boldsymbol{V}}^*} $ | (6) |
其中,Σ是一个r×r的对角矩阵,有非0的对角元素{σ1, …, σr},并且,U和V为酉矩阵。
U∈CM×r,并且U*U=I
V∈Cr×N,并且V*V=I
将式(5)和式(6)代入式(4)中,可得:
| $ \mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{U}}^*}\mathit{\boldsymbol{V}}_2^N\mathit{\boldsymbol{V}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{-1}} $ | (7) |
F即为A的最优低维估计矩阵,由此通过求解F的特征值和特征向量即可得到DMD分析结果。
假设F是一个r维子空间内的精确映射矩阵而不是对A的估计,那么
| $ {\mathit{\boldsymbol{x}}_{k + 1}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_k} $ | (8) |
则A的POD模态U可以看作从xk到vk的近似映射,则
| $ {\mathit{\boldsymbol{v}}_k} \approx \mathit{\boldsymbol{Ux}} $ | (9) |
如果F的特征向量个数与秩相等且都线性独立,那么F可以写做如下形式
| $ \mathit{\boldsymbol{F}} = \left[{{\mathit{\boldsymbol{y}}_1} \cdots {\mathit{\boldsymbol{y}}_r}} \right]\left[{\begin{array}{*{20}{l}} {{\mu _1}}&{}&0 \\ {}& \ddots &{} \\ 0&{}&{{\mu _r}} \end{array}} \right]\left[\begin{gathered} z_1^* \hfill \\ \vdots \hfill \\ z_r^* \hfill \\ \end{gathered} \right] $ | (10) |
其中yi是其特征向量,μi为其特征值,每一个yi的模为一个单位长度,yi*yi=1, zi*是F*的特征向量,F*相应的特征值为μi, zi*和yi满足如下的条件:
| $ z_i^*{\mathit{\boldsymbol{y}}_j} = \left\{ \begin{gathered} 1, \;\;\;i = j \hfill \\ 0, \;\;i \ne j \hfill \\ \end{gathered} \right. $ | (11) |
| $ 则\;\;\;\;{\mathit{\boldsymbol{x}}_k} = \mathit{\boldsymbol{YD}}_\mu ^k{\mathit{\boldsymbol{Z}}^*} = \sum\limits_{i = 1}^r {{\mathit{\boldsymbol{y}}_i}\mu _i^kz_i^*{\mathit{\boldsymbol{x}}_0}} = \sum\limits_{i = 1}^r {{\mathit{\boldsymbol{y}}_i}\mu _i^k{\alpha _i}} $ | (12) |
其中,αi=zi*x0表示初始条件对第i个模态的影响程度,所以可以利用DMD模态的线性组合来估计数据快照,模态为Φi=Uyi,则:
| $ {\mathit{\boldsymbol{v}}_k} \approx \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{x}}_k} = \sum\limits_{i = 1}^r {{\boldsymbol{\mathit{\phi}} _i}\mu _i^k{\alpha _i}} $ | (13) |
由此可得:
| $ \begin{gathered} \left[{{v_1}, {v_2}, \cdots, {v_{N-1}}} \right] \approx \left[{{\boldsymbol{\mathit{\phi}} _1}, {\boldsymbol{\mathit{\phi}} _2}, \cdots, {\boldsymbol{\mathit{\phi}} _r}} \right] \cdot \hfill \\ \left[{\begin{array}{*{20}{l}} {{\alpha _1}}&{}&{}&0 \\ {}&{{\alpha _2}}&{}&{} \\ {}&{}& \ddots &{} \\ 0&{}&{}&{{\alpha _r}} \end{array}} \right]\left[{\begin{array}{*{20}{l}} 1&{{\mu _1}}& \cdots &{\mu _1^{N-1}} \\ 1&{{\mu _2}}& \cdots &{\mu _2^{N-1}} \\ \vdots&\vdots&\ddots&\vdots \\ 1&{{\mu _r}}& \cdots &{\mu _r^{N-1}} \end{array}} \right] \hfill \\ \end{gathered} $ | (14) |
动态模态分解获得的最重要的结果是模态ϕi和模态对应的特征值μi, lg(μi/Δt)的实部为对应模态的放大率,其虚部表示对应模态的频率。在进行稳定性判断时,放大率为正,则对应的模态发散;放大率为负,则对应的模态收敛;若放大率为0,则对应的模态为稳定极限环模态。同样也可以将μi置于复平面的单位圆上进行判断,若在单位圆内,则收敛;单位圆外,则发散;单位圆上,则为稳定周期性模态。
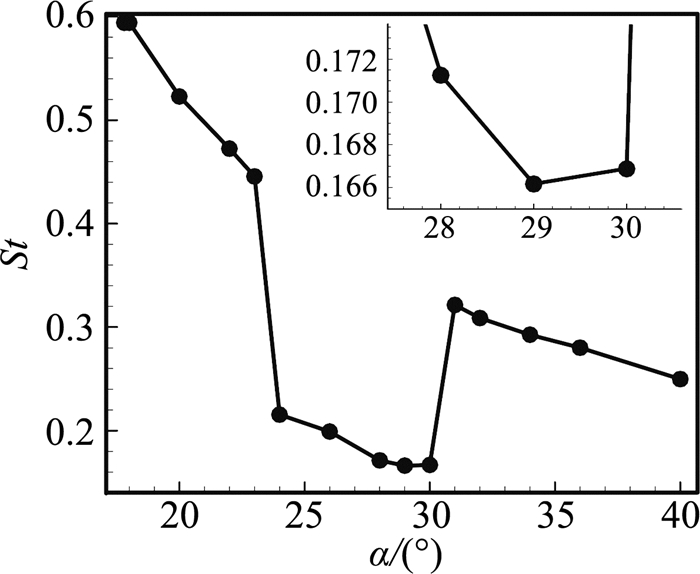
3 计算结果分析本文在验证算例中实验条件的马赫数和雷诺数下对NACA0012大迎角失速翼型流场的涡稳定性演化规律进行研究。首先,对迎角在17.8°至40°范围内的状态进行非定常计算,其中22°至24°的计算中,迎角间隔为1°。图 5为Strouhal数(St)随迎角的变化曲线,
|
图 5 升力系数的St随迎角的变化 Figure 5 St of lift coefficient varying with α |
| $ St = fC/{U_\infty } $ | (15) |
式中f为频率,C为弦长,U∞为来流速度。
可以看出,St随迎角的增加并不是呈现单调减小的规律。当迎角在17.8°至23°范围内,随迎角的增加,St基本呈线性减小;当迎角由23°增加到24°时,St大幅减小;当迎角在24°至29°范围内,St随迎角增加缓慢减小,并且迎角为29°时,St达到最小,为0.166168;迎角由29°增加到30°时,St有微幅的增加;当迎角进一步由30°增加到31°时,St大幅增加;迎角从31°增加到40°时,St再次基本呈线性减小。因此,采用DMD方法分别对以下3种迎角状态下的分离流场进行稳定性分析:(1)迎角为17.8°时,流动刚刚进入失速状态,称为失速初始状态;(2)迎角增加到24°,流动进一步分离,St突然大幅减小,称为浅失速状态;(3)迎角进一步增加到29°时,St达到最小,称为深失速状态。
由于在上述三种迎角下,流场最后均表现为稳定极限环状态,升力系数均呈现周期性变化。因此,采用DMD方法进行稳定性分析时,DMD采样中仅提取一个周期的瞬态流场数据,三种迎角下的样本数量分别为65、182、234。
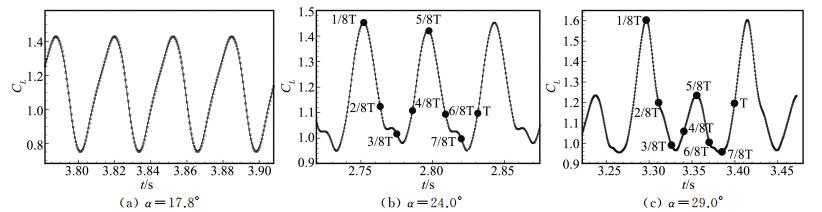
3.1 DMD稳定性分析图 6为升力系数随时间的变化。三种状态下,升力系数在一个周期内的变化相差较大。失速初始状态下,升力系数一个周期内呈现类似正弦曲线的变化,周期性变化规律简单,一个周期中仅有一个极大值和一个极小值,最大值与最小值相对均值的振荡幅值分别为28.6%和32.2%。浅失速状态中,升力系数一个周期内的变化较复杂,一个周期中存在四个极大值和四个极小值,在5/8T时刻附近达到的极大值略小于1/8T时刻的最大值,最大值与最小值相对均值的振荡幅值分别为24.4%和18.6%。深失速状态中,升力系数在一个周期中存在两个极大值和两个极小值,且在5/8T时刻附近达到的极大值小于1/8T时刻的最大值。最大值与最小值相对均值的振荡幅值分别为38.3%和17.6%。
|
图 6 升力系数随时间的变化 Figure 6 Lift coefficient varying with time for the three states |
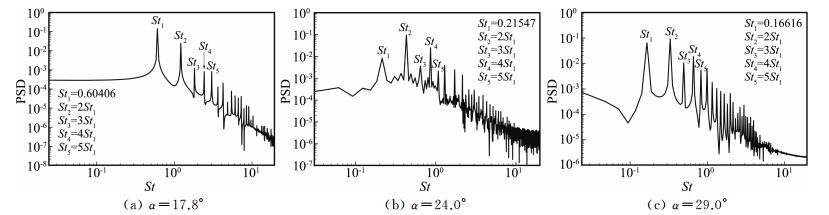
图 7为升力系数FFT分析结果。可见FFT可提取其主频及高阶倍频,图中仅标出前五阶频率,按照St对应的峰值对St进行排序,三种状态的顺序各不相同。失速初始状态,St的顺序为:St1,St2,St3,St4,St5;浅失速状态,St的顺序为:St2,St4,St1,St3,St5;深失速状态,St的顺序为:St2,St1,St4,St3,St5。
|
图 7 升力系数FFT分析结果 Figure 7 FFT results of lift coefficient |
表 1为DMD方法提取频率与FFT分析结果的对比,两者之间频率最大差异为0.15037%,说明DMD方法可以非常准确地提取流动中的频率。
| 表 1 FFT与DMD分析得到的St的对比 Table 1 Comparison of St between FFT and DMD |
|
|
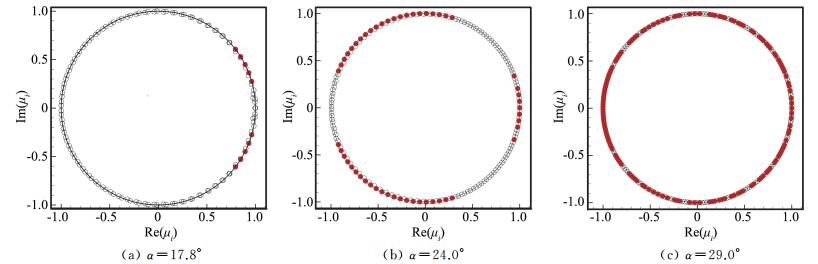
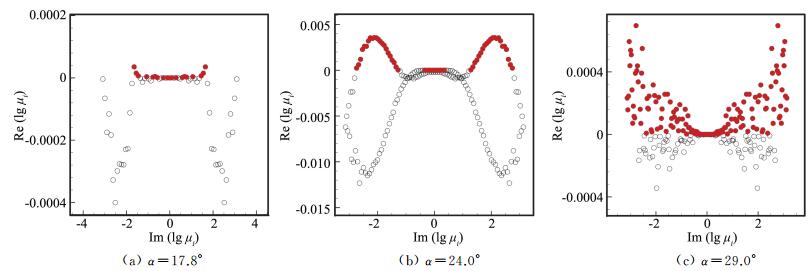
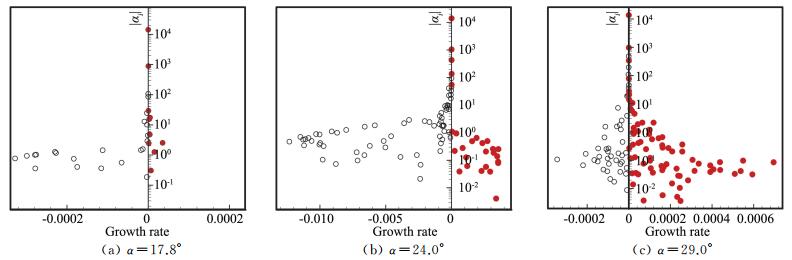
基于DMD方法分别对三种状态下的流场进行稳定性分析。图 8为翼型三种迎角状态下DMD特征值的实部和虚部在单位圆上的分布,图中黑色点表示在单位圆上或单位圆内,红色点表示在单位圆外。图 9为特征值取对数之后的实部和虚部的分布,图中黑色点表示实部等于0或小于0,红色的点表示实部大于0。图 10为模态幅值与放大率之间的关系,图中红色的表示放大率正,黑色表示放大率为负或0。由前面DMD方法介绍中,这三个图中黑色点对应的模态为收敛模态或稳定极限环模态,而红色点对应的模态为发散模态。三种迎角状态下,不稳定模态占总模态数量的比例分别为29.23%、29.28%和62.52%。
|
图 8 特征值的实部与虚部在单位圆上的分布 Figure 8 Eigenvalues on unit circle for the three states |
|
图 9 特征值取对数后的实部与虚部的分布 Figure 9 Logarithmic eigenvalues on unit circle for the three states |
|
图 10 放大率与幅值之间的关系 Figure 10 Amplitude varying with growth rate for the three states |
从图 8看,所有模态的特征值基本都落在单位圆上,且从图 9和图 10中可以看出,所有发散模态对应的放大率都非常小,最大放大率分别为3.53×10-5,3.56×10-3和6.95×10-4,这些不稳定模态处于弱发散状态,其他模态处于收敛或极限环状态。
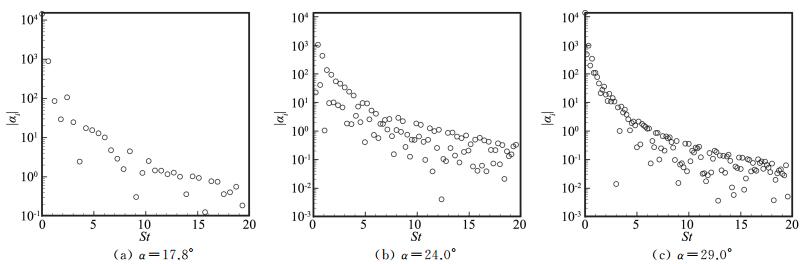
图 11为模态系数幅值随St的变化,可以看出,模态系数幅值随St的增加,基本呈现逐渐减小的趋势,说明St较低的模态在流场中占据主要影响。同时,DMD提取的St范围为0~20,覆盖了脱落涡主频St的0~33倍,说明DMD方法提取到流动频率范围很宽。
|
图 11 幅值随St的变化 Figure 11 Amplitude varying with St for the three states |
图 12为失速初始状态下一个周期中8个瞬态流场的涡量图以及流线图,其中1/8T和5/8T时刻分别对应升力系数最大和最小状态。在1/8T时刻,翼型上表面存在一个顺时针的大分离涡(主涡),同时后缘存在一个较小的逆时针尾涡,并且翼型中段物面附近处存在一个由于剪切层分离形成的分离泡。当进入2/8T时刻时,前缘处生成一个前缘涡,同时翼型中段处的一个分离泡演化为两个分离泡。当进入3/8T时刻时,2/8T时刻中靠近后缘处的的分离泡消失,同时靠近前缘处的分离泡和前缘涡进一步发展,尾涡逐渐变小。当进入4/8T时刻时,在后缘处形成一个新的小分离涡,同时翼型中段处的分离泡和前缘涡进一步发展,尾涡进一步变小。当进入5/8T时刻时,尾涡脱落消失,同时主涡,前缘涡、翼型中段处的分离泡和后缘处分离涡进一步发展。当进入6/8T时刻时,在后缘处分离涡发展成为新的尾涡,同时前缘涡、主涡和翼型中段处的分离泡均变小,且主涡呈现脱落的趋势。当进入7/8T时刻时,主涡脱落消失,尾涡变大,前缘涡进一步向后发展,翼型中段处的分离泡消失。当进入T时刻时,前缘涡进一步发展成为新的主涡,尾涡也进一步变大,流动开始向下一个周期发展。总体来看,分离涡在一个周期的演化过程中,前缘涡、主涡、翼型中段处的分离泡以及尾涡都经历了一次形成、发展、消失、再形成。
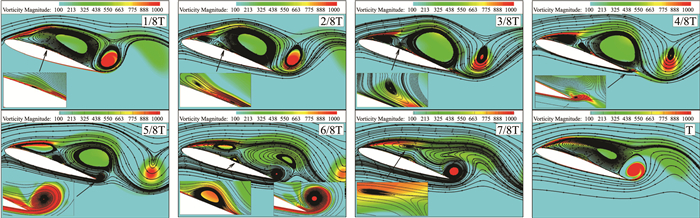
|
图 12 一个周期中涡结构的演化 Figure 12 Evolution of the vortex structure in a cycle |
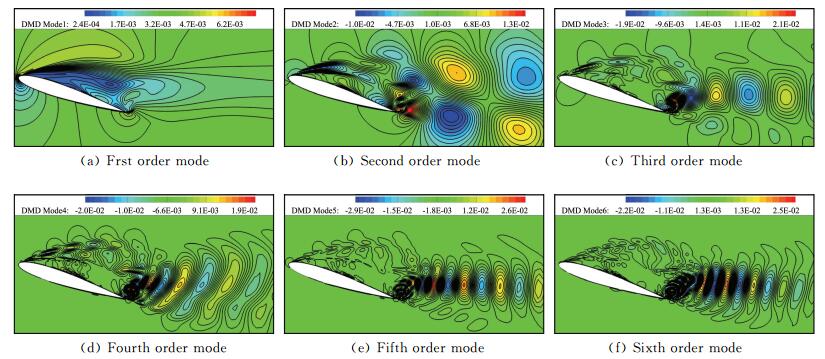
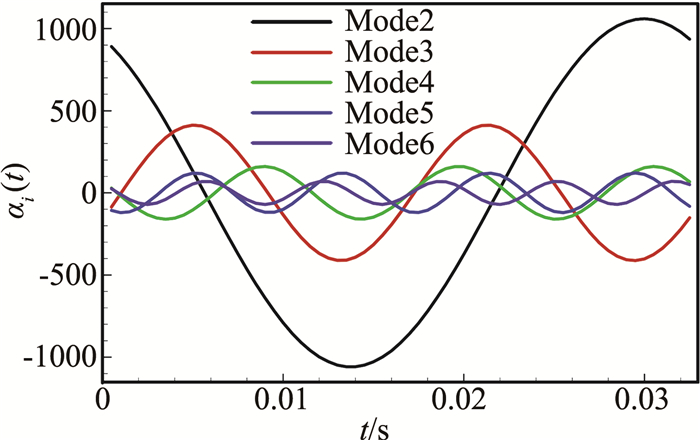
图 13为前六阶DMD模态的速度云图,其中Mode1对应的St为0,Mode2~Mode6分别对应St1~St5(浅失速状态和深失速状态与此相同)。可以看出,Mode1主要表现为整个翼型上表面的大分离涡结构,其模态系数幅值不随时间变化,说明此模态的分离涡结构为翼型分离涡演化过程中最主要的静止模态。Mode2主要表现为前缘涡、翼型中段处的分离泡, 以及后缘处的尾涡结构,且其对应的频率为升力系数的主频,结合一个周期中流场涡结构的演化过程可以发现,此模态对应的涡结构与流动中以此频率进行演化的涡结构比较一致。Mode3~Mode6主要表现为后缘附近小尺度的尾涡以及尾迹区的涡结构,其对应的频率为高阶倍频。图 14为模态系数随时间的变化,可以看出不同模态系数之间不仅频率不同,并且不同系数之间存在明显的相位差,说明分离涡流动中不同频率对应的涡结构运动不同步。按照模态系数最大幅值对Mode2~Mode6进行排序,发现排序后的模态对应的St为St1、St2、St3、St4、St5,这与图 7(a)中频率按峰值排序一致。
|
图 13 DMD模态速度云图 Figure 13 Contours of velocity for DMD modes |
|
图 14 DMD模态系数随时间的变化 Figure 14 DMD mode amplitude varying with time |
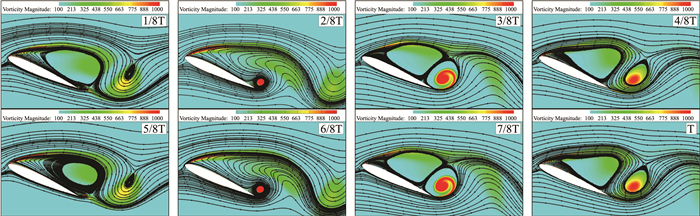
图 15为浅失速状态下一个周期中8个瞬态流场的涡量图以及流线图。可以看出,1/8T与5/8T、2/8T与6/8T、3/8T与7/8T、4/8T与T,每一对时刻的流场均非常相似。从图 6(b)中可以看出,1/8T和5/8T时刻对应升力系数的两个较大的极值点;2/8T、4/8T、6/8T以及T时刻对应升力系数的值较接近,但其中2/8T与6/8T时刻升力系数处于下降阶段,4/8T与T时刻升力系数处于上升阶段,3/8T和7/8T时刻的升力系数接近且均处于升力系数下降阶段。
|
图 15 一个周期中涡结构的演化 Figure 15 Evolution of the vortex structure in a cycle |
流场中涡的演化过程为:在1/8T时刻,翼型上表面存在一个顺时针的大分离涡(主涡),其后存在一个逆时针的二次涡,同时后缘处存在一个较小的逆时针分离涡;当进入2/8T时刻时,主涡和二次涡脱落消失,后缘处的小分离涡进一步发展;3/8T时刻,主涡再次形成,后缘处的小分离涡发展为较大的二次涡;当进入4/8T时刻时,主涡和二次涡向下游发展;5/8T时刻时,二次涡进一步向下游发展,后缘处再次形成一个小分离;之后分离涡演化过程与2/8T至4/8T的过程类似。
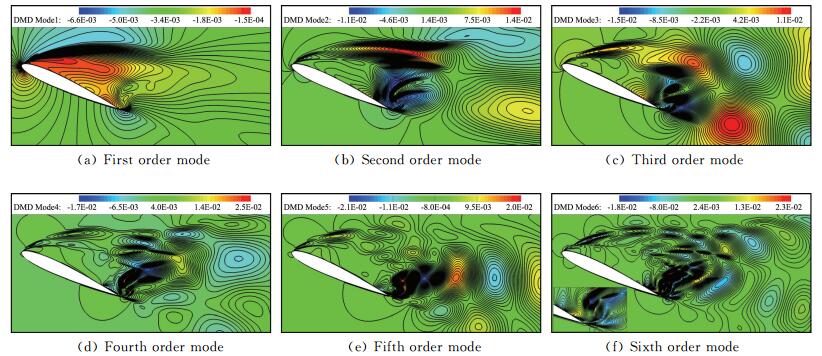
图 16为前六阶DMD模态的速度云图。Mode1主要表现为整个翼型上表面的大分离涡结构,这与失速初始状态类似,该分离涡结构为分离涡演化过程中最主要的静止模态。与失速初始状态不同的是,Mode2、Mode3和Mode4主要表现为翼型后缘分离涡和主涡上方区域的一些涡结构,Mode5和Mode6主要表现为尾迹区的涡结构。实际上,随着迎角的增加,翼型上表面逐渐成为一个背风区,在空间上,流场中涡不再仅仅从靠近后缘区域脱落,整个翼型上表面上方区域会有涡脱落。例如圆柱和竖直平板的流动,可看成迎角为90°的翼型。文献[4]和文献[9]中分别采用LES和DES方法,在对翼型分离流动的模拟中,均捕捉到了这种分离涡结构。本文DMD方法提取的Mode2、Mode3和Mode4对应的涡结构与这一流动规律吻合。
|
图 16 DMD模态速度云图 Figure 16 Counters of velocity for DMD modes |
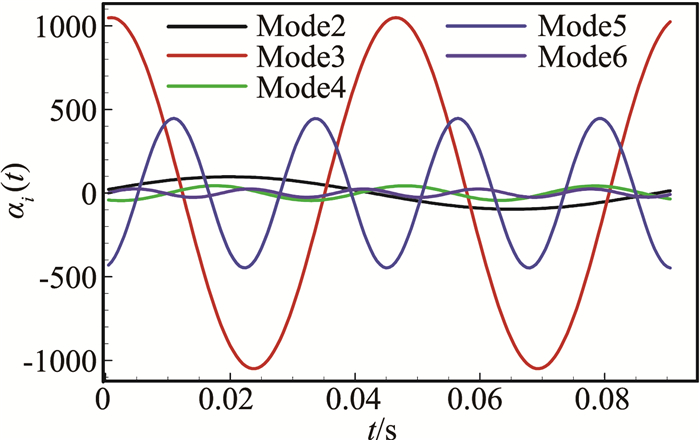
图 17为模态系数随时间的变化,可以看出,不同系数之间也存在明显的相位差。按照模态系数最大幅值对Mode2~Mode6进行排序,发现排序后的模态对应的St为St2、St4、St1、St3、St5,这与图 7(b)中的频率按峰值排序一致。
|
图 17 DMD模态系数随时间的变化 Figure 17 DMD mode amplitude varying with time |
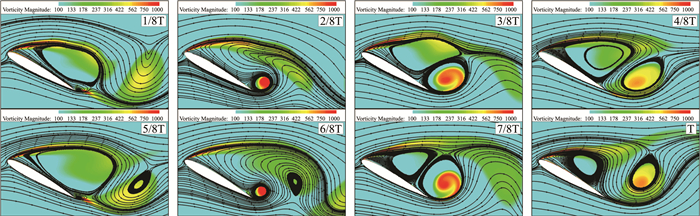
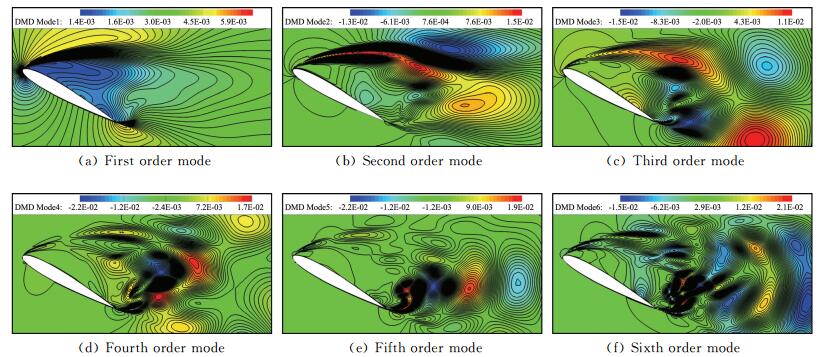
图 18为深失速状态下一个周期中8个瞬态流场的涡量图以及流线图,流场中分离涡的演化规律与浅失速时类似,与之不同的是,翼型上表面的分离区域进一步增大。图 19为前六阶DMD模态的速度云图。其中Mode1依然反应的是整个翼型上表面的大分离涡结构。与浅失速状态相比,Mode2、Mode3和Mode4进一步表现为了随迎角增大而形成的后缘分离涡和主涡上方区域的一些涡结构,同时Mode5和Mode6主要表现为后缘分离涡和尾迹区的涡结构。
|
图 18 一个周期中涡结构的演化 Figure 18 Evolution of the vortex structure in a cycle |
|
图 19 DMD模态速度云图 Figure 19 Contours of velocity for DMD modes |
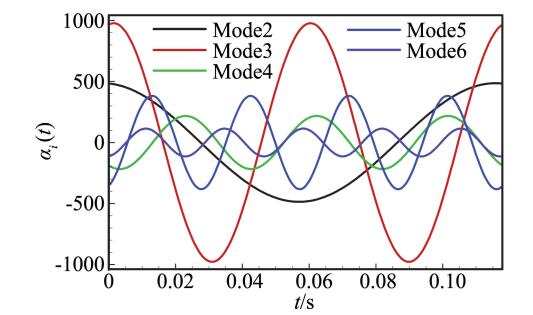
图 20为模态系数随时间的变化,可以看出,不同系数之间依然存在明显的相位差。按照模态系数最大幅值对Mode2~Mode6进行排序,发现排序后的模态对应的St为St2、St1、St4、St3、St5,这与图 7(c)中的频率按峰值排序一致。这说明DMD提取的模态频率不仅与FFT分析结果相差极小,并且两者提取的频率在流动中的主导作用顺序也一致。
|
图 20 DMD模态系数随时间的变化 Figure 20 DMD mode amplitude varying with time |
本文基于SST-DDES混合方法对NACA0012大迎角分离流动进行非定常数值模拟,采用DMD方法对三种典型大迎角失速状态下流场的涡稳定性演化规律进行研究。对于本文的计算模型及条件,得到以下结论:
1) DMD方法可以准确地提取翼型大迎角流动中的主频和高阶倍频及对应的流场模态结构。与FFT分析结果相比,频率最大相差小于0.16%,且可通过特征值对相应的模态进行稳定性分析。由于三种迎角下所有模态的放大率均接近0,因此所有模态处于弱发散、弱收敛或极限环状态。
2) 三种流动状态下,DMD提取的一阶模态主要表现为分离涡演化过程中最主要的静止分离涡结构。前三阶低频对应的模态涡结构与流动中以此频率进行演化的涡结构比较一致。更高阶的倍频主要表现为尾涡和尾迹区的涡结构。
3) DMD提取的模态频率不仅与FFT分析结果相差极小,两者提取的频率在流动中的主导作用顺序也一致。不同DMD模态系数之间存在相位差,说明分离涡流动中不同频率对应的涡结构运动不同步。
| [1] |
Alferez N, Mary I, Lamballais E. Study of stall development around an airfoil by means of high fidelity large eddy simulation[J]. Flow Turbulence Combust, 2013, 91: 623-641. DOI:10.1007/s10494-013-9483-7 (  0) 0) |
| [2] |
Chen Pei. Simulation and analysis of airfoil deep stall flow at high angle of attack[C]//8th Cross-straits Conference on Aeronautics and Astronautics. BeiJing, 2012: 218-225. (in Chinese) 陈培. 翼型大迎角深失速流动的模拟和分析[C]//第八届海峡两岸航空航天学术研讨会. 北京, 2012: 218-225. (  0) 0) |
| [3] |
Mellen C P, Fr-Ograve J, Hlich, et al. Lessons from LESFOIL project on large-eddy simulation of flow around an airfoil[J]. AIAA Journal, 2012, 41(4): 573-581. (  0) 0) |
| [4] |
Almutairi J H, Alqadi I M. Large-eddy simulation of natural low-frequency oscillations of separating-reattaching flow near stall conditions[J]. AIAA Journal, 2013, 51(4): 981-991. DOI:10.2514/1.J052165 (  0) 0) |
| [5] |
Spalart P R. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 181-202. DOI:10.1146/annurev.fluid.010908.165130 (  0) 0) |
| [6] |
Liu Z, Yang Y J, Zhou W J, et al. Study of unsteady separation flow around airfoil at high angle of attack using hybrid RANS-LES method[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 372-380. (in Chinese) 刘周, 杨云军, 周伟江, 等. 基于RANS-LES混合方法的翼型大迎角非定常分离流动研究[J]. 航空学报, 2014, 35(2): 372-380. (  0) 0) |
| [7] |
Richez F, Pape A L, Costes M. Zonal detached-eddy simulation of separated flow around a finite-span wing[J]. AIAA Journal, 2015, 53(11): 3157-3166. DOI:10.2514/1.J053636 (  0) 0) |
| [8] |
Mittal S, Saxena P. Prediction of hysteresis associated with static stall of an airfoil[J]. AIAA Journal, 2000, 38(5): 933-935. DOI:10.2514/2.1051 (  0) 0) |
| [9] |
Zhang J Z, Li K L, Chen L Y. Nonlinear dynamics of static stall of airfoil and its control[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(12): 2163-2173. (in Chinese) 张家忠, 李凯伦, 陈丽莺. 翼型失速的非线性动力学特性及其控制[J]. 航空学报, 2011, 32(12): 2163-2173. (  0) 0) |
| [10] |
Lumley J L. The structure of inhomogeneous turbulence flows[J]. Atmospheric Turbulence and Radio Wave Propagation, 1967, 166-176. (  0) 0) |
| [11] |
Sirovich L. Turbulent and the dynamics of coherent structures. Parts Ⅰ-Ⅲ[J]. Quarterly of Applied Mathematics, 1987, XLV(3): 561-582. (  0) 0) |
| [12] |
Kang W, Dai X Y, Liu N. Multi-modal interaction and flow instability of flow around an airfoil at low reynolds number[J]. Journal of Northwestern Polytechnical University, 2015, 33(3): 382-387. (in Chinese) 康伟, 代向艳, 刘凝. 低速翼型绕流的多模态耦合与流动稳定性研究[J]. 西北工业大学学报, 2015, 33(3): 382-387. (  0) 0) |
| [13] |
Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanical, 2010, 656: 5-28. DOI:10.1017/S0022112010001217 (  0) 0) |
| [14] |
Rowley C W, Mezic I, Bagheri S, et al. Spectral analysis of nonlinear flows[J]. Journal of Fluid Mechanical, 2009, 641: 115-127. DOI:10.1017/S0022112009992059 (  0) 0) |
| [15] |
Roy S, Hua J C, Barnhill W, et al. Deconvolution of reacting-flow dynamics using proper orthogonal and dynamic mode decomposetions[J]. Physical Review E, 2015, 91: 013001. DOI:10.1103/PhysRevE.91.013001 (  0) 0) |
| [16] |
Jovanović M R, Schmid P J, Nichols J W. Sparsity-promoting dynamic mode of decomposition[J]. Physics of Fluids, 2014, 26: 024103. DOI:10.1063/1.4863670 (  0) 0) |
| [17] |
Seena A, Sung H J. Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations[J]. International Journal of Heat and Fluid Flow, 2011, 32(6): 1098-1110. DOI:10.1016/j.ijheatfluidflow.2011.09.008 (  0) 0) |
| [18] |
Muld T W, Efraimsson G, Henningson D S. Flow structures around a high-speed train extracted using proper orthogonal decomposition and dynamic mode decomposition[J]. Computers & Fluids, 2012, 57: 87-97. (  0) 0) |
| [19] |
Pan C, Chen H, Wang J J. Dynamical mode decomposition of complex flow field[C]//8th National Conference on Experimental Fluid Mechanics. Guangzhou, 2010: 77-82. (in Chinese) 潘翀, 陈皇, 王晋军. 复杂流场的动力学模态分解[C]//第八届全国实验流体力学学术会议论文集. 广州, 2010: 77-82. (  0) 0) |
| [20] |
Mariappan S, Gardner A D, Richter K, et al. Analysis of dynamic stall using dynamic mode decomposition technique[J]. AIAA Journal, 2014, 52(11): 2427-2439. DOI:10.2514/1.J052858 (  0) 0) |
| [21] |
Mohan A T, Gaitonde D V, Visbal M R. Model reduction and analysis of deep dynamic stall on a plunging airfoil using dynamic mode decomposition[R]. AIAA 2015-1058.
(  0) 0) |
| [22] |
Spalart P R. Young person's guide to detached-eddy simulation grids[R]. NASA CR-2001-211032.
(  0) 0) |
| [23] |
Mccroskey W J. A critical assessment of wind tunnel results for the NACA 0012 airfoil[R]. NASA TM 1987-100019.
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36


