从20世纪70年代开始,喷流噪声的飞行效应开始得到研究者的关注。早期的飞行试验[1]和风洞试验[2]都表明:飞行状态下的喷流噪声水平比静止情况低,也发展了理论或半经验公式[3-4]来预计飞行速度对喷流噪声的影响。然而,由飞行试验和由不同风洞试验中得到的飞行速度影响有很大的不同[5]。因此,获得飞行状态下的噪声源特征及飞行速度对喷流噪声的影响规律,具有重要的意义。
已有较多的风洞试验研究了飞行速度对喷流声源和远场噪声的影响,如Morris等[6]测量了飞行速度对近场流动的影响规律,试验飞行速度与喷流的比值λ从0.096变化到0.497,遗憾的是,喷流马赫数偏小,仅为0.47。Larson等[7]测量了飞行速度对混合层的增长率、湍流水平、对流速度、积分尺度和时间尺度的影响。Soares等[8]测量了λ从0到0.5情况下的近场流场,分析了飞行速度对波包的影响,在一定程度上阐释了飞行速度对声源改变与远场噪声改变之间的联系。André等[9]则测量了飞行速度对超声速欠膨胀喷流的影响。Packman等[10]和Viswanathan等[11]测量了不同飞行速度下的远场声场,发现不同辐射角度下噪声和相对速度呈指数关系,但没有给出声源测量结果。
对喷流噪声的飞行效应数值研究较少。Shur等[12-13]采用隐式大涡模拟(ILES)来计算飞行速度对喷流流场和噪声的影响,但其重点在于计算方法和流动控制,并未对飞行效应做详细分析。Sandberg等[14]则直接数值模拟(DNS)喷流流场,发现不同环向模态噪声与相对速度的指数关系相同。
由于喷流与飞行速度之间通常存在速度差,会形成剪切层和混合层,它们失稳后形成的噪声带宽较大。因此,要精确预测近场流动和远场噪声,势必要求采用近流场解析方法,如LES、DNS等;而远声场则通常采用声比拟方法,如求解FW-H方程。
然而,无论LES还是DNS,在预测高雷诺数流动时,其计算资源的消耗都是非常巨大的。为节约计算资源,人们还常采用RANS-LES混合方法,其中分离涡模拟方法(DES)是最流行的混合方法之一,它结合了RANS和LES方法的优点,具有构造简单、计算量可接受的优点,得到了广泛应用[15],能解决喷流计算中包含喷管边界层等的工程问题。尽管DES类方法固有的“灰区”问题会极大延迟剪切层失稳[16],但已找到减缓方法[17];此外,DES类方法在喷流噪声的预测中也有部分应用[18-21]。
本文采用改进长度尺度定义的IDDES方法预测近场流动,FW-H方程求解远场噪声,来研究飞行速度对喷流流场和声场的影响。首先,介绍所使用的数值方法;其次,通过比较稀密网格和不同积分面,验证方法和网格;最后,分析飞行速度对喷流流场和声场的影响。
1 计算方法 1.1 IDDES方法本文所使用的IDDES方法,其基准模式为SST,主要通过修改湍动能方程中的长度尺度,实现RANS和LES之间的互相转变。IDDES方法中的湍动能输运方程可修改为[22]:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {U_i}k} \right)}}{{\partial {x_i}}} = {P_k}- \frac{{\rho {k^{\frac{3}{2}}}}}{{{L_{{\rm{hybrid}}}}}} + \frac{\partial }{{\partial {x_i}}}\left[{\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_i}}}} \right] $ | (1) |
式(1)中混合长度尺度的定义为:
| $ {L_{{\rm{IDDES}}}} = {\tilde f_d}\left( {1 + {f_e}} \right){L_{{\rm{RANS}}}} + \left( {1-{{\tilde f}_d}} \right){L_{{\rm{LES}}}} $ | (2) |
式(2)中SST模式中湍流长度尺度定义为:
| $ {L_{{\rm{RANS}}}} = \sqrt k /\left( {{\beta ^*}\omega } \right) $ | (3) |
LES的滤波尺度定义为:
| $ {L_{{\rm{LES}}}} = \left[{{F_1}{C_{{\rm{DES, }}k-\omega }} + \left( {1-{F_1}} \right){C_{{\rm{DES}}, k-\varepsilon }}} \right]\Delta $ | (4) |
式(4)中CDES, k-ω和CDES, k-ε是基于SST模式两个分支的系数,具体取值通常需要各项同性湍流衰减算例进行标定。
IDDES中网格尺度的定义:
| $ \Delta = \min \left( {\max \left( {{C_w}{\Delta _{\max }}, {C_w}d, {\Delta _{\min }}} \right), {\Delta _{\max }}} \right) $ | (5) |
其中Δmax=max(Δx, Δy, Δz),Δmin=min(Δx, Δy, Δz)。其它参数形式可参见文献[23]。
1.2 减缓灰区的方法DES类方法,尤其在流向,存在一个由RANS到LES之间模糊的区域,称之为“灰区”,会严重影响喷流剪切层的发展与失稳,需克服。
对于喷流而言,流向网格通常可加密,但是周向网格加密会带来巨量网格增加。因此,“灰区”在剪切层发展初期,则极可能因周向网格过稀而出现。针对喷流流动,减缓“灰区”的办法为——改变网格尺度定义,使其适应周向稀网格。
在喷流喷口附近,周向网格大于其它两方向,式(5)中长度尺度定义,会产生较大的物理黏性,从而形成严重的“灰区”问题。考虑涡轴的方向修改网格尺度,最大效率利用网格的解析能力,新的定义为式(6)和式(7)[24]:
| $ {\Delta _\omega } = \frac{1}{{\sqrt 3 }}\max \left| {{\mathit{\boldsymbol{l}}_n}-{\mathit{\boldsymbol{l}}_m}} \right|, \left( {m, n = 1, 2, \ldots, 8} \right) $ | (6) |
| $ {\mathit{\boldsymbol{l}}_n} = {\mathit{\boldsymbol{n}}_\omega } \times \left( {{\mathit{\boldsymbol{r}}_n}-\mathit{\boldsymbol{r}}} \right), \left( {n = 1, 2, \ldots, 8} \right) $ | (7) |
其中nω为单位涡矢量,rn-r为从网格单元顶点到网格单元中心的矢量(此处为结构网格形式)。
1.3 空间离散格式和时间推进方法仅用先进的DES类方法还不够,还需要与之匹配的自适应耗散空间离散格式及至少二阶的时间推进方法。
实际工程非定常湍流问题中,外形和流动较为复杂,要求数值格式适用性强、鲁棒性好,然而,要解析小尺度结构,却要求格式精度高、耗散小,二者的要求其实是矛盾的,很难统一。比如,在物面、远场、激波等,当地局部扰动大,需要稳定、大耗散,耗散小了计算易发散。可是在分离区域,流动接近各向同性,需要高精度、小耗散甚至无耗散,耗散大会抑制涡的生成。
采用下述自适应耗散格式,可同时满足上述需求,且具有可实现性[25]:
| $ {F_{i + 1/2}} = {F_{{\rm{symmetric, }}i + 1/2}}- \phi \frac{1}{2}\left[{\left| {{{\tilde A}_{{\rm{inv}}}}} \right|\left( {{U_R}-{U_L}} \right)} \right] $ | (8) |
右端第一项为纯对称格式通量,无耗散,仅有色散且由对称格式精度决定;第二项无色散,纯耗散且由插值精度、插值方式和熵修正特性等决定。在式(8)第二项中引入与DES类方法匹配的自适应耗散系数ϕ,它是[0,1]之间的变量,应包含到物面距离、模化涡黏系数、时间尺度、运动长度尺度、网格尺度、应变率与涡量等物理信息。在物面附近、远场无旋区内为1,湍流占主导的区域则趋于0。它能有效抑制数值振荡,同时尽可能地解析小尺度运动。借鉴SST模式中的混合函数可构建函数ϕ:
| $ \phi = \max \left[{{\phi _{\min }}, \tanh \left( {{A^{CH1}}} \right)} \right] $ | (9) |
其中ϕmin为耗散系数下限,本程序中一般取0.05至0.2之间,用于保证计算的稳定性,其它参数的计算如式(10)~(14)所示:
| $ A = CH2 \cdot \max \left\{ {\left[{\left( {\frac{{{L_{{\rm{LES}}}}}}{{g{l_t}}}} \right)-0.5} \right], 0} \right\} $ | (10) |
| $ {l_t} = \sqrt {\frac{{v + {v_t}}}{{C_\mu ^{1.5}K}}} $ | (11) |
| $ K = \max \left\{ {{{\left[{\left. {{{\left( S \right)}^2} + {W^2}} \right)/2} \right]}^{1/2}}, 0.1} \right\} $ | (12) |
| $ g = \tanh {B^4} $ | (13) |
| $ B = \frac{{CH3W\;\max \left( {S, W} \right)}}{{\max \left[{\left( {{S^2} + {W^2}} \right)/2, {{10}^{-20}}} \right]}} $ | (14) |
其中常数分别为CH1=3, CH2=1, CH3=2。其中S和W分别为
时间推进方面,隐式LU-SGS可采用较大的时间步长,在足够子迭代的情况下,可实现二阶精度。
耦合DES类混合方法、自适应耗散空间离散格式和含子迭代的LU-SGS时间推进方法在新型飞行器气动仿真与总体设计实验室(LASD)中得到了广泛的验证,如低速起落架大范围分离流动[23]、跨声速OAT15A翼型激波抖振及控制[26]、超声速空腔流动及其控制[28]、高超声速空腔诱导边界层转捩[27]等。
1.4 FW-H声比拟方法对于喷流噪声的传播过程,理论上可直接求解N-S方程得到,但这样需要非常大的计算资源。常用的方法为声比拟方法,如可穿透积分面的FW-H方法,它不求解计算域内四极子项的体积分,但积分面需包括全部的噪声源。其积分解如式(15),具体的推导过程详见文献[29-30]。
| $ \begin{gathered} 4\pi p' = \iint\limits_S {{{\left[{\frac{{{\rho _0}\left( {{{\dot U}_i}{n_i} + {U_i}{{\dot n}_i}} \right)}}{{r{{\left| {1-{M_r}} \right|}^2}}} + \frac{{{\rho _0}{U_i}{n_i}K}}{{{r^2}{{\left| {1-{M_r}} \right|}^3}}}} \right]}_{{\text{ret}}}}{\text{d}}S + } \hfill \\ \;\;\;\;\;\;\;\;\;\;{\iint\limits_S {\left[{\frac{{{F_i}{{\hat r}_i}-{F_i}{M_i}}}{{{r^2}{{\left| {1-{M_r}} \right|}^2}}}} \right]}_{{\text{ret}}}}{\text{d}}S + \hfill \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{c}\iint\limits_S {{{\left[{\frac{{{{\dot F}_i}{{\hat r}_i}}}{{r{{\left| {1-{M_r}} \right|}^2}}} + \frac{{{F_i}{{\hat r}_i}K}}{{{r^2}{{\left| {1-{M_r}} \right|}^3}}}} \right]}_{{\text{ret}}}}{\text{d}}S} \hfill \\ \end{gathered} $ | (15) |
该方程的求解,可采用预先时间步[31],即根据声源时间求解接收点的时间,
| $ \begin{array}{l} {t_{{\rm{observer}}}} = t + \Delta \tau \\ \Delta \tau = \frac{{\left| {x\left( {t + \Delta \tau } \right)-y\left( t \right)} \right|}}{c} \end{array} $ | (16) |
接收点时间方向的插值采用二阶方法。每得到一个接收点时刻,做如下处理:
| $ {j_{{\rm{adv}}}} = {\mathop{\rm int}} \left( {\frac{{t_{{\rm{adv}}}^j}}{{\Delta t}}} \right), \;\;\;\;\;\;w = \frac{{t_{{\rm{adv}}}^j}}{{\Delta t}}-{j_{{\rm{adv}}}} $ | (17) |
Δt和jadv分别为接收点时间离散间隔和序号,然后将该接收时刻插值到时间离散点上,
| $ p_i^j = \left\{ \begin{array}{l} p_i^j = p', \;\;\;\;\;w_i^j = w\;\;\;{\rm{if}}\;\;\;\;p_i^j = 0\\ p'-w\frac{{p_i^j-p'}}{{w_i^j-w}}, \;\;w_i^j = 0\;\;\;\;{\rm{if}}\;\;\;p_i^j \ne 0 \end{array} \right. $ | (18) |
采用具有风洞试验数据的喷流进行验证,马赫数Ma=0.9,对应喷流速度UJ=308 m/s,基于喷管直径D的雷诺数Re=1.1×106,喷流总温与背景温度相同,喷流外侧保留了马赫数为0.05的伴随流动。
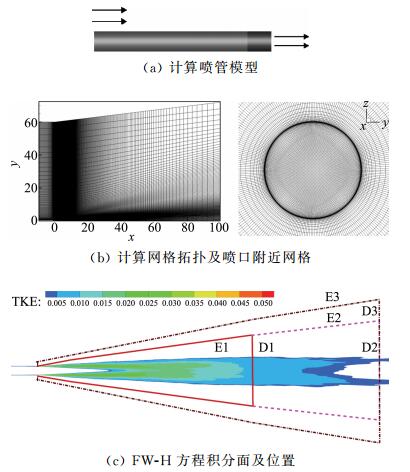
喷管直径D=0.06223 m,圆形,喷管长度为10D,如图 1(a)所示。计算网格如图 1(b)所示,计算域流向-10D~100D,径向60D~72D。
|
图 1 喷管示意图和计算网格 Figure 1 Schematic of the nozzle and nearfield mesh |
由于可穿透的FW-H方程积分面要求封闭,不能有旋涡通过,在喷流噪声问题中难以实现。为研究FW-H方程积分面的影响,选取5个积分面,如图 1(c)所示。开口积分面S1(漏斗形开口E1旋转形成)、闭口积分面S2(S1和D1封闭)、开口积分面S3(E1和E2旋转所得)、闭口积分面S4(S3和D2封闭)和封闭积分面S5(E3旋转加上D2和D3封闭所得)。
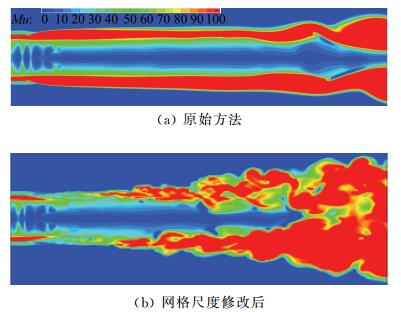
为对比网格尺度的影响,采用两套拓扑结构一致的结构化网格,网格单元分别为400万和1800万。稀网格自身耗散大,如果修改网格尺度定义的方法在稀网格的基础上效果不错的话,密网格的表现应更好。图 2给出原始和修订长度尺度后获得的模化涡粘系数对比,发现修订后的长度尺度能有效减小剪切层初期模化黏性,加速剪切层失稳,改善了DES类方法在喷流计算中的“灰区”缺陷。此外,在剪切层失稳下游,修订后的旋涡尺度更小。
|
图 2 网格尺度修改前后模化的湍流粘性 Figure 2 Comparisons of modeled turbulence viscosity |
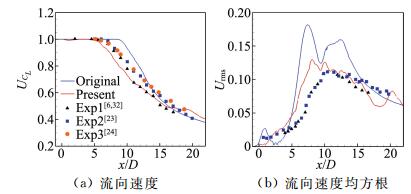
为定量对比网格尺度定义的影响,给出中心线平均流向速度和及其均方根变化,见图 3。由于“灰区”问题,原始方法的剪切层失稳过缓,势流区长度太长,势流区结束之后的耗散更大,流向速度的脉动值也偏大。修改网格尺度后,有效地促进剪切层的失稳,改善了脉动速度的预测。预测的剪切层失稳较试验略提前,与相同网格量的LES表现类似[13]。
|
图 3 网格尺度修改前后喷流中线处的平均流向速度和其脉动均方根的对比 Figure 3 Comparisons of mean and RMS streamwise velocity on the central line |
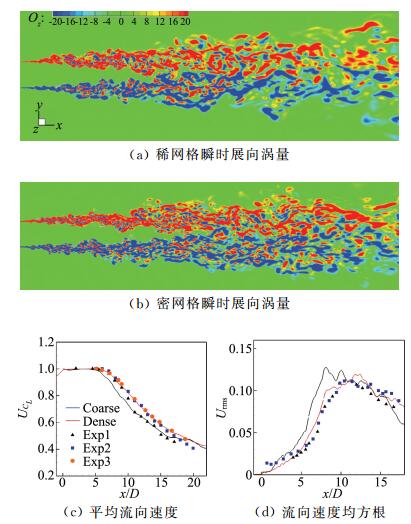
图 4(a)和图 4(b)给出了稀网格和密网格的瞬时涡量对比,两套网格都捕捉到了相似的流动特点,即剪切层失稳及破碎,其中密网格获得的流动结构更精细。图 4(c)给出了两套网格预测的中心线处平均流向速度(UCL)分布,密网格预测的喷流势流核更长,与试验更接近,相应的中心线处流向脉动速度均方根(Urms)的预测也得到改善(图 4d)。
|
图 4 稀网格和密网格流场结果对比 Figure 4 Comparisons of results between the coarse and dense mesh |
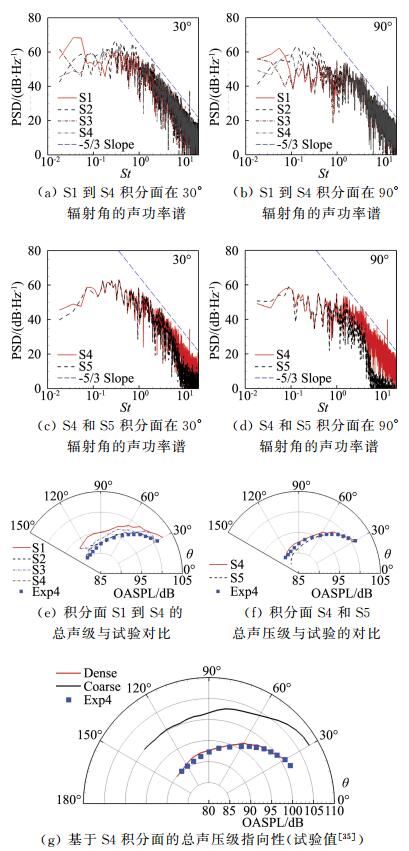
图 5(a)~(d)给出不同积分面在30°和90°辐射角度上的声功率谱的对比,该结果是基于密网格的结果。接收点距离喷流出口98D,喷流下游为0°,从下游到上游逐渐过渡到180°。首先,对比开口S1和闭口S2。S1在低频(St < 0.08,St=fD/UJ)高于S2,以30°位置为例,在低频截止位置处(St=0.018)处,S1比S2高约14 dB。在90°位置,S2在中频(0.1 < St < 0.5)附近要高于S1,该频带内的总能量差别约9.5 dB,它们在高频的能量谱基本重合。其次,比较开口S3和闭口S4。同样地,S3在低频(St < 0.04)高于S4,同样以30°位置为例,在低频截止位置处(St=0.018)处S3比S4高约16 dB。两套积分面都表明开口FW-H方程会高估低频噪声,与文献结论一致[36];但是,S3与S4有差别的频率为St=0.04之前,小于S1和S2差别开始的频率St=0.08,说明随着积分面长度增加,开口对低频的高估会减弱。然后,比较闭口S2和S4。S2在中频(0.1 < St < 0.5)附近能量高于S4,该频带内的能量差别约为7.8 dB。这是由于S2距离喷管更近,仍有较强的湍流结构通过产生的。最后,比较闭口S4和S5影响。由于S4已包含所有声源结构,故S4和S5的能谱在中低频一致;在高频部分,S5衰减较快是因为S5处大网格尺度导致。在本算例的5个积分面中S4是最合适的,即减小了涡通过积分面造成的伪噪声,又解析了足够多的高频噪声。
|
图 5 不同积分面的噪声结果及与试验值的比较 Figure 5 Comparisons of results among different FW-H integral surfaces and measurements |
图 5(e)和图 5(f)分别展示了5个积分面的总声压级及与试验值的对比,S4积分面得到的结果与试验最为接近。本文后续对噪声的讨论都将针对S4积分面的结果进行。图 5(g)则展示了两套网格远场噪声指向(S4积分面)及与试验值的对比。稀网格会高估远场噪声,与其在近场高估湍流脉动的结果相一致。两套网格得到的远场噪声指向性形态一致,密网格与试验值更为接近。
通过对比分析近场流场和远场噪声结果,均表明网格收敛了,且接近风洞试验值,密网格结果具有可靠性。
3 飞行速度影响喷流马赫数及雷诺数与前相同,外界飞行马赫数分别为Ma∞=0.05和Ma∞ =0.2。Ma∞从0.05到0.2的变化可以用来近似飞机从静止状态到起飞状态之间的转变。该部分的计算采用密网格进行。
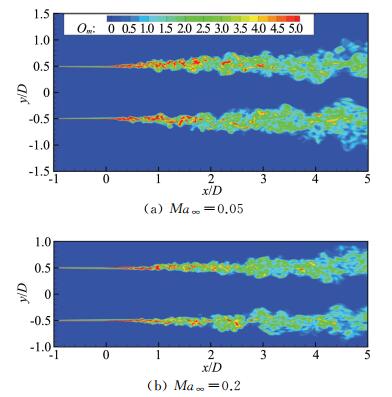
图 6给出两个飞行速度下的瞬时涡量(Om)云图。由图 6可知,随着飞行速度提高,喷流混合层之间的剪切作用减弱,但仍然捕捉到了与低飞行速度接近的剪切层失稳位置。图 7则给出了两个飞行速度下的Q=10(UJ/D)2等值面图(UJ为喷流出口速度),它能反映三维涡结构的生成、演化、发展、失稳及相互作用。由图可知,在喷管出口处剪切层就已经发展并逐渐形成准二维环向结构;在向下游发展的过程中,卷起速度不一致的三维流动结构;再下游,形成一些相对规则的发卡涡,它们在三维力的作用下被拉伸,形成流向三维小尺度结构,并最终失稳形成尺度更小且具有宽频特征的小尺度旋涡。从图中也可以看出,当Ma∞=0.2时,准二维结构形成的流向距离更长,剪切层的失稳略微后移,且在径向的发展也慢于Ma∞=0.05情况。
|
图 6 过中心线截面的涡量云图 Figure 6 Flight effects on instantaneous vortices |

|
图 7 Q=10(UJ/D)2的等值面(以Ma染色) Figure 7 Iso-surface of Q=10(UJ/D)2(colored by Ma) |
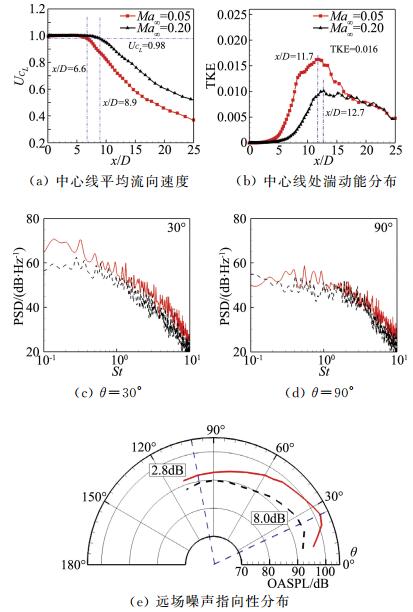
图 8给出飞行速度对近场流动及远声场的影响规律。其中,图 8(a)和图 8(b)给出了中心线处平均流向速度及其对应的湍动能对比。随着飞行速度的提高,喷流势流核心区增长。假设喷流速度为喷口出口速度的0.98倍时,势流区结束[13],则Ma∞=0.05时,势核区长度为6.6D;当Ma∞=0.2时,核心区长度变为8.9D。此外,当Ma∞从0.05增加到0.2时,湍动能最大值的位置从11.7D增加到12.7D,最大值则从0.016减小到0.010。
|
图 8 飞行速度对近场和远场噪声的影响 Figure 8 Flight effects on near-field flow quantities and far-field noise |
图 8(c)和图 8(d)给出了30°和90°辐射角度声功率谱的对比。Ma∞=0.2在整个能量频带上都低于Ma∞=0.05,30°位置处总能量差别6.8 dB,90°位置处总能量差别位2.8 dB。
图 8(e)给出远场声指向性结果。从总声压级上来看,在25°位置附近时,两者差距最大,为8.0 dB;随着角度的增加,其差距在减小,在100°位置时,差距约为2.8 dB。Viswanathan等[11]的试验结果表明,总声压级随来流速度变化关系为ΔOASPL=m10lg(UJ/(UJ-Vt)),Vt为飞行速度,在不同方位角具有不同的值,在25°辐射角度下约为8.0 dB,在100°辐射角度下约为3.0 dB。本文计算中,在25°和100°时因来流速度引起的总声压级降低分别为8.7 dB和3.3 dB,与他们的试验结果基本吻合。
4 结论本文使用修正长度尺度的IDDES方法、自适应耗散格式和可穿透积分面的FW-H方程,计算了飞行速度对喷流流场和远场噪声的影响。
首先,计算与分析了已有风洞试验数据的喷流流场及其远声场。在稀网格基础上,通过与试验结果的对比,说明改进网格尺度定义的IDDES方法在减缓“灰区”方面是成功且可靠的。
其次,比较了稀、密两套网格的流场和声场,说明了网格的收敛性。然后基于密网格的5个FW-H积分面得到的噪声结果,积分面的选取应综合考虑声源范围和当地网格尺度的影响,选取紧邻噪声源但包含所有噪声源的积分面最为合适,即本文中的S4积分面。
最后,详细讨论了飞行速度对喷流近场和远场噪声的影响。通过对比发现,飞行速度增加会增加喷流势流核的长度,降低势流核附近湍动能,在势流核完全结束之后,飞行速度对湍动能的影响减小;飞行速度对远场噪声的影响规律及其具体幅值,也与试验测量吻合良好,说明该方法在预测喷流噪声的飞行速度效应时也是适用的。
| [1] |
Bushell K W. Measurement and prediction of jet noise in flight[R]. AIAA 75-461, 1975.
(  0) 0) |
| [2] |
Tanna H K, Morris P J. In-flight simulation experiments on turbulent jet mixing noise[J]. Journal of Sound and Vibration, 1977, 53(3): 389-405. DOI:10.1016/0022-460X(77)90422-9 (  0) 0) |
| [3] |
Michalke A, Michel U. Relation between static and in-flight directivities of jet noise[J]. Journal of Sound and Vibration, 1979, 63(4): 602-605. DOI:10.1016/0022-460X(79)90834-4 (  0) 0) |
| [4] |
Michalke A, Michel U. Prediction of jet-noise in flight from static tests[J]. Journal of Sound and Vibration, 1979, 67(3): 341-367. DOI:10.1016/0022-460X(79)90541-8 (  0) 0) |
| [5] |
Michel U. On the systematic error in measurements of jet noise flight effects using open jet wind tunnels[R]. AIAA 2015-2996.
(  0) 0) |
| [6] |
Lau J C, Morris P J, Fisher M J. Measurements in subsonic and supersonic free jets using a laser velocimeter[J]. Journal of Fluid Mechanics, 1979, 93(1): 1-27. DOI:10.1017/S0022112079001750 (  0) 0) |
| [7] |
Larson R S, Mecolgan C J, Packman A B. Jet noise source modification due to forward flight[J]. AIAA Journal, 1978, 16(3): 225-232. DOI:10.2514/3.60881 (  0) 0) |
| [8] |
Mourão Soares L F, Cavalieri A V, Kopiev V, et al. Flight effects on turbulent-jet wavepackets[C]//23rd AIAA/CEAS Aeroacoustics Conference. Denver, Colorado, 2017.
(  0) 0) |
| [9] |
André B, Castelain T, Bailly C. Experimental study of flight effects on slightly underexpanded supersonic jets[J]. AIAA Journal, 2017, 55(1): 57-67. DOI:10.2514/1.J054797 (  0) 0) |
| [10] |
A B Packman K W N, Paterson R N. Effect of simulated forward flight on subsonic jet exhaust noise[J]. Journal of Aircraft, 1976, 13(12): 1007-1012. DOI:10.2514/3.58741 (  0) 0) |
| [11] |
Viswanathan K, Czech M. Measurement and modeling of effect of forward flight on jet noise[J]. AIAA Journal, 2011, 49(1): 216-234. DOI:10.2514/1.J050719 (  0) 0) |
| [12] |
Shur M L, Spalart P R, Strelets M K. Noise prediction for increasingly complex jets. Part Ⅱ:applications[J]. International Journal of Aeroacoustics, 2005, 4(3&4): 247-266. (  0) 0) |
| [13] |
Shur M L, Spalart P R, Strelets M K. LES-based evaluation of a microjet noise reduction concept in static and flight conditions[J]. Journal of Sound and Vibration, 2011, 330(17): 4083-4097. DOI:10.1016/j.jsv.2011.02.013 (  0) 0) |
| [14] |
Sandberg R D, Tester B J. Mach-number scaling of individual azimuthal modes of subsonic co-flowingjets[J]. Journal of Fluid Mechanics, 2016, 793: 209-228. DOI:10.1017/jfm.2016.133 (  0) 0) |
| [15] |
Spalart P R. Detached-eddy simulation[J]. Annual Review of Fluid Mechanics, 2009, 41: 181-202. DOI:10.1146/annurev.fluid.010908.165130 (  0) 0) |
| [16] |
Yan J, Tawackolian K, Michel U, et al. Computation of jet noise using a hybrid approach[R]. AIAA 2007-3621, 2007.
(  0) 0) |
| [17] |
Shur M L, Spalart P R, Strelets M, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649. DOI:10.1016/j.ijheatfluidflow.2008.07.001 (  0) 0) |
| [18] |
Yan J, Panek L, Thiele F. Simulation of jet noise from a long-cowl nozzle with serrations[R]. AIAA 2007-3635, 2007.
(  0) 0) |
| [19] |
Chauvet N, Deck S, Jacquin L. Zonal detached eddy simulation of a controlled propulsive Jet[J]. AIAA Journal, 2007, 45(10): 2458-2473. DOI:10.2514/1.28562 (  0) 0) |
| [20] |
Verrière J, Gand F, Deck S. Zonal detached-eddy simulations of a dual-stream Jet[J]. AIAA Journal, 2016, 54(10): 3176-3190. DOI:10.2514/1.J054896 (  0) 0) |
| [21] |
Verriere J, Gand F, Deck S. Zonal detached eddy simulations of a dual-stream jet:turbulence rate sensitivity[J]. AIAA Journal, 2017, 55(8): 2503-2521. DOI:10.2514/1.J055535 (  0) 0) |
| [22] |
Xiao Z X, Liu J, Huang J B, et al. Numerical dissipation effects on massive separation around tandem cylinders[J]. AIAA Journal, 2012, 50(5): 1119-1136. DOI:10.2514/1.J051299 (  0) 0) |
| [23] |
Xiao Z X, Liu J, Luo K Y, et al. Investigation of flows around a rudimentary landing gear with advanced detached-eddy-simulation approaches[J]. AIAA Journal, 2013, 51(1): 107-125. DOI:10.2514/1.J051598 (  0) 0) |
| [24] |
Shur M L, Spalart P R, Strelets M K. Jet noise computation based on enhanced DES formulations accelerating the RANS-to-LES transition in free shear layers[J]. International Journal of Aeroacoustics, 2016, 15(6-7): 595-613. DOI:10.1177/1475472X16659388 (  0) 0) |
| [25] |
Xiao Z X, Luo K Y, Liu J. Developments and applications of hybrid RANS-LES methods for wide-speed-rangeflows[J]. Acta Aerodynamica Sinica, 2017, 35(3): 338-353. (in Chinese) 肖志祥, 罗堃宇, 刘健. 宽速域RANS-LES混合方法的发展及应用[J]. 空气动力学学报, 2017, 35(3): 338-353. (  0) 0) |
| [26] |
Huang J, Xiao Z X, Liu J, et al. Simulation of shock wave buffet and its suppression on an OAT15A supercritical airfoil by IDDES[J]. Science China Physics, Mechanics and Astronomy, 2012, 55(2): 260-271. DOI:10.1007/s11433-011-4601-9 (  0) 0) |
| [27] |
Xiao L H, Xiao Z X, Duan Z W, et al. Improved-delayed-detached-eddy simulation of cavity-induced transition in hypersonic boundary layer[J]. International Journal of Heat and Fluid Flow, 2015, 51: 138-150. DOI:10.1016/j.ijheatfluidflow.2014.10.007 (  0) 0) |
| [28] |
Luo K Y, Weng Z, Xiao Z X, et al. Improved delayed detached-eddy simulations ofsawtooth spoiler control before supersonic cavity[J]. International Journal of Heat and Fluid Flow, 2017, 63: 172-189. DOI:10.1016/j.ijheatfluidflow.2017.01.012 (  0) 0) |
| [29] |
Di Francescantonio P. A new boundary integral formulation for the prediction of sound radiation[J]. Journal of Sound and Vibration, 1997, 202(4): 491-509. DOI:10.1006/jsvi.1996.0843 (  0) 0) |
| [30] |
Brentner K S, Farassat F. An analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces[J]. American Institute of Aeronautics and Astronautics Journal, 1998, 36: 1379-1386. DOI:10.2514/2.558 (  0) 0) |
| [31] |
Casalino D. An advanced time approach for acoustic analogy predictions[J]. Journal of Sound and Vibration, 2003, 261(4): 583-612. DOI:10.1016/S0022-460X(02)00986-0 (  0) 0) |
| [32] |
Lau J C. Effects of exit Mach number and temperature on mean-flow and turbulence characteristics in roundjets[J]. Journal of Fluid Mechanics, 1981, 105: 193-218. DOI:10.1017/S0022112081003170 (  0) 0) |
| [33] |
Arakeri V H, Krothapalli A, Siddavaram V, et al. On the use of microjets to suppress turbulence in a Mach 0.9 axisymmetric jet[J]. Journal of Fluid Mechanics, 2003, 490: 75-98. DOI:10.1017/S0022112003005202 (  0) 0) |
| [34] |
Smimonich J C, Narayanan S. Aeroacoustic characterization noise reduction and dimensional scaling effects of high subsonic jets[J]. AIAA Journal, 2001, 39(11): 2062-2069. DOI:10.2514/2.1228 (  0) 0) |
| [35] |
Viswanathan K. Aeroacoustics of hotjets[J]. Journal of Fluid Mechanics, 2004, 516: 39-82. DOI:10.1017/S0022112004000151 (  0) 0) |
| [36] |
Shur M L, Spalart P R, Strelets M K. Noise prediction for increasingly complex jets, Part 1:methods and tests[J]. International Journal of Aeroacoustics, 2005(3-4): 213-246. (  0) 0) |
 2018, Vol. 36
2018, Vol. 36

