流动由层流转变成湍流的过程称为转捩,转捩现象普遍存在于流体流动中[1]。例如,大型民机、高空无人机、高空螺旋桨、风力机叶片及微型飞行器表面都存在流动转捩现象。由于影响因素众多、物理机理复杂,转捩问题一直是流体力学中尚未完全解决的前沿问题之一[2]。层流和湍流两种流态下物体表面的摩擦阻力、热传导速率和流动分离位置等特性大为不同,故转捩位置直接影响飞行器气动力计算的精确性,其中对阻力预测的影响尤为显著。空中客车公司专家指出未来要提高大型飞机的空气动力学效率,大幅度降低油耗和污染排放,层流减阻技术是一个非常有前途的发展方向[3]。因此,发展高效可靠的转捩预测方法是飞行器减阻设计的关键。
随着计算机技术的高速发展,大涡模拟(LES)[4]和直接数值模拟(DNS)[5]方法已经能够对流动转捩进行精细化研究。但由于其计算量过大,还不适合广泛的工程应用。目前针对层流减阻设计常用的转捩预测方法为:基于线性稳定性理论的eN方法[6]和基于流场当地变量的γ-Reθ转捩模型[7]。最近一种基于动模态分解的DMD/eN转捩预测方法[8]也被提出,并展现出良好的发展前景。下面分别对这三种方法进行详细介绍。
基于线性稳定性理论的eN方法是目前在工程实践中得到最广泛认可的转捩预测方法[6],eN方法由Smith[9]和Ingen[10]首次提出,目前国外研究机构已经围绕翼型、机翼边界层流动转捩预测开展了大量的研究工作[11-26]。而针对翼身组合体等复杂三维外形,国外开展的边界层转捩预测方法研究相对较少,且主要使用简化的eN数据库转捩预测方法。如法国宇航院(ONERA)在其雷诺平均Navier-Stokes(RANS)方程求解器elsA中加入了Arnal[15]和Casalis[18]发展的eN数据库方法,分别用来计算TS波和CF波诱导的转捩,并开展了带增升装置的翼身组合体外形的转捩预测研究[27]。德国宇航院(DLR)在其结构化网格RANS求解器FLOWer[28]和非结构/混合网格RANS求解器TAU[29]中加入了eN数据库方法,开展了三维复杂外形的转捩预测研究。美国斯坦福大学的Lee和Jameson[30]开展了基于耦合eN数据库方法的RANS求解器的层流机翼优化设计工作。eN数据库方法并不求解线性稳定性方程,而只是根据边界层的形状因子、速度型拐点信息等部分特征参数,在数据库中查询事先求解的平板边界层不稳定扰动累积放大因子的包络线。目前,国内已开展的转捩预测研究工作主要针对翼型、机翼绕流进行,也鲜有使用eN方法对翼身组合体等复杂三维外形开展转捩预测的研究工作。在使用稳定性理论和eN方法进行后掠机翼边界层稳定性及转捩预测研究方面,张坤[31]通过线性稳定性理论(Linear Stability Theory,LST),左岁寒[32]通过线性抛物化稳定性方程(Linear Parabolized Stability Equations,LPSE)开展了机翼边界层转捩预测研究。孙朋朋[33]、靖振荣[34]和黄章峰[35]等通过LST开展了一系列的后掠机翼边界层稳定性及转捩研究,以及使用扩展的O-S方程(Extended Orr-Sommerfeld equation,EOS)和LPSE进行了机翼边界层的横流稳定性分析和转捩预测研究。韩忠华等[36]开展了基于线性稳定性理论的双eN方法耦合RANS求解器进行自然层流后掠机翼优化设计的工作。
基于流场当地变量的γ-Reθ转捩模型是由Menter和Langtry等[7]提出的经验预测模型。该模型严格基于流场当地变量构建,与现代CFD方法兼容,在边界层流动转捩模拟中获得了广泛的应用。经典的γ-Reθ模型只能预测流向TS波不稳定性导致的转捩,为了能够预测后掠机翼上横流CF波不稳定性主导的转捩,需要在现有转捩模型的基础上添加横流转捩预测准则。德国宇航院的Krumbein等[37-38]提出了横流雷诺数和当地后掠角的概念,实现了横流雷诺数的当地求解,并进行了C1准则和γ-Reθ模型的耦合研究。韩国的Choi和Kwon等[39]对当地横流雷诺数和当地后掠角的概念进行了讨论,将一些非当地变量用完全当地变量代替,对模型做了进一步改进。国内西北工业大学的徐家宽等[40]开展了基于γ-Reθ模型和C1准则的横流转捩研究。
基于动模态分解的DMD/eN方法是一种新的转捩预测方法,由韩忠华等[8, 41-42]于2017年最新提出。该方法通过DMD[43-46]来进行稳定性分析,并结合eN方法实现转捩预测。DMD/eN方法用于翼型转捩预测与其他转捩预测方法的主要区别是,不需要平行流假设,也不需要求解稳定性或经验关系式方程,而是直接从CFD数值模拟的结果中提取出流动稳定性信息。因此该方法是一种数据驱动的方法。目前该方法已被应用于若干翼型流动转捩预测算例,将计算结果与实验值和其他转捩预测方法的计算结果进行了比较,结果吻合良好,表明该方法具备预测翼型流动转捩的能力。
本文对这三种实用的转捩预测方法进行了详细介绍,展示了所发展方法的有效性,并在原有研究的基础上进一步开展了改进研究,主要工作体现在:1)针对民机后掠机翼的横流转捩问题,对经典γ-Reθ模型添加了当地C1横流转捩预测准则,形成了可以预测流向和横流转捩的三维γ-Reθ-C1模型;2)针对DMD/eN方法中的DMD分析进行了完善,避免了数值误差对转捩位置的影响,进一步增强了该方法的鲁棒性,并通过NLF0416自然层流翼型转捩预测算例进行了验证;3)基于双eN转捩预测方法,开展了设计升力系数为0.5的中短程民机的自然层流机翼减阻优化设计工作,充分展示了该方法的工程实用价值。
1 基于线性稳定性理论的双eN转捩预测方法本文使用多块结构化网格和三维雷诺平均Navier-Stokes方程求解器,耦合边界层方程求解和基于线性稳定性理论的双eN方法,发展了一套可同时计及Tollmien-Schlichting波和横流不稳定性扰动诱导转捩的翼身组合体流动转捩自动判断方法。eN方法的思想是对边界层流动中的小扰动进行线性稳定性分析,如果扰动逐渐衰减,则是稳定的,如果扰动被放大,则是不稳定的。对于不稳定的扰动,从其开始放大处起,沿下游方向计算其累积的线性放大倍数,当累积放大倍数到达扰动开始放大处振幅的eN倍时,认为转捩发生。基于平行流假设的三维小扰动形式为:
| $ q'\left( {x, y, z, t} \right) = \hat q\left( y \right){{\rm{e}}^{-\left( {{\alpha _i}x + {\beta _i}z} \right)}}{{\rm{e}}^{{\rm{i}}\left( {{\alpha _r}x + {\beta _r}z-\omega t} \right)}} $ | (1) |
式中:x、y、z为机翼的非正交贴体坐标系方向;

|
图 1 空间放大理论中扰动波数矢量k与扰动增长矢量A Figure 1 Disturbance wave number vector and disturbance amplification vector in spatial amplification theory |
| $ \begin{array}{l} \psi = \arctan \left( {{\beta _r}/{\alpha _r}} \right)\\ \bar \psi = \arctan \left( {{\beta _i}/{\alpha _i}} \right) \end{array} $ | (2) |
基于线性稳定性理论的eN方法,对机翼边界层信息求解线性稳定性方程,进行扰动累积放大因子的计算,而不对数据库进行查询,因此不存在近似和简化。eN方法进行边界层转捩位置的判断分两步进行:首先,计算中性曲线,即扰动的稳定区域和不稳定区域的分界线。通过中性曲线就可以确定不稳定扰动的频率范围、波数范围和不同扰动各自开始被放大的位置;然后,按照适当的积分策略,对这些频率的扰动放大率从中性曲线下半支出发,沿着扰动传播路径进行积分,得到扰动累积放大因子N。这两步都需要求解三维可压缩线性稳定性方程,其数值求解方法为:(a)采用连续法获得具有较高精确度的特征变量初值;(b)将高阶的线性稳定性控制方程组转化为一阶的控制方程组;(c)采用中心差分方法离散控制方程组;(d)采用牛顿法线化离散后的控制方程组;(e)采用块矩阵消去法求解方程组。
1.1 RANS求解器与转捩预测方法耦合流程采用耦合双eN方法的三维RANS求解器PMNS3D开展面向翼身组合体外形的机翼边界层转捩自动判断方法研究。求解器主要由3个模块构成:1)三维RANS求解器模块。本模块采用多块结构化网格、有限体积法、LU-SGS(Lower-Upper Symmetric Gauss-Seidel)时间推进、多重网格加速收敛技术。湍流流动模拟采用Spalart-Allmaras(S-A)湍流模型。此模块对翼身组合体黏性绕流进行数值模拟,并从计算结果中提取机翼边界层外边界流向速度ue、展向速度we、温度Te等流动参数,作为三维层流边界层方程求解的边界条件;2)三维层流边界层方程求解模块。因直接从RANS方程解提取的层流边界层信息难以满足线性稳定性分析的精度要求,此模块通过非正交贴体坐标系对机翼边界层方程进行求解,可在对网格量没有过高要求的条件下,得到满足三维边界层稳定性分析所需的高精度速度型u、温度型T以及它们在物面法向的一阶导数

|
图 2 RANS求解器耦合转捩预测模型的流程 Figure 2 Coupling structure of RANS solver and transition prediction model |
对于TS波不稳定(TSI)扰动,原有的包络线方法[47]始终寻找扰动放大率最大的波角方向进行积分,如果存在较强的CF波,可能会错误的把CF波扰动积分到NTS中。本文采用固定波角方法计算TS波扰动累积放大因子,即
| $ {N_{{\rm{TS}}}} = \mathop {\max }\limits_{f, \psi = 0} \int_{{x_0}}^x {-{\alpha _i}{\rm{d}}x} $ | (3) |
式中:NTS为TS波扰动累积放大因子;f为TS波频率;x0为中性曲线计算出的小扰动开始放大的x位置。本文采用的固定波角方法,选择扰动波波角ψ= 0°方向即边界层外边界速度方向,计算不同频率f扰动的放大率并进行积分,因此能够保证始终对TS波扰动进行积分,不会混入CF波扰动。
通过后掠角10°和20°的无限翼展机翼边界层转捩预测算例,验证固定波角方法对TS波不稳定扰动主导转捩预测的正确性。计算模型为以NACA642A015翼型为剖面翼型并垂直前缘布置的无限翼展机翼,计算状态和转捩位置所参考的实验数据来自美国NASA Ams研究中心在其12英尺低湍流风洞中开展的相关实验[48]。计算采用结构化C-H网格,网格量为353×105×9。计算马赫数为0.27,雷诺数范围从5×106到25×106,迎角分别固定为0.5°和1°,TS波扰动放大因子转捩阀值取为10.5。图 3~图 6分别给出了后掠角分别为10°和20°时机翼上表面转捩位置计算值与实验值的比较,以及计算压力分布和TS波扰动累积放大因子曲线。可见,采用固定波角方法计算的转捩位置与实验吻合较好,且从扰动累积放大因子曲线可以看出,当机翼上表面出现逆压梯度时,TS波剧烈增长,最终其扰动放大因子达到预设的转捩放大因子10.5,判定转捩发生。通过以上算例可以证明本文将固定波角方法用于TS波诱导边界层流动转捩的预测是十分可靠的。

|
图 3 10°后掠无限翼展NACA642A015机翼上表面计算转捩位置与实验值比较 Figure 3 Calculated transition locations on the upper surface of infinite swept wing (NACA642A015, λ=10°) compared with experiments |

|
图 4 20°后掠无限翼展NACA642A015机翼上表面计算转捩位置与实验值比较 Figure 4 Calculated transition locations on the upper surface of infinite swept wing (NACA642A015, λ=20°) compared with experiments |

|
图 5 10°后掠无限翼展NACA642A015机翼上表面计算压力分布与TS波扰动累积放大曲线 Figure 5 Pressure coefficients and N factors of TSI on the upper surface of infinite swept wing (NACA642A015, λ=10°) |

|
图 6 20°后掠无限翼展NACA642A015机翼上表面计算压力分布与TS波扰动累积放大曲线 Figure 6 Pressure coefficients and N factors of TSI on the upper surface of infinite swept wing(NACA642A015, λ=20°) |
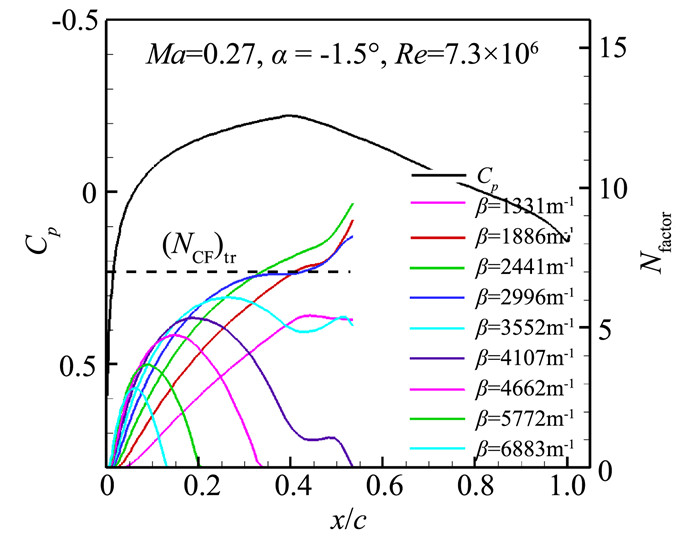
对于CF波不稳定(CFI)扰动诱导的转捩,本文采用固定βr/固定f方法[49]计算CF波扰动累积放大因子,即
| $ {N_{{\rm{CF}}}} = \mathop {\max }\limits_{{\beta _r}, f = 0} \int_{{x_0}}^x {-{\alpha _i}{\rm{d}}x} $ | (4) |
式中:NCF为CF波扰动累积放大因子;βr即横流展向波数;f为横流行波频率,f = 0Hz时则为横流驻波;x0为中性曲线计算出的小扰动开始放大的x位置;αi为x方向的扰动放大率。针对本文中短程民机巡航状态,选择对不同展向波数βr的横流驻波进行扰动放大率的积分,计算横流扰动累积放大因子NCF。对于CF波不稳定扰动,基于平行流假设的线性稳定性理论没有考虑扰动幅值本身的变化,存在一定偏差。根据黄章峰等[35]的研究,线性稳定性方程计算得到的扰动放大增长因子与考虑扰动幅值本身变化的抛物化稳定性方程相比,形态趋势一致但相对偏小。参考此结论,本文采用基于线性稳定性方程预测CF波不稳定诱导的转捩时,采用较小的转捩阀值。
通过后掠角40°和50°的无限翼展机翼边界层转捩预测算例,验证固定βr/固定f方法对CF波不稳定扰动主导的转捩预测的正确性。机翼剖面仍为NACA642A015翼型,计算状态和转捩位置实验值也来自参考文献[48]。计算采用结构化C-H网格,网格量为353×105×9,计算马赫数为0.27,雷诺数范围从4.3×106到7.3×106,迎角为-1.5°,CF波扰动放大因子转捩阀值取为7.0。图 7和图 8给出了计算转捩位置和实验值的比较,吻合较好。本文在CF波扰动计算时仅考虑CF驻波,因此CF波频率固定为0,分别计算不同波数的扰动累积放大因子,图 9和图 10分别给出了40°和50°后掠角计算模型在雷诺数6.1×106时上表面压力分布和CF波扰动累积放大因子曲线,50°后掠角时计算出的CF波扰动增长更快,相对于40°后掠模型,转捩更加靠前。通过以上算例证明将固定βr/固定f方法用于CF波主导的边界层流动转捩预测是可靠的。

|
图 7 40°后掠无限翼展NACA642A015机翼上表面计算转捩位置与实验值比较 Figure 7 Calculated transition locations on the upper surface of infinite swept wing (NACA642A015, λ=40°) compared with experiments |

|
图 8 50°后掠无限翼展NACA642A015机翼上表面计算转捩位置与实验值比较 Figure 8 Calculated transition locations on the upper surface of infinite swept wing (NACA642A015, λ=50°) compared with experiments |
|
图 9 40°后掠无限翼展NACA642A015机翼上表面计算压力分布与CF波扰动累积放大曲线 Figure 9 Pressure coefficients and N factors of CFI on the upper surface of infinite swept wing(NACA642A015, λ=40°) |

|
图 10 50°后掠无限翼展NACA642A015机翼上表面计算压力分布与CF波扰动累积放大曲线 Figure 10 Pressure coefficients and N factors of CFI on the upper surface of infinite swept wing(NACA642A015, λ=50°) |
如前所述,基于线性稳定性理论的eN方法是一种半经验的转捩判断方法,需要与实验转捩位置对比标定N值。研究表明,机翼后掠角不超过20°时,转捩一般为TS波不稳定(TSI)扰动诱导。当机翼后掠角增大时,机翼展向流动增强,产生CF波不稳定(CFI)诱导的横流转捩。一般机翼后掠角大于30°时,边界层发生横流转捩。但是对于实际问题,并不能事先预知是TSI诱导的转捩,还是CFI诱导的转捩。因此,本文采用既能判断TS波不稳定诱导转捩,也能判断CF波不稳定诱导转捩的双eN方法。双eN方法是一种转捩预测方法的构架,可以针对TS波和CF波选择不同的扰动放大率积分策略构建不同的转捩预测方法。对于TS波的扰动放大增长因子NTS,采用固定波角方法计算;对于CF波的扰动放大增长因子NCF,采用固定βr/固定f方法计算。该方法可由公式(5)表示:
| $ \begin{array}{l} {x_{{\rm{tr}}}} = \min \left( {{x_{{\rm{TS}}}}, {x_{{\rm{CF}}}}} \right), \\ \left\{ \begin{array}{l} {x_{{\rm{TS}}}} = x', {\rm{when}}\;\mathop {\max }\limits_{f, \psi = 0} \int_{{x_0}}^{x'} {-{\alpha _{i, {\rm{TS}}}}{\rm{d}}x} = {\left( {{N_{{\rm{TS}}}}} \right)_{{\rm{tr}}}}\\ {x_{{\rm{CF}}}} = x', {\rm{when}}\;\mathop {\max }\limits_{{\beta _r}, f = 0} \int_{{x_0}}^{x'} {-{\alpha _{i, {\rm{CF}}}}{\rm{d}}x} = {\left( {{N_{{\rm{CF}}}}} \right)_{{\rm{tr}}}} \end{array} \right. \end{array} $ | (5) |
根据事先给定的转捩阀值[(NTS)tr, (NCF)tr],确定机翼边界层的转捩位置。如果NTS先到达其对应的阀值(NTS)tr,就认为TS波在xTS处诱导转捩发生;如果NCF先到达其对应的阀值(NCF)tr,则认为边界层流动转捩由CF波在xCF处诱导转捩发生。
本文对原双eN方法[47]进行改进。原双eN方法采用包络线方法计算NTS,改进后的双eN方法采用固定波角方法计算NTS,克服了原双eN方法在存在较强的CF波时,会错误的把CF波扰动积分到NTS中的问题。下面给出一个后掠角为40°的无限翼展机翼算例,说明改进的有效性。计算模型为垂直前缘剖面是NACA642A015翼型的无限翼展机翼,后掠角为40°,马赫数为0.27,雷诺数为7×106,迎角为-1.0°,计算状态和转捩位置实验值也来自参考文献[48]。图 11展示的是使用改进前后的双eN方法计算得到的机翼上表面TS波(虚线)和CF波(实线)不稳定性扰动放大积分因子发展规律。其中,图 11(a)使用原有的双eN方法,判断出的机翼上表面转捩位置在流向19%处,而实验转捩位置为33%,原因是大后掠角时包络线方法对NTS的计算是错误的。图 11(b)使用改进后的双eN方法,判断出的转捩位置在流向37%处,与实验结果吻合较好,证明了改进的有效性。

|
图 11 机翼上表面TS波和CF波不稳定性扰动放大积分因子 Figure 11 N factors of TSI and CFI on upper surface of wing |
采用本文方法,对DLR-F4翼身组合体外形机翼边界层进行自由转捩数值模拟,以验证本文方法对复杂外形绕流转捩判断的正确性。对于翼身组合体等三维复杂外形,如果使用非结构网格,虽没有严格的网格拓扑结构要求,但在计算扰动累积放大因子时,因其相邻网格单元的无序性,需要采取专门的积分路径确定方法[50]。本文针对复杂外形流动,建立了一种便于实现转捩自动判断的,且通用的翼身组合体结构化网格拓扑结构处理方法,对所有翼面类部件均适用,在计算扰动累积放大因子时,积分路径可以直接使用机翼表面网格线,相对非结构网格较为简单便利。具体方法如下:包裹整个机翼(不包含翼梢端面和机翼后缘厚度端面)边界层生成一块完整的C型单块网格,网格块示意图如图 12中线框所示。

|
图 12 DLR-F4翼身组合机外形机翼边界层转捩预测结构网格拓扑结构 Figure 12 Topology of structured grid for boundary layer transition prediction of wing of DLR-F4 wing-body configuration |
对于这块网格,执行图 2中右侧虚线框内的转捩自动判断流程。因为机翼表面流向网格线完整连续,这样在计算扰动累积放大因子时,积分路径可以直接使用机翼表面网格线。如果需要对平尾、垂尾等翼面的边界层进行转捩自动判断,上述方法同样适用。而机身部分则不存在网格拓扑结构的特殊要求,可按照常规方法自由生成网格。
计算状态参考DLR在欧洲跨声速风洞(European Transonic Wind Tunnel,ETW)使用温敏漆(Temperature Sensitive Paint,TSP)技术进行的翼身组合体机翼边界层转捩测量试验[51]:Ma = 0.785,Re = 6.0×106,α=-0.87°。计算网格为多块结构化网格,y+约为0.8,整个翼身组合体网格量为420万,其中包裹机翼的网格块机翼流向分布185个网格点,展向分布49个网格点,法向分布105个网格点。采用S-A湍流模型模拟湍流流动。放大因子转捩阀值[(NTS)tr, (NCF)tr]根据经验取[10.5, 7.5]。
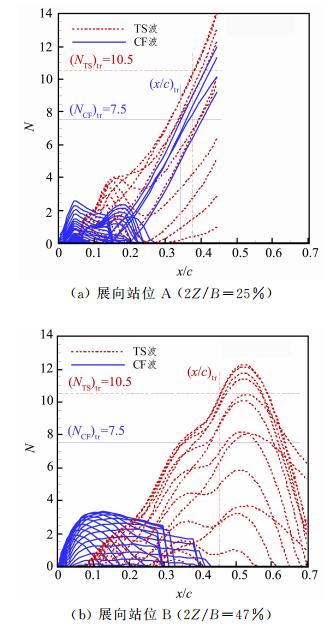
使用本文方法预测的机翼边界层转捩位置与试验对比,如图 13所示,其中云图为TSP试验结果[51],浅色部分为层流区域,深色部分为湍流区域,其中,从机翼前缘拖出的三角形湍流区域是因为机翼表面不光滑造成的湍流楔,并非小扰动引发的自然转捩;黑色实线为本文方法计算得到的机翼上表面转捩线,和试验转捩位置基本一致。Fey等[51]分析试验结果TSP照片认为机翼内段可能为横流驻波不稳定性诱发的转捩。而本文计算结果同样表明,翼根区域为横流驻波不稳定性扰动导致转捩:图 14为展向25%处站位A和47%处站位B的机翼上表面TS波(虚线)和CF波(实线)不稳定性扰动放大积分因子发展规律。由图 14(a)可见,展向站位A在流向x/c=0.34位置处,CF波扰动累积放大因子先于TS波达到其对应阀值,即CF波不稳定性在此站位诱发转捩。而图 14(b)的展向站位B处为TS波不稳定性诱发转捩,转捩位置在流向x/c=0.45位置处。

|
图 13 本文方法对DLR-F4机翼边界层转捩预测结果与TSP试验照片对比 Figure 13 Transition line on upper surface of DLR-F4 wing predicted by proposed method and TSP image |
|
图 14 机翼上表面TS波和CF波不稳定性扰动放大积分因子 Figure 14 N factors of TSI and CFI on upper surface of wing |
此算例表明,本文发展的双eN方法不仅能够对机翼边界层转捩位置进行较为准确的预测,同时能够判断出机翼内段转捩是由横流不稳定性主导的机理,与TSP试验结果分析[51]研究结论一致。验证了本文方法的正确性,说明本文发展的方法,针对翼身组合体复杂外形,能够实现对机翼边界层的转捩自动判断。
2 基于流场当地变量的γ-Reθ转捩预测模型经典γ-Reθ转捩模型是Menter和Lantry等[7]于2004年提出的基于流场当地变量和经验关系式的转捩预测模型,包含两个输运方程,如下:
| $ \rho \frac{{\partial \gamma }}{{\partial t}} + \rho {U_j}\frac{{\partial \gamma }}{{\partial {x_j}}} = {P_r}- {E_r} + \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _f}}}} \right)\frac{{\partial \gamma }}{{\partial {x_j}}}} \right] $ | (6) |
| $ \begin{array}{l} \rho \frac{{\partial \overline {\mathit{R}{\mathit{e}_{\theta t}}} }}{{\partial t}} + \rho {U_j}\frac{{\partial \overline {\mathit{R}{\mathit{e}_{\theta t}}} }}{{\partial {x_j}}} = \\ \;\;\;\;{P_{\theta t}} + \frac{\partial }{{\partial {x_j}}}\left[{{\sigma _{\theta t}}\left( {\mu + {\mu _t}} \right)\frac{{\partial \overline {\mathit{R}{\mathit{e}_{\theta t}}} }}{{\partial {x_j}}}} \right] \end{array} $ | (7) |
其中,间歇因子γ表示流动处于湍流和层流的时间比例,通过和湍流模型进行耦合,控制湍动能的生成,从而模拟转捩的发生。
针对经典γ-Reθ模型无法预测横流转捩的问题,本文做出以下改进:在经典γ-Reθ模型的基础上引入横流C1准则,发展了一种可以预测流向和横流转捩的γ-Reθ-C1三维转捩模型。
2.1 基于当地C1准则的横流转捩预测模型横流C1准则是由法国宇航院的Arnal等[52]基于大量的实验数据,归纳总结提出的关于临界横流位移厚度雷诺数Reδ2t和边界层形状因子H12的经验准则。C1准则可以表示为:
| $ \mathit{R}{\mathit{e}_{\delta 2t}} = \left\{ \begin{array}{l} \frac{{300}}{{\rm{ \mathsf{ π} }}}{\tan ^{- 1}}\left[{\frac{{0.106}}{{{{\left( {{H_{12}}-2.3} \right)}^{2.05}}}}} \right], 2.3 \le {H_{12}} \le 2.7\\ 150.0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{H_{12}} < 2.3 \end{array} \right. $ | (8) |
当横流位移厚度雷诺数Reδ2>Reδ2t时,认为转捩发生。Reδ2的表达式为:
| $ \mathit{R}{\mathit{e}_{\delta 2}} = \frac{{\rho {Q_e}{\delta _2}}}{\mu }, \;\;\;\;\;{\delta _2} = \int\limits_0^\infty {\frac{{\left| {0-w} \right|}}{{{Q_e}}}{\rm{d}}y} $ | (9) |
其中δ2是边界层横流位移厚度,Qe是三维边界层外边界的势流速度,w是横流速度。
由于Reδ2和Reδ2t的求解需要沿边界层法向积分操作,增加了计算的难度和计算量,需对C1准则进行当地化改造。通过求解三维边界层的Falkner-Skan-Cooke相似性方程,可以建立Hartree参数βH、压力梯度因子λθ、形状因子H12和当地后掠角φ(当地压力梯度方向和当地速度方向的夹角)之间相互关系的数据库(可参考文献[53]),其中λθ在经典γ-Reθ模型中是和
| $ \begin{array}{l} \mathit{R}{\mathit{e}_{\delta 2}} = \frac{{\mathit{R}{\mathit{e}_w}}}{{f\left( {{\lambda _\theta }, \varphi } \right)}}\\ \mathit{R}{\mathit{e}_{\delta 2t}} = g\left( {{H_{12}}} \right) = g\left( {{\lambda _\theta }, \varphi } \right) \end{array} $ | (10) |
其中,
将当地C1准则作为横流转捩判据加入γ-Reθ模型间歇因子输送方程的源项,形成γ-Reθ-C1三维转捩模型。间歇因子输送方程的源项修改为:
| $ {P_{\gamma \_3D}} = {F_{{\rm{length}}}}{c_{a1}}\rho S{\left( {\gamma {F_{{\rm{onset\_3}}D}}} \right)^{0.5}}\left( {1-{c_{e1}}\gamma } \right) $ | (11) |
其中Fonset_3D的表达式为:
| $ \left\{ \begin{array}{l} {F_{{\rm{onset1\_TS}}}} = \frac{{\mathit{R}{\mathit{e}_v}}}{{2.193\mathit{R}{\mathit{e}_{\theta c}}}}, {F_{{\rm{onset1\_}}C1}} = \frac{{\mathit{R}{\mathit{e}_w}}}{{f\left( {{\lambda _\theta }, \varphi } \right)\mathit{R}{\mathit{e}_{\delta 2t}}}}\\ {F_{{\rm{onset1\_3D}}}} = \max \left( {{F_{{\rm{onset1\_TS}}}}, {F_{{\rm{onset1\_C1}}}}} \right)\\ {F_{{\rm{onset2\_3D}}}} = \min \left( {\max \left( {{F_{{\rm{onset1\_3D}}}}, F_{{\rm{onset1\_3D}}}^4} \right), 2.0} \right)\\ {F_{{\rm{onset3\_3D}}}} = \max \left( {1-{{\left( {\frac{{RT}}{{2.5}}} \right)}^3}, 0.0} \right)\\ {F_{{\rm{onset\_3D}}}} = \max \left( {{F_{{\rm{onset}}2\_3{\rm{D}}}}-{F_{{\rm{onset}}3\_3{\rm{D}}}}, 0.0} \right) \end{array} \right. $ | (12) |
图 15说明了γ-Reθ-C1转捩模型和RANS方程求解的耦合过程。

|
图 15 RANS求解器耦合γ-Reθ-C1转捩模型的流程 Figure 15 Coupling structure of RANS solver and γ-Reθ-C1 transition prediction model |
选取了镰刀形机翼算例来验证耦合横流转捩准则的γ-Reθ-C1转捩模型的正确性。镰刀形机翼[54]是专门设计用来验证横流转捩预测方法的一副机翼,分为不同后掠角的几段,从翼根到翼梢的前缘后掠角分别是0°、30°、45°和55°。由于在每一段的前缘后掠角保持不变,镰刀形机翼很适合对基于Falkner-Skan-Cooke相似性方程解的当地C1准则进行验证。不仅如此,在机翼各分段之间的拐折处的横流效应明显,会导致由横流不稳定造成的前缘转捩,对横流转捩预测方法的适用性要求很高。实验在布伦瑞克德国宇航院的低湍流度闭环风洞中进行[54],风洞湍流度为0.17%,自由来流风速55 m/s,单位弦长雷诺数为2.75×106。机翼无后掠部分的弦长为0.8m,迎角-2.6°,平均表面粗糙度为9.78μm。
采用γ-Reθ-C1模型对镰刀机翼上表面的横流转捩进行模拟,计算状态为Ma=0.162, Re=2.2×106, α=-2.6°, Tu=0.3%, RT=3。表面网格如图 16所示,计算网格的网格量为400万,壁面第一层网格高度5×10-6,保证y+小于1。

|
图 16 镰刀机翼几何模型和表面网格 Figure 16 Sickle wing geometric model and surface grid |
计算得到的表面摩擦系数云图如图 17所示,可以看出,相比于不能预测横流转捩的经典γ-Reθ模型,γ-Reθ-C1模型能够捕捉到后掠段的横流转捩,也能够捕捉到拐折处由于横流不稳定导致的前缘转捩尖角,说明γ-Reθ-C1模型在进行复杂机翼外形的横流转捩预测时适用性较强。但γ-Reθ-C1模型对于后掠角30°分段的转捩位置预测仍不够精确,预测的转捩位置和实验转捩位置相比稍微靠前,需要进一步的研究和改进。总体来说,γ-Reθ-C1模型对机翼外形的横流流动转捩能够进行较好的模拟。

|
图 17 γ-Reθ-C1模型计算得到的镰刀机翼上表面的表面摩擦系数云图 Figure 17 Calculated surface friction coefficient contour of the upper surface over sickle wing |
该部分对DMD方法的实现过程进行简要介绍。DMD理论的详细介绍可参见参考文献[43]。
将从数值计算中获得的流场数据表示成下面快照序列的形式:
| $ \mathit{\boldsymbol{V}}_1^n = \left\{ {{v_1}, {v_2}, {v_3}, \cdots, {v_n}} \right\} $ | (13) |
其中,n为快照数;V1n是流场快照矩阵,相邻两个快照之间的空间间隔(Δx)相同。
假设整个抽样空间中两个相邻的流场快照vi和vi+1可以由线性变化A联系起来:
| $ {\mathit{\boldsymbol{v}}_{i + 1}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_i} $ | (14) |
因此,流动序列表示为如下矩阵形式:
| $ \mathit{\boldsymbol{A}}V_1^{n-1} = \mathit{\boldsymbol{V}}_2^n $ | (15) |
其中,矩阵A是一个反应流场内在动力学机制,且具体形式未知的高维矩阵,所以DMD方法采一个低维满秩矩阵
下面简述满秩矩阵
对由流场快照组成的矩阵
| $ \mathit{\boldsymbol{V}}_1^{n-1} = \mathit{\boldsymbol{U}}\mathit{\Sigma }{\mathit{\boldsymbol{W}}^{\rm{T}}} $ | (16) |
将式(16)代入式(15),并在式(16)两端左乘UT和右乘以WΣ-1得到:
| $ {\mathit{\boldsymbol{U}}^T}\mathit{\boldsymbol{V}}_2^n\mathit{\boldsymbol{W}}{\mathit{\Sigma }^{-1}} = {\mathit{\boldsymbol{U}}^T}\mathit{\boldsymbol{AU}} \equiv \mathit{\boldsymbol{\tilde S}} $ | (17) |
这样就得到了满秩矩阵
在原始的方法中[8, 41-42],矩阵V1n-1分解结果为
随后求
对DMD得到的A的特征值进行对数映射,得到空间模式下的特征值:
| $ \lambda = \lg \mu /\Delta x = {\lambda _{{\rm{re}}}} + {\lambda _{{\rm{im}}}}{\rm{i}} $ | (18) |
其中,λre是指数放大率或衰减率,λim是空间波数,i表示虚数(i2=-1)。
3.2 DMD/eN转捩预测方法本文提出将DMD方法和eN转捩方法结合的过程如下:
1) 以驻点为起点,沿弧长s对上、下表面的流场数据进行划分。我们将翼型表面分成L段,如图 18所示。根据理论分析和经验,我们取L=10。则(0~0.1)s/c为第1段,(0~0.2)s/c为第2段,以此类推(这里的c为无量纲化为1的翼型弦长);

|
图 18 翼型表面分段示意图 Figure 18 Schematic of segments to perform DMD analysis |
2) 沿翼型流向进行推进求解,对翼型表面每一段的流场数据进行DMD计算,得到该段的稳定性特征值;
3) 确定有效特征值。本文采用两种快照数对某段流场进行DMD分析,选择不稳定特征值(λi, λr)中重叠性最好的特征值分别作为各自流场快照数在本段的有效特征值,对应的模态即是本段的特征模态。研究中发现数值噪声对DMD分析的结果影响较大,在这里选取重叠性最好的特征值的目的是为了避免数值噪声干扰。由于不同快照的特征值中重叠最好的两个也存在些微小差异(并不是完全重合),故我们以流场快照数多的结果为准;
4) N因子计算方法如公式(19)所示。即对DMD分析得到的空间放大率乘以对应段的长度,得到翼型表面每段对应的扰动放大因子Ni(下标i为段标号);
| $ {N_i} = {s_i} \times {\lambda _{{\rm{ri}}}} $ | (19) |
5) 找出Ni超过转捩阀值Ncrit时对应的段标号,记为s;连接该段及以前每段末的扰动放大因子N1、N2、……、Ns,得到一条类似包络线的N值增长曲线,如图 19所示。在该曲线上线性插值得到转捩阀值对应的弧长位置s/c,再通过比较翼型表面网格点弧长与弦长的对应关系,插值得到对应的转捩点弦长位置x/c。

|
图 19 N因子积分示意图 Figure 19 Diagram of N factor integration |
以上为DMD/eN方法[8, 41-42]的实现步骤,下面将该方法与RANS求解器进行耦合。图 20为绕翼型定常流动的转捩预测过程。首先,采用RANS求解器对绕翼型的流动进行固定转捩数值模拟,需选取足够靠后的初始转捩位置,保证流场充分收敛;其次,提取层流边界层内部的速度信息,形成用于DMD分析的流场快照;而后,采用DMD/eN方法进行流动转捩预测;最后,将判断的转捩点位置回带到RANS求解器进行迭代,直至得到收敛的结果。

|
图 20 N-S求解器与DMD/eN方法耦合转捩预测示意图 Figure 20 Diagram of transition prediction using N-S solver coupling with DMD/eN method |
开展不同迎角下NLF0416翼型的转捩预测计算对该方法进行验证。计算状态是Ma=0.1, Re=4×106。转捩后的湍流区域采用SA湍流模型。NLF0416翼型计算网格如图 21所示,计算网格量为641×241,第一层网格高度1×10-6c。下面以迎角α=1°为例,较为详细地展示计算结果。

|
图 21 NLF0416翼型计算网格 Figure 21 Computational grids of NFL0416 airfoil |
采用总快照数100和200对翼型表面进行DMD分析,分别计算出上、下表面的N值增长。将推进求解中N值达到阀值及之前段的N值表示为随x方向变化的曲线,并与LST/eN方法的N值增长曲线进行对比,如图 22和图 23所示。根据以往的经验,在利用eN方法进行NLF0416翼型流动的转捩预测时,阀值N取为6较为合适。由图可见,上表面DMD/eN方法推进求解得到的N值增长曲线与LST/eN方法的包络线吻合很好,而下表面DMD/eN方法的N值比LST/eN方法增长要早,但总体趋势是可比的。

|
图 22 NLF0416翼型上表面DMD/eN与LST/eN方法的N值增长对比图(α=1°) Figure 22 Comparison of N growth between DMD/eN and LST/eN method on upper surface of NLF0416 airfoil |

|
图 23 NLF0416翼型下表面DMD/eN与LST/eN方法的N值增长对比图(α=1°) Figure 23 Comparison of N growth between DMD/eN and LST/eN method on lower surface of NLF0416 airfoil |
表 1为DMD/eN方法与LST/eN方法计算得到的上、下表面转捩点位置与实验值的对比。实验测出了翼型表面层流与湍流区的位置,转捩发生在两者之间。由表可知,上表面DMD/eN方法计算的转捩点位置比LST/eN方法更接近实验值,但两者都比实验值稍靠前。下表面两者均在层流点到湍流点之间,与实验值吻合良好。
| 表 1 NLF0416翼型上/下表面转捩点位置计算与实验值比较(α=1°) Table 1 Comparison of predicted transition location with experimental data on upper/lower surface of NLF0416 airfoil (α=1°) |
|
|
由于层流粘性系数远小于湍流粘性系数,故这两种流态下翼型表面的摩擦阻力差异很大。图 24为NLF0416翼型全湍流和自由转捩状态下的物面摩擦力系数分布图。其中,黑色虚线是全湍流模拟的摩阻系数,蓝色点画线和红色实线是考虑转捩的分别采用LST/eN和DMD/eN方法计算得出的结果。可见,LST/eN和DMD/eN两种方法得到的摩阻系数分布吻合良好。翼型上、下表面对应的摩阻系数分别在各自转捩点附近有一个突增,对应位置在0.33和0.5左右。转捩点之前为层流,全湍流模拟的Cf远大于自由转捩的结果,而转捩点之后进入湍流,两者Cf的值开始逐步接近。

|
图 24 NLF0416翼型全湍流与自由转捩表面摩擦力系数对比图 Figure 24 Comparison of skin friction (Cf) for NLF0416 airfoil between full turbulence and free transition |
以上迎角1°的算例较为详细的展示了DMD/eN方法对NLF0416翼型的转捩预测结果,验证了本文方法的正确性。下面,将对-6°~6°中的多个迎角状态的NLF0416翼型绕流进行转捩点预测,并与实验值、文献[55]及LST/eN方法的计算结果进行对比。
图 25和图 26给出了NLF0416翼型上、下表面采用以上三种方法计算得到的转捩点随迎角的变化曲线。其中,黑色空心点和实心点分别为实验测得的层流和湍流位置;蓝色、红色、绿色线分别代表文献[55]、DMD/eN方法和LST/eN方法计算得到的转捩点位置所连成的曲线;Xtr_up和Xtr_low分别代表翼型上、下表面的转捩点位置。由图 25可见,随着迎角的增大,上表面转捩点逐步向翼型前缘移动。DMD/eN的计算结果基本位于层流和湍流点之间,且和文献结果符合较好,而LST/eN方法计算的结果比实验值略靠前。由图 26可知,不同迎角下三种方法的转捩点计算结果均符合较好,且变化趋势一致,进一步验证了本文方法的正确性。可见随着迎角的增大,下表面转捩点向翼型后缘移动。这是由于随着迎角的增加,下表面作为压力面,顺压梯度增加,更易保持层流,故转捩点后移。上表面的规律与之相反,但原理是类似的。

|
图 25 NLF0416翼型上表面转捩点位置随迎角的变化 Figure 25 Variations of transition location along with the angles of attack on upper surface of NLF0416 airfoil |

|
图 26 NLF0416翼型下表面转捩点位置随迎角的变化 Figure 26 Variations of transition location along with the angles of attack on lower surface of NLF0416 airfoil |
综上,NLF0416翼型不同迎角下的转捩预测结果与实验结果吻合良好,验证了本文发展DMD/eN转捩预测方法的正确性。
4 转捩预测方法在中短程民机机翼减阻设计中的应用为了证明本文所述转捩预测方法的实用性,以双eN转捩预测方法为例,将该转捩预测方法添加到RANS方程求解器中,并在此基础上利用自主发展的优化平台SurroOpt[56]开展跨声速自然层流机翼优化设计研究工作。
目前,在现代民用客机跨声速高雷诺数的典型飞行状态下,为保持翼面大范围层流流动,既要求机翼前缘后掠角尽量小于20°,又要求上翼面前部分具有适当顺压梯度。而在相同飞行速度下,以上两方面设计均会导致翼面激波的增强,从而部分抵消增大层流范围带来的减阻效果。由此可见,应用于现代客机的跨声速自然层流机翼气动设计难点在于如何在保持大范围翼面层流面积的同时保持较小的激波强度。
经过仔细考虑,本节首先配置了适用于现代中短程民机的自然层流机翼,该机翼的剖面翼型为顺气流布置的自然层流超临界翼型NPU-LSC-72613,该翼型设计状态为Ma=0.72,Re=2.0×107,CL=0.6,该状态下翼型压力分布如图 27。机翼几何尺寸和设计状态参考了空客A320相关数据,机翼面积123 m2,展长为35 m,展弦比为10.5,梢根比为0.3,前缘后掠角为19°,翼根和翼尖扭转分别为0°和-2°,基于平均气动弦长的无量纲机翼几何形状由图 28给出。初始机翼的设计巡航状态为Ma=0.75,Re=2.0×107,CL=0.5。本节首先在设计状态下对初始机翼进行考虑转捩影响的绕流数值模拟计算,计算网格为C-H型结构化网格,大小为257×105×73,其中机翼表面流向布置200个网格,展向布置48个网格,如图 29所示。扰动放大因子转捩阀值取[(NTS)tr, (NCF)tr]=[9.0, 8.5]。

|
图 27 NPU-LSC-72613翼型在设计状态下的压力分布(Ma=0.72, Re=2.0×107,CL=0.6) Figure 27 Pressure coefficients of the NPU-LSC-72613 airfoil at Ma=0.72, Re=2.0×107, CL=0.6 |

|
图 28 适用于中短程民机的机翼平面形状 Figure 28 Wing geometry for the short-to mid-range aircraft |

|
图 29 针对中短程民机的机翼C-H结构化网格示意图 Figure 29 C-H structured grid for the wing geometry of the short-to mid-range aircraft |
图 30(a)给出了设计状态下初始机翼的压力分布和上/下表面转捩线。可以看出,机翼上表面虽然保持了大范围的层流流动,但是产生了很强的激波;而机翼下表面靠近翼根处层流范围急剧减小。

|
图 30 初始机翼和优化机翼上表面压力云图对比 Figure 30 Pressure coefficient contours on upper surface of the baseline and the optimum wing |
为了减小机翼阻力,提升气动性能,在设计状态Ma=0.75,Re=2.0×107,α=1.76°下开展机翼的优化设计工作。公式(20)给出了具体的优化目标和约束表达式,优化过程中保持初始迎角不变,优化目标是最小化机翼总阻力,约束为保持机翼的升力系数不小于原升力,力矩绝对值不增大,同时,为保持机翼内部容积,翼根(标记为r)和35%展向位置(标记为k)处翼型相对厚度不减,翼尖位置(标记为t)翼型相对厚度不小于12%。
| $ \begin{array}{l} {\rm{Min}}\;\;\;\;\;\;\;{C_D}\\ {\rm{W}}.{\rm{r}}.{\rm{t}}\;\;\;\;\;\;x \in \left[{-0.2, 0.2} \right]\\ {\rm{S}}.{\rm{t}}.\;\;\;\;\;\;\;\;\;{C_L} \ge {C_{L0}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left| {{C_M}} \right| \le \left| {{C_{M0}}} \right|\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {t/c} \right)_{r, k}} \ge {\left( {t/c} \right)_{r0}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {t/c} \right)_t} \ge 12\% \end{array} $ | (20) |
经过400次CFD计算,优化收敛。最终机翼阻力下降了11.3框(counts),且在优化机翼处,阻力系数的代理模型预测值与真实CFD计算值的相对误差仅有0.05%,说明代理模型在最优点附近空间内已经十分精确。图 31给出了优化收敛历程,可见优化目标阻力系数为117.3框,而初始机翼在该状态下阻力系数为128.6框,阻力降低了8.8%。表 2和表 3给出了优化前后机翼力系数和控制剖面相对厚度的比较,可见相比于初始机翼,优化机翼的阻力系数下降了11.3框,其中摩擦力系数下降1.6框,压差阻力下降9.7框,而升力保持不变,力矩系数绝对值减小,机翼相对厚度约束严格满足。

|
图 31 适用于中短程民机的机翼优化设计收敛曲线 Figure 31 Convergence history of the optimization process |
| 表 2 优化前后机翼气动力系数比较 Table 2 Comparisons of aerodynamic coefficients between the baseline and the optimum wing |
|
|
| 表 3 优化前后机翼不同展向位置处相对厚度比较 Table 3 Comparisons of relative thicknesses between the baseline and the optimum wing |
|
|
图 30给出了优化前后机翼上翼面压力分布云图以及上/下翼面转捩线位置。在上翼面,初始机翼已经有大范围层流流动(占机翼上表面约62.5%),而优化机翼较好地保持了这一优良特性,层流流动覆盖57.8%,且很大程度上减弱了激波强度;在下翼面,初始机翼翼根部分出现了由三维边界层内横流扰动诱导的前缘转捩,而优化机翼有效地抑制了CF波诱导的翼根位置提前转捩,从而显著推迟层流向湍流的自然转捩,将机翼下翼面翼根位置层流范围从初始机翼靠近前缘点处扩大到54.8%。图 32给出了优化前后机翼典型展向站位截面压力分布及转捩位置比较。可见,初始机翼设计中为稳定边界层内TS波,采用了较大的顺压梯度,导致了较高波前马赫数,从而产生较强激波,所以尽管实现了翼面大范围的层流流动,激波阻力的增加抵消了部分层流减阻的效果。优化机翼则将上翼面顺压梯度保持在合适的强度,这样既能稳定边界层内TS波的发展,又不至于产生较强的激波,从而实现机翼总阻力的降低。而在展向15%站位处,可观察到优化机翼下表面在前缘加速区后保持一段变化缓慢的压力区,实现了前缘转捩的推迟。

|
图 32 初始和优化机翼典型展向位置截面压力分布对比 Figure 32 Pressure coefficient comparisons of the baseline and the optimum wing at typical spanwise stations |
以上不难看出,将双eN转捩预测方法与RANS方程求解器进行耦合,可以有效地预测TS波和CF波导致的转捩,进而推动层流机翼设计工作的进行,同时证明了发展的转捩预测方法有很好的工程实用价值。
5 结论本文对面向层流减阻设计的转捩预测方法进行了研究,得出如下结论:
1) 将求解线性稳定性方程的双eN转捩预测方法推广到了三维复杂外形。DLR-F4翼身组合体算例表明,本文发展的针对三维复杂外形的转捩自动判断方法可同时计及TS波和CF波扰动诱导的转捩,较为准确的判断转捩位置,且能够正确判断转捩诱发机制。
2) 实现了当地C1横流转捩准则和经典γ-Reθ模型的耦合,形成了γ-Reθ-C1三维转捩模型。利用该模型较为准确的预测了镰刀形机翼表面的转捩位置,表明其具有良好的工程应用前景。
3) 改进的DMD/eN转捩预测方法可用于翼型流动转捩判断,计算的转捩位置与实验值吻合良好,展现出较好的工程应用价值,可作为层流减阻设计的有力工具。
4) 以双eN方法的工程应用为例,利用该转捩预测方法,同时结合代理优化方法,开展了针对中短程民机的跨声速层流机翼优化设计研究。最终结果表明,相对于基准机翼,优化机翼减阻效果明显,设计点气动性能有很大提升,证明了本文发展的转捩预测方法鲁棒可靠,有很高的工程应用价值。
| [1] |
Fu S, Wang L. Progress in turbulence/transition modelling[J]. Advances in Mechacics, 2007, 37(3): 409-416. (in Chinese) 符松, 王亮. 湍流转捩模式研究进展[J]. 力学进展, 2007, 37(3): 409-416. DOI:10.6052/1000-0992-2007-3-J2006-159 (  0) 0) |
| [2] |
Zhou H. Studies on transition and turbulence[C]//2003 Advanced Research Papers on Aerodynamics. Beijing: Aerodynamic society of China, 2003: 87-93. (in Chinese) 周恒. 关于转捩和湍流的研究[C]//2003空气动力学前沿研究论文集. 北京: 中国空气动力学会, 2003: 87-93. (  0) 0) |
| [3] |
Seitz A, Kruse M, Wunderlich T, et al. The DLR Project LamAiR: design of a NLF forward sweep wing for short and medium range transport application[C]//29th AIAA Applied Aerodynamics Conferences, AIAA-2011-3526, 2011. https://link.springer.com/chapter/10.1007/978-3-319-64519-3_18
(  0) 0) |
| [4] |
Urbin G, Knight D. Large-eddy simulation of a supersonic boundary layer using an unstructured grid[J]. AIAA Journal, 2001, 39(7): 1288-1295. DOI:10.2514/2.1471 (  0) 0) |
| [5] |
Schlatter S. Assessment of direct numerical simulation data of turbulent boundary layers[J]. Journal of Fluid Mechanics, 2010, 659: 116-126. DOI:10.1017/S0022112010003113 (  0) 0) |
| [6] |
Krumbein A, Krimmelbein N, Grabe C. Streamline-based transition prediction techniques in an unstructured computational fluid dynamics code[J]. AIAA Journal, 2017, 55(5): 1548-1564. DOI:10.2514/1.J054990 (  0) 0) |
| [7] |
Menter F R, Langtry R B, Likki S R, et al. A correlation-based transition model using local variables:part I-model formulation[J]. Journal of Turbomachinery, 2004, 128(3): 413-422. (  0) 0) |
| [8] |
Han z h, Wang S N, Han L, et al. Transition prediction based ondynamic mode decomposition for flows over airfoils[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 120034-1. (in Chinese) 韩忠华, 王绍楠, 韩莉, 等. 一种基于动模态分解的翼型转捩预测新方法[J]. 航空学报, 2017, 38(1): 120034-1. (  0) 0) |
| [9] |
Smith A M O, Gamberoni N. Transition, pressure gradient and stability theory[M]. Long Beach: Douglas Aircraft Company, 1956.
(  0) 0) |
| [10] |
Ingen J L V. A suggested semi-empirical method for the calculation of the boundary layer transition region. VTH-74[R]. Delft: Delft University of Technology, 1956. https://link.springer.com/content/pdf/10.1007%2F978-1-4612-4724-1_1.pdf
(  0) 0) |
| [11] |
Drela M. Newton solution of coupled viscous/inviscid multielement airfoil flows[C]//21st Fluid Dynamics, Plasma Dynamics and Lasers Conference. 1990: 1470. https://link.springer.com/chapter/10.1007/978-3-319-27279-5_26
(  0) 0) |
| [12] |
Cebeci T, Stewartson K. On stability and transition in three-dimensional flows[J]. AIAA Journal, 1980, 18(4): 398-405. DOI:10.2514/3.50772 (  0) 0) |
| [13] |
Malik M R. COSAL: A black-box compressible stability analysis code for transition prediction in three-dimensional boundary layers. NASA-CR-165925[R]. Washington D C: NASA, 1982 http://www.worldcat.org/title/cosal-a-black-box-compressible-stability-analysis-code-for-transition-prediction-in-three-dimensional-boundary-layers/oclc/11673405
(  0) 0) |
| [14] |
Mack L M. Stability of three-dimensional boundary layers on swept wings at transonic speeds[C]//IUTAM. Symposium Transsonicum Ⅲ. Berlin Heidelberg: Springer, 1989: 209-223. https://link.springer.com/chapter/10.1007/978-3-642-83584-1_18
(  0) 0) |
| [15] |
Arnal D. Transition prediction in transonic flow[C]//IUTAM. Symposium Transsonicum Ⅲ. Berlin Heidelberg: Springer, 1989: 253-262. http://www.springer.com/us/book/9783642835865
(  0) 0) |
| [16] |
Arnal D, Casalis G, Juillen J C. Experimental and theoretical analysis of natural transition on "infinite" swept wing[C]//IUTAM. Laminar-Turbulent Transition. Berlin Heidelberg: Springer, 1990: 311-325.
(  0) 0) |
| [17] |
Radespiel R, Graage K, Brodersen O. Transition predictions using Reynolds-averaged Navier-Stokes and linear stability analysis methods. AIAA-1991-1641[R]. Reston: AIAA, 1991. https://link.springer.com/chapter/10.1007/978-3-540-33287-9_24
(  0) 0) |
| [18] |
Casalis G, Arnal D. ELFIN Ⅱ subtask 2. 3: Database method-Development and validation of the simplified method for pure cross-flow instability at low speed: ELFIN Ⅱ-145[R]. Toulouse: ONERA-CERT, 1996.
(  0) 0) |
| [19] |
Stock H W, Haase W. Feasibility study ofeN transition prediction in Navier-Stokes methods for airfoils[J]. AIAA Journal, 1999, 37(10): 1187-1196. DOI:10.2514/2.612 (  0) 0) |
| [20] |
Nebel C, Radespiel R, Wolf T. Transition prediction for 3D flows using a Reynolds-averaged Navier-Stokes code and N-factor methods. AIAA-2003-3593[R]. Reston: AIAA, 2003. https://link.springer.com/chapter/10.1007/3-540-32382-1_18
(  0) 0) |
| [21] |
Krumbein A. Automatic transition prediction and application to high-lift multi-element configurations. AIAA-2004-2543[R]. Reston: AIAA, 2004. https://www.sciencedirect.com/science/article/pii/S1270963808000254
(  0) 0) |
| [22] |
Stock H W. Infinite swept wingNavier-Stokes computations with eN transition prediction[J]. AIAA Journal, 2005, 43(6): 1221-1229. DOI:10.2514/1.12487 (  0) 0) |
| [23] |
Krumbein A. Automatic transition prediction and application to 3D wing configurations. AIAA-2006-0914[R]. Reston: AIAA, 2006. http://elib.dlr.de/view/type/conference=5Fitem/2005.html
(  0) 0) |
| [24] |
Cliquetj, Houdeville R, Arnal D. Application of laminar-turbulent transition criteria in Navier-Stokes computations. AIAA-2007-515[R]. Reston: AIAA, 2007.
(  0) 0) |
| [25] |
Krumbein A. eN transition prediction for 3D wing configurations using database methods and a local, linear stability code[J]. Aerospace Science and Technology, 2008, 12(8): 592-598. DOI:10.1016/j.ast.2008.01.005 (  0) 0) |
| [26] |
Perraud J, Arnal D, Casalis G, Archambaud J P, Donelli R. Automatic transition predictions using simplified methods[J]. AIAA Journal, 2009, 47(11): 2676-2684. DOI:10.2514/1.42990 (  0) 0) |
| [27] |
Perraudj, Cliquet J, Houdeville R, et al. Transport aircraft three-dimensional high-lift wing numerical transition prediction[J]. Journal of Aircraft, 2008, 45(5): 1554-1563. DOI:10.2514/1.32529 (  0) 0) |
| [28] |
Krumbein A. Automatic transition prediction and application to 3D high-lift configurations. AIAA-2006-3164[R]. Reston: AIAA, 2006. https://link.springer.com/chapter/10.1007/978-3-642-14243-7_13
(  0) 0) |
| [29] |
Krimmelbein N, Radespiel R, Nebel C. Numerical aspects of transition prediction for three-dimensional configurations. AIAA-2005-4764[R]. Reston: AIAA, 2005. https://rd.springer.com/chapter/10.1007/978-3-642-04093-1_7
(  0) 0) |
| [30] |
Lee J D, Jameson A. Natural-laminar-flow airfoil and wing design byadjoint method and automatic transition prediction. AIAA-2009-897[R]. Reston: AIAA, 2009.
(  0) 0) |
| [31] |
Zhang K, Song W P. Application of the full eN transition method to the infinite swept-wing's transition prediction[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 142-147. (in Chinese) 张坤, 宋文萍. eN方法在无限展长后掠翼边界层转捩预测中的初步应用[J]. 西北工业大学学报, 2011, 29(1): 142-147. (  0) 0) |
| [32] |
Zuo S H, Yang Y, Li D. Investigation on cross-flow instabilities in swept-wing boundary layers with linear parabolized stability equations[J]. Chinese Journal of Computational Physics, 2010, 27(5): 665-670. (in Chinese) 左岁寒, 杨永, 李栋. 基于线性抛物化稳定性方程的后掠翼边界层内横流稳定性研究[J]. 计算物理, 2010, 27(5): 665-670. (  0) 0) |
| [33] |
Sun P P, Huang Z F. Effect of sweep angle on stability and transition in a swept-wing boundary layer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(7): 1313-1321. (in Chinese) 孙朋朋, 黄章峰. 后掠角对后掠机翼边界层稳定性及转捩的影响[J]. 北京航空航天大学学报, 2015, 41(7): 1313-1321. (  0) 0) |
| [34] |
Jing Z R, Sun P P, Huang Z F. Effect of attack angle on stability and transition in a swept-wing boundary layer[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2177-2183. (in Chinese) 靖振荣, 孙朋朋, 黄章峰. 小迎角对后掠机翼边界层稳定性及转捩的影响[J]. 北京航空航天大学学报, 2015, 41(11): 2177-2183. (  0) 0) |
| [35] |
Huang Z F, Lu X Z, Yu G T. Cross-flow instability analysis and transition prediction of airfoil boundary layer[J]. Acta Aerodynamica Sinica, 2014, 32(1): 14-20. (in Chinese) 黄章峰, 逯学志, 于高通. 机翼边界层的横流稳定性分析和转捩预测[J]. 空气动力学学报, 2014, 32(1): 14-20. DOI:10.7638/kqdlxxb-2012.0062 (  0) 0) |
| [36] |
Han Z H, Chen J, Zhu Z, et al. Aerodynamic design of transonic natural-laminar-flow (NLF) wing via surrogate-based global optimization. AIAA 2016-2041[R]. Reston: AIAA, 2016.
(  0) 0) |
| [37] |
Grabe C, Krumbein A. Correlation-based transition transport modeling for three-dimensional aerodynamic configurations[J]. Journal of Aircraft, 2013. (  0) 0) |
| [38] |
Grabe C, Krumbein A. Extension of the γ-Reθt model for prediction of crossflow transition. AIAA 2014-1269[R]. Reston: AIAA, 2014.
(  0) 0) |
| [39] |
Choi J H, Kwon O J. Enhancement of a correlation-based transition turbulence model for simulating crossflow instability[J]. AIAA Journal, 2015. (  0) 0) |
| [40] |
Xu J K, Bai J Q, Qiao L, et al. Transition model for predicting crossflow instabilities[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1814-1822. (in Chinese) 徐家宽, 白俊强, 乔磊, 等. 横流不稳定性转捩预测模型[J]. 航空学报, 2015, 36(6): 1814-1822. (  0) 0) |
| [41] |
Wang S N, Han Z H, Song W P. A data-driven transition prediction method for flows over airfoils[J]. Physics of Gases, 2017, 2(3): 5-16. (in Chinese) 王绍楠, 韩忠华, 宋文萍. 一种数据驱动的翼型流动转捩预测方法[J]. 气体物理, 2017, 2(3): 5-16. (  0) 0) |
| [42] |
WU M M, Han Z H, Wang S N, et al. A DMD-based automatic transition prediction method for flows over airfoils. AIAA 2017-4303[R]. Reston: AIAA, 2017.
(  0) 0) |
| [43] |
Schmid P J. Dynamic mode decomposition of numerical and experimental data[J]. Journal of Fluid Mechanics, 2010(656): 5-28. (  0) 0) |
| [44] |
Rowley C W, Mezic I, Bagheri S, et al. Spectral analysis of nonlinear flows[J]. Journal of Fluid Mechanics, 2009(641): 115-127. (  0) 0) |
| [45] |
Jovanovic M R, Schmid P J, Nichols J W. Sparsity-promoting dynamic mode decomposition[J]. physics of fluids, 2014, 26(2): 024103-1-024103-22. (  0) 0) |
| [46] |
Seena A, Sung H J. Dynamic mode decomposition of turbulent cavity flows for self-sustained oscillations[J]. International Journal of Heat and Fluid Flow, 2011, 32: 1098-1110. DOI:10.1016/j.ijheatfluidflow.2011.09.008 (  0) 0) |
| [47] |
Zhang K, Song W P. Application of the full en transition method to the infinite swept-wing's transition prediction[J]. Journal of Northwestern Polytechnical University, 2011, 29(1): 142-147. (in Chinese) 张坤, 宋文萍. eN法在无限展长后掠翼边界层转捩判断中的初步应用[J]. 西北工业大学学报, 2011, 29(1): 142-147. (  0) 0) |
| [48] |
Boltz F W, Kenyon G, Allen C Q. Effects of sweep angle on the boundary-layer stability characteristics of an untapered wing at low speeds[R]. NASA 19980227185(1960).
(  0) 0) |
| [49] |
Zhang K, Song W P. VariedeN methods used in the three dimensional boundary layer flows[C]//11th Russian-Chinese Conference on Fundamental problems of Aircraft Aerodynamics, Flight Dynamics, Strength and Flight Safety 2011. Zhukovsky: TsAGI, 2011.
(  0) 0) |
| [50] |
Krumbein A, Krimmelbein N, Grabe C. Streamline-based transition prediction techniques in an unstructured computational fluid dynamics code[J]. AIAA Journal, 2017, 55(5): 1548-1564. DOI:10.2514/1.J054990 (  0) 0) |
| [51] |
Fey U, Egami Y, Engler R. High Reynolds number transition detection by means of temperature sensitive paint. AIAA 2006-0514[R]. Reston: AIAA, 2006. http://elib.dlr.de/view/type/conference=5Fitem/2006.html
(  0) 0) |
| [52] |
Arnal D, Coustols E, Juillen J C. Experimental and theoretical study of transition phenomena on an infinite swept wing[J]. La Recherche Aerospatiale(English Edition), 1984(4): 39-54. (  0) 0) |
| [53] |
Cooke J C, Howarth L. The boundary layer of a class of infinite yawed cylinders[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 2008, 46(4): 645-648. (  0) 0) |
| [54] |
Petzold R, Radespiel R. Transition on a wing with spanwise varying crossflow evaluated with linear stability theory[C]//43rd AIAA Fluid Dynamics Conference. 2013: 2466.
(  0) 0) |
| [55] |
Basha W. Accurate drag prediction for transitional external flow over airfoils[D]. Concordia University, Canada, 2006: 56-85. https://spectrum.library.concordia.ca/view/year/2006.default.html
(  0) 0) |
| [56] |
Han Z H. SURROOPT: A generic surrogate-based optimization code for aerodynamic and multidisciplinary design. In: 30th congress of the international council of the aeronautical sciences. Korea, 2016. http://elib.dlr.de/view/year/2016.html
(  0) 0) |
 2018, Vol. 36
2018, Vol. 36


