2. 上海机电工程研究所, 上海 200233;
3. 西北工业大学, 陕西 西安 710072
2. Shanghai Electro-mechanical Engineering Institute, Shanghai 200233, China;
3. NorthwesternPolytechnical University, Xi'an 710072, China
机载导弹能否从载机上安全、平稳地分离影响到载机的安全与导弹后续作战任务的顺利完成[1-2],文献[3-6]中研究指出,在分离过程中加入舵面控制可以有效地改善分离特性。现有的机载导弹分离研究中,重点是发展基于高精度CFD方法(如动态嵌套网格技术等)的分离轨迹仿真技术[7]。
本文探讨的分离轨迹优化问题不同于单次的分离轨迹数值模拟,由于轨迹优化是一个迭代过程,在迭代过程中嵌套CFD计算的计算量太大。目前的轨迹优化一般采用参数化气动模型[8],即有足够精度的解析气动系数表达式,因此,构建起一个有足够精度的分离过程中的导弹参数化气动模型是进行分离轨迹优化的前提。相对于CFD嵌套仿真技术与栅格化的气动数据库,参数化气动模型更加方便直观,便于敏感性分析和分离过程中导弹控制系统设计。自由流条件下的飞行器气动建模技术相对比较成熟[9-11],而机-弹分离过程中导弹气动力系数和力矩系数除了与迎角、侧滑角有关外,还与导弹相对载机的空间位置和姿态相关,其气动建模问题更加复杂,相关文献十分有限。
本文采用“自由流模型+扰动量模型”的方法建立起了分离过程中导弹参数化气动模型,在此基础上,考虑分离过程的安全性、平稳性与分离终端时刻姿态稳定性,构建了纵向平面内最优分离轨迹的最优控制问题[12]。以升降舵偏角为控制量,通过高斯伪谱法(Gauss Pseudospectral Method,GPM)[13-14]求解了该纵向平面内的分离轨迹优化问题,得到了纵向平面内的最优分离轨迹。对结果的分析表明,优化后得到的分离轨迹确保了分离过程的安全平稳。
1 分离过程中导弹气动系数参数化模型 1.1 模型概述针对机-弹分离过程,文献[1]中提出了“自由流模型+扰动量模型”的气动模型,即分离过程中,导弹气动系数可视为自由流场中气动系数与受载机影响下气动系数扰动量的叠加,表述如下:
| $ C = {C_U}\left( {M{a_M}, {\alpha _M}, {\beta _M}, \delta } \right) + \Delta {C_{NU}}\left( {{r_{M/A}}, {\mathit{\Omega }_{M/A}}} \right) $ | (1) |
其中,CU表示自由流条件下的导弹气动系数,是导弹迎角αM、侧滑角βM、马赫数MaM和舵偏角δ的函数,ΔCNU表示载机干扰下的导弹气动系数扰动量,是导弹与载机的相对位置rM/A和相对姿态ΩM/A的函数。
本文讨论导弹在载机的纵向对称面x-z平面(欧美坐标系)内分离的情况,假设分离过程中载机定态飞行且导弹滚转通道稳定。由于分离过程时间很短,故可以认为MaM不变。以往的研究表明,相对于纵向相对位置x和横向相对位置y,垂向相对位置z为气动干扰的主要影响因素[15]。在以上假设条件下,ΔCNU可简化为导弹俯仰角ϑ、偏航角ψ和z的函数,如式(2)所示。
| $ C = {C_U}\left( {\alpha, \beta, \delta } \right) + \Delta {C_{NU}}\left( {z, \vartheta, \psi } \right) $ | (2) |
自由流场中,CU模型一般为以α和β为变量的多项式回归模型,如下所示:
| $ \begin{array}{l} {C_U}\left( {\alpha, \beta } \right) = {c_1}{\xi _1}\left( {\alpha, \beta } \right) + \cdots + {c_i}{\xi _i}\left( {\alpha, \beta } \right) + \cdots \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + {c_m}{\xi _m}\left( {\alpha, \beta } \right) + C_U^\delta \delta \end{array} $ | (3) |
其中,CUδ为舵偏角效率,本文假定舵偏角δ对气动力的影响较小,只考虑其对力矩系数的影响。
1.3 ΔCNU的参数化模型如式(2)所示,ΔCNU的影响因素中除了导弹姿态角之外,还有导弹相对飞机的垂向距离z。取若干离散的z值(z=z1, z2, …, zh)(分离过程中,导弹受载机影响的主要范围在1至1.5倍机身长度内[1],因此,根据具体的载机情况选取z值),在每个离散的z值处,ϑ和ψ以一定规则生成试验样本点,通过CFD计算得到相应的载机干扰数据ΔCNUzi(i=1, …, h)。
根据ΔCNUzi以及相应的样本点(ϑ, ψ),在每个不同的z值处,可以建立关于姿态角的多项式模型:
| $ \left. {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\Delta {C_{NU}}\left( {z = {z_1}} \right) = {c_{11}}{\xi _1}\left( {\vartheta, \psi } \right) + \cdots + {c_{1j}}{\xi _j}\left( {\vartheta, \psi } \right)}\\ { + \cdots + {c_{1n}}{\xi _n}\left( {\vartheta, \psi } \right)}\\ {\Delta {C_{NU}}\left( {z = {z_2}} \right) = {c_{21}}{\xi _1}\left( {\vartheta, \psi } \right) + \cdots + {c_{2j}}{\xi _j}\left( {\vartheta, \psi } \right)}\\ { + \cdots + {c_{2n}}{\xi _n}\left( {\vartheta, \psi } \right)}\\ { \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {\Delta {C_{NU}}\left( {z = {z_h}} \right) = {c_{h1}}{\xi _1}\left( {\vartheta, \psi } \right) + \cdots + {c_{hj}}{\xi _j}\left( {\vartheta, \psi } \right)} \end{array}}\\ { + \cdots + {c_{hn}}{\xi _n}\left( {\vartheta, \psi } \right)} \end{array}} \end{array}} \right\} $ | (4) |
其中,ξj为模型中第j个多项式回归项;cij为zi处模型的第j项ξj对应的系数;n为多项式回归项的个数。
由式(4)知,不同z值处的模型中,同一回归项对应的系数不同,这些系数(c1j, c2j, …, chj)分别对应着垂向距离(z1, z2, …, zh), 因此,可以将其看作是距离z的函数,记为fj(z)。
分离过程中,随着距离z的增加,载机对导弹的干扰作用会趋近于0,即存在如下边界条件:
| $ \mathop {\lim }\limits_{z \to \infty } \Delta {C_{NU}} = 0 \Rightarrow \mathop {\lim }\limits_{z \to \infty } {f_j}\left( z \right) = 0\;\;\forall j = 1, \cdots, n $ | (5) |
当机-弹分离的马赫数超过1时,由于激波等因素的影响,导弹的ΔCNU并不是随z单调下降,而是会经过波动再趋向于0[1],综合以上两点,采用如下的函数形式:
| $ {f_j}\left( z \right) = {e^{-\varphi z}}\left( {{\eta _0} + {\eta _1}z + {\eta _2}{z^2} + \cdots + {\eta _s}{z^s}} \right) $ | (6) |
其中的e-φz项可以保证满足边界条件,(η0+η1z+η2z2+…+ηszs)项可以描述过程中的波动规律。本文中取s=3。而φ与ηi则是待估计的参数。至此,可以将ΔCNU模型表示如下:
| $ \begin{array}{l} \Delta {C_{NU}}\left( {z, \vartheta, \psi } \right) = {f_1}\left( z \right){\xi _1}\left( {\vartheta, \psi } \right) + \cdots + {f_j}\left( z \right){\xi _j}\left( {\vartheta, \psi } \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + \cdots + {f_n}\left( z \right){\xi _n}\left( {\vartheta, \psi } \right) \end{array} $ | (7) |
上节中给出了分离过程中导弹气动系数的参数化表达形式,如式(3)和式(7)。采用多元正交函数最小二乘法可以确定式(3)和式(4)中的模型结构及对应的系数。在常规的最小二乘法中,存在回归项线性相关的风险,从而造成矩阵病态,导致求解困难,而多元正交函数最小二乘法较好地解决了这一问题。式(6)中各待定参数的值的求解方法如下。
将φ与η(η=[η0, …, ηm])视为优化变量,可以构造如下的参数优化问题:
| $ \begin{array}{l} \min J\;\;\;\sum\limits_{i = 1}^h {{{\left( {{f_j}\left( {\varphi, \eta } \right){|_{z = {z_i}}}-{c_{ij}}} \right)}^2}} \\ s.\;t.\;\;\;\;\;{\varphi _{\min }} \le \varphi \le {\varphi _{\max }}\\ \;\;\;\;\;\;\;\;\;\;\;{\eta _{\min }} \le \eta \le {\eta _{\max }} \end{array} $ | (8) |
文中采用“遗传算法+序列二次规划算法”的混合优化方法对该参数优化问题进行求解,完成fj(z)的参数估计。
3 纵向平面内的分离轨迹优化问题在得到气动系数参数化模型后,可以构建纵向平面内的分离轨迹优化问题。机载导弹分离过程中,为了避免导弹与载机相撞,一般认为导弹越快速地远离载机越好,而迎角为负的情况下升力向下,气动力促使导弹远离载机,因此选取迎角的积分来表征导弹远离载机的快速性,从而保证分离过程的安全;又考虑到分离过程结束后导弹能顺利地完成后续作战任务,对分离过程结束时的导弹迎角和俯仰角速度提出了要求,采用了如下加权形式的目标函数[12]:
| $ \min J = {\omega _1}\int_{{t_0}}^{{t_f}} {\alpha \left( t \right){\rm{d}}t} + {\omega _2}\left| {\alpha \left( {{t_f}} \right)} \right| + {\omega _3}\left| {{\omega _y}\left( {{t_f}} \right)} \right| $ | (9) |
考虑到导弹在分离过程中的姿态稳定性与舵偏限制,提出如下路径约束与控制约束:
| $ \begin{array}{l} {\alpha _{\min }} \le \alpha \le {\alpha _{\max }}\;\;\;\;\;\;{\vartheta _{\min }} \le \vartheta \le {\vartheta _{\max }}\\ {\omega _{{y_{\min }}}} \le {\omega _y} \le {\omega _{{y_{\max }}}}\;\;\;\;{\delta _{{y_{\min }}}} \le {\delta _y} \le {\delta _{{y_{\max }}}} \end{array} $ | (10) |
采用GPM方法将该分离轨迹优化问题转化为非线性规划问题,并通过序列二次规划算法求解。
4 数值算例以某型导弹在载机纵向对称面内弹射分离过程为研究对象,进行导弹的气动系数参数化建模和轨迹优化。分离时载机以1.5Ma平飞,以升力cz为例说明建模过程。
4.1 气动系数的参数化建模 4.1.1 CU的参数化建模采用多元正交函数最小二乘法完成CU的参数化建模。以升力系数cz为例,得到的czU如下:
| $ c{z_U} = 0.002455{\alpha ^2} + 0.1518\alpha $ | (11) |
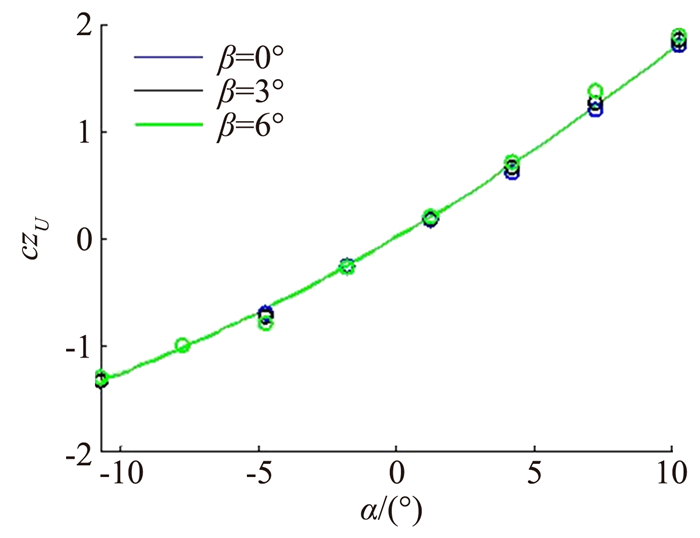
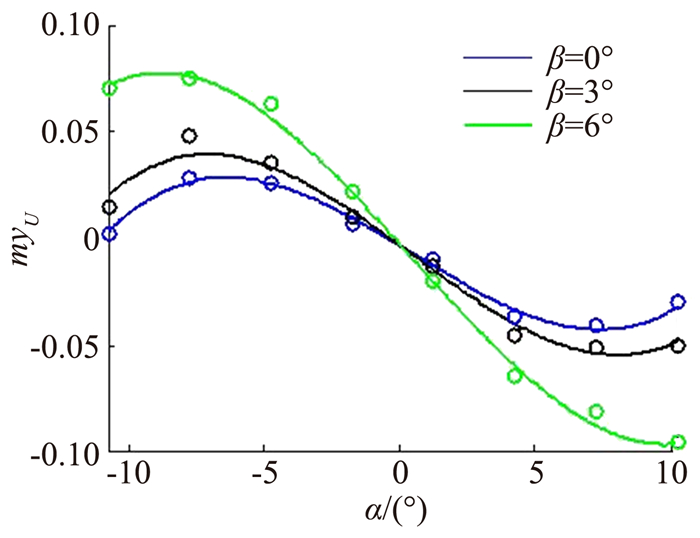
将式(11)得到的数据与CFD源数据进行对比,如图 1和图 2所示(图中实线代表参数化气动模型拟合值,符号‘°’代表对应的CFD源数据),可以看出,模型(11)有较好的拟合精度,且表达式较为精简,避免了过拟合。
|
图 1 参数化模型得到的czU数据与CFD源数据对比图 Figure 1 Comparison of czU data resulting from parametric model with CFD data |
|
图 2 参数化模型得到的myU与CFD源数据对比图 Figure 2 Comparison of myU data resulting from parametric model with CFD data |
采用前述方法,得到ΔCNU的表达式如下:
| $ \begin{array}{l} \Delta c{z_{NU}} = {\exp ^{-0.55z}}\left( {0.27-0.24z + 0.18{z^2}-0.071{z^3}} \right)\\ + {\exp ^{ - 0.54z}}\left( {0.011 - 0.059z + 0.037{z^2} - 0.0065{z^3}} \right)\vartheta \\ + {\exp ^{ - 2.3z}}\left( { - 0.033 - 0.14z + 0.22{z^2} - 0.31{z^3}} \right)\psi \\ + {\exp ^{ - 0.41z}}\left( { - 0.0049 - 0.0051z - 0.00012{z^2}} \right)\vartheta \psi \\ + {\exp ^{ - 0.35z}}\left( { - 0.0021 - 0.00073z + 0.00010{z^2}} \right){\vartheta ^2}\\ + {\exp ^{ - 2.2z}}\left( { - 0.0061 + 0.53z - 0.081{z^2} + 0.051{z^3}} \right)\vartheta {\psi ^2}\\ + {\exp ^{ - 1.5z}}\left( {0.0024 - 0.011z + 0.020{z^2} - 0.0068{z^3}} \right){\psi ^2} \end{array} $ | (12) |
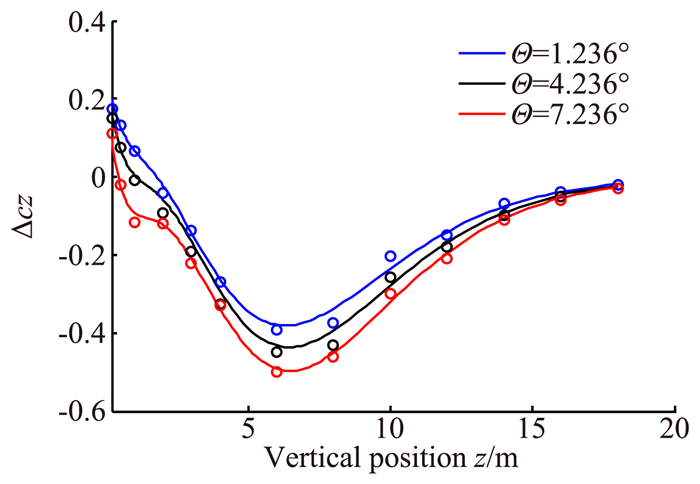
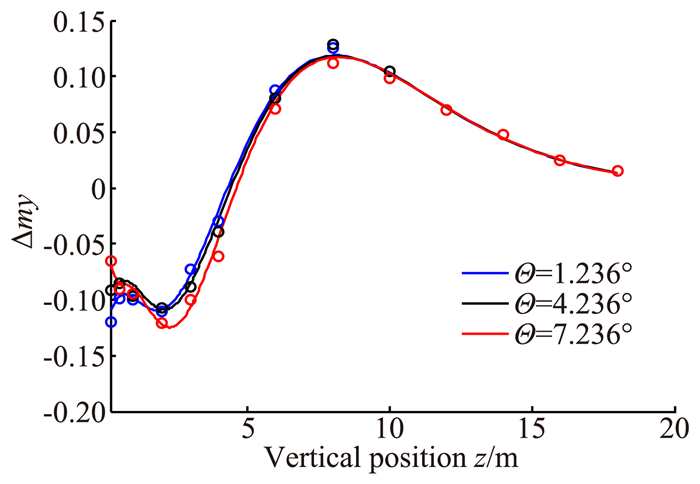
图 3和图 4显示了模型预测值与CFD源数据的对比(图中实线代表参数化气动模型值,符号‘°’代表CFD源数据),可以看出,所得气动系数模型有较高的精度。
|
图 3 参数化模型得到的ΔczNU与CFD源数据对比图 Figure 3 Comparison of ΔczNU data resulting from parametric model with CFD data |
|
图 4 参数化模型得到的ΔmyNU数据与CFD源数据对比图 Figure 4 Comparison of ΔmyNU data resulting from parametric model with CFD data |
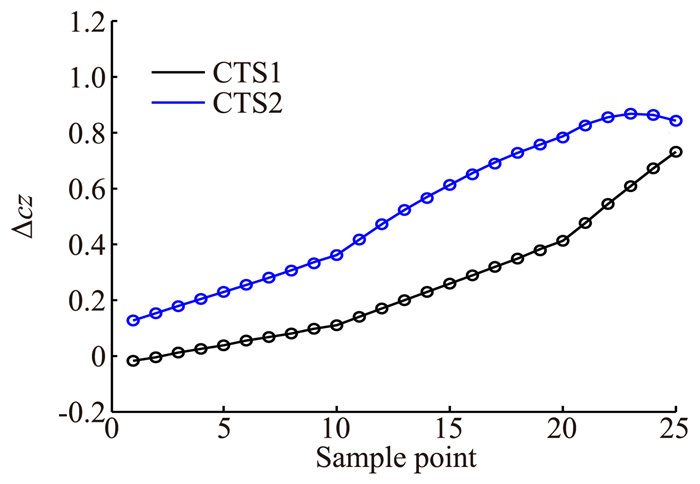
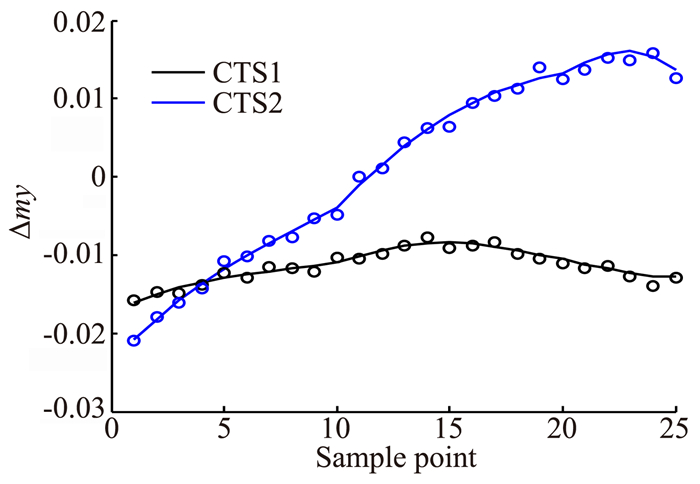
为了进一步验证本文所采用的模型及其求解方法的正确性,将参数化模型预测值与马赫数1.5下的两组CTS(Captive trajectory system)风洞实测数据进行了对比,如图 5和图 6所示(实线代表参数化气动模型拟合值的连线,符号‘°’代表采样点上的CTS实验风洞数据)。可以看出,模型预测值与实际风洞数据基本吻合。其中ΔczNU模型对CTS1与CTS2预测的最大相对误差分别为4.58%和2.06%,ΔmyNU模型对于CTS1与CTS2预测的最大相对误差分别为8.43%和9.51%,均在可接受的范围内,说明文中方法得到的ΔCNU可以较好地反应载机对于导弹的气动干扰规律。
|
图 5 参数化模型得到的ΔczNU数据与CTS实验数据对比图 Figure 5 Comparison of ΔczNU data resulting from parametric model with CTS experiment data |
|
图 6 参数化模型得到的ΔmyNU数据与CTS实验数据对比图 Figure 6 Comparison of ΔmyNU data resulting from parametric model with CTS experiment data |
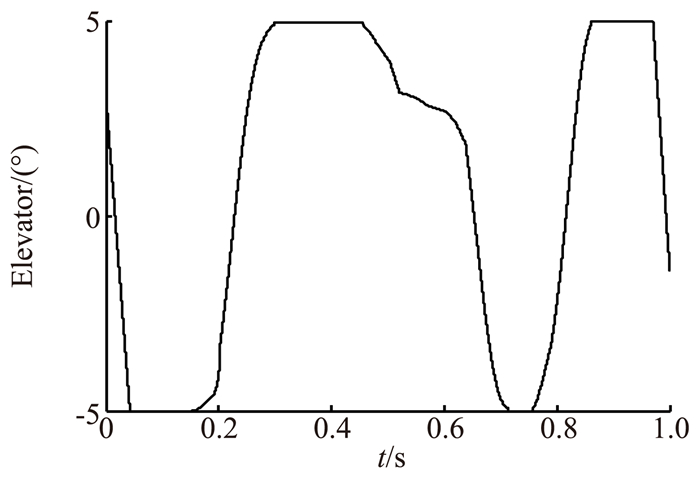
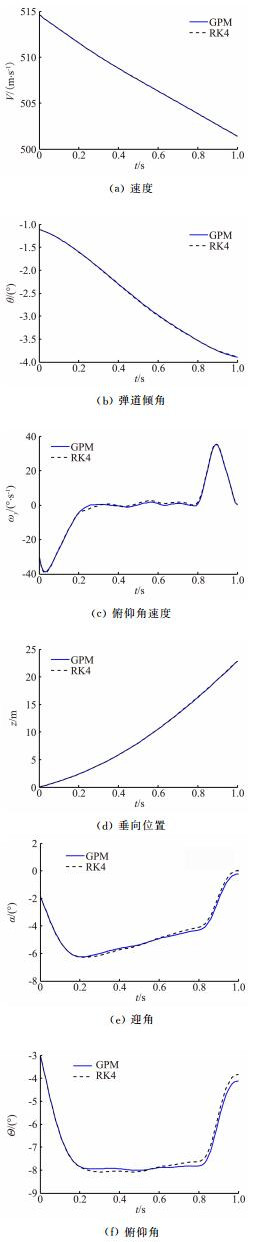
根据前文中得到的参数化气动模型,采用GPM方法求解纵向平面内分离轨迹优化问题。参考相关文献[12],给出状态初值。取升降舵偏角为控制变量,采用GPM求解该分离弹道的优化问题,可以得到最优开环控制规律,如图 7所示。将得到的最优开环控制规律带入到运动方程中,采用四阶龙格库塔法求解微分方程组,得到对应的状态量,将其与轨迹优化得到的状态量变化规律绘制在图 8中。
|
图 7 最优开环控制规律 Figure 7 Open-loop optimal control law |
|
图 8 最优分离弹道的状态量变化规律 Figure 8 States of optimal separation trajectory |
如图 8所示,导弹俯仰角变化平稳,避免了由于姿态不稳定而造成的碰撞;分离末端时刻的俯仰角速度与迎角均为0,从而使导弹有一个较好的起始点火状态;导弹迎角始终为负值,保证了导弹所受的气动力始终向下,从而可使导弹快速地远离载机,保证了分离过程的安全性。
5 结论1) 参数化的“自由流模型+干扰模型”能较好地反映出机-弹分离过程中导弹气动系数的变化规律,具有一定的工程应用价值。
2) 通过基于参数化气动模型的分离轨迹优化,能够得到一条安全、平稳的分离轨迹,为导弹后续作战任务的完成打下扎实的基础。
3) 本文考虑的是一个开环的最优控制问题,在初始条件存在偏差的情况下,开环最优控制规律将不再适用,考虑初始条件扰动的闭环控制器设计将是后续的主要工作。
| [1] |
Carter R, Lind R. Parametric modeling for store separation aerodynamics using system identification[C]//AIAA Atmospheric Flight Mechanics Conference, AIAA 2012-4510. http://arc.aiaa.org/doi/abs/10.2514/6.2012-4510
(  0) 0) |
| [2] |
Song Guibao, Liu Jimin, Gao Shiqing, et al. Numerical simulation research situation for missile separated from aircraft[J]. Winged Missiles Journal, 2006, 10: 26-28. (in Chinese) 宋贵宝, 刘济民, 高世清, 等. 导弹与载机分离数值模拟研究现状[J]. 飞航导弹, 2006, 10: 26-28. DOI:10.3969/j.issn.1009-1319.2006.10.009 (  0) 0) |
| [3] |
Wang Xiaopeng. The numerical investigation on separation track of missile ejected from aircraft[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3): 69-72. (in Chinese) 王晓鹏. 导弹弹射发射分离轨迹的数值研究[J]. 弹箭与制导学报, 2012, 32(3): 69-72. DOI:10.3969/j.issn.1673-9728.2012.03.019 (  0) 0) |
| [4] |
Nichols R H, Denny A G. Numerical simulation of a store in controlled separation[C]//17th Applied Aerodynamics Conference, AIAA 1999-3128. http://arc.aiaa.org/doi/abs/10.2514/6.1999-3128
(  0) 0) |
| [5] |
Atwood C A. Computation of a controlled store separation from a cavity[J]. Journal of Aircraft, 1995, 32(4): 846-852. DOI:10.2514/3.46800 (  0) 0) |
| [6] |
Yan Cheng, Li Xiuhong. The realization of CTS test with control law[J]. Experiments and Measurements in Fluid Mechanics, 2003, 17(1): 24-27. (in Chinese) 阎成, 黎秀红. 带控制律CTS试验的实现[J]. 流体力学实验与测量, 2003, 17(1): 24-27. DOI:10.3969/j.issn.1672-9897.2003.01.006 (  0) 0) |
| [7] |
Liu Gang, Xiao Zhongyun, Wang Jiantao, et al. Numerical simulation of missile air launching process under rail slideway constraints[J]. Acta Aerodynamica Sinica, 2015, 33(2): 192-197. (in Chinese) 刘刚, 肖中云, 王建涛, 等. 考虑约束的机载导弹导轨发射数值模拟[J]. 空气动力学学报, 2015, 33(2): 192-197. DOI:10.7638/kqdlxxb-2013.0109 (  0) 0) |
| [8] |
Hargraves C R, Paris S W. Direct trajectory optimization using nonlinear programming and collocation[J]. Journal of Guidance, Control, and Dynamics, 1987, 10(4): 338-342. DOI:10.2514/3.20223 (  0) 0) |
| [9] |
Morelli E A. Global nonlinear aerodynamic modeling using multivariate orthogonal functions[J]. Journal of Aircraft, 1995, 32(2): 270-277. DOI:10.2514/3.46712 (  0) 0) |
| [10] |
Morelli E A, Klein V. Accuracy of aerodynamic model parameters estimated from flight test data[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 74-80. DOI:10.2514/2.3997 (  0) 0) |
| [11] |
Grauer J A, Morelli E A. Generic global aerodynamic model for aircraft[J]. Journal of Aircraft, 2015, 52(1): 13-20. DOI:10.2514/1.C032888 (  0) 0) |
| [12] |
Carter R, Lind R. Trajectory optimization for guided store separation[C]//AIAA Guidance, Navigation, and Control Conference. AIAA 2012-4686. https://arc.aiaa.org/doi/abs/10.2514/6.2012-4686
(  0) 0) |
| [13] |
Benson D. A Gauss pseudospectral transcription for optimal control[D]. Massachusetts Institute of Technology, 2005. http://www.researchgate.net/publication/35215358_A_Gauss_pseudospectral_transcription_for_optimal_control_
(  0) 0) |
| [14] |
Yong E, Tang G, Chen L. Rapid trajectory optimization for hypersonic reentry vehicle via Gauss pseudospectral method[J]. Journal of Astronautics, 2008, 6(29): 1766-1772. (  0) 0) |
| [15] |
Ching T K. Grid survey approach to store separation trajectory prediction[J]. Journal of Aircraft, 2000, 37(4): 736-738. DOI:10.2514/2.2662 (  0) 0) |
| [16] |
Barron A. The predicted squared error:a criterion for automatic model selection[M]. New York: Self-Organizing Methods in Modeling, Marcel Dekker, 1984, 87-103.
(  0) 0) |
| [17] |
Xie Yu. Regression Analysis[M]. Social Sciences Academic Press, 2010. (in Chinese) 谢宇. 回归分析[M]. 社会科学文献出版社, 2010. (  0) 0) |
| [18] |
He Xiaoqun, Liu Wenqing. Applied regresion analysis[M]. China Renmin University Press, 2007. (in Chinese) 何晓群, 刘文卿. 应用回归分析[M]. 中国人民大学出版社, 2007. (  0) 0) |
 2018, Vol. 36
2018, Vol. 36

