自20世纪五、六十年代起,人们逐渐认识到直升机在下滑飞行中存在着一种严重不稳定的状态,即涡环状态(Vortex-Ring State,VRS)[1]。国内外学者利用试验和仿真等手段对直升机涡环状态的现象、本质和对直升机飞行安全带来的影响进行了深入研究。文献[2]采用叶素模型和自由尾迹模型分析涡环状态中单旋翼、共轴双旋翼和倾转旋翼机尾迹状态的异同;文献[3]对涡环状态之于直升机飞行性能的影响进行了建模;文献[4]将计算流体力学引入直升机涡环状态流场仿真。鉴于涡环状态对飞行安全的巨大威胁,涡环边界的精确计算尤为重要。文献[5-7]通过模型试验总结规律,提出了计算涡环状态边界的不同判据,确定了直升机陷入涡环状态的速度边界,得以广泛应用。其中高-辛判据[8]被认为得出了直升机进入涡环状态的首要现象,其结果与飞行试验值一致性较好[8-10]。
但是,高-辛判据试验中,模型直升机旋翼与机身为刚性连接,无法反映桨盘在飞行中的姿态变化,因此,根据涡环判据直接得出的涡环边界与试飞值之间存在一定的偏差。
据此,本文依据高-辛判据试验装置和实际飞行的区别,讨论了斜下滑阶段直升机各姿态角与力的关系,通过与涡环判据相结合,计算了两种情况下的涡环边界并与试飞数据进行了对比,据此分析了桨盘倾角对旋翼涡环边界的影响。
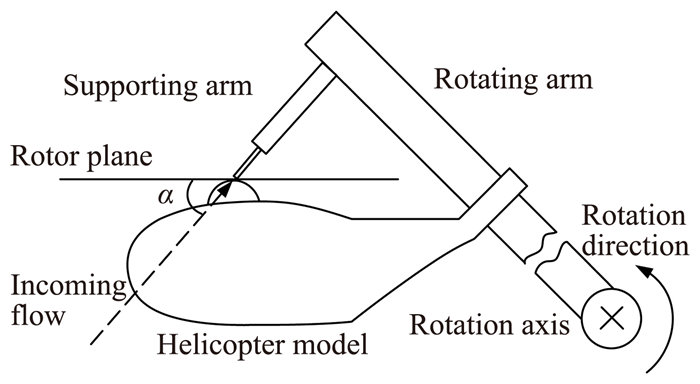
1 桨盘倾角对VRS判据的影响 1.1 模型试验中直升机下滑角如图 1所示,在模型试验中:旋转轴带动旋转大臂在水平面内逆时针旋转,支撑小臂处线速度方向与小臂同轴;支撑小臂与桨盘平面之间夹角设定为α,通过连接,带动模型直升机一起转动;旋翼与机身保持固定的位置与角度,相对气流反方向吹来,垂直于旋转大臂,与桨盘平面夹角为α。此时模拟的是直升机沿下滑角α斜下滑的情况。
|
图 1 模型试验中直升机下滑角 Figure 1 Glide angle of helicopter in model test |
由此可见,影响直升机进入涡环状态的是桨盘下滑角,即旋翼桨尖平面倾角(αTPP),应以之为标准计算涡环边界。而在试验中,直升机下滑角与桨盘下滑角是相同的,并不加以区分。
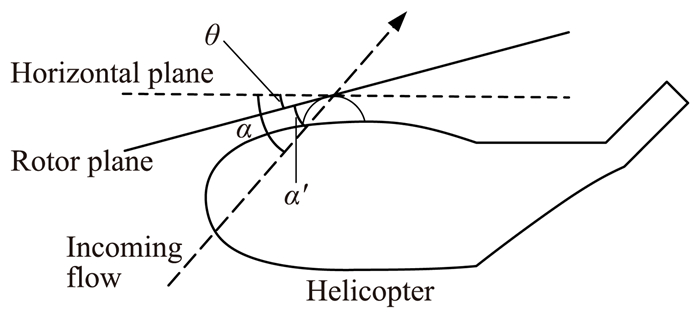
1.2 实飞中直升机下滑角实际飞行中,直升机在斜下滑时有一定的前飞速度,旋翼桨盘前倒,使旋翼拉力产生向前的分量。如图 2所示,若直升机同样以下滑角α斜下降,桨盘倾斜产生桨盘倾角θ,则桨盘下滑角α′=α-θ。
|
图 2 实飞直升机下滑角 Figure 2 Glide angle of helicopter in real flight |
对于同一直升机,桨盘倾角与直升机前飞速度有关;对于不同直升机,以同样速度前飞时,产生的桨盘倾角也不同。因此实际飞行中的涡环边界的计算应将桨盘倾角纳入其中。
2 涡环边界修正模型及求解 2.1 直升机下滑状态姿态角由于前飞速度和桨盘倾角之间的复杂关系,需要对直升机斜下滑状态的平衡方程进行求解。
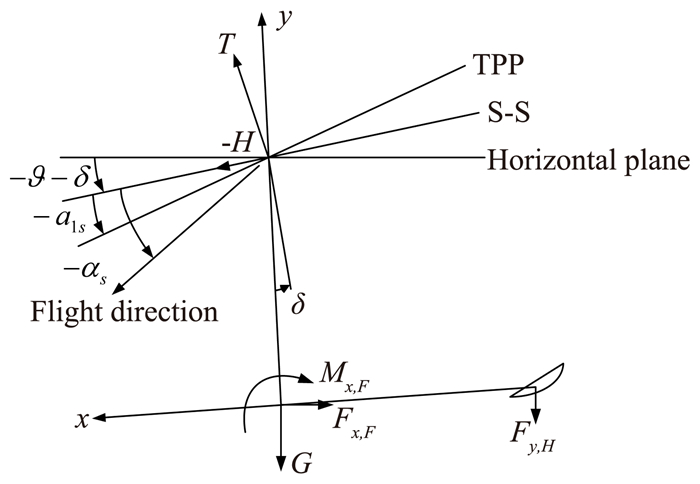
如图 3所示,ϑ为直升机俯仰角,δ为桨轴前倾角,a1s为旋翼后倒角,αs为旋翼迎角。则图 2与图 3中角度对应关系为:
|
图 3 直升机斜下滑时的受力及姿态角 Figure 3 Forces and attitudes of helicopter in declined decent |
| $ \left\{ \begin{array}{l} \theta =-\vartheta-\delta-{a_{1s}}\\ \alpha ' = - {\alpha _s} + {a_{1s}}\\ \alpha = \vartheta - \delta - {\alpha_s} \end{array} \right. $ | (1) |
据此,先简要分析配平各参数随前飞速度变化的规律。
1) 将各力投影到桨毂平面,则有:
| $ \begin{array}{l} -H + G\sin \left( {-\vartheta-\delta } \right) - {F_{x, F}}\cos \left( { - \vartheta - \delta } \right)\\ + {F_{y, H}}\sin \left( { - \vartheta - \delta } \right) = 0 \end{array} $ | (2) |
由于(-ϑ-δ)为小量,左边第四项可忽略,则
-H+G(-ϑ-δ)-Fx, Fcos(-ϑ-δ)=0
即:
| $ \left( {-\vartheta-\delta } \right) = \frac{{H + {F_{x, F}}}}{G} $ | (3) |
式中,Fx, F与前飞速度的平方成正比,因此(-ϑ-δ)随前飞速度增加而增大。
2) 将各力投影到水平面上,则有:
| $ -H-{F_{x, F}} + T\left( {-\vartheta - \delta } \right) = 0 $ | (4) |
由于-H≈T(-a1s),则式(4)成为:
T(-ϑ-δ-a1s)=Fx, F
即:
| $ T\theta = {F_{x, F}} $ | (5) |
可见,θ随前飞速度增大而增加。
2.2 平衡方程根据平衡条件可得直升机斜下滑平衡方程
| $ \left\{ \begin{array}{l} {F_{x, M}} + {F_{x, H}} + {F_{x, V}} + {F_{x, F}}-G\sin \vartheta = 0\\ {F_{y, M}} + {F_{y, H}} + {F_{y, F}}-G\cos \vartheta \cos \gamma = 0\\ {F_{z, M}} + {F_{x, T}} + {F_{x, V}} + {F_{x, F}} + G\sin \vartheta \sin \lambda = 0\\ {M_{x, M}} + {M_{x, T}} + {M_{x, V}} + {M_{x, F}} = 0\\ {M_{y, M}} + {M_{y, T}} + {M_{y, V}} + {M_{y, F}} = 0\\ {M_{z, M}} + {M_{z, T}} + {M_{z, H}} + {M_{z, F}} = 0 \end{array} \right. $ | (6) |
式中,Fi, M、Fi, T、Fi, H、Fi, V、Fi, F分别为旋翼、尾桨、平尾、垂尾、机身气动力在体轴系中i方向的分量,Mi, X为相应的力矩分量。采用数值方法求解该非线性方程,得到配平的操纵量和姿态角,求解过程不再赘述。
2.3 涡环判据高-辛判据经过飞行试验验证[5-6]具有一定的精度,其作为直升机主旋翼涡环边界判据的表达式为:
| $ \frac{{{{\tilde V}^2}-\tilde v \cdot \tilde V \cdot \sin \alpha }}{{\sqrt {{{\tilde V}^2}-2\tilde v \cdot \tilde V \cdot \sin \alpha + {{\tilde v}^2}} }} =-0.28 $ | (7) |
入流方程为:
| $ {{\tilde v}^2} \cdot \left( {{{\tilde V}^2}-2\tilde v \cdot \tilde V \cdot \sin \alpha + {{\tilde v}^2}} \right) = 1 $ | (8) |
式中:
由于所涉及方程式难以建立相关参数的解析表达式,采取如下求解步骤:
步骤一 将涡环判据和入流方程转换为关于水平速度分量
步骤二 在未修正的涡环边界曲线上等
1) 求解该点的桨盘下滑角:
| $ \alpha ' = \arctan \left( {{{\tilde V}_y}/{{\tilde V}_x}} \right) $ | (9) |
和飞行速度:
| $ \tilde V = \sqrt {\tilde V_x^2 + \tilde V_y^2} $ | (10) |
2) 气动力计算:根据飞行速度计算直升机各部件气动力,由于小速度下滑时α′和α差别不大,可采用α′近似计算。
3) 用式(6)进行配平计算,得到ϑ和a1s,通过式(1)得到θ和α。
4) 求解实际临界点(
步骤三 对所得n个实际飞行临界点进行拟合,得到连续的实际飞行涡环边界曲线。
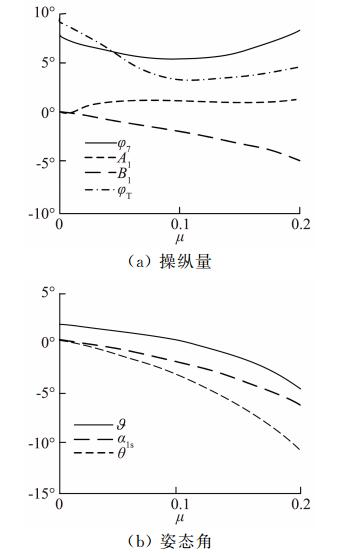
3 算例及分析 3.1 配平分析运用上述方法对样例直升机进行斜下滑时的配平计算,确定直升机斜下滑时的操纵量和姿态角。图 4是不同前飞速度下的配平结果。
|
图 4 样例直升机在不同前飞速度时的配平结果 Figure 4 Results of helicopter trimming in different forward speeds |
观察图 4(b)可知,随前飞速度的增加,旋翼后倒角的增大近似呈线性,而直升机俯仰角增大的斜率越来越大。由于桨轴倾角是固定的,作为三者之和,在起飞速度增大时桨盘倾角增大的斜率最大。
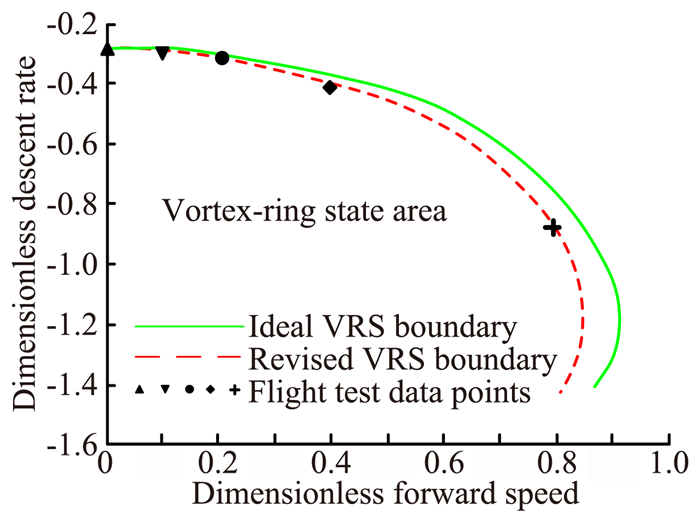
3.2 试飞数据点的验证根据得到的样例直升机的桨盘倾角与前飞速度之间的关系,求解其实飞状态下的涡环边界曲线。图 5将得到的理想涡环边界曲线和修正的涡环边界曲线与文献[7]中用于高-辛判据验证的试飞数据点进行了对比。其中,所有速度参数都进行了无量纲化,因此消除了机型各参数不同带来的差异,涡环边界具有可比性。
|
图 5 涡环边界计算值与试飞数据的对比 Figure 5 Contrast of vortex-ring boundary calculation result and flight test data |
图中可以看出,试飞数据点和理想涡环边界之间的差距随前飞速度的增大不断扩大,而桨盘倾角的计算结果与此趋势相同。因此,考虑桨盘倾角的计算大大消除了计算值与试飞值之间的误差,使实飞涡环边界曲线与试飞数据点吻合程度更高。
进一步地,理想涡环边界的涡环区域较大,结果偏保守。造成这一现象的原因是在以同样的下滑速度进入涡环时,旋翼桨盘同样出现了涡环现象,此时的旋翼下滑角相等,而实飞的直升机下滑角大于理想情况。因此,实际飞行涡环边界向理想涡环边界左下方偏转。
3.3 实飞涡环边界曲线的特性根据平衡分析所得出的结论,对于不同的直升机,其姿态角随前飞速度的变化可能不同,因此应针对机型计算各自的实飞涡环边界曲线。
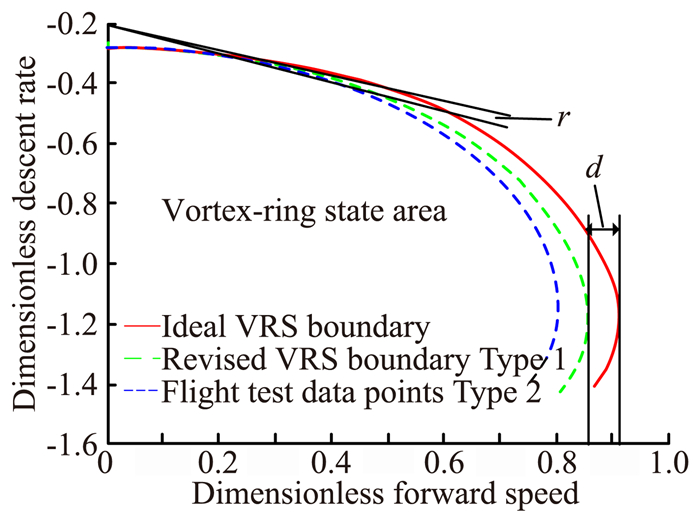
图 6是两种机型实飞涡环边界曲线的对比,该结果一方面验证了根据平衡方程所作出的结论,另一方面说明不同机型都可以通过高-辛理想涡环边界计算得到自身的实飞涡环边界,更反映了高-辛判据的基础性和普适价值。
|
图 6 不同机型实飞涡环边界曲线的对比 Figure 6 Contrast of vortex-ring boundary curves in real flight of different helicopter types |
另外,涡环边界的临界值是指直升机将要进入涡环时刻的参数,包括临界垂直下降率、临界下滑角、临界前飞速度。图 6中r表示直升机临界下滑角在理想与实际两情况下计算值之差,d表示直升机最大临界前飞速度之差。可得以下结论:
1) 两者的临界垂直下降率相同。桨盘倾角对临界下降率的影响随前飞速度的增大而增大。
2) 实际飞行中直升机的临界下滑角大于理想涡环边界的计算值。经计算,本算例r约为2°。
3) 直升机前飞速度超过临界前飞速度时,直升机不会有发生涡环事故的危险。实际飞行中直升机的临界下滑角大于理想涡环边界的计算值。经计算,本算例d折算飞行速度约9.0km/h。
4 结论本文分析了高-辛涡环判据的建立过程,考虑桨盘倾角对涡环边界的影响,建立了用于实际飞行的涡环边界求解计算模型,将实飞的涡环边界曲线和理想涡环边界曲线与试飞数据进行了对比。结果表明:直升机前飞时导致的桨盘倾角是导致理想涡环边界曲线偏离试飞数据点的主要原因,修正的涡环边界曲线与试飞值吻合良好,用于实飞的直升机涡环边界计算模型是对高辛涡环判据的有力补充。同时,由于桨盘倾角随前飞速度变化因机型而异,不同直升机应计算各自的实飞涡环边界。
| [1] |
U. S. Department of transportation federal aviation administration. rotorcraft flying handbook[M]. Washington D. C. : Government Printing Office, 2000: 11-6.
(  0) 0) |
| [2] |
Leishman J G, Ananthan S. Free-vortex wake predictions of the vortex ring state for single-rotor and multi-rotor configurations[C]//AHS International, 58th Annual Forum Proceedings, 2002, 1: 642-671.
(  0) 0) |
| [3] |
Johnson W. Model for vortex ring state influence on rotorcraft flight dynamics[R]. NASA Moffett Field CA Ames Research Center, 2004. https://www.researchgate.net/publication/228786128_Model_for_Vortex_Ring_State_Influence_on_Rotorcraft_Flight_Dynamics
(  0) 0) |
| [4] |
Hoinville E, Renaud T. CFD simulation of helicopter rotor in the Vortex Ring State regime[C]//Annual Forum Proceedings American Helicopter Society. American Helicopter Society, Inc, 2007, 63(2): 1165. https://www.researchgate.net/publication/290715772_CFD_simulation_of_helicopter_rotor_in_the_Vortex_Ring_State_regime
(  0) 0) |
| [5] |
Wolkovitch J. Analytical prediction of vortex-ring boundaries for helicopters in steep descents[J]. Journal of the American Helicopter Society, 1972, 17(3): 13-19. DOI:10.4050/JAHS.17.13 (  0) 0) |
| [6] |
Peters D A, Chen S Y. Momentum theory, dynamic inflow, and the vortex-ring state[J]. Journal of the American Helicopter Society, 1982, 27(3): 18-24. DOI:10.4050/JAHS.27.18 (  0) 0) |
| [7] |
辛宏, 高正. 直升机涡环状态速度边界的实验研究[J]. 南京航空航天大学学报, 1995, 27(4): 439-444. (  0) 0) |
| [8] |
陆洋, 高正, 黄文明, 等. 直升机涡环状态边界的试飞验证[C]//第十七届全国直升机年会, 2001: 232-237.
(  0) 0) |
| [9] |
张西, 孙杰. 直升机垂直下降时旋翼涡环飞行试验分析[J]. 飞行力学, 2010, 28(4): 82-84. (  0) 0) |
| [10] |
汤连刚, 朱宇, 李显耀, 等. 直升机尾桨涡环飞行试验研究[J]. 飞行力学, 2008, 26(5): 63-66. (  0) 0) |
 2018, Vol. 36
2018, Vol. 36

