推进系统与飞机后体之间的优化布局设计,一直是现代高性能战机关注的关键技术之一,尤其是对于高敏捷性、具备过失速能力机动飞行[1]的三代战机及其改进机型,以及把推力矢量作为标准配置的四代战机。一方面,这些飞机通常会装配几何外形可变的发动机喷管,以期在飞机全马赫数范围以及全发动机落压比条件下,提供高效的推力性能。另一方面,相对于推力性能的实现,喷管与后体间的布局设计也是十分重要的。因为它会影响飞机后体的形状,最终引起飞机阻力特性的变化。大量的研究表明,由于喷管与后体之间的不利干扰,将会改变飞机后体表面的压力分布,引起气流分离,最终在飞机的后体部位,产生较大的阻力损失,而且这种损失在喷管巡航状态下,比喷管在加力状态表现得更为明显[2-3]。对于双喷构型的飞机,由于两个喷管之间存在强干扰,加剧了流场的复杂性,阻力损失情况也更为复杂。
由于喷管与后体相互干扰而表现出来的这种复杂的气动现象,各航空技术发达国家均开展了大量的试验研究工作。以NASA兰利研究中心为例,在20世纪70、80年代,发展了完善的全机和飞机后体喷流测力、测压试验设备及推力转向喷管地面试验台,进行了大量的研究试验,在喷流影响研究以及推力转向试验技术的发展过程中起到了重要作用[4-6]。俄罗斯在多座低速风洞均具有喷流影响及推力转向试验技术,模拟落压比NPR最大可达10[7]。英国也在喷流影响以及推力转向试验领域开展了大量的风洞试验研究工作[8]。
另外AEDC也具备完善的喷流影响和推力转向试验设备及成熟的试验技术,其中喷流影响测力试验中飞机阻力系数测量精度可以达到0.0005,与我国常规测力精度合格指标一致,另外值得一提的是,其发展的后体压力技术形式的喷流影响风洞试验,其阻力精度可达0.0001[9]。
中国空气动力研究与发展中心在20世纪80年代末开始喷流影响以及推力转向风洞试验技术的研究工作,主要目标是研制适用于进行大迎角、大侧滑角状态下喷流影响以及推力转向控制风洞试验的试验设备,并掌握相应的试验技术,形成能满足我国第三代歼击机改型以及第四代歼击机研制进行喷流影响以及推力转向风洞试验的能力[10]。
“十二五”期间,中航工业空气动力研究院(以下简称气动院)在FL-3风洞全面建设了推力矢量高速风洞试验设备,并开展了分离形式及一体形式喷流模型试验技术的研究工作,使得气动院完全具备了承担推力转向气动特性研究和试验的能力,能够为型号提供优质全面的综合技术服务。
目前,受限于基础设备能力薄弱,国内后体喷流试验主要还是采用分离形式,试验方法简单,数据处理容易,国内喷流影响以及推力转向试验领域普遍采用。但由于分离形式喷流模型尾部缝隙的存在,一方面缩小了尾喷管的面积,使得几何模拟不真实,另一方面由于高压喷流的引射作用,使得喷管与模型内壁面之间的空腔压力与风洞环境压力不相等,产生附加的气动力作用到模型上[11-12],需要对天平数据进行精确修正,由于腔压对阻力的影响很大[13-15],且很难进行准确的测量,导致阻力数据精度不高,实际工程应用价值不高。
为提高分离形式后体喷流模型阻力测量的精度,2014年11月,在中航工业空气动力研究院FL-3风洞开展了某型飞机后体喷流测力试验,解决了模型后体与支撑系统之间的密封问题,保证了腔压在试验过程中的稳定性,发展了一套成熟的后体阻力测量与修正试验技术,从而提高了阻力数据修正的精度,与国外同类型试验阻力测量精度一致。
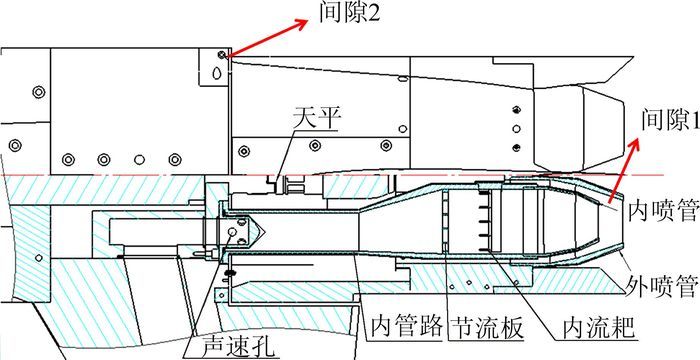
1 试验方法 1.1 试验原理试验采用分离形式后体喷流模型,如图 1所示。供气管路只与支撑系统相连,喷管与模型之间存在缝隙,即图 1所示的间隙1。模型沿展向从某处截开,模型前端以及整个机翼作为支撑系统的一部分,与天平固定端、支撑系统相连。模型后体作为测量部件与天平测量端相连。模型前后体之间存在缝隙,即图 1所示的间隙2。天平只会测量到模型后体,包括平尾以及垂尾产生的气动力,喷管的气动力不会传递到天平上。通过有无喷流之间的差值,即得到喷流对模型后体的影响量。
|
图 1 分离形式后体喷流模型剖面图 Figure 1 Section of sleeve-type after-body jet model |
本次试验模拟的相似参数,除了模型几何尺寸相似的严格模拟之外,在气动上,主要模拟的相似参数包括外流马赫数、尾喷管出口马赫数、落压比。其中,外流马赫数由吹风条件严格保证,尾喷管出口马赫数由喷管面积比以及落压比共同保证,落压比由高压控制系统精确控制尾喷管入口总压保证,环境静压取每次试验时的驻室静压。
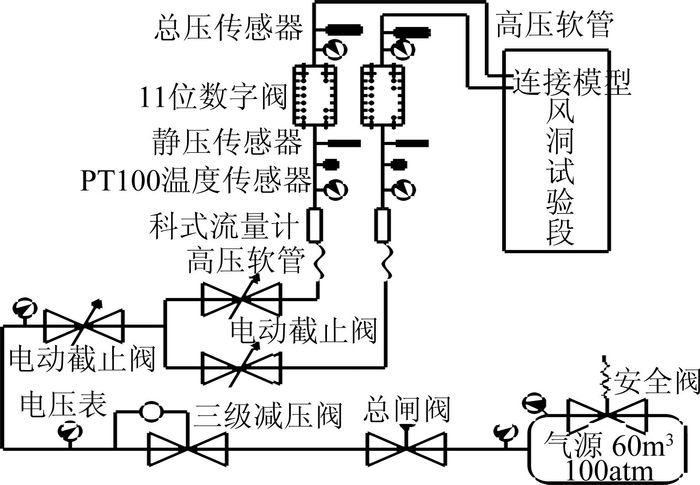
2 喷流试验专有设备 2.1 高压气源系统整个高压供气系统如图 2所示,压缩空气自气源流出,经安全阀、总闸阀、三级减压阀、电动截止阀、科式流量计后进入数字阀,进行喷流、TPS等试验时,高压气体在经过数字阀后调节压力之后通过供气胶管、供气软接头和供气支撑进入飞行器模型喷管喷出。
|
图 2 FL-3风洞高压供气系统示意图 Figure 2 Sketch of the high pressure air supply system for FL-3 tunnel |
FL-3风洞采用两台高精度数字阀进行流量及压力的精确控制,见图 3。该数字阀压力控制精度高、可调范围宽、响应时间快、效果平稳无毛刺,承压能力10MPa,工作压力点3.5MPa左右,流量调节范围5g/s~5kg/s,单次调节达到目标值并在误差范围带内稳定所需时间小于20s,小流量时所需时间小于10s,流量波动误差小于±5g/s,相对精度达0.1%~0.2%,喷流总压控制精度约优于0.5%。

|
图 3 FL-3风洞喷流压力控制系统 Figure 3 Control system of pressure for jet test in FL-3 tunnel |
FL-3风洞喷流气体流量测量选用德国西门子生产的科式流量计,对流体参数(温度、压力、密度、黏度等)进行了全面测量修正,在国外进行过专门的校准,测量精度有保证,流量测量精度0.2%~0.3%。
3 关键技术问题及设计方法 3.1 模型截断面以及密封设计套筒形式的后体测力主要有2个间隙的设计,即1.1节所示的间隙1和间隙2。对于间隙1,套筒形式的方案一般取为1.5mm~2.0mm之间。对于间隙2,一般选择1.5mm左右,中间使用肽氟龙进行密封。
同时需要综合考虑其它因素的影响,间隙的设计原则如下:
(1) 首先在整体方案中确定天平的形式以及具体的安装位置,以天平在最大后体载荷下的弹性变形量为基本设计依据;
|
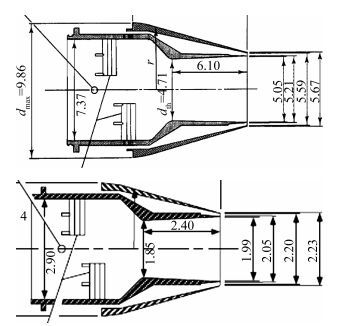
图 4 国外典型喷管间隙示意图 Figure 4 Sketches of the typical gap between nozzle and model shell used in abroad |
(2) 若需要同时考虑测压方案,则间隙兼顾测压尾罩测压管的引出;
(3) 考虑加工、安装引起间隙的偏差,缝隙适当的大,减少风险。
本文取值较一般性原则保守,最终间隙1选择为刚度计算结果的3倍左右,间隙2确定为2.5mm,中间采用肽氟龙密封。
3.2 后体腔压影响的修正套筒形式的后体测力方案,天平所测阻力包含三个部分:天平测量阻力=后体阻力+截断面压差阻力+底部阻力。从掌握的资料来看[3],由于受到高压喷流的引射效应以及体积效应的影响,后体腔压与来流静压存在较大的差值,而且差值还会随着马赫数的变化,呈现出反号的现象,即产生的附加力既有可能是推力,又有可能是阻力。文献[2]对此修正方法进行了详细的介绍。
本次试验取密封环内腔静压等于喷管出口静压,则阻力影响修正公式可简化为:
| $\begin{array}{l} D = {D_{{\rm{bal}}}} - \left( {{P_{{\rm{es}}}} - {P_\infty }} \right)\left( {{A_{{\rm{fus}}}} - {A_{{\rm{seal}}}}} \right) - \\ \quad \quad ({P_{{\rm{in}}}} - {P_\infty })({A_{{\rm{seal}}}} - {A_{{\rm{an}}}}) \end{array}$ | (1) |
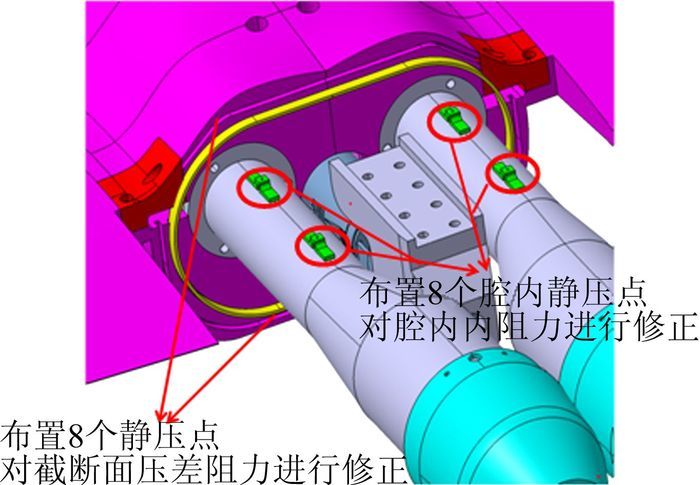
式中:D为后体阻力;Dbal为天平的测量值;Pes为肽氟龙密封环外的静压值;本试验中,沿周向布置了8个静压点,试验数据处理中,Pes取这8个静压的平均值;P∞为来流静压,试验中取为驻室参考压力,或在模型头部设置一静压测量点;Afus为截断面整体的投影面积;Aseal为肽氟龙密封环内部截断面的投影面积,即图 7所示黄色密封环内部截面积;Pin为肽氟龙密封环内静压,本试验中,沿喷流管道外壁对称布置了8个静压点,数据处理中,Pin取这8个静压的平均值;Aan值为喷管在截断面上所侵占的面积,本试验中,取为两个喷管侵占面积之和。图 5为测点布置方案图。
|
图 5 测压点布置方案 Figure 5 Sketches of the positions of pressure measured in cavity |
从腔压修正公式可以看出,要实现后体阻力的精确修正,需要截断面处的密封效果较好,使得腔内无内外串流现象,以便Pes以及Pin这两个参数在试验过程中能被准确地测量。
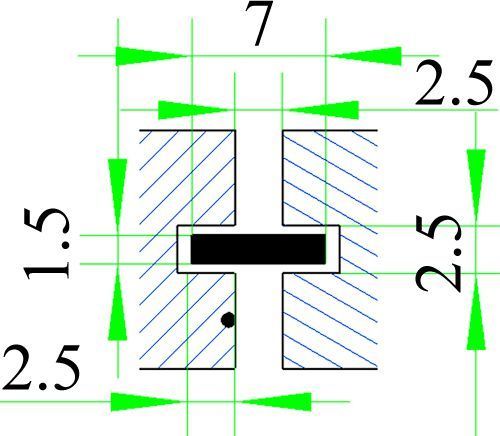
传统迷宫形式密封效果难以满足上述要求,本次试验采用肽氟龙接触式密封。其原理是在前后体截断面开槽,搁置肽氟龙密封圈,在轴向及高度方向留有一定的余量,使其可以自由移动,由于肽氟龙材质较为柔软光滑,几乎不影响天平的测量精度,同时又能承受一定的压力,阻止外部气流串流,从而能保证其密封效果。具体的设计方案如图 6所示。
|
图 6 肽氟龙密封方案 Figure 6 Teflon seal project |
经过对天平性能和刚度特性的准确评估,以及对间隙设计原则的准确把握,本次试验中未出现碰触现象,试验数据全部有效。
4.1 腔压测量结果分析表 1是模型在Ma=0.8、迎角2°条件下,进行5次重复性试验时,腔压的测量结果。从表 1可以看出,同期进行的5次重复性试验,密封环外腔压最大值与最小值之间仅相差144.5Pa,密封环内腔压最大值与最小值之间仅相差198.2Pa,相对误差仅分别为0.19%和0.27%,可见内腔流动还是比较稳定的,内外串流现象不明显。腔压结果换算到阻力修正结果Dc如表 2所示(取阻力方向为正)。
| 表 1 腔压重复性试验结果 Table 1 Result of repeat test for pressure in cavity |
|
|
| 表 2 阻力修正值重复性试验结果 Table 2 Result of repeat test for drag correction |
|
|
从表 2可以看出,上述的腔压结果换算到阻力修正结果Dc,最大值与最小值之间仅相差2.6716N,约占阻力修正结果的2.2%。此时天平的测量值也会随着阻力修正结果的波动,而产生变化。利用公式4进行处理,最终换算到后体阻力系数的结果如表 3所示。其中,X*为天平测量值,Cx风轴系下的后体阻力系数(取阻力方向为正)。
| 表 3 后体阻力系数重复性试验结果 Table 3 Result of repeat test for after-body drag coefficient |
|
|
从表 3可以看出,天平的测量值由于受到腔压的严重影响,表现为测得一个推力结果,可见腔压修正对于后体阻力试验的重要性。同期进行的5次重复性试验,经过修正后,后体阻力系数最大值与最小值仅相差0.00034,优于国军标常规测力试验阻力测量精度0.0005的要求。
4.2 阻力修正结果分析某些马赫数情况下的阻力修正试验结果如表 4所示。从表 4中可以看出,在亚声速时,腔压影响结果为一个较大的推力;在Ma=1.18时,变为阻力;且随着马赫数的增加急剧增大,腔压对天平测量结果的影响在量值上很大。从表 5可以清楚的看到,在各马赫数条件下,腔压结果与天平测量结果的比值都是不容忽视的,在Ma=0.8时,达到最大值,为天平测量结果的1.54倍;腔压影响结果随着马赫数的增加,呈现出了正负号的变化。即在Ma=0.6~0.9时,由于喷流的强引射作用,腔压小于风洞静压,从而形成了附加的推力;而当马赫数为超声速之后,喷流的引射作用不再占据主导地位,体积效应阻碍了腔内气流的流动,形成滞止区,腔压高于风洞静压,从而形成了附加的阻力。
| 表 4 不同马赫数条件下的试验结果 Table 4 Variation of test result with Mach number |
|
|
| 表 5 腔压修正值与天平测量值之比 Table 5 Ratio between the value of pressure correction in cavity and the value of balance measuring |
|
|
对喷流的影响规律进行了分析,如表 6所示,在有喷流状态下,后体阻力比无喷流状态下有较为明显的增加。在Ma=0.6、迎角2°时,后体阻力增量约为13N,占比30%左右,后体阻力系数也呈明显的增大趋势。
| 表 6 喷流对后体阻力的影响 Table 6 Jet-effects to after-body drag |
|
|
随着马赫数的变化,同一状态下,后体阻力系数也呈现出了一定的规律。在马赫数0.6~0.9范围内,后体阻力系数随马赫数的增加而有一定程度的减小;Ma=0.9~1.18时,后体阻力系数急剧增加;之后直至Ma=1.516,后体阻力系数继续增加,但趋势放缓。如表 7所示(NPR为喷管落压比)。
| 表 7 后体阻力系数随马赫数的变化规律 Table 7 Variation of after-body drag coefficient with Mach number |
|
|
同一马赫数条件下,不断改变模型喷管总压,即落压比条件,后体阻力系数随喷流落压比的增大而增大;但当落压比大于某个特定值之后,后体阻力系数不再随喷流落压比的增大而增大。如表 8所示。
| 表 8 后体阻力系数随落压比的变化规律 Table 8 Variation of after-body drag coefficient with NPR |
|
|
(1) 分离形式后体喷流模型腔压对后体阻力的影响是一个大量,甚至能在亚声速条件下,导致天平测量结果反号,必须要经过精确的腔压影响修正,才能得到准确的后体阻力数据。
(2) 以本文提出的分离形式后体喷流模型间隙设计原则,对喷管间隙以及模型前后体间隙进行设计,布置防碰报警装置监视整个试验过程中模型的状态,利用肽氟龙对模型前后体间隙进行接触式密封,能很好地阻滞串流,保证腔内流动稳定,腔压测量准确可靠,重复性测量相对误差仅为0.27%左右,能够实现对后体阻力的精确修正。
(3) 经过修正后的后体阻力数据,喷流影响规律正确,阻力测量精度约为0.0005,与国外同类型试验一致,同时也满足国军标常规测力试验阻力精度要求,可以有效应用于此类型试验。
| [1] |
Little F K, et al. Internal aerodynamics manual[M]. North American Rockwell Corporation Columbus, Ohio, 1970.
(  0) 0) |
| [2] |
Leavitt L D. Effect of empennage location on twin-engine afterbody/nozzle aerodynam characteristics at mach numbers from 0.6 to 1.2[R]. NASA TP-2116, 1983.
(  0) 0) |
| [3] |
Wing D J. Afterbody/nozzle pressure distributions of a twin-tail twin-engine fighter with axisymmetric nozzles at mach numbers from 0.6 to 1.2[R]. NASA TP-3509, 1995.
(  0) 0) |
| [4] |
Francis J Capone, Linda S Bangert, Scott C Asbury, et al. The NASA Langley 16-Foot Transonic Tunnel historical overview, facility description, calibration, flow characteristics, and test capabilities[R]. NASA TP-3521, 1995.
(  0) 0) |
| [5] |
Staff of the Propulsion Aerodynamics Branch. A user's guide to the Langley 16-Foot Transonic Tunnel comples[R]. NASA TM-102750, 1990.
(  0) 0) |
| [6] |
Paryz R W. Upgrades at the NASA Langley Research Center national transonic facility[R]. NASA Langley Research Center, Hampton, VA 23681-2199.
(  0) 0) |
| [7] |
李明华, 曾冬娟. 俄罗斯中央空气流体动力研究院1970~2000年的工作及前景展望[M]. 沈阳飞机设计研究所, 2001.
(  0) 0) |
| [8] |
Bouis X, Chair W G. Sonic nozzles for mass flow measurement and reference nozzles for thrust verification[D]. AGARD AR-321, 1997.
(  0) 0) |
| [9] |
Smith C L, Bergmann J C, Riddle T R. Current airframe propulsion integration testing techniques at AEDC[R]. AIAA 2004-6819.
(  0) 0) |
| [10] |
郭旦平, 林俊. 2. 4m跨声速风洞带涡轮动力模拟器实验技术研究[C]//2007年近代空气动力学年会. 银川, 2007.
(  0) 0) |
| [11] |
Carlson J R, Pao S P. Aerodynamic performance predictions of single and twin jet afterbodies[C]//31th Joint Propulsion Conference and Exhibit. San Diego, CA, USA, 1995.
(  0) 0) |
| [12] |
Pozniak O M, Haines A B. Afterbody drag measurement at transonic speeds on a series of Ttwin and single jet afterbodies terminating at the jet-exit[R]. NASA CP-1266, 1973.
(  0) 0) |
| [13] |
Ferri A. Improver nozzle testing techniques in transonic flow[R]. AGARD 208, 1974.
(  0) 0) |
| [14] |
Jr Price E A. An investigation of F-16 nozzle-afterbody foeces at transonic mach numbers with emphasis on model scale effects[R]. AEDC TR-80-57. AFWAL-TR-81-2110.
(  0) 0) |
| [15] |
Capone F J. Aeropropulsive characteristics at Mach numbers up to 2.2 of axisymmetric and nonaxisymmetric nozzles installed on an F-18 model[R]. NASA TP-2044, 1982.
(  0) 0) |
 2017, Vol. 35
2017, Vol. 35

