气膜冷却作为燃气轮机涡轮部件的主要冷却方式之一,广泛应用于涡轮端壁、叶片前缘和叶片尾缘等部位。气膜冷却所用冷却气一般是从压气机中引入,这必然会降低燃气轮机的功率输出,另外气膜冷却及其出流还会带来掺混损失,因此,在保证冷却效果的前提下,进一步提高气膜冷却效率以减少冷却气用量是气膜冷却研究的一个重要目标。大量研究表明,气膜孔出口形状是影响气膜冷却性能的一个重要因素,近年来也不断有新型气膜孔孔形及其布置方式的提出及应用[1-3]。
Leylek[4]、Goldstein[5]、Okita[6]、Kusterer[7]、Heidmann[8]等对圆形孔、扩张孔、箭头形孔、双射流孔和肩臂孔等不同冷却孔形的气膜冷却特性研究表明,与传统圆形气膜冷却孔相比,扩张孔和能产生反肾形涡结构的肩臂孔等气膜孔结构均可显著改善气膜冷却效率。本文提出渐扩后倾肩臂孔的概念,结构设计拟结合扩张孔和肩臂孔反肾形涡的优点,以进一步改进气膜冷却效果。
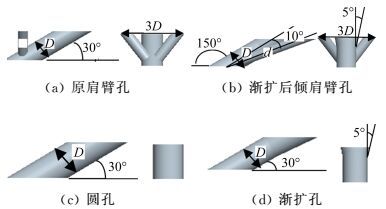
1 渐扩后倾肩臂孔及对比孔型的几何结构Heidmann[8]等所研究的肩臂孔是由一个与主流成30°夹角的主射流孔和两个侧孔组成,均为圆形孔,两侧孔的直径d为主射流孔直径D的一半(本文计算取D=20mm),两侧孔的展向宽度为3D,如图 1(a)所示。考虑到原肩臂孔两侧孔与主流方向夹角较大,侧孔冷却气随吹风比增大时易脱离壁面,故将两侧孔的中心平面向后倾,与主射流孔中心平面成10°夹角,主射流孔采用扩张角为5°的渐扩扩张孔,如图 1(b)。因渐扩后倾肩臂孔的冷却气入口面积与圆柱孔的入口面积相同,在给定入口速度的情况下冷却气流量相同,因此在与相同入口面积的单圆孔(如图 1(c)所示,中心轴线与主流成30°夹角)、扩张角为5°的渐扩孔(如图 1(d)所示,中心轴线与主流成30°夹角)和原肩臂孔做方案对比时所消耗的冷却气用量相同。
|
图 1 不同气膜孔通道结构几何示意图 Figure 1 Geometry of different gas film hole channels |
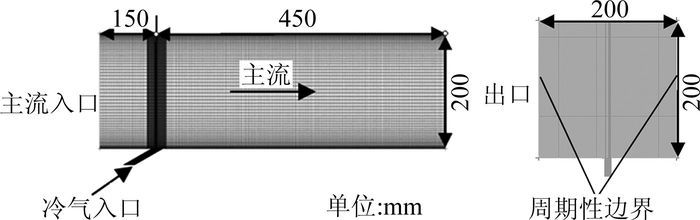
为保证网格质量和运行效率,对计算域进行多块结构化网格划分,其中冷气射流孔计算块采用O型剖分,对壁面进行加密处理。图 2所示为圆孔气膜冷却的计算域,计算总网格数为110万。
|
图 2 圆孔气膜冷却计算域 Figure 2 Film cooling of calculation domain of circular hole |
计算过程中湍流模型选用基于k-ω的SST湍流模型加Gamma-Theta转捩模型,主流风速20m/s,入口湍流度为5%,冷却气进口风速按相应吹风比确定。主流温度350K,射流入口温度300K,为方便计算绝热气膜冷却效率,采用绝热壁面。
2.2 参数定义及计算模型可行性分析大量研究表明吹风比[9-16]相对密度比和湍流度等流动参数而言是气膜冷却研究中最重要的参数,它表征了冷气量的大小。文中用M表示吹风比。
本文选用展向平均绝热气膜冷却效率作为评定气膜冷却效果的主要参数。平均绝热气膜冷却效率的定义为:
| $\bar{\eta }=\frac{{{T}_{\infty }}-{{{\bar{T}}}_{aw}}}{{{T}_{\infty }}-{{T}_{c}}}$ | (1) |
其中,T∞为主流温度,Tc为冷却气温度,Taw为绝热壁面的展向平均恢复温度。由于计算中采用了绝热措施, 所以Taw等于绝热壁面的展向平均温度。
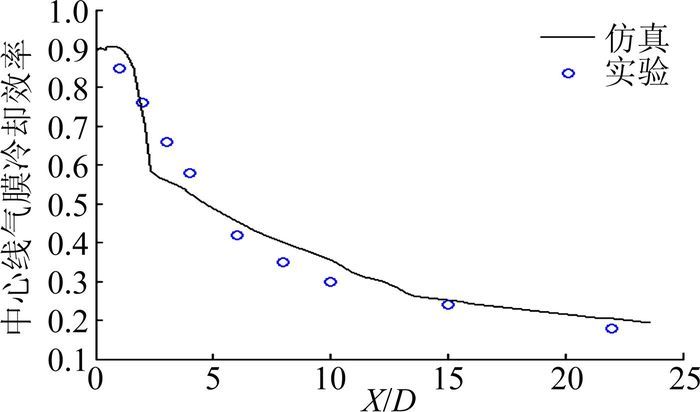
为验证计算结果,建立与文献[17]试验条件相同的几何模型进行了比较,仿真与试验结果对比如图 3所示。从图 3中可以看出绝热气膜冷却效率的变化趋势基本一致,说明所选用模型可用于气膜冷却孔冷却效果的对比研究。
|
图 3 M=0.5时圆孔中心线气膜冷却效率 Figure 3 Center line film cooling efficiency of the circular hole at M=0.5 |
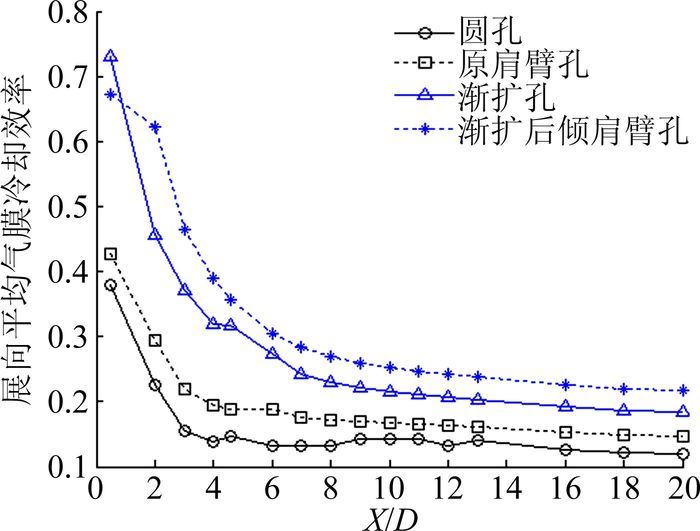
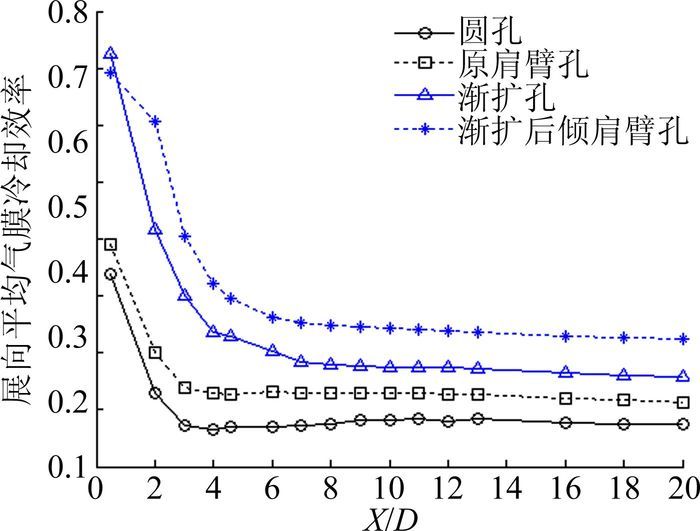
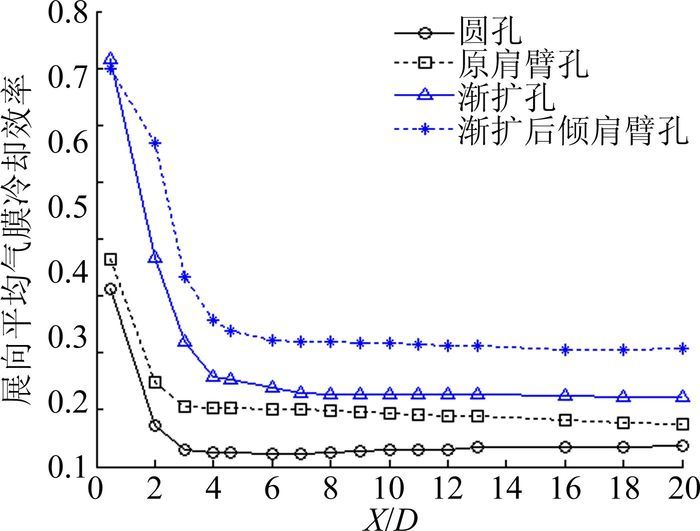
图 4~图 7为吹风比为0.5、1.0、1.5和2.0时不同孔形的展向气膜冷却效率对比结果。从图中可以看出,在吹风比为0.5时,渐扩后倾肩臂孔和渐扩孔的展向平均气膜冷却效率相当,均高于圆孔和原肩臂孔的值;吹风比大于1.0时,渐扩后倾肩臂孔的展向气膜冷却效率开始明显高于其它孔形,渐扩孔次之,原肩臂孔略高于圆孔。由此可见,渐扩后倾肩臂孔的性能实现了设计初衷,在相同冷却气消耗量的情况下,可更好地保护被冷却壁面。

|
图 4 M=0.5时不同孔形的展向平均气膜冷却效率 Figure 4 Average film cooling efficiency of different hole geometries at M=0.5 |
|
图 5 M=1.0时不同孔形的展向平均气膜冷却效率 Figure 5 Average film cooling efficiency of different hole geometries at M=1.0 |
|
图 6 M=1.5时不同孔形的展向平均气膜冷却效率 Figure 6 Average film cooling efficiency of different hole geometries at M=1.5 |
|
图 7 M=2.0时不同孔形的展向平均气膜冷却效率 Figure 7 Average film cooling efficiency of different hole geometries at M=2.0 |
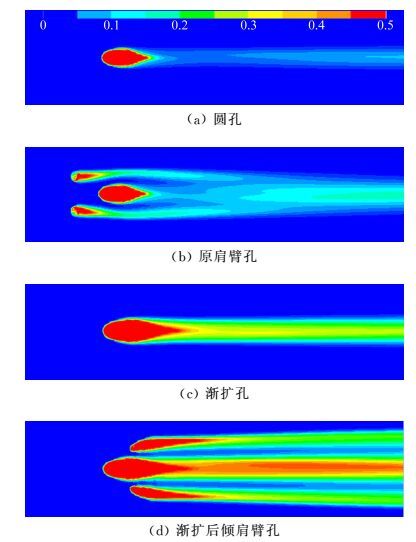
图 8所示为吹风比2.0时的四种气膜孔出流壁面的绝热气膜冷却效率分布图。从图 8中可以看出圆孔在高吹风比时壁面的绝热气膜冷却效率最低,且在圆孔下游气膜展向的作用范围较窄。原肩臂孔展向的作用范围较圆孔要宽很多,但在其作用范围上的气膜冷却效率仍偏低。渐扩后倾肩臂孔的展向绝热气膜冷却效率最高,侧向扩散较均匀。其与效率次之的扩张孔相比,不仅在中心线以外绝热气膜冷却效率值较高,即使是中心线附近的绝热气膜冷却效率也有明显提高。
|
图 8 出流孔壁面的气膜冷却效率 Figure 8 Film cooling efficiency of different hole geometries |
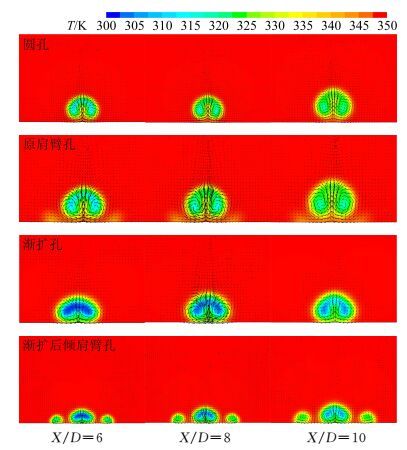
图 9所示为不同孔形在吹风比M=2.0时距出流口X/D=6、8和10处流场截面的温度场及涡系结构分布图。从图 9中可以看出在高吹风比时,圆孔和原肩臂孔出流口下游流场截面中心处的流场及温度场相似,不过原肩臂孔两侧存在两个出流小孔,对中心的肾形涡具有一定的抑制作用,中心的肾形涡更贴近被冷却壁面。扩张孔与渐扩后倾肩臂孔出流口下游截面中心处的流场及温度场相似,不过在图上可以清晰地看到,渐扩后倾肩臂孔两侧的两个出流小孔对中心的肾形涡的抑制作用,这也是渐扩后倾肩臂孔中心线附近的绝热气膜冷却效率也比渐扩孔要高的原因。
|
图 9 距出流口不同距离处流场截面的温度场和涡系结构分布图 Figure 9 Temperature field and the distribution of the vortex in the flow field at different distances |
1) 渐扩后倾肩臂孔的展向绝热气膜冷却效率值在不同吹风比下均最高,且吹风比2.0时,渐扩后倾肩臂孔的绝热气膜冷却效率值分布较其它孔型更均匀。
2) 吹风比2.0时,渐扩后倾肩臂孔两侧的两个出流小孔对中心的肾形涡有一定的抑制作用,从而使渐扩后倾肩臂孔中心线附近的绝热气膜冷却效率也比渐扩孔要高。
| [1] |
朱延鑫, 谭晓茗, 郭文, 等. 出流孔型对平板气膜冷却影响机理的研究[J]. 推进技术, 2013, 34(4): 499-505. (  0) 0) |
| [2] |
葛绍岩, 徐靖中. 气膜冷却[M]. 北京: 科学出版社, 1985.
(  0) 0) |
| [3] |
李少华, 宋东辉, 刘建红, 等. 不同孔型平板气膜冷却的数值模拟[J]. 中国电机工程学报, 2006, 26(17): 112-116. DOI:10.3321/j.issn:0258-8013.2006.17.020 (  0) 0) |
| [4] |
Leylek J H, Zerkle R D. Discrete jet film-cooling:A comparison of computational results with experiments[J]. ASME Journal of Transaction, 1994, 116: 358-368. (  0) 0) |
| [5] |
Goldstein R J, Eckert E R, Burggraf F. Effects of hole geometry and density on three-dimensional film cooling[J]. International Journal of Heat Mass Transfer, 1974, 17(5): 595-607. DOI:10.1016/0017-9310(74)90007-6 (  0) 0) |
| [6] |
Okita Y, Nishiura M. Film effectiveness performance of an arrowhead-shaped film-cooling hole geometry[J]. Journal of Turbomachinery, 2007, 129(2): 331-339. DOI:10.1115/1.2437781 (  0) 0) |
| [7] |
Kusterer K, Bohn D, Sugimoto T, et al. Double-jet ejection of cooling air for improved film cooling[J]. Journal of Turbomachinery, 2007, 129(4): 809-815. DOI:10.1115/1.2720508 (  0) 0) |
| [8] |
Heidmann J D, Ekkad S. A novel antivortex turbine film-cooling hole concept[J]. Journal of Turbomachinery, 2008, 130(3): 487-496. (  0) 0) |
| [9] |
Gustafson R, Mahmood G I, Acharya S. Flowfield in a film-cooled three-dimensional endwall passage:aerodynamic measurements[R]. ASME GT 2007-28154, 2007.
(  0) 0) |
| [10] |
Goldstein R J. Heat transfer[M]. 1971:321-379.
(  0) 0) |
| [11] |
Bunker R S. A review of shaped hole turbine film-cooling technology[J]. ASME J. Heat Transfer, 2005, 127: 441-453. DOI:10.1115/1.1860562 (  0) 0) |
| [12] |
Ekkad S V, Ou S, Rivir R B. Effect of jet pulsation and duty cycle on film cooling from a single jet on a leading edge model[J]. ASME J. Turbomach., 2005, 128: 564-571. (  0) 0) |
| [13] |
Kapadia S, Roy S, Heidmann J. First hybrid turbulence modeling for turbine blade cooling[J]. Thermophys Heat Transfer, 2004, 181: 154-156. (  0) 0) |
| [14] |
Bunker R S. Film cooling effectiveness due to discrete holes within a transverse surface slot[R]. ASME GT 2002-30178.
(  0) 0) |
| [15] |
Dhungel S, Phillips A, Ekkad S V, et al. Experimental investigation of a novel anti-vortex film cooling hole design[R]. ASME GT 2007-27419.
(  0) 0) |
| [16] |
Bogard D G, Thole K A. Gas turbine film cooling[J]. Propul Power, 2006, 222: 249-270. (  0) 0) |
| [17] |
Sinha A K, Bogard D G. Film-cooling effectiveness downstream of a single row of holes with variable density ratio[J]. ASME Journal of Turbomachinery, 1991, 113(3): 441-449. (  0) 0) |
 2017, Vol. 35
2017, Vol. 35

